Тема 9. Нормальный закон распределения
Нормальным называется распределение непрерывной случайной величины X функция плотности распределения которой имеет вид
,
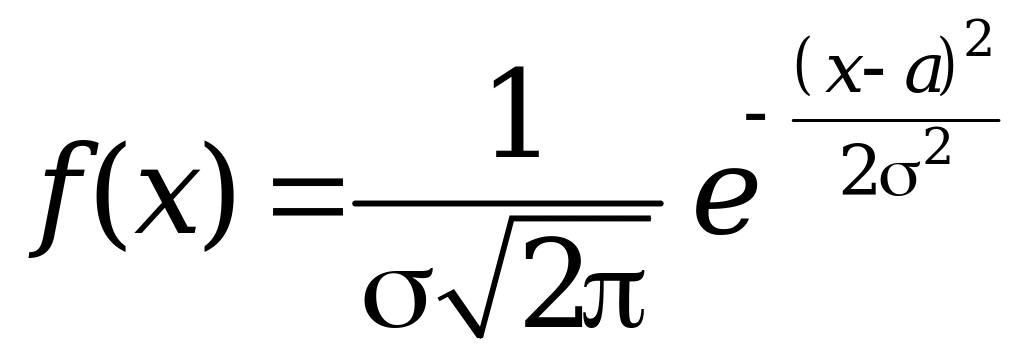где a – математическое ожидание, а – среднее квадратическое отклонение случайной величины X.
Вероятность
того, что случайная величина X
примет значение, принадлежащее
интервалу
,
определяется по формуле
.
где
– функция Лапласа, равная
.
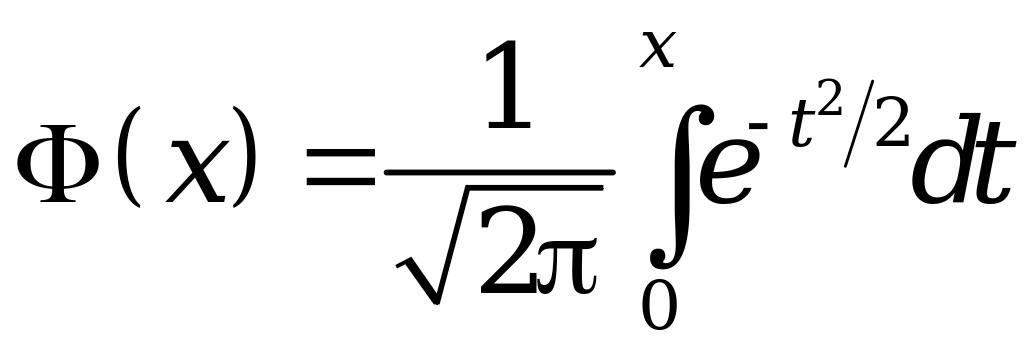Таблица значений функции Лапласа приводится в приложении 2.
Вероятность того, что нормально распределенная случайная величина X отклонится по модулю от своего математического ожидания а на величину, меньшую положительного числа определяется по формуле
.
В
частности,
.
Это свойство известно под названием
правила «трех сигм».
Свойства функции Лапласа
Свойство
1. Функция
Лапласа – нечетная
функция, т.е.
.
Свойство
2. Функция Лапласа – монотонная
возрастающая ограниченная функция
на всей области определения
.
Свойство 3. Верно следующее предельное равенство
причем,
при
можно считать, что
.
Вопросы для самопроверки
1. Запишите дифференциальную функцию для нормального закона распределения непрерывной случайной величины.
2. Какой вид имеет нормальная кривая? Поясните геометрический смысл параметров a и нормального распределения.
3. Как найти математическое ожидание и дисперсию нормально распределенной случайной величины?
4. Как определяется вероятность попадания нормально распределенной случайной величины в заданный интервал .
5. Как
определяется вероятность отклонения
нормально распределенной случайной
величины по модулю от своего математического
ожидания
.
6. Сформулируйте правило «трех сигм».
Задание 13. В задачах 13.1–13.30 станок-автомат на поточной линии разливает фруктовый сок в пакеты объемом а мл с точностью .
Считая
что случайные ошибки при разливе
подчинены нормальному закону, найти
вероятность того, что в наугад взятом
пакете окажется не более
и не менее мл
сока. Каков процент пакетов с ошибкой
разлива не более
мл? Каков гарантированный минимум
и возможный максимум объема сока в
пакете? Построить график функции
распределения
и проиллюстрировать полученное решение
графически.
№ |
a |
σ |
|
|
|
13.1. |
250 |
35 |
220 |
290 |
15 |
13.2. |
500 |
60 |
470 |
520 |
30 |
13.3. |
1000 |
65 |
980 |
1100 |
35 |
13.4. |
1500 |
90 |
1470 |
1550 |
45 |
13.5. |
250 |
15 |
240 |
275 |
10 |
13.6. |
500 |
70 |
480 |
550 |
35 |
13.7. |
1000 |
70 |
960 |
1050 |
40 |
13.8. |
1500 |
95 |
1430 |
1520 |
45 |
13.9. |
250 |
25 |
230 |
270 |
15 |
13.10. |
500 |
75 |
490 |
510 |
30 |
13.11. |
1000 |
90 |
990 |
1075 |
45 |
13.12. |
1500 |
75 |
1440 |
1580 |
35 |
13.13. |
250 |
20 |
210 |
290 |
10 |
13.14. |
500 |
65 |
475 |
570 |
30 |
13.15. |
1000 |
50 |
985 |
1080 |
20 |
13.16. |
1500 |
55 |
1455 |
1540 |
20 |
13.17. |
250 |
30 |
245 |
295 |
10 |
13.18. |
500 |
40 |
495 |
525 |
20 |
13.19. |
1000 |
60 |
975 |
1055 |
30 |
13.20. |
1500 |
65 |
1475 |
1565 |
35 |
13.21. |
250 |
35 |
225 |
265 |
15 |
13.22. |
500 |
50 |
465 |
530 |
20 |
13.23. |
1000 |
60 |
995 |
1035 |
25 |
13.24. |
1500 |
75 |
1490 |
1545 |
30 |
13.25. |
250 |
40 |
235 |
285 |
15 |
13.26. |
500 |
70 |
450 |
600 |
30 |
13.27. |
1000 |
95 |
950 |
1100 |
50 |
13.28. |
1500 |
75 |
1450 |
1600 |
55 |
13.29. |
250 |
55 |
200 |
350 |
25 |
13.30. |
500 |
45 |
425 |
575 |
35 |