Глава 2. Электромагнитная индукция §2.1. Опыты Фарадея. Закон Фарадея и правило Ленца

Из опытов Эрстеда и Ампера следовало, что с помощью электрического тока можно сузить магнитное поле. Следуя идеям о неразрывной связи и взаимодействии сил природы, Фарадей в 1831 г. открыл новое физическое явление электромагнитной индукции, состоящее в возникновении электрического тока с помощью магнитного поля.

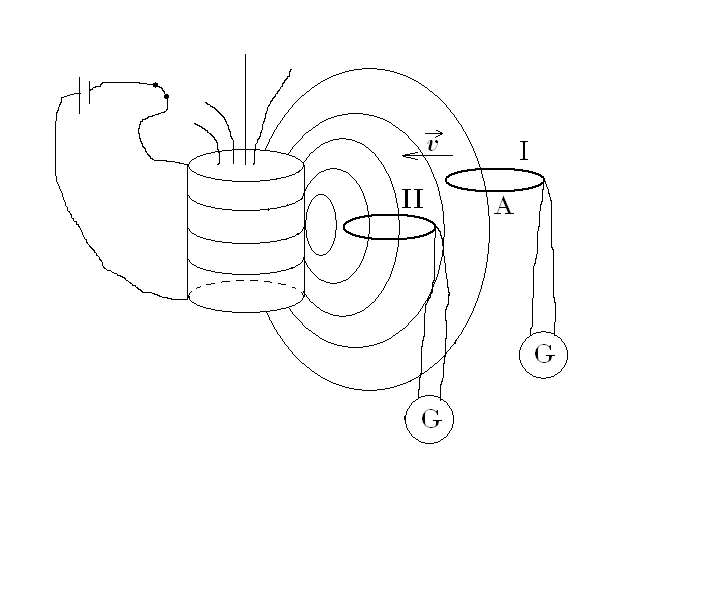
Все опыты Фарадея по электромагнитной индукции можно условно разделить на три группы: первая – источник магнитного поля покоится, контур движется (рис.23,а); вторая – источник магнитного поля движется, контур покоится; третья – два неподвижных контура, но в одном из них меняют силу тока (рис.23б). Из этих опытов следовало, что в контуре, соединённом с гальванометром, возникает индукционный ток I_i при всяком изменении магнитного потока, пронизывающего данный контур. По закону Ома электрический ток появляется в замкнутом контуре, если в этой цепи действует ЭДС:

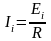, (2.1)

где 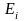- ЭДС электромагнитной индукции возникающая в данном контуре;

R – сопротивление контура. Из рисунка 24а видно, что при перемещении

а б

Рис.23.

контура из положения 1 в положение 2, число силовых линий пронизывающих контур растёт, т.е. возрастает магнитный поток. То же самое наблюдается в третьей группе опытов (рис.23б), при росте силы тока в контуре С (рис.23б).

Опыты также показали, что с увеличением скорости движения контура в магнитном поле или скорости движения магнита относительно контура и быстроты изменения силы тока в контуре С, возникает величина эдс индукции в контуре А (рис.23). Таким образом, Фарадей экспериментально установил, что эдс индукции по абсолютной величине равна скорости изменения магнитного потока, пронизывающего данный контур:

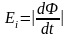, (2.2)

где Ф – магнитный поток пронизывающий контур площадью S:

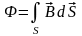. (2.3)

Если контур А перемещать из положения 2 в положение 1 (рис.23а), а в контуре С уменьшать силу тока (рис.23б), то направление индукционного тока сменится на противоположное.

Учитывая этот факт, закон Фарадея, выражаемый формулой (2.2), можно переписать, как

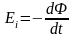. (2.4)

Направление индукционного тока определяется правилом Ленца: индукционный ток всегда направлен так, что своим магнитным полем препятствует тому изменению магнитного потока, который вызвал его. Правило Ленца является следствием закона сохранения энергии так, как в противном случае контур А (рис.24а) без видимой причины начал бы ускоряться и увеличивать свою кинетическую энергию.

§ 2.2. Физический смысл эдс индукции

По определению ЭДС индукции можно записать:

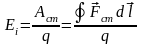. (2.5)

Выясним физическую природу сторонних сил эдс индукции, возникающих в опытах Фарадея.

Рассмотрим поступательное движение контура со скоростью в неоднородном стационарном магнитном поле. Пусть за время dt контур переместился параллельно самому себе из положения L₁ в положение L₂ на расстояние . В положение L₁ магнитный поток пронизывающий петлю был равен Ф_L1 . В положении L₂ поверхность стягивающая контур увеличилась на величину поверхности ободка S_об. Таким образом, магнитный поток в положении контура L₂ равен

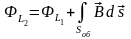, (2.6)

где

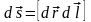. (2.7)

Согласно закону Фарадея (2.4), получим

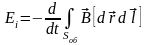. (2.8)

Полученный результат справедлив для контура любой формы и движущегося любым способом. Сравнивая уравнения (2.4),(2.5) и (2.8), можно записать

.

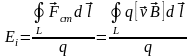Из этого выражения видно, что. в качестве сторонней силы эдс выступает сила Лоренца, которая действует на заряд q, движущийся вместе с контуром.

К такому же выводу можно прийти, рассмотрев следующий пример. Пусть в однородном стационарном магнитном поле находится контур с подвижной стороной длиной l .Эта сторона может свободно скользить по двум параллельным сторонам контура (рис.24).

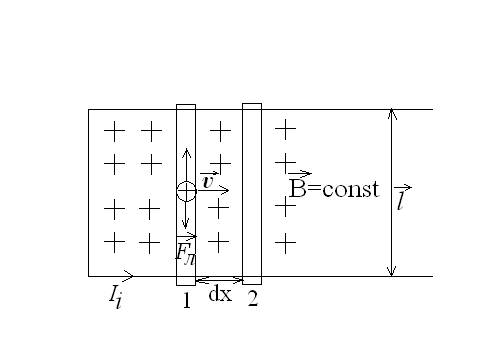
Рис.24.

При перемещении проводника длиной l со скоростью на dx из положения 1 в положение 2 в контуре возникает индукционный ток. Возникшая эдс индукции по определению равна

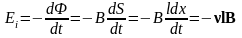(2.9)

С другой стороны, на заряд, движущийся вместе с проводником действует сила Лоренца. Эта сила смещает заряд вдоль проводника и совершает работу: 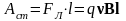. Тогда эдс индукции

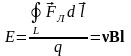(2.10)

В случае, когда контур покоится, а источник магнитного поля движется, используя принцип относительности, приходим к тому же самому результату: эдс индукции обусловлена возникновением силы Лоренца.

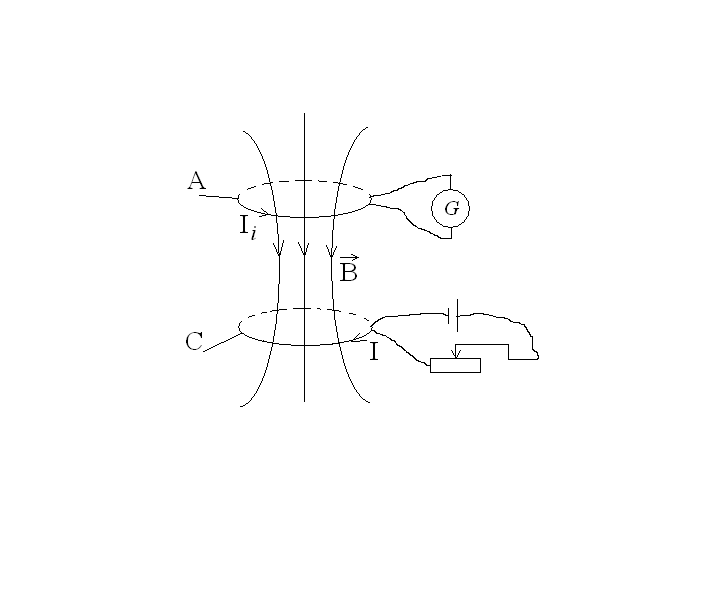
В третьей группе опытов Фарадея оба контура покоятся, но в контуре А возникает эдс индукции и индукционный ток (рис.23б):

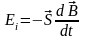(2.11)

На свободные электрические заряды в контуре может действовать сила Лоренца

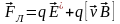
В данном случае магнитная составляющая равна нулю (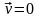 ). Остаётся предположить, что возникает электрическое поле , источником которого является меняющееся во времени магнитное поле:

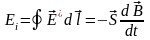. (2.12)

Из этого уравнения следует, что циркуляция вектора не равна нулю: 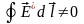и поле не является потенциальным, оно является вихревым.

Таким образом, Фарадей открыл новый вид электрического поля – вихревое электрическое поле, источником которого является меняющееся во времени магнитное поле. Проволочный контур А (рис.23б) играет всего лишь роль индикатора, в котором эдс индукции обусловлена возникновением вихревого электрического поля. Используя уравнение (2.3) перепишем уравнение (2.12):

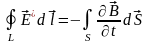(2.13)

Переход к частной производной в первой части связан с тем, что речь идёт об изменении вектора в определённой точке пространства. Перестановка порядка действий в первой части уравнения допустима, так как дифференцирование выполняется по времени, а интегрирование по поверхности S, стягиваемой контуром L.

На рис. 25 изображены силовые линии вихревого электрического поля в случаях возрастания (рис.25а) или убывания (рис.25б) магнитного поля со временем.

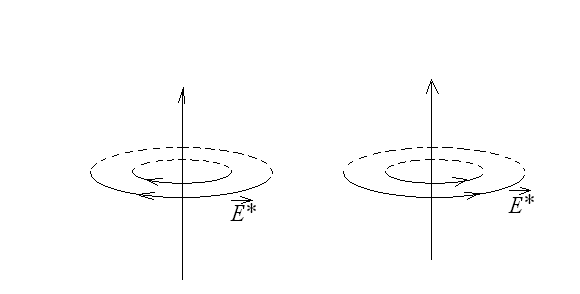
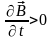
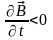
а б

Рис.25.

Из сказанного можно сделать вывод, что в общем случае эдс индукции возникла за счёт двух причин: вихревого электрического поля и силы Лоренца, т.е.

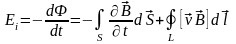. (2.14)