Вопросы и качественные задачи

1. Докажите, что для вычисления энергии сферического конденсатора можно пользоваться формулой

.

2. Плоский конденсатор заряжается от батареи, которая затем отключается. Между обкладками помещается пластина из диэлектрика. Как изменится заряд, разность потенциалов между обкладками, напряженность поля, емкость конденсатора и запасенная в нем энергия? Почему изменилась энергия? Рассмотреть те же вопросы в случае, если батарея не отключается.

3. Какую работу надо совершить, чтобы увеличить расстояние между обкладками плоского конденсатора вдвое (начальная разность потенциалов U, а емкость С)? Рассмотреть два случая: источник напряжения отсоединен и присоединен.

4. Когда конденсатор присоединили к батарее, он приобрел энергию 1 Дж. Какую работу совершила батарея? Какая энергия перешла в тепло?

Глава 5. Постоянный электрический ток § 5. 1. Электрический ток. Плотность и сила тока. Закон Ома. Закон Джоуля-Ленца

Заряженные частицы (электроны и ионы), входящие в состав вещества, совершают хаотическое тепловое движение. При этом в единицу времени через произвольно выбранную площадку в веществе в одном и другом направлении проходит одинаковое количество зарядов, т.е. суммарный заряд, проходящий через данную площадку равен нулю. Если по какой либо причине возникает упорядоченное или направленное движение заряженных частиц, то говорят о возникновении электрического тока.

Для возникновения и существования электрического тока в веществе необходимы два условия: наличие свободных заряженных частиц и наличие электрического поля (или разности потенциалов),которое действует на эти частицы с некоторой силой в определенном направлении.

О наличии тока можно судить последующим внешним эффектам: нагревание проводника, по которому идет ток; свечение газа, в котором создан ток, притяжение или отталкивание проводников с током; силовое взаимодействие между проводником с током и магнитной стрелкой.

Для количественного описания электрического тока во­дятся такие понятия как сила тока и вектор плотности тока j.

Силой тока называется скалярная величина, равная отношению электрического заряда dq, прошедшего через поперечное сечение проводника за промежуток времени dt, к данному промежутку времени:

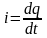. (5. 1)

Вектор плотности тока численно равен силе тока di через расположенную в данной точке перпендикулярную к направлению движения заряженных частиц площадку , отнесенной к величине этой площадки:

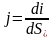. (5. 2)

За направление j принимается направление вектора скорости упорядоченного движения положительно заряженных частиц (положительных носителей тока).

Зная вектор плотности тока в каждой точке проводника, можно рассчитать силу тока через любую поверхность S:

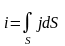, (5. 3)

где dS – вектор элемента площади.

Вектор плотности тока можно выразить через концентрацию носителей тока n и их скорость упорядоченного движения v. Выделим внутри проводника элементарный объем в виде цилиндра ( рис. 5. 1) таким образом, чтобы во всех его точках вектор j оставался неизменным. Тогда уравнение (5. 3) будет иметь вид

или ,

где - элементарный заряд, прошедший за время dt через сечение S; е- заряд носителей тока. Учитывая, что вектора v и j сонаправлены, окончательно получим:

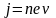(5. 4)

Если в веществе возможно движение носителей тока разного знака, то полная плотность тока определяется векторной суммой плотностей тока зарядов каждого знака.

Электрический ток, плотность и сила которого не меняются со временем, называется постоянным.

Обозначим силу постоянного тока I и выражение (5. 1) можно заменить как

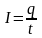, 5)

где q- заряд переносимый через рассматриваемую поверхность за время t.

В электротехнике большое значение имеет понятие о линейном проводнике. Линейный проводник – это длинный и очень тонкий провод (сечение проводника мало по сравнению с его длиной).

Допустим, что по линейному проводнику (рис. 5. 2) протекает постоянный электрический ток, который обусловлен напряжением , приложенным к концам проводника. Опыты показывают, что в этом случае сила тока пропорциональна напряжению на проводнике:

, (5. 6)

где величина R называется электрическим сопротивлением проводника. Величина сопротивления при данной температу­ре зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного линейного проводника с постоянной площадью сечения (S=const)

, (5. 7)

где l - длина проводника, S – площадь его поперечного сечения, - удельное электрическое сопротивление проводника.

Для большинства металлов растет с повышением температуры по линейному закону:

, (5. 8)

где -удельное сопротивление при проводника при 00 С

t0-температура по шкале Цельсия, - температурный коэффициент сопротивления, численно равный примерно 1/2730С.

Формула (5. 6) выражает закон Ома для участка цепи.

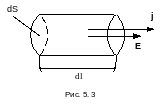
Закон Ома можно записать в дифференциальной форме. Выделим в окрестности некоторой точки внутри проводника элементарный цилиндрический объем (рис. 5. 3) с образующими, параллельными вектору плотности тока j в данной точке. Через поперечное сечение цилиндра течет ток силой 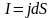. Напряжение, приложенное к цилиндру равно 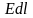, где E – напряженность электрического поля в данном объеме. Сопротивление цилиндра, согласно формуле (5. 7)

равно . Подставив эти значения в формулу (5. 6), получим

.

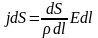Учитывая, что в изотропных средах вектора j и Е направлены одинаково, перепишем предыдущее уравнение так

, (5. 9)

где - величина, называемая удельной проводимостью вещества проводника.

Уравнение (5. 9) представляет закон Ома в дифференциальной форме, применимой в каждой точке проводника.

При прохождении по проводнику тока (рис. 5. 2) проводник нагревается. Экспериментально было установлено, что количество теплоты Q, которое выделяется в проводнике, пропорционально его сопротивлению, квадрату силы тока и времени протекания тока:

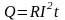. (5. 10)

Если сила тока изменяется со временем, то

. (5. 11)

Эти уравнения выражают закон Джоуля – Ленца. Покажем, что нагревание проводника происходит за счет работы электрического поля. За время dt через каждое сечение проводника проходит заряд При этом электрическое поле совершает работу 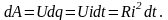Интегрируя данное уравнение, получим выражение, совпадающее с соотношением (5. 11).

Таким образом, работа сил электрического поля в неподвижном проводнике, по которому идет ток, расходуется на изменение его внутренней энергии, выражающееся в выделении тепла данным проводником.

Закон Джоуля – Ленца можно выразить в дифференциальной форме. Выделим в проводнике таким же образом, как это было сделано выше при выводе формулы (5. 9), элементарный объем ( dV=dldS) в виде цилиндра. Согласно (5.11), в этом объеме за время dt выделится количество теплоты

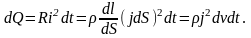(5.12)

Количество теплоты dQ, отнесенное к единице времени и единице объема, называют удельным количеством теплоты или удельной мощностью тока w. Из уравнения (5. 12) получим

, 5.13)

или, с учетом (5. 9)

. 14)

Две последних формулы выражают закон Джоуля-Ленца в дифференциальной форме.