
3830
.pdfМинистерство образования и науки Российской Федерации Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«Хабаровская государственная академия экономики и права»
Кафедра математики и математических методов в экономике
ВЫСШАЯ МАТЕМАТИКА
Программа, методические указания, варианты контрольной работы № 1 для студентов 1-го курса
заочного отделения всех специальностей
Хабаровск 2007
2
ББК В 11
Х12
Математика : программа, методические указания, варианты контрольной работы №1 для студентов 1-го курса заочного отделения всех специальностей / сост. В. А. Вербицкий, Е. Н. Кравченко. – Хабаровск : РИЦ ХГАЭП, 2007. – 20 с.
Рецензент В. М. Манаков, канд. физ.-мат. наук, доцент кафедры высшей математики ТГТУ
Утверждено издательско-библиотечным советом в качестве методических указаний
Виктор Александрович Вербицкий Елена Николаевна Кравченко
ВЫСШАЯ МАТЕМАТИКА
Программа, методические указания, варианты контрольной работы № 1 для студентов 1-го курса
заочного отделения всех специальностей
Редактор Г.С. Одинцова
Подписано к печати |
Формат 60×84/16. |
Бумага писчая. |
|
Печать офсетная. |
Ус.печ.л. 1,2. |
Уч.-изд.л. 0,8. |
Тираж 300 экз. |
Заказ № |
|
|
|
680042, Хабаровск, ул. Тихоокеанская, 134, ХГАЭП, РИЦ
© Хабаровская государственная академия экономики и права, 2007
3
Предисловие
Цель преподавания математических дисциплин в экономическом вузе – ознакомить студентов с основами математического аппарата, необходимого для решения теоретических и практических задач экономики; привить студентам умение самостоятельно изучать литературу по математике и её приложениям в экономике; развить логическое мышление и повысить общий уровень математической культуры; выработать навыки математического исследования прикладных вопросов и умение перевести экономическую задачу на математический язык.
Студенты первого курса всех специальностей изучают высшую математику, выполняют по этой дисциплине две контрольные работы, сдают экзамен и зачёт.
4
КОНТРОЛЬНЫЕ ЗАДАНИЯ, ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ
Вариант для контрольного задания студент выбирает в соответствии с двумя последними цифрами своего шифра по следующему правилу: вторая цифра номера варианта должна совпадать с последней цифрой шифра. Далее, если предпоследняя цифра шифра чётная, то первая цифра номера варианта должна быть равна 0 или 2; если же предпоследняя цифра нечётная, то первая цифра номера варианта должна быть 1. Например, при учебном номере (шифре) 955027 студент решает 07 вариант, при шифре 953054 – вариант 14 и т.д.
Номера |
|
Номера задач |
для контрольного |
задания |
||
вариантов |
|
|
|
|
|
|
|
|
|
|
|
|
|
01 |
1 |
|
21 |
|
41 |
61 |
02 |
2 |
|
22 |
|
42 |
62 |
03 |
3 |
|
23 |
|
43 |
63 |
04 |
4 |
|
24 |
|
44 |
64 |
05 |
5 |
|
25 |
|
45 |
65 |
06 |
6 |
|
26 |
|
46 |
66 |
07 |
7 |
|
27 |
|
47 |
67 |
08 |
8 |
|
28 |
|
48 |
68 |
09 |
9 |
|
29 |
|
49 |
69 |
10 |
10 |
|
30 |
|
50 |
70 |
11 |
11 |
|
31 |
|
51 |
71 |
12 |
12 |
|
32 |
|
52 |
72 |
13 |
13 |
|
33 |
|
53 |
73 |
14 |
14 |
|
34 |
|
54 |
74 |
15 |
15 |
|
35 |
|
55 |
75 |
16 |
16 |
|
36 |
|
56 |
76 |
17 |
17 |
|
37 |
|
57 |
77 |
18 |
18 |
|
38 |
|
58 |
78 |
19 |
19 |
|
39 |
|
59 |
79 |
20 |
20 |
|
40 |
|
60 |
80 |
При выполнении контрольной работы надо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студентам для переработки.
1.Контрольные работы выполнять в тетради пастой или чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.
2.На обложке тетради должны быть ясно написаны фамилия студента, его инициалы, шифр, название дисциплины и номер контрольной работы; здесь же следует указать дату отсылки работы в институт и почтовый адрес студента.
3.В работу должны быть включены все задачи, указанные в задании, строго по своему варианту. Контрольные работы, содержащие не все задания, а также
5
содержащие задачи не своего варианта, не зачитываются.
4.Решение задач надо располагать в порядке, указанном в заданиях, сохраняя номера задач.
5.Перед решением каждой задачи надо выписать полностью её условие. Если несколько задач имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными из соответствующего номера.
6.После получения прорецензированной работы (как зачтённой, так и незачтённой) студент должен исправить в ней все отмеченные рецензентом ошибки и недочёты. В связи с этим следует оставлять в конце тетради чистые листы для работы над ошибками. Вносить исправления в сам текст работы после её рецензирования запрещается.
7.Выполнив работу над ошибками, необходимо выслать работу в наиболее короткий срок.
8.В конце работы следует указать литературу, которую изучал студент, выполняя данную работу.
9.Студент должен подписать работу и поставить дату.
10.Зачтённые контрольные работы вместе с рецензиями обязательно предъявляются на зачёте и экзамене.
11.Перед сдачей зачёта и экзамена студент обязан защитить контрольную работу
|
БИБЛИОГРАФИЧЕСКИЙ СПИСОК |
1. |
Вербицкий В. А. и др. Математика в экономике : учеб. пособие. – |
Хабаровск : РИЦ ХГАЭП, 1999. |
|
2. |
Высшая математика для экономистов : учеб. пособие / под |
ред. Н. Ш. Кремера. – М. : ЮНИТИ, 2003.
3.Карасев А. И., Аксютина З. М., Савельева Т. К. Курс высшей математики для экономических вузов. Ч. 1. – М. : Высшая школа, 1982.
4.Красс М. С. Чупрынов Б. П. Основы математики и её проложение в экономическом образовании. – М. : Дело, 2001.
5.Лихолетов И. И. Высшая математика, теория вероятностей и математическая статистика. – Минск : Вышейшая школа, 1976.
6.Лихолетов И. И., Мацкевич И. П. Руководство к решению задач по высшей математике, теории вероятностей и математической статистике. – Минск : Вышейшая школа, 1976.
7.Лунгу К. Н. и др. Сборник задач по высшей математике. Ч. 1,2. – М. :
Айрис, 2004.
8.Минорский В. П. Сборник задач по высшей математике. – М. : Наука, 1977.
9.Тиунчик М. Ф. Элементы линейной алгебры и аналитической геометрии. Ч.1. – Хабаровск : РИЦ ХГАЭП, 1996.
10.Тиунчик М. Ф. Элементы линейной алгебры и аналитической геометрии. Ч.2. – Хабаровск : РИЦ ХГАЭП, 1997.
6
ПРОГРАММА ДИСЦИПЛИНЫ
1. Понятие об уравнении линии. Уравнение прямой с угловым коэффициентом. Общее уравнение прямой. Угол между двумя прямыми; условия параллельности и перпендикулярности прямых. Уравнение прямой через две точки. Пересечение двух прямых. Канонические уравнения кривых второго порядка: окружности, эллипса, гиперболы, параболы.
2. Матрица, виды матриц, операции над матрицами. Определитель матрицы. Определители 2-го и 3-го порядка. Миноры. Алгебраические дополнения. Разложение определителя по элементам строки. Обратная матрица. Система линейных алгебраических уравнений. Матричный метод решения систем линейных уравнений. Метод Крамера. Система с базисом. Метод Жордано–Гаусса. Векторы. Сложение и вычитание векторов. Умножение вектора на число. Длина вектора. Расстояние между двумя точками. Координаты вектора. Скалярное произведение векторов. Система координат на плоскости. Основные задачи на метод координат (расстояние между двумя точками, деление отрезка в данном отношении).
3.Функция одной переменной. Область определения функции. Способы задания. Основные элементарные функции, их графики. Монотонность функции, ограниченность функции. Обратные и сложные функции.
4.Числовая последовательность. Предел числовой последовательности.
Теоремы о единственности предела числовой последовательности, об ограниченности последовательности, имеющей предел. Бесконечно малые величины. Теоремы о бесконечно малых. Бесконечно большие величины. Связь между бесконечно малыми и бесконечно большими величинами. Теорема о связи переменной, её предела и бесконечно малой. Предел суммы, произведения, частного. Предельный переход в неравенствах. Признак существования предела монотонной последовательности. Предел функции. Теорема о пределе функции. Раскрытие неопределённостей. Первый замечательный предел. Второй замечательный предел. Сравнение бесконечно малых. Эквивалентные бесконечно малые и их применение для вычисления пределов.
5.Производная y=f(x). Геометрический смысл производной. Уравнение касательной. Теорема о непрерывности функции, имеющей производную. Производная суммы, произведения, дроби. Производные тригонометрической функции, показательной функции, степенной функции, обратных тригонометрических функций. Производные обратной и сложной функции. Производные высших порядков. Дифференциал. Геометрический смысл дифференциала.
6.Теорема Ферма. Теоремы Ролля, Лагранжа, их геометрический смысл. Правило Лопиталя. Признак возрастания (убывания) функции на
интервале. |
Экстремум функции |
у = |
f(x). |
Необходимое условие |
|
экстремума. |
Второе достаточное |
условие |
экстремума. |
Наименьшее и |
|
наибольшее значение у=f(x) на [а,b]. Выпуклость, вогнутость, точки перегиба. Асимптоты кривых. Вертикальные и наклонные асимптоты.
7
7. Функции нескольких переменных. Область определения. Способы задания. Понятие предела для функции двух переменных. Непрерывность функции Z=f(х,у). Частные приращения, частные производные. Полное приращение, полный дифференциал Z=f(х,у). Экстремум функции двух
переменных. Метод наименьших квадратов.
8.Первообразная функции. Теорема о первообразных. Определение неопределённого интеграла. Свойства неопределённого интеграла. Замена переменной в неопределённом интеграле. Интегрирование по частям. Интегрирование рациональных дробей, тригонометрических выражений, иррациональных функций. Задача о площади криволинейной трапеции. Интегральная сумма. Определённый интеграл. Свойства определённого интеграла. Определённый интеграл с переменным верхним пределом. Формула Ньютона – Лейбница. Замена переменной в определённом интеграле. Площадь плоской фигуры. Несобственные интегралы.
9.Числовой ряд. Сходимость числового ряда. Свойства рядов. Геометрический ряд. Гармонический ряд. Необходимый признак. Признак сравнения. Признак Даламбера. Интегральный признак. Знакочередующийся
ряд. Признак Лейбница. Степенной ряд. Радиус сходимости. Ряд Маклорена. Условия разложимости в ряд. Ряды Маклорена для y=sinх, y=cosх, у=ех, у=(1+х)m. Приближенные вычисления с помощью рядов.
В настоящих методических указаниях ссылка на пособие из библиографического списка обозначается его порядковым номером, заключенным в квадратные скобки. Например, запись 5 гл.3, 8 № 66, 68. Это означает следующее: изучите материал, изложенный в главе 3 учебника Лихолетова И.И. “Высшая математика ” и решите задачи № 66, 68 из учебника Минорского В.П.
Указания к выполнению контрольной работы №1
Тема 1. Аналитическая геометрия
1 гл. 4.
3 гл. 3, 4.
5 гл. 3, 4.
8 гл.1 № 62, 63, 87, 95, 165, 187, 213.
Примеры решения задач
Задача 1. Даны вершины треугольника ABC (рис. 1): А(-4,8), В(5,-4), С(10, 6).
Найти:
1)длину стороны АВ;
2)уравнение высоты СД и её длину;
3)уравнение медианы, проведённой из вершины А;
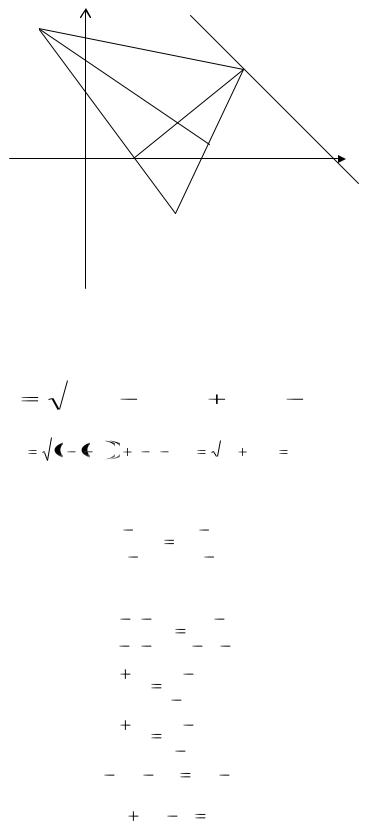
8
4) записать уравнение прямой, проходящей через точку С параллельно стороне АВ.
Решение
А Y
C
Р
D |
X |
B
Рис.1
1. Расстояние d между точками М1(x1у1) и М2(х2у2) определяется по формуле
|
d |
|
|
( x |
2 |
x )2 |
( y |
2 |
y )2 |
. (1) |
|||
|
|
|
|
|
1 |
|
|
1 |
|
||||
Подставим в формулу (1) |
координаты точек А и В, получим |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
2 |
( 4 8)2 |
|
|
|
|
15 . |
|
|
АВ |
5 4 |
|
81 144 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Уравнение прямой, проходящей через точки М1(x1у1) и М2(х2у2), имеет вид
х |
х1 |
|
у |
у1 |
. |
(2) |
|
|
|
|
|
||
х2 |
х1 |
|
у2 |
у1 |
|
|
Подставив в формулу (2) координаты точек А и В, получим уравнение прямой АВ:
х |
( |
4) |
|
|
у |
|
8 |
; |
||
5 |
( |
4) |
|
|
4 |
8 |
||||
|
|
|
||||||||
х |
4 |
|
|
у |
8 |
|
; |
|
|
|
9 |
|
|
|
|
12 |
|
|
|
||
|
|
|
|
|
|
|
|
|||
х |
4 |
|
|
у |
8 |
|
; |
|
|
|
3 |
|
|
|
|
4 |
|
|
|
||
|
|
|
|
|
|
|
|
|||
4x |
16 |
|
3y |
24; |
||||||
4x |
3y |
8 |
|
|
0 |
( AB). |
||||

9
Для нахождения углового коэффициента kАВ |
прямой АВ разрешим полученное |
|||||||||||||||
уравнение относительно у: |
у |
|
4 |
х |
8 |
. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|||
Отсюда kAB |
|
4 |
. Т.к. высота |
СD |
|
перпендикулярна АВ, |
то угловой |
|||||||||
|
3 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
коэффициент k |
|
будет равен k |
|
|
1 |
, |
|
k |
1/( 4 / 3) |
3 |
. |
|
||||
|
CD |
|
|
|
CD |
|
|
kАВ |
|
CD |
|
4 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Искомая высота проходит |
через |
точку |
|
С(10,6). Воспользуемся |
уравнением |
|||||||||||
прямой, проходящей через данную точку, с заданным угловым коэффициентом:
|
|
|
(y–yо) = k(x–xo); |
|
|
|
|
(3) |
|||||
y – 6= |
3 |
(x–10); 3x–4y–6 = 0 |
(СD). |
|
|||||||||
4 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для нахождения длины СD определим координаты точки D, решив систему |
|||||||||||||
|
|
4х 3у 8 |
0 |
|
|
|
|
|
|
||||
уравнений (АВ) и (СD): 3х |
|
|
4у |
6 |
0 , откуда х = 2, у = 0, т.е. D(2,0). |
||||||||
Подставив в формулу (1) координаты точек С и Д, находим |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2)2 |
|
0)2 |
|
|
|
|
|
|
CD |
|
(10 |
(6 |
64 |
36 |
|
10. |
|||||
3. Обозначим основание искомой медианы через М. По определению медианы М делит сторону ВС пополам. Координаты точки М найдём по формуле
|
|
|
|
|
|
|
|
( |
х1 |
|
х2 |
; |
|
y1 |
|
y2 |
); |
|
|
|
|
|
|
|
|
|
(4) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
М ( |
5 |
|
10 |
; |
|
4 |
|
6 |
) |
( |
15 |
|
;1). |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||
Чтобы |
записать |
уравнение |
|
медианы |
AM, |
воспользуемся |
формулой (2). |
||||||||||||||||||||||||||||||
|
x ( |
4) |
|
y |
8 |
, |
|
x 4 |
|
|
y |
8 |
, |
|
2(x |
4) |
|
|
|
|
y |
8 |
; 14x |
23y 128 0 (АМ). |
|||||||||||||
15/ 2 |
( 4) |
1 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
23/ 2 |
|
|
|
7 |
|
|
|
|
|
|
23 |
|
|
|
|
|
|
7 |
|
|
|
|
|
||||||||||||
4. Обозначим искомую прямую СР. Угловой коэффициент kAB |
|
4 |
, т.к. АВ и |
||||||||||||||||||||||||||||||||||
3 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
СР параллельны, то kAB |
kCP |
искомая прямая проходит через |
точку С (10,6). |
||||||||||||||||||||||||||||||||||
Воспользуемся уравнением (3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
у |
6 |
|
4 |
(х |
10) ; 3y 18 |
4x |
40; 4x |
|
|
3y |
58 |
0 (СP). |
|
|
|
|||||||||||||||||||||
|
3 |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Задача 2. Уравнение кривой привести к каноническому виду и построить
линию.
1) х2 + 4у2 – 4х + 16у – 16 = 0.
Решение: выделим полные квадраты при х и у:
(х2 – 4х+4) – 4+4(у2+4у+4)–16–16 = 0; (х–2)2+4(у+2)2–36 = 0 (х–2)2+4(у+2)2–36;
10
|
(х 2)2 |
|
|
( у |
2)2 |
1. |
|
|
|||
|
36 |
9 |
|
|
|
||||||
|
|
|
|
|
|
||||||
Получили уравнение вида |
|
(х |
)2 ( у |
|
)2 |
1 – |
(5) |
каноническое |
|||
|
а2 |
|
|
|
|
b2 |
|
||||
|
|
|
|
|
|
|
|
|
|
||
уравнение эллипса. |
|
|
|
|
|
|
|
|
|
|
|
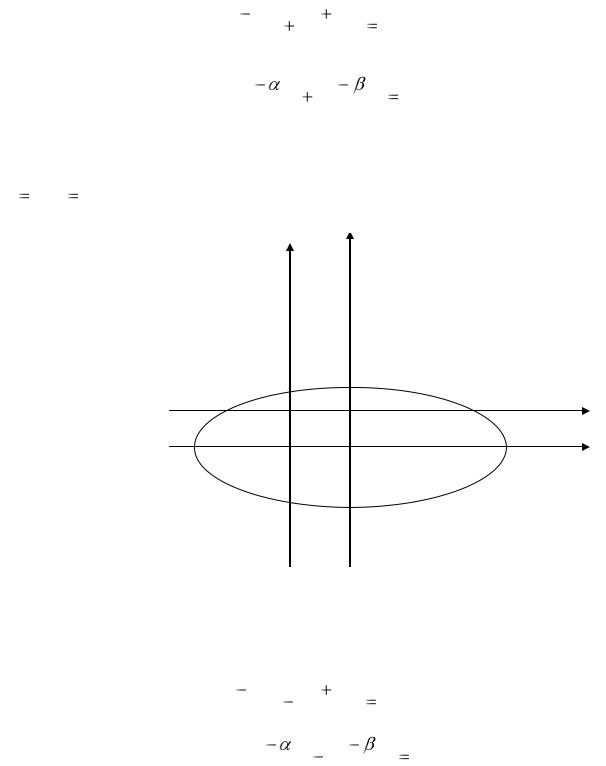
Центр эллипса лежит в точке O/(α,β), оси параллельны осям координат |
|||||||||||
(рис. 2). O/(2, –2) – центр данного эллипса. |
Отложим от |
точки O/ отрезки |
|||||||||
a 6 b 3 в направлениях, параллельных ОХ и OY, CС/ = 2 a =12; ВВ/ = 2 b = 6; 2) 9x2 – 4y2 – 54x – 8y + 41 = 0.
У У/
|
|
В/ |
|
3 |
|
|
|
|
|
|
|
||
-6 |
|
О |
|
|
6 |
Х |
|
|
|
|
|||
|
|
|
|
|
С/ |
Х\ |
С |
|
|
О/ |
|||
|
|
|
|
|
|
|
|
|
В |
-3 |
|
|
|
Выделим полные квадраты при х и у.
9(х2 – 6х + 9) – 81– 4((у2 + 2у + 1) + 4 + 41 = 0;
9(х – 3)2 – 4(у+1)2–36 = 0; 9(х–3)24(у+1)2 = 36;
|
|
(х 3)2 |
|
( у |
1) |
2 |
|
1. |
|
|
|||||
|
|
|
4 |
|
|
|
|
9 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Получили |
уравнение вида: |
|
(х |
)2 |
|
|
( у |
|
|
)2 |
1– |
(6) каноническое |
|||
|
а2 |
|
|
|
|
|
b2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
уравнение |
гиперболы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Центр гиперболы лежит в точке А(α,β), оси параллельны осям координат. Центр
данной гиперболы лежит в точке А(3, –1), |
a = 2, |
b = 3. Построим основной |
прямоугольник гиперболы, откладывая от |
точки |
А отрезки a =2, b =3 в |
направлениях, параллельных основным осям координат. BB/=2 a =4, СС/=2 b =6. Диагонали прямоугольника будут являться асимптотами. Вершины гиперболы – точки B и B/ (рис. 3).
