5493

ББК У 9 (2) 26 Х 12

Финансовая математика : метод. указания и варианты контрольных заданий для бакалаврантов направления 38.03.02 «Экономика» / В. Н. Руденко. – Хабаровск : РИЦ ХГАЭП, 2015. – 24 с.

Написана на основе компетентного подхода в соответствии с программой курса «Финансовая математика» для бакалаврантов. Предназначена как для практических занятий, так и для самостоятельного изучения изучаемого курса. Содержит достаточное количество теоретического материала и практических заданий для прочного и творческого усвоения студентами основ финансовой математики.

Рецензент:

С. Н. Осипов, доктор экономический наук, профессор кафедры финансов ДВИ-филиал РАНХиГС

Утверждено издательско-библиотечным советом академии в качестве методических указаний для студентов

Руденко В. Н., 2015 Хабаровская государственная академия экономики и права, 2015

2

Введение

В последнее время в России началось возрождение, изучение и активное развитие финансовой математики на различных уровнях. Даже обычному гражданину, а тем более специалисту в области финансов, приходится принимать решения при осуществлении платежей, вложений, займов и иных финансовых операций. Поэтому знание и понимание основ финансовой математики становится неотъемлемым атрибутом всей нашей жизни.

Внастоящих методических указаниях рассмотрены основы классической финансовой математики, изложен традиционный материал без громоздких выводов и формул, но с достаточно наглядными практическими примерами, характеризующими основные схемы финансовых операций.

При изложении материала предполагалось, что студенты знакомы с основными понятиями экономической теории, математики, теории финансов.

После изложения материала даны задачи для контрольных, лабораторных и иных работ.

Рекомендуемая литература позволит студентам основательно изучить дисциплину.

Изучение основ финансовой математики базируется на процессах наращения

идисконтирования, поэтому им и моделям, их описывающих, уделено основное внимание автора.

Врезультате изучения дисциплины «Финансовая математика» студент должен

знать:

– связь реальной и номинальной процентных ставок;

– основные кредитные схемы и виды кредитных операций;

уметь:

– вычислить наращенную сумму в случае простых и сложных процентов;

– сравнивать наращение по простой и сложной ставкам процентов;

– производить дисконтирование по простой и сложной ставке;

– учитывать влияние негативных факторов на ставку процента;

– рассчитывать эффективную процентную ставку для различных схем наращения;

– рассчитывать его приведённую и наращенную величины по схемам постнумерандо и пренумерандо;

– рассчитывать доходность за несколько периодов;

3

–рассчитывать основные параметры ипотечных кредитов и аннуитетов;

–производить сравнение различных схем погашения долга;

владеть:

–понятием эффективной процентной ставки;

–понятием финансового потока;

–понятиями дохода и доходности финансовой операции;

–понятием конверсии, коинтеграции (замены, объединения) платежей.

1. Основные понятия и обозначения

Одна из базовых концепций экономики (финансов, менеджмента, анализа и оценки бизнеса, теории принятия решений) – концепция стоимости активов состоит в том, что стоимость актива (инструмента, капитала), а в конечном счёте определённой суммы денег – это функция от времени возникновения денежных доходов и расходов.

В основе финансовой математики лежит понятие временной стоимости денег. Денежная единица, полученная сегодня, стоит дороже такой же денежной единицы, которая будет получена в течение какого-либо периода в будущем (т.е. время обесценивает деньги). Единственное условие жизнеспособности этой концепции – положительный уровень процента, под который можно инвестировать фонды (активы, капитал), иначе время неумолимо обесценивает настоящие (сегодняшние) стоимости. Известный афоризм «время – деньги» как нельзя лучше выражает сущность современного количественного финансового анализа. Знание того, как правильно рассчитывать стоимость денег во времени и воплощать в конкретные решения, чрезвычайно важно для экономической практики, а в теории – для понимания финансов вообще.

Расчёт и анализ любой финансовой операции начинается в первую очередь с приведения всех денежных потоков, появляющихся в различные моменты времени, к одному моменту (неважно – в настоящем или в будущем), только после этого денежные суммы можно сравнивать между собой, складывать и вычитать.

Основные обозначения (символы) и их перевод взяты такими, какие используются в мировой финансовой литературе:

CF – денежный поток, поток платежей (cash flow), ассоциированный финансовой операцией в условных денежных единицах (у.д.е.);

4

CFt – денежный поток (поток платежей) в периоде t, представляющий собой

n – число периодов экономической жизни финансовой операции;

PV (present value) – настоящая (приведённая, текущая, сегодняшняя, современная) стоимость денежных потоков;

FVn (future value) – будущая стоимость денежных потоков в конце периода n. i % − процентная ставка (годовая) наращения (APR);

r = 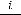− коэффициент наращения (процент, доходность, норма прибыли,

ставка процента) (interеst rate);

m – число наращений в году по схеме сложных процентов (компаундинга).

2. Наращение

Под наращением (генерацией, накоплением) понимается процесс увеличения первоначального объёма капитала (величины, стоимости актива) в результате начисления процентов.

Процесс наращения (генерации) капитала можно изобразить в принятых обозначениях схематично так:

PV .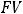

Экономический смысл процесса наращения состоит в определении величины, которая будет (или может быть) получена из некоторой первоначальной (текущей) суммы в результате проведения финансовой операции во времени.

Описание изменения денежных сумм во времени производится путём вычисления дохода от инвестирования средств, т.е. путём начисления процентов на первоначальную сумму. Теория процентных ставок является основой для количественного описания изменения величины (стоимости) денежных сумм (капитала) во времени (временной стоимости денег).

Существуют две основные модели (схемы) процесса наращения:

1. Модель простых процентов, когда базой для наращения служит первоначальная сумма PV во всех периодах: FVn = PV(1 + 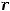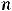) (2.1), где r – годовой коэффициент наращения является неизменным, а n – число лет операции.

5

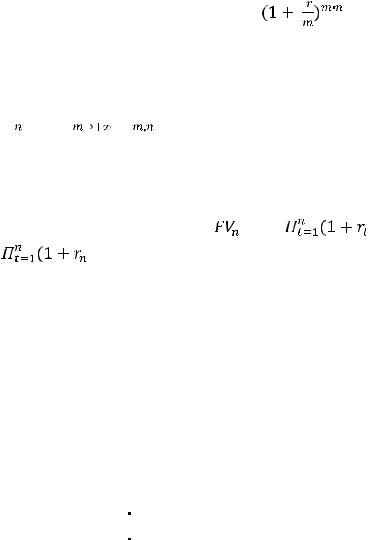
Эта модель применяется, как правило, для краткосрочных финансовых операций (со сроком до года). Если период считается в днях, то r делят на фактическое число дней в году (365 или 366) т.е. получают ежедневную ставку и умножают на число полных дней операции. Аналогично можно поступить, если счёт вести полугодиями, кварталами, месяцами.

2. Модель (схема) сложных процентов применяется (как правило) в долгосрочных финансовых операциях (со сроком более года), в ней – база наращения переменная (увеличивается в каждом периоде в результате реинвестирования генерированных в предыдущих периодах сумм): FVn = PV(1 + + r)n (2.2).

Очевидно, что первая модель в период до года даёт большой рост, чем вторая. А после года наоборот.

Если m – число начислений процентов в году по второй модели, то формула (2.2)

Процесс капитализации в этом случае ускоряется.

При m →∞ (непрерывная капитализация) из формулы (2.3), применив второй замечательный предел (см. общий курс математики), получаем:

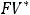
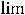
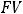
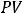
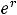
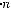
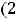
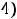, где е = 2,718 28… − основание натурального логарифма.

Если ставки наращения по годам меняются то формула (2.2)

1+rt, a rt – ставка в периоде t. Итак, процесс наращивания во времени приводит настоящие стоимости к будущим с нормой доходности r. Это прямая задача.

Проиллюстрируем вышесказанное примерами. Пример 2.1. Вложена сумма на 4 года.

1.PV = 1 000 у.д.е. n = 4 года i = 15% годовых постоянно. Вычислить суммы

вконце каждого года по схеме простых и сложных процентов.

Решение Схема простых процентов (применяется формула (2.1)).

FV1=1 000(1+0,15)=1 150 (у.д.е.).

FV2=1 000(1+0,15 2)=1 300 (у.д.е.).

FV3=1 000(1+0,15 3)=1 450 (у.д.е.).

6

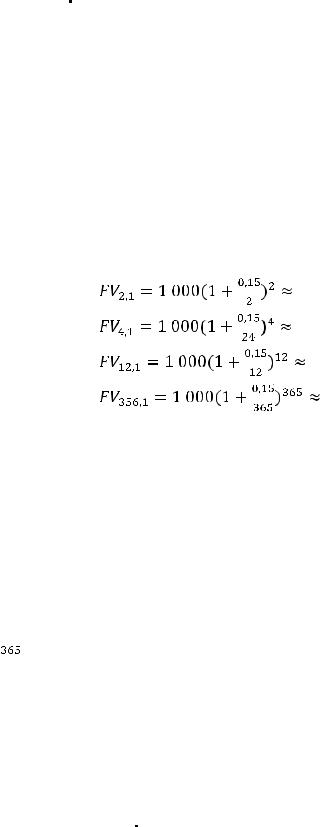
FV4 =1 000(1+0,15 4)=1 600 (у.д.е.).

Схема сложных процентов (применяется формула (2.2)).

FV1=1 000(1+0,15)1= 1 150 (у.д.е.).

FV2=1 000(1+0,15)2= 1 322,5 (у.д.е.).

FV3=1 000(1+0,15)3= 1 520,8 (у.д.е.).

FV4 =1 000(1+0,15)4= 1 749,01 (у.д.е.).

Очевидно, что модель сложных процентов обеспечивает больший рост при t >1.

Пример 2.2. По условиям примера 2.1 рассмотреть начисление процентов в течение первого года по схеме сложных процентов а) по полугодиям; б) поквартально; в) помесячно; г) по дням.

Решение. Применяется формула (2.3)

Очевидно, что чем больше m (т.е. чем чаще начисляются проценты при прочих равных условиях), тех будущая стоимость будет больше.

Пример 2.3. Клиент вносит в банк сумму PV = 40 000 рублей на срок 3 года и 219 дней под 12 % годовых. Какая сумма денег будет у этого клиента к концу этого срока?

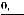
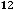
Решение. Поскольку срок смешанный и дробный, то общепринято общее число лет оценивать по модели сложных процентов, а оставшееся число дней по модели простых процентов, т.е. будущая сумма за этот период PV = 40 000(1 + + 0,12)3(1 + 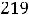) = 60 243,3 (рубля).

Пример 2.4. Некто планирует занять (взять) в одном банке 5 000 000 рублей на 10 лет под 14% годовых с оплатой в конце этого срока и вложить эту сумму сразу же в другой банк под 12 % на этот же срок. Оценить итог этой операции.

Решение. Так как заём производится по модели простых процентов, а вложение – по модели сложных процентов, то применяем формулы (2.1) и (2.2) и получаем итог этой операции

FV1,0 = −5 000 000(1 + 0,14 10) + 5 000 000(1 + 0,12)10 = −12 000 000 + 15 529 241= 3 529 241 (рублей) > 0 операция рентабельна.

Пример 2.5. Родители, заинтересованные в обеспечении материальной независимости (защищённости) ребёнка открывают счёт в банке и вкладывают

7

800 000 рублей на 15 лет под 10 % годовых с условием возможности снятия средств. Начиная с 11 года на обучение ребёнка в начале каждого года снимается 100 000 рублей. Какая сумма денег образуется на этом счёте к концу 15 года?

Решение. Применяем формулу 2.2, получаем по условию задачи следующую модель данной операции:

FV15=((((((800 000 1,110– 100 000)1,1 – 100 000)1,1−100 000)1,1− 100 000)1,1− − 100 000)1,1 = 800 000 1,115 – 100 000(1,15 + 1,14 + 1,13 + 1,12 + 1,1) = 800 000

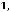
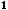
1.115 − 100 000 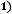) = 3 341 798 – 10 000 11 0,610 51=3 341 798 − 671 561=

= 2 670 237 (руб).

Накопленная сумма достаточна (даже с учётом негативных факторов) для поддержки ребёнка, например вложение средств в ипотечное строительство.

Пример 2.6. Компания планирует купить оборудование, стоимость которого сегодня PV = 500 000 у.д.е. Какую сумму должна будет уплатить компания продавцу оборудования через (или за) три года, если принятая ставка ежегодной доходности r = 0,2 постоянна в течение всего срока при условиях: 1) оплата будет производиться по прошествии трёх лет одним платежом; 2) оплата будет производиться по полугодиям равными суммами (в конце каждого полугодия).

Расчёт оплаты следует производить исходя из того, что полученные сегодня (или в любой другой момент времени) средства продавец может вложить по ставке r = 0,2. Поэтому, применяя формулы (2.2) и (2.3), получаем:

1)FV3 = 500 000(1 + 0,2)3 = 864 000 у.д.е.

2)CF 1,1 1,22 + CF 1,22 + CF 1,1 1,2 + CF 1,2 + CF 1,1 + CF = 864 000→

CF=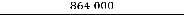=113 029, 8

в сумме, где CF – величина полугодового платежа;

FV2,3 = 113029,8 * 6=6781789.

Варианты (сценарии) оплаты 500 000 у.д.е. сегодня, 864 000 у.д.е. через три года и по 113 029,8 в конце каждого полугодия в течение трёх лет эквивалентны (т.е. стоимости их равновесны) с точки зрения временной стоимости денег.

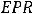
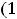
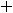
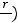
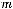
Для сравнения различных схем наращения применяется годовая эффективная процентная ставка EPR (effective percentage rate), которая вычисляется по формуле 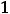(2.6) , где r – годовая процентная ставка, а m –

число начислений процентов в году по схеме сложных процентов. Годовая эффективная процентная ставка делает эквивалентным начисление процентов m раз в году по схеме сложных процентов с годовой ставкой r начислению

8

процентов один раз в год по эффективной ставке EPR. Поэтому её называют ещё ставкой сравнения.

Пример 2.7. Сравнить три варианта вложений средств:

1)при годовой ставке r1 = 0,10 (i1 = 10%) проценты начисляются два раза в год (по полугодиям);

2)при годовой ставке r2 = 0,096 (i2 = 9,6%) проценты начисляются четыре раза в год (поквартально);

3)при годовой ставке r3 = 0,084 (i3 = 8,4%) проценты начисляются двенадцать раза в год (помесячно);

Решение. Применяется формула (2.6)

Первый вариант самый выгодный для вложении, так как эффективная ставка EPR1=0,1025 больше всех остальных.

Концепция учёта негативных факторов (инфляции, риска, ликвидности и других) в финансовых операциях заключаются в необходимости реального отражения стоимости активов и денежных потоков, а также в обеспечении компенсации потерь доходов, вызываемых негативными факторами и процессами. Методический инструментарий следующий:

Iнорм = Iреал Iнегат (2.7), т.е. индекс номинальной (с учётом негативных факторов) доходности актива Iнорм равен произведению индекса реальной доходности Iреал и индекса негатива, объединяющего все негативные факторы. Таким образом, учёт негативных факторов производится на мультипликативной основе.

В частности, для учёта фактора инфляции получаем: 1+ rном= (1+ rреал)(1 +

Если с инфляцией одновременно учитывается риск, то из формулы (2.7) получим:

(2.1).

При анализе оценки финансовых операций применяется номинальная ставка, поэтому в формулах (2.1), (2.2), (2.3) , (2.4) r – есть номинальная годовая ставка, а в формуле (2.5) rt тоже номинальная годовая ставка в периоде t.

9

Пример 2.8. Реальная ставка доходности 25 % годовых, темп инфляции 10% в год. Вычислить номинальную годовую ставку.

Решение. Применяется формула Фишера (2.8)

rном = rреал + rинф + rреал rинф. Подставляя rреал = 0,25, rинф = 0,10, получим rном =

= 0,25 + 0,10 + 0,25 0,10 = 0,375 или iном = rном 100% = 37,5 %.

Пример 2.9. Определить реальную доходность операции ,если её номинальная доходность rнорм = 0,56, rриска = 0,20.

Решение. Реальная доходность rреал равна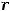

или в процентах iреал = rреал 100% = 0,30 100% = 30%.

Пример 2.10. Оценить номинальную ставку доходности финансовой операции, если годовая ставка реальной доходности rреал = 0,4, годовая инфляция ожидается не менее 10%, а риск – не менее 5% в год.

Решение. Поскольку негативные факторы инфляция и риск накладываются друг на друга (мультипликативны), то, применяя формулу (2.7), получим:

Т. е. номинальная ставка доходности должна быть не меньше 0,617 или iном ≥

≥ 0,617 100% ≥ 61,7 %.

3. Дисконтирование

Процесс нахождения величины (стоимости) капитала на настоящий (сегодняшний, текущий) момент времени по её известному или предполагаемому значению в будущем называется дисконтированием.

Дисконтирование – это, по сути, зеркальное отражение наращения, обратная процессу наращения задача, в которой значение будущей величины FVn приводится к текущей величине PV с коэффициентом дисконтирования d.

математического дисконтирования по схеме простых 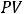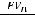(3.1) и сложных

(3.2) процентов, где d – коэффициент дисконтирования (как

правило, годовой). На практике величина d определяется альтернативной доходностью операции, ассоциированной с риском, инфляцией и другими факторами.

10