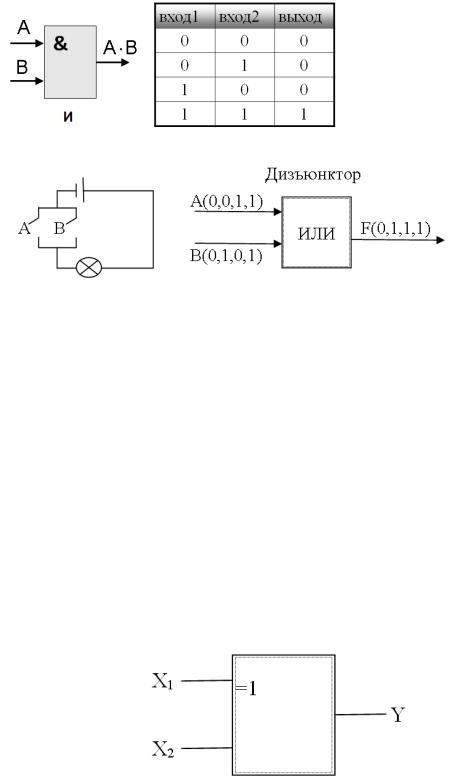
25

Тогда ток через лампочку идёт и она горит.

Таблица истинности логического элемента «И»

8.3.Логический элемент ИЛИ (дизъюнктор)

Оба контакта в положении «выкл». Тока нет. Лампочка не горит.

Первый контакт в положении «выкл», второй – в положении «вкл». Ток идёт, лампочка горит.

Обратная ситуация. Лампочка горит. Оба контакта в положении «включено».

Тогда ток через лампочку идёт и она горит.

8.4.Логический элемент «ИСКЛЮЧАЮЩЕЕ ИЛИ»

Схематически элемент элемент «ИСКЛЮЧАЮЩЕЕ ИЛИ» обозначается следующим образом:

Элемент «ИСКЛЮЧАЮЩЕЕ ИЛИ» Составим таблицу истинности логического элемента «ИСКЛЮЧАЮЩЕЕ

ИЛИ» (таблица 17).

26

Таблица 17 – Таблица истинности элемента «ИСКЛЮЧАЮЩЕЕ ИЛИ»

Составим таблицу условных обозначений основных логических элементов компьютера (таблица 18).

9. Таблица 18 – Условные обозначения логических элементов компьютера

27

10.Вопросы для самопроверки

1.Какие существуют основные формы мышления?

2.В чём состоит разница между содержанием и объёмом понятия?

3.Может ли быть высказывание выражено в форме вопросительного предложения?

4.Как определяется истинность или ложность простого высказывания? Составного высказывания?

5.Что содержат таблицы истинности и каков порядок их построения?

6.Какие логические выражения называются равносильными?

7.Какое количество логических функций двух аргументов существует и почему?

8.Какие логические функции двух аргументов имеют свои названия?

9.Какое существует количество логических функций трёх аргументов?

28

11.Решение логических задач

11.1.Примеры решения задач

Пример 1

Какой логической операции соответствует таблица истинности?

A B

0 0

01

10

1 1

F=A → B

Таблица истинности соответствует логической функции «импликация».

Пример 2

Найти значение логического выражения ,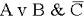

при А=0 (false), В=1 (True), С=0 (False).

Решение: подставим значения переменных в выражение и вычислим его согласно приоритету выполнения операций:

=0 v 1 & 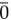=0 v 1& 1=0 v 1=1 (True).

Ответ: данное логическое выражение имеет значение True.

Пример 3

Найти значение логического выражения: (А<В) v (В>2) v (А ≠ 5) при А=5, В=-4. Решение: Подставим значения переменных в выражение и вычислим его со-

гласно приоритету выполнения операций:

(5<-4) v (-4>2) v (5 ≠ 5)=0 v 0 v 0=0.

Пример 4

Упростить логическое выражение: (А & В) v (А & ). Правильность упрощения проверить с помощью таблиц истинности.

Решение: Воспользуемся законом диструбтивности и вынесем за скобки А:

(А & В) v (А & ) = А & (В v ).

По закону исключённого третьего В v = 1, следовательно,

А & (В v ) = А & 1 = А.

Таким образом

(А & В) v (А & 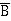) = А.

29

Составим таблицу истинности для выражения (А & В) v (А & )

Пример 5

По заданной логической схеме составить логическое выражение и заполнить для него таблицу истинности.

Решение: Используя обозначения логических элементов, составим логическое выражение .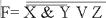

Заполним для F таблицу истинности

Пример 6

Какое из приведённых имён удовлетворяет логическому условию:

(первая буква согласная → вторая буква согласная) Λ (предпоследняя буква гласная → последняя буква гласная)?

1)КРИСТИНА

2)МАКСИМ

3)СТЕПАН

4)МАРИЯ

30

Решение: Имя должно удовлетворять условию, значит, F=1. Заменим выражения на логические переменные:

первая буква согласная – А вторая буква согласная – В предпоследняя буква гласная – С последняя буква гласная – D (A→B)Λ(C→D) = 1.

Расставляем приоритеты логических операций. Сначала должна выполняться конъюнкция. Чтобы выражение было равно 1, необходимо, чтобы (A→B) = 1 и

(C→D) = 1.

Теперь рассмотрим импликации. В каждой из них есть по 3 возможных варианта, когда импликация равна 1.

A→B = 1.

Теперь будем проверять каждое имя.

КРИСТИНА: А=1, В=1, С=0, D=1 .A→B=1.C→D=1. Следовательно, это имя подходит.

МАКСИМ: А=1, В=0, С=1, D=0. A→B=0. C→D=0. Следовательно, это имя не подходит.

СТЕПАН: А=1 ,В=1, С=1, D=0 .A→B=1 .C→D=0. Следовательно, это имя не подходит.

МАРИЯ: А=1,В=0,С=1,D=1.A→B=0.C→D=1. Следовательно, это имя не подходит.

31

Пример 7

Дан фрагмент таблицы истинности выражения F:

Какое выражение соответствует F?

1)X Λ Y Λ Z

2)¬X V ¬Y V Z

3)X V Y V Z

4)¬XΛ¬YΛ¬Z

Решение: Будем решать подстановкой предлагаемых вариантов.

1) F=X Λ Y Λ Z = 1 только в случае, когда X, Y, Z = 1. Проверяем по таблице. Этому условию не удовлетворяют вторая и третья строки таблицы. Не подходит.

2) F=¬XV¬Y V Z. Подставляем значения из таблицы:

для первой строки F=0 V 0 V 1=1 в случае, когда хотя бы одно из значений X, Y или Z =1

для второй строки F = 0 V 0 V 0=0. Следовательно, не подходит.

3)F=X V Y V Z=1 Проверяем по таблице. Подходит для всех трёх строк таблицы.

4)F=¬XΛ¬YΛ¬Z. Подставляем значения из таблицы:

F = 0 Λ 0 Λ 0=0. Следовательно, не подходит. Ответ: выражение 3) F=X V Y V Z=1

Пример 8

Укажите, какое логическое выражение равносильно выражению:

A V ¬(¬B Λ¬C):

1)¬A V B V ¬C

2)A V (B Λ C)

3)A V B V C

4)A V ¬B V ¬C

Решение: выносим за скобки операцию отрицания AV¬(¬BΛ¬C)=AV¬¬(BΛC) двойное отрицание логического выражения AV¬¬(BΛC) даёт выражение

A V (B ΛC)

Ответ: AV¬(¬BΛ¬C) = A V (B Λ C).