21

Это означает, что результат логического сложения высказывания и его отрицания всегда принимает значение «истина»:

А v Ā=1.

7.4.Закон двойного отрицания

Если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание:

=А.

7.5.Законы де Моргана (общей инверсии)

= Ā & ;

= Ā .

Важное значение для выполнения преобразований логических выражений имеют законы алгебраических преобразований. Многие из них имеют аналоги в обычной алгебре.

7.6.Закон коммутативности (переместительный)

Вобычной алгебре слагаемые и множители можно менять местами. В алгебре высказываний можно менять местами логические переменные при операциях логического умножения и логического сложения:

7.7.Закон ассоциативности (сочетательный)

Если в логическом выражении используются только операция логического умножения или только операция логического сложения, то можно пренебрегать скобками или произвольно их расставлять:

22

7.8.Закон дистрибутивности (распределительный)

Вотличие от обычной алгебры, где за скобки можно выносить только общие множители, в алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые:

Рассмотрим в качестве примера применения законов логики преобразование логического выражения. Пусть нам необходимо упростить логическое выраже-

ние (А & В) v (А & ).

Воспользуемся законом дистрибутивности и вынесем за скобки А: (А & В) v (А & 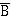) = А & (B v ).

По закону исключённого третьего В v 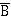=1, следовательно:

А & ( В v ) = А & 1 = А .

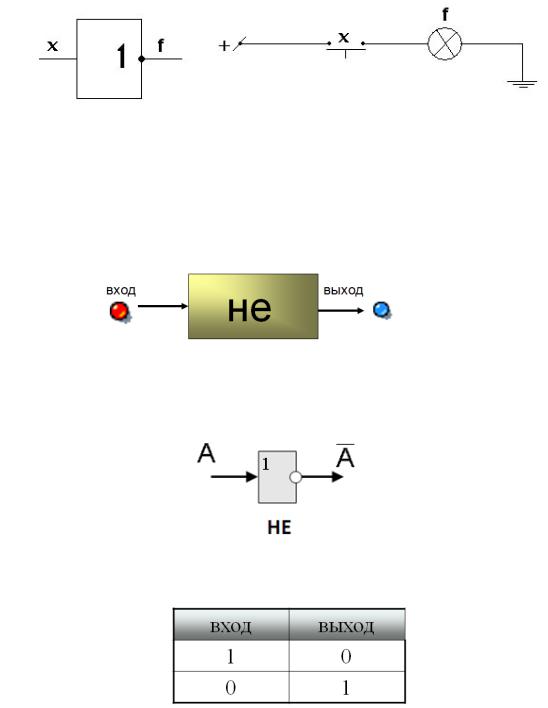
8. Логические элементы

Работа современных вычислительных машин сводится к обработке последовательностей нулей и единиц, которыми закодирована различная информация (числовая, графическая звуковая), и пересылки этой информации. Такую обработку производит арифметико-логическое устройство, являющееся частью процессора. Состоит оно из логических элементов.

Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие (называемые также вентилями), а также триггер.

С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.

Чтобы представить два логических состояния — “1” и “0” в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт.

Высокий уровень обычно соответствует значению “истина” (“1”), а низкий — значению “ложь” (“0”).

Каждый логический элемент имеет своё условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электрон-

23

ная схема в нём реализована. Это упрощает запись и понимание сложных логических схем.

Работу логических элементов описывают с помощью таблиц истинности.

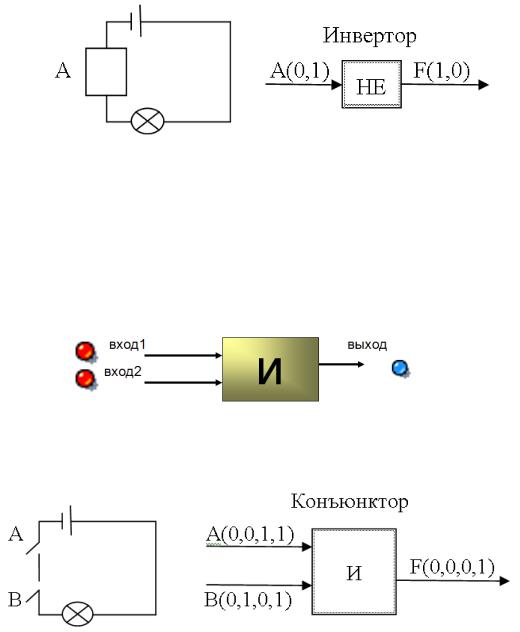
8.1.Простейший логический элемент НЕ (инвертор)

ВЭВМ операция инверсии физически реализуется стандартным логическим элементом «не» – инвертором.

В этом устройстве в качестве переключателя используется автоматический ключ. Когда тока в нём нет, пластинка замыкает контакты и лампочка горит. Если на переключатель подать напряжение, то цепь размыкается. Лампочка не горит.

Он имеет один вход и один выход. Работа этого элемента заключается в инвертировании (т.е. замене на противоположный) значения поступившего в него сигнала.

Зависимость входных и выходных сигналов можно представить в виде таблицы истинности.

24

ИНВЕРСИЯ

АF

01

10

Базовый набор операций

С помощью операций И, ИЛИ и НЕ можно реализовать любую логическую операцию.

8.2.Логический элемент И (конъюнктор)

Его работа заключается в том, что на выходе получается сигнал, равный «1», когда на оба входа был подан единичный сигнал. Элемент имеет два входа и один выход.

Оба контакта в положении «выкл». Тока нет. Лампочка не горит.

Первый контакт в положении «выкл», второй – в положении «вкл». Ток не идёт, лампочка не горит.

Обратная ситуация. Лампочка не горит. Оба контакта в положении «включено».