
- •Министерство образования Российской Федерации
- •Хабаровская государственная академия экономики и права
- •КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ И ПРОГНОЗИРОВАНИЕ
- •1. Задача
- •Задания для выполнения лабораторной работы
- •Щелкнув мышью по первой строке Numeric Data, появится список (рис.6):
- •Выберем второй пункт Multiple – Variable Analysis, откроется диалоговое окно для ввода переменных (рис.7).
- •Таблица 1
- •Таблица 2
- •Таблица 4
- •Таблица 10
- •Таблица 11
- •Уравнения линейных трендов
- •Таблица 15
- •Таблица 16
- •Таблица 17
- •Прогнозные расчеты
- •Ход работы
- •Анализ матрицы коэффициентов корреляции
- •Варианты заданий
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 15
- •Критические точки распределения Стъюдента
- •Приложение 3
- •Окончание прил. 4
- •Библиографический список
- •ВОПРОСЫ И ЗАДАНИЯ ДЛЯ ЗАЩИТЫ ЛАБОРАТОРНОЙ РАБОТЫ
- •Корреляционно-регрессионный анализ и прогнозирование
- •Подписано в печать . Формат 60х84/16. Бумага писчая.
- •Выписка из протокола № 7
|
13 |
|
|
|
|
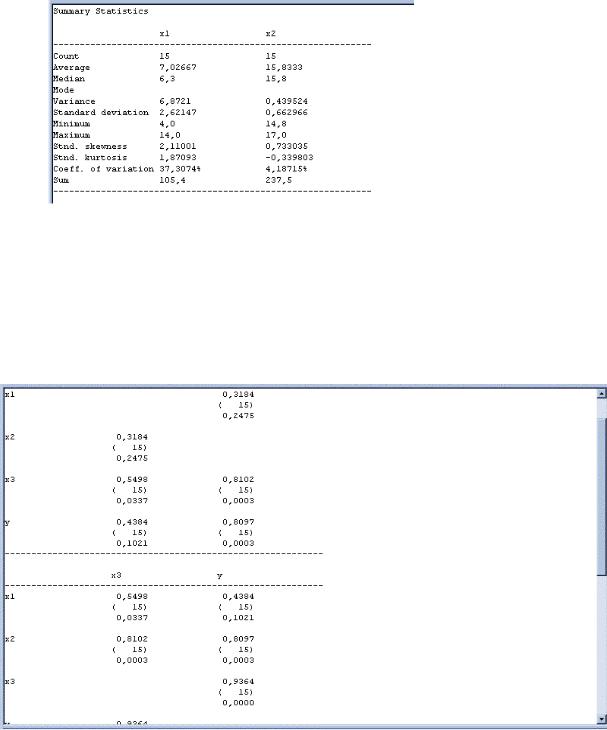
Стандартное |
Межквартильный |
сумма |
отклонение |
размах |
|
Std. Error |
|
|
Стандартная ошибка |
|
|
В табл. 3 мы получили дополнительный список общих статистик Таблица 3
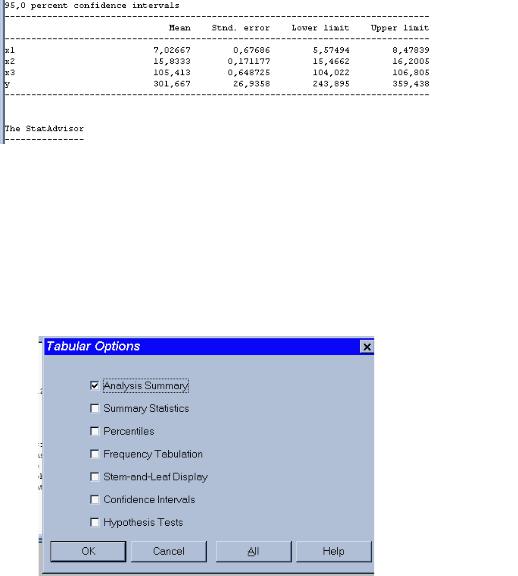
2.4.Для получения матрицы парных коэффициентов корреляции выберите
вокне табличных опций (рис.10) Correlations. Нажмите кнопку ОК. На экране появится табл. 4. Первое число является коэффициентом корреляции Пирсона, второе (под первым) представляет собой число наблюдений, а третье – уровень значимости
Таблица 4
14
В табл. 5 получены интервальные оценки среднего значения соответствующих переменных генеральной совокупности.
Таблица 5
2.5. Интервальные оценки дисперсий
Закройте рабочее окно.
Выберите Dеscribe / Numeric Data / One – Variable Analysis.
Введите в анализ переменную Y, затем нажмите кнопку табличных опций в рабочем окне. Появится окно табличных опций (рис.13).
Рис. 13
Выберите Confidence Intervals (доверительные интервалы), затем нажмите OK. Таким образом, получили интервальную оценку для среднего значения и стандартного отклонения переменной Y (табл. 6).
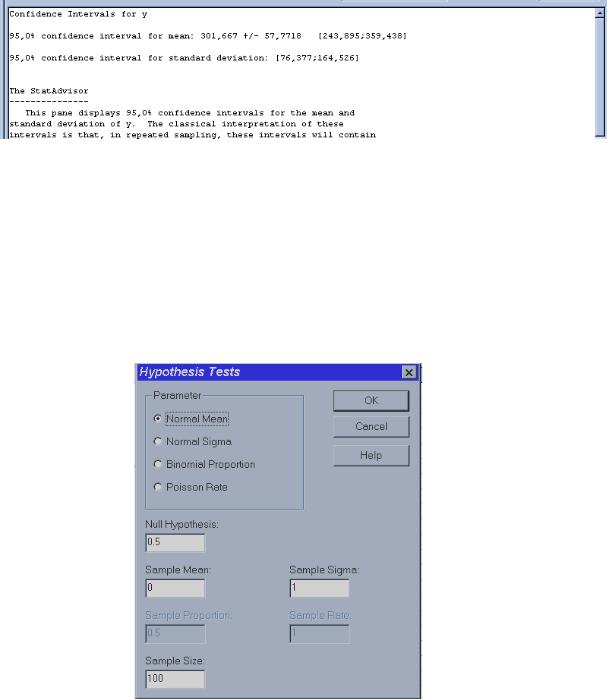
15
Таблица 6
Аналогично получите интервальные оценки для переменных х1, х2, х3. Доверительный интервал для стандартного отклонения генеральной
совокупности можно получить, проверив гипотезу Н0: σв=σг, при конкурирующей гипотезе Нα: σв≠σг.
Войдите в основное окно, пометьте столбец значений переменной Y, щелкнув мышкой по Y, затем Describe / Hypthesis Tests (проверка гипотез), на экране появится диалоговое окно (рис. 14).
Рис. 14
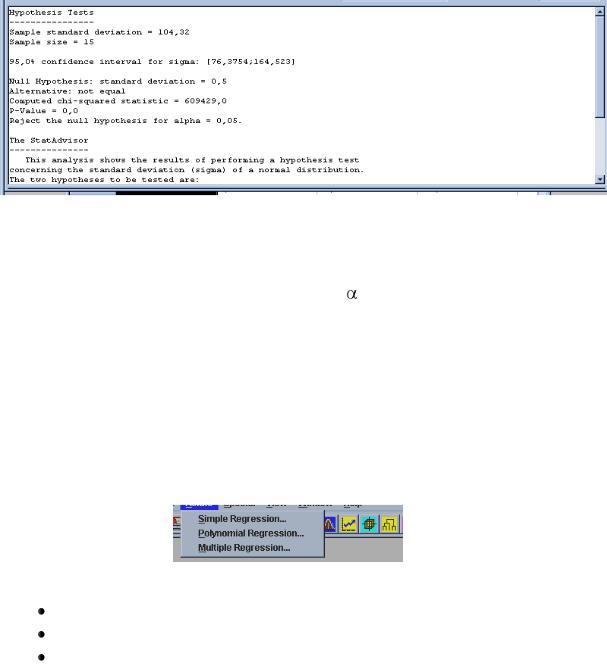
В поле Parameter Sigma введите значение стандартного отклонения переменной Y из табл. 1 - 104,32, в поле Sample Size введите объем выборки 15.
16
На экране появится отчет (табл. 7)
Таблица 7
Из отчета следует, что стандартное отклонение σг попадает в доверительный интервал (76; 3754; 164; 523) с надежностью 95%. Нулевая гипотеза Н0: σг=0,5 отвергается, при уровне значимости =0,05.
2.6.Уравнения регрессии
Встроке меню основного окна выберем команду Relate, на экране появится список регрессивных моделей (рис.15).
Рис. 15
простая регрессия, полиномиальная регрессия, множественная регрессия.
17
Выполним режим множественной регрессии Multiple Regression. На экране высветится диалоговое окно (рис. 16).
Рис. 16
Введите сначала переменную Y в поле Depended Variable (зависимая переменная), х1, х2 и х3 в поле Independed Variables (независимые переменные). Нажмите OK.
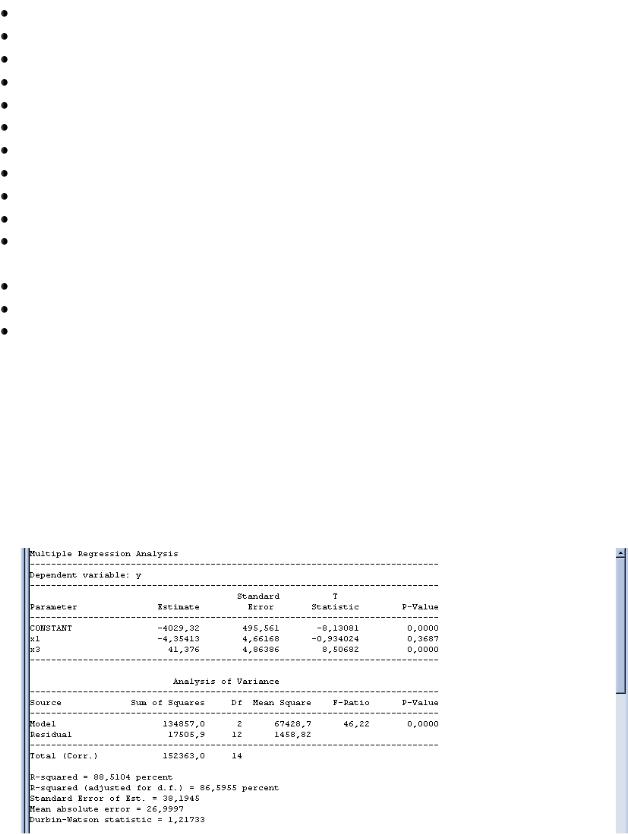
Получим сводку проведенного анализа (табл. 8).
Таблица 8
18
Estimate – оценка
St. Error – ст. ошибка
T Statistic – Т критерий (статистика) P-Value – Р- значение
Source – источник
Sum of Squares – сумма квадратов Df – степени свободы
Mean Square – средний квадрат F – Ratio – F – критерий
R – Squared – коэффициент множественной детерминации.
R squared (adjusted for d.f.) коэффициент детерминации с учетом степеней свободы
Standard Error if Est – стандартная ошибка остатков Mean absolute error – средняя абсолютная ошибка
Durbin – Watson Statistic – статистика Дарбина – Уотсона
Аналогично получите отчеты о множественной регрессии Y(х1х2), Y(х1х3), Y (х2х3), Y(х1), Y(х2), Y(х3), а также отчет об уравнениях трендов
х1(х4); х2(х4); х3(х4). (табл. 9-17).
Уравнения парной регрессии получите, используя режим множественной регрессии, так как анализ парной регрессии не содержит статистику Дарбина – Уотсона.
Таблица 9
