
- •II. Пределы и непрерывность
- •§ 4. Пределы функций
- •Предел дробно-рациональной функции в точке
- •3) , Тогда ;
- •Пределы дробно-рациональных функций с квадратичными выражениями
- •Предел дробно-рациональной функции в бесконечности
- •3) , Тогда .
- •Пределы иррациональных функций
- •Примеры сопряжённых выражений
- •Тригонометрические пределы. Первый замечательный предел
- •Второй замечательный предел
- •§ 5. Непрерывность функций
- •Исследование кусочно-заданных функций на непрерывность
- •Непрерывность дробно-рациональных функций
- •Непрерывность некоторых сложных функций
Тригонометрические пределы. Первый замечательный предел
ПР13. Найдите тригонометрические пределы простой подстановкой:
1) а)
; б)
 ; в)
; в)
![]() ; г)
; г)
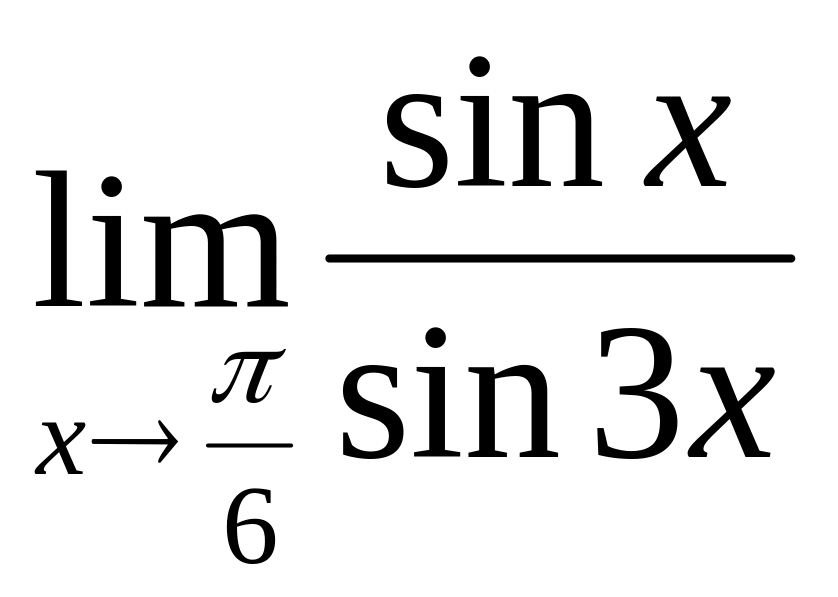 ;
д)
;
д)
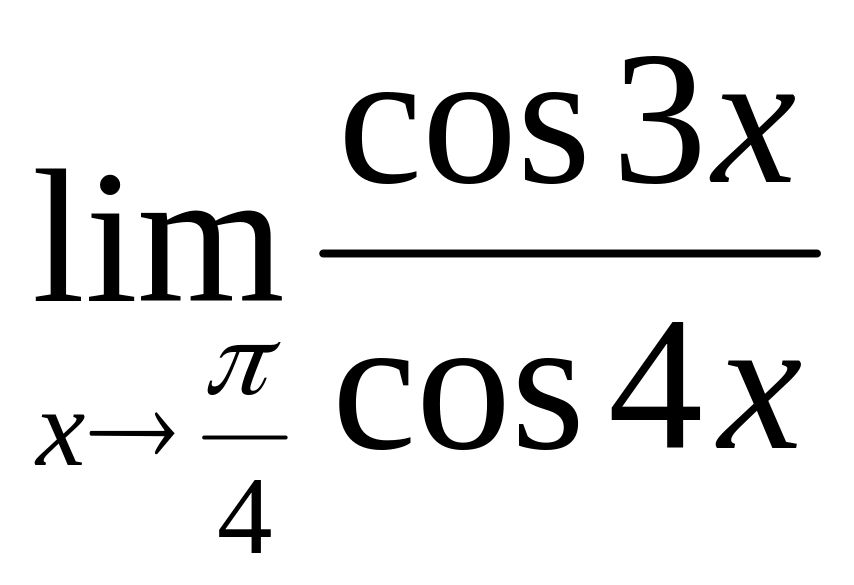 ;
;
2) а)
 ; б)
; б)
![]() ; в)
; в)
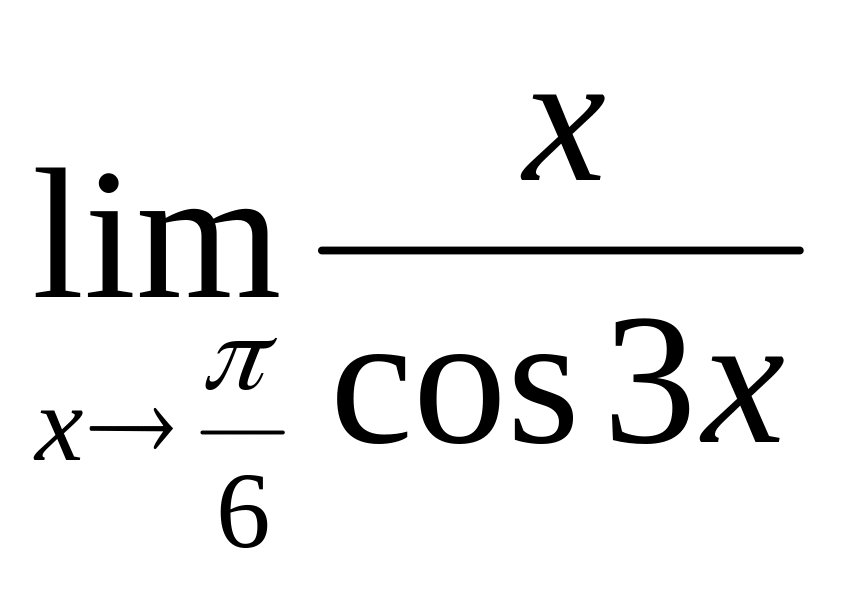 ; г)
; г)
![]() ;
д)
;
д)
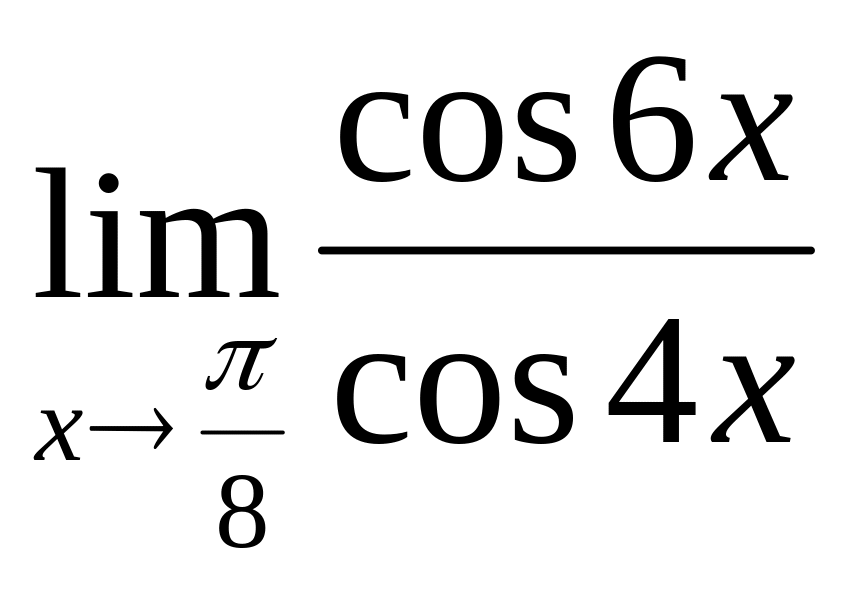 .
.
Пример 19. Легко видеть, что
а)
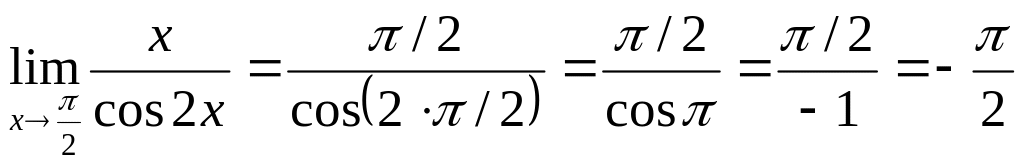 ;
;
б)
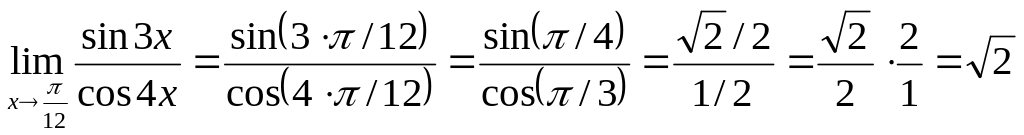 .
.
Предел
![]() помогает, если при вычислении
тригонометрических функций получается
неопределённость
.
Оказывается, если при
помогает, если при вычислении
тригонометрических функций получается
неопределённость
.
Оказывается, если при
![]() функция
функция
![]() ,
то выполнено приближённое равенство
,
то выполнено приближённое равенство
![]() ,
,
и все 4 функции примерно равны собственному аргументу. Тем самым, если аргумент , указанные функции являются эквивалентными бесконечно малыми (предел их соотношения равен 1).
Так,
![]() ,
,
![]() ,
поскольку
,
поскольку
![]() .
Как применить это при вычислении
пределов, показано в примерах.
.
Как применить это при вычислении
пределов, показано в примерах.
ПР14. Раскройте неопределённость при помощи эквивалентных бесконечно малых величин:
1)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() ; д)
; д)
![]() ;
;
2)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() ; д)
; д)
![]() .
.
Пример 20. Если заменить функции собственным аргументом, то
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
ПР15.
Раскройте неопределённость
при помощи эквивалентных бесконечно
малых и тождества
![]() :
:
1) а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() ;
;
2) а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
Пример 21.
![]()
![]() .
.
Пример 22.
![]()
![]()
(учли, что по смыслу
задачи
,
иначе
![]() не существует).
не существует).
При переходе к эквивалентным бесконечно малым следует проявлять осторожность, когда присутствует разность или сумма функций, тем более, если после упрощений получается 0 в числителе или знаменателе:
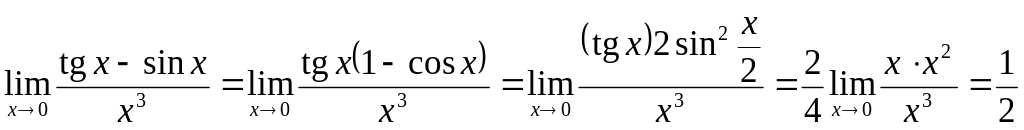 .
.
Попытка перейти
в числителе к разности
![]() приведёт к ошибке: либо решим, что в
числителе «чистый» 0, и потому ответ
равен 0, либо вовсе зайдём в тупик.
приведёт к ошибке: либо решим, что в
числителе «чистый» 0, и потому ответ
равен 0, либо вовсе зайдём в тупик.
Второй замечательный предел
Предел
![]() применяют для раскрытия неопределённостей
вида
,
связанных с показательными функциями
применяют для раскрытия неопределённостей
вида
,
связанных с показательными функциями
![]() .
Равносильное
свойство:
.
Равносильное
свойство:
![]()
Однако, как при вычислении любого предела, начинать следует с подстановки предельной точки. Если вместо точки указана бесконечность, пытаются упростить пример, найдя предел основания, степени и т.п. И только при возникновении неопределённости применяют замечательный предел.
Схема применения 2-го замечательного предела
Пусть при
оказалось, что
![]() ,
а
,
а
![]() .
Тогда
.
Тогда
![]() .
.
Считаем, что
![]() ,
где
при
.
Тогда
,
где
при
.
Тогда
![]() .
.
Поскольку
![]() ,
то
,
то
![]() .
.
Найдём предел
![]() ,
и если он равен числу A,
то весь предел равен
,
и если он равен числу A,
то весь предел равен
![]() .
.
ПР16. Найдите пределы простой подстановкой:
1) а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() ;
;
2) а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
Пример 23.
![]() .
.
ПР17.
Найдите пределы, воспользовавшись
свойствами показательной функции
![]() ,
а именно – её значениями при
,
а именно – её значениями при
![]() ,
когда
,
когда
![]() или
или
![]() :
:
1) а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() ;
;
2) а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
В задании 2 в каждом примере получаются 2 ответа – в зависимости от знака бесконечности.
Пояснение. Если
,
то
![]() и
и
![]() .
Если
,
то
.
Если
,
то
![]() и
и
![]() .
При
.
При
![]() зависимость
не является функцией (точнее, это функция,
разрывная в каждой действительной
точке).
зависимость
не является функцией (точнее, это функция,
разрывная в каждой действительной
точке).
Пример 24.
![]() Видно, что
Видно, что
![]() .
.
Тогда, поскольку
при
![]() величина
величина
![]() обращается в 0,
обращается в 0,
![]() .
.
Пример 25.
![]() Находим
Находим
![]() .
.
Основание
![]() ,
а в этом случае
,
а в этом случае
![]() .
Поэтому
.
Поэтому
![]() .
.
Пример 26.
![]() Здесь
Здесь
![]() .
.
Но функция
![]() – это то же, что
– это то же, что
![]() .
А эта функция стремится к 0 при
.
А эта функция стремится к 0 при
![]() и обращается в
и обращается в
![]() при
при
![]() .
Тогда
.
Тогда
![]() .
.
ПР18. При помощи 2-го замечательного предела раскройте неопределённость , когда аргумент стремится к бесконечности:
1) а)
![]() б)
б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() ;
;
2) а)
![]() б)
б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() ;
;
3) а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() ;
;
4) а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() ;
;
5) а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
Пример 27.
![]() .
.
Пример 28.
Найдём
![]() .
Представим основание так:
.
Представим основание так:
![]()
(а лучше сразу
заметить, что
![]() ).
).
Тогда
![]() .
.
Но
![]() .
Поэтому
.
Поэтому
![]() .
.
ПР19. При помощи 2-го замечательного предела раскройте неопределённость , когда аргумент стремится к 0:
1) а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() ;
;
2) а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
Пример 29. Преобразовав степень, получаем
а)
![]() ;
;
б)
![]() .
.
ПР20. Найдите пределы
1) а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() ;
;
2) а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
Пример 30.
Найдём
![]() .
Здесь
.
Здесь
![]() ,
,
и тогда
![]() .
.
В степени присутствует
,
но
![]() ,
поэтому
,
поэтому
![]() .
Это и есть ответ.
.
Это и есть ответ.
Пример 31.
Найдём
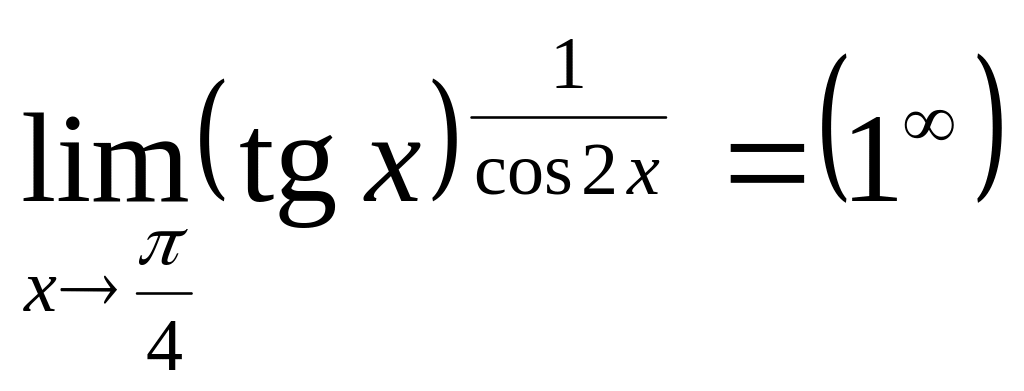 .
Представив
.
Представив
![]() ,
получаем, что
,
получаем, что
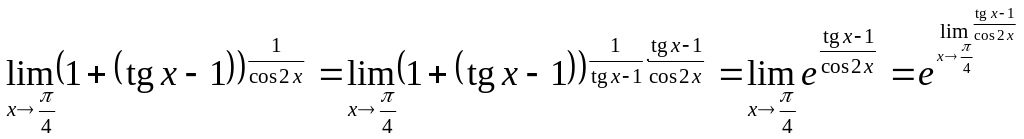 .
.
Теперь находим
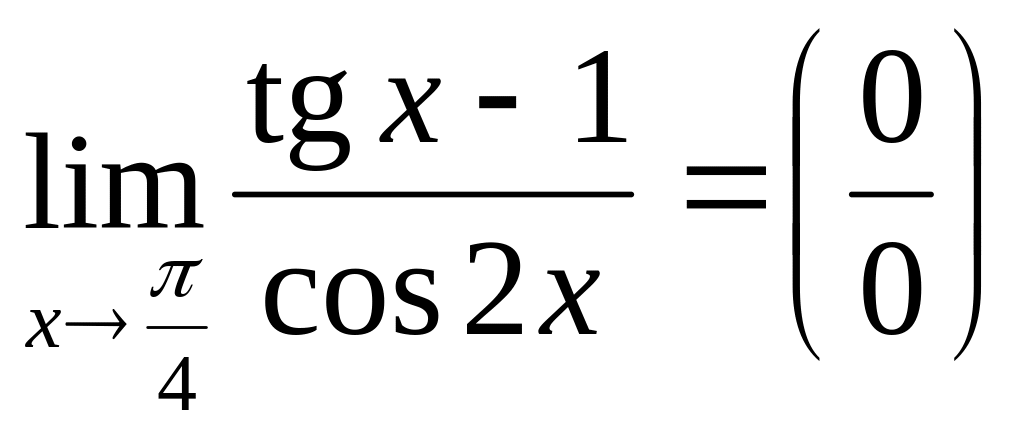 .
Преобразуем показатель степени так:
.
Преобразуем показатель степени так:
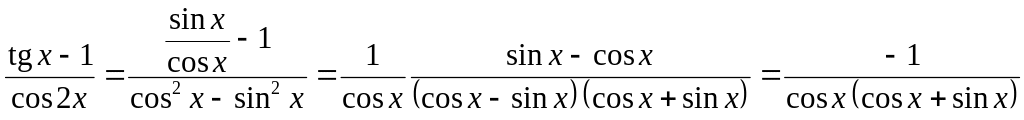 .
.
Тогда
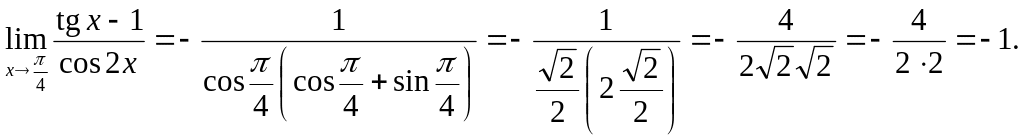
Ответ:
![]() .
.
