681_Trofimov_V.K._Teoremy_kodirovanija_neravnoznachnymi_

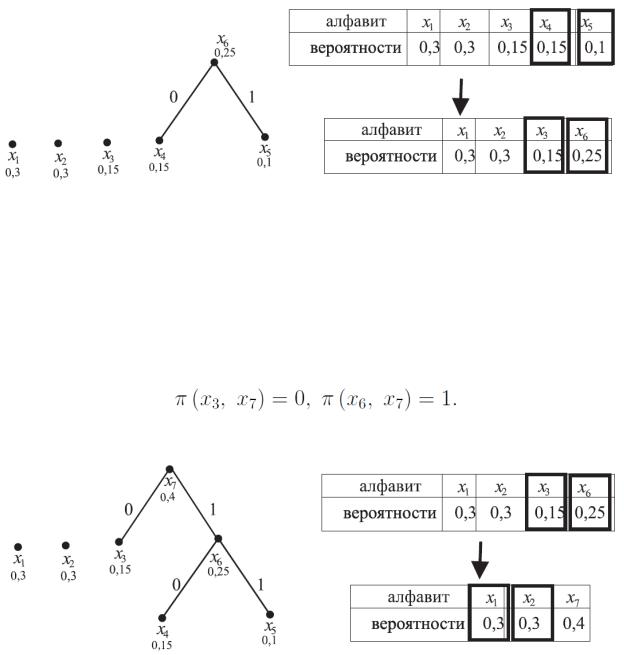
Замечание. Вместо буквы x4 на данном шаге могла быть выбрана буква x3

с такой же вероятностью. При присвоении меток можно было бы поменять их местами: π (x4, x6) = 1, π (x5, x6) = 0. При построении кода это не важно, так как не влияет на эффективность кодирования, а именно, на среднюю длину ко-

дового слова.

.

Рис. 3.

На втором шаге построения кода (рис. 4), работая уже с алфавитом

x1, x2 , x3, x6 , выбираем буквы x3, x6 , удаляем их из алфавита, заменяя на букву x7 с вероятностью p(x7) = 0.4. Вершины кодового дерева, соответствующие бук-

вам x3, x6 , соединяем ребрами с вершиной, соответствующей x7 . Метки ребер:

Рис. 4.

21

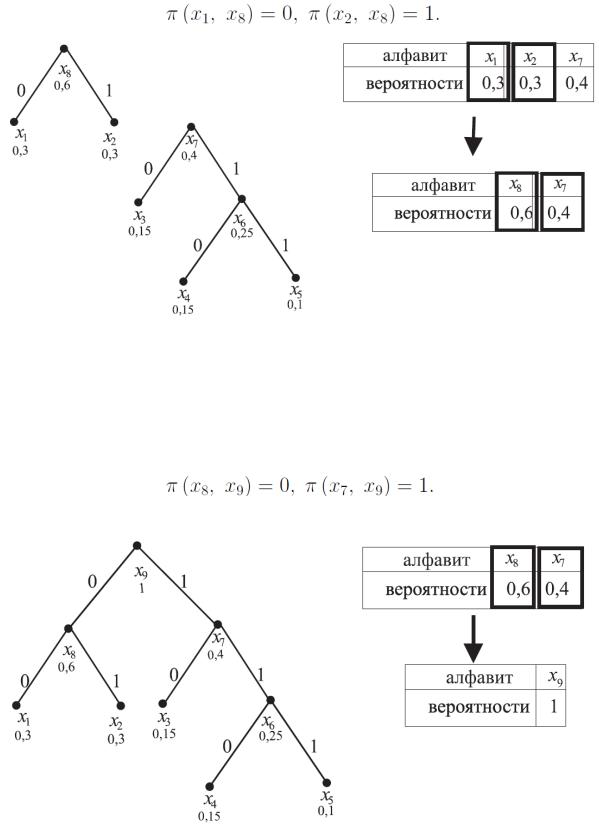
На третьем шаге (рис. 5), удаляем из алфавита x1, x2 , x7 буквы x1, x2 ,

вводя букву x8 , где полагаем p( x8 ) = 0.6. Добавляем к кодовому дереву ребра

x1, x8 и x2 , x8 с метками

Рис. 5.

На четвертом, последнем, шаге (рис. 6) заменяем две оставшиеся буквы x7 , x8 на букву x9, p(x9) = 1. Добавляем к кодовому дереву ребра ( x7 , x9 ) и ( x8 , x9 ) с метками

Рис. 6.

22

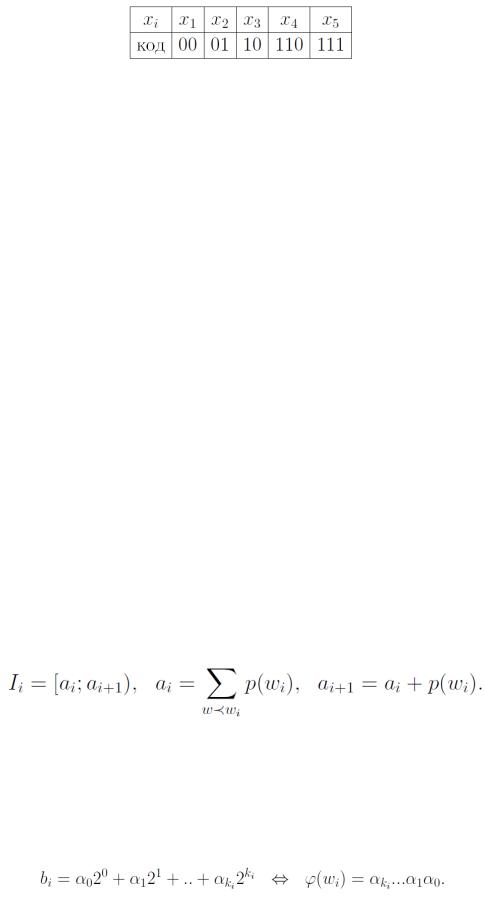
Запишем кодовые слова для букв исходного алфавита (табл. 2).

Табл. 2.

2.2. Арифметическое кодирование

Одним из наиболее известных алгоритмов сжатия данных является арифме-

тическое кодирование [12, 17, 39, 40, 55, 56, 66]. Сообщения источника коди-

руются вещественным числом из полузакрытого слева единичного интервала.

Каждый следующий символ сообщения источника сужает выбираемый интер-

вал согласно закону распределения вероятности появления символа в сообще-

нии. После окончательного определения интервала, соответствующего слову источника, остается число, определяющее код сообщения: двоичная запись числителя дроби, принадлежащей данному интервалу, знаменатель которой яв-

ляется наименьшей возможной степенью двойки.

Идея арифметического кодирования была предложена П. Элайесом, опи-

сана Н. Абрамсоном в 1963 г. [33] и усовершенствована Й. Риссайненом

[55, 56].

Пусть заданы алфавит X x1, x2 ,..., xk и закон распределения p. Упоря-

дочим все слова источника лексикографически. Разобьем интервал [0; 1) на по-

лузакрытые слева интервалы

числа bi :

23

Пример выполнения арифметического кодирования.

Рассмотрим множество слов над алфавитом X a; b; c; d бернулли-

евского источника. Пусть задана вероятность появления символов алфавита в сообщениях: p a 0.3; p b 0.4; p c 0.1; p d 0.2.

Определим кодовое слово для сообщения "adcc".

Для этого разобьем единичный интервал на четыре интервала, соответ-

ствующих буквам алфавита (по порядку):

[0;1) = [0;0.3) [0.3;0.7) [0.7;0.8) [0.8;1).

Выберем интервал, соответствующий первой букве сообщения "a": a  [0; 0.3).

Разобьем интервал [0; 0.3) на четыре интервала, соответствующих буквам ал-

фавита, масштабируя предыдущее разбиение [0; 1):

[0;0.3) = [0;0.09) [0.09;0.21) [0.21;0.24) [0.24;0.3).

Выберем интервал, соответствующий второй букве сообщения "d": ad  [0.24; 0.3).

Разобьем интервал [0.24; 0.3) на четыре интервала, соответствующих буквам алфавита, масштабируя предыдущее разбиение:

0.24; 0.3 0.24; 0.24 0.018 0.24 0.018; 0.24 0.042

0.24 0.042;0.24 0.048 0.24 0.048;0.24 0, 06 ;

0.24;0.3 0.24;0.258 0.258;0.282 0.282; 0.288 0.288; 0.3 .

Выберем интервал, соответствующий третьей букве сообщения "c": adc  [0.282; 0.288).

Разобьем интервал [0.282; 0.288) на четыре интервала, соответствующих бук-

вам алфавита, масштабируя предыдущее разбиение:

0.282;0.288 0.282;0.282 0.0018 0.282 0.0018;0.282 0.00420.282 0.0042;0.282 0.0048 0.282 0.0048;0.282 0.006 ;

0.282;0.288 0.282;0.2838 0.2838;0.2862 0.2862; 0.2868 0.2868; 0.288 .

Выберем интервал, соответствующий четвертой букве сообщения "c":

24

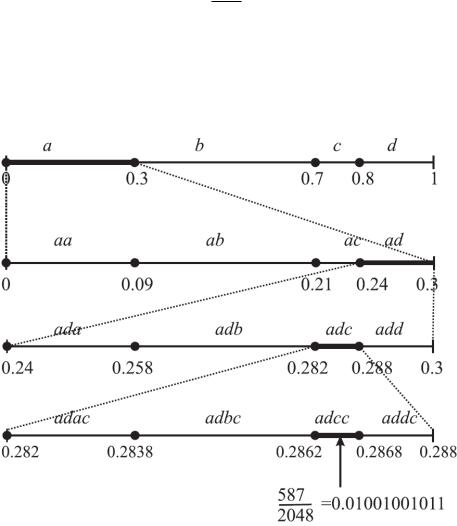
adcc [0.2862;0.2868).

Выберем правильную дробь с наименьшим возможным знаменателем степени числа 2:

0.2862 587211 0.2868 ,

и представим в двоичной записи:

Рис. 7.

Итак, φ(adc)=01001001011.

Иллюстрация арифметического кодирования дана на рис.7.

Арифметическое кодирование широко используется при сжатии изображений,

втом числе и видео. Модификации арифметического кодирования предложены

вработах И. Уиттена [66], Б.Я. Рябко [16] и Ю.М. Штарькова [30].

25

2.3. Код Лемпела-Зива

Код Лемпела-Зива (LZ), предложенный в 1977-78 гг. [67, 68], относится к словарным методам кодирования. В процессе просмотра текста создается сло-

варь из закодированных последовательностей, расширяющийся по мере про-

смотра текста.

Базовая идея схемы Лемпела-Зива заключается в следующем.

Просматриваем последовательность символов w xi1 xi2 · · · xin алфавита

X x1, x2 ,..., xk до тех пор, пока не встретим повторяющийся символ:

Просматривая последовательность далее, выделим максимальный по длине префикс (подслово), который уже встречался в предыдущем тексте

Добавим данный префикс в качестве нового слова к "словарю". При этом при-

своим новому слову двойную метку, состоящую из

1)номера позиции первого символа самого раннего вхождения данного слова в текст;

2)количества букв в обрабатываемом слове:

Продемонстрируем данную схему на примере, закодировав слово "abrabarabra".

1)abrabarabra → (a)brabarabra;

2)(a)brabarabra → (ab)rabarabra;

3)(ab)rabarabra → (abr)abarabra;

4)(abr)abarabra → (abr)(1, 2)arabra; буква "a" уже встречалась ранее: "a" –

первый символ последовательности; добавляем в словарь "ab" слово длины два,

следовательно, вместо слова "ab" оставляем метку (1,2);

26

5) (abr)(1, 2)arabra → (abr)(1, 2)(1, 1)rabra; буква "a" уже встречалась ра-

нее: "a" – первый символ последовательности; добавляем в словарь "a" одно-

буквенное слово, следовательно, вместо слова "a" оставляем метку (1,1);

6) (abr)(1, 2)(1, 1)rabra → (abr)(1, 2)(1, 1)(3, 3)ra; буква "r" встречалась ра-

нее (третий символ входной последовательности); добавляем в словарь "rab" ,

оставляем метку (3,3);

7) (abr)(1, 2)(1, 1)(3, 3)ra → (abr)(1, 2)(1, 1)(3, 3)(3, 2), добавляем в словарь

"ra", оставляем метку (3,2).

В версии LZ77 вводится два параметра: длина скользящего "окна", охва-

тывающего последовательность, и максимальная длина последовательности в словаре. При этом рассматриваемым подсловам ставятся в соответствие трой-

ные метки, состоящие из указателя на смещение слова в словаре, длины нового подслова и последующей за ним буквы. Используем в качестве примера слово

"abrabarabra" и закодируем его посредством LZ77 с длиной окна, равной 6, и

размером словаря 4 (табл. 3).

Табл. 3.

На четвертом символе обнаружено совпадение: смещение буквы "a" относи-

тельно начала окна равно 1, длина совпадающего подслова 2. После создания первых двух кодовых символов окно смещается на две ячейки вправо. Следу-

ющая буква "a" (табл. 4)

Табл. 4.

27

Обнаружено совпадение со словарем: смещение буквы "a" относительно начала окна 2, длина совпадающего подслова 1. Окно смещается вправо на одну ячей-

ку. Следующая буква "r" (табл. 5).

Табл. 5.

Обнаружено совпадение со словарем: смещение буквы "r" относительно начала окна отсутствует, длина совпадающего подслова 2. Окно смещается на две ячейки вправо. Следующая буква "b" (табл. 6).

Табл. 6.

Длину буфера (оставшейся от словаря части окна), очевидно, не имеет смысла делать больше, чем длину словаря. Закодируем "abrabarabra" посредством LZ77

с длиной окна, равной 8, и размером словаря 4 (табл. 7).

Табл. 7.

В версии LZ78 словарь изначально содержит все буквы алфавита и при просмотре текста расширяется посредством добавления новых слов, которые получаются из уже имеющихся добавлением новых букв в конец слова.

28

При этом для нового слова формируется двойная метка, состоящая из ссылки-указателя на слово в словаре и добавляемой к этому слову буквы.

Закодируем "abrabarabra", используя LZ78 (табл. 8).

Табл. 8.

Существует множество модификаций LZ-схемы, подробный обзор по

этой теме содержится, например, в [34].

3.Кодирование известного источника неравнозначными символами

3.1.Предварительные построения

Рассмотрим кодовый алфавит Y y1, y2,..., ym c вектором длительно-

стей кодовых символов tY t1,t2 ,...,tm . Пусть 0 tY – наибольший положи-

тельный корень уравнения

t1 t2 .. tm 1.

которое состоит из m непересекающихся интервалов I j a;b определяется

следующим образом:

29

i 1

Утверждение. Длина интервала I j a;b обратно пропорциональна дли-

тельности буквы y j .

Доказательство. В самом деле, согласно определению разбиения полу-

чаем:

Утверждение доказано.

Через Yn a;b обозначим разбиение, полученное n-кратным примене-

нием процедуры разбиения Y a;b к интервалу a;b , т.е. «разбиение разби-

ений»:

довый алфавит и известны длительности кодовых символов t(0)=1 и t(1)=8.