
567_Kozljaev_JU._D._SAbornik_zadach_i_uprazhnenij_po_kursu_EHlektropitanie_
.pdf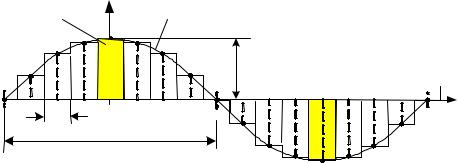
импульсного сигнала и его первой гармоники, как показано на рисунке при значениях D1 = 0.2, D2 = 0.5, D3 = 0.8, D4 = 1.0.
2. При каких значениях D в спектре сигнала обращаются в ноль третья, пятая и седьмая гармоники.
3. Вычислить значения коэффициента искажения импульсного сигнала при указанных в п. 1 значениях коэффициента заполнения D.
Коэффициент искажения определяется отношением действующего значения первой гармоники S1 к действующему значению сигнала Sд (см. раздел 1.2).
3.2. Задачи повышенной сложности (Б)
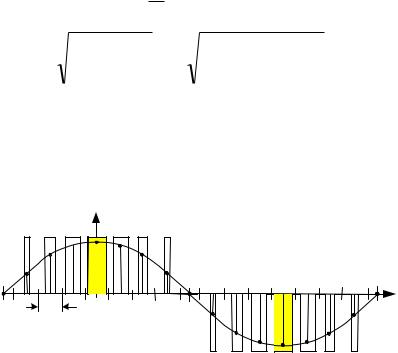
Б.1. Синусоидальный сигнал s(t) с амплитудой А аппроксимируется ансамблем из N импульсных прямоугольных знакопеременных сигналов. Для наглядности h n (t) с номером n = 0 на рисунке отмечен затемнением. В после-
дующем, такие сигналы будем обозначать термином «биэлементарный» или для краткости БЭС. Кратность длительности половины периода сигнала s(t) по отношению к длительности импульса (Tт) сигнала h(t), равна четной величине N = 8. Соответственно, общее число БЭС в ансамбле равно N.
s,h
ho(t) |
|
s(t) |
|
|
|
|
|
|
|
|
M=T/TT=16, |
|
|
|
N=M/2=8 |
|
|
|
А |
TT |
0 |
0.5Т |
t |
|
|
||
|
|
|
Определить действующее значение и амплитуды первой (k = 1) и третьей (k = 3) гармоник функции h(t) = hn (t) . Высота импульсов h n (t) равна значе-
нию s(t) в центре тактового интервала (ТТ) с порядковым номером n. Сравните действующие значения сигналов s(t) и h(t).
Пояснения к решению задачи:
1. Вычислить относительную длительностью импульсов и высоту импульсов
An (t) с порядковым номером n D = TT/0.5T = /N: А n = A cos( n / N ) .
2. C учетом числа БЭС определить фазовый сдвиг между соседними сигналами
1 / N .
3. Амплитуды гармоник БЭС с номером k вычисляются по формуле табл. приложения П.1 сигнал № 5.
4. Для вычисления амплитуд гармоники сигнала, представленного ансамблем произвести суммирование гармоник биэлементарных сигналов с учетом их фазового сдвига:
21
|
N Б ЭС |
|
|
|
|
|
||||
|
|
2 |
|
|
|
4An |
|
D |
|
|
Umk = U mk (n) |
cos(n k 1 ) , где Umk(n) = |
sin(k |
) . |
|||||||
|
2 |
|||||||||
n |
N "C |
|
k |
|
||||||
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
5. При вычислении действующего значения ансамбля учесть, что БЭС образуют ортогональную последовательность из N функций. Действующее значение
каждой БЭС равно U БЭС An 
 D ,
D ,
|
N / 2 |
|
N / 2 |
следовательно: U = |
U БЭС2 |
(n) A |
cos 2 (n / N ) . |
|
N / 2 |
|
N 2 |
Б.2. Импульсный сигнал образован последовательностью из N = 0.5T/Тт биэлементарных импульсов* с высотой равной А. Длительность импульсов модулирована по закону косинуса таким образом, что их ширина пропорциональна мгновенной величине модулирующего сигнала
|
s |
|
|
|
M=T/Tт=16 |
|
|
0.5Т |
TT |
0 |
t |
s(t) = m cos(n TT ) , где m ‒ коэффициент модуляции, n ‒ порядковый номер элементарного импульса в ансамбле. Кратность частоты модулирующего сигнала и тактовой частоты модуляции равна четному числу М = 2N.
Определить действующее значение сигнала s(t) и величины амплитуд первой и третьей гармоник его спектра.
Алгоритм решения аналогичен решению задачи Б.1.
Б.3. Синусоидальный сигнал s(t) апроксимируется треугольным h1(t) и прямоугольным h2(t) сигналами (рис. 1.3). При заданной амплитуде синусоидального сигнала Еm и относительной длительности D = Ти/0.5Тs вычислить значения амплитуд аппроксимирующих сигналов Eh1, Eh2 при условии равен-
ства нулю ошибки 1 .
Б.4. В техническом устройстве планируется при отказе источника синусоидального напряжения использовать резервный источник импульсного напряжения. Сигналы s(t) и h(t), соответствующие названным напряжениям, показанные на рисунке.
__________________________________________________________________
*Пример импульсного знакопеременного «биэлементарного» сигнала показан в приложении, табл. П.1, сигнал № 3.
22

|
|
s |
|
|
|
|
|
|
Es |
|
|
-Ts/4 |
0 |
|
Ts/4 |
Ts/2 |
t |
|
|
h |
|
|
|
|
|
|
|
Eh |
|
|
|
Tи |
Th |
|
t |
|
|
|
|
|
|
Определить необходимые величины Еh при заданных Еs, D = Tи/Th и |
|||||
М = Ts/Th для выполнения условий: |
|
|
|||
а) действующие значения сигналов s(t) и h)t) равны; |
|
||||
б) средние значения модулей сигналов (So, Ho) равны. |
|
||||
Б.5. Выразите расчетные соотношения рассмотренной выше задачи (А.4) через параметр А и угол отсечки . Определите средние значения (So, Ho) и действующие значения сигналов (Sд, Hд) при заданных параметрах А и .
Б.6. Сложный сигнал образован суммированием синусоидального сигнала s1(t) с амплитудой А1 и модулированной по синусоидальному закону последовательности импульсов пилообразной формы s2(t) c максимальной амплитудой А2. Кратность периодов сигналов М=200.
Получить общее решение для оценки действующего значения сигнала s(t) и определить величину Sд при заданных параметрах А1, А2.
s |
S1 |
|
|
A2 |
|
|
|
|
|
|
А1 |
0 |
Tт |
t |
|
0.5T |
|
s2 |
|
А2 |
|
|
|
|
|
t |
S3 |
0.5Тт |
A2 |
|
|
|
|
|
t |
|
|
23 |
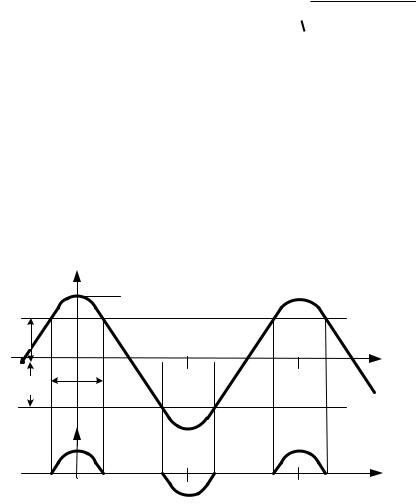
Пояснения к решению задачи. Сигналы s1(t) s2(t) являются ортогональ-
ными, следовательно, действующее значение Sд = 
 S2(S1) S 2(S 2) , где Sд(S1) ‒
S2(S1) S 2(S 2) , где Sд(S1) ‒
действующее значение синусоидального сигнала s1(t), Sд(S2) ‒ действующее значение сигнала s2(t), равное по величине действующему значению сигнала s3(t) =│s2(t)│ (см. раздел 2, пример П.2.8).
Б.7. Сигнал s2(t) образован «отсечением» вершин каждой полуволны синусоидального сигнала s1(ωt) на уровне В = Асos(ψ/2). Параметры А и В заданы в таблице.
Определить: угол отсечки θ; амплитуду первой гармоники сигнала s2(t): его действующее значение (Sд); значения коэффициента формы (Кф) и коэффициента амплитуды (Ка).
s1
|
А |
|
|
В |
|
|
|
|
|
|
t |
-В |
|
|
|
s2 |
|
|
|
0 |
|
|
t |
|
|
|
Пояснения к решению задачи. Аналогичная задача для однополярных сигналов s(ωt) рассмотрена в примере П.2.7. Если s(ωt) представить разностью двух последовательностей однополярных импульсных сигналов (положительной и отрицательной, отвечающих условию ортогональности), для каждой из которых расчетные соотношения относительно амплитуды основной гармоники и действующего значения применимы решения примера П.2.7, то результирующее решение может быть найдено с использованием закономерностей, полученных при рассмотрении свойств комбинированных сигналов (раздел 1.1, п. А, Б).
3.3. Задачи высокого уровня сложности (В)
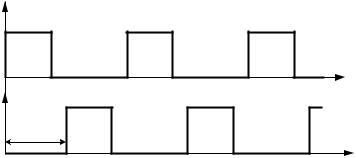
В.1. Сформулируйте закономерности изменения спектров и действующих значений элементарных сигналов s1(t), s2(t) при формировании «комбинирован-
ных» сигналов s3(t) = s1(t) + s2(t) и s4(t) = s1(t) ‒ s2(t). Сигналы s1(t) и s2(t) имеют одинаковые форму, частоту следования, длительности импульсов (рис. В.1). Взаимный сдвиг во времени импульсных последовательностей равен 0.5Т.
При заданных значениях высоты импульсов (А), относительной длительности (D = Ти/0.5Т) определите действующие значения частоты и амплитуды основных гармоник комбинированных сигналов.
24
s1 |
|
|
Ти |
Т |
t |
s2 |
|
|
Tc |
|
|
|
|
t |
|
|
Рис. В.1 |
Для решения задачи необходимо представить исходные сигналы рядом Фурье в комплексной форме. Очевидно, из-за «одинаковости» форм сигналов
их спектры амплитуд одинаковы, а спектры фаз различаются на угол k k .
Из изложенного выше следует, что результат суммирования или вычитания элементарных сигналов существенно изменяет амплитуды для гармоник с четным и нечетным номером k.
При оценке действующих значений комбинированных сигналов следует учесть, что исходные сигналы являются ортогональными, поэтому в комбинированных сигналах отсутствует составляющая «взаимной энергии» исходных сигналов.
В результате решения следует сформулировать:
А. При формировании сигнала s3(t) амплитуды четных /нечетных гармоник исходных сигналов не изменяются/возрастают/уменьшаются, во сколько раз.
Б. При формировании сигнала s4(t) амплитуды четных/нечетных гармоник исходных сигналов возрастают/уменьшаются, во сколько раз.
В. Присутствуют ли в спектрах сигналов s3(t), s4(t), гармонические составляющие с частотами, отсутствующими в спектрах исходных сигналов.
Г. Как изменятся выводы по п. А, Б при условии неодинаковости форм исходных сигналов (например, импульсные последовательности s3(t), s4(t) различаются по амплитуде, по длительности).
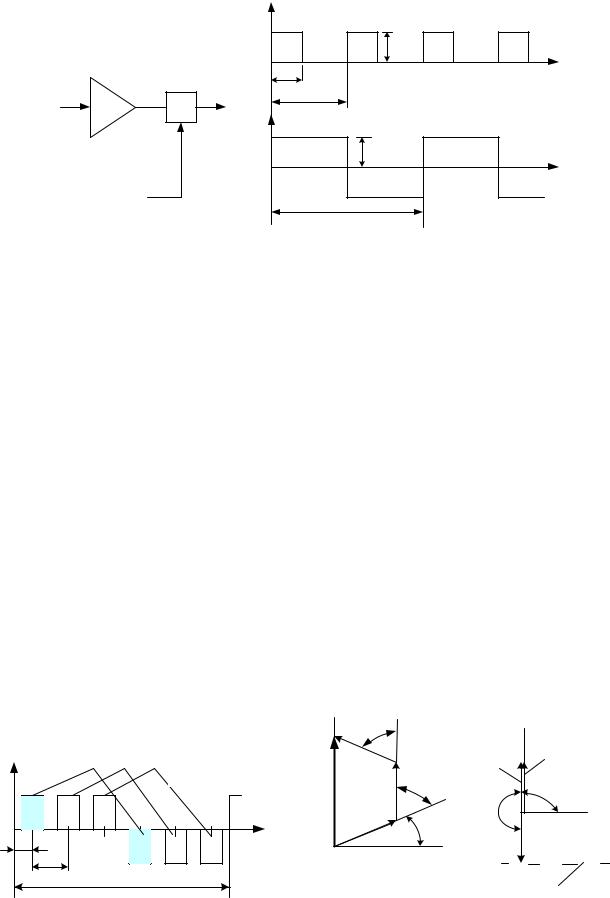
В.2. Электрический сигнал s1(t) преобразуется схемой, показанной на рис. В.2. На один из входов перемножителя (М) поступает усиленный в k раз сигнал s1(t), на второй вход перемножителя поступает сигнал переключения s2(t) с единичной амплитудой импульсов. Коэффициент заполнения импульсов сигнала s1(t) равен значению D.
25
|
|
S1 |
|
|
|
|
A1 |
|
М |
Tи |
t |
|
|
||
S1(t) |
S(t) |
T1 |
|
|
|
|
|
K |
X |
|
|
|
|
S2 |
|
|
|
|
A2=1.0 |
|
S2(t) |
|
t |
|
|
|
|
|
|
T2 |
|
|
|
Рис. В.2 |
|
Приведите график ожидаемого выходного сигнала s(t). Вычислите действующее значение выходного сигнала; значения амплитуд гармоник с номером k = 1,3,5, значения частоты гармоник.
Во сколько раз следует изменить величину коэффициента заполнения импульсов сигнала s1(t) при увеличении А1 на 20 % для поддержания неизменной величины амплитуды первой гармоники выходного сигнала s(t)?
В.3. Предложите геометрическую интерпретацию формирования амплитуд гармоник ШИМС-сигнала [5], образованного ансамблем элементарных импульсов, модулированных по синусоидальному закону (пример сигнала показан на рисунке к задаче КБ.2). Приведите иллюстрацию формирования векторов амплитуд первой и третьей гармоник для заданных значений импульсов (А), коэффициента модуляции (m) и кратности (М) частоты тактовых импульсов по отношению к частоте выходного сигнала. Вычислите значения амплитуд первой и третьей гармоник сигнала.
Пояснение к решению задачи приведем на примере сигнала ШИМП (модуляция ширины импульсов по «прямоугольному» закону, все импульсы сигнала имеют одинаковую длительность, как показано на рис. В.3). В рассматриваемом примере число БЭС N = 3. В случае ШИМС длительности импульсов от такта к такту меняется по синусоидальному закону.
s |
s1 |
s2 |
s3 |
|
|
|
N=3; |
|
|||
|
|
|
|
||
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a) |
|
|
|
|
|
|
|
|
|
U1-3 |
|
U3=U3-3 |
|
|
|
U3-1 |
|
|
|
|
|
|
|
U1 |
U1-2 |
|
=3 |
|
|
|
|
||
|
|
|
|
|
|
U1-1 |
|
|
|
|
|
|
|
|
|
|
|
U3-2 |
|
U1=U1-1+U1-2+U1-3 |
U3=U3-1+U3-2+U3-3 |
|||
|
|
|
||
|
б) |
|
в) |
|
|
|
|
|
|
Рис. В.3
26
Особенности сигнала s(t):
M / 2
а) s(t) = sn (t) , то есть представляет последовательность из N = M/2 одина-
n 1
ковых, сдвинутых по фазе на угол T = / N биэлементарных сигналов (БЭС), следовательно, результирующие гармоники сигнала представляются геометрической суммой гармоник трех БЭС, сдвинутых по фазе на угол n n T , n ‒ порядковый номер БЭС. «Первый» БЭС (s1(t)) в структуре сложного сигнала показан затемнением (рис. В.3 а);
б) амплитуды гармоник элементарных импульсов определяются их высотой и относительной длительностью (характеристики сигнала № 3, табл. П.1);
в) амплитуда гармоники с номером k = 1 функции s(t) определяется геометрической суммой амплитуд гармоник составляющих функций с взаимным фазовым сдвигом T (рис. В.3 б, 0 / 6, T / N / 3) ;
г) амплитуды гармоник с номером k = 3,5, находятся по аналогии с п. В с учетом взаимного фазового сдвига суммируемых компонент k k T .
Пример. Сигнал ШИМП. А = 100 В, M = 6, D = Ти/0.5Т = 0.25:
a) вычисляем амплитуды гармоник с номерами k = 1,3,5 биэлементарного сигнала по формуле
Umk = |
4А |
sin(k |
D |
) находим: Um1 = |
100 |
4 |
sin( |
0.25 |
) 38.2 |
B ; |
||||||||||||
|
2 |
|
|
|
||||||||||||||||||
|
k |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||
Um3 = 100 |
4 |
|
|
sin(3 |
0.25 |
) 39.23 B ; |
Um5 = 100 |
|
4 |
|
sin(5 |
|
0.25 |
) 23.54 B ; |
||||||||
|
3 |
2 |
|
|
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
5 |
|
||||||||||
б) число биэлементарных импульсов N в сигнале s(t) равно трём, фазовый сдвиг между импульсами Т / N / 3, фазовый сдвиг первого импульса (его центра) относительно начала координат 0 / 2 / 6 ;
в) взаимный фазовый сдвиг гармоник с номером k смежных (двух «соседних») элементарных сигналов k k Т . Например, для k = 3 k 3 ,
для k = 5 k 5 = 5 / 6 и т. д.
С учетом изложенных замечаний на рис. В.3 б, в построены векторные диаграммы для гармоник с k = 1 и k = 3. Наглядно виден эффект увеличения амплитуды первой гармоники сигнала и сохранения неизменной значения амплитуды первой гармоники.
При переходе от ШИМП сигнала к ШИМС сигналу следует ожидать существенного снижения гармоник с номером k > 1. Строгое решение в этом случае находится по формуле [4].
|
|
|
N |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
k |
|
|
|
k |
|
|
|
4 |
2 |
|
|
|
|
|
|
|||||
Umk = |
|
[sin(m |
cos(n |
)) cos(n |
)], |
||||||||
|
|
|
|
||||||||||
|
k n |
|
N |
|
2N |
|
N |
|
N |
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
|
||||
где m ‒ коэффициент модуляции. В рассматриваемом примере следует принять m = 1.0.
27
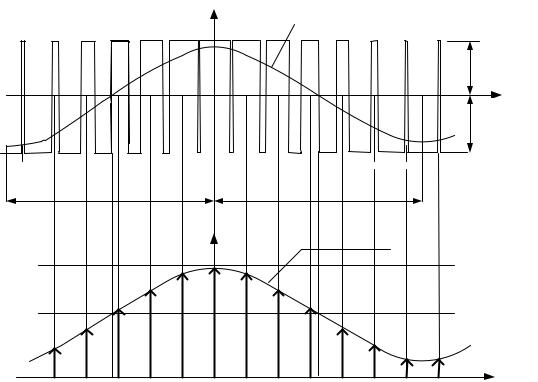
В.4. Ниже, на рисунке показан принцип формирования двухполярного импульсного сигнала с модуляцией длительности (ширины) импульсов по синусоидальному закону (ДШИМС [5]). Кратность тактовой частоты импульсов по отношению к основной частоте сигнала s(t) равна нечетному числу М. Нижний фрагмент рисунка показывает, что относительная длительность положительных импульсов сигнала пропорциональна множителю Dn = 0.5(1 + m cos(2πn/M), где m ‒ коэффициент модуляции (регулирования), n ‒ порядковый номер импульса в структуре сигнала. Значения Dn соответствуют длинам стрелок (выделены жирной линией) на графике D = f(t/Тт). График s1 в приближенном виде отображает ожидаемый уровень основной гармоники сигнала.
|
|
|
s |
|
|
s1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
E |
t/Tт |
|
|
|
|
|
|
|
|
|
|
|
|
-0.5(М-1) |
|
|
|
|
|
|
|
0.5(М-1) |
|
|
|
0.5M |
|
|
|
|
|
|
0.5M |
|
|
|
|
|
|
|
+D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.5(1+Smod) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.0 |
|
|
|
|
|
|
|
|
|
|
|
0.5 |
|
-5 -4 |
-3 -2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
t/Tт |
|
|
|
|
|
|||||||
При заданных значениях Е, m и М определить:
А. Амплитуду основной гармоники сигнала и её действующее значение. Б. Действующее значение сигнала (Sд).
В. Коэффициент искажения (Ки) и коэффициент гармоник (Кг).
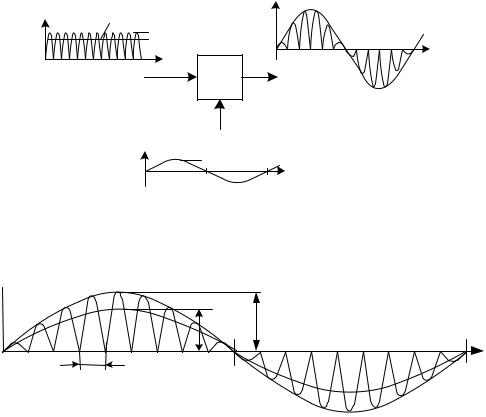
В.5. Сигнал s(t) сформирован перемножением пульсирующего сигнала s1(t) = Sm1│sin(2Nωо t)│и гармонического сигнала s2(t) = sin( ωо t) с единичной амплитудой (рис. В.5 а), где ωо ‒ круговая частота гармонического сигнала s2(t), N ‒ кратность отношения длительности половины интервала полупериода s2(t) к тактовой длительности последовательности импульсов (Тт), образующих сигнал s1(t). Индексом So на графике обозначено среднее значение (постоянная составляющая) сигнала s1(t). Пунктиром показаны огибающая сигнала s(t) с амплитудой А, связанная с «высотой» импульсов s1(t) и ожидаемая диаграмма первой гармоники выходного сигнала с амплитудой S(m1).
28
s1 |
|
|
|
s |
so |
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
t |
|
t |
|
|
х |
|
|
|
s1 |
|
s |
|
|
|
|
||
|
|
|
|
s2 |
|
s2 |
|
|
|
|
|
Sm=1.0 |
||
|
|
|
|
t |
а)
 s
s
S(m1) A N=0.5T/Tт=9
Тт |
0.5Т |
Т |
t |
|
|||
|
|
в) Рис. В.5
Докажите или опровергните следующие утверждения:
А. Амплитуда первой гармоники выходного сигнала S(m1) определяется величиной среднего значения So сигнала s1(t). Вычислите величину S(m1) при заданных значениях.
Б. Ближайшие паразитные гармоники (гармоники искажения) имеют частоты ωн = ωо(N ‒ 1) ωв = ωo(N + 1), а их амплитуды равны между собой. Определите ожидаемую величину амплитуд гармоник.
В. Действующее значение сигнала s2 совпадает с действующим значением функции, огибающей сигнал s(t). Вычислите величину действующего значения сигнала.
Примечание:
1. Решение задачи во многом совпадает с рассмотренным выше примером П.2.8. Отличия обусловлены только спецификой спектрального состава сигнала s1(t) (Uo = 2A/π; Umk = 2A/(k² ‒ 1).
2. В качестве иллюстрации к задаче в приложении № 2 показан пример моделирования «похожего» сигнала и его спектральной диаграммы.
29
Список литературы
1.Дмитриков В.Ф., Тонкаль В.Е., Островский М.Я. Теория Ключевых Фор-
мирователей гармонических колебаний. ‒ Киев: Наукова Думка, 1993.
2.Гоноровский И.С. Радиотехнические цепи и сигналы. ‒ М.: Радио и связь,
1986 .
3.Сергиенко А.Б. Цифровая обработка сигналов : Учебник для вузов. ‒ Санкт-Петербург: Питер, 2002.
4.Баскаков С.И. Радиотехнические цепи и сигналы. ‒ М.: Высшая школа,
1983.
5.Косулина Н.Ю., Козляев Ю.Д. Инверторы напряжения для источников бесперебойного питания : Учебное пособие. ‒ Новосибирск: СибГУТИ, 2010.
30
