
567_Kozljaev_JU._D._SAbornik_zadach_i_uprazhnenij_po_kursu_EHlektropitanie_
.pdfФедеральное агентство связи
Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования
«Сибирский государственный университет телекоммуникаций и информатики» (ФГОБУ ВПО «СибГУТИ»)
Ю.Д. Козляев
СБОРНИК ЗАДАЧ И УПРАЖНЕНИЙ ПО КУРСУ «ЭЛЕКТРОПИТАНИЕ УСТРОЙСТВ
И СИСТЕМ ТЕЛЕКОММУНИКАЦИЙ»
Учебно-методическое пособие
НОВОСИБИРСК 2015
УДК 621.31(07)
Козляев Ю.Д. Сборник задач и упражнений по курсу «Электропитание устройств и систем телекоммуникаций» : Учебно-методическое пособие. – Новосибирск: Изд-во СибГУТИ, 2015. – 82 с.
Учебно-методическое пособие содержит вводные замечания, справочные материалы и методические указания к решению задач, контрольные задачи. Пособие ориентировано на студентов разных уровней обучения (бакалавров, специалистов, магистров), изучающих базовые разделы дисциплины «Силовая электроника» и её специальные приложения, вошедшие в учебный курс «Электропитание устройств и систем телекоммуникаций» (ЭПУСТ).
Кафедра радиотехнических устройств
Список литературы – 17 наименований
Рецензент: канд. техн. наук Резван И.И.
Утверждено редакционно-издательским советом СибГУТИ в качестве учебно-методического пособия.
©Козляев Ю.Д., 2015
©Сибирский государственный университет телекоммуникаций и информатики, 2015
СОДЕРЖАНИЕ |
|
Введение………………………………………………………………………. |
5 |
ЧАСТЬ 1. Электрические сигналы. Основные характеристики |
|
сигналов………………………………………………………………………. |
6 |
1.1. Количественные характеристики сигналов…………………………. |
6 |
1.2. Показатели качества сигналов……………………………………….. |
9 |
1.3. Аппроксимация сигналов. Критерии аппроксимации……………… |
10 |
2. Примеры задач и пояснения к их решению……………………………… |
11 |
3. Контрольные задачи……………………………………………………….. |
18 |
3.1. Задачи тестового уровня……………………………………………… |
18 |
3.2. Задачи повышенной сложности……………………………………… |
21 |
3.3. Задачи высокого уровня сложности…………………………………. |
24 |
Список литературы…………………………………………………………... |
30 |
Приложения…………………………………………………………………… |
31 |
П.1. Таблица параметров распространенных сигналов………………… |
31 |
П.2. Пример результата моделирования сложного сигнала…………….. |
33 |
П.3. Таблицы вариантов заданий…………………………………………. |
34 |
ЧАСТЬ 2. Источники электрической энергии. Рабочие характеристики |
|
источников…………………………………………………………………….. |
37 |
1. Полная мощность переменного тока. Составляющие полной |
|
мощности потребления……………………………………………………….. |
37 |
2. Основные энергетические характеристики и показатели источников |
|
питания............................................................................................................. |
38 |
3. Источники переменного тока……………………………………………... |
43 |
4. Источники постоянного тока……………………………………………… |
45 |
4.1. Аккумуляторы, аккумуляторные батареи свинцового типа………... |
45 |
4.2. Общая характеристика промышленных аккумуляторов…………... |
48 |
4.3. Примеры задач по теме п. 4.1………………………………………… |
49 |
4.4. Солнечные элементы и батареи……………………………………… |
51 |
4.5. Примеры задач по теме п. 4.4………………………………………… |
52 |
5. Контрольные задачи................................................................................... |
55 |
Приложения…………………………………………………………………… |
59 |
П.1. Справочные параметры промышленных аккумуляторов |
|
и аккумуляторных батарей............................................................................. |
59 |
П.2. Справочные параметры солнечных батарей серии SY для систем |
|
питания напряжением 12, 24 В……………………………………………… |
62 |
ЧАСТЬ 3. Элементы систем распределения электрической энергии. |
|
Показатели энергопотребления……………………………………………… |
64 |
3.1. Структура построения систем электропитания предприятия……… |
64 |
3.2. Приборы и устройства коммутации тока........................................... |
66 |
3.3. Показатели качества и эффективности электропотребления……… |
69 |
3.4. Типовые примеры задач и пояснения к их решению......................... |
71 |
3.5. Контрольные задачи…………………………………………………... |
73 |
3 |
|
Приложения…………………………………………………………………… 77
1.Справочные параметры коммутирующих приборов……………………. 77
2.Определение сопротивления цепи при оценке тока короткого
замыкания........................................................................................................ |
78 |
|
3. |
Плавкие предохранители............................................................................ |
79 |
4. |
Таблица обозначений элементов систем электропитания........................ |
80 |
Список литературы…………………………………………………………… |
81 |
|
4
ВВЕДЕНИЕ
Особенность курса «Электропитание устройств и систем телекоммуникаций» (ЭПУСТ) обусловлена широким вовлечением знаний из ряда общеобразовательных и профессиональных дисциплин (физики, теории линейных и нелинейных электрических систем, радиотехники, электронной и микроэлектронной техники, силовых полупроводниковых приборов и др.). Это связано, в частности, с широким использованием в современных технологиях преобразования электрической энергии в источниках питания приемов и методов преобразования радиотехнических сигналов. Не менее сложным аспектом изучения дисциплины является практическая направленность курса, при этом понятия эффективности, надежности технических решений, качества электропитания оборудования телекоммуникационного комплекса сопряжены как с нормативными ограничениями, так и с необходимостью существенных капитальных вложений для их реализации. Многие из перечисленных проблем изучаются в теоретическом курсе ЭПУСТ, на лабораторных и практических занятиях.
Настоящее пособие является первым из планируемой серии и концентрирует внимание на задачах, рассматриваемых в учебном курсе, знакомит студентов с кругом ожидаемых научно-технических проблем и методах их решения. Каждый раздел пособия предварен краткими теоретическими выкладками и ссылками на литературу, обсуждающую подобные задачи.
Тематика задач соответствует программе учебного курса. Сложность контрольных задач ранжирована по уровням, соответствующим задачам и целям обучения:
А ‒ ориентирован на проверку и активизацию базовых знаний, необходимых для изучения курса или определенного раздела.
Б ‒ ориентирован на проверку и закрепление знаний изучаемого раздела.
В‒ повышенной сложности, требующий знания смежных разделов, привлечения методов математического анализа или методов компьютерного моделирования.
Вприложениях изложены справочные данные, необходимые для решения некоторых типов задач.
5
ЧАСТЬ 1. ЭЛЕКТРИЧЕСКИЕ СИГНАЛЫ
СИГНАЛЫ. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СИГНАЛОВ
Под сигналом понимается функциональная зависимость явлений и процессов различной физической природы. В преобразовательной технике сигналами отображают процессы в электрических и энергетических системах. В приложении к задачам электротехники термином «сигнал» будем определять временные зависимости определенных физических процессов, связанных с передачей энергии. В пособии рассматриваются детерминированные аналоговые периодические сигналы, обозначаемые в общем случае индексом s(t). В технике электропитания ими описывают напряжения, токи, мощность, освещенность, потоки тепла или другие носители энергии. Характеристики сигнала жестко определяют качественные и количественные показатели эффективности передачи и преобразования энергии. Именно этими особенностями обусловлена актуальность изучаемой темы [1].
1.1. Количественные характеристики сигналов
А. Среднее значение или постоянная составляющая сигнала (So):
|
|
t Т |
|
So |
1 |
x s(t)dt. |
|
T |
(1.1) |
tx
Так как интеграл определяет значение площади (S), ограниченной функцией s(t) на интервале периода Т, то для ряда сигналов очевидны следующие соотношения:
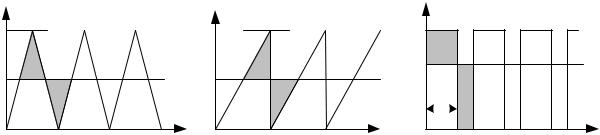
1.Треугольный (пилообразный) сигнал (рис.1.1 а, б): S = 0.5AT, So = 0.5A.
2.Импульсный сигнал прямоугольной формы (рис.1.1 в) с относительной длительностью импульсов D = Tи/Т: S = ATи , So = ATи/T = AD.
s |
|
A |
|
|
So |
0 |
T |
|
|
|
a) |
|
s |
|
|
s |
|
|
|
|
A |
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
So |
|
|
|
So |
|
|
|
|
|
|
|
|
DT |
|
t |
0 |
T |
t |
0 |
T |
t |
|
||||||
|
|
б) |
|
|
|
в) |
Рис.1.1. Импульсные сигналы с отображением уровня постоянной составляющей So (пунктирная линия)
6
3.Среднее значение знакопеременного сигнала равно нулю при условии равенства площадей положительной и отрицательной полуволны.
4.В ряде случаев сложный сигнал s(t) может быть представлен комбинаци-
ей (суммой) «простейших* или элементарных» сигналов Sn(t) при этом
N
So Son , где N ‒ число элементарных сигналов в структуре s(t).
n 1
5.Графически уровень среднего значения отображается линией So таким
образом, чтобы площади отсеченных фрагментов s(t) ‒ So и Sо ‒ s(t) (на рис. 1.1 они обозначены затемнением) были равны. В ряде случаев такой прием позволяет ориентировочно оценить ожидаемую величину среднего значения сложного сигнала.
Б. Амплитуды гармонических составляющих сигнала, обладающего свойством четности (s(-t) = s(t)):
|
2 |
0.5Т |
|
4 |
0.5T |
|
|
|
Smk |
|
s(t)cos(k t)dt |
|
s(t) cos(k t)dt, |
(1.2) |
|||
Т |
T |
|||||||
|
0.5Т |
|
0 |
|
|
|||
|
|
|
|
|
|
|||
где k ‒ порядковый номер гармоники, Т ‒ период, |
2 / Т ‒ круговая частота |
|||||||
сигнала.
|
|
|
|
s1 |
|
|
|
|
s |
|
|
|
|
A1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
So1 |
|
A1 |
|
|
|
T |
|
|
|
|
|
|
So |
|
|
|
|
|
|
|
|
|
|
|
|
|
A2А2 |
|
0 |
T1 |
T |
t |
|
|
|
|
||||
|
|
|
|
s2 |
|
||
|
|
|
|
A2 |
|
|
|
|
|
|
|
|
|
|
|
0 |
T1 |
T2 |
T |
t |
|
So2 |
|
|
|
|
|||||
|
|
|
|
0 |
T1 |
T2 |
t |
|
|
|
|
|
|||
|
|
|
|
а) |
|
|
|
s |
|
|
|
s1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
So1 |
|
|
|
|
So |
|
|
|
|
|
|
|
t |
|
s2=-So2 |
|
|
|
|
|
б) |
|
|
|
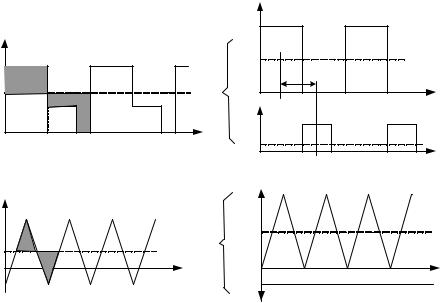
Рис.1.2. Примеры представления сложных сигналов суммой «элементарных»
__________________________________________________________________
*Термин «простейший сигнал» введен И.С. Гоноровским. Анализ прямоугольного, треугольного, пилообразного сигналов рассмотрены в [2].
7

В ряде случаев амплитуда k-й гармоники «сложного» сигнала, представленного суммой элементарных (ЭС), может быть найдена как сумма амплитуд гармоник ЭС с учетом их взаимного фазового сдвига k .
Так, например, сигналы s1 (t), s 2 (t) (рис. 1.2 а), сдвинуты во времени наT 0.5T1 0.5(T 2 T1) 0.5T2 . Следовательно, взаимный фазовый сдвиг гармоник с номером k двух сигналов равен k 2 k T / T. Примеры решения подобных задач будут рассмотрены ниже.
В. Энергетические показатели периодического сигнала
В общей теории сигналов термины «энергия и мощность сигнала» используется как показатели сравнения сигналов с различной формой, поэтому в теории сигналов исключают из рассмотрения резистор нагрузки, на котором выделяется энергия или, точнее, по умолчанию принимают R = 1.0. В электротехнике обсуждаются задачи количества, качества и эффективности передаваемой потребителю энергии и мощности. Для того чтобы отличать показатели мощности или энергии сигнала от энергии или мощности, передаваемых в нагрузку, обозначения первых будем дополнять индексом «s» (ES, PS). Заметим также, что с формальных позиций по указанной выше причине размерности мощности и энергии в электрических цепях (Вт, Вт с ) отличаются от соответствующих размерностей показателей сигнала (В 2 , В 2 с ‒ для сигнала напряжения и А 2 , А 2 с ‒ для сигнала тока [2]).
Энергия за время Т и мощность сигнала определяются соотношениями:
t1 |
T |
|
1 |
t1 |
T |
|
ES= s2 (t)dt; |
РS= |
|
s2 (t)dt. |
(1.3) |
||
T |
|
|||||
|
t |
|
|
t |
|
|
|
1 |
|
|
|
1 |
|
Из (1.3) следует, что только для знакопеременного прямоугольного сигнала c высотой импульсов равной А и постоянного сигнала s(t) = A значения ЕS и РS равны максимальной величине А 2 Т и А 2 соответственно.
Г. Действующее (среднеквадратическое или эффективное) значение сигнала (Sд) определяется выражением:
|
1 tx t |
|
|
|
Sд = |
Т |
|
s(t)2dt. |
(1.4 а) |
|
|
t |
|
|
|
|
x |
|
|
С учетом равенства Парсеваля [2,5] действующее значение может быть выражено через гармонические компоненты сигнала, полученные разложением s(t) в ряд Фурье:
|
|
|
|
Sд = So2 0.5 Smk2 , |
(1.4 б) |
||
|
k 1 |
|
|
где So, Smk ‒ постоянная составляющая и амплитуда гармоники с номером k, соответственно. В преобразовательной технике распространены сигналы без постоянной составляющей (So = 0), а гармоническая составляющая с порядковым
8

номером k = 1 является основной. В таких случаях расчетное выражение для действующего значения удобно представлять в виде:
|
Sm1 |
|
2 |
|
|
||
Sд= |
|
Smk |
Sд1 K Г . |
(1.4 в) |
|||
|
|
|
2 |
||||
2 |
|
||||||
|
|
k 2 |
Sm1 |
|
|
||
Введенный в выражение коэффициент Кг (коэффициент гармоник) учитывает «вклад» гармонических составляющих с номером k > 1 в увеличение Sд по отношению к действующему значению первой гармоники Sд1.
Из (1.4) следует:
1. Для сложного сигнала, представимого суммой N «неперекрываемых» элементарных сигналов (НЭС), величина Sд определяется «квадратической» суммой действующих значений ЭС:
N |
|
Sд = Sд2(т) . |
(1.4 г) |
т 1 |
|
Таким образом, НЭС обладают свойством ортогональности [3]. |
|
2.Действующие значения сигнала s1(t) и его модуля s2(t) = s1 (t) равны.
3.Действующее значение «постоянного» сигнала s(t) = А равно А.
Д. Амплитуда сигнала (Sm) определяет его наибольшее значение. Примеры распространенных в технике электропитания сигналов и их пока-
затели при единичной амплитуде (Sm = 1.0) приведены в приложении к разделу (табл. П.1).
1.2. Показатели качества сигналов (ПКС)
ПКС позволяют сравнивать сигналы по ряду критериев с целью анализа и выбора наилучшего варианта при решении конкретной технической задачи. Ряд показателей количественно иллюстрируют различия сопоставляемых сигналов, отличающихся по форме.
Основные ПКС:
Коэффициент формы: Кф = Sд/So(0.5Т), где Sд ‒ действующее значение сигнала, So(0.5Т) ‒ среднее значение сигнала на интервале полупериода.
Коэффициент амплитуды: Ка = Sm/Sд.
Коэффициент искажения: Ки = Sд(1)/Sд, где Sд(1) ‒ действующее значение первой гармоники сигнала.
Коэффициент гармоник:
|
|
|
|
|
2 |
|
|
|
1 |
|
|
Sд |
|
||
|
2 |
|
|
||||
Кг = |
|
|
Sk |
= |
|
1. |
|
|
|
2 |
|||||
S1 |
|||||||
|
|
k 2 |
|
Sд(1) |
|
||
9

Очевидно, коэффициент гармоник сигнала «жестко» связан с показателем
|
|
|
|
|
|
Ки: Кг = |
1 |
1 . |
|||
К |
2 |
||||
|
|
|
|||
|
И |
|
|
||
|
|
|
|
||
Примеры значений ПКС простейших сигналов:
Синусоидальный сигнал: Кф = 1.1, Ка = 1.41, Ки = 1.0, Кг = 0.
«Прямоугольный синус» (меандр): Кф = 1.0, Ка = 1.0, Ки = 1.225, Кг = 0.47.
«Треугольный синус» (табл. П.1, сигнал № 5 при То = 0.5Т): Кф = 1.154, Ка = 1.733, Ки = 0.997, Кг = 0.0953.
1.3. Аппроксимация сигналов. Критерии аппроксимации
При решении инженерных задач часто возникает проблема замены (аппроксимации) сложного сигнала s(t) более простым и удобным для анализа (h(t)). В этом случае возникает задача оценки и допустимости погрешности аппроксимации. В зависимости от решаемой задачи могут быть использованы критерии ошибки первого порядка и второго порядка [3]. В первом случае сигналы сопоставляются по интегральной величине разности модулей сигналов («площадь» ошибки) или усредненной величине ошибки ( 1 ) за время Т:
Т |
|
|
||||||||
1 [ |
|
s(t) |
|
|
|
h(t) |
|
]dt (S0 H0 )Т , |
1 = 1 /Т. |
(1.5 а) |
|
|
|
|
|||||||
|
|
|
|
|||||||
0 |
|
|
|
|
|
|
|
|
|
|
Во втором случае критериями могут служить «квадратическая» ошибка аппроксимации сигнала ( 2 ) или её средне квадратическое значение ( 2 ) :
|
Т |
|
|
|
|
2 |
{ [s(t) h(t)]2 dt}1/ 2 , |
|
|
|
|
2 = 2 / Т . |
(1.5 б) |
||||
|
0 |
|
|
|
|
Выражения (1.5) применимы как для сигналов с равными периодами, так и для сигналов с кратными периодами. Во втором случае интервал интегрирования «Т» соответствует периоду сигнала с меньшей частотой. Таким образом, низкочастотный сигнал, например s(t), сопоставляется с ансамблем из k фрагментов сигнала h(t) , где k = Ts/Th кратность периодов сигналов (рис. 1.3).
10
