555_Innovatsii_inauchno-tekhnicheskoe_tvorchestvo_molodezhi2014_

результаты, чем нечёткая система оценки недвижимости FuzzyExtent. А система в целом, поможет пользователю получить быструю и независящую от риелтора оценку недвижимости.

РАЗРАБОТКА ПРИЛОЖЕНИЯ РАСПОЗНАВАНИЯ ОБРАЗОВ С ИСПОЛЬЗОВАНИЕМ МЕТОДОВ СТОХАСТИЧЕСКОЙ ГЕОМЕТРИИ И ФУНКЦИОНАЛЬНОГО АНАЛИЗА

(по работам Федотова Н.Г.)

Халяпин К.И. НГТУ, Новосибирск

e-mail: kirill.halypin@gmail.com, alex1207@ngs.ru

Научный руководитель – Попов А.А., профессор НГТУ

Целью данной работы является создание приложения основанного на теории признаков распознавания образов с позиции стохастической геометрии и функционального анализа. Разработка ведется с ориентацией на возможность использования данного приложения для решения широкого спектра задач распознавания на персональных компьютерах.

В модуле предварительной обработки в качестве алгоритма сегментации мною был выбран метод, основанный на пороговой бинаризации изображения. Алгоритм автоматически находит оптимальный порог бинаризации, на основе дискриминантного критерия [3]. Данный метод рассмотрен применительно к двум классам или типам участков, из которых состоит изображение с распределением w x , где 0 x 255 значение пикселя. Причем, существует оптимальная граница x0 , разделяющая эти участки наилучшим образом в некотором смысле. Данная граница считается оптимальным порогом бинаризации и в качестве нее берется максимум межклассовой дисперсии, т.е.

x0 argmax B2 x0* , где x0* – величина пробного порога, разбивающего

x0*

изображение на классы.

Данный метод используется мною с рядом модификаций. Для компенсации нестационарности был введен алгоритм пороговой бинаризации со скользящим окном, при котором рабочая область охватывает не все изображение, а некоторое окно радиусом r .Каждое новое положение рабочей области отличается от предыдущего только на один шаг по строке или по столбцу. Находимый на каждом шаге оптимальный порог относится к центральной точке текущей области. Таким образом, порог изменяется в каждой точке изображения, причем эти изменения имеют характер, сопоставимый с характером нестационарности самого изображения.

Однако процедура обработки значительно усложняется, поэтому для повышения скорости работы был введен алгоритм пороговой бинаризации с прыгающим окном, когда окно рабочей области перемещается по изображению на несколько шагов. Порог в «пропущенных» точках определяется с помощью

371

интерполяции (в данном случае линейной) значений порога по его найденным значениям в ближайших точках.

Также в реализацию включен алгоритм медианной фильтрации и фильтрации методом скользящего среднего с возможностью установки веса обрабатываемого пикселя. Оба алгоритма достаточно просты в реализации и дают неплохие результаты в подавлении разного рода шумов (шум «соль и перец», импульсный шум, гауссов шум), а также сглаживании контуров. К тому же медианный фильтр обладает устойчивостью к выбросам и может быть применен после бинаризации исходного изображения.

Для выделения объектов (разбиения изображения) применяется метод, основанный на рекурсивной функции разметки произвольной замкнутой области изображения. Таким образом, на входе модуля распознавания мы получаем ряд объектов, каждый из которых обладает оригинальной меткой.

Описанный метод сегментации может быть применен для широкого спектра задач, таких как выделение различных печатных знаков, информативных областей лица, в медицинской и технической диагностике, геологии, биометрии и т.д.

Для распознавания объектов планируется использовать группу признаков называемых триплетными признаками, характерной особенностью которых

интенсивности описывающей изображение. В данном случае, функция F – это некоторое бинарное изображение, полученное после сегментации.

Основой для формирования признаков распознавания является введенное новое геометрическое trace–преобразование[1], связанное со сканированием изображения линиями по случайным направлениям.

Функционал называется trace–функционалом и применяется к изображению. Для каждой прямой он дает число индексированное и зависящее от двух параметров , , нормальных координат сканирующей прямой L , . В случае сканирования изображения данные параметры являются дискретными, поэтому в итоге мы получаем trace–матрицу. По столбцам параметр (расстояние, изменяющееся на интервале R R), по строкам параметр (угол наклона прямой, изменяющееся на интервале0 2 ). В данной работе решено применить следующие функционалы для бинарных изображений:

Суммарная длина всех отрезков, которые порождает прямая на изображении.

Максимальная длина из всех отрезков, которые порождает прямая на изображении. На рисунке максимальной длиной будет обладать отрезок t1,t2 .

372

Литература:

1.Федотов Н.Г. Методы стохастической геометрии в распознавании образов. – М.: Радио и связь, 1990. – 144 с.

2.Федотов Н.Г. Теория признаков распознавания образов на основе стохастической геометрии и функционального анализа. – М. :Физматлит, 2009.

– 304 с.

3.Грузман И.С., Киричук В.С., Косых В.П., Перетягин Г.И., Спектор А.А. Цифровая обработка изображений в информационных системах: Учебное пособие.- Новосибирск: Изд-во НГТУ, 2002. - 352 c.

АЛГОРИТМЫ СТЕГОАНАЛИЗА ИЗОБРАЖЕНИЙ

Шевчук П.П. НГТУ, Новосибирск

Научный руководитель – Попов А.А., профессор НГТУ

Исследование проблем разработки, совершенствования и применения методов защиты информации в процессе её хранения и передачи привлекает внимание множества исследователей.

В современных системах защиты информации огромную роль играет стеганография. Классическая задача стеганографии – скрыть факт передачи сообщения. Указанная задача стеганографии решается посредством внедрения сообщений в объекты данных, называемые контейнерами. Обратная задача стеганографии называется стегоанализом. Стегоанализ, в первую очередь, направлен на выявление наличия скрытых сообщений в контейнерах.

Один из наиболее активно используемых и исследуемых видов контейнеров – это цифровые изображения. Одним из самых простых и распространенных методов встраивания сообщений в цифровые изображения является метод замены младших бит (LSB replacement). В этом методе младшие биты каждого элемента контейнера заменяются на биты сообщения. Задача стегоанализа данного стеганографического преобразования является актуальной в настоящее время.

При замене младшего бита цветовой компоненты очередного пикселя контейнера на очередной бит стегосообщения статистика контейнера изменяется.

Яркость одной цветовой компоненты изображения в формате BMP может принимать значения от 0 до 255. В двоичной системе исчисления – от 0000 0000

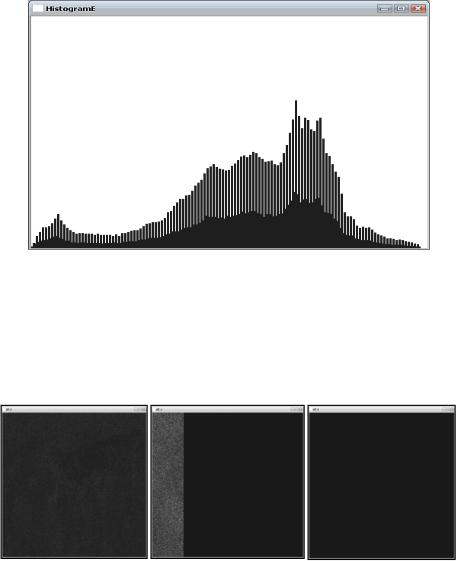
до 1111 1111. Пары соседних значений яркости: 0000 0000-0000 0001, 0000 0010-0000 0011, …, 1111 1100-1111 1101, 1111 1110-1111 1111 – отличаются друг от друга только в младшем бите. Вероятности появления каждого значения из пары в пустых контейнера существенно различаются. В случае стеганографического встраивания количество пикселей в парах выравнивается. Данный факт можно использовать для построения статистического теста хиквадрат. Для повышения эффективности это метод может быть применен к частям изображения.

374

Тогда общее описания алгоритма будет выглядеть следующим образом: Каждую цветовую компоненту исходного изображения разбиваем на

непересекающиеся прямоугольные блоки достаточной величины.

Для каждого блока строим эмпирическую (по данной области изображения) гистограмму, а также теоретическую гистограмму на основе эмпирической по следующим формулам:

,

,

где – число пикселей той яркости эмпирической гистограммы, – число пикселей ой яркости эмпирической гистограммы.

Для каждого блока сравним схожесть теоретической и эмпирической гистограмм с помощью статистики хи-квадрат.

Теоретическая и эмпирическая гистограммы считаются схожими, если полученное эмпирическое значение статистики хи-квадрат меньше теоретического значения статистики хи-квадрат при заданном уровне значимости и количестве степеней свободы N.

Если данное неравенство справедливо, то мы обнаружили встраивание в проверяемый блок.

Исследования реализованного алгоритма проводились на изображении в формате BMP, размером 800*600 пикселей. Приведем график зависимости процента изображения, в котором обнаружилось встраивание, от количества разбиений изображения (рисунок 1) при наполненности контейнера на 98%, 40% и 0%. Как мы видим из графика, при слишком больших и слишком малых разбиениях контейнеры оказываются статистически неотличимыми друг от друга.

Рисунок 1 - График зависимости для G-канала изображения.

375

В ходе исследований также были получены результаты, которые не согласуются с положениями о распределении яркостей пикселей в заполненном контейнере. Так, например, если встраиваемое сообщение представляет собой многократно повторяющуюся символьную последовательность, то вид гистограммы значительно меняется. Соседние яркости не выравниваются, а дублируются с точностью до некоторого значения (рисунок 2).

Рисунок 2 - Эмпирическая гистограмма распределения яркостей для G-канала изображения.

Так же было проведено исследование стегоаналитического алгоритма на основе известного пустого контейнера. Его суть заключается в попиксельном сравнении контейнера-оригинала и контейнера-результата. При обнаружении различий в пикселях детектируется встраивание (рисунок 3).

Рисунок 3 - Изображение R-, G-, B-каналов (слева направо) при наполненности контейнера на 40%.

Таким образом, в рамках проделанной работы был разработан и исследован стегоаналитический метод с использованием критерия хи-квадрат, а также алгоритм с использованием известного пустого контейнера для цифровых изображений в формате BMP. Были получены зависимости процента обнаруженной скрытой информации от числа разбиении изображения. Была обнаружена зависимость вида гистограммы от вида встраиваемой информации. Результаты данной работы могут быть применены для улучшения методов стеганографии и стегоанализа, а также методов защиты информации в целом.

376

Литература:

1.Барсуков В.С. Компьютерная стенография вчера, сегодня, завтра. / Барсуков В.С., Романцов А.П. // Специальная техника. – 1998. – № 4-5. – С. 6-7.

2.Грибунин В.Г. Цифровая стеганография / Грибунин В.Г., Оков И.Н., Туринцев И.В. – М : "Солон-Пресс", 2002. – 272 с.

3.Конахович Г.Ф. Компьютерная стеганография. Теория и практика. / Конахович Г.Ф., Пузыренко А.Ю.. – К.: "МК-Пресс", 2006. – 288 с.

ЭФФЕКТИВНЫЕ МОДИФИКАЦИИ АЛГОРИТМА КЛАССИФИКАЦИИ KNN (МЕТОД K БЛИЖАЙШИХ СОСЕДЕЙ)

Щербакова А.А. НГТУ, Новосибирск

e-mail: anastasNSK@gmail.com, тел.: (913) 759-93-85

Научный руководитель – Попов А.А., профессор НГТУ

Введение.

Внастоящее время широко используются задачи распознавания образов, которые, по существу, представляют собой дискретные аналоги задач поиска оптимальных решений. Однако интерес представляет более широкий класс задач, в которых требуется установить, обладают ли изучаемые объекты конечным набором свойств, позволяющим отнести их к определенному классу.

Втаких задачах (задачи распознавания и классификации) используются методы классификации. Аналогичная информация о конечном множестве служит для выяснения, в какой области из множества областей через определенный период времени будут находиться процессы – задача прогнозирования.

Автоматизация функций распознавания, классификации и прогнозирования являются актуальными задачами для автоматизации процессов принятия решения.

Анализ проблемы.

Определим понятие «задача классификации». Задача разбиения множества объектов или наблюдений на априорно заданные группы, называемые классами, внутри каждой из которых они предполагаются похожими друг на друга, имеющими примерно одинаковые свойства и признаки, называется задачей классификации.

Внастоящее время классификация применяется при определении лояльности клиентов, при оценке кредитоспособности заемщиков, распознавании образов, медицинской диагностике и многих других приложениях. Если аналитику известны свойства объектов каждого класса, то когда новое наблюдение относится к определенному классу, данные свойства автоматически распространяются и на него.

Существует большое множество алгоритмов, реализующих методы классификации. Как один из методов классификации, метод k ближайших соседей (kNN – k nearest neighbors), очень прост для понимания: близкие точки

377

похожи. Но такая «формулировка» требует пояснения. Что значит близки? Здесь появляется понятие метрики: евклидово расстояние, косинусная мера, расстояние Махаланобиса, Кульбака-Лейблера и т.д. Что значит похожи? Необходимо выбрать критерий схожести: близкие значения целевой функции, возможности простой аппроксимации, схожее распределение и т.д. Что значит точки? Это могут быть точки из обучающей выборки, центроиды классов, прочие прототипные точки.

Вдальнейшем необходимо осуществить оптимизацию вычислительной сложности алгоритма для повышения скорости обработки больших объемов данных.

Постановка задачи исследования.

Формально классификация производится на основе разбиения пространства признаков на области, в пределах каждой из которых многомерные векторы рассматриваются как идентичные. Другими словами, если объект попал в область пространства, ассоциированную с определенным классом, он к нему и относится.

Целью исследования является отбор наиболее эффективных модификаций алгоритма классификации kNN как по времени, так и по точности.

Метод kNN реализован в виде алгоритма, принцип работы которого заключается в отнесении элемента выборки к такому классу, к которому относится наибольшее количество k соседей данного элемента из обучающей выборки.

Вкачестве одной из модификаций алгоритма является взвешенное голосование – каждый сосед данного элемента имеет свой вес (степень важности) при голосовании. Разнообразный выбор весовой функции позволяет выбрать наилучший вариант для выборки.

Также результат классификации зависит от выбора числа k соседей. При этом крайние значения k не показывают хороший результат. И это объяснимо – при k=1 алгоритм неустойчив к шумовым выбросам: он дает ошибочные классификации не только на самих объектах-выбросах, но и на ближайших к ним объектах других классов. При k=m, где m – количество наблюдений в выборке, алгоритм чрезмерно устойчив и вырождается в константу. Поэтому, значение параметра k определяется по критерию скользящего контроля, а именно – методом исключения объектов по одному (LOO – leave-one-out).

Существует несколько проблем при работе с методом k ближайших соседей. Во-первых, отсев шума (выбросов). Среди объектов обучения могут быть типичные представители классов (эталоны); объекты, плотно окруженные объектами того же класса, и если их удалить из выборки, это практически не скажется на качестве классификации (неинформативные); объекты, окруженные объектами чужого класса (шумовые выбросы). Если учитывать принадлежность каждого объекта к эталону, неинформативному объекту и

шумовому выбросу, то качество классификации улучшается.

При сверхбольших выборках (m >> 103) возникают чисто технические проблемы: необходимость хранить большой объем данных, скорость нахождения k ближайших соседей. Но у этой проблемы есть два способа

378

решения. Во-первых, прореживание выборки путем выбрасывания неинформативных объектов и шумовых выбросов. Во-вторых, применение специальных индексов и эффективных структур данных для быстрого поиска k ближайших соседей (например, kd-деревья).

Т.к. основополагающим критерием отнесения объекта к определенному классу является расстояние, то возникает проблема выбора метрики. Первое, что приходит в голову – это евклидова метрика. Но эта метрика не гарантирует нам «идеального случая». При этом, необходимо помнить, что все признаки должны быть измерены «в одном масштабе», а еще лучше – отнормированы. Но и нормировка остается сомнительной эвристикой, т.к. остается вопрос: разве все признаки одинаково значимы и должны учитываться с одинаковым весом?

Имеет место проблема проклятия размерности, если признаков слишком много. Получается, что в пространстве высокой размерности все объекты примерно одинаково далеки друг от друга; выбор числа k ближайших соседей становится практически произвольным. Такую проблему можно решить только путем отбора небольшого количества информативных признаков, по мнению эксперта, и построения опорных множеств признаков.

Выводы.

Вработе проведено исследование методов классификации: kNN и его модификаторы. Осуществлен выбор наиболее эффективных модификаторов. Такими модификаторами являются kNN с взвешенным голосованием и Fuzzy kNN.

Вкачестве обучения в работе предусмотрено запоминание обучающей выборки с предварительным отсевом неинформативных объектов и шумовых выбросов, а также с выделение эталонных объектов каждого класса.

379