
555_Innovatsii_inauchno-tekhnicheskoe_tvorchestvo_molodezhi2014_
.pdfПриведём далее особенности программной реализации разработанного демонстрационного приложения. Был выбран язык разработки C#, так как именно он позволяет наиболее полно раскрыть возможности выбранной облачной платформы, без необходимости углубления в особенности реализации сервиса Live Connect. Демонстрационное приложение имеет графический интерфейс.
Помимо вышеуказанного, платформа Microsoft .NET Framework 4.5 позволяет с лёгкостью использовать асинхронные процедуры при взаимодействии пользователя с графическим интерфейсом. Для разработки также необходим пакет Live SDK.
С точки зрения проектирования, приложение разработано с применением шаблона проектирования «Модель-Представление-Контроллер» (англ. MVC) [6]. Также учитывались рекомендации, изложенные в [7] и [8].
Литература:
1.Frank Gens. IDC’s New IT Cloud Services Forecast: 2009-2013 // IDC. 2005. Дата обновления: 05.10.2009. URL: http://blogs.idc.com/ie/?p=543 (дата обращения 12.01.2014);
2.Peter Mell, Timothy Grance. The NIST definition of cloud computing (draft) // NIST special publication. 2011/1;
3.Балабаев Н.Д. Разработка модуля учета новорожденных для информационной системы муниципальных учреждений здравоохранения г. Новокузнецка. В кн.: «Студент и научно-технический прогресс»: Информационные технологии, Новосибирск, 12–18 апреля 2013: материалы. Новосибирск: Новосиб. гос. ун-т., 2013. С. 62;
4.Балабаев Н.Д. Разработка информационной системы с многоуровневой архитектурой / Н.Д. Балабаев; науч. рук. В.Г. Кобылянский // Наука. Технологии. Инновации : материалы Всерос. науч. конф. молодых ученых, Новосибирск, 21–24 нояб. 2013 г.: в 10 ч. – Новосибирск : Изд-во НГТУ, 2013. – Ч. 2. – С. 34–37;
5.Руководство разработчика Live SDK // Центр разработчиков Live Connect :
сайт. 2013. URL: http://msdn.microsoft.com/ru-ru/library/live/hh243641(дата обращения 18.01.2014);
6.Э. Гамма, Р. Хелм, Р. Джонсон, Дж. Влиссидес. Приемы объектноориентированного проектирования. Паттерны проектирования. – СПб: «Питер», 2007. – С. 366;
7.Макконнелл С. Совершенный код. Мастер-класс / Пер. с англ. — М. : Издательско-торговый дом «Русская Редакция»; СПб.: Питер, 2005. — 896 стр.: ил.;
8.Фаулер М. Рефакторинг: улучшение существующего кода. — Пер. с англ. — Спб: Символ-Плюс, 2003. — 432с., ил.
311
ИССЛЕДОВАНИЕ РАСПРЕДЕЛЕНИЙ СТАТИСТИК И МОЩНОСТИ ПАРАМЕТРИЧЕСКИХ КРИТЕРИЕВ ОДНОРОДНОСТИ ДЛЯ ЦЕНЗУРИРОВАННЫХ ВЫБОРОК
Валова А.С., Семёнова М.А. НГТУ, Новосибирск e-mail: alexandra4892@mail.ru
Научный руководитель – Чимитова Е.В., доцент НГТУ
Статистический анализ продолжительности жизни имеет долгую историю. Интерес к этой теме связан главным образом с медицинской статистикой, а также с задачами испытаний на надежность в промышленности и во многих других областях, где необходимо оценить вероятность наступления некоторого системного события.
Надежностью называется свойство технического объекта сохранять свои характеристики (параметры) в определенных пределах при данных условиях эксплуатации. Переформулировав данное понятие в терминах анализа выживаемости, введем понятие выживаемость, которая является оценкой вероятности того, что больной останется живым к конкретному моменту после начала лечения.
Функция выживаемости определяется следующим соотношением:
S(t) P(T t) f (u)du 1 F(t).
t
В общем случае, данные, полученные в результате исследований выживаемости, можно представить в виде
(t1, 1),(t2, 2 ),...,(tn , n ),
где n – объем выборки, ti – время до наступления системного события или момента цензурирования, i – индикатор цензурирования, который принимает значение 1, если наблюдение полное, и 0, если цензурированное. Степень цензурирования – отношение количества цензурированных наблюдений в выборке к общему количеству наблюдений в выборке.
Проверка однородности выборок – часто возникающая на практике задача статистического анализа. Это связано с тем, что для практических целей, как правило, характерны задачи сравнения двух и более групп наблюдений.
В настоящее время проблеме проверки однородности выборок с помощью непараметрических критериев однородности посвящено достаточно большое количество публикаций [1], [2], [3], [4], [5], [6], в то время как параметрические критерии однородности практически не исследованы.
Для описания данных типа времени жизни чаще всего используются следующие вероятностные модели: распределение Вейбулла, гаммараспределение, экспоненциальное распределение, логнормальное распределение и другие.
312

Предположим, что в двух группах n1 и n2 наблюдений, в первой группе r1
полных {(x1, 1),...,(xr |
, r )} и |
n1 r1 |
цензурированных {(xr 1 |
, r |
1),...,(xn |
, n )} |
||||||||||
|
|
|
|
|
|
1 |
1 |
|
– r2 |
|
|
|
1 |
1 |
1 |
1 |
наблюдений, |
а во |
второй |
полных |
{(y1, 1),...,(yr |
, r |
)} и n2 r2 |
||||||||||
цензурированных {(yr 1, r 1),...,(yn |
, n )} наблюдений. |
|
2 |
2 |
|
|||||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
2 |
2 |
2 |
2 |
|
|
|
|
|
|
Если |
|
|
|
известно, |
что две группы наблюдений принадлежат |
|||||||||||
экспоненциальному |
закону |
распределения |
с плотностью |
распределения |
||||||||||||
1 |
|
|
1 |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
f (t) |
|
e |
|
|
,t 0, 0, |
с параметрами масштаба и |
2 |
, то для их сравнения |
||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
используются: критерий отношения правдоподобия; F-критерий Кокса.
Если известно, что две группы наблюдений принадлежат закону распределения Вейбулла или закону гамма-распределения с плотностью
распределения |
f (t) |
1 |
( |
1 |
t) 1 exp[ ( |
1 |
t) ],t 0, 0, 0 |
и |
|||||||
|
|
|
|||||||||||||
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
||||
f (t) |
( |
t) 1 exp[ ( |
t)],t 0, 0, 0, |
с параметрами масштаба |
и |
||||||||||
|
|
|
|||||||||||||
|
( ) |
|
|
|
|
|
|
|
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|||||||
2 , и параметрами |
формы 1 и 2 , то для их сравнения необходимо сначала |
||||||||||||||
проверить гипотезу о равенстве параметров формы, а затем проверить гипотезу о равенстве параметров масштаба [2].
Для вычисления статистики критерия отношения правдоподобия необходимо оценить значения параметров масштаба двух распределений по
следующим формулам: ˆ1 r1 |
n1 |
ˆ2 |
r2 |
n2 |
|
|
|
|
|
|
|
||||
xi , |
yi |
. Для полученных оценок |
|||||||||||||
|
|
|
|
i 1 |
|
|
|
i 1 |
|
|
|
|
|
|
|
параметров |
ˆ ˆ |
|
вычислить значение |
|
ˆ ˆ |
ˆr1 ˆr2 |
|
ˆ |
n1 |
ˆ |
n2 |
|
|||
, |
2 |
L( , |
) |
|
exp |
( x ) |
( y ) . |
||||||||
|
1 |
|
|
|
|
1 2 |
1 2 |
|
1 |
i |
2 |
i |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
i 1 |
|
Оценить |
параметр |
масштаба |
экспоненциального |
распределения, |
||||
соответствующего |
обеим |
выборкам, вычислить функции |
правдоподобия и |
|||||
|
|
|
|
|
ˆ r1 |
r2 |
n1 |
n2 |
значения |
|
|
статистики: |
xi |
yi , |
|||
|
|
|
|
|
2log L( ˆ, ˆ) L( ˆ1, ˆ2) . |
i 1 |
i 1 |
|
|
|
n1 |
n2 |
|
|
|
||
L( ˆ, ˆ) ˆr1 r2 exp ˆ( xi |
yi ) , XL |
|
|
|||||
|
|
i 1 |
i 1 |
|
|
|
|
|
Если XL 12, , то гипотеза об однородности отвергается и, следовательно, |
||||||||
два экспоненциальных распределения |
не одинаковы, где |
12, |
– хи-квадрат |
|||||
распределение с одной степенью свободы, – заданный уровень значимости. Для вычисления статистики F-критерий Кокса необходимо вычислить
|
n1 |
n2 |
|
|
ˆ |
|
|
|
ˆ |
|
ˆ |
|
|
|
||
|
tˆ1 xi |
r1 , tˆ2 yi |
|
|
t |
2 |
|
|
|
|
|
t |
2 |
|
|
|
значения |
r2 . |
Если |
|
F2r1,2r2,1 /2 |
|
1 |
|
|
F2r1,2r2, /2 |
, |
то |
|||||
ˆ |
ˆ |
ˆ |
||||||||||||||
|
i 1 |
i 1 |
|
|
t1 |
|
|
|
2 |
|
t1 |
|
|
|
||
гипотеза |
об |
однородности |
не |
отвергается, |
|
следовательно, |
|
два |
||||||||
экспоненциальных распределения одинаковы, где F2r ,2r ,1 /2 |
– распределение |
|||||||||||||||
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
313

Фишера с 2r1,2r2 степенями свободы и заданным уровнем значимости
1 /2 [1].
Вычисление статистики критерия сравнения параметров формы выглядит следующим образом: оценить значение параметров формы ˆ1, ˆ2 , вычислить значение ˆ1 ˆ2 . Если ˆ1
ˆ2 . Если ˆ1 ˆ2 l ,то гипотеза отвергается, параметры формы различны, следовательно, два распределения различны, где l – табличное значение [6] с заданным уровнем значимости [2].
ˆ2 l ,то гипотеза отвергается, параметры формы различны, следовательно, два распределения различны, где l – табличное значение [6] с заданным уровнем значимости [2].
Для распределения Вейбулла для вычисления статистики критерия сравнения параметров масштаба необходимо: оценить значение параметров масштаба ˆ1, ˆ2 , используя полученные значения ˆ1, ˆ2 и оценки ˆ1, ˆ2 , полученные при проверке гипотезы о равенстве параметров формы H0 : 1 2 ,
вычислить статистику G 1(ˆ1 ˆ2)(log ˆ2 log ˆ1) [2].
2
Если G z , то гипотеза не отвергается, и два распределения Вейбулла одинаковы, где z – табличное значение [2] с заданным уровнем значимости .
Для гамма-распределения для вычисления статистики критерия сравнения
|
|
|
|
|
|
|
n1 |
|
|
n2 |
параметров |
|
масштаба необходимо вычислить |
x |
xi |
n1 , |
y |
yi n2 , |
|||
посчитать |
x |
|
y |
. |
|
|
i 1 |
|
|
i 1 |
|
|
|
|
|
||||||
Если |
x |
|
y |
F2n 1,2n 2, , то гипотеза не отвергается, |
и два гамма |
|||||
распределения одинаковы, где F2n 1,2n 2, – распределение Фишера с 2n 1,2n 2
степенями свободы и заданным уровнем значимости .
В данной работе было проведено исследование распределение статистик и мощности параметрических критериев однородности в зависимости от объемов и степени цензурирования выборок. Исследования проводились для экспоненциального распределения, распределения Вейбулла, а также для гамма-распределения.
Литература:
1.Lawless, J. F. (1982). Statistical Methods and Model for Lifetime Data. Wiley, New York.
2.Lee E.T., Wang J.W. Statistical Methods for Survival Data Analysis. John Wiley & Sons Inc., Hoboken, New Jersey, 2003. – 513 p.
3.Mann, N.R., R.E. Schafer and N.D. Singpurwalla, Methods for Statistical Analysis of Reliability and Life Data, John Wiley & Sons, Inc., New York, 1974.
4.Nelson, W., Applied Life Data Analysis, John Wiley & Sons, Inc., New York, 1982.
5.Rao, C. R. (1952). Advanced Statistical Methods in Biometric Research. Wiley, New York.
6.Кокс, Д. Анализ данных типа времени жизни / Д. Кокс, Д. Оукс. – М. : Финансы и статистика, 1988. – 191 с.
314
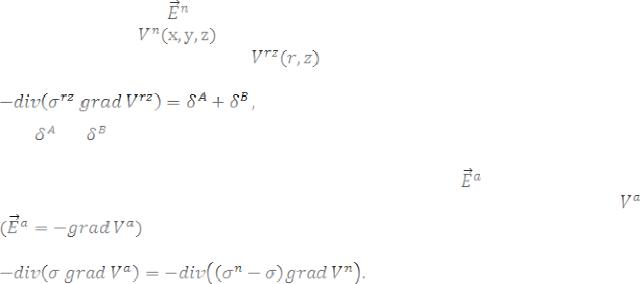
РАЗРАБОТКА И РЕАЛИЗАЦИЯ ВЫЧИСЛИТЕЛЬНЫХ СХЕМ ДЛЯ РЕШЕНИЯ ЗАДАЧ ГЕОЭЛЕКТРИКИ С ИСТОЧНИКОМ В ВИДЕ ВЭЛ
Демина В.О. НГТУ, Новосибирск
e-mail: vdemina@hotmail.com, тел.: 8(953)888-07-73
Научный руководитель - Персова М.Г., профессор НГТУ
На сегодняшний день электрическое зондирование остается одним из самых применяемых электроразведочных методов для поиска залежей углеводородов и восполнения их запасов. Возрастающие требования к точности восстановления глубинного распределения удельного сопротивления среды делают все более актуальным использование 3D моделирования при интерпретации электроразведочных данных. Одним из методов решения задач электромагнетизма является метод конечных элементов (МКЭ)[1]. Но при конечноэлементном моделировании трехмерных геоэлектромагнитных полей для достижения хорошей точности часто требуются очень высокие вычислительные затраты. Предложенный в работах [2, 3] метод, основанный на выделении поля вмещающей горизонтально-слоистой среды, позволяет существенно уменьшить вычислительные затраты. Данная работа посвящена описанию этого метода для контролируемого источника в виде вертикальной электрической линии (ВЭЛ), а также приведены примеры 3D моделирования геоэлектромагнитных полей.
В освещаемом нами методе искомое трехмерное электромагнитное поле ищется в виде суммы нормального поля горизонтально-слоистой среды и аномального поля влияния трехмерных объектов.
Сначала рассмотрим математические модели стационарных магнитного и электрического полей ВЭЛ при включенном токе с учетом их разделения на
двумерную и трехмерную составляющие. |
|
|
|||||
|
Во вмещающей горизонтально-слоистой (или осесимметричной) среде |
||||||
электрическое поле |
полностью описывается потенциалом. |
При этом для |
|||||
ВЭЛ потенциал |
|
может быть найден путем перерасчета (с учетом |
|||||
положения |
источника) поля |
, найденного из решения двумерной |
|||||
краевой задачи в цилиндрических координатах: |
|
(1) |
|||||
|
|
|
|
|
|
|
|
где |
и |
— положительный и отрицательный источники, описывающий |
|||||
токи, стекающие с электродов A и B. |
|
|
|
||||
|
Аномальная |
(трехмерная) |
составляющая |
напряженности |
|||
электрического |
поля |
полностью описывается |
скалярным потенциалом |
||||
краевой задачи: |
, который может быть получен как решение следующей |
||||||
|
|
|
|
|
|||
|
|
|
|
|
|
|
(2) |
|
Математическая |
модель для |
расчета |
стационарного |
трехмерного |
||
магнитного поля при условии, что магнитная проницаемость среде является
315
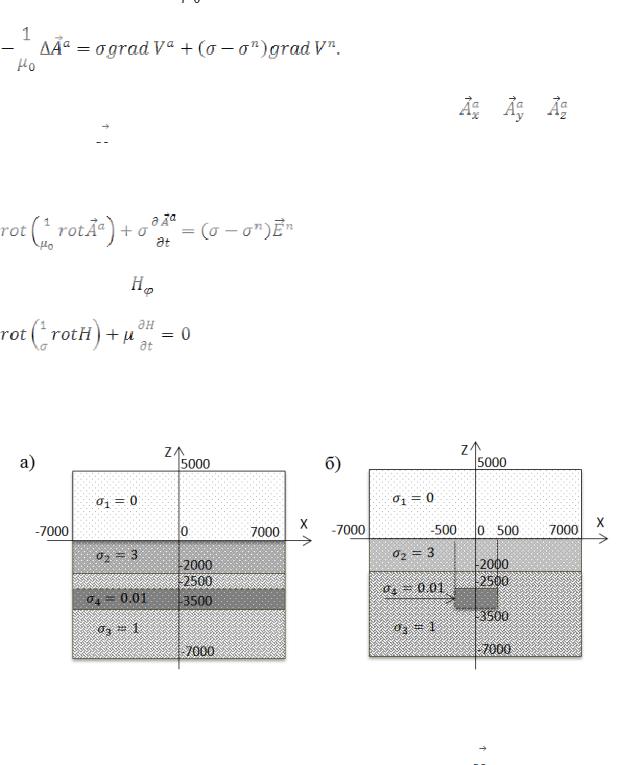
постоянной, равной 


 — магнитной проницаемости вакуума, выглядит следующим образом:
— магнитной проницаемости вакуума, выглядит следующим образом:
|
|
|
|
(3) |
|
|
|
|
|
|
|
Векторное уравнение (3) фактически является совокупностью трех |
||
независимых скалярных уравнений для компонент , |
, |
вектор- |
||
потенциала 


 .
.
На этапе становления поля изменение его характеристик во времени изучается при выключенном в ВЭЛ токе. Для описания этого процесса
используется модель вида: |
|
|||||||
|
|
|
|
|
|
|
. |
(4) |
|
|
|
|
|
|
|
||
Нормальное поле для рассматриваемого источника удобно искать в виде |
||||||||
распределения |
|
в цилиндрической системе координат. |
Математическая |
|||||
модель для расчета нестационарного поля ВЭЛ имеет вид: |
|
|||||||
|
|
|
|
|
|
. |
(5) |
|
|
|
|
|
|
|
|||
В качестве примера, демонстрирующего адекватность реализованных методов трехмерного моделирования, приведем результаты расчета для горизонтально-слоистой среды, вид которой представлен на рисунке 1. ВЭЛ заземлена на дневной поверхности и находится на глубине 1700 м.
Рисунок 1 - Геоэлектрические модели сред, на которых проводились исследования.
Приведем распределение X-компоненты вектора 


 , полученной из решения стационарной (рисунок 2a) и нестационарной (в момент времени
, полученной из решения стационарной (рисунок 2a) и нестационарной (в момент времени 



 , рисунок 2б) задач, в области, содержащей аномальный слой (Рисунок 1а), в сечение XY в середине слоя.
, рисунок 2б) задач, в области, содержащей аномальный слой (Рисунок 1а), в сечение XY в середине слоя.
316
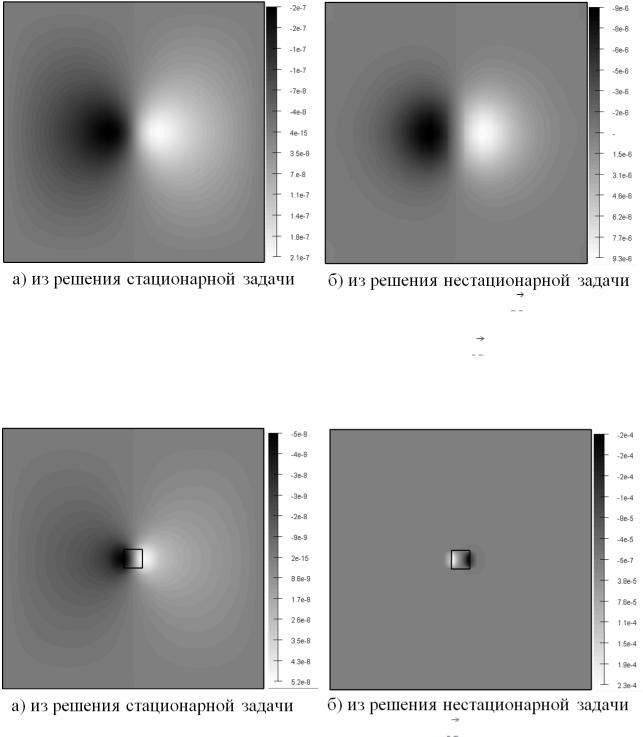
Рисунок 2 - Распределение X-компоненты вектора 

 .
.
Покажем распределение X-компоненты вектора 


 , полученной из решения стационарной (рисунок 3a) и нестационарной (в момент времени
, полученной из решения стационарной (рисунок 3a) и нестационарной (в момент времени 



 , рисунок 3б) задач, в области, содержащей аномальный объект (рисунок 1б), в сечение XY в середине объекта.
, рисунок 3б) задач, в области, содержащей аномальный объект (рисунок 1б), в сечение XY в середине объекта.
Рисунок 3 – Распределение X-компоненты вектора 



Литература:
1.Соловейчик Ю.Г., Рояк М.Э., Персова М.Г. Метод конечных элементов для решения скалярных и векторных задач // Учебное пособие. Сер. “Учебники НГТУ”. Новосибирск: НГТУ. 2007. 899 с.
2.Соловейчик Ю.Г., Рояк М.Э., Моисеев В.С. Математическое моделирование на базе метода конечных элементов трехмерных электрических полей в задачах электроразведки // Физика Земли. 1997. № 9. С. 67–71.
3.Персова М.Г., Соловейчик Ю.Г., Тригубович Г.М. Компьютерное моделирование геоэлектромагнитных полей в трехмерных средах методом конечных элементов // Физика Земли. 2011. № 2. С. 3–14.
317

МЕТОД РАСПОЗНАВАНИЯ КОММУНИКАТИВНЫХ СИГНАЛОВ КИТОВ НА ФОНЕ ПОМЕХ
Жарков К.Ю. НГТУ, Новосибирск e-mail: new_neo@mail.ru
Научный руководитель – Неделько В.М., доцент НГТУ
Многочисленные исследования ученых показали, что низкочастотный шум морских судов создаёт большие помехи для китов и негативно сказывается на их существовании. Была разработана система, корректирующая курс судов при обнаружении китов. Но возникла необходимость в эффективном способе распознавания сигналов китов.
Поэтому была поставлена задача: изучить звуковые коммуникативные сигналы китов, разработать метод их распознавания и протестировать на большой выборке неизвестных сигналов [1].
Объект исследования - огромная выборка неизвестных звуковых сигналов (30000 звуковых фрагментов), которая представлена в виде звуковых спектрограмм.
На рисунке пример спектрограммы звукового фрагмента с ярко выраженным коммуникативным сигналом кита.
Рисунок - Спектрограмма с выделенным коммуникативным сигналом кита.
318
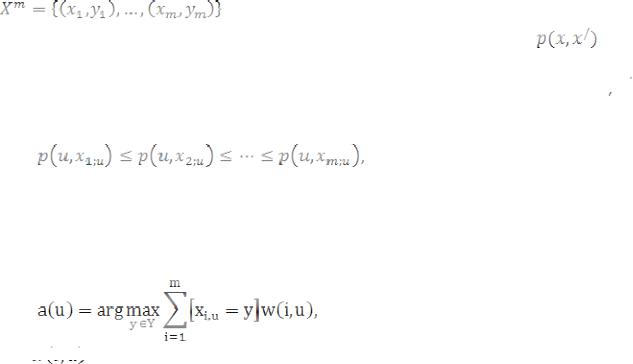
Метод ближайших соседей был выбран для решения задачи [2].
Для повышения надёжности классификации объект относится к тому классу, которому принадлежит большинство из его соседей — k ближайших к
нему объектов обучающей выборки xi. |
пар |
«объект—ответ» |
||||
Пусть |
задана |
обучающая |
выборка |
|||
|
|
. |
|
|
|
|
Пусть |
на множестве |
объектов |
задана функция |
расстояния |
. Эта |
|
функция должна быть достаточно адекватной моделью сходства объектов. Чем больше значение этой функции, тем менее схожими являются два объекта 




 .
.
Для произвольного объекта uрасположим объекты обучающей выборки xiв порядке возрастания расстояний до u:
где через xi,u обозначается тот объект обучающей выборки, который является i- м соседом объекта u. Аналогичное обозначение введём и для ответа на i-м соседе: yi,u. Таким образом, произвольный объект u порождает свою перенумерацию выборки.
В наиболее общем виде алгоритм ближайших соседей есть
где 






 — заданная весовая функция, которая оценивает степень важности i- го соседа для классификации объекта u. Естественно полагать, что эта функция неотрицательна и не возрастает по i.
— заданная весовая функция, которая оценивает степень важности i- го соседа для классификации объекта u. Естественно полагать, что эта функция неотрицательна и не возрастает по i.
Результаты исследований приведены в таблице.
Таблица - Исследование точности распознавания метода ближайших соседей
Количество звуковых фрагментов |
Количество звуковых |
|
|
фрагментов тестируемой |
AUC |
||
обучающей выборки |
|||
выборки |
|
||
|
|
||
|
|
|
|
1000 |
5000 |
0.654 |
|
2500 |
5000 |
0.690 |
|
5000 |
5000 |
0.705 |
|
1000 |
1000 |
0.841 |
|
15000 |
1000 |
0.943 |
|
25000 |
1000 |
0.960 |
|
10000 |
20000 |
0.907 |
Показатель AUC - площадь, ограниченная ROC-кривой и осью доли ложных положительных классификаций. Чем выше показатель AUC, тем качественнее классификатор. ROC-кривая (кривая ошибок) – графическая характеристика качества бинарного классификатора, зависимость доли верных
319
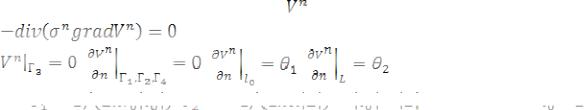
положительных классификаций от доли ложных положительных классификаций.
Результаты исследований показали, что метод ближайших соседей перспективен для задачи распознавания звуковых коммуникативных сигналов китов, при тесте большой выборки (20000 элементов) значение AUC = 0.907.
В дальнейшем планируется найти способы улучшающие качество работы метода, например использование кластеризации с выделением регрессии.
Литература:
1. Description - The Marinexplore and Cornell University Whale Detection Challenge [Электронныйресурс]. – Режимдоступа: https://www.kaggle.com/c/whale-detection-challenge
2.Гайдышев, И. Анализ и обработка данных / И. Гайдышев – СанктПетербург: Питер, 2001. – 750 с.
РАЗРАБОТКА ПРОГРАММЫ 3D-МОДЕЛИРОВАНИЯ ГЕОЭЛЕКТРОМАГНИТНОГО ПОЛЯ КРУГОВОГО ЭЛЕКТРИЧЕСКОГО ДИПОЛЯ
Епанчинцева Т.Б. НГТУ, Новосибирск
e-mail: etb-tatiana@mail.ru, тел. 8(960)789-19-22
Научный руководитель - Персова М.Г., профессор НГТУ
В данной работе представлен алгоритм решения прямых трехмерных задач для установки КЭД, который представляет собой несколько симметрично расположенных радиально направленных горизонтальных линий (лучей), один электрод которых расположен близко к центру установки, а другой удален на некоторое расстояние, называемое внешним радиусом КЭД. Подход, предложенный в работах [1,2], позволяет моделировать с использованием МКЭ стационарные и нестационарные ЭМ процессы для источника «круговой электрический диполь» (КЭД) с высокой точностью при минимальных вычислительных затратах. Математическая модель основана на разделении искомого электромагнитного поля на двумерную (нормальную) и трехмерную (аномальную) составляющие [3]. Приведены примеры 3D моделирования геоэлектромагнитных полей.
Большие перспективы применения этого источника могут быть связаны с морской электроразведкой, где его использование может повысить
разрешающую способность. |
|
|
|
|
||||
Двумерное стационарное поле |
|
находится из решения краевой задачи: |
||||||
|
, |
|
|
|
|
|
(1) |
|
, |
|
, |
|
|
, |
|
, |
(2) |
|
|
|
|
|
||||
где 



















 ,
, 





















 , а
, а 


 и
и 


 - длины ребер
- длины ребер 
 и
и 
 . Цилиндрическая расчетная область показана на рисунке 1.
. Цилиндрическая расчетная область показана на рисунке 1.
320
