Загребаев Лектсии по теории вероятностеы и математическоы статистике 2015

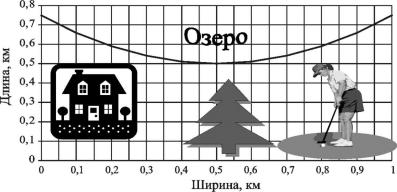
Определенный интеграл. Предположим, что некто, продвигая на рынок «высокоинтеллектуальный» заграничный товар, например детские подгузники с крылышками или зубные щетки с абразивным напылением, «заработал» десятки миллионов «бакинских» рублей и решил, наконец, купить себе усадьбу. Конечно, под Москвой, конечно, на берегу водохранилища, конечно, с яхтой и полем для гольфа! (рис. 4.7).

Рис. 4.7. Усадьба

Наконец, некто нашел подходящий участок и, не веря представленным документам (покупает землю у такого же «бизнесмена»), решил точно определить площадь участка. Если бы участок был прямоугольным – проблем нет. В нашем случае граница с озером не является прямой линией. Подсчитать площадь приближенно можно следующим образом. Разобьем участок вертикальными полосами шириной x = 0,1 км . Длину полосы будет определять граница с

озером на линии полуширины полосы ( x1 = 0,05 ). Например, для крайней левой полосы ее длина составляет величину f (x1) = 0,7 км.

41

дей 10 участков.) Понятно, чем ýже мы брали бы полоску, тем на большее число полосок пришлось бы разбивать участок и тем точнее подсчитали бы площадь. Если существует предел последовательности, S1, S2..., Sn ..., то он называется определенным инте-

гралом S = lim Sn . При этом значок трансформируется в , а

смотренном примере граница участка с озером описывается функцией f (x) = 0,5 + (x − 0,5)2 , тогда площадь участка есть

1

[0,5 + (x − 0,5)2 ] dx = 0,583 км2. Как видите, наше приближенное

0

вычисление почти совпадает с точным значением.

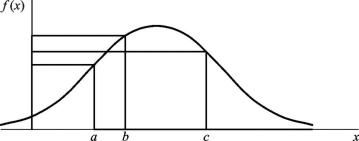
Каверзный вопрос. Иногда на экзамене я задаю следующий вопрос. На рис.(4.8) изображена плотность вероятности некоторой случайной величины. Вероятность появления какого значения случайной величины больше: a, b или c? Комбинации выдавали самые

разные: P(b) > P(c) > P(a) − самый распространенный, выстроенный по убыванию значений f (x) ; P(c) > P(b) > P(a) − выстроенный по убыванию площадей под функцией f (x) и, наконец, P(b) > P(c) P(c) > P(a) , поэтому!!! P(a) = P(c) !!! Понятно, что правильный ответ: P(a) = P(b) = P(c) = 0 .

Рис. 4.8. Каверзный вопрос

42

Лекция 5. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН

Ранее мы рассматривали различные формы закона распределения, каждая из которых полностью, с вероятностной точки зрения, характеризует случайную величину:

•для дискретных случайных величин − это ряд распределения P(x) и функция распределения F(x);

•для непрерывных – функция распределения F(x) и плотность распределения f (x).

Однако на практике зачастую интересуются не законом распределения случайной величины, а лишь частными особенностями ее поведения. Например, средним ее значением, степенью разбросанности и т.д.

Числовыми характеристиками случайных величин называют величины, позволяющие в сжатой форме выразить наиболее существенные особенности закона распределения случайной величины. При этом иногда решить поставленную задачу можно, лишь оперируя числовыми характеристиками.

Например, при массовом производстве молодежной женской одежды нет необходимости знать закон распределения прекрасного пола по какому-либо размеру (объему талии), достаточно знать средние габариты для данной категории (70 см) и возмож-

ный средний разброс (± 30 см).

Математическое ожидание, мода, медиана

Пусть имеется дискретная случайная величина X, которая в n опытах приняла следующие значения:

x1 → m1 раз; ….………

xn → mn раз.

Тогда сумма всех значений, принятых случайной величиной X в n независимых опытах есть

x1m1 + ... + xk mk .

43

Допустим, что число испытаний n велико, тогда относительные частоты будут по вероятности сходится к возможности появления

соответствующих значений, т.е. wi → pi . Следовательно,

Таким образом, математическое ожидание дискретной случайной величины

i=1

где xi – ее возможные значения.

_______________________________________________________

Отступление. Последовательность случайных величин Xn схо-

дится по вероятности к А, если для любого ε > 0 вероятность неравенства Xn − A < ε с увеличением n неограниченно приближается к

единице

lim P( Xn − A < ε) = 1.

n→∞

Давайте, сравним это определение предела последовательности с известным вам из курса математического анализа:

последовательность чисел Xn сходится к A, если для любого ε > 0

найдется такой номер N, что для всех n > N выполняется неравенство

Xn − A < ε.

Существенная разница заключается вот в чем. Классическое определение предела говорит о том, что число A является пределом последова-

тельности Xn , если dы для заданного ε > 0 нашли такой номер N, то для всех n больших, чем N, все члены последовательности Xn «находятся на

расстоянии от предела A менее, чем на это ε». Сходимость же по вероятности допускает, что отдельные значения последовательности Xn

могут «выбрасываться из отрезка Xn − A < ε », но вероятность этого

44

события тем меньше, чем больше n. (Да простят меня математики за это объяснение!)

Анекдот (истинная правда) Принимая экзамен по данному курсу у одного из студентов ИИМ, я на экзаменационном листе увидел фразу «сходится к A по вер.». На мой вопрос: Что значит «по вер.?», я услышал ответ: «по вертикали!»

____________________________________________________

Математическое ожидание непрерывной случайной величины определяется как

−∞

Математическое ожидание является неслучайной величиной. Отметим одно важное обстоятельство. Выражение M [X ], с од-

ной стороны, может обозначать число – математическое ожидание случайной величины, а с другой – операцию нахождения математического ожидания от случайной величины X. Здесь ситуация аналогичная производной функции. Действительно, с одной стороны,

df (x) есть производная функции, т.е. некая функция, а с другой − dx

dfdx понимается как операция нахождения производной от функции f (x).

Свойства математического ожидания

1) математическое ожидание постоянной неслучайной величины равно самой этой величине:

2) математическое ожидание от произведения постоянной величины c на случайную величину X равно произведению постоянной на математическое ожидание случайной величины

Доказательство. Для дискретной случайной величины

45

Для непрерывной случайной величины

M[cx] = −∞∞ cxf (x)dx = c −∞∞ xf (x)dx = cM[x].

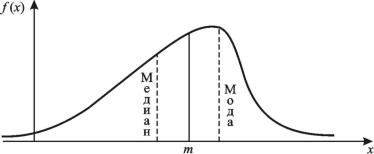
Модой дискретной случайной величины X называется ее наиболее вероятное значение μ.

Модой непрерывной случайной величины X называется то её значение, при котором плотность вероятности максимальна (обо-

значается так же − μ). Для непрерывной случайной величины нельзя говорить о наиболее вероятном значении, так как вероятность любого конкретного значения одинакова и равна нулю.

Медианой случайной величины X называется такое её значение, для которого выполняется равенство P(X > μe ) = P(X < μe ), то есть

прямая x = μe делит площадь под кривой функции f (x) на две рав-

ные части.

Если многоугольник (плотность) распределения имеют один максимум, то такое распределение называется унимодальным, более одного – полимодальным. Если имеет один минимум, то антимодальным. Геометрический смысл числовых характеристик показан на рис. 5.1 для непрерывной случайной величины.

Рис. 5.1. Геометрический смысл числовых характеристик

46

Моменты случайной величины

Начальным моментом k-го порядка дискретной случайной величины называется сумма

i=1

Начальным моментом k-го порядка непрерывной случайной величины называется интеграл

−∞

Здесь возможные значения случайной величины возводятся в степень k.

Таким образом, введенная ранее величина – математическое ожидание (см. формулы (5.3) и (5.4)) − есть не что иное, как первый (k = 1) начальный момент случайной величины X.

Обобщая формулы (5.7) и (5.8), можно записать

Центрированной случайной величиной называется случайная величина, представляющая собой отклонение от математического

ожидания: X = X − mx = X − M [ X ].

Центрирование случайной величины означает перенос начала отсчета в точку с координатой равной математическому ожиданию. Действительно, очевидны следующие соотношения как для дискретной, так и непрерывной случайной величины

Моменты центрированной случайной величины носят название центральных. Центральный момент k-го порядка по определению есть

47

Наиболее важной характеристикой, наряду с математическим ожиданием, является второй центральный момент μ2 , называемый

дисперсией. Введем для этой величины специальное обозначение Dx или, понимая под символом D операцию нахождения диспер-

сии, D[ X ]. В явном виде эта величина имеет следующие выраже-

ния:

для дискретной случайной величины

i=1

для непрерывной случайной величины

−∞

Дисперсия есть мера рассеянности, разбросанности, случайной величины около ее математического ожидания.

Между центральными и начальными моментами существует однозначная связь. Например, для момента второго порядка − дисперсии − получим

Дисперсия имеет размерность квадрата соответствующей случайной величины. Для наглядной характеристики рассеивания удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Для этого из дисперсии извлекают квадратный корень. Полученная величина называет средним

48

квадратическим отклонением случайной величины: σx = Dx .

На рис. 5.2 показан пример вида функции плотности распределения двух случайных величин, имеющих одно и то же математическое ожидание, но разные дисперсии.

Рис. 5.2. Графическая иллюстрация моментов случайной величины

Случай на экзамене. На экзаменационном листе студента ИИМ в формуле (5.14) индекс при дисперсии был написан очень крупно, приблизительно так: DX . В ответ на мой вопрос: «Что

здесь написано?» будущий инновационный менеджер ответил: «D умноженное на X»!!!

Лекция 6 . ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ.

ЗАКОН РАВНОМЕРНОЙ ПЛОТНОСТИ

Если известно, что значение случайной величины находится в пределах некоторого интервала, а плотность вероятности распределения в пределах этого интервала постоянна, то говорят, что случайная величина подчинена закону равномерной плотности.

Пусть, например, известно, что поезда метро идут с фиксированным интервалом в 2 минуты. Если пассажир вышел на платформу в произвольный момент времени в отсутствие поезда, то время ожидания есть случайная величина, распределенная с равномерной плотностью на отрезке [0, 2].

49

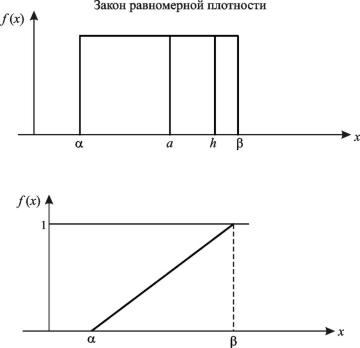
Закон равномерной плотности или равномерный закон распределения непрерывной случайной величины имеет функцию плотности распределения вида

рис. 6.2 – функция распределения F(x) для закона равномерной плотности.

Рис. 6.1. Функция плотности распределения

Рис. 6.2. Функция распределения для закона равномерной плотности

50