
Мишулина Основы теории вероятностей 2011
.pdf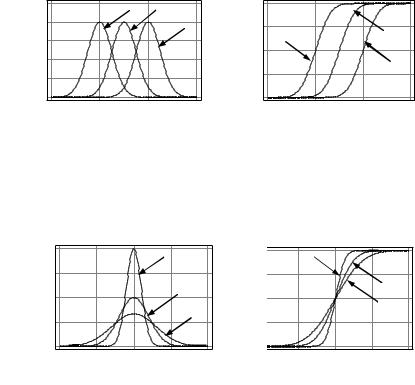
Плотность распределения является симметричной функцией относительно x = m. Изменение математического ожидания приводит к параллельному переносу вдоль координатной оси x графика плотности вероятности. Мода нормального распределения совпадает со значением математического ожидания m. На рис. 2.15, б показаны соответствующие графики функции распределения нормального закона.
f (x) |
|
|
|
F (x) |
|
|
|
0,5 |
|
0 |
2 |
1 |
|
|
|
|
|
|
|
|
|
||
0,4 |
|
|
4 |
0,75 |
|
|
|
|
|
|
0 |
|
2 |
||
0,3 |
|
|
|
|
|
||
|
|
|
0,5 |
|
|
||
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
0,25 |
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
-4 |
0 |
4 |
8 x |
-4 |
0 |
4 |
8 x |
|
|
a |
|
|
|
б |
|
Рис. 2.15. Распределение вероятностей нормального закона для трех значений m = 0, 2, 4 при ζ = 1: a – плотность распределе-
ния, б – функция распределения вероятностей
f (x) |
|
|
|
|
0,4 |
|
|
1 |
|
|
|
|
|
|
0,3 |
|
|
|
|
0,2 |
|
|
|
2 |
|
|
|
|
|
0,1 |
|
|
|
3 |
|
|
|
|
|
0 |
|
|
|
|
-10 |
-5 |
0 |
5 |
10 |
|
|
|
a |
|
|
F (x) |
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
0,75 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
0,25 |
|
|
|
|
|
|
0 |
|
|
|
|
|
x |
-10 |
-5 |
0 |
5 |
10 |
x |
|
|
|
|
б |
|
|
Рис. 2.16. Распределение вероятностей нормального закона для трех значений ζ = 1, 2, 3 при m = 0: a – плотность вероятности; б – функция распределения вероятностей
101
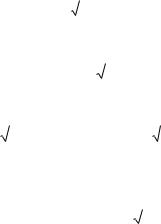
На рис. 2.16, а представлено влияние параметра ζ на форму графика плотности вероятности. Три показанные на рисунке графика соответствуют значениям ζ = 1, 2, 3 и фиксированному математическому ожиданию m = 0. На рис. 2.16, б показаны соответствующие графики функции распределения нормального закона.
Чтобы получить выражение для функции распределения вероятностей нормального закона, воспользуемся известной формулой связи F(x) и f(x):
x
F (x) f (x) dx .
Тогда для функции F(x) получим следующее выражение:
|
|
|
|
|
|
|
|
1 |
|
|
|
|
x |
|
|
|
|
(x m)2 |
|
|
|
||||||||||||
|
|
|
F (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2 |
exp |
|
|
2 |
2 |
|
|
dx |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
z 2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
2 |
exp |
2 |
|
|
dz |
|
(2.83) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x m |
|
|
|
|
|
|
||||
|
|
1 |
0 |
|
|
|
z 2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
z 2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
exp |
|
2 |
|
|
dz |
|
2 |
|
|
|
exp |
|
2 |
dz . |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||||||||||
Функция распределения закона Гаусса не выражается в элементарных функциях. Определим следующую функцию:
|
|
1 |
|
x |
|
|
z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
(x) |
|
|
|
|
|
||||
2 |
|
exp |
2 |
dz , |
(2.84) |
||||
|
|
0 |
|
|
|
|
|||
которую называют функцией Лапласа, или интегралом вероятно-
стей. Для преобразования выражения (2.83) для F(x) используем очевидные свойства функции Лапласа:
(x) – (x) |
и ( ) 1/ 2 . |
(2.85) |
Последнее свойство следует из равенства (2.82) при m = 0 и ζ = 1 и симметрии подынтегральной функции. В результате преобразований получаем следующее выражение:
|
1 |
x m |
|
||
F (x) |
|
|
|
. |
(2.86) |
|
|
||||
|
2 |
|
|
|
|
102
Выражение (2.86) для функции распределения вероятностей F(x) позволяет записать расчетную формулу для вероятности попадания нормально распределенной случайной величины в произвольный интервал [α, β):
|
m |
|
m |
||
P ( X ) F ( ) F ( ) |
|
|
|
|
. (2.87) |
|
|
|
|
||
Заметим, что в силу непрерывности нормального распределения вероятность попадания случайной величины в фиксированную
точку равна нулю и, следовательно, формула (2.87) определяет также вероятности P( X ) и P( X ) .
Рассмотрим вероятность попадания нормальной случайной величины в интервал (m – ε, m + ε), расположенный симметрично относительно математического ожидания. Для получения расчетной формулы воспользуемся выражением (2.87) и свойством (2.85) нечетной симметрии функции Лапласа:
P (m X m ) P (m X m )
|
|
|
|
|
|
||
F (m ) F (m ) |
|
|
|
|
2 |
|
. |
|
|
||||||
|
|
|
|
|
|
||
Таким образом, получена следующая расчетная формула:
|
|
|
|
P (| x m | ) 2 |
|
. |
(2.88) |
|
|||
|
|
|
|
Функция Лапласа табулирована, что позволяет выполнить неко-
торые показательные расчеты:
P (| x m | ) 2 (1) 0,8627; P (| x m | 2 ) 2 (2) 0,9545; P (| x m | 3 ) 2 (3) 0,9973;
P (| x m | 4 ) 2 (4) 0,99994.
Из приведенных расчетов, в частности, следует, что с вероятностью 0,9973 нормально распределенная случайная величина отклоняется от своего математического ожидания не более, чем на 3ζ.
Характеристическая функция нормально распределенной случайной величины рассчитывается согласно определению (2.71):
|
j X |
|
|
1 |
|
|
j x |
|
|
(x m)2 |
||
|
|
|
|
|
e |
|
|
|
|
|
||
( ) M[e |
|
] |
|
|
|
|
exp |
|
|
|
dx |
|
|
|
|
|
|
2 |
2 |
||||||
|
|
|
||||||||||
|
|
|
|
2 |
|
|
|
|
|
|||
103

|
j m |
|
1 |
|
|
|
|
y2 |
|
|
|
2 2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
e |
|
|
|
|
exp |
|
2 |
|
2 |
j y dy exp j m |
2 |
|
. (2.89) |
||
|
|
|
2 |
|
|
|
|
|
|
|
|||||
o
Центрированная случайная величина X X mX , распределенная нормально, имеет характеристическую функцию
|
|
|
|
2 2 |
(2.90) |
|
0 |
( ) exp |
|
. |
|||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Ранее было установлено, что разложением характеристической функции в ряд Маклорена можно определить моменты случайной величины (2.79). Представим 0 ( ) рядом Маклорена:
|
|
|
|
2 |
2 |
|
|
2k |
|
2k |
|
|
0 |
( ) exp |
|
|
|
1 ( 1)k |
k |
|
|
|
|||
|
|
|
|
2 |
|
|
|
2 |
k! |
|
||
|
|
|
|
|
|
k 1 |
|
|
||||
|
|
|
|
( j)2k |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2k (2k 1)!! , |
|
|
|
|
(2.91) |
|
|
|
(2 k)! |
|
|
|
|
|
|||||
|
k 1 |
|
|
|
|
|
|
|
||||
где (2k – 1)!! = 1·3·5·…·(2k – 1). Поскольку коэффициентами при
( j)k в разложении Маклорена характеристической функции
( k)!
0 ( ) центрированной случайной величины являются ее цен-
тральные моменты, получаем на основании разложения (2.91) следующие выражения для центральных моментов нормально распределенной случайной величины:
μ2k+1 = 0, k = 0, 1, 2, …
μ2k = (2k – 1)!! ζ2k, k = 1, 2, … . (2.92)
Из (2.92) при k = 2 получаем выражение для четвертого централь-
ного момента:
μ4 = 3ζ4,
откуда следует, что эксцесс, определенный выражением (2.55), для нормально распределенной случайной величины равен нулю.
Допустим, что нормально распределенная случайная величина X подвергнута линейному преобразованию Y = aX +b. Возникает вопрос: какому распределению вероятностей подчиняется случайная величина Y? Для ответа на поставленный вопрос воспользуемся доказанным ранее свойством (2.75), которое устанавливает, что
104
характеристические функции φX(λ) и φY(λ) случайных величин X и
Y связаны следующим выражением:
φY (λ) = e jbλ φX (aλ).
Согласно выражению (2.89)
|
|
|
|
|
|
|
2 |
2 |
|
|
|
||
|
X |
( ) exp j m |
X |
|
|
X |
|
, |
|
||||
|
|
|
|
|
|||||||||
|
|
|
|
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
откуда следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
a |
2 |
|
2 |
|
|
φY (λ) = exp j(m |
X |
b) |
|
|
|
X |
. |
||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
Полученное выражение для характеристической функции φY(λ) означает, что случайная величина Y распределена, как и X, по закону Гаусса, но имеет другие параметры:
mY = mX + b, ζY = |a| ζX .
Контрольные вопросы и задачи
1.Чему равна плотность вероятности нормально распределенной случайной величины?
2.Покажите, что плотность вероятности нормального закона удовлетворяет условию нормировки.
3.Какова область возможных значений нормально распределенной случайной величины?
4.От каких параметров зависит нормальный закон распределения вероятностей?
5.Объясните, почему начальные и центральные моменты произвольного порядка нормально распределенной случайной величины выражаются через математическое ожидание и стандартное отклонение.
6.Чем различаются графики плотности вероятности нормального распределения случайных величин, характеризующихся разными математическими ожиданиями и одинаковыми стандартными отклонениями?
7.Как изменится форма графика плотности вероятности нормально распределенной случайной величины, если увеличить ее стандартное отклонение?
105
8.Напишите выражение для функции распределения вероятностей закона Гаусса.
9.Дайте определение функции Лапласа.
10.Какими свойствами обладает функция Лапласа? Нарисуйте
ееграфик.
11.Напишите выражение для вероятности попадания нормально распределенной случайной величины в произвольный интервал [α, β). Зависит ли эта вероятность от включения или исключения из интервала граничных точек?
12.Укажите для нормально распределенной случайной величины интервал, расположенный симметрично относительно центра распределения вероятностей, в который она попадает с вероятностью, превышающей 0,95.
13.Напишите выражение для характеристической функции нормально распределенной случайной величины.
14.На основании какого свойства характеристической функции могут быть найдены моменты случайной величины?
15.Чему равны центральные моменты нечетного порядка для нормально распределенной случайной величины?
16.Чему равны центральные моменты четного порядка для нормально распределенной случайной величины?
17.Чему равен эксцесс нормального распределения вероятностей? Дайте обоснование к своему ответу.
18.Как изменяется закон распределения вероятностей при линейном преобразовании нормально распределенной случайной величины?
106

Глава 3. СЛУЧАЙНЫЕ ВЕКТОРЫ
§ 20. Распределение вероятностей случайного вектора
При решении прикладных задач обычно каждый объект, явление или испытание характеризуется не одним числом, а совокупностью n чисел. Например, технические характеристики компьютера включают в себя тактовую частоту процессора, тип материнской платы, объем оперативной памяти и пр. Метеосводка содержит ряд показателей: скорость ветра, температуру и влажность воздуха, атмосферное давление и пр. Допустим, что таких показателей n. Назовем их X1, X2, …, Xn . Они образуют вектор X = col(X1, X2, …, Xn), где col(·) означает вектор-столбец (column), координаты которого записаны строкой. Если показатели X1, X2, …, Xn являются случайными величинами, то в совокупности они образуют случайный вектор X размерности n, или n-мерную случайную величину X.
Возможные значения случайного вектора X будем обозначать x = col(x1, x2, …, xn). Обратим внимание на то, что координаты случайного вектора могут иметь разную физическую природу и измеряться в различных единицах.
Свойства случайного вектора X в общем случае не исчерпываются свойствами его отдельных случайных координат X1, X2, …, Xn . Это объясняется возможной статистической или функциональной зависимостью рассматриваемых случайных величин.
Статистические свойства случайного вектора X полностью оп-
ределяются его n-мерной функцией распределения вероятностей
FX1 , X 2 ,..., X n (x1, x2 , ..., xn ) : |
|
|
|
|
|
|
|
|
|
F |
(x , |
|
|
|
n |
( X |
|
|
|
x , ..., x ) P |
|
i |
x ) |
||||||
X1, X 2 ,..., X n |
1 |
2 |
n |
|
|
i |
(3.1) |
||
|
|
|
|
i 1 |
|
|
|||
P ((X1 x1) ( X 2 |
x2 ) ... ( X n xn )). |
||||||||
|
|
|
|
|
|
|
|
|
107 |
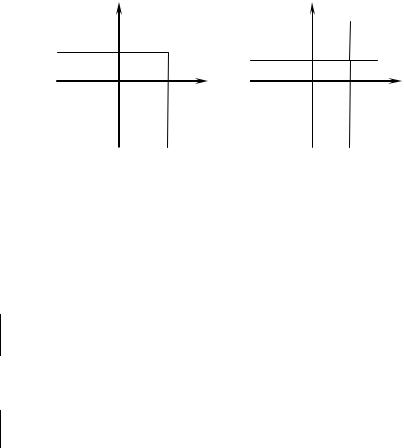
В формуле (3.1) под знаком вероятности стоит произведение событий ( Xi xi ) , i = 1, 2, …, n. В частности, для двумерного случайного вектора (n = 2) функция распределения вероятностей FX1 , X 2 (x1, x2 ) при аргументах (a1, a2) представляет собой вероят-
ность P ((X1 a1 ) (X 2 a2 )) попадания случайного вектора X = col(X1, X2) в прямоугольник, заштрихованный на рис. 3.1, a.
x2 |
|
|
x2 |
|
|
|
|
|
|
a2 |
|
|
b2 |
|
|
D |
E |
|
|
|
|
|
a2 |
|
a1 |
x1 |
a1 b1 |
x1 |
|
|
|
A |
C |
|
a |
|
|
|
|
|
|
б |
||
Рис. 3.1. Иллюстрация к определению (3.1) (a) и свойству (3.6) (б) функции распределения вероятностей FX1, X2 (x1, x2 )
В дальнейшем будем также использовать краткую форму для обозначения функции распределения вероятностей случайного вектора: FX (x1, x2 , ..., xn ) или FX (x) в зависимости от контекста.
Рассмотрим основные свойства функции FX (x1, x2 , ..., xn ) , справедливые для любых типов распределений вероятностей.
1. Для любых xi , i = 1, 2, …, n,
0 ≤ FX (x1, x2 , ..., xn ) ≤ 1. |
(3.2) |
Это утверждение следует из определения FX (x) как вероятности случайного события, состоящего в одновременном выполнении событий ( Xi xi ) , i = 1, 2, …, n.
2. Справедливы следующие равенства:
FX ( , , ..., ) 1, FX ( , , ..., ) 0 . (3.3)
Здесь и далее используются следующие краткие обозначения:
FX ( , , ..., ) lim |
FX (x1, x2 , ..., xn ), |
x1 , x2 ,..., xn |
|
108

FX ( , , ..., ) lim |
FX (x1, x2 , ..., xn ). |
x1, x2 ,..., xn |
|
|
n |
Равенства (3.3) следуют из того, что событие ( X i ) являет- |
|
|
i 1 |
n |
|
ся достоверным, а ( X i ) – невозможным. |
|
i 1 |
|
Первое из равенств (3.3) отражает условие нормировки вероят- |
|
ности, распределенной на множестве возможных значений случайного вектора.
|
3. Пусть X – n-мерный случайный вектор. Тогда для любого k, |
|||||||||||||||||||||||||||||||
1 k n , и произвольных значений |
|
x1, ..., xk 1, |
xk 1, ..., xn |
вероят- |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
X |
|
b ) |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ность события |
(a |
k |
k |
|
( X |
i |
x ) |
, a |
k |
b |
, определяет- |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
i |
|
|
k |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1, i k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ся выражением: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
X |
|
b ) |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P (a |
k |
k |
|
( X |
i |
x ) |
|
|
|
|
|
|
|
|
(3.4) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1, i k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
FX (x1, ..., xk 1, bk , xk 1, ..., xn ) FX (x1, ..., xk 1, ak , |
xk 1, ..., xn ). |
||||||||||||||||||||||||||||||
|
Равенство (3.4) следует из представления случайного события |
|||||||||||||||||||||||||||||||
|
|
|
b ) |
n |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( X |
k |
|
( X |
|
i |
) |
суммой двух несовместных событий: |
|||||||||||||||||||||||||
|
|
k |
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
i 1, i k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
b ) |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( X |
k |
|
( X |
i |
x ) |
= |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1, i k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
a |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
b ) |
|
n |
|
|
|
|
|
|
|||
|
|
= ( X |
k |
k |
) |
|
( X |
i |
x ) |
+ (a |
k |
|
X |
k |
|
|
( X |
i |
x ) |
|||||||||||||
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
k |
|
|
|
|
i |
|
||||||||||
|
|
|
|
|
|
|
i 1, i |
k |
|
|
|
|
|
|
|
|
|
|
|
|
i 1, i k |
|
|
|
|
|
||||||
и последующего применения формулы сложения вероятностей для несовместных событий.
Для n = 2 формула (3.4) принимает следующий вид:
k 1: P ((a1 X1 b1 ) ( X 2 x2 )) FX (b1 , x2 ) FX (a1 , x2 ), |
(3.5) |
k 2 : P((X1 x1 ) (a2 X 2 b2 )) FX (x1 , b2 ) FX (x1 , a2 ). |
|
|
109 |

4. Рассмотрим |
для |
двумерной случайной |
величины |
X = col(X1, X2) |
|
случайное |
событие |
E= ((a1 X1 b1 ) (a2 |
X 2 |
b2 )) . Это случайное событие состоит |
|
в попадании случайной величины X в прямоугольник, заштрихованный на рис. 3.1, б прямой сеткой.
Вероятность события E определяется выражением:
P(E) P((a1 X1 b1 ) (a2 X 2 |
b2 )) |
(3.6) |
|
FX (b1 , b2 ) FX (b1 , a2 ) FX (a1 , b2 ) FX (a1 , a2 ). |
|||
|
|||
Для доказательства равенства (3.6) рассмотрим следующие случайные события, которые выделены на рис. 3.1, б разной штриховкой:
A ((X1 a1 ) ( X 2 a2 )) ; |
B ((X1 b1 ) ( X 2 b2 )); |
C ((a1 X1 b1 ) ( X 2 a2 )); |
D ((X1 a1 ) (a2 X 2 b2 )). |
Случайные события A, C, D и E несовместны и связаны равенством: В = A + C + D + E. Раскрывая вероятности событий A, В, C, D и E с использованием равенств (3.5) и применяя простейшие преобразования, получим равенство (3.6).
5. Вероятность попадания случайного вектора в прямоугольный параллелепипед, определенная в (3.6) для двумерного случайного вектора, может быть обобщена на случай вектора произвольной размерности n:
|
n |
|
ax1 , b1 |
ax2 , b2 |
... axn , bn FX (x1, x2 , ..., xn ) , (3.7) |
P |
(ak X k bk ) |
||||
|
|
|
1 |
2 |
n |
k 1 |
|
|
|
|
|
где оператор ax, b (x) определен выражением:
ax, b (x) (b) (a) .
Равенство (3.7) может быть установлено методом математиче-
ской индукции. |
|
|
6. Одномерная |
функция распределения |
вероятностей |
FX i (xi ) координаты Xi |
случайного вектора X может быть получена |
|
из известной функции |
FX (x1, x2 , ..., xn ) в соответствии с равенст- |
|
вом: |
|
|
FX i (xi ) FX ( , ..., , xi , , ..., ) . |
(3.8) |
|
110 |
|
|
