
Сандаков Векторная алгебра Учебно-методическое пособие 2012
.pdf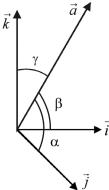
Числа α, , называются координатами вектора a в базисе p, q, r. Пишут также a ( , , ).
Замечание 1.3. Два вектора равны тогда и только тогда, когда равны их соответствующие координаты.
На плоскости и в пространстве справедлива следующая теорема. Теорема 1.6. При сложении любых двух векторов их соответствующие координаты относительно любого базиса складываются, а при умножении вектора на любое число R все координаты
этого вектора умножаются на это число .
В дальнейшем все определения, теоремы и свойства будут сформулированы для пространства. Они автоматически справедливы и для плоскости (достаточно опустить одну координату).
|
Аффинная (косоугольная) система координат в пространстве |
||||||||||||||
определяется выбором начальной точки O (началом координат) и |
|||||||||||||||
какого-либо базиса |
p, q, |
r |
пространства. |
|
|
|
|||||||||
|
Координатами точки М в данной аффинной системе координат |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
называются координаты вектора OM в выбранном базисе p, q, r. |
|||||||||||||||
|
|
|
|
|
|
|
|
то пишут M (x; |
y; z) . Если вектор a задан |
||||||
Если OM xp yq zr, |
|||||||||||||||
своими началом и концом, т.е. |
|
(причем известны коор- |
|||||||||||||
a M M |
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
динаты точек |
M1(x1; y1; z1) |
|
и |
M2(x2; y2; z2) |
в заданной системе |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
находятся по форму- |
||
координат Opqr), |
то координаты вектора a |
||||||||||||||
лам: a (x |
2 |
x ; |
y |
2 |
y ; z |
2 |
z ) . |
|
|
|
|||||
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|||
|
Чаще всего будем иметь дело с декартовой |
|
|||||||||||||
прямоугольной системой координат в про- |
|
||||||||||||||
странстве, которая определяется заданием |
|
||||||||||||||
начальной точки О (началом координат) и ка- |
|
||||||||||||||
кого-либо ортонормированного базиса (ОНБ) |
|
||||||||||||||
e , |
e |
, e . Обычно этот ортонормированный |
|
||||||||||||
1 |
2 |
3 |
|
|
|
j; k . В нем i ; j; k |
|
|
|
||||||
базис обозначают i ; |
|
вза- |
|
||||||||||||
имно-перпендикулярны и по длине равны |
|
||||||||||||||
единице. Обозначим через |
, , углы, обра- |
|
|||||||||||||
зованные вектором |
a |
(a |
|
|
с базисными |
|
|||||||||
0) |
|
||||||||||||||
векторами i ; |
j; k (рис. 1.10). |
|
|
|
|
Рис. 1.10 |
|||||||||
11
Если a (x; y; z) в базисе i ; |
j; k , |
то x |
|
x |
|
cos ; |
|
y |
|
y |
|
cos ; |
||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
z |
|
z |
|
cos . По теореме Пифагора |
|
a |
|
|
|
x2 y2 z2. |
Следователь- |
|||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
но, cos2 cos2 cos2 1, |
|
cos ; |
|
cos ; |
|
|
cos |
|
называются |
|||||||||||||||||||
направляющими косинусами вектора a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Ортом ненулевого вектора |
|
a |
|
(обозначается ea ) |
называется |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
единичный вектор, направление которого совпадает с a . |
|
|
|
|
|
|
||||||||||||||||||||||
Координаты орта вектора a имеют вид: e (cos ; cos ; cos ) . |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|||||||
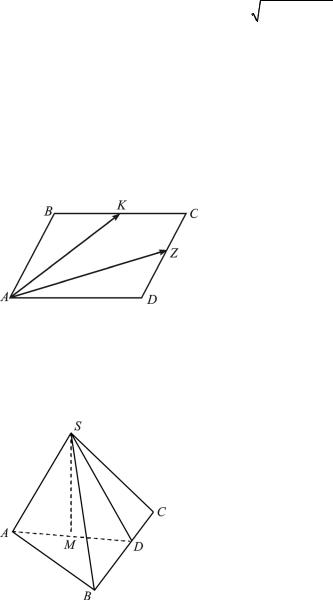
Задача 1.1. Точки K и Z служат серединами сторон BC и CD |
||||||||||||||||||||||||||||
параллелограмма ABCD. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Выразите векторы ВС и |
CD |
через векторы AK и |
AK. |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Из определения ра- |
||||||||||||||||
|
|
|
|
|
|
|
|
венства векторов, суммы векто- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
ров и умножения вектора на |
||||||||||||||||||||
|
|
|
|
|
|
|
|
число следует (рис. 1.11), что |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
AK |
AB BK CD |
2 |
|
|
BC, |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||||||||
|
|
|
|
Рис. 1.11 |
|
|
|
|
|
|
|
AZ |
AD DZ BC |
2 CD. |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разрешая получившуюся систему: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
BC |
CD |
AK; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
BC |
2 |
CD |
AZ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
относительно векторов |
|
|
и |
, |
|||||||||||||||||||
|
|
|
|
|
|
BC |
|
CD |
||||||||||||||||||||
|
|
|
|
|
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
4AZ |
2AK |
|
|
|
2AZ |
|
4AK |
. |
|||||||||||||
|
|
|
|
|
BC |
|
|
|
|
|
3 |
|
|
; CD |
|
3 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
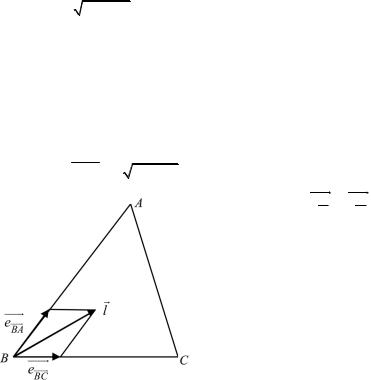
Задача 1.2. Пусть М – точка пере- |
|||||||||||||||||||||
|
|
|
|
|
сечения медиан грани ABC треуголь- |
|||||||||||||||||||||||
|
|
|
|
|
ной пирамиды SABC. Разложите век- |
|||||||||||||||||||||||
|
|
|
|
|
тор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
SM |
по базису e |
SA, |
e |
SB, |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
||||||||||
|
|
|
|
|
e3 SC. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Рис. 1.12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12
|
Решение. Из рис. 1.12 имеем (согласно определению суммы век- |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
торов) SM |
SA |
AM. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Так как точка М является точкой пересечения медиан треуголь- |
||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ника ABC, то AM |
3 |
AD. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.11) |
||||||||||
|
SM |
SA |
3 |
AD . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С другой стороны, |
|
|
|
|
|
|
Так как |
|
1 |
|||||||||||||||||
|
AD |
SD |
SA. |
SD |
2 |
(SB SC), то |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
AD |
|
|
|
|
|
|
|
(1.12) |
||||||||||||
|
|
|
|
|
|
|
2 |
SB |
2 |
SC |
SA. |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Подставляя (1.12) в (1.11), получим |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
||||||||||
|
|
SM |
|
3 |
(SA SB |
SC) |
3 |
e |
3 |
e |
3 |
e . |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
3 |
|
|||||
|
Задача 1.3. На плоскости даны три вектора a (5; 16), |
b (2; 1), |
|||||||||||||||||||||||||
c |
(1; 2). Найдите разложение каждого из них по двум другим. |
||||||||||||||||||||||||||
|
Решение. Заметим, что векторы b |
|
и c |
неколлинеарны. Следова- |
|||||||||||||||||||||||
тельно, векторы b |
и c |
образуют базис на плоскости. Запишем раз- |
|||||||||||||||||||||||||
ложение вектора a |
|
по базису b, |
с |
|
с неизвестными коэффициента- |
||||||||||||||||||||||
ми , : a b c, т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
(5;16) (2;1) (1; 2) (2 ; ) ( ; 2 ) (2 ); 2 ). |
||||||||||||||||||||||||||
|
Приравнивая соответствующие координаты получим: |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
5 2 ; |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 2 . |
|
|
|
|
|
|
|
|
|
||||||||
|
Решая эту систему, найдем 2; |
|
9 . Итак, |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
a 2b 9c. |
|
|
|
|
|
|
|
|
(1.13) |
|||||||||
Из равенства (1.13) находим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
|
9 |
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
||||
|
|
|
|
b 2 a |
|
|
2 c, |
|
|
c |
|
|
9 a |
|
9 c. |
|
|
|
|
|
|||||||
Это разложения векторов b |
|
и c, соответственно, по базисам a, c и |
|||||||||||||||||||||||||
a, b. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13
Задача 1.4. Даны точки А(1; 0; 2), B( 1; 1; 0), C(3; |
5; 2). Най- |
||||||||||||||||||||||||||||||
дите: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
а) координаты вектора 2AB |
BC; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
б) орт и направляющие косинусы вектора |
; |
|
|
|
|
|
|
|||||||||||||||||||||||
|
AB |
|
|
|
|
|
|
||||||||||||||||||||||||
|
в) какой-нибудь вектор, направленный по биссектрисе внут- |
||||||||||||||||||||||||||||||
реннего угла B треугольника ABC. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
( 1 1; 1 0; 0 2) |
|
( 2; 1; 2) ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
А. AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
(3 |
( 1); 5 1; 2 |
0) (4; 4; 2) ; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
BC |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2AB BC ( 2 2 4; 2 1 4; 2( 2) ( 2)) ( 8; 2; 2) . |
|
||||||||||||||||||||||||||||||
Б. Орт вектора |
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
AB обозначим |
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
4 1 |
4 3 ; |
|
|
AB |
|
1 |
|
|
|
2 |
; |
1 |
; |
2 |
; |
||||||||||||||
|
AB |
|
e |
|
|
|
|
AB |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB |
|
|
|
AB |
|
3 |
|
|
|
3 |
|
3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
cos 2 |
; |
cos 1 ; |
|
cos |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В. Найдем орты векторов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
BA и |
BC : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
32 ; 13 ; 32 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
eBA |
eAB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
BC |
|
|
BC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
e |
|
|
|
|
|
|
|
|
3 |
; |
3 |
; |
|
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 4 4 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
BC |
|
|
BC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
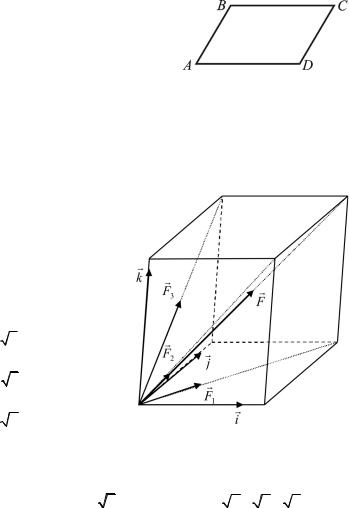
Вектор e eAB eBC |
направ- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лен по биссектрисе внутреннего |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
угла B треугольника ABC (так как |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
является |
|
диагональю |
ромба) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 1.13). |
|
4 |
|
1 |
|
1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
; |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
3 |
3 |
|
. |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вместо |
|
вектора |
|
e |
можно |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
взять |
вектор |
|
(4; 1; 1) , |
колли- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|||||||||||||||||
|
|
|
Рис. 1.13 |
|
|
|
|
|
неарный вектору e |
|
и одинаково |
||||||||||||||||||||
|
|
|
|
|
|
|
|
с ним направленный. |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
14
Задача |
1.5. |
Даны три вершины параллелограмма |
A( 2; 1), |
||||
B(1; 3), C(4; 0). Найдите четвертую вершину D. |
|
|
|||||
Решение. Так как ABCD параллелограмм |
то |
(рис. 1.14) |
|||||
|
|
но |
|
( 3; |
2) . |
Следовательно, |
|
CD |
BA, |
BA ( 2 1; 1 3) |
|||||
|
( 3; |
2) . Обозначим через x и |
|
|
|
|
|
CD |
|
|
|
|
|||
y координаты вершины D параллело- |
|
|
|
|
|||
грамма ABCD, т.е. D(x, y). Тогда |
|
|
|
|
|||
|
x 4; y 0 . |
|
|
|
|
||
CD |
|
|
|
|
|||
Так как, с другой стороны, |
Рис. 1.14 |
CD 3; 2 , , отсюда имеем: |
|
x 4 3; |
y 2. |
Таким образом, координаты вершины D есть пара чисел (1; 2). Задача 1.6. К вершине куба приложены три силы, равные по величине 1, 2, 3 и направленные по диагоналям граней куба, прохо-
дящим через эту вершину. Найдите величину равнодействующей этих трех сил.
Решение. Направим от вершины О по ребрам куба
вектора i , j, k. Тогда данные силы примут вид (рис. 1.15):
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
(i |
j), |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
F |
|
|
|
(i |
k ), |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
F |
|
|
|
|
(k |
j). |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.15 |
|
|
||||||
Равнодействующая этих трех |
|
|
|
|
|
||||||||||||||||
сил F равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
3i |
4 j |
5k |
|
|
3 |
|
4 |
|
5 |
. |
||||||||||
F F |
F |
F |
, или |
F |
; |
; |
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
1 |
|
2 |
|
3 |
|
2 |
|
|
|
|
2 |
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||
Следовательно, величина равнодействующей этих трех сил равна длине вектора F , или
15

|
|
|
|
3 |
2 |
4 2 |
|
5 2 |
|
|
|||||
|
|
|
|
||||||||||||
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
5. |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2 |
|
2 |
|
|
2 |
|
|
||||
|
|
|
|
|
|
||||||||||
Задача 1.7. Даны три некомпланарных вектора a, b, c. Проверь- |
|||||||||||||||
те, будут ли линейно зависимы векторы: |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||
c; |
m a |
b c и |
n |
a |
b |
c. |
|||||||||
В случае положительного ответа указать линейную зависимость, их связывающую.
Решение. Рассмотрим соотношения 1 2m 3n 0.
Подставляя в это равенство выражения для , m и n, получим:
1c 2(a b c) 3(a b c) 0 .
Запишем последнее равенство и виде:
( 1 2)a ( 2 3)b ( 1 2 3)c 0 .
Так как a, b, c линейно независимы (по условию они некомпланарны), то
|
|
|
|
1 3 |
0; |
|
|
|
|
||||
|
|
|
|
|
3 |
0; |
|
|
|
|
|||
|
|
|
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
0. |
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|||||
|
|
|
|
1 |
|
|
|
|
|
|
|||
Очевидно 1 |
2, |
|
2 1, 3 |
1 |
являются ненулевым решением |
||||||||
последней системы. Следовательно, |
|
|
|
|
|||||||||
, |
m и |
n линейно зависимы. |
|||||||||||
Кроме того, 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
m n |
0 . |
|
|
|
|
|
|
|
|
||||
Задачи для самостоятельного решения |
|
|
|||||||||||
1. Определите начало вектора a (2; 3; 1), |
если конец его совпа- |
||||||||||||
дает с точкой М( 2; 1; 3). |
|
|
|
|
|
|
|
|
|||||
2. В треугольнике АВС даны: A( 1; 3; 2), |
|||||||||||||
AB (3; 1; 1) и |
BC |
||||||||||||
=(1; 2; 5). Найдите координаты точек В, С и длину стороны АС.
3.Вектор b составляет с осями ОХ и OY углы α = 60°, β = 120° соответственно. Какой угол он составляет с осью OZ? Найдите ко-
ординаты этого вектора, если b 4.
16
4. |
Найдите |
модуль |
и направляющие косинусы вектора a |
|||
(2; 3; 6). |
|
|
|
|
|
|
5. |
Определите, может ли вектор a |
составлять с координатными |
||||
осями углы: |
|
|
|
|
|
|
а) α = 30°, |
β = 60°, |
|
γ = 150°; |
|
|
|
б) α = 45°, |
β = 60°, |
|
γ = 120°. |
|
|
|
6. |
|
|
(2; 3; 6) и |
( 1; 2; 1) являются сторо- |
||
Два вектора AB |
AC |
|||||
нами треугольника АВС. Найдите векторы, совпадающие с медианами этого треугольника.
7. Два вектора a (4; 3; 0) и b (2; 4; 4) приложены к одной точке. Определите координаты вектора c, направленного по биссек-
трисе угла между векторами a и b, при условии |
|
с |
|
|
4 3. |
||||
|
|
||||||||
8. |
На плоскости даны два вектора |
p |
(1; 2), |
q (0, 3). Найдите |
|||||
разложение вектора a (2; 5) по базису |
p, q. |
|
|
|
|
|
|
||
9. |
Даны три вектора p (2;1;0), |
q (1; 1; 2), |
r (2; 2; 1). |
||||||
Найдите разложение вектора c (3; 7; |
7) по базису |
|
p, q, r. |
||||||
10.Найдите координаты центра тяжести треугольника с верши-
нами А(2; 3; 4); В(3; 1; 2) и С(4; 1; 3)
11.К одной и той же точке приложены две силы Р и Q, действу-
ющие под углом в 120 , причем |P| = 7 и |Q| = 4. Найти величину равнодействующей силы R.
12. Найдите равнодействующую пяти компланарных сил, равных по величине и приложенных к одной и той же точке, зная, что
углы между каждыми двумя последовательными силами равны 72 . |
||||||||||||||
13. Докажите, что для любых трех векторов |
a, b, c и любых |
|||||||||||||
трех чисел , , |
векторы a b; |
b |
c; |
c a линейно за- |
||||||||||
висимы. |
|
|
|
|
|
|
|
|
|
|
|
|
||
14. Даны три некомпланарных вектора a, b, c. Проверьте, будут |
||||||||||||||
ли линейно зависимы векторы: |
|
|
|
|
|
|||||||||
а) |
|
|
|
|
|
|
|
|
|
|||||
|
2a b |
c; |
m 2b |
c |
a и n |
2c a b; |
||||||||
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
c; |
m b |
c и n c a. |
|
|
||||||||
15. В случае положительного ответа указать линейную зависимость, их связывающую.
17

§2. Скалярное произведение двух векторов. Проекция вектора на ось
Скалярным произведением двух векторов
действительное число (скаляр) (обозначение
изведению длин этих векторов на косинус угла
(a, b) a b cos ,
где угол между векторами a и b .
Проекцией вектора a на ось вектора b
прba a cos .
a и b называется (a, b)), равное промежду ними, т.е.
называется число:
С помощью понятия проекции скалярное произведение двух |
||||||||||||
векторов a |
и b |
принимает вид: |
|
|
|
|
|
|
||||
|
|
(a, b) |
|
b |
|
пр a |
|
|
a |
|
пр b. |
(2.1) |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
b |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
||
Справедливы следующие свойства скалярного произведения для |
||
любых векторов a и b и любого R : |
|
|
1) (a, b) (b, a); |
|
|
2) (a b, c) (a, c) (b, c); |
|
|
3) ( a, b) (a, b); |
|
и b ортого- |
4) (a, b) 0 тогда и только тогда, когда вектора |
a |
|
нальны между собой (критерий ортогональности двух векторов); 5) (a, a) 0 для любого a 0 .
Найдем выражение скалярного произведения через координаты
перемножаемых векторов в ортонормированном базисе. |
|
|
и b |
||||||||||
Если в ортонормированном базисе i , |
j, k |
сомножители a |
|||||||||||
имеют координаты a x ; |
y ; |
z , b |
x |
; y |
2 |
; z |
2 |
, то их скалярное |
|||||
1 |
1 |
1 |
2 |
|
|
|
|
|
|
|
|
||
произведение вычисляется по формуле (a, b) x1x2 y1y2 z1z2 . |
|||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
3, |
|
4. |
Задача 2.1. Векторы a и b |
образуют угол 3 , |
a |
b |
||||||||||
Найдите b: 1) (a, b); 2) (3a 2b; a 2b); |
3) (3a 2b)2 |
. |
|
|
|
||||||||
18
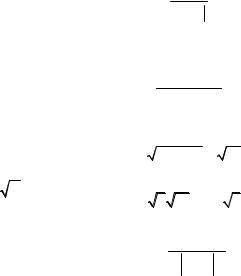
|
|
|
|
|
|
|
|
|
|
|
cos |
2 |
|
3 4 |
|
|
1 |
|
6. |
|
||||
Решение. 1. (a, b) |
a |
|
b |
3 |
|
2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. (3a 2b; a 2b) 3(a, a) 6(a, b) 2(b, a) 4(b, b) |
||||||||||||||||||||||||
3 |
|
|
|
2 |
|
4 |
|
|
|
2 |
3 3 |
2 |
4 |
|
|
|
1 |
4 4 |
2 |
61. |
||||
|
|
|
|
|
|
|||||||||||||||||||
|
a |
|
|
4(a, b) |
|
b |
|
|
|
|
3 4 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
Здесь были использованы свойства 1) 3) скалярного произве-
дения. |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3. (3a |
2b) |
|
|
|
(3a |
2b; 3a |
|
2b) |
9(a, a) 12(a, b) 4(b, b) |
|||||||||||||||||||||||||
9 |
|
|
|
2 |
12 |
|
|
|
|
|
|
|
|
|
1 |
4 |
|
|
|
2 |
9 (3) |
2 |
12 |
|
|
|
1 |
|
4 |
2 |
217. |
|||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
a |
|
|
|
a |
|
|
b |
|
|
|
|
b |
|
|
|
3 4 |
|
4 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
Задача 2.2. Даны два вектора a (1; 1; 0) |
и b |
(2; 0; 1). Най- |
||||||||||||||||||||||||||||||||
дите: 1) угол между векторами a и a 2b; |
2) |
проекцию вектора b |
||||||||||||||||||||||||||||||||
на направление вектора a b. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Решение. 1. Из определения скалярного произведения двух век- |
|||||||||||||||||||||||||||
торов x |
и y |
следует, что угол между этими векторами может быть |
||||||||||||||||||||||||||
найден по формуле |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
cos |
|
|
(x |
, |
|
y) |
. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
y |
|
|
|
|
|
|
a 2b вычис- |
|||||
Согласно этой формуле угол между векторами a и |
||||||||||||||||||||||||||||
ляется по формуле |
|
|
(a, a |
2b) |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
cos |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
a |
2b |
|
. |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Так как |
|
a 2b (1 4; 1; |
0 2( 1)) ( 3; 1; 2), |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
a 2b |
|
9 1 4 14 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 1 0 |
|
|
|
|
|
1 |
|
|
|||||||||||
и |
|
a |
|
|
2, то |
|
cos |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 14 |
|
|
|
7 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
прa bb (b,aa bb) .
19
Так как a b (1 2; 1 0; 0 1) (3; 1; 1) и |
|
a b |
|
|
|
|
9 1 1 |
11, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 2 ( 1) 0 ( 1) ( 1) |
|
|
|
7 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
пр |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|||||||||||||||
|
|
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A( 1; 2; 4), |
|||||||||
Задача 2.3. |
Даны |
|
|
вершины |
треугольника |
|
|
|
|||||||||||||||||||||||||||||||
B( 4; 2; 0), C(3; 2; 1). Найдите: 1) внешний угол при вершине С; |
|||||||||||||||||||||||||||||||||||||||
2) проекцию медианы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
AM |
на сторону BC. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
1. Внешний |
угол |
при |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
вершине С равен углу между векторами |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
AC и CB (рис. 2.1). Из формулы ска- |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
лярного произведения между двумя век- |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
торами следует, что |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
(AC, CB) |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||||||||
Рис. 2.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AC |
C B |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
(3 ( 1); 2 ( 2); 1 4) (4; 0; 3), |
|
|
|
|||||||||||||||||||||||||||||||||||
|
AC |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
( 4 |
|
3; 2 ( 2); 0 |
1) ( 7; 0; 1) |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
CB |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
и |
|
|
|
|
|
|
16 9 5, |
|
|
|
|
49 1 5 |
|
2, |
|
|
|
|
|
||||||||||||||||||||
|
AC |
|
|
|
CB |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
то |
|
|
|
|
|
|
|
|
|
|
cos |
28 3 |
|
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
3 |
|
5 5 2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Следовательно, |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. Так как М середина отрезка [B, C], то координаты точки М |
|||||||||||||||||||||||||||||||||||||||
|
4 3 |
; |
|
2 2 |
; |
0 1 |
|
|
M |
|
1 |
; 2; |
|
1 |
|
|
|
|
|||||||||||||||||||||
имеют вид M |
|
2 |
|
|
|
|
|
2 |
|
2 |
, или |
|
|
2 |
|
2 |
, и |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(AM , BC) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
пр |
AM |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
BC |
|
|
|
|
BC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
7 |
|
|
||||||||
Так как |
AM |
|
2 |
( 1); |
2 |
( 2); |
2 |
|
4 |
|
|
|
; 0; |
2 |
, |
BC |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(3 ( 4); 2 ( 2); 1 0) (7; 0; 1) и |
BC |
|
|
|
|
|
49 1 |
|
50, то |
|
|||||||||||||||||||||||||||||
20
