
Ратушный Лабораторный практикум по курсу Материалы и елементы 2012
.pdf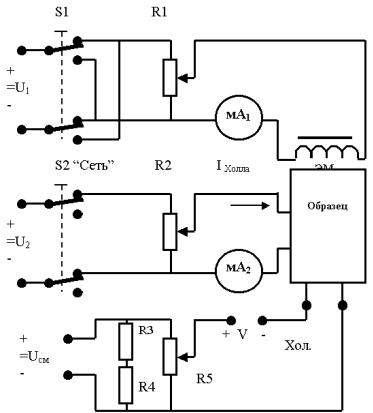
2)электрическая цепь тока, проходящего через образец: пере-
ключатель S2, резистор R2, миллиамперметр mA2 (предел измерения 30 мА).
3)электрическая цепь напряжения смещения: делитель напря-
жения (резисторы R3, R4 и R5), клеммы для подключения вольтметра.
Рис. 3.3. Электрическая схема стенда для экспериментального исследования эффекта Холла
Напряжение смещения Uсм последовательно с εх подается на вольтметр универсальный цифровой В7-38 и позволяет производить измерения не изменяя полярность включения вольтметра.
31

Задание
1.Определить постоянную Холла.
2.Определить концентрацию носителей в образце.
3.Установить тип проводимости изучаемого полупроводника.
4.Рассчитать удельное электрическое сопротивление образца
иопределить материал (вещество), из которого изготовлен образец.
Ход работы
1.Подключить к стенду вольтметр В7-38.
2.Подключить стенд к сети.
3.Резистором R5 установить произвольное значение Uсм.
4.Ввести в щель стенда образец.
5.Включить переключатель S2 в положение «Сеть» (красная
кнопка).
6.Резистором R2 установить минимальный ток по миллиамперметру mA2 (0 – 13 мA), проходящий через испытуемый образец.
7.Включить переключатель S1 в одно из двух положений.
Резистором R1 по миллиамперметру mA1 установить ток электромагнита. Зафиксировать значение алгебраической суммы Ucм+εх по вольтметру В7-38.
8.Переключить S1 в другое положение и повторить замер.
9.Увеличивая резистором R2 ток, протекающий через обра-
зец сделать несколько замеров величины Uсм+εх при обоих положениях переключателя S1.
10.Результаты измерений предоставить в виде табл. 3.2.
Таблица 3.2. Зависимость ЭДС Холла от силы тока, протекающего через образец
Iэм=_____________; Uсм=__________________
Iх, мА
Uсм+εх, В
Uсм - εх, В
32

11.Установить среднее значение Iх.
12.Установить произвольное значение Uсм.
13.Резистором R1 по миллиамперметру mA1 установить минимальное значение тока электромагнита. Измерить алгебраическую
сумму Uсм+εх при обоих положениях переключателя S1; увеличивая резистором R1 ток электромагнита, повторить замеры.
14.Результаты предоставить в виде табл. 3.3.
Таблица 3.3. Зависимость ЭДС Холла от силы тока, протекающего через электромагнит
Iх =_____________; Uсм=__________________
Iэм, мА
Uсм+εх, В
Uсм – εх, В
Обработка результатов
1. Определение постоянной Холла.
Чтобы определить постоянную Холла, нужно рассчитать удель-
ную ЭДС Холла по формуле:
ε* = |
εхb |
, |
(3.11) |
|
I |
||||
|
|
|
где εх –ЭДС Холла, полученная по формуле (3.13); b – толщина образца; I – ток, протекающий через образец.
При этом стоит заметить, что удельная ЭДС Холла ε* |
прямо |
пропорциональна индукции магнитного поля B: |
|
ε* = RxB, |
(3.12) |
где Rx – постоянная Холла.
Затем построить график зависимости ε*(В) и по тангенсу угла наклона прямой определить постоянную Холла.
) При экспериментальном определении ЭДС Холла следует обратить внимание на то, что наряду с эффектом Холла наблюдаются также некоторые другие гальваномагнитные эффекты: эффект Эттинсгаузена, эффект Нернста, а также термомагнитные эффекты: поперечный эффект Эттинсгаузена–Нернста, поперечный эффект Риги–Ледюка, продольный
33
эффект Эттинсгаузена–Нернста и другие. Для исключения влияния побочных эффектов используют четность этих эффектов, т. е. их независимость от направления магнитного поля. Между тем, эффект Холла, являясь нечетным, меняет свой знак при изменениинаправлениямагнитного поля.
Для того чтобы исключить побочные эффекты и определить истинное значение ЭДС Холла, напряжение между холловскими контактами измеряют при двух направлениях магнитного поля. Действительно, при выбранном направлении магнитного поля напряжение между холловскими контактами U1 = εх + εдоб, при изменении направления магнитного поля на противоположное напряжение – U2 = εх + εдоб. Отсюда
εх |
= |
|
|
U1 |
|
+ |
|
U2 |
|
|
, |
(3.13) |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
|
|||||
т.е. εдоб, обусловленное побочными четными эффектами, исключается.
2.По Rх (постоянной Холла) и εх (ЭДС Холла) определить концентрацию носителей в образце и установить тип изучаемого образца.
3.Расчет удельного электрического сопротивления образца.
Для определения удельного электрического сопротивления
изучаемого полупроводника, нужно измерить электрическое сопротивление между двумя контактами, расположенными на длинной поверхности образца на расстоянии l. С этой целью, необходимо пропустить электрический ток I вдоль длины образца и измерить падение напряжения U между указанными контактами. Затем удельное электрическое сопротивление рассчитать по формуле:
ρ = |
U |
|
bd |
, |
(3.14) |
|
I |
l |
|||||
|
|
|
|
где b, d – поперечное сечение образца.
4. По величине ρ (удельного электрического сопротивления),
определить материал (вещество), из которого изготовлен образец.
Данные для проведения расчетов:
1.Размеры испытуемого образца: l = 6 мм; d = 2 мм; b = 1 мм.
2.Количество витков электромагнита w = 9080.
3.Длина средней силовой линии магнитного поля электромаг-
нита lм = 0,414 м.
4.Абсолютная магнитная проницаемость электростали μμ0 =
=0,015 Гн/м.
34

5. Индукция магнитного поля: B =μμ0 Iэм w. lм
Отчет о работе
Отчет должен содержать:
1)название и цель работы;
2)краткие теоретические сведения и расчетные формулы;
3)результаты измерений;
4)расчеты постоянной Холла, ЭДС Холла, концентрации но-
сителей в образце, удельного электрического сопротивления. График зависимости ε*(В);
5)установленный тип изучаемого образца и материал (вещество), из которого изготовлен образец;
6)вывод по работе.
Контрольные вопросы
1.В чем заключается эффект Холла? Какова причина классического эффекта Холла?
2.Как вычисляется концентрация носителей заряда?
3.Что понимают под термином подвижность носителей тока?
Как связаны подвижность носителей тока с электропроводностью вещества? Как определяется подвижность носителей?
4.Каким образом производят вывод выражения для расчета ЭДС Холла? Какие существуют способы ее экспериментального определения?
35
Лабораторная работа № 4
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ЛИНЕЙНОГО РАСШИРЕНИЯ ТВЕРДЫХ ТЕЛ
Цель работы: изучить метод определения коэффициента линейного расширения.
Теоретические сведения
Для объяснения теплового расширения твердых тел необходимо принимать во внимание тот факт, что силы взаимодействия между атомами в решетке не совсем упругие, т.е. они зависят от смещения атомов из положения равновесия не линейно, а содержат ангармонические члены второй и более высоких степеней, влияние которых возрастает с ростом температуры.
Рассмотрим простую модель двух атомов, расположенных по соседству. Допустим, что между этими атомами имеет место упругая сила взаимодействия. Тогда линейной зависимости силы от смещения х атома из положения равновесия при х = х0 будет соответствовать параболический ход потенциальной энергии:
U (x) = |
Cx2 |
=βx |
2 |
, |
(4.1) |
2 |
|
||||
|
|
|
|
|
где С = 2β – коэффициент квазиупругой силы.
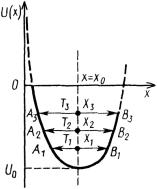
Как видно из рис. 4.1, при температуре Т1 атомы колеблются так, что межатомное расстояние изменяется от А1 до В1 со средним значением <х1> = х0, при Т2 межатомное расстояние меняется от А2 до В2 со средним значением <х2> = х0 и т.д. Поскольку кривая потенциальной энергии симметрична относительно прямой <х> = х0,то <х> не зависит от амплитуды колебаний атомов и остается равным х0 при любой температуре.
Таким образом, расстояние между атомами, совершающими гармонические колебания, при нагревании не изменяется, так как их среднее смещение <х> = 0, а следовательно, и тепловое расширение должно отсутствовать, что противоречит реальной ситуации. Все твердые тела при нагревании расширяются. Относительная величина этого расширения на один градус для большинства твердых
36
тел порядка 10-5. В табл. 4.1 приведены значения коэффициентов линейного расширения для некоторых веществ.
Рис. 4.1. Зависимость потенциальной энергии от смещения атома
без учета ангармонических членов;
T1<T2<T3
Таблица 4.1. Температурные коэффициенты линейного расширения для разных веществ (при комнатной температуре)
Вещество |
α, 106 К-1 |
Вещество |
α, 106 К-1 |
Li |
56 |
Fe |
12 |
B |
2 |
Co |
12 |
Cu |
16,6 |
Ag |
19 |
Ga |
18 |
Cd |
32,5 |
Ge |
5,8 |
Au |
14 |
Тепловое расширение решетки обусловлено асимметрией взаимодействия между атомами, вызванной тем, что сила отталкивания возрастает быстрее при сближении атомов, чем сила притяжения при их удалении друг от друга. Это приводит к непараболическому виду кривой потенциальной энергии взаимодействия (рис. 4.2):
|
|
|
|
|
|
U(x) = –U0 + βx2 – gx3 + ..., |
(4.2) |
||||||
|
1 |
d 2U |
|
g = − |
1 |
d 3U |
|
||||||
где β = |
|
|
|
|
|
, |
|
|
|
|
. |
|
|
2 |
dx |
2 |
6 |
|
3 |
|
|||||||
|
|
|
x= x0 |
|
|
dx |
|
x=x0 |
|
||||
При температуре Т1 атомы колеблются так, что межатомное расстояние изменяется от А1 до В1 со средним значением <х1> (cм. рис. 4.2) . При более высокой температуре Т2 межатомное расстояние изменяется от А2 до В2 со средним значением <х2> > <х1> и т.д.
37
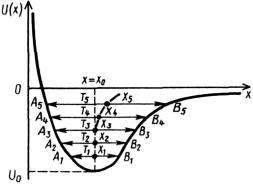
Так как <х1> < <х2> < <х3>, то твердое тело с повышением температуры расширяется.
Рис. 4.2. Зависимость потенциальной энергии взаимодействия между двумя атомами с учетом ангармонических членов; T1<T2<T3
Расширение твердых веществ при нагревании происходит одинаково по всем направлениям. Однако во многих случаях на практике приходится учитывать расширение только в одном направлении. Изменение одного определенного размера твердого тела при изменениях температуры называется линейным расширением (линейным сжатием). Рассмотрим особенности этого расширения.
Пусть дан стержень, длина которого при 0 °С равна l0, а при температуре t равна lt. Следовательно, изменение длины стержня при его нагревании на t = t – 0 = t будет равно l = lt – l0. На основании опытов легко установить, что изменение длины стержня
l прямо пропорционально приросту температуры |
t и его длине |
при 0 °С l0, т.е. |
|
l = αl0t. |
(4.3) |
Зависимость l от рода вещества выражается коэффициентом пропорциональности α.
Величина α, характеризующая зависимость линейного расширения при нагревании от рода вещества и внешних условий, называется коэффициентом линейного расширения. Коэффициент линейного расширения показывает, на какую часть длины тела, взя-
того при 0 °С, изменяется его длина при нагревании на 1 °С: |
|
||
α = |
l |
l . |
(4.4) |
|
t |
|
|
|
0 |
|
|
38
Вычислим длину тела при различных температурах по известной длине l0. Из (4.3) имеем
lt – l0 = αl0t
или |
|
lt = l0(1 + αt). |
(4.5) |
Чтобы по длине тела l1 при температуре t1 найти его длину l2 при температуре t2, вообще говоря, сначала нужно найти l0 с помощью формулы (4.5), а затем по этой же формуле вычислить l2. Однако, учитывая, что α – очень маленькое число, l2 можно находить по следующей приближенной формуле:
l2 ≈ l1[1 + α(t2 – t1)]. |
(4.6) |
Из формулы (4.6) получаем приближенную формулу для вычисления коэффициента линейного расширения твердого вещества:
α = |
|
l2 −l1 |
|
. |
(4.7) |
||
|
|
) |
|||||
|
l (t |
2 |
−t |
|
|
||
|
1 |
|
1 |
|
|
|
|
Описание установки
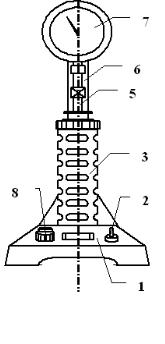
Данная установка (рис. 4.3) состоит из корпуса 1, к которому крепится защитный кожух 3, а также кнопочный выключатель 2 и индикаторная лампа 8. В защитном кожухе находится стеклянная пробирка 4, в которую вставляется стержень 5. Для измерения относительного удлинения к стойке 6 с кронштейном крепится индикатор малых перемещений 7. В защитном кожухе также находится нагреватель.
Принцип работы прибора очень прост: испытуемый образец твердого тела помещается в стеклянную пробирку с водой. Изменение длины нагретого образца по сравнению с его первоначальной длиной (при комнатной температуре) измеряется индикатором малых
Рис. 4.3. Схематическое изображение измерительной установки
39
перемещений и вводится в известную формулу для определения линейного расширения.
Задание
1. Определить коэффициент линейного расширения твердых
тел.
2. Рассчитать относительную погрешность.
Ход работы
1.Пробирки наполнить на 0,5 объема водой комнатной температуры, опустив в каждую по испытуемому стержню сферическим концом вниз.
2.Поместить пробирки в штатив.
3.В поворотный кронштейн вставить индикатор и отвести его на четверть оборота в сторону до упора.
4.Пробирку с испытуемым стержнем через резиновую прокладку и отверстие в крышке прибора ввести в нагреватель.
5.Замерить положение стрелки на шкале индикатора (для первого опыта стрелку лучше ставить на нулевую отметку).
6.Только после этого можно включить питание прибора кнопочным выключателем. При этом должна загореться индикаторная лампа. При закипании воды в пробирке испытуемый образец принимает температуру, равную температуре кипения воды. Увеличение длины образца определяется по отклонению стрелки индикатора от первоначального положения. Отсчет ведут с точностью до половины деления шкалы индикатора, т.е. с точностью до 5 мкм.
7.Кнопочным выключателем отключить питание прибора.
8.Индикатор на поворотном кронштейне отвести в сторону до упора, предварительно оттянув шток индикатора вверх.
9.Извлечь из прибора нагретую пробирку и поместить ее в штатив.
Внимание! Нагретую пробирку извлекать только с помощью
специального держателя.
10. Повторить операции для другого образца.
Для более точного определения коэффициента линейного расширения рекомендуется проводить несколько замеров (минимум 5)
40
