
Демина Геометрические принтсипы теории функтсиы комплексного 2015
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ЯДЕРНЫЙ УНИВЕРСИТЕТ «МИФИ»
М.В. Демина
ГЕОМЕТРИЧЕСКИЕ ПРИНЦИПЫ ТЕОРИИ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Рекомендовано к изданию УМО «Ядерные физика и технологии»
Москва 2015
УДК 517.54(075.8) ББК 22.16я7 Д 30
Демина М.В. Геометрические принципы теории функций комплексного переменного: Учебное пособие. − М.: НИЯУ МИФИ, 2015. − 72 с.
В настоящем учебном пособии рассматриваются некоторые вопросы теории функций комплексного переменного, не входящие в классический курс. Пособие включает в себя разделы, посвященные распределению нулей однозначных аналитических функций, общей теории конформных отображений, а также применению конформных отображений при решении задач математической физики. Каждый раздел содержит необходимый набор теоретических сведений, подробные решения наиболее важных типовых задач, а также задачи для самостоятельной работы.
Пособие предназначено для студентов НИЯУ МИФИ, обучающихся по направлению «Прикладная математика и информатика», а также может быть использовано студентами и аспирантами высших технических учебных заведений при изучении курса «Теория функций комплексного переменного» по расширенной программе.
Подготовлено в рамках Программы создания и развития НИЯУ МИФИ.
Рецензент доц., канд. физ.-мат. наук В.Б. Шерстюков.
ISBN 978-5-7262-2109-0 |
♥ Национальный исследовательский |
|
ядерный университет «МИФИ», 2015. |
Оглавление
Предисловие . . . . . . . . . . . . . . . . . . . . . . . . . |
4 |
1.Приращение аргумента аналитической функции
|
вдоль кривой . . . . . . . . . . . . . . . . . . . . . . |
5 |
2. |
Принцип аргумента и распределение нулей . . . . |
8 |
3. |
Общие вопросы теории конформных отображений |
17 |
4.Принцип симметрии . . . . . . . . . . . . . . . . . . 36
5.Конформные отображения многоугольников . . . 49
6.Решение двумерных краевых задач
математической физики . . . . . . . . . . . . . . . |
58 |
Список литературы . . . . . . . . . . . . . . . . . . . . . |
71 |
3
Предисловие
Геометрическая теория функций комплексного переменного изучает классы функций, определяемые какими–либо геометрическими свойствами, и наоборот, геометрические свойства различных классов функций. Например, одной из задач геометрической теории является исследование существования и единственности конформного отображения некоторой области на другую, включающее в себя нахождение классов функций, осуществляющих такие отображения.
В учебном пособии большое внимание уделяется применению принципа симметрии и формулы Кристоффеля–Шварца при построении конформных отображений, подробно рассматриваются задачи распределения нулей однозначных функций и многочленов, играющие большую роль в теории устойчивости решений дифференциальных уравнений и систем, описывается метод решения ряда задач математической физики, основанный на построении некоторого конформного отображения для заданной области.
Предполагается, что читатели знакомы с ключевыми понятиями теории функций комплексного переменного, такими как область, аналитическая функция, кривая Жордана и т.п.
4

1.Приращение аргумента аналитической функции вдоль кривой
1.Приращение аргумента аналитической функции вдоль кривой
Пусть γ — ориентированная гладкая или кусочно-гладкая кривая. Рассмотрим функцию f(z), аналитическую и не обращающуюся в нуль на γ. Приращением аргумента функции f(z) вдоль кривой γ называют число
∫
∆γ arg f = Im |
γ |
|
dz. |
(1.1) |
f(z) |
С геометрической точки зрения приращение аргумента функции f(z) вдоль кривой γ представляет собой угол поворота вектора w = f(z) от начальной точки f(a) до конечной f(b), где a
— начальная точка кривой γ, b — конечная. Напомним, что функция f(z) является аналитической на некоторой кривой γ, если найдется такая область D C, целиком содержащая эту кривую, что функция f(z) будет аналитична в области D.
При практическом подсчете приращений аргумента удобно использовать следующее утверждение.
Утверждение 1.1. Для функций f1(z) и f2(z), аналитических и не обращающихся в нуль на ориентированной гладкой или кусочно-гладкой кривой γ, справедливы равенства
∆γ arg(f1f2) = ∆γ arg f1 + ∆γ arg f2, |
|
||||
|
|
1 |
= −∆γ arg f1 |
(1.2) |
|
∆γ arg |
|
|
|||
f1 |
|
||||
и, как следствие, |
|
|
|
|
|
∆γ arg |
f1 |
= ∆γ arg f1 − ∆γ arg f2. |
(1.3) |
||
f2 |
|||||
Рассмотрим примеры.
5
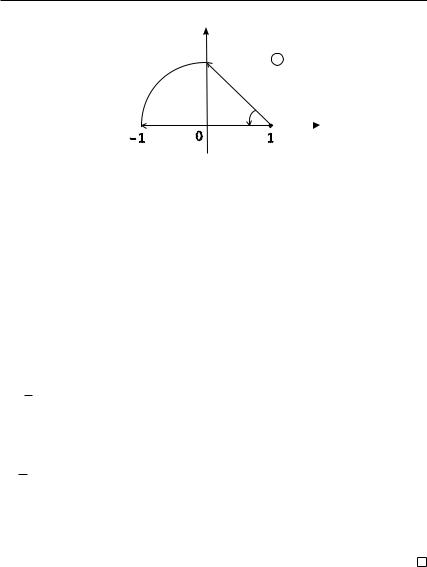
1. Приращение аргумента аналитической функции вдоль кривой
|
|
|
y |
|
|
|
|
|
|
i |
z |
|
|
|
|
|
γ |
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
Рис. 1.1 |
|
|
|
Задача 1.1. |
Найти приращение |
аргумента |
функции |
|||
f(z) = z(z − 1)2 |
вдоль четверти окружности: z = |
eiφ, φ |
||||
|
π |
|
|
|
|
|
[ |
|
, π]. |
|
|
|
|
2 |
|
|
|
|
||
Решение. Используя утверждение 1.1, находим: |
|
|||||
|
|
∆γ arg f = ∆γ arg z + 2∆γ arg(z − 1). |
(1.4) |
|||
Приращение ∆γ arg z равняется углу поворота вектора z от начальной точки i до конечной −1. Другими словами, ∆γ arg z = = π2 . Аналогично приращение ∆γ arg(z − 1) равняется углу поворота вектора z − 1, когда точка z пробегает по кривой γ от начальной точки до конечной. Начальное и конечное положения вектора z − 1 изображены на рис. 1.1. Тогда ∆γ arg(z − 1) = = π4 . Соответствующий угол на рис. 1.1 обозначен символом β. Окончательно получаем
∆γ arg f = |
π |
+ 2 · |
π |
= π. |
(1.5) |
2 |
4 |
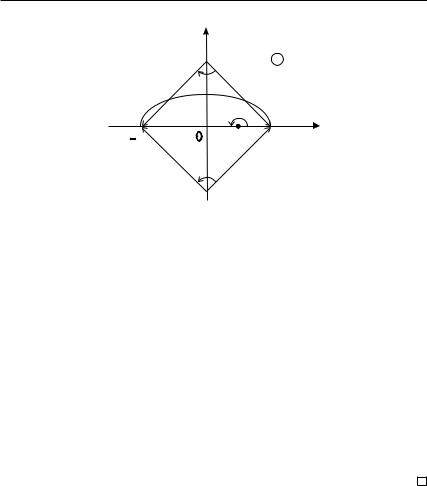
Задача 1.2. |
Найти приращение аргумента функции |
||
f(z) = |
z2 + 4 |
|
вдоль кривой: z = 2 cos φ + i sin φ, φ [0, π]. |
(z − 1)2 |
|||
6
1. Приращение аргумента аналитической функции вдоль кривой
|
y |
|
2 i |
z |
|
i |
β1 |
|
|
||
γ |
β3 |
|
|
||
2 |
x |
|
2 |
||
|
||
|
β2 |
Рис. 1.2
Решение. Раскладывая числитель функции f(z) на множители и используя соотношения (1.2), (1.3), получаем:
∆γ arg f = ∆γ arg(z + 2i) + ∆γ arg(z − 2i) − 2∆γ arg(z − 1).
Кривая γ представляет собой дугу эллипса (см. рис. 1.2). Углы поворота векторов z −2i, z + 2i, z −1, когда точка z пробегает по кривой γ от начальной точки до конечной, на рис. 1.2 обозначены
символами |
β1, |
β2, β3 соответственно. Нетрудно убедиться в |
||||||||||
|
|
|
π |
|
|
|
|
|
||||
том, что β1 = |
−β2 = − |
|
, β3 |
= π. Следовательно, искомое |
||||||||
2 |
||||||||||||
приращение аргумента равняется |
|
|
|
|||||||||
|
|
|
|
|
π |
π |
|
|
(1.6) |
|||
|
|
∆γ arg f = |
− |
|
+ |
|
− 2 · |
π = −2π. |
|
|||
|
|
2 |
2 |
|
||||||||
Задача |
1.3. |
Найти |
приращение |
аргумента |
π |
функции |
||||||
f(z) = z2 − 1 вдоль кривой: z = 2 cos φ + 5i sin φ, φ [ |
, π]. |
|||||||||||
|
||||||||||||
2 |
||||||||||||
Ответ: ∆γ arg f = π.
Задача 1.4. Найти приращение аргумента |
|
функции |
||
f(z) = |
z + i |
вдоль дуги окружности: z = eiφ, φ [0, |
π |
]. |
|
|
|||
z − i |
4 |
|||
Ответ: ∆γ arg f = 0.
7

2.Принцип аргумента и распределение нулей
2.Принцип аргумента и распределение нулей
Сприкладной точки зрения большой интерес представляет задача об исследовании расположения на комплексной плоскости нулей некоторой функции f(z).
Теорема 2.1 (Принцип аргумента). Пусть функция f(z)
аналитична в замыкании области D за исключением, быть может, конечного числа полюсов, расположенных в D, и не обращается в нуль на границе ∂D области D, представляющей собой замкнутую гладкую или кусочногладкую кривую Жордана. Тогда разность между числом нулей Nf, D и числом полюсов Pf, D функции f в области D равна алгебраическому числу оборотов, которые совершает вектор w = f(z) вокруг точки w = 0 при обходе точкой z кривой ∂D один раз в положительном направлении.
Заметим, что число нулей необходимо считать с учетом их кратностей, а число полюсов — с учетом порядков. В каждой точке кривой ∂D определены значения аргумента функции f, поскольку функция аналитична и не обращается в нуль на кривой ∂D. Алгебраическое число оборотов, о котором идет речь в этой теореме, равно деленному на 2π приращению аргумента функции f при обходе точкой z кривой ∂D один раз в положительном направлении. Таким образом, утверждение теоремы 2.1 можно записать в виде
1 |
|
(2.1) |
|
2π ∂D arg f = Nf, D − Pf, D. |
|||
|
|||
Теорема 2.2 (Теорема Руше). Пусть функции f(z), g(z)
аналитичны в замыкании области D, и на границе ∂D, представляющей собой замкнутую гладкую или кусочногладкую кривую Жордана, выполнено неравенство |f(z)| > > |g(z)|. Тогда функции f(z) и f(z) + g(z) имеют одинаковое число нулей в области D: Nf,D = Nf+g,D.
8

2. Принцип аргумента и распределение нулей
Из теоремы Руше непосредственно следует справедливость основной теоремы алгебры.
Теорема 2.3 (Основная теорема алгебры).
Любой многочлен степени n имеет на комплексной плоскости ровно n нулей с учетом их кратностей.
Задача 2.1. Найти количество нулей многочлена P (z) = z8 + + 2z5 + 5z − 1 в круге K1 = {z C : |z| < 1}.
Решение. Представим многочлен P (z) в виде P (z) = f(z) + + g(z), где f(z) = 5z, g(z) = z8 + 2z5 − 1. Тогда на окружности z = eiφ, φ [0, 2π) справедливы соотношения: |f(eiφ)| = 5,
|g(eiφ)| ≤ |e8iφ| + |2e5iφ| + 1 = 4. Таким образом, |f(eiφ)| > > |g(eiφ)|. Многочлен f(z) = 5z в круге K1 имеет один простой нуль: Nf, K1 = 1. Согласно теореме Руше, количества нулей многочленов P (z) и f(z) в круге K1 совпадают. Окончательно имеем NP, K1 = Nf, K1 = 1.
Задача 2.2. Найти количество нулей многочлена P (z) = = z5 − 2z4 − 2z3 + z2 + 7z − 3 в круге K = {z C : |z − 1| < 1}.
Решение. Для удобства дальнейших вычислений сделаем замену s = z − 1. Тогда задача нахождения нулей многочлена P (z) в круге K сводится к задаче нахождения нулей многочлена Q(s) = P (s + 1) в круге S = {s C : |s| < 1}. Многочлен Q(s) выглядит следующим образом: Q(s) = s5 +3s4 −7s2 +2. Разобьем многочлен Q(s) на сумму двух многочленов Q(s) = f(s) + g(s), где f(s) = −7s2, g(s) = s5 + 3s4 + 2. На окружности s = eiφ, φ [0, 2π) имеют место соотношения: |f(eiφ)| = | − 7e2iφ| = 7,
|g(eiφ)| ≤ |e5iφ|+|3e4iφ|+2 = 6. Следовательно, |f(eiφ)| > |g(eiφ)|. Многочлен f(s) = −7s2 в круге S имеет один нуль кратности два: Nf, S = 2. Воспользуемся теоремой Руше, получим NQ, S =
= Nf, S = 2. Тогда NP, K = NQ, S = 2.
9

2. Принцип аргумента и распределение нулей
C III |
IV |
I II |
III IV |
I |
II |
|
v |
- - |
|
+ |
+ |
- - |
+ |
+ |
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
u |
- |
+ |
|
+ |
- |
- |
+ |
+ |
- |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-3 |
- |
3 |
-1 0 |
|
1 |
3 |
3 |
y |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Рис. 2.1 |
|
|
|
|
|
|
Задача |
2.3. Найти |
количество |
нулей многочлена P (z) = |
|||||||||
= z5 − z3 + 2z2 − z + 6 в кольце G = {z C : 1 < |z| < 2}. |
|
|
||||||||||
Решение. Сначала найдем число нулей многочлена P (z) в
круге K2 = {z C : |z| < 2}. Представим многочлен P (z) в
виде: P (z) = f1(z)+g1(z), где f1(z) = z5, g1(z) = −z3 +2z2 −z+6. На окружности z = 2eiφ, φ [0, 2π) справедливы соотношения:
|f1(2eiφ)| = |25e5iφ| = 32, |g1(2eiφ)| ≤ |23e3iφ|+|23e2iφ|+|2eiφ|+6 =
=24. Следовательно, |f1(2eiφ)| > |g1(2eiφ)|. Многочлен f1(z) =
=z5 в круге K2 имеет один нуль кратности пять: Nf1, K2 = 5. По теореме Руше находим NP, K2 = Nf1, K2 = 5. Далее рассмотрим круг K1 = {z C : |z| < 1}. Определим, сколько нулей многочлена P (z) попадает в круг K1. Разбивая многочлен P (z)
следующим образом: P (z) = f2(z) + g2(z), где f2(z) = 6, g1(z) = = z5 − z3 + 2z2 − z, находим |f2(eiφ)| = 6, |g2(eiφ)| ≤ |e5iφ| + + |e3iφ| + |2e2iφ| + |eiφ| = 5, φ [0, 2π). Тогда |f2(eiφ)| > |g2(eiφ)|.
Многочлен f2(z) = 6 вообще не имеет нулей. Следовательно, по теореме Руше в круге K1 нет нулей многочлена P (z). Таким образом, все пять нулей многочлена P (z) находятся в кольце G:
NP, G = NP, K2 − NP, K1 = 5.
Задача 2.4. Доказать, что многочлен P (z) = azn + z − 1, где n ≥ 2 — целое число, a C, a ≠ 0 имеет хотя бы один нуль в
10
