Белобородов Надежност тестов 2012

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ЯДЕРНЫЙ УНИВЕРСИТЕТ «МИФИ»

В.Н. Белобородов

Надежность тестов

Рекомендовано УМО «Ядерные физика и технологии» в качестве учебно-методического пособия

Москва 2012

легко понять, если учесть что при неизменном суммарном числе заданий теста на отдельный раздел заданий становится меньше, что увеличивает случайную погрешность измерения.

Помимо случайных погрешностей существуют систематические погрешности. Если стрельба из винтовки ведется кучно, но центр попаданий смещен относительно центра мишени, то прицел явно сбит. В случае тестирования задания могут проверять не совсем то или совсем не то, для чего их намеревались использовать. В тестировании соответствие теста и цели тестирования в самом общем понимании называется валидностью теста, т.е. пригодностью теста. Если для проверки знания механики используются тесты, содержащие задания по другим разделам физики, то такое тестирование является содержательно невалидным. То же можно сказать и про тест по механике для россиян, если его использовать без перевода в стране с другим государственным языком. Тест может оказаться невалидным по причине низкого качества отдельных тестовых заданий [1, 2].

Точность определения уровня подготовки обучающихся в некоторых случаях лимитируется «ценой деления» – это, как правило, единица на шкале суммы баллов за отдельные задания. Если максимальный балл за тест 10, то 1 балл определяет относительную погрешность отсчета 1/10 = 10%.

В современной теории тестирования акцент сделан на выполнении не теста в целом, а отдельных его заданий. При этом предполагается реализованным условие независимости результатов выполнения заданий в группе испытуемых с одинаковой подготовкой. Если классическая теория тестирования оперирует вероятностью выполнения заданий Р, то в современной теории тестирования обычно анализируются шансы выполнения заданий Р/(1 – Р) или логарифмы от шансов. Такое логарифмическое преобразование объекта математического исследования растягивает область значений вероятности [0, 1] на всю числовую ось для логарифма шансов.

Отдельной проблемой является технологическая надежность теста. Речь идет о правильности распознавания и оценивания ответов обучающихся. Ошибки распознавания ответов характерны для бумажной формы тестирования. В случае компьютерного тестирования ошибки распознавания, как правило, исключаются. Ошибки оценивания возникают при проверке экспертами выполнения зада-

5

ний с развернутым ответом. Уменьшение влияния случайных ошибок экспертов достигается на этапе проведения экзамена введением нескольких независимых проверок выполнения заданий. В дальнейшем изложении предполагается, что технологически тесты надежны.

1.НАДЕЖНОСТЬ ТЕСТА

ВКЛАССИЧЕСКОЙ ТЕОРИИ ТЕСТИРОВАНИЯ

Надежность в классической теории тестирования – мера воспроизводимости результата тестирования при использовании эквивалентных, или параллельных, форм теста. Параллельная форма теста – другой вариант теста, собранный по тем же правилам из других заданий одного банка заданий, характеризующих проверяемую область знаний. Процедуры, позволяющие оценивать надежность тестов, могут быть пояснены следующими примерами. Пример 1 – оценка у разных преподавателей одного и того же учащегося по одному предмету. Пример 2 – повторное тестирование эквивалентным тестом – ретестовая надежность. Надежность как величина – коэффициент корреляции результатов по параллельным формам теста. В классической теории тестирования по умолчанию применяются методы, основанные на предположении о применимости к результатам тестирования нормальной функции распределения, для которой разработан достаточно обширный математический аппарат. В качестве количественной меры надежности теста используется коэффициент корреляции результатов выполнения параллельных форм тестов Rxx′ (X и X′ – баллы за параллельные

формы теста). Максимальное значение коэффициента корреляции R = 1 соответствует абсолютно надежному тесту, минимальное значение коэффициента корреляции R = –1 соответствует самому ненадежному тесту, вернее его назвать «антинадежным», если такое значение получается при вычислении корреляции результатов по исследуемому тесту и по всем другим возможным тестам. «Антинадежный» тест, как легко понять, можно сделать надежным простой перекодировкой результатов. Поэтому будем по умолчанию считать, что R ≥ 0. Ненадежный тест имеет коэффициент корреляции, близкий к нулю со всеми остальными тестами. Нулевой коэффициент корреляции означает отсутствие значимой зависимости между результатами выполнения разных форм тестов.

6

Если сложить m эквивалентных тестов в один, то надежность результирующего теста изменяется (увеличивается). Для вычисления надежности результирующего теста используем (пока без вывода) формулу Спирмена–Брауна [1]:

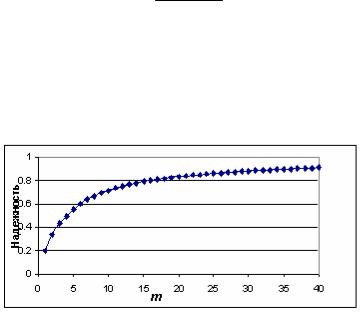
где R – надежность отдельного компонента. Из формулы (1.1) получаем, что при m → ∞ R→1. Отсюда следует, что надежность теста можно повышать, увеличивая его длину, т.е. количество заданий. Поэтому для получения тестов приемлемой надежности используется, как правило, несколько десятков заданий. Зависимость надежности теста от его длины изображена на рис. 1.1.

Рис.1.1. Надежность теста как функция количества частей m в тесте при надежности одной части R = 0,2

Из рис. 1.1 видно, что при надежности исходного теста 0,2 надежность 0,9 достигается увеличением его длины в 35 раз. Легко проверить, что при исходной надежности теста 0,5 надежность 0,9 достигается увеличением длины теста только в 9 раз. Таким образом, увеличение длины теста является экстенсивным способом повышения надежности теста. Более целесообразно повышать надежность на основе содержательного подхода.

Так как повторное тестирование по эквивалентному тесту в большинстве случаев нереально (за исключением физиологического), интересующий тест разбивают на две эквивалентные части

7

равной длины и применяют частный случай формулы Спирмена– Брауна для m = 2

где r – коэффициент корреляции баллов по половинам одного и того же теста. Разбиение теста на половины должно проводиться так, чтобы они были максимально эквивалентны. Самый простой способ – разделение исходного теста на два, состоящих из четных и нечетных заданий соответственно. Возможно проведение предварительного ранжирования заданий по трудности с последующим разделением на четные и нечетные.

Существуют методы расчета надежности теста, основанные на вычислении дисперсий результатов отдельных частей теста и теста как целого. Используются формулы Кронбаха и Кудера–Ричардсо- на, Рюлона и их модификации [3].

Считается, что тест по надежности пригоден к использованию для диагностических целей, если R ≥0,7. При проведении аттестационных экзаменов используются тесты, для которых R ≥0,9 [2].

Расчет коэффициента корреляции результатов по половинам теста

Пусть xij – ответ i-го учащегося на j-е задание. Учащихся – N,

заданий – n. Введем дихотомическую систему оценивания выполнения задания:

j − нечетное

8

где σx – стандартное отклонение, являющееся мерой разброса значений баллов в группе обучающихся.

Коэффициент корреляции (Пирсона) баллов по четным и нечетным заданиям вычисляется так:

где стандартные отклонения баллов по четным и нечетным заданиям σy ,σz определяются в соответствии с формулой (1.3):

Будем считать, что смещение оценки дисперсии из-за конечности N несущественно.

Значения коэффициента корреляции (1.4) лежат в интервале от минус единицы до плюс единицы: rzy [−1, 1] .

Можно показать, что коэффициент корреляции результатов по четным и нечетным заданиям может быть также вычислен по формуле:

9

Альфа (α) Кронбаха и формулы Кудера–Ричардсона

Для вывода формул, позволяющих вычислять надежность тестов, используем метод индукции. Сначала рассмотрим простой пример, а затем построим общие выражения, следуя методике, содержащейся в книге [1].

Рассмотрим результаты выполнения двух форм теста (А и B) из трех заданий небольшой группой студентов из пяти человек

(табл. 1.1 – 1.3).

10