Лекция_4

Добавил:

AD Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тверской Государственный Университет

Предмет:

Векторный и тензорный анализ

Файл:

Определитель метрического тензора

g det g 2 .

Компоненты

.pdf

Скачиваний:

Добавлен:

07.11.2022

Размер:

974.96 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Лекция 4. Криволинейные координаты

1. Криволинейные координаты. В ряде случаев, определяемых

симметрией задачи, удобно перейти к криволинейным координатам

q1, q2 , q3 , которые в механике называются обобщёнными. Декартовы координаты связаны с криволинейными координатами следующим

соотношением:

r r q1, q2 , q3 x q1, q2 , q3 i y q1,q2 ,q3 j z q1,q2 ,q3 k

(75)

или x x q . Будем считать, что эти функции непрерывно

дифференцируемы определенное количество раз (гладкое отображение) и

взаимно-однозначны. Если при этом обратное отображение тоже гладко, то

(75) называется диффеоморфизмом. Из (75) следуют равенства

q q x .	(76)
Если мы приравняем какую-либо координату q	постоянной величине C , то

получим уравнение поверхности, которая	называется координатной

поверхностью, соответствующей этой координате q C . Пересечение двух координатных поверхностей даёт координатную линию, вдоль которой изменяется только одна координата. Пересечение же трёх координатных

поверхностей даёт точку P , положение которой мы и определяем (рис.				9).
Ввиду дифференцируемости функций (75) можно ввести производные

	e	r	,	(77)
	e	q	,	(77)
		q


Рис. 9. Локальный базис.	которые		образуют	векторы,
называемые векторами локального	базиса	(репера) P,e1,e2 ,e3 . Эти
векторы направлены по касательным к координатным линиям в точке P . В
отличие от орт декартовой системы координат,		векторы e меняются при

переходе от одной точки к другой (отсюда и название локальный базис).

Векторы e и i	( i1 i,i2 j,i3 k ) связаны друг с другом посредством
якобиевых матриц	A	:

A i

(78)

Здесь мы учли, что

r x i

и базисные векторы i

декартовой системы

координат постоянны. Ввиду взаимной однозначности преобразования

координат det A 0. Тогда

существует

обратная

якобиева матрица,

которую обозначим

A A

(79)

2. Коэффициенты Ламэ. Векторы e

в общем случае имеют отличную

от единицы длину. В физике в основном используются орты единичной длины, составляющие ортонормированный базис. Единичные орты определяются следующим выражением

(80)

где H

– коэффициенты

Ламэ. Следует

отметить, что

коэффициенты Ламэ имеет смысл вводить только в ортогональных системах координат, в которых метрический тензор имеет диагональный вид.

Задание 14. Убедитесь в том, что в ортогональных системах координат

метрический тензор диагональный.

Диагональные компоненты при этом равны квадратам соответствующих коэффициентов Ламэ. Покажем это. Метрический тензор в криволинейной системе координат имеет вид

e e

(81)

Здесь – метрический тензор в декартовой системе координат (см.

формулу (43)). Фактически мы получили закон преобразования компонент тензора второго ранга. Если векторы локального базиса взаимно ортогональны, то

g	e e		H H e* e*	H	H	H 2	(82)

Здесь суммирования по нет. Итак, мы показали, что метрический тензор в ортогональной системе координат имеет вид:

	H		2	0	0
		1
2		0		2	0		(83)
G g H		0		H2	0	.	(83)
		0		0	2
		0		0	H3

Примерами криволинейных систем координат являются цилиндрическая и сферическая системы координат, рассмотренные нами ранее.

Т.к. согласно (46)
	e e			(84)

и нормированные векторы основного базиса равны (см. формулу (80))
e*	e /
e*	e /	g	,	(85)

то нормированные векторы взаимного базиса имеют вид:

e* e g		.	(86)

В качестве примера найдем выражение для метрического тензора и коэффициентов Ламэ в цилиндрической системе координат (см. рис. 4).

Цилиндрические координаты

q1 , q2 , q3 z

(87)

связаны с декартовыми координатами следующим образом (формулы (11)):

x cos ,

y sin ,

z z .

(88)

Поэтому

i1 cos i

2 sin,

i1 sin i2 cos ,

(89)

i3.

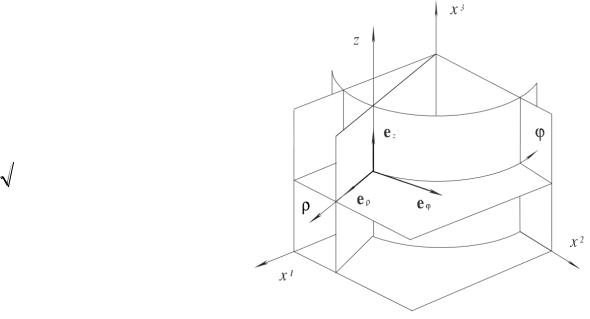
Координатные линии и поверхности показаны на рис.10. Поверхностями являются круговой цилиндр

	x2 y2	и		плоскости
z z ,	arctg		y	.	Легко

			x
убедиться, что		e e			g .

Это значит, что цилиндрическая система координат – ортогональная. В

самом деле, проводя прямые вычисления, найдем:

Рис. 10. Цилиндрическая система

координат x cos ,

y sin ,

z z

e e ezez eze e ez e e e e

i1 cos i2 sin i1 sin i2 cos cos sin cos sin 0,

i3i3 1,

i1 sin i2 cos i3 0,

i1 cos i2 sin i3 0,

i1 cos i2 sin i1 cos i2 sin 1,

i1 sin i2 cos i1 sin i2 cos 2.

Поэтому метрический тензор имеет вид:

обратного тензора в случае ортогональных координат (тензор диагональный)

g 1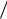 g . Ось Oz , для которой 0 , представляет собой геометрическое место особых точек, в которых базис не определен. Поэтому векторы,

заданные на оси Oz описывать с помощью цилиндрической системы координат нельзя. Коэффициенты Ламе определяются элементарно:

H 1, H , H z 1.

(91)

Задание 15. Найдите выражение для векторов взаимного базиса цилиндрической системы координат.

Задание 16. Для следующих криволинейных координат найти координатные линии и поверхности, выражения для векторов исходного и взаимного базисов, метрический тензор и коэффициенты Ламэ.

a.Сферические координаты q1 r, q2 , q3 , 0 r , 0 ,

0 2 .

b. Эллиптические координаты	q1 , q2 , q3 z ,	1 ,
1 1.

x c ,

y c 2 1 1 2 ,

z z.

Параболические

координаты

q1 , q2

, q3 ,

0 ,

0 , 0 2 ,

x cos ,

y sin ,

z 2

Тородоидальные

q1 ,

q2 , q3 ,

0 ,

sh cos

x c

ch cos

sh sin

y c

ch cos

sin

z c

ch cos

Вытянутые

сфероидальные

координаты

q1 ,

, q3

1 , 1 1, 0 2 .

x c ,

1 1 2 cos ,

z c

1 1 2 sin .

Сплюснутые

сфероидальные

координаты q1 ,

, q3

1 , 1 1, 0 2 .

x c sin ,

y c 2 1 1 2 ,

z c cos .

Символы

Кристоффеля.

Найдем производные

от

базисных

векторов криволинейной системы координат. Прежде всего, отметим, что

изменение вектора de e q dq e q определяется разностью, которая в общем случае уже не является вектором, т.к. вычитаемые векторы взяты в

разных точках q	и q dq . Чтобы в	результате de	стал вектором,
необходимо вектор	e q dq путем	параллельного	переноса (но в

криволинейных координатах!) перенести в точку нахождения вектора e q .

При таком переносе приращение de определяется с помощью коэффициентов связности пространства или символов Кристоффеля второго

рода	:

	de		e dq .			(92)

						равны
Итак, по определению символы Кристоффеля второго рода						равны

		e		e	.	(93)
		e		q	.	(93)
				q

Определим теперь символы Кристоффеля первого рода следующим образом:

e	e	e	2r	e	e	.	(94)

q		q q		q

Связь между символами Кристоффеля первого и второго родов осуществляется посредством метрического тензора:

e	e	g e	e	g .	(95)
	q
		q

Вспоминая определение метрического тензора (42), можно получить полезное при расчетах выражение для символа Кристоффеля первого рода:

1	g	g	g	.	(96)


2	q	q	q

Пример. Символы Кристоффеля первого рода в цилиндрической системе координат вычисляем с использованием формул (95) и (90):

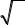
1 g			g		g	0,
2						0,
2
	1	g		g		g
							,
							,
	2
	2

.....

так

далее.

Ненулевыми символами

являются только

Из

символов Кристоффеля

второго рода отличаются

от нуля

4. Элементы длины, объема и поверхности в криволинейных

системах координат. Между определителем метрического тензора и якобианом существует простая связь. Найдем ее. Прежде всего, заметим, что выражение (81)

Учитывая, что определитель произведения матриц равен произведению определителей сомножителей, имеем:

g det AT det E det A .

Так как определитель единичной матрицы равен единице, а определитель транспонированной матрицы равен определителю исходной, то

g det A 2 .

Определитель якобиевой матрицы называют якобианом	J det A	x	.
		q
Следовательно,

J g .		(99)

Расстояние между двумя бесконечно близкими точками выражается с помощью метрического тензора

ds2 drdr	r	dq	r	dq e e	dq dq g	dq dq .	(100)
	q		q

В любой точке пространства можно привести метрический тензор к диагональному виду. Это значит, что можно выбрать ортогональную систему координат. В таком случае

ds2 H 2 dq dq H1dq1 2 H2dq2 2 H3dq3 2 .

(101)

В такой форме квадрат длины в криволинейной системе координат определяется как в декартовой системе координат, с помощью теоремы

Пифагора. Только

этом

случае dx

заменяется на

элемент длины

dq . Обратим

внимание, что в

не

зависимости

от размерности

обобщенной координаты q , элемент длины dl

имеет размерность длины.

Элемент объема в этих координатах имеет вид

dV dl dl dl H H

H dq1dq2dq3

detGdq1dq2dq3

g dq1dq2dq3 Jdq1dq2dq3.

(102)

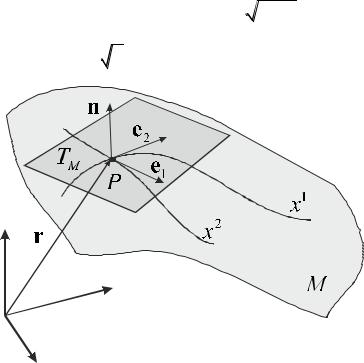
Рис. 11. Положение точки P на поверхности M . Векторы e1 и e2

определяют локальный базис в касательной плоскости TP – плоскости,

касающейся поверхности в точке P .

Очевидно, что значение элемента объема не зависит от выбора системы координат. Следовательно, выражение (102) имеет место быть в любой допустимой системе координат.

Соотношение (102) имеет общий характер. Т.е. (102) справедливо при любой размерности. Например, рассмотрим метрику на двумерной поверхности, погружённую в трехмерное пространство, в котором определена евклидова метрика.

Зададим координаты на этой поверхности q1 и q2 (так называемые Гауссовы параметры). Тогда в некоторой точке P этой поверхности можно ввести векторы локального базиса

e	r	,	e		r	.
	q1
1				2	q2

Эти векторы лежат в касательной плоскости Tp . Вектор нормали к

поверхности в точке

определяется векторным произведением базисных

векторов

e1 e2

(103)

e e

В силу тождества Лагранжа (68)

q1 q2

g11

g12

(104)

r r

g21

g22

q2 q1

q2 q2

Здесь, конечно, g –

это определитель метрики на поверхности. Из (104)

следует

e1 e2

gn .

(105)

Поэтому вектор элемента площади поверхности

dS e dq1 e

dq2

gndq1dq2 ndS.

(106)

Следовательно, элемент площади имеет вид

gdq1dq2 ,

(107)

1 / 21 2 > Следующая >>>

Соседние файлы в предмете Векторный и тензорный анализ

#
07.11.2022682.31 Кб5Лекция 6.pdf
#
07.11.2022713.53 Кб4Лекция 7.pdf
#
07.11.20221.23 Mб10Лекция_1.pdf
#
07.11.2022708.28 Кб7Лекция_2.pdf
#
07.11.2022853.22 Кб10Лекция_3.pdf
#
07.11.2022974.96 Кб10Лекция_4.pdf
#
07.11.2022727.38 Кб12Лекция_5.pdf
#
21.12.20221.03 Mб8Операции с тензорами 15.12.pdf
#
21.12.2022484.96 Кб3разбор теста.jpg