2 Основы скалярной теории дифракции

Дифракция – явление нарушения прямолинейного распространения оптических лучей при наличии препятствий в окружающем пространстве.

Расчёт э.м. полей при наличии дифракции является одной из наиболее сложных задач электродинамики и поэтому при её решении зачастую прибегают к приближённым методам в основе которых лежат положения волновой оптики, разработанные Х. Гюйгенсом и О. Френелем в XVIII и XIX веках.

Одно из основных допущений – рассматривается не векторное, а скалярное поле.

Результаты скалярной теории дифракции получаются достаточно точными, если выполняются два условия:

1. отверстия в экранах, на которых дифрагируют волны велики по сравнению с длиной волны;

2. дифрагированные волны наблюдаются не слишком близко от экранов.

Интегральная теорема Гельмгольца-Кирхгофа

Решение дифракционной задачи исторически имело несколько этапов, на каждом из которых исследователями вводились дополнительные уточняющие и упрощающие предположения относительно свойств поля и получались новые, более точные и удобные для практического применения результаты (§1.2 в уч. пос. [1]).

В основе решения дифракционной задачи лежат однородное уравнение Гельмгольца (1.4) и теорема Грина

, (1.8)

где U и G – произвольные комплексные функции, удовлетворяющие уравнению Гельмгольца (1.4) и непрерывные вместе со своими частными производными первого и второго порядков в объёме V и на ограничивающей его поверхности S; n – направление внешней нормали к поверхности S.

Соотношение (1.8) можно рассматривать как уравнение с двумя неизвестными функциями. Если одна из этих функций известна или задана, то вторую функцию можно в общем случае определить из этого уравнения.

В постановке Кирхгофа решение дифракционной задачи заключается в выражении решения уравнения Гельмгольца в произвольной точке Р₀ через значение этого решения и его первой производной на произвольной замкнутой поверхности S, окружающей эту точку.

Для решения задачи Кирхгоф ввёл в уравнение (1.8) в качестве функции G функцию Грина свободного пространства

которая представляет собой сферическую волну единичной амплитуды, распространяющуюся из точки Р₀.

Т.к. функции U и G удовлетворяют уравнению Гельмгольца (1.4), то объёмный интеграл в левой части (1.8) обращается в нуль, а из правой части путём определённых математических приёмов находится решение дифракционной задачи в форме т.н. интегральной теоремы Гельмгольца-Кирхгофа:

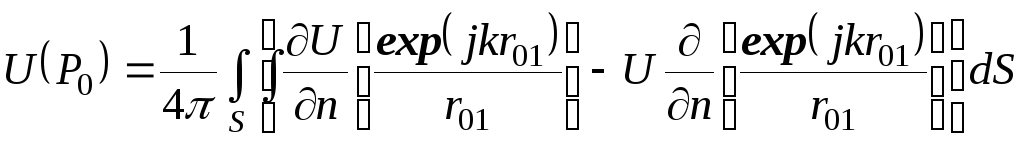. (1.9)

Эта теорема играет важную роль в скалярной теории дифракции, т.к. позволяет выразить поле в любой точке Р₀ через граничное значение волны на любой замкнутой поверхности, окружающей эту точку.

Формула Гюйгенса-Френеля в приближении Кирхгофа

В данном случае рассматривается задача о дифракции световой волны на отверстии в плоском бесконечном экране. Геометрия задачи представлена на рисунке.

В данном случае поверхность S, охватывающая точку Р₀, равна S₁ + S₂, где S₁ – часть теневой поверхности экрана, включая площадь отверстия Σ; S₂ – часть поверхности сферы радиуса R.

Применение интегральной теоремы Г-К к данному случаю приводит к соотношению

(1.10)

Как показывается в электродинамике, все реальные поля должны удовлетворять условию излучения Зоммерфельда

.

При выполнении этого условия интеграл по поверхности S₂ в (1.10) при R→∞ стремится к нулю и мы приходим к формуле

. (1.11)

Учитывая, что экран непрозрачен везде, кроме отверстия, Кирхгоф ввёл два приближённых допущения (граничных условия):

1. на поверхности Σ поле U и его производная имеют точно такие же значения, какие они имели бы в отсутствие экрана;

2. на поверхности S₁ за пределами отверстия Σ амплитуда поля U и его производной равны нулю.

При учёте этих граничных условий выражение (1.11) преобразуется к виду

. (1.12)

(Пояснить в чём заключается приближенный характер наложенных граничных условий)

Формула дифракции Френеля-Кирхгофа. Принцип Гюйгенса-Френеля

Если в предыдущей задаче положить, что расстояние r₀₁ от отверстия до точки наблюдения много больше длины волны, т. е k >> 1/ r₀₁, то выполняется приближённое соотношение

,

с учётом которого выражение (1.12) приобретает вид

. (1.13)

Если предположить, что отверстие Σ освещается сферической волной,

исходящей от точечного источника, расположенного в точке Р₂ , то из (1.13) получим

. (1.14)

Полученное соотношение называется формулой дифракции Френеля-Кирхгофа.

Соотношение (1.14) можно представить в виде

, (1.15)

где

Соотношение (1.15) является математическим выражением принципа Гюйгенса-Френеля.

Формула Рэлея-Зоммерфельда

С точки зрения математической теории потенциала принятие приближённых граничных условий Кирхгофа приводит к тому, что искомая функция U(P₀) обращается всюду в нуль. Чтобы избежать этого противоречия, Зоммерфельд ввёл новую симметричную функцию грина.

Данная функция во всех точках на поверхности экрана обращается в нуль, а её производная по нормали – нет. Это позволяет отказаться от жёсткого условия равенства нулю производной по нормали функции U на поверхности экрана, что снимает выявленное выше противоречие с теорией потенциала.

Подстановка новой функции Грина в (1.12) приводит к более точному решению граничной задачи

. (1.16)

Если поле в точке Р₁ в дифракционном отверстии Σ создаётся точечным источником, расположенным перед экраном в точке Р₂, то выражение (1.16) переходит в формулу дифракции Рэлея-Зоммерфельда

. (1.17)

Выражение (1.16) представляет собой интеграл суперпозиции

(1.18)

где - импульсный отклик слоя пространства, разделяющего экран и точку наблюдения.

Интеграл суперпозиции применяется только для описания линейных систем, к которым могут быть отнесены э.м. поля при наличии экранов.