13. Распределение Максвелла (функция распределения частиц по скоростям, вычисление средних значений, среднее значение относительной скорости, среднее значение кинетической энергии)

Функция распр-я частиц по скоростям – показывает относительное число частиц, скорости которых лежат в интервале от u до u+du

Где - относительная скорость - наиболее вероятная скорость частиц и.г.

Вычисление средних значений – , необходима формула

, где

Среднее значение относительной скорости u частиц газа - Среднее значение кинетической энергии ε частиц газа -

14. Распределение энергии по степеням свободы

Число степеней свободы физ. Объекта – минимальное кол-во независимых координат, необходимых для описания движений этого объекта. Частицы и.г. имеют 3 степени свободы, значит на каждую степень -»

2 -атомная молекула – материальные точки имеют 2 внутренних степени свободы Итого i=3+2=5

И скусственно можно создать ситуацию с 4 степенями свободы, если 2-атомную молекулу зажать между 2 плоскостями, тогда она сможет совершать движение лишь в какой-то 1 плоскости. Максимум – 6 степеней свобод ы.

Полная энергия частиц идеального газа вычисляется по формуле:

15. Теплоемкость многоатомных газов

Внутренняя энергия газа –

Теплоёмкость при постоянном объёме –

Теплоёмкость при постоянном давлении -

16. Распределение Максвелла для компонент импульса

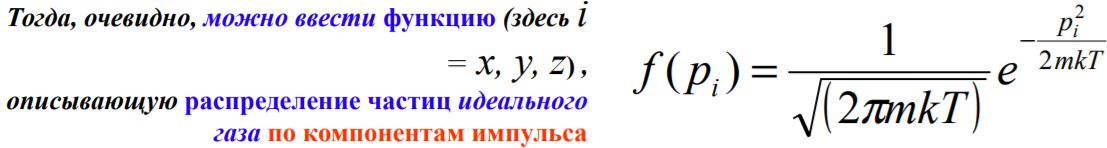
1 7. Распределение Больцмана (при T=const)

выч-ем элем-е кол-во частиц газа в элем-м объёме в потенц-м поле константа на экспоненту в степени (пот. Энергия делёная на тепловую энергию)

18. Распределение Максвелла-Больцмана

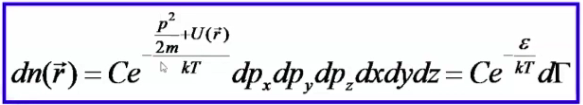
элемент фазового объёма–элем-й объём 6-мерного пространства

19. Фермионы и бозоны: распределение Бозе-Эйнштейна

Бозоны – частицы, с целым спином(собственный момент движения), полностью эквивалентные м/у собой.

Фермионы – частицы, с полуцелым спином, подчиняющиеся принципу Паули

Принцип Паули – в каждой ячейке μ - пространства м.б. не > 1 фермиона и хоть сколько бозонов μ – пространство, 6-тимерное пространство, т.е. имеющее 6 измерений px, py, pz, x, y, z шестимерное координатно-импульсное пространство

Р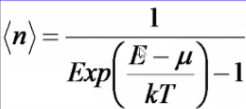 аспределение Бозе-Эйнштейна для бозонов: - -» Вероятное кол-во частиц в каждом квантовом состоянии - -» Е – полная энергия системы

20. Фермионы и бозоны: распределение Ферми-Дирака для фермионов.

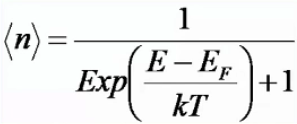
Доказательства ко 2 коллоквиуму:

7. Уравнение Майера –

доказательство в 12 лекции 1:24:00

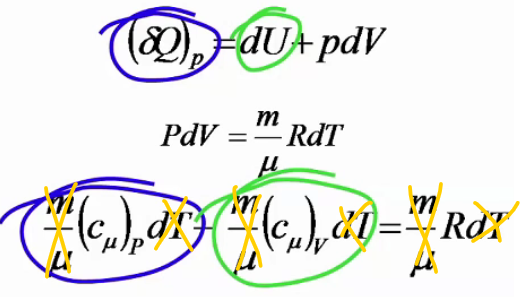
8. Адиабатический процесс

Доказательство в 12 лекции 1:26:30

9. Теплота и работа при изопроцессах

И зотермический (T=const) - Элементарная работа -» - подставим Р из ур-я М-К –» Проинтегрируем -» Внутренняя энергия через т-ть при V=const -»

Первое начало ТМ -»

И 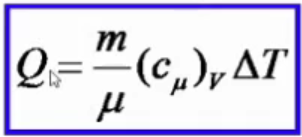зохорический (V=const) Элементарная работа -»

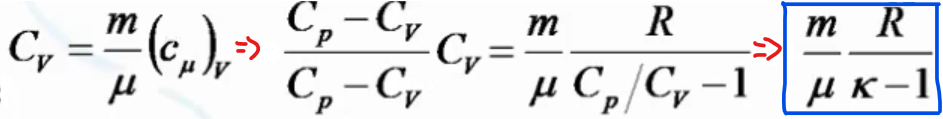Тогда из первого н. ТМ -» -» Интегрируем -» Для т-ти используем ур-е Майера -»

А диабатический (Q=const)

П ервое начало ТМ -» Тогда элем. Работа -»

Интегрируем -»

13. Среднее значение кинетической энергии ε частиц газа

16. Распределение Максвелла для компонент импульса

19. Распределение Бозе-Эйнштейна

Пусть: Wi – число способов, которыми можно разместить Ni частиц (в состоянии i) в gi ячейках Ni! -число перестановок частиц, не дающих новых способов (gi-1)! – число перегородок м/у ячейками Тогда W –ТМ вероятность - число способов разделения частиц по разл. состояниям (в 1 сост. – N1 частиц, во 2 – N2)

20. Распределение Ферми-Дирака

Лекция 17 - 11 минута Пусть: Wi – число способов, которыми можно разместить Ni частиц (в состоянии i) в gi ячейках Ni! -число перестановок частиц, не дающих новых способов (gi-1)! – число перегородок м/у ячейками gi! - число перестановок всех ячеек Тогда W –ТМ вероятность - число способов разделения частиц по разл. состояниям (в 1 сост. – N1 частиц, во 2 – N2)