МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение

высшего профессионального образования

ЮЖНО-РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ ЭКОНОМИКИ И СЕРВИСА

(ЮРГУЭС)

ЛИНЕЙНАЯ АЛГЕБРА

Учебное пособие

Рекомендовано для самостоятельной работы

студентов очной, заочной и дистанционной форм

обучения всех специальностей

Шахты 2008

УДК

ББК

Составители:

к.ф.-м.н., доцент кафедры «Математика» ЮРГУЭС

А.Б. Михайлов

к.т.н., доцент кафедры «Математика» ЮРГУЭС

Г.Р. Саакян

к.т.н., старший преподаватель кафедры «Математика» ЮРГУЭС

И.Д. Михайлова

Рецензенты:

к.т.н., доцент кафедры «Математика» ЮРГУЭС

Л.Д. Алексеенко

к.э.н., доцент кафедры «Математика» ЮРГУЭС

О.И. Охрименко

Михайлов А.Б. Линейная алгебра: учебно-методическое пособие/

А.Б. Михайлов, Г.Р. Саакян, И.Д. Михайлова, Ю.А. Хоменко.- Шахты: Изд-во ЮРГУЭС, 2008. – 27 с.

Учебно-методическое пособие предназначено в помощь студентам при изучении раздела высшей математики «Линейная алгебра».

Пособие содержит в большом объеме теоретический материал. Подробно разобраны решения практических заданий, приведены задачи для самостоятельного решения и ответы к ним.

Пособие рекомендовано для студентов очной, заочной и дистанционной форм обучения.

Матрицы

Прямоугольная таблица чисел

,

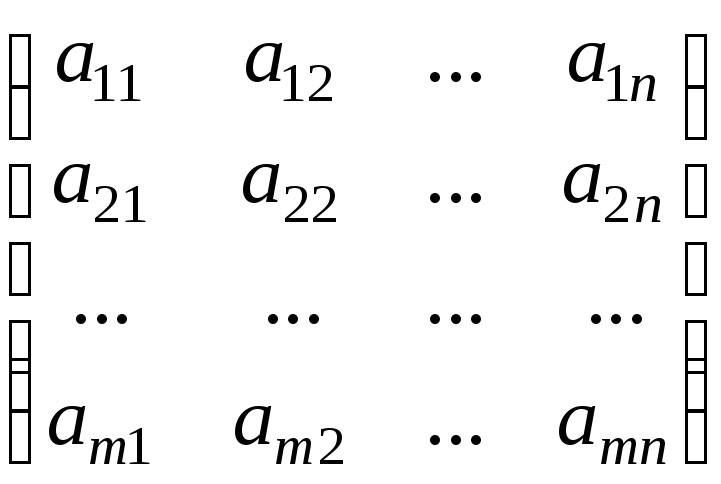содержащая строк истолбцов, называетсяматрицей размеров . Числа называютсяэлементами матрицы. Каждый элемент матрицы снабжен двумя индексами: первый индекс указывает номер строки, второй – номер столбца, в которых расположен этот элемент. Часто вместо подробной записи употребляют сокращенную: или даже. Если число строк матрицы равно числу ее столбцов, то матрица называетсяквадратной порядка . Диагональквадратной матрицы называетсяглавной диагональю, а диагональ –побочной диагональю.

Среди квадратных матриц одного и того же порядка (например, порядка , т.е. размеров) важную роль играет матрица вида

,

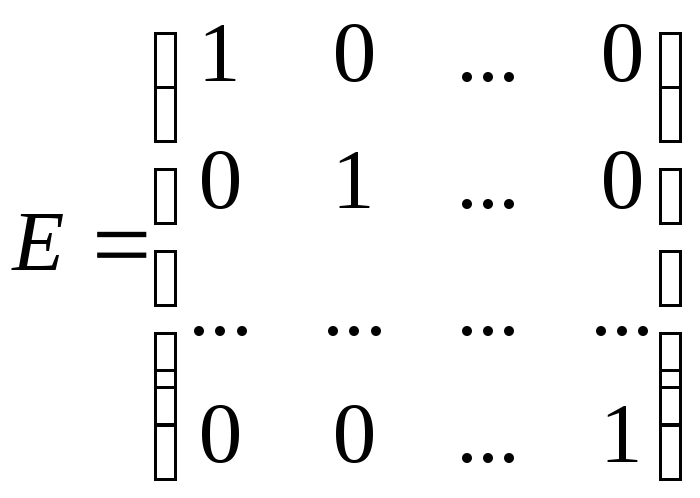которую называют единичной матрицей.

Пример 1. Матрица

имеет размеры 3×4, например, элементы ,.

Матрица

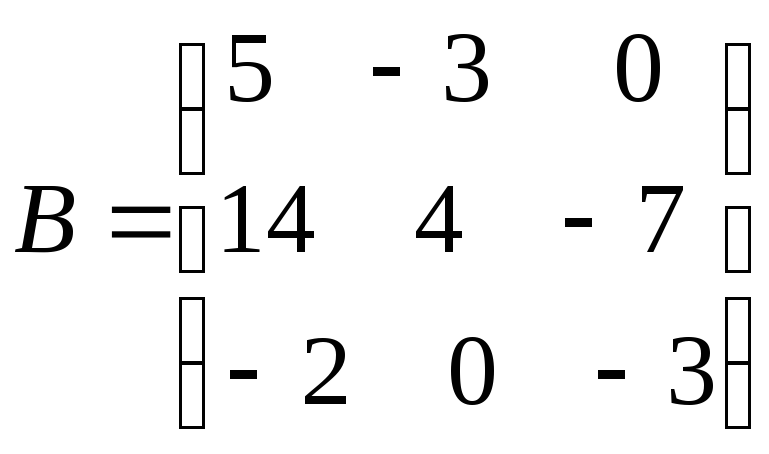
является квадратной порядка 3. Элементы 5, 4, –3 образуют главную диагональ, а элементы 0, 4, –2 матрицы – побочную диагональ.

Умножение матрицы на число. Для того чтобы умножить матрицу на число, нужно каждый элемент матрицыумножить на это число:.

Сложение матриц. Складывать можно только матрицы с одинаковым числом строк и столбцов, т.е. матрицы одинаковых размеров. Суммой матриц иназывается матрица, элементы которой равны суммам соответствующих элементов матрици, т.е.для любых индексов,.

Умножение матриц. Произведение матрицы на матрицу(обозначается) определено только в том случае, когда число столбцов матрицыравно числу строк матрицы. В результате умножения получим матрицу, у которой столько же строк, сколько их в матрице, и столько же столбцов, сколько их в матрице. Для удобства запоминания запишем это кратко:

Если ,и, то элементыопределяются следующим образом:

,

где .

Это правило можно сформулировать и словесно: элемент ,стоящий на пересечении -й строки и-го столбца матрицы, равен сумме попарных произведений соответствующих элементов-й строки матрицыи-го столбца матрицы. Другими словами, элементявляется результатом скалярного произведения -й вектор-строки и-го вектор-столбца.

Пример 2. Выполнить действия:

.

Пример 3. Перемножить матрицы:

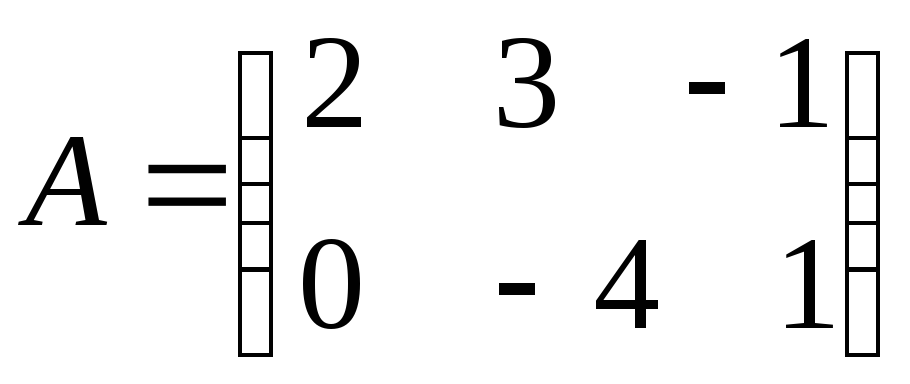и .

Матрица имеет размерность 2×3, матрицаимеет размерность 3×4, значит, матрицы можно перемножить. Размерность матрицы произведенияС – 2×4. Чтобы получить первый элемент матрицы С перемножим элементы первой строки матрицы А на соответствующие элементы первого столбца матрицы В. Элементы ,,получим умножением элементов первой строки матрицыА на соответствующие элементы второго, третьего, четвертого столбцов матрицы В.

2 3 –1 2 3 –1 2 3 –1 2 3 –1

–5 0 3 3 –2 2 1 –1 2 0 3 –4

–10+0– 3= –13 6 – 6 – 2 =–2 2 – 3 – 2= –3 0 + 9 + 4=13.

Элементы получим умножением элементов второй строки матрицыА на соответствующие элементы первого, второго, третьего, четвертого столбцов матрицы В.

0 –4 1 0 –4 1 0 –4 1 0 –4 1

–5 0 3 3 –2 2 1 –1 2 0 3 –4

0 – 0 + 3=3 0 + 8 + 2=10 0 + 4 + 2 =6 0 – 12 – 4= –16

Итак, матрица произведения С имеет вид:

.
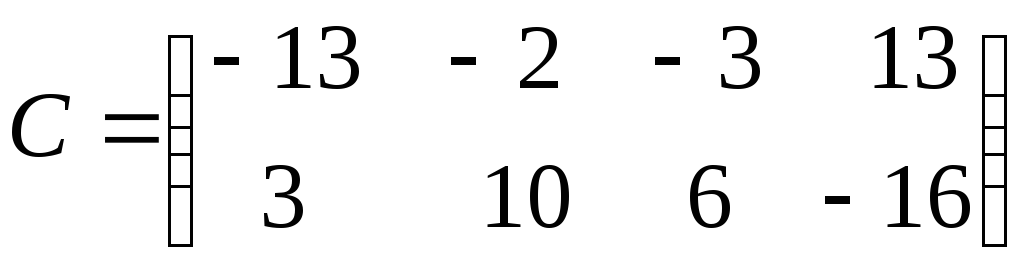