2. Модель мс.
2.1 Полагаем, что система состоит из материальных точек постоянной массы.
Определения. Параметры.
- система материальных точек -совокупность конечного числа материальных точек;
-
импульс
системы
(момент импульса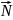
)
векторная сумма импульсов (моментов
импульса) материальных точек
;
(
= [
-
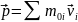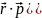
момент
силы системы
относительно точки принятой за начало
называется векторная сумма моментов
сил, приложенных к точкам системы
(внешних и внутренних).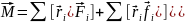
;
-
центром
масс
системы называют точку с радиус- вектором
,
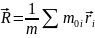(2) ,
здесь
m-
масса покоя системы,
-
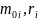масса покоя и радиус-вектор i-ой
материальной точки системы.
Если
материальные точки не связаны друг с
другом жесткими связями, то положение
каждой точки определяется из решения
дифференциального уравнения второго
закона динамики для i-ой
точки
=
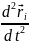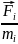. (3)
Продифференцируем
дважды соотношение (2) по времени:
=
=
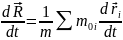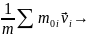
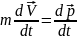Это уравнение в
нерелятивистском случае определяет
движение точки центра масс системы.
Здесь
-результирующий
вектор внешних сил. Внутренние силы
системы (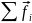
=0) не могут изменить положение её центра
масс
Уравнение:
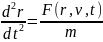есть дифференциальное уравнение
второго порядка в переменных (r,t)
Решение (3) даёт кинематический закон
движения в явном виде
,
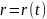при
заданной силе и начальным условиям .
2.2.Динамика тел переменной массы.
Постановка задачи. Пусть система состоит из материальных точек, масса которых изменяется со временем. Найдём дифференциальное уравнение движения одного из тел системы. Импульс тела
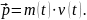Второй
закон:
=
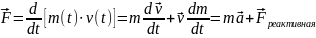
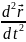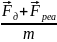
Явный вид реактивной силы находится для конкретного задания.
2.3 Механическая система, состояние которой описывается энергетическими параметрами.
Преобразуем
второй закон:
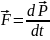Умножим
скалярно на
)=
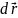
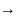
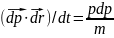т.к
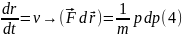
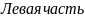(4)
есть элементарная механическая работа.
Энергия - это способность системы)
совершать
работу, тогда правая часть (4) есть
элементарная энергия
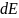
При
совершении работы силой энергия
изменяется, то есть:
.
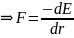(4)
Таким образом, действие силы во времени изменяет импульс тела; действие силы в пространстве - изменяет энергию тела. Для получения кинематических уравнений движения нужно решать дифференциальное уравнение вида (1), (3 или (4). В первом случае решение называется в переменных Ньютона, во втором, в переменных Гамильтона.
Механическая энергия делится на энергию
движения (кинетическую), зависящую от
скорости движения (или импульса) тела
и энергию, зависящую от положения
(координат) взаимодействующих тел
(потенциальную). Полная энергия:
+
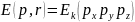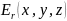Решение уравнения (4) в переменных
Гамильтона обычно используется в
системах, состоящих из большого числа
элементов (частиц), в которых состояние
системы определяется её энергетическим
состоянием, а не координатами частиц:
.
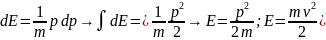Для
нахождения потенциальной энергии нужно
задать силу взаимодействия частиц или
силу, действующую со стороны силового
поля, в котором частицы находятся.