
- •Задание 1
- •1.Текст задания
- •2. Вариант.
- •3. Выполнение задания
- •4. Ответы на вопросы.
- •Вопрос 1. Какой вид имеет асимптотическая логарифмическая амплитудно-частотная характеристика (лачх) соединения (привести график) и ? Ответ:
- •Задание 2
- •1.Текст задания
- •2. Вариант.
- •3. Выполнение задания
- •4. Ответы на вопросы.
- •Вопрос 1. Какому типовому звену соответствуют переходная и частотные характеристики соединения?
- •Вопрос 2. Является ли система второго порядка с пф полностью управляемой и наблюдаемой? Объяснить почему.
- •Су управляема
- •Задание 3
- •1.Текст задания
- •2. Вариант.
- •3. Выполнение задания
- •4. Ответы на вопросы.
- •Вопрос 1. Как проявляются свойства неустойчивой части в последовательном соединении звеньев и на характеристиках соединения в целом с пф ?
- •Вопрос 2. Как отражается на характеристиках соединения с пф в корневой, временной и частотной областях неполная компенсация неустойчивого полюса пф ?
- •Задание 4
- •1.Текст задания
- •2. Вариант.
- •3. Выполнение задания
- •4. Ответы на вопросы.
- •Вопрос 1. Построить асимптотические лачх и логарифмические фазочастотные характеристики (лфчх).
- •Вопрос 2. Какие фильтрующие свойства проявляют звенья на низких и высоких частотах?
Вопрос 2. Как отражается на характеристиках соединения с пф в корневой, временной и частотной областях неполная компенсация неустойчивого полюса пф ?
Ответ:
Неполная компенсация происходит в том случае, когда соответствующие нуль и полюс не совпадают, хотя могут быть близкими, т. е. располагаться на плоскости корней друг относительно друга на сколь угодно малом расстоянии. Рассмотрим следующие ПФ:
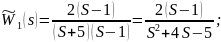
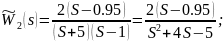
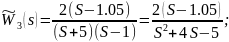
Построим графики переходной характеристики, АФХ, ЛАЧХ и ЛФЧХ, используя программное средство MATLAB/Simulink:
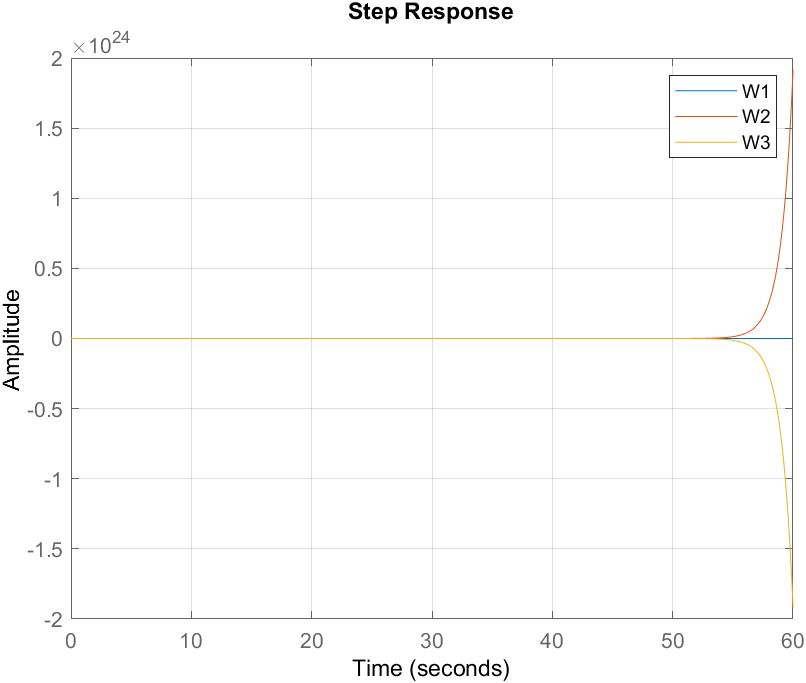 Рис.
22. ПХ для
Рис.
22. ПХ для
 и
и
 .
.
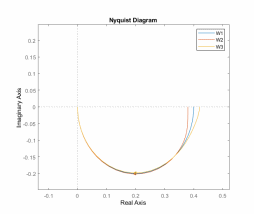 Рис.
23. АФХ для
и
.
Рис.
23. АФХ для
и
.
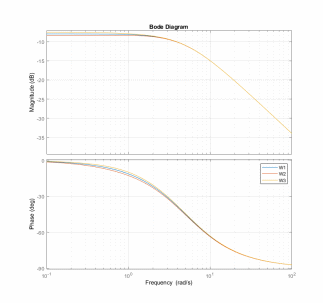 Рис.
24. ЛАЧХ и ЛФЧХ для
и
.
Рис.
24. ЛАЧХ и ЛФЧХ для
и
.
Исходя из полученных результатов на графиках, можно сделать вывод о том, что при полной компенсации система становится устойчивой и проявляет свойства апериодического звена первого порядка. В свою очередь, неполная компенсация даёт расходящийся переходный процесс.
Задание 4
1.Текст задания
Найти ПФ
 типовых звеньев, параллельные соединения
которых описываются эквивалентными
дифференциальными уравнениями вида:
типовых звеньев, параллельные соединения
которых описываются эквивалентными
дифференциальными уравнениями вида:
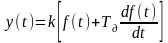 ;
;

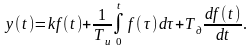
2. Вариант.
Вариант
№13:

Согласно заданному варианту дифференциальные уравнения описаны следующими выражениями:
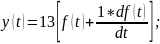


3. Выполнение задания
Найдем ПФ звена, параллельные соединение которого описываются следующим дифференциальными уравнением:
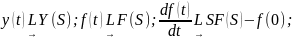
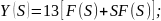
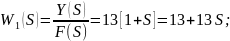
Отметим:
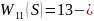 усилительное (пропорциональное) звено.
усилительное (пропорциональное) звено.
 дифференцирующее
звено.
дифференцирующее
звено.
Найдем ПФ
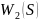 звена, параллельные соединение которого
описываются следующим дифференциальными
уравнением:
звена, параллельные соединение которого
описываются следующим дифференциальными
уравнением:

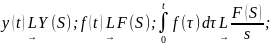

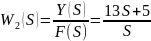
Отметим:
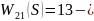 усилительное (пропорциональное) звено.
усилительное (пропорциональное) звено.
 интегрирующее
звено.
интегрирующее
звено.
Найдем ПФ
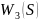 звена, параллельные соединение которого
описываются следующим дифференциальными
уравнением:
звена, параллельные соединение которого
описываются следующим дифференциальными
уравнением:
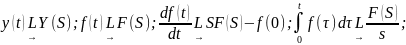


Отметим:
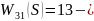 усилительное (пропорциональное) звено.
усилительное (пропорциональное) звено.
 интегрирующее
звено.
интегрирующее
звено.
 дифференцирующее
звено.
дифференцирующее
звено.
4. Ответы на вопросы.
Вопрос 1. Построить асимптотические лачх и логарифмические фазочастотные характеристики (лфчх).
Ответ:

Рис. 25. АЛАЧХ и ЛФЧХ для .
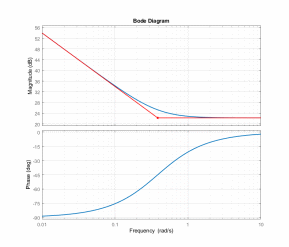 Рис.
26. АЛАЧХ и ЛФЧХ для
.
Рис.
26. АЛАЧХ и ЛФЧХ для
.
 Рис.
27. АЛАЧХ и ЛФЧХ для
.
Рис.
27. АЛАЧХ и ЛФЧХ для
.
Вопрос 2. Какие фильтрующие свойства проявляют звенья на низких и высоких частотах?
Ответ:
АЛАЧХ
на низких частотах (до 1
рад/с) имеет
наклон 0 дБ/дек, после на высоких частотах
наклон составляет 20 дБ/дек. ЛФЧХ
изменяется
от 0 до 90° , причем на
сопрягающей частоте
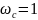 она равна 45°. Получившаяся
система обладает свойствами фильтра
высоких частот.
она равна 45°. Получившаяся
система обладает свойствами фильтра
высоких частот.
АЛАЧХ
на низких частотах (до частоты
 рад/с) имеет наклон -20 дБ/дек, после нее
0 дБ/дек на высоких частотах. ЛФЧХ
изменяется
от −90° до 0 , причем на
сопрягающей частоте
рад/с) имеет наклон -20 дБ/дек, после нее
0 дБ/дек на высоких частотах. ЛФЧХ
изменяется
от −90° до 0 , причем на
сопрягающей частоте
 она равна −45°. Получившаяся
система обладает свойствами фильтра
низких частот.
она равна −45°. Получившаяся
система обладает свойствами фильтра
низких частот.
АЛАЧХ
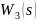 имеет две точки перегиба: наклон до
частоты
рад/с составляет -20 дБ/дек, после нее и
до частоты
имеет две точки перегиба: наклон до
частоты
рад/с составляет -20 дБ/дек, после нее и
до частоты
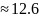 рад/с наклон составляет 0 дБ/дек, и на
высоких частотах наклон составляет 20
дБ/дек. ЛФЧХ на низких частотах изменяется
от -90
рад/с наклон составляет 0 дБ/дек, и на
высоких частотах наклон составляет 20
дБ/дек. ЛФЧХ на низких частотах изменяется
от -90 до 0
,
на средних частотах держится в пределах
0
,
и далее на высоких частотах увеличивается
от 0
до 90
до 0
,
на средних частотах держится в пределах
0
,
и далее на высоких частотах увеличивается
от 0
до 90 Получившаяся
система обладает свойствами режекторного
фильтра.
Получившаяся
система обладает свойствами режекторного
фильтра.
