Лекции_по_дисциплине

Компьютерное моделирование

Теперь попробуем повторить предыдущую процедуру. Для уменьшения f надо уменьшить либо x1, либо x2, но это невозможно, так как в этом базисе

х1=0, х2 =0.

Таким образом, данное базисное решение является оптимальным, и min

f =-1 при x, = 0,x2 = 0, x3=1, x4=3.

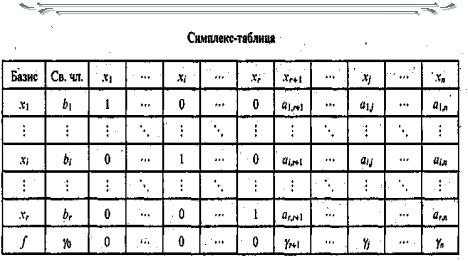
Приведем алгоритм симплекс-метода в общем виде. Обычно все вычисления по симплекс-методу сводят в стандартные таблицы. Запишем систему ограничений в виде

Тогда очередной шаг симплекс-процесса будет состоять в переходе от старого базиса к новому таким образом, чтобы значение линейной функции, по крайней мере, не увеличивалось. Данные о коэффициентах уравнений и линейной функции занесем в табл.7.1.

Таблица 7.1 Симплекс-таблица

111

Тарова Инна Николаевна

Сформулируем алгоритм симплекс-метода применительно к данным, внесенным в табл. 7.1.

1. Выяснить, имеются ли в последней строке таблицы положительные числа ( 0 не принимается во внимание). Если все числа отрицательны, то процесс закончен; базисное решение (b1, b2, …, br , 0, ..., 0) является оптимальным; соответствующее значение целевой функции f= 0. Если в последней строке имеются положительные числа, перейти к п. 2.

2.Просмотреть столбец, соответствующий положительному числу из последней строки, и выяснить, имеются ли в нем положительные числа. Если ни в одном из таких столбцов положительных чисел нет, то оптимального решения не существует. Если найден столбец, содержащий хотя бы один положительный элемент (если таких столбцов несколько, взять любой из них), пометить этот столбец и перейти к п. 3.

3.Разделить свободные члены на соответствующие положительные числа из выделенного столбца и выбрать наименьшее частное. Отметить строку таблицы, соответствующую наименьшему частному. Выделить разрешающий элемент, стоящий на пересечении отмеченных строки и столбца. Перейти к п. 4.

4.Разделить элементы выделенной строки исходной таблицы на разрешающий элемент (на месте разрешающего элемента появится единица). Полученная таким образом новая строка пишется на место прежней в новой таблице. Перейти к п. 5.

5.Каждая следующая строка новой таблицы образуется сложением со-

112

Компьютерное моделирование

ответствующей строки исходной таблицы и строки, записанной в п. 4, которая предварительно умножается на такое число, чтобы в клетках выделенного столбца при сложении появились нули. На этом процесс заполнения новой таблицы заканчивается, и происходит переход к п. 1.

Таким образом, используя алгоритм симплекс-метода применительно к симплекс-таблице, мы можем найти оптимальное решение или показать, что его не существует. Результативность симплекс-метода гарантируется следующей теоремой (приведем ее без доказательства): если существует оптимальное решение задачи линейного программирования, то существует и базисное оптимальное решение. Это решение может быть получено через конечное число шагов симплекс-методом, причем начинать можно с любого исходного базиса.

Ранее мы предполагали, что если система ограничений задана в виде (7.1), то перед первым шагом она уже приведена и виду (7.3), где bi 0 (i = 1, 2, ..., r). Последнее условие необходимо для использования симплексметода. Рассмотрим вопрос об отыскании начального базиса. Один из ме-

тодов его получения - метод симплексного преобразования. Прежде всего,

проверяем, есть ли среди свободных членов отрицательные. Если свободные члены не являются числами неотрицательными, то добиться их не отрицательности можно несколькими способами:

1)умножить уравнения, содержащие отрицательные свободные члены,

на-1;

2)найти среди уравнений, содержащих отрицательные свободные члены, уравнение, с максимальным по абсолютной величине отрицательным свободным членом и затем сложить это уравнение со всеми остальными, содержащими отрицательные свободные члены, предварительно умножив его на-1.

Затем, используя действия, аналогичные указанным в пп. 3-5 алгоритма симплекс-метода, совершаем преобразования исходной таблицы до тех пор, пока не получим неотрицательное базисное решение.

Транспортная задача Рассмотрим некоторую производственную ситуацию. Например, организация, занимающаяся механизацией трудоемких работ, располагает набором однородных технических средств в количестве

30 единиц, которые размещаются на трех базах: А1, А2 и А3 . При этом базы А1 и А2 имеют по 11 единиц техники, а база А3 – 8 единиц. Использование этой техники планируется на четырех объектах В1, В2, В3, В4. Причем объект В1 нуждается в 5 единицах, объекты В2 В3 – в 9 единицах каждый, а

113

Тарова Инна Николаевна

объект В4 – в 7 единицах. Эффективность эксплуатации техники во многом зависит от того, насколько интенсивно они используются, т.е. чем меньше простои, тем выше эффективность. В данном случае простой машин определяется главным образом тем, на каком объекте они работают. Например, машины базы А3, занятые на объекте В1 простаивают в среднем 6 ч в неделю, а те же машины на объекте В3 – 1 час. Общая картина использования техники с указанием ее наличия в базах и потребностей на объектах показана в таблице.

Таблица 7.2:

8

Решение: Необходимо разработать такой план распределения машин по объектам, при котором суммарное время простоя техники будет наимень-

шим. Это будет так называемая транспортная задача математического программирования. Одним из наиболее распространенных способов ее решения является метод потенциалов. Прежде всего, составим исходный план распределения машин по объектам. В первые верхние углы клеток таблицы поместим цифры простоя машин, освободив тем самым нижнюю половину для цифр, отражающих количество распределяемых единиц техники. Первоначально заполняется первая строка плана. Распределение целесообразно выполнить по тому направлению, где время простоя минимально, т.е. А1В4. Здесь время простоя С14=3. Количество машин на этом направлении устанавливается как минимальное из их общего количества, имеющегося на А1 и потребного для В4, оно = 7. Таким образом, достигается либо полный расход техники данной базы, либо полное насыщение объекта. В нашем случае полностью насыщается объект. После указанной операции на базе А1 остаются 4 единицы техники, которые записываем в скобках радом с цифрой 11. Этот остаток целесообразно направить на объект В3, так как простои будут минимальными из оставшихся. Теперь все ресурсы базы А1 оказались исчерпаны, а на объекте В3 остается потребность в 5

114

Компьютерное моделирование

единицах (эту цифру записываем рядом с 9 в скобках). Поскольку все ресурсы базы А1 израсходованы, то переходим к строке плана, где описание операций повторяется, и т.д.

Таблица 7.3:

В результате получаем первый, исходный план распределения машин по объектам. Чтобы определить оптимальность полученного плана, время простоя будем рассматривать в качестве некоторой стоимости: чем меньше время простоя, тем меньше стоимость работы. Введѐм понятие потенциала. Потенциалом являются некоторые числа UBi и UAi, приписываемые соответственно базам и объектам, сумма которых для клеток плана, содержащих цифры распределенных машин, равна стоимости результата времени простоя, т.е. UBi+UAi=Сij, а для тех клеток, где распределения нет, эта сумма будет не более стоимости результата, т.е. UBi +UAi<=Сij.(Условие 1)

План, все клетки которого отвечают этим условиям, является оптимальным. Чтобы определить оптимальность указанного исходного плана, рассчитаем и внесем в таблицу 7.3 значения потенциалов баз и объектов. Примем, что UAi=0, тогда

UB3=C13-UA1=5-0=5 UB4=C14-UA1=3-0=3 UA3=C33-UB3=1-5=-4 UB3=C23-UA3=-3-(-4)=7 UA2=C22-UB2=4-7=-3 UB1=C21-UA2=2-(-3)=5

Проверим теперь, соблюдается ли условие потенциальности для свободных клеток. Просуммируем для каждой клетки соответствующие потенциалы баз и объектов и сравним полученный результат с временем простоя, поставленным в правых верхних углах клеток. Суммы потенциалов для свободных клеток называются псевдостоимостями и обозначаются Сij. Их записывают в левых верхних углах. Из выражений следует, что для оптимального плана Сij- Сij<=0. Так как (условие 1) выполняется для всех свободных клеток, то этот план – оптимальный. Если условие оптимальности не выполняется, план подлежит улучшению.

115

Тарова Инна Николаевна

7.3. РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ В EXCEL

7.3.1. Задачи оптимизации

Очень широкий класс задач составляют задачи оптимизации или, как их еще называют, экстремальные задачи. Обычно их решение сопряжено с большим количеством вычислений, что затрудняет их решение вручную. Мы рассмотрим следующие типы задач оптимизации:

решение уравнений с одним неизвестным,

задачи линейного программирования;

аппроксимация функций.

Постановка задачи оптимизации

Взадачах оптимизации требуется найти значения параметров или функций, реализующих максимум или минимум некоторой завися-

щей от них величины, например: Z=f(x1, x2,…, xn) (7.4) часто при дополнительных условиях-неравенствах:

φ(x1, x2,…, xn) <=0 (i=1,2,…,n) (7.5)

Во многих инженерных и экономических задачах, например, желательно найти максимум меры выполнения или минимум стоимости.

Другим приложением задач оптимизации является получение приближенных решений выбором неизвестных значений параметров или функций так, чтобы они давали минимум ошибки.

Впростейшем случае одной независимой переменной х локальные максимум и минимум функции определяются следующим образом. Действительная функция f(x), определенная при х=а, имеет в точке а (локальный) минимум или (локальный) максимум f(a), если сущест-

вует такое положительное число δ, что при всех x = х - а, для кото-

f f (a x) f ( f ) 0

Максимум и минимум функции объединяются общим названием

экстремума функции. Определение локальный подчеркивает тот факт, что понятие экстремума связано лишь с достаточно малой ок-

116

Компьютерное моделирование

рестностью точки а. При решении оптимизационных задач важно нахождение не локальных экстремумов, а глобального максимума или глобального минимума (наибольшего или наименьшего значений) функции на промежутке X.

Для поиска экстремумов существуют различные методы. Часто случается, что при отыскании максимумов и минимумов функций многих переменных получают сложную систему уравнений, в этих случаях экстремумы находятся численными методами, то есть при помощи последовательного применения метода проб. При этом применение компьютера является практически единственным способом решения задачи.

7.3.2. Решение уравнений с одним неизвестным

Одним из приложений задач оптимизации является численное решение систем уравнений с одним или несколькими неизвестными

Нахождение корней уравнения вида (7.6) даже в случае алгебраических уравнений выше третьей степени представляет достаточно сложную задачу. Трансцендентные же уравнения чаще всего вообще не имеют аналитического решения. В этих случаях единственным путем является получение приближенных решений, выбором неизвестных значений параметров так, чтобы они давали минимум ошибки некоторой целевой функции (как правило, квадратичной). Обычно используются итерационные методы, когда вначале выбирают некоторое начальное приближение, затем вычисляют последовательные

Итерационные методы обеспечивают сходимость таких приближений к искомому значению х. В MS Excel для решения уравнений вида (7.6) используется удобный и простой для понимания инструмент Подбор параметра. Он реализует алгоритм численного решения уравнения, зависящего от одной переменной.

Процесс решения с помощью процедуры Подбор параметра распадается на два этапа:

117

Тарова Инна Николаевна

1.Задание на рабочем листе ячейки, содержащей переменную решаемого уравнения (так называемой влияющей ячейки), и ячейки содержащей формулу уравнения (зависящей или целевой ячейки).

2.Ввод адресов влияющей и целевой ячеек в диалоговом окне Подбор параметра и получение ответа (или сообщения о его отсутствии или невозможности нахождения, поскольку уравнение может не иметь решений или алгоритм решения (оптимизации) может оказаться расходящимся в конкретных условиях).

К сожалению, с помощью процедуры Подбор параметра могут быть решены только некоторые типы уравнений.

7.3.3 Линейное программирование

В случае, когда оптимизируемая целевая функция (7.4) и ограничения (7.5) линейны, задача оптимизации решается методами линейного программирования и обычно называется задачей линейного программирования. Задача линейного программирования заключается в нахождении n переменных x1, х2,..., хn, минимизирующих данную линейную функцию (целевую функцию):

Z=f(x1, x2,…, xn)=c1x1+c2x2+…+cnxn (7.7)

(или максимизирующую — Z) при линейных ограничениях-

Часто задачу линейного программирования (7.7.-7.9) сводят путем введения в случае необходимости вспомогательных переменных к стандартной форме (основной задаче линейного программирования). При этом требуется минимизировать целевую функцию:

Z=f(x1, x2,…, xn)≡c1x1+c2x2+…+cnxn (7.10)

118

Компьютерное моделирование

Допустимым решением (планом) задачи линейного программирования является упорядоченное множество чисел (x1, x2,…, xn), удовлетворяющих ограничениям (7.11) и (7.12). Это точка в n-мерном пространстве. Допустимое решение, минимизирующее целевую функцию (7.10), называется оптимальным решением (оптимальным планом).

Чаще всего оптимальное решение, если оно существует, является и единственным. Однако возможны случаи, когда оптимальных решений бесчисленное множество. Процесс решения задачи линейного программирования обычно состоит из ряда этапов:

1-й этап: осмысление задачи, выделение наиболее важных качеств, свойств, величин, параметров. Это можно делать, составляя схемы, таблицы, графики и т. п.;

2-й этап: введение обозначений (неизвестных). Желательно ограничиваться как можно меньшим количеством неизвестных, выражая по возможности одни величины через другие;

3-й этап: создание целевой функции. Обычно в качестве цели могут выступать максимальная стоимость всего объема продукции, максимальная прибыль, минимальные затраты и т. п. Целевая функция записывается в виде (7.7) или (7.10).

4-й этап: составление системы ограничений, которым должны удовлетворять введенные величины (7.8), (7.9) или (7.11), (7.12).

5-й этап: решение задачи на компьютере.

Инструментом для поиска решений задач оптимизации в Excel служит процедура Поиск решения (Сервис > Поиск решения). При этом открывается диалоговое окно Поиск решения. Оно содержит следующие рабочие поля:

Установить целевую ячейку — служит для указания целевой ячейки, значение которой необходимо максимизировать, минимизировать или установить равным заданному числу. Эта ячейка должна содержать формулу;

Равной — служит для выбора варианта оптимизации значения целевой ячейки (максимизация, минимизация или подбор задан-

119

Тарова Инна Николаевна

ного числа). Чтобы установить число, необходимо ввести его в поле;

Изменяя ячейки — служит для указания ячеек, значения которых изменяются в процессе поиска решения до тех пор, пока не будут выполнены наложенные ограничения и условие оптимизации значения ячейки, указанной в поле Установить целевую ячейку;

Предположить — используется для автоматического поиска ячеек, влияющих на формулу, ссылка на которую дана в поле Установить целевую ячейку. Результат поиска отображается в поле

Изменяя ячейки;

Ограничения — служит для отображения списка граничных условий поставленной задачи;

Добавить — используется для отображения диалогового окна До-

бавить ограничение;

Изменить — применяется для отображения диалогового окна Из-

менить ограничение;

Удалить — служит для снятия указанного ограничения;

Выполнить — используется для запуска поиска решения поставленной задачи;

Закрыть — служит для выхода из окна диалога без запуска поиска решения поставленной задачи. При этом сохраняются установки, сделанные в окнах диалога, появлявшихся после нажатий на кнопки Параметры, Добавить, Изменить или Удалить;

Параметры — применяется для отображения диалогового окна Параметры поиска решения, в котором можно загрузить или сохранить оптимизируемую модель и указать предусмотренные варианты поиска решения;

Восстановить — служит для очистки полей окна диалога и восстановления значений параметров поиска решения, используе-

мых по умолчанию.

Другими типовыми примерами задач линейного программирования являются задачи:

О рационе питания.

Об оптимальных перевозках.

120