Площадь. Единицы площади

Классная доска висит на стене. Можно сказать, что площадь классной доски меньше, чем площадь этой стены.

Ковёр лежит на полу и полностью его закрывает. Пло­щадь ковра и площадь пола равны.

Площадь четырёхугольника больше, чем площадь тре­угольника. Это видно на глаз.

Сравнить площади круга и квадрата на глаз трудно. В таком случае используют способ наложения фи­гур.

Круг весь поместился внутри квадрата. Значит, пло­щадь круга ... , чем площадь квадрата, а площадь квадрата ... , чем площадь круга.

Часто бывает, что способом наложения сравнить пло­щади фигур нельзя.

В этом случае можно подсчитать квадраты с одина­ковой площадью, на которые разбита каждая фигура, и сравнить полученные числа.

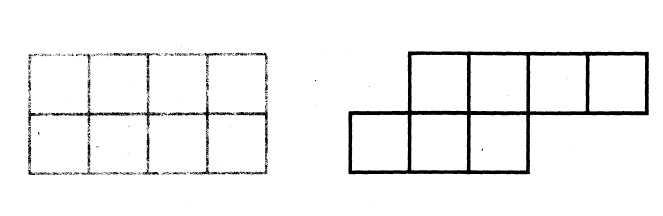
Это поможет учащимся осознать тот факт, что найти площадь прямоугольника — значит узнать, сколько квадратных сантиметров в нем содержится. Од­нако найти число этих квадратных сантиметров можно рациональ­нее: путем умножения длины на ширину.

При введении новой единицы площади — квадратного децимет­ра можно поступить следующим образом: нарисовать на доске пря­моугольник и предложить учащимся измерить его площадь, поль­зуясь двумя моделями — квадратного сантиметра и квадратного дециметра. Учащиеся убеждаются практически, что использование квадратного сантиметра для измерения площади данной фигуры нерационально. Гораздо удобнее пользоваться большей меркой — квадратным дециметром. У каждого ученика должна быть модель квадратного дециметра, разбитая на квадратные сантиметры. Учащиеся самостоятельно устанавливают соотношение между данными единицами площади: 1 кв. дм = 100 кв. см.

При знакомстве с квадратным метром необходимо иметь его демонстрационную модель, разбитую на квадратные дециметры.

Соотношения между единицами площади закрепляются в про­цессе выполнения различных упражнений.

Арифметические действия с величинами

Рассматривается сложение и вычитание однородных величин, умножение и деление величины на число.

Приведем пример различного объяснения того, как выполнено действие

42 м 65 см + 26 м 83 см = 69 м 48 см:

1) 4265 2) 42 м 65 см

+ +

2683 или 26 м 83 см

6948 см 69 м 48 см

69 м 48 см

Однако в любом случае дети должны понимать, что сложение и вычитание длины, массы и т. д. выполняется так же, как сло­жение и вычитание многозначных чисел.

Аналогично для умножения и деления величины на число.

4. Методика изучения дробей

В соответствии с программой по математике в начальных классах должна быть проведена подготовка к изучению дробей в последующих классах. Это значит, в начальных классах надо создать конкретные представления о доле и дроби. С этой целью npедусматривается в III классе ознакомить детей с долями, записью, научить сравнивать доли на наглядной основе, решать задачи на нахождение доли числа и числа по его доле.

В IV классе ознакомить с дробями, их записью, научить сравнивать доли и дроби. Все названные вопросы раскрываются на наглядной основе.

4.1.Ознакомление с долями (М. 3, ч.1, с.96-99).

Ознакомить детей с долями - значит сформировать конкретные представления о долях, т. е. научить детей образовывать доли практически. Например, чтобы получить одну четвертую долю круга, надо круг разделить на четыре равные части и взять одну такую часть; чтобы получить одну пятую долю отрезка, надо разделить его на пять равных частей и взять одну такую часть.

Для формирования правильных представлений о долях надо использовать достаточное количество разнообразных наглядных пособий. Как показал опыт, наиболее удобными пособиями являются геометрические фигуры, вырезанные из бумаги; можно использовать рисунки фигур, выполненные на бумаге или в диапозитивах (круги, прямоугольники, треугольники, бруски, отрезки и т. п.). Очень важно, чтобы пособия были не только у учителя, но и у каждого из учащихся. Правильные представления о долях, а позднее о дробях будут сформированы тогда, когда ученики будут своими руками получать, например, половину круга, квадрата и т. п., четверть отрезка и т. п.

Покажем, как можно ознакомить детей с долями.

У каждого из учащихся и у учителя несколько одинаковых кругов, прямоугольников (квадратов). Возьмите два одинаковых круга. Один из них paзделите на 2 равные части (показывает, как надо перегнуть и как разрезать круг).

Это целый круг, а это половина круга иначе говорят, одна вторая доля круга. Сколько вторых долей в целом круге? (2.) Покажите их. Возьмите квадрат. Как по­лучить одну вторую долю, или половину квадрата? (Разделить его на дне равные части и взять одну такую часть.) Выпол­няйте.

Учащиеся могут это сделать разными способами, например: разрезать квадрат по диагонали и получить два равных тре­угольника или же разрезать по средней линии, тогда получат­ся два прямоугольника. Некоторые учащиеся могут предложить и другие способы деления квадрата на две равные части (см. рис.)

Как получили одну вторую часть круга? (Разделили круг на две равные части и взяли одну такую часть.) Как получили одну вторую долю квадрата? Как иначе называют одну вторую долю круга, квадрата? (Половина круга, половина квадрата.)

Сколько половин круга в целом круге? (2.) Учащиеся накладывают половины круга на целый круг.

Доли записывают с помощью двух чисел. Одна вторая доля круга, квадрата обозначается так: . Число 2 показывает, что круг, квадрат или другая фигура (или предмет) разделены на две равные части, а число 1 показывает, что взяли одну такую часть.

Учащиеся записывают на половинах круга «» и объясня­ют, что показывает в этой записи каждое число.

Так же образуются доли и др. и объясняют, что показывает в этой записи каждое число.

При этом учащиеся должны уяснить, что для получения, например, отрезка (прямоугольника, бумажной полоски и т.п.) надо данный отрезок (прямоугольник, полоску и т.п.) разделить на 5 равных частей и взять одну такую часть, что в данном отрезке (прямоугольнике, полоске и т.п.) 5 пятых долей, что одна пятая доля записывается так: , что в этой записи число 5 обозначает, на сколько равных частей разделили отрезок (прямоугольник, полоску и т.п.), а число 1 показывает, что взята только одна часть.

Для закрепления этих знаний и умений учащимся предлагаются различные задания.

Это, прежде всего, задания в назывании и записи долей. Назовите и запишите, какая доля квадрата (круга) отрезана (закрашена, заштрихована).

Можно предлагать самим детям изобразить какую-либо до­лю отрезка (круга, квадрата и др.) и записать эту долю.

В каждом случае надо спрашивать, сколько всего долей в целом. Например, сколько четвертых долей круга в целом круге? Сколько третьих долей отрезка во всем отрезке? и т. п.

Решение задач на нахождение доли числа и числа по его доле также способствует формированию пред­ставлений о долях величины. В этом их основное назначение. Поэтому решение задач на нахождение доли числа и числа по его доле выполняется на наглядной основе.

Рассмотрим, как можно ознакомить учащихся с решением задач каждого вида.

Сначала вводятся задачи на нахождение доли числа. Для ознакомления с решенном задач лучше предлагать задачи, ко­торые легко иллюстрировать. Например, предлагается задача:

«От полоски длиной 15 см отрезали —1/3 ее. Чему равна длина отрезанного куска полоски?» Ученики вырезают полоску длиной 15 см. Затем выясняется, как найти одну третью часть полоски (разделить ее на 3 равные части и взять одну такую часть). Учащиеся практически выполняют деление (перегибают полос­ку), а затем отрезают одну третью часть. Запись решения вы­полняется так:

15:3 = 5 (см) –длина отрезанного куска.

Ответ: 5 см.

При решении других задач достаточно воспользоваться чер­тежом: число изобразить отрезком, который учащиеся делят на заданное число равных частей, обозначают долю, после чего выполняют решение устно или письменно.

В дальнейшем задачи на нахождение доли числа должны включаться для устной и письменной работы. Следует больше включать заданий вида: сколько сантиметров в м; в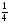м? Сколько минут вчаса; вчаса и т. д.?

Надо объяснить детям, почему принято говорить: «половина второго», «без четверти 10» и т. п.

Задачи на нахождение числа по его доле вначале надо брать такие, чтобы их можно было непосред­ственно иллюстрировать, например: «Серёжа отрезал от куска проволоки 4 см. Это всего куска. Какой длины был кусок?»

Изобразим кусок проволоки, который отрезал Сережа. (Чер­тят отрезок длиной 4 см.) Какую часть всего куска составляет отрезанный кусок (одну третью часть). Как изобразить весь кусок? (Взять 3 раза по 4 см.) Почему? (4 см — это куска проволоки, а во всём куске будет три трети.) Начертите (выполняют). Какой длины был кусок? (12см.) Как узнали?

Запись решения: 4· 3 = 12(см) –длина всего куска проволоки.

Ответ: 12 см.

Далее оба вида задач предлагаются в перемежении и предлагаются как для устного решения, так и для письменного решения.

4.2. Углубление знаний о долях (М.4, часть 2, с. 103-104).

Образование дробей, как и образование долей рассматривается с помощью наглядных пособий ( термин «дробь» по традиционной программе не используется, что весьма непонятно).

Разделите круг на 4 равные части. Как назвать каждую такую часть? Запишите. Покажите три четвертые доли. Вы получили дробь — три четвертых. Кто сможет записать эту дробь? Что показывает число 4? (На сколько равных частей разделили круг.) Что показывает число 3? (Столько таких частей взяли.) Аналогичным образом учащиеся получают и записывают другие дроби, объясняя, что показывает каждое число.

Для закрепления полученных знаний выполняются такие же задания, как и при ознакомлении с долями: по данным иллюстрациям называют и записывают, какие дроби изображены, или же изображают дробь с помощью чертежа, рисунка. Уяснению конкретного смысла доли помогают задания по сравнению долей на наглядной основе.

Для сравнения долей обычно используются иллюстрации с равными прямоугольниками. Учащимся предлагается начертить в тетради прямоугольник, длина которого 16 см, а ширина 1 см.

Это один прямоугольник. Запишем. (В пepвом прямоугольнике записывают число 1.) Начертите под пepвым прямоугольником такой же второй и разделите его на 2 равные части. (Выполняют.) Какие доли получили? (Вторые, половины.) Сколько вторых долей в целом прямоугольнике? Подпишите. Ниже начертите такой же прямоугольник и разделите его на 4 равные части. Как называется каждая часть? Сколько четвертых долей в целом прямоугольнике? Сколько четвертых долой в половине? Что больше: одна вторая или одна четвертая; одна вторая или две четвертые; одна четвертая или три четвертые; две вторые или четыре четвертые?

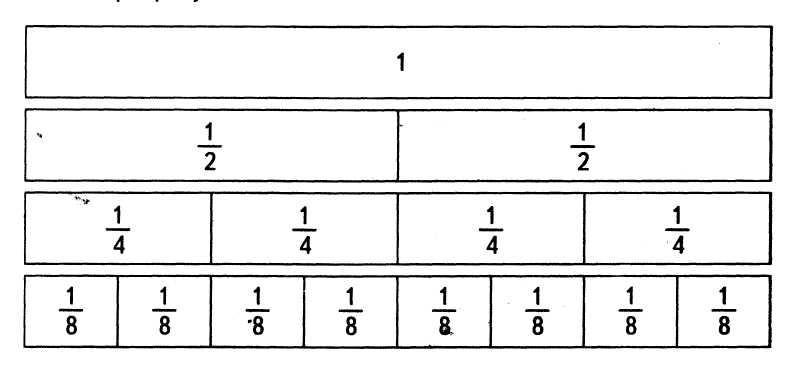
Начертите четвёртый такой же прямоугольник и разделите его на 8 равных час­тей. Как называются полученные доли? Сколько восьмых долей в целом? Сколько восьмых долей в одной четверти; в половине прямоугольника? Что больше: три восьмых или одна четвертая? Какой дроби равна одна вторая?

Ответы на все перечисленные вопросы дети дают, глядя на рисунок.

Таким же путем сравниваются и другие дроби, но для их сравнения выполняются другие иллюстрации: например, для сравнения дробей со знаменателями 3, 6, 9 равные прямоугольники де­лятся соответственно на 3, 6 и 9 равных частей, а для сравне­нии дробей со знаменателями 2, 5 и 10 равные прямоугольники делятся соответственно на 2, 5 и 10 равных частей.

Предлагаются специальные задания на сравнение долей:

Выполняя такие и подобные задания, учащиеся прибе­гают к соответствующим иллюстрациям с прямоугольниками или заново изображают дроби с помощью, например, отрезков.

Эффективным упражнением для формирования представле­ний о долях является сравнение долей одной и той же величи­ны, которое выполняется чисто практически с помощью нагляд­ных пособий.