
- •Числовые ряды. Признаки сходимости.
- •Необходимый признак сходимости
- •Необходимый признак следует понимать
- •Достаточные признаки сходимости знакоположительных рядов
- •Признак
- •Эталонные ряды
- •Например, сходящимися рядами будут являться следующие ряды
- •Признак
- •Таблица эквивалентных бесконечно малых величин
- •Признак Даламбера
- •Признак Даламбера применяется для решения вопроса о сходимости таких рядов, общие члены которых
- •При применении признака Даламбераожет встретиться необходимост
- •Радикальный признак Коши
- •Интегральный признак Коши
- •Интегральный признак Коши применяется для решения
Числовые ряды. Признаки сходимости.
Необходимый признак сходимости
Если числовой ряд u1 u2 u3 ... un ... = n=1un.
сходится, то предел его общего члена обязательнонулю, т.е.
равен |
|
lim un = 0. |
|
|
|
|
|
n |
|
|
|
Если |
необходимый |
признак |
сходимости |
не |
|
выполняется, т.е. |
lim un 0, |
|
|
||
|
|
n |
|
|
|
то ряд расходится.
Сходимость ряда исследуется по следующей схеме:
1.Проверяется необходимый признак сходимости.
2.Если необходимый признак выполняется, то окончательный вывод о сходимости ряда решается с помощью достаточных признаков сходимости.
Необходимый признак следует понимать |
|
|
|
|
|
|
|||||||||||||||||||
так: |
|
|
lim un = 0, то ряд может сходиться, |
|
|
|
|
||||||||||||||||||
|
Если |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
но |
может |
и |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
расходиться. |
|
|
|
|
|
|
||
|
Если |
|
lim un |
|
0, |
ряд |
точно |
|
|
|
|
||||||||||||||
|
|
|
расходится. |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
2n 1 |
|
2 |
|
|
||||||||
2n 1 |
|
1 3 5 |
|
|
|
|
limn |
= |
0. |
||||||||||||||||
n=1 3n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3n 1 |
3 |
|||||||
|
4 |
|
|
7 |
|
|
10 |
|
|
|
|||||||||||||||
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
.... |
|
|
|
|
|
|
|
||||
1 |
|
1 |
|
|
1 |
|
|
|
|
|
1 |
....расходится, хотяlimn |
|
1 |
|
|
|||||||||
n=1 |
|
|
= |
|
|
|
|
|
|
|
= 0. |
||||||||||||||
|
|
4 |
7 |
|
|
|
|
3n 1 |
|||||||||||||||||
3n 1 |
10 |
||||||||||||||||||||||||
В дальнейшем, если предел общего члена ряда |
||||||||||||
окажется равным нулю, то будем говорить, что ряд |
||||||||||||
может сходится, и продолжать исследование на |
||||||||||||
сходимость с помощью достаточных признаков |
||||||||||||
|
5n |
5 |
10 |
15 |
lim |
|
|
5n |
= 0 |
|||
|
3 |
|
|
|||||||||
n=1 |
|
|
= |
|
27 |
86 .... |
n |
3n |
|
2n 1 |
|
|
3n3 |
2n 1 |
4 |
|
|
||||||||
|
|
|
|
|
|
|
ряд может сходится |
|||||
Достаточные признаки сходимости знакоположительных рядов
Числовой ряд является знакоположительным, если все его члены положительны
Признак
сравнения 1 |
|
|
|
|
Пусть даны два знакоположительных |
|
|||
ряда |
n=1un = u1 u2 |
u3 ... un ... |
(1) |
|
|
||||
|
n=1vn = v1 v2 |
v3 ... vn ..., |
(2) |
|
причем, начиная с некоторого |
n = N, выполняется условие |
|||
номера |
un vn |
|
|
|
Тогда(1),из сходимости ряда (2) всегда следует сходимость и ряда |
||||
(2). |
из расходимости ряда (1) следует и расходимость ряда |
|||
Признак |
сравнения |
2 |
||
(предельный) |
|
|
|
|
Если существует конечный, отличный от нуля предел |
||||
отношения |
|
u |
|
|
|
limn |
n |
|
= A 0, |
|
v |
|||
n
то оба ряда (1) и (2) одновременно либо сходятся, либо асходятся.
При применении признака сравнения данный ряд сопоставляется с одним из, так называемых, эталонных
рядов, сходимость или расходимость которых установлена.
Эталонные ряды
1.Геометрический ряд
|
Если |
| q |< 1 ряд сходится |
qn : |
Если |
| q | 1 ряд расходится |
n=1 |
|
|
2. Обобщенный гармонический ряд
|
1 |
|
Если |
k > 1, |
то ряд |
n=1 |
: |
|
k 1, |
сходится |
|
|
|
||||
nk |
Если |
то ряд |
|||
3. Гармонический ряд |
расходится |
||||
|
|||||
|
1 |
1 |
1 |
1 |
|
n=1 n |
= 1 2 |
3 n ряд расходится |
|||

Например, сходящимися рядами будут являться следующие ряды
k > 1:
|
1 |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
1 |
|
|
|
1 |
|
||||||
|
, |
|
|
|
, |
|
|
|
|
, |
|
|
, |
|
|
, |
|
|
|
, |
|||||||||||||
|
|
3n |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
n |
2 |
2 |
|
2n |
3 |
1 |
n |
5 |
|
|
n |
3/ 2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
7 / 2 |
||||||||||||||||||||||||||
|
|
|
|
n |
7 |
||||||||||||||||||||||||||||
n=1 |
|
|
n=1 |
|
|
|
n=1 |
|
|
n=1 |
|
|
|
|
n=1 |
|
n=1 |
|
|
|
n=1 |
n |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| q |< 1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
3 n |
|
|
|
1 n |
|
|
|
2 n |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
7 |
, |
|
|
|
|
, |
|
|
5 |
, |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
n=1 |
|
|
|
|
n=1 |
2 |
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Например, расходящимися рядами будут являться следующие ряд
k 1:
|
1 |
|
|
|
1 |
, |
|
|
|
|
1 |
|
|
|
1 |
, |
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
, |
||||||
|
|
|
|
|
|
1/ 2 |
|
|
|
|
|
|
|
|
|
1/ 3 |
|
|
|
|
|
|
|
|
|
|
|
|
3/ 5 |
|||||||
|
n |
|
|
n |
|
|
3 |
|
n |
|
|
n |
|
|
5 |
2n |
3 |
|
|
|
5 |
2 n |
|
|||||||||||||
n=1 |
|
|
|
n=1 |
|
|
|
n=1 |
|
|
|
n=1 |
|
|
|
n=1 |
|
|
|
|
n=1 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
n |
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
| q | 1: |
|
|
|
|
, |
|
2 , |
|
|
|
1 , |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
( 1) , |
|
|
|
|
||||||||||||||||||||||
|
|
|
n=1 |
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||

Признак |
сравнения |
применяется |
|
для |
|
решения |
|
|
||||||||||||||
опроса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о сходимости, к примеру, рядов |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
1 |
|
|
|
|
n 5 |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
n=1 |
|
|
|
|
|
, n=1 |
|
|
|
|
, n=1ln |
1 |
|
|
|
|
, n=2 |
|
, |
|||
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||
n |
|
3n 1 |
3 n7 |
4n5 2 |
n |
3 |
ln n |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 |
|
|
|
|
|
n=1sin |
|
|
|
|
|
, n=1 |
1 |
5 |
|
|
|
|
|||
|
n |
2 |
|||||
|
|
|
|
|
|
|
|
cos 2n
|
|
|
|
e |
|||
, |
|
||
|
n=1 |
||
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|||
|
n |
|
1 |
|
|
|
|
|
||
|
|
|
|
|
||||||
|
|
, |
n=1 |
n arctg |
|
|
. |
|||
|
|
n |
4 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При использовании этого признака нужно привести данный ряд к эквивалентному ряду вида
A |
|
n |
A |
|
||
n=1 |
|
n=1A q |
|
n=1 |
|
n=1A qn |
nk |
|
|||||
|
nk |
|||||
При этом очень часто используется прием выделения главных членов выражения, а также таблица эквивалентных бесконечно малых величин
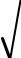
Таблица эквивалентных бесконечно малых величин
(x) 0
sin (x) ~ (x), |
|
arcsin (x) ~ (x), |
|||||||
tg (x) ~ (x), |
|
arctg (x) ~ (x), |
|||||||
1 |
cos (x) ~ |
2 (x) |
, |
e ( x) 1 ~ (x), |
|||||
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
||
n |
|
|
1 ~ |
(x) |
. |
ln(1 (x)) ~ (x), |
|||
1 |
(x) |
||||||||
|
|||||||||
|
|
|
|
|
n |
|
|
||

|
1 |
1 |
|
1 |
||
1. |
n=2 |
ln n-- ряд расходится, так как |
|
|
> n |
|
ln n |
||||||
|
|
а гармонический ряд |
1 |
расходится. |
||
|
|
|
n=2 n |
|
||
|
|
sin2 n |
-- ряд сходится, так |
|||
2. |
n=1 |
|
2 |
|
как |
|
n |
n |
|||||
|
|
|
|
|||
sin2 n |
|
1 |
|
а ряд |
1 |
|||
|
|
|
|
|||||
< |
, |
n=1 n5/2 |
||||||
n2 |
|
n5/2 |
||||||
n |
|
|||||||
сходится как обобщенный |
k = 5/2 > 1. |
гармоническийпоказателемс |

3. |
|
|
1 2n |
|
-- ряд расходится, так как |
||||||||||||||||||||||
n=1 |
|
|
|
|
|
|
2 |
|
члены его для достаточно |
||||||||||||||||||
|
|
|
|
1 |
n |
|
|
эквивалентны |
членам |
|
n |
||||||||||||||||
|
|
|
|
|
|
гармонического |
|||||||||||||||||||||
1 2n |
|
|
|
|
рядабольших |
|
|
|
|
2 |
|
|
|
расходи |
|||||||||||||
|
|
2n |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
2 ~ |
|
|
|
2 |
|
|
~ |
|
|
|
, а ряд |
n=1 |
n |
тся. |
|||||||||||
n |
n |
|
|
|
n |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
2n 1 |
|
|
|
|
2n |
|
|
2 |
|
|
|||||||||
4. n=1 |
|
|
|
|
~ n=1 n3 |
= n=1 |
|
|
|
||||||||||||||||||
n (1 n) (n 2) |
n2 |
|
|||||||||||||||||||||||||
ряд сходится |
|
|
обобщенный гармонический ряд с |
||||||||||||||||||||||||
как |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
показателем |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
= 2 > 1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
ряд расходится как обобщенный |
||||||||
5. n=1 3 |
|
|
|
|
|
|
|
|
|
|
~ n=1 |
|
|
||||||||||||||
n |
2 |
|
|
|
|
|
|
n |
2/3 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
4n |
|
|
|
|
|
|
|
|
||||||||||
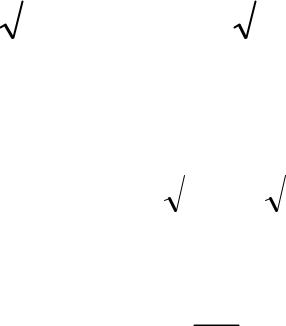
гармонический ряд с показателемk = 2/3 < 1
|
1 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
||||||
6. n=1 |
|
sin |
|
|
|
~ n=1 |
|
|
|
|
|
|
|
|
|
|
|
= n=1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3/2 |
||||||||||
3n 4 |
2 |
n |
3n 2 n |
6n |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
ряд сходится как обобщенный гармонический ряд с |
|
||||||||||||||||||||||||||
показателем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
k = 3/2 > 1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
при |
n |
||||||||
Здесь использовано то, что |
sin |
|
|
|
|
|
~ |
|
|
||||||||||||||||||
2 |
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||
|
n |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
||||||||||||
|
|
1 |
|
1 |
|
1 |
|
|||
7. |
n=1n arctg |
|
|
~ n=1n |
|
4 |
= n=1 |
|
|
|
n |
4 |
|
n |
3 |
||||||
|
|
|
n |
|
|
|
|
|||
ряд сходится как обобщенный гармонический ряд с казателем
k = 3 > 1
Здесь использована эквивалентность
1 |
1 |
при n |
||
arctg |
n4 |
~ |
n4 |
|

|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|||
8. n=1 |
|
|
|
|
|
|
cos |
|
|
|
|
|
~ n=1 |
|
ряд расходится |
||||||||
3n 4 |
2 |
|
|
|
3n |
||||||||||||||||||
|
n |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
В данном случае использовано то обстоятельство, что |
|||||||||||||||||||||||
|
cos |
|
1 |
|
|
|
1 |
|
|
|
при |
|
n |
|
|
||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
n |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
9. |
n=1 |
1 |
|
cos |
|
|
~ |
n=1 |
|
|
|
ряд сходится |
|||||||||||
|
n |
2 |
2n |
4 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
как обобщенный гармонический ряд с показателемk = 4 >1 Здесь мы воспользовались тем, что nпри
1 |
cos |
1 |
~ |
(1/n2 )2 |
= |
1 |
. |
|
n2 |
2 |
2n4 |
||||||
|
|
|
|
|
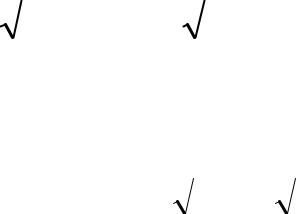
10. |
|
|
|
|
|
|
|
2 |
|
|
|
~ |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
= 2 |
|
1 |
|
|
|
|||||||||||||
|
|
ln 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
n=1 n1/2 |
ряд расходится |
|||||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
как обобщенный гармонический с |
|
|
|
|
|
|
k =1/2 <1. |
|
|||||||||||||||||||||||||||||||||||
|
показателем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Здесь использовано |
|
|
|
|
|
|
|
|
|
|
|
|
при n |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
1 |
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
n |
|
|
|
|
|
|
|||||
11. |
n=1 sin |
|
|
|
~ n=1 |
|
|
|
= |
n=1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
2 |
n |
|
2 |
n |
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ряд сходится как геометрический сознаменателем q 1/ 2 1 |
||||||||||||||||||||||||||||||||||||||||||||
12. |
|
|
|
3n |
e |
2n |
|
|
|
53n |
|
|
53 n |
|
|
|
|
|||||||||||||||||||||||||||
n=15 |
|
|
|
|
|
|
|
~ n=1 |
|
|
|
|
2n = n=1 |
|
2 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
125 |
|
|||||
ряд расходится как геометрический со |
|
|
|
|
|
|
q = e2 |
> 1. |
||||||||||||||||||||||||||||||||||||
знаменателем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
