Математичні основи аналітичної фотограмметрії

Тема лекції. Математичні основи аналітичної фотограмметрії

1. Основи векторної алгебри

При розгляді фізичних та геометричних основ фотограмметрії ми постійно оперуємо з поняттям вектора.

В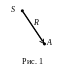 ектор - це величина, що має довжину і напрямок. Промінь, що виходить з центра проекції S до точки об'єкта А (рис.1) є вектором; стрілкою показаний напрям вектора, а його довжина - це віддаль між точками S і А.

Вільний вектор - вектор, в якому початкова точка (в даному випадку S) може лежати будь-де.

Зв'язаний вектор - вектор, в якому початкова точка (в даному випадку S) є фіксованою.

Якщо кілька векторів R₁, R₂, R₃ лежать в одній площині, то сумою векторів є:

(1.1)

Сума векторів має ті ж властивості, що й звичайна арифметична сума (властивості переміщення та об'єднання):

R₁+R₂=R₂+R₁, (1.2)

R₁+R₂+R₃=(R₁+R₂)+R₃=R₁+(R₂+R₃). (1.3)

Добуток вектора на скаляр записується так:

R = nr, (1.4)

тобто вектор R зберігає напрямок вектора r, а його довжина збільшується в n-разів.

Якщо вектори R та r мають однакові або протилежні напрямки і між ними існує залежність (1.4), то можна записати в узагальненому вигляді:

aR+br=0, (1.5)

де

. (1.6)

Розглянемо два вектори r₁ i r₂, що лежать в одній площині (рис. 2).

Рис. 2

Збільшимо вектор r₁ в n разів, так що отримаємо

R₁=nr₁, (1.7)

а вектор r₂ відповідно в m-разів; маємо:

R₂=mr₂. (1.8)

Сумарний вектор

R=R₁+R₂=nr₁+mr₂. (1.9)

Очевидно, що

R=kr=-pr, (1.10)

R₁+R₂-R=0, (1.11)

і остаточно

nr₁+mr₂+pr=0. (1.12)

Умова (1.12) називається умовою компланарності трьох векторів і формулюється наступним чином: якщо три вектори лежать в одній площині, то для них справедливе рівняння (1.12).

Важливим для аналітичної фотограмметрії є представлення вектора через три не компланарні вектори. Заслуговує особливої уваги випадок, коли ці три не компланарні вектори утворюють просторову прямокутну систему координат.

Звернемось до рис. 3. Будь-який вектор можна представити як діагональ паралелепіпеда, три ребра якого паралельні векторам r_x, r_y, r_z.

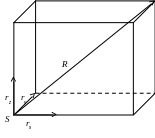
Рис. 3

Отже, вектор R можна записати як суму

R = nr_x + mr_y + pr_z. (1.13)

У випадку просторової прямокутної системи координат вводиться поняття ортів – це вектори i, j, k, що мають довжини, рівні одиниці, а напрямки їх співпадають з осями координат x, y, z. Тоді (1.13) записується так:

. (1.14)

Отже, будь-який вектор можна розкласти на його складові (проекції) на осі координат.

Якщо для вектора R необхідно знайти проекцію на деякий напрямок L в просторі, то маємо:

. (1.15)

Тут - довжина вектора R, - кут між напрямками L та R.

Скалярний добуток двох векторів R₁ та R₂ є величина

. (1.16)

Якщо вектори R₁ i R₂ утворюють прямий кут, то

. (1.17)

Тому для ортів маємо очевидне

. (1.18)

Якщо між ортами кут рівний нулю (випадок двох паралельних систем координат), то маємо

. (1.19)

Без викладок запишемо для добутку двох векторів

. (1.20)

Для скалярного добутку є справедливим розподільчий закон:

. (1.21)

В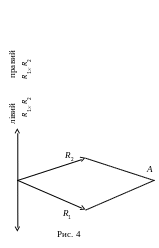 екторний добуток двох векторів є вектор, по величині рівний площі паралелограма, побудованого на цих векторах, а по напрямку співпадає з перпендикуляром до площини, яку утворюють ці два вектори (рис.4).

, (1.22)

. (1.23)

Напрям вектора R залежить від орієнтування системи координат або від уявної точки А, де стоїть спостерігач. Тоді для нього перпендикуляр може бути або ліворуч (лівий), або праворуч (правий).

Згідно з визначенням векторного добутку та на підставі рис.4 можемо записати:

(1.24)

Для векторного добутку є справедливим розподільчий закон:

.

В прямокутній системі координат XYZ добуток двох векторів виражається так:

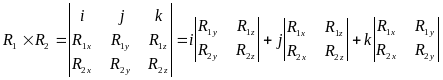, (1.25)

де - проекції відповідних векторів на осі координат.

Співвідношення між скалярним та векторним добутками.

Запишемо скалярний добуток вектора R на векторний добуток , тобто . Згідно з (1.25) та (1.23)

. (1.26)

Отже, скалярний добуток (1.26) виражає об’єм паралелепіпеда, побудованого на векторах R, R₁, R₂. Знак залежить від орієнтування координатних осей.

Якщо три вектори R, R₁, R₂ компланарні (тобто лежать в одній площині), то об’єм паралелепіпеда, побудованого на них, рівний нулю. Тобто:

=0. (1.27)

Це фундаментальне рівняння аналітичної фотограмметрії; використовується при розв'язанні задачі взаємного орієнтування і звучить так:

якщо три вектори R, R₁, R₂ компланарні, то їх змішаний скалярно-векторний добуток рівний нулю.

1.2. Операції з матрицями.

Матриця - сукупність чисел або деяких об'єктів, розташованих у вигляді прямокутної таблиці.

m - число рядків

n - число стовпчиків

Якщо матриця має один стовпчик - це матриця-стовпчик;

Якщо матриця має один рядок - це матриця-рядок.

Якщо m=n, то матриця називається квадратною.

Якщо в квадратній матриці поза головною діагоналлю всі елементи є нульовими, то матриця називається діагональною. В одиничній матриці на діагоналі є одиниці:

.

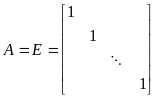Якщо всі елементи матриці рівні нулю, то матрицю називають нульовою.

Квадратна матриця називається верхньою (нижньою) трикутною, якщо нижче (вище) головної діагоналі всі елементи дорівнюють нулю.

Для матриць прийнято позначення у вигляді великих букв А, В, …. Розмірність матриці - це кількість рядків m і кількість стовпчиків n . Вигідно позначати матрицю та її розмірність так: .

Сума двох матриць:

, (1.28)

. (1.29)

Множення матриці на число:

. (1.30)

Це означає, що в результаті операції (1.30) кожний елемент матриці B отримується так:

. (1.31)

Справедливі такі дії:

, (1.32)

. (1.33)

Перемноження матриць:

. (1.34)

Перемножувати матриці можна лише за умови відповідності їх розмірів. В нашому прикладі (1.34) кількість стовпчиків n в матриці А відповідає кількості рядків n в матриці В. Для матриці С результуюча розмірність є . Кожний елемент матриці С отримується як сума добутків відповідних елементів матриць А і В:

. (1.35)

В загальному випадку множення матриць не підлягає комутативному правилу, тобто

. (1.36)

Це не стосується множення зліва чи справа на одиничну матрицю:

. (1.37)

Транспонування матриць.

Операція перестановки (заміни) всіх стовпчиків на рядки (і навпаки) в матриці називається транспонуванням. Якщо основна матриця є , то транспонована позначається і має розмірність .

Якщо квадратна матриця співпадає зі своєю транспонованою, то вона називається симетричною.

Матриця, для якої - , називається кососиметричною.

Запис системи лінійних рівнянь за допомогою матриць.

Система лінійних рівнянь типу:

,

, (1.37)

……………………………...

,

за допомогою матриць представляється так:

, (1.38)

де

, , .

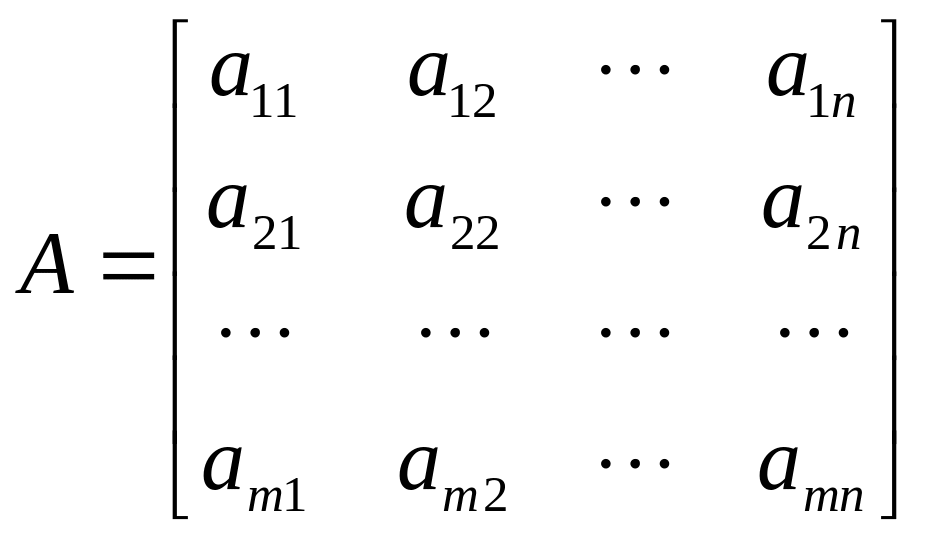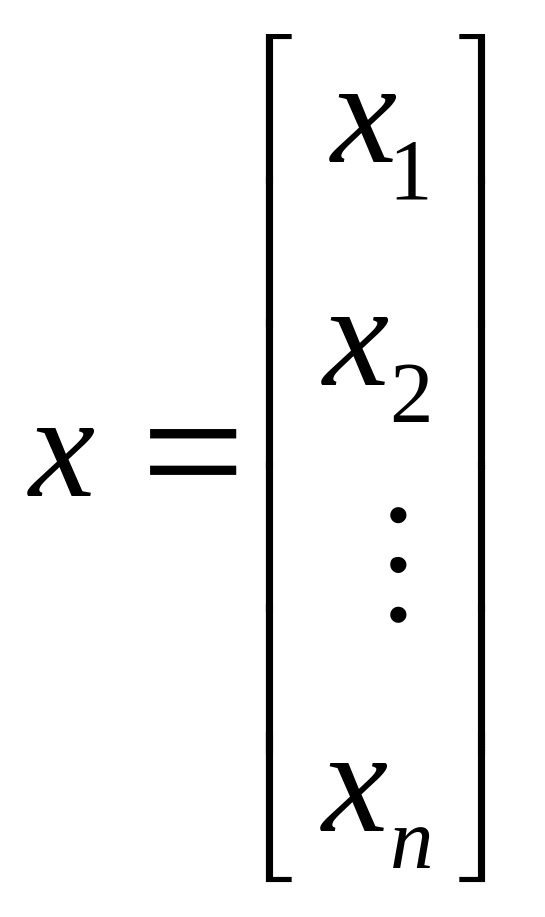Рівняння (1.38) можна назвати лінійним перетворенням, бо діючи на матрицю-стовпчик x матрицею А отримуємо нову матрицю-стовпчик y.

Обернена матриця.

У звичайній алгебрі для числа K є завжди таке число , при перемноженні яких маємо одиницю. Аналогічно для матриці А існує така матриця В, при перемноженні яких отримаємо одиничну матрицю: ; матрицю В називають оберненою і позначають . Тому маємо:

. (1.39)

Тут справедливе правило:

. (1.40)

Знаходження оберненої матриці не є простою операцією і в своїй суті є аналогією до розв'язання системи лінійних рівнянь. Якщо з рівняння (1.38) необхідно знайти величину x, то маємо:

і . (1.41)

Визначник матриці.

Визначник матриці є число, яке обчислюється за певними правилами.

Нехай у визначнику n-го порядку виділено k різних рядків і стільки ж стовпчиків; всі елементи, які розташовані на перетині цих рядків і стовпчиків, утворюють визначник, який називають мінором k-го порядку:

. (1.42)

Якщо з визначника усунути всі елементи, які належать мінору , то всі залишкові елементи утворять визначник - порядку, який називають доповнюючим мінором:

. (1.43)

Алгебраїчним доповненням мінора k-го порядку називають величину

, (1.44)

де - сума номерів рядків і стовпчиків, які утворюють мінор .

Обчислення невідомих для системи лінійних рівнянь за правилом Крамера.

У відповідності до правила Крамера для рівняння (1.41) маємо:

. (1.45)

де - визначник системи, - алгебраїчні доповнення.

Приклад обчислення визначника.

Розкладання визначника по елементах рядка або стовпчика вигідно, коли там є тільки один ненульовий елемент.

.

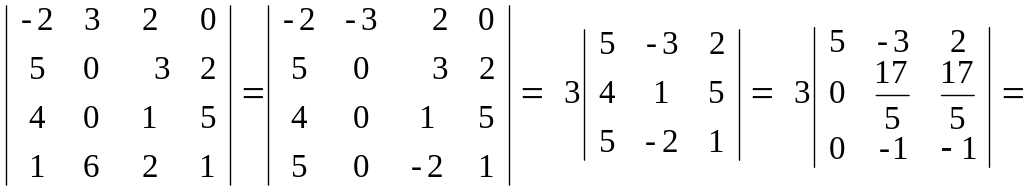
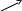
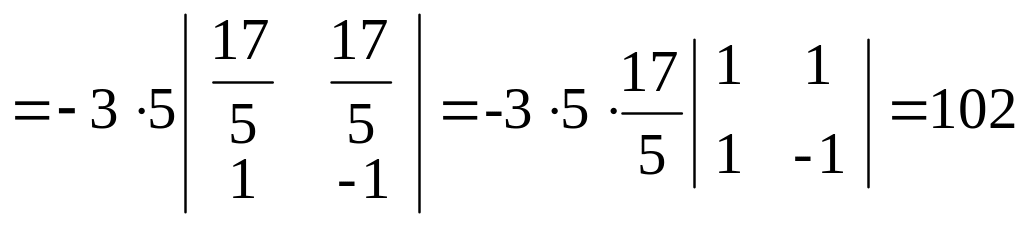Блочні матриці.

Часто матрицю вигідно розбивати вертикальними і горизонтальними лініями, утворюючи блоки-матриці менших розмірів.

Розіб'ємо матрицю А так, що вона матиме блоки:

.

Матрицю В розіб'ємо так:

.

Перемноження матриць дає:

. (1.46)

Для блочної матриці S n-го порядку та оберненої матриці при розбитті на блоки

, (1.47)

можна вичислити обернену матрицю так:

1-а формула Фробеніуса:

. (1.48)

2-а формула Фробеніуса:

. (1.49)

Тут

, , , . (1.50)

1.3. Геометричні перетворення.

В фотограмметрії приходиться оперувати такою математичною категорією як перетворення простору. Найбільш уживаним є проективне перетворення дво- або тримірного простору. Подамо в стислій формі найбільш поширені в фотограмметрії типи перетворень.

1. Проективне; має вигляд:

, (1.51)

де А - матриця перетворень, ( ), y - вектор початковий, - вектор перетворений.

2. Афінне; має вигляд:

, (1.52)

де А - матриця перетворення, x, x´, b - вектори-стовпчики.

Властивості цього перетворення: площина, лінія і відрізок переходять відповідно у площину, лінію і відрізок; не порушується паралельність прямих і площин; зберігається метрика векторів; трикутник переходить в трикутник.

Особливий випадок цього типу перетворення:

, (1.53)

при умові, що

, (1.54)

тобто А - ортогональна матриця, а вектор R є діагональною матрицею, тобто

. (1.55)

3. Афінне при співпадінні осей координат; має вигляд:

, (1.56)

тут .

4. Афінне зі збереженням подібності; має вигляд:

, (1.57)

де k>0, .

Властивості цього перетворення:

• кути зберігаються;

• зберігається подібність фігур;

• зберігається пропорційність відрізків;

• не порушується перпендикулярність векторів.

5. Афінне подібне середнє:

, (1.58)

тобто отримане з (1.57) за умови b=0. В цьому випадку зберігається початок системи координат.

6. Гомотетія:

, (1.59)

тобто з (1.58) k=1.

7. Ізометрія:

. (1.60)

Тут зберігаються довжини векторів.

8. Ізометрія середня:

. (1.61)

Тут збігаються початки систем координат.

9. Поворот простору:

, (1.62)

де , .

10. Перенос:

, (1.63)

, .

Властивість: міняється початок системи координат.

11. Симетричне відображення:

, (1.64)

, , витікає з (1.58).

Властивість: міняється орієнтування в просторі.

12. Ідентичне перетворення:

, (1.65)

тут зберігаються всі елементи.

Звернемо тепер увагу на деякі аспекти геометричних перетворень. Спочатку розглянемо перетворення площини в площину (рис.5).

Для визначення положення точки а на площині прийнята довільна (не прямокутна) система координат . Для так званих невласних точок (перетин двох паралельних прямих) ці координати не дозволяють визначити їх положення. Тому в проективній геометрії положення точки визначається його напрямком. Напрямок вектора визначається співвідношенням його складових . Тому для будь-якої точки а (рис.5) визначальним є відношення:

. (1.66)

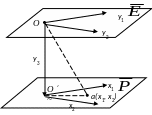
Рис. 5

Координати називають однорідними координатами точки а в системі . Співвідношення (1.66) означає пропорційність складових k.

Для кожної точки площини можна записати

. (1.67)

Звідси можна зробити висновок, що системі однорідних координат у (n+1) - мірному просторі може відповідати довільна система координат n - вимірного простору.

З (1.66) маємо:

, . (1.68)

Для тривимірного простору необхідно взяти чотири числа, тобто (1.66) запишеться так:

, (1.69)

.

Якщо прийняти до уваги (1.51) - лінійне перетворення, то для четвірки чисел запишемо:

,

, (1.70)

,

.

З (1.70) та (1.69) легко отримуємо формули для обчислення координат при геометричних проективних перетвореннях.

Для тривимірного простору:

,

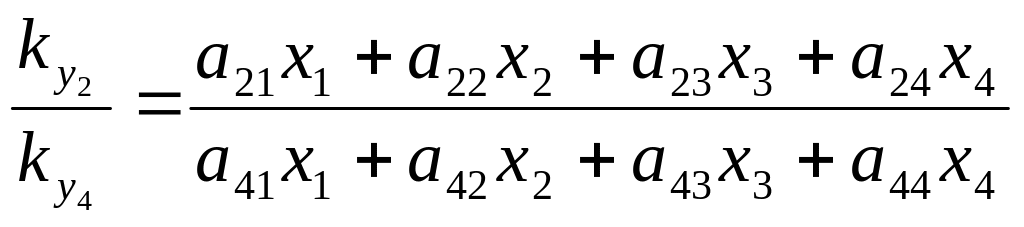, (1.71)

.

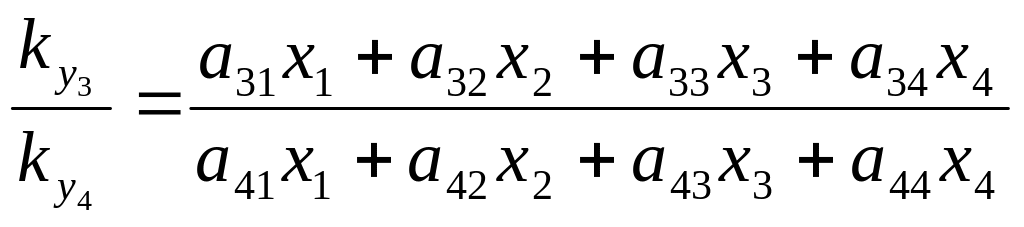Ставиться вимога, що .

Рівняння (1.71) можна спростити, розділивши чисельник і знаменник в (1.71) на .

Ввівши позначення для величин

, , і т.д., (1.72)

отримаємо:

,

, (1.73)

.

Для двомірного простору (перетворення площини в площину) маємо і відповідно: