Розділ 5 вимірювання других похідних потенціалу сили ваги

Для вимірювання других похідних потенціалу сили ваги використовують гравітаційні варіометри і градієнтометри. Якщо гравітаційними варіометрами можна виміряти горизонтальні градієнти сили вагиW_xz, W_yz і градієнти кривини рівневої поверхніW_xy,W_, то гравітаційним градієнтометром - тільки горизонтальні градієнти сили ваги. В кінці XIX століття угорським фізиком Етвешом була розроблена теорія варіометра і перший прилад для вимірювання других похідних потенціалу сили ваги. Всімоделігравітаційних варіометрів і градієнтометрів побудовані за принципом крутильної ваги Кулона. Така крутильна вага Кулона являє собою легке горизонтальне коромисло з двома тягарцями на кінцях, яке всередині підвішене на дуже тонкій нитці, навколо якої воно може повертатися (рис. 27)

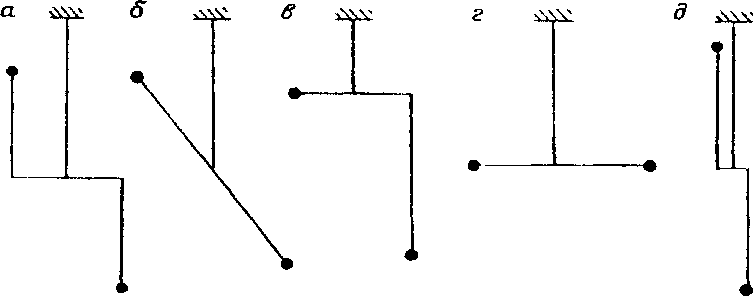
Рис, 27. Схеми коромисел крутильної ваги

На рис. 27 подані Z - подібні - (а,d), нахилені - (б); L - подібні - (в) і горизонтальні -(г) коромисла. Крутильну вагу Кулона (горизонтальні коромисла) Етвеш назвав вагою першого роду, а вагу з тягарцями на різних висотах - вагою другого роду. На протязі деякого часу крутильна вага здійснює затухаючі коливання, і після цього вона займає у деякому певному азимуті положення рівноваги В однорідному гравітаційному полі на тягарці діють однакові сили і положення рівноваги буде при розкрученому стані нитки. Насправді гравітаційне поле є неоднорідним, і тому положення рівноваги коромисла буде залежати від параметрів коромисла і гравітаційних сил.

1. Теорія гравітаційного варіометра

Залежність між гравітаційними силами і параметрами коромисла в положенні рівноваги називається основним рівнянням гравітаційного варіометра. Для того, щоб одержати це рівняння, розглянемо рис. 28, на якому точка 0 - початок системи прямокутних просторових координат х, у,z. Вісь z направлена вертикально вниз вздовж нитки, вісь х- на північ, а вісь у- на схід.

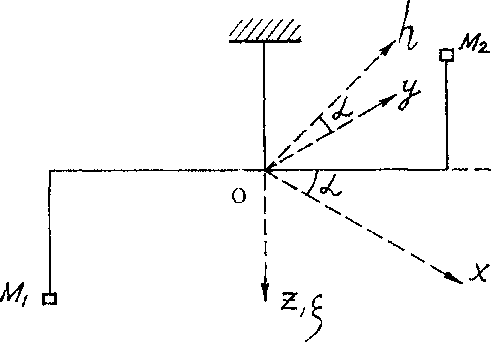
Рис. 28. До теорії гравітаційного варіометра

Для будь-якої точки нашої системи з елементарною масою dт і координатами х, у,z розкладемо діючу силу ваги gна три складові за осями координатg_x, g_y, g_z. Як відомо із теоретичної механіки, складові g_x і g_y створюють елементарний крутильний момент, а складова g_zє паралельною нитці і не викликає повороту навколо вертикальної осі коромисла. Тоді крутильний момент, який діє на всю систему, дорівнює інтегралу по всьому об'єму коромисла.

(5.1)

Під дією моментаM_z коромисло повернеться навколо осі z, а в крутильній нитці виникнутьпружинні сили, які протидіють повороту. Цей крутильний момент нитки М_Тбуде пропорційний кутові ϑ повороту коромисла. Кут ϑ відраховують від положення коромисла при розкрученому стані нитки, тобто від положення рівноваги в однорідному гравітаційному полі. Це положення безпосередньо ми не можемо спостерігати, тому що завжди проводять спостереження в неоднорідному гравітаційному полі, а нитка буде в закрученомустані. Позначимо через ϑ₀- відлік за горизонтальною шкалою, який виражається в радіанах і відповідає розкрученому

п оложенню нитки. Звідси основне рівняння гравітаційного варіометра, яке виражає положення рівноваги систем записують у вигляді

(5.2)

де

τ- стала крутильної нитки, яка залежить від її розмірів і матеріалу, з якого вона виготовлена.

Розміри чутливої системи варіометра невеликі, тому можна прийняти сталими другі похідні потенціалу сили ваги в об'ємі, який займає чутлива система. Використовуючи

р

(5.3)

(5.4)

яд Тейлора і обмежуючись при розкладі членами першого порядку, для величин g_x і g_yзапишемо:

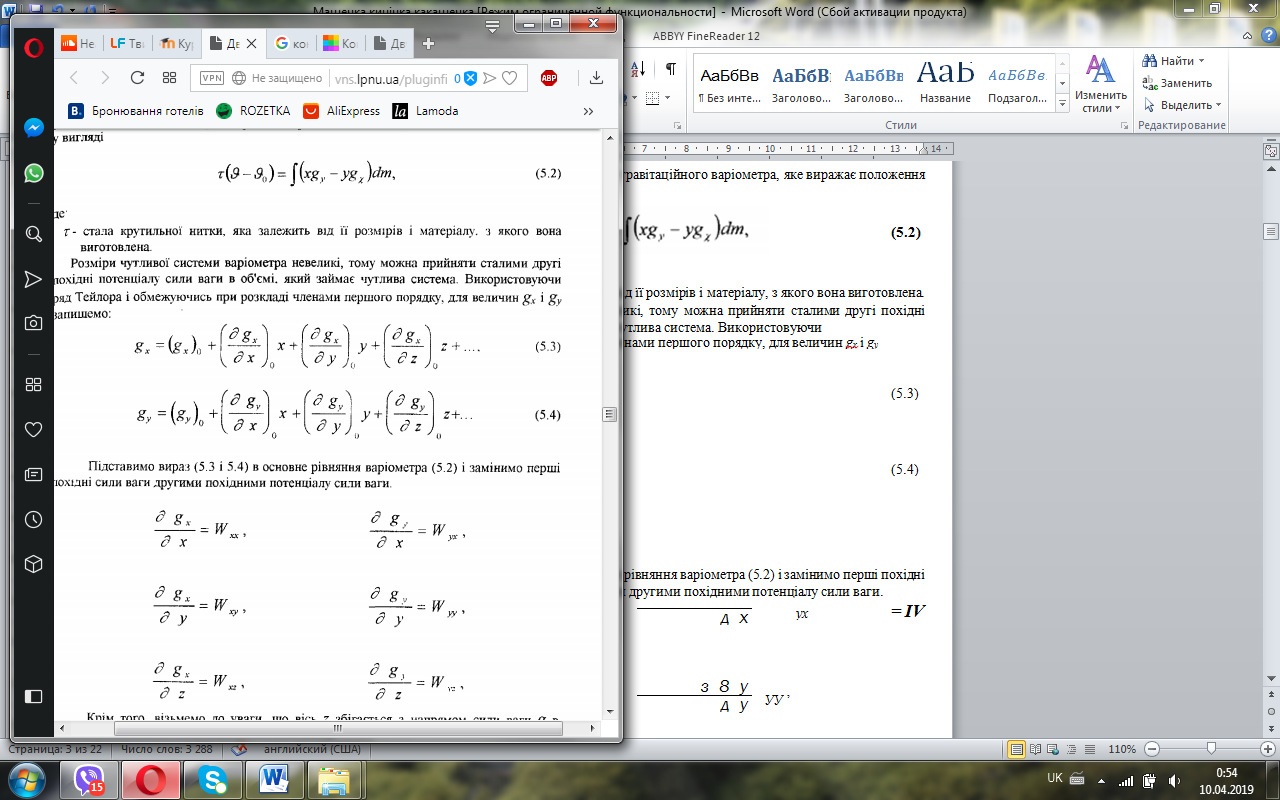
Підставимо вираз (5.3 і 5.4) в основне рівняння варіометра (5.2) і замінимо перші похідні сили ваги другими похідними потенціалу сили ваги.

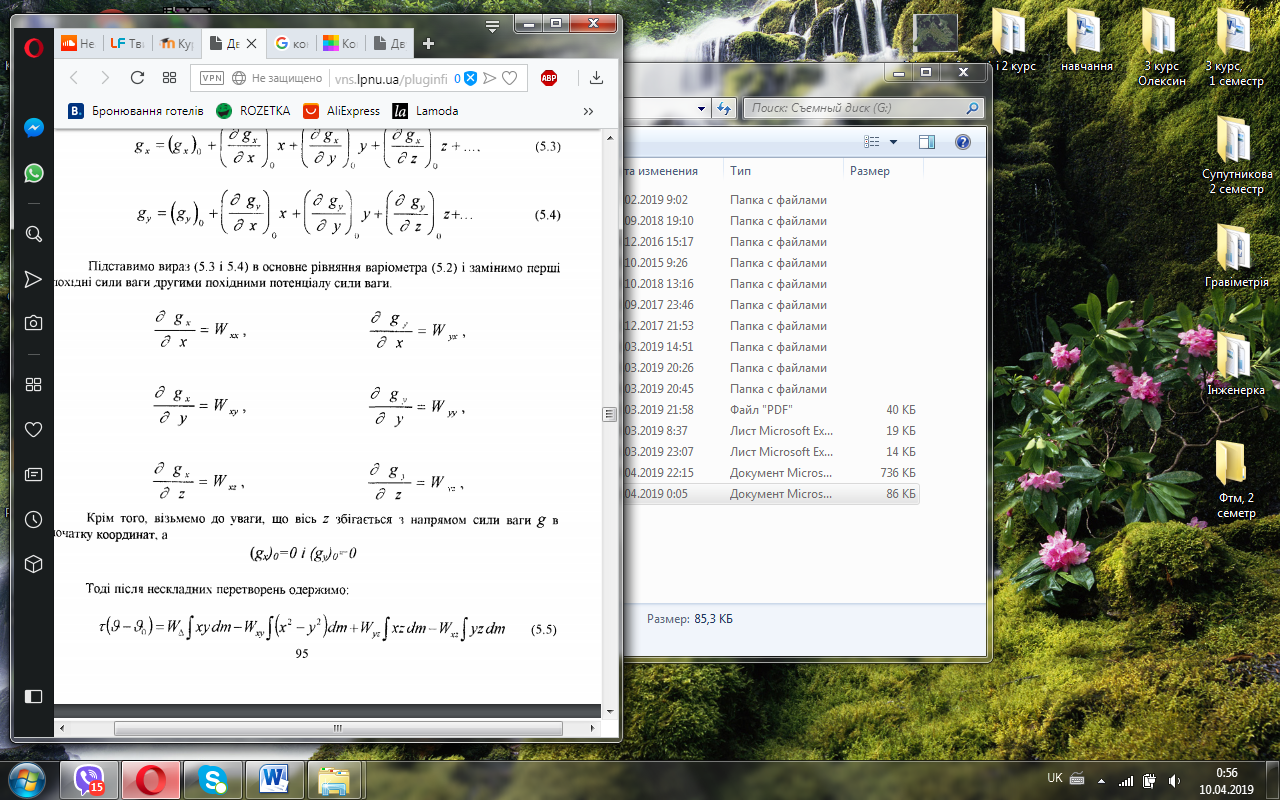
Крім того, візьмемо до уваги, що вісь г збігається з напрямом сили ваги g в початку координат, а

(g_x)₀=0 і (g_y)₀=0

Т

(5.5)

оді після нескладних перетворень одержимо:

95

Інтеграли в правій частині рівняння залежать від форми, розмірів коромисла і його положення в просторі. Для того, щоб спростити обчислення інтегралів, введемо нову систему координат Ɛ, ɳ, ς нерухомо зв’язану з коромислом. Початок нової системи координат співпадає з центром ваги коромисла, вісь Ɛ направлена вздовж коромисла, вісь ɳ -в перпендикулярному напрямі, а вісь ς збігається з напрямом z. Кут між осями х і Ɛ, який є азимутом коромисла, позначимо черезα. Тоді основне рівняння варіометра (5.5) з врахуванням переходу від однієї системи координат до іншої

x=Ɛ cos α - ɳ sin α,

y=Ɛ sin α + ɳ cos α,

z=ς

набере вигляду після нескладних перетворень

(5.6)

Знаючи форму та розмір коромил, можна обчислити інтеграли, які входять і рівняння (5.6).

Р озглянемо інтеграли виду 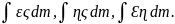Для всіх типів коромисла зберігається

с иметрія відносно площини ɳ=0, а через те і Знайдемо вираз

д ля

(5.7)

де

/ - довжина плеча коромисла,

к - віддаль між центрами ваг тягарців,

т - маса кожного тягарця

Т ут при обчисленні інтеграла ми приймаємо що маса тягарця зосереджена в йогоцентрі ваги з

Координатами

І нтеграл представимо в виді

(5 8)

Де- момент інерції коромисла відносно С,

П оперечні розміри коромисла малі в порівнянні з його довжиною, і можна з похибкою до 0,1% прийняти, що

(5 9)

О тже основне рівняння гравітаційного варіометра одержимо у вигляді

(5.10)

В це рівнянні входять пять невідомих величин ( ϑ₀, W_, W_xy, W_xz, W_yz)іпять параметрів (К, h, 1, т, τ). Величина кута поворот, коромисла ϑ в заданому азимуті αвимірюється. Для визначення всіх п'яти невідомих необхідно виконати спостереження в п’ятирізних азимутах, а саме при α=0°, 72°, 144°, 216°, 288°. Задаючи підвісній системі різну форму можна одержувати рівняння типу (5.10), в яке будуть входити не всі другі похідні потенціалу сили ваги. Так, для крутильної ваги першого роду h=0 то тоді основне рівняння гравітаційного варіометра запишуть так

(5.11)

при К=0 одержують основне рівняння градієнтометра

( 5.12)

Для скорочення часу спостережень у варіометрах і градієнтометрах встановлюють крутильні системи які повернуті одна відносно іншої на 180˚.