
МВ обч гравіметр звязку двох пунктів
.pdfМІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ “ЛЬВІВСЬКА ПОЛІТЕХНІКА”
ОБЧИСЛЕННЯ
ГРАВІМЕТРИЧНОГО ЗВ’ЯЗКУ ДВОХ ПУНКТІВ, ВИКОНАНОГО СУЧАСНИМИ МАЯТНИКОВИМИ ПРИЛАДАМИ ТА СТАТИЧНИМИ ГРАВІМЕТРАМИ
МЕТОДИЧНІ ВКАЗІВКИ
до виконання лабораторних робіт з курсу “Основи гравіметрії” для студентів базового напряму
“Геодезія, картографія та землеустрій”
Затверджено на засіданні кафедри вищої
геодезії та астрономії. Протокол № 1 від 29.08.2013 р.
Львів – 2013
Обчислення гравіметричного зв’язку двох пунктів, виконаного сучасними маятниковими приладами та статичними гравіметрами :
Методичні вказівки до виконання лабораторних робіт з курсу “Основи гравіметрії” для студентів базового напряму “Геодезія, картографія та землеустрій” / уклад.: П. Д. Двуліт, О. В. Ломпас – Львів: Видавництво Львівської політехніки, 2013. – 20 с.
Укладачі |
Двуліт П. Д., д-р техн. наук, проф., |
|
Ломпас О. В., канд. техн. наук, асист. |
Відповідальний за випуск Заблоцький Ф.Д., д-р техн. наук, проф.
Рецензент Марченко О.М., д-р фіз.-мат. наук, проф.
2
ВСТУП
Як відомо, під час відносних вимірювань прискорення вільного падіння гравіметричним приладом можна безпосередньо або посередньо виміряти одну з двох основних величин (час або шлях), за яким визначають прискорення. Невизначеність отримують вимірюванням цієї самої величини на наступному пункті, а другу вимірювальну величину вважають незмінною. За виміряним приростом часу або шляху обчислюють прирости прискорення вільного падіння між пунктами спостереження. Відносні вимірювання є ефективніші за економічними затратами, ніж абсолютні вимірювання.
Відносний метод вимірювання прискорення вільного падіння маятниковими приладами (за незмінної зведеної довжини маятника) став дуже ефективним і його використовували протягом тривалого часу.
З розвитком науки і техніки маятникову апаратуру вдосконалювали. Були розроблені досконаліші маятникові прилади, нові способи реєстрації періодів коливання маятників, а також покращена методика вимірювань. Розвивалась як теорія маятникового методу, так і способи спостережень, врахування впливу навколишнього середовища (температура, тиск, вологість тощо). Якісний стрибок у розвиток маятникової апаратури відбувся від впровадження фотоелектронної реєстрації періодів коливання маятників та їх амплітуд. Цей метод дав можливість автоматизувати реєстрацію періоду та амплітуду коливань маятника з застосуванням ЕОМ.
У 30-х роках ХХ століття з’явився новий клас гравіметричних приладів – статичні гравіметри, які в середині 60-х років ХХ ст. витіснили маятникові прилади. Точність вимірювань приросту прискорення вільного падіння маятниковими приладами досягла 0.01 мГала у 2000 р. У той же час точність таких вимірювань статичними гравіметрами збільшилась з 30-х років ХХ ст. на два порядки ( від 1 мГала до 1 мкГала). Але статичні гравіметри мають два істотних недоліки: зміну нуль-пункту і необхідність визначати ціну поділки відлікової шкали. Маятники перед гравіметрами мають такі переваги: висока стабільність, відсутність нуль-пункту, немає потреби виконувати еталонування, незалежність результатів від вимірюваного значення приросту прискорення вільного падіння і від тривалості рейсу. Завдяки цим перевагам маятникову апаратуру почали використовувати для створення опорних високоточних гравіметричних мереж і базисів для еталонування гравіметрів. Крім того, почав розвиватися метод сумісного визначення прискорення вільного падіння статичними гравіметрами і маятниковими приладами як найбільш прогресивний і раціональний за методики робіт в умовах морів та океанів.
3
Отже, відносні вимірювання прискорення вільного падіння сучасними маятниковими приладами і статичними гравіметрами виконують для створення високоточної Державної мережі опорних гравіметричних пунктів. Створені опорні гравіметричні пункти підвищеної точності слугують для еталонування гравіметрів, врахування зміщення нуль-пункту гравіметра з часом і для приведення результатів гравіметричного знімання в єдину систему. Це досягається застосуванням високоточних маятникових приладів, статичних гравіметрів, удосконаленням методики спостережень, багаторазовими вимірюваннями, скороченням тривалості гравіметрових рейсів і сприятливих температурних умов тощо.
Обчислення гравіметричного зв’язку та оцінка точності вимірювань сучасними маятниковими приладами
У різних країнах світу сьогодні розроблені і набули широкого використання сучасні маятникові прилади. До них належать американський маятниковий прилад з кварцовими маятниками, англійський (Кембриджський) прилад з інварними маятниками, німецький чотиримаятниковий прилад “Askania”, канадський маятниковий прилад, двомаятниковий прилад “Агат”, виготовлений у СРСР. Маятниковий комплекс “Агат”, який був розроблений у ЦНДІГАІК, об’єднує три двомаятникових, термостатованих і вакуумованих прилади. Визначення прискорення вільного падіння здійснюється методом Венінг-Мей- неса. Середня квадратична помилка вимірювання приросту g одним приладом становить 0,08 мГал, а їх комплектом – 0,05 мГал.
Програма спостережень на пункті залежить від точності гравіметричного зв’язку, від величини похибок приладу, впливу мікросейсми і вібрацій, від умов транспортування приладу і зношення лез маятників. Програма спостережень з сучасним маятниковим приладом “Агат” має деякі особливості:
1.Тривалість однієї серії спостережень на пункті становить 2048 коливань ( ≈ 17 хв).
2.У симетричні моменти відносно середнього моменту серії вимірюють амплітуду коливань фіктивного маятника і тиск всередині штатива.
3.Для зменшення впливу похибок аретування, варіацій частоти кварцового генератора, мікросейсм і вібрацій на пункті вимірюють період коливання у 6–8 серіях.
4.Порівнюють частоту кварцових генераторів кожної доби, а на опор-
ному пункті їх контролюють за еталонною частотою Служби часу. Спостереження виконують за схемою А-В-А або А-В-…-В-А з кожним
приладом комплекту, а у вихідному пункті А спостерігають два рази з метою контролю незмінності зведеної довжини маятника. Період коливань фіктивного маятника T обчислюють за формулою
4

|
T = T ' + T + |
T + |
T + |
T |
f |
+ |
T |
, |
(1) |
|
α |
t |
D |
|
|
прип. |
|
|
|
де T ' – виміряний період коливання за допомогою реєстратора; |
|
||||||||
Tα |
– поправка за амплітуду; |
|
|
|
|
|
|
|
|
Tt |
– поправка за температуру; |
|
|
|
|
|
|
|
|
DTD – поправка за густину навколишнього середовища; |
|
|
|||||||
DTf |
– поправка за частоту кварцового генератора; |
|
|
|
|||||
DTприп. – поправка за припливні варіації прискорення вільного падіння.
Потім обчислюють для кожного приладу приріст прискорення вільного падіння g , використовуючи середнє значення періоду коливання у вихідному пункті А і значення періоду коливання у визначальному пункті В. Тоді
|
T 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
g B = g A × |
A |
|
або |
Dg = g |
B |
- g |
A |
= Dg |
1 |
+ Dg |
2 |
, |
(2) |
|
T 2 |
|
|||||||||||||
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
де |
|
Dg1 = -2g A |
× DT , |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
TB |
|
|
|
|
|
|
|
|
|
|
|
|
|
éDT ù |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Dg2 |
= g A × ê T |
ú |
, |
|
|
|
|
|
|
|
|
|
|
|
|
ë |
B û |
|
|
|
|
|
|
|
|
|
|
DT = TB -TA .
При рівноточних вимірюваннях усіма приладами за остаточне значення g приймають середнє арифметичне із результатів окремих значень кожного
приладу
|
n |
|
|
|
|
å Dgi |
|
|
|
Dgсер = |
i=1 |
. |
(3) |
|
n |
||||
|
|
|
Похибку гравіметричного зв’язку остаточного результату, виконаного n приладами, отримують за формулою
M g = |
m g |
, |
(4) |
|
n |
||||
|
|
|
|
|
n |
|
|
|
|
å(δi )2 |
|
|
де |
m g = |
i=1 |
, |
|
n -1 |
||||
|
|
|
δi = Dgi - Dgсер .
Така оцінка точності за внутрішньою збіжністю не враховує можливих систематичних похибок і дає, зазвичай, неправильне уявлення про точність вимірювань. У разі суворої оцінки точності вимірювань необхідно враховува-
5
ти джерела помилок випадкового, напівсистематичного і систематичного характеру. Цього можна досягти на підставі аналізу великої кількості вимірювань, виконаних різними приладами за однорідних умов спостережень, а також лабораторних досліджень кожного приладу. Тоді похибка одного при- ладу-зв’язку обчислюється за такими виразами:
é2g |
|
ù |
|
|
|
||
m2g = ê |
|
×10−8 |
ú |
×m2T |
= k ×m2T , |
(5) |
|
T |
|||||||
ë |
|
û |
|
|
|
||
|
|
|
|
|
m2 |
= m2 |
+ m2 , |
|
|
|
(6) |
|||
|
|
|
|
|
T |
|
|
0 |
|
T |
|
|
|
|
де m0 |
– похибка визначення середнього періоду у вихідному пункті; |
|
||||||||||||
|
mT |
– похибка середнього періоду для цього приладу у визначальному пункті; |
||||||||||||
|
m T |
|
– похибка приросту періоду коливань маятника |
T . |
|
|||||||||
|
Похибки m0 |
і mT |
подамо у вигляді |
|
|
|
|
|
||||||
|
|
|
|
|
m02 = 1 (mA2 |
+ mA2 |
)+σ 2 , |
|
|
|
(7) |
|||
|
|
|
|
|
4 |
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ = 1 (TA |
|
-TA ) , |
|
|
|
(8) |
|||
|
|
|
|
|
2 |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 = m |
2 |
+ μ 2 , |
|
|
|
(9) |
|||
|
|
|
|
|
T |
T ' |
|
|
|
|
|
|
|
|
|
|
|
μ 2 = m2 × Dp2 + A2 × m2 |
+ m2 |
×Dt 2 +α 2 × m2 |
+ m2 |
× m2 , |
(10) |
||||||
|
|
|
|
A |
p |
|
|
α |
|
t |
|
f |
a |
|
де |
mA |
і |
mA – похибки визначення середніх періодів при спостереженнях на |
|||||||||||
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
опорному пункті; |
|
|
|
|
|
|
|
|
|
|||
|
σ |
– похибка, зумовлена впливом нелінійності зміни зведеної довжини та |
||||||||||||
|
|
|
інших джерел помилок; |
|
|
|
|
|
|
|
|
|
||
|
mT ' – випадкова похибка періоду коливання у визначальному пункті; |
|
||||||||||||
|
μ |
– напівсистематична стала похибка для певного пункту, але змінна від |
||||||||||||
|
|
|
одного пункту до іншого. Для її обчислення враховують технічні ха- |
|||||||||||
|
|
|
рактеристики маятникового комплексу “Агат”. |
|
|
|
|
|||||||
|
α і A – температурний і барометричний коефіцієнт маятника; |
|
||||||||||||
|
t і |
p – відхилення температури і тиску всередині штативу від їх серед- |
||||||||||||
|
|
|
нього значення на вихідному пункті; |
|
|
|
|
|||||||
|
m f |
і ma – похибки визначення поправок за частоту кварцового генератора |
||||||||||||
|
|
|
і похибки за амплітуду; |
|
|
|
|
|
|
|
|
|
||
|
mA , |
mα , m t , |
m p – похибки перерахованих вище величин. |
|
||||||||||
|
Похибки mA |
, mA |
і mT ' визначають за внутрішньою збіжністю періодів, |
|||||||||||
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
виправлених усіма поправками, використовуючи формулу
6
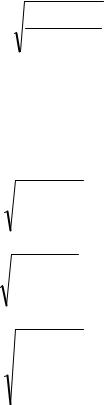
m = |
åV 2 |
|
N ×(N -1) , |
(11) |
де V – відхилення кожного періоду від середнього на пункті для кожного приладу;
N – кількість серій спостереження з цим приладом на пункті.
Після цього визначають середню квадратичну похибку результату із всіх n приладів комплекту. ЇЇ можна визначати за такими формулами:
M gсер |
= |
|
(m2g )сер |
(12) |
|||||||
|
|
n |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||
M |
' |
= |
|
|
åV 2 |
|
|
|
(13) |
||
gсер |
|
|
|
|
|
|
|
|
|||
|
n × |
(n -1) |
|||||||||
|
|
|
|
|
|||||||
M '' gсер |
= |
|
(m2g )сер |
(14) |
|||||||
|
|
n |
|
|
|
||||||
|
|
|
|
|
|
å Pi |
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
n |
|
|
× Dgi |
|
|
|
|
|
|
|
|
å Pi |
|
|
|
|
||||
Dg .в. = |
i=1 |
|
|
|
|
|
|
|
(15) |
||
|
|
n |
|
|
|
|
|
||||
|
|
|
|
å Pi |
|
|
|
|
|||
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
P = |
(m2g )сер |
|
. |
|
(16) |
|||||
|
|
m2g |
|
||||||||
|
|
|
|
|
|
|
|
||||
У цих формулах:
(m2g )сер – середнє арифметичне значення квадратів похибок або квадрат
похибки одиниці ваги; n – кількість приладів;
P – вага виміру;
g .в. – середнє вагове значення приросту прискорення вільного падіння. Оцінити точність результату вимірювань можна з найбільшою достовірністю, якщо ввести ваги вимірювань. Виконуючи повторні гравіметричні зв’язки з іншими маятниковими приладами, можемо виявити інші джерела помилок, як систематичного, так і напівсистематичного характеру. Приклад обчислення гравіметричного зв’язку та його оцінка точності між пунктами А і В, виконаного за схемою А1 – В – А2 комплектом п’яти маятникових приладів під час рівноточних та нерівноточних вимірів, наведено у табл. 1–3. Період
7
коливання маятника трьох приладів становить приблизно на 0,5 с, а двох інших – 0,75 с. Похибки m0 , σ і mT виражають у міліГалах, використовуючи наближене значення (з 2–3 значущими цифрами) коефіцієнта переходу К.
|
|
Вихідні дані |
|
Таблиця 1 |
|
|
|
|
|
||
|
|
|
|
|
|
Варіант 1 |
gа= |
978430,11 мГал |
|
|
|
Номер |
Номер |
Кількість |
Період |
Похибка |
|
приладу |
пункту |
серій |
Т, с |
m |
, 10-8 с |
|
|
|
|
T |
|
1 |
А1 |
6 |
0,491237479 |
|
±0,31 |
В |
8 |
0,491155867 |
|
0,48 |
|
|
А2 |
7 |
0,491237487 |
|
0,58 |
2 |
А1 |
5 |
0,490634542 |
|
±0,69 |
В |
8 |
0,490552992 |
|
0,39 |
|
|
А2 |
7 |
0,490634528 |
|
0,50 |
3 |
А1 |
6 |
0,484993252 |
|
±0,53 |
В |
6 |
0,484912690 |
|
0,45 |
|
|
А2 |
7 |
0,484993250 |
|
0,31 |
4 |
А1 |
8 |
0,739476357 |
|
±0,91 |
В |
6 |
0,739353472 |
|
0,31 |
|
|
А2 |
7 |
0,739476344 |
|
-0,68 |
5 |
А1 |
6 |
0,746344220 |
|
±0,33 |
В |
6 |
0,746220209 |
|
0,33 |
|
|
А2 |
6 |
0,746344184 |
|
0,47 |
8

|
|
|
|
Обчислення гравіметричного зв’язку |
|
Таблиця 2 |
||||||
|
|
|
|
|
|
|
||||||
|
Зв’язок А1 – В – А2 |
|
|
|
|
gа=978430,11 мГал, |
2gа= 1956860,22 мГал |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mT |
|
|
|
ΔТ, 10-8, с |
g1 , мГал |
|
|
|
Номер |
Номер |
Кількість |
Період |
|
Період |
|
ΔТ/Т, 10-8, с |
g2 , мГал |
δ |
||
|
приладу |
пункту |
серій |
Т, с |
10-8, с |
|
мГал |
Т, с |
|
(ΔТ/Т)2, 10-16, с |
g , мГал |
мГал |
|
|
|||||||||||
|
|
A1 |
6 |
0,491237479 |
0,31 |
|
0,012 |
|
|
-8161,6 |
325,174 |
|
|
1 |
B |
8 |
0,491155867 |
0,48 |
|
0,019 |
0,491237483 |
|
-16617,1 |
0,027 |
-0,014 |
|
|
A2 |
7 |
0,491237487 |
0,58 |
|
0,023 |
|
|
2,8 |
325,147 |
|
|
|
|
|
К1=0,040 |
σ=0,40 |
|
0,016 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
A1 |
5 |
0,490634542 |
0,69 |
|
0,028 |
|
|
-8154,3 |
325,282 |
|
|
2 |
B |
8 |
0,490552992 |
0,39 |
|
0,016 |
0,490634535 |
|
-16622,7 |
0,027 |
0,095 |
|
|
A2 |
7 |
0,490634528 |
0,50 |
|
0,020 |
|
|
2,8 |
325,255 |
|
9 |
|
|
|
К2=0,040 |
σ=-0,70 |
|
-0,028 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
A1 |
6 |
0,484993252 |
0,53 |
|
0,021 |
|
|
-8056,1 |
325,103 |
|
|
|
|
|
|
|
|
|||||||
|
3 |
B |
6 |
0,484912690 |
0,45 |
|
0,018 |
0,484993251 |
|
-16613,5 |
0,027 |
-0,085 |
|
|
A2 |
7 |
0,484993250 |
0,31 |
|
0,013 |
|
|
2,8 |
325,076 |
|
|
|
|
|
К3=0,040 |
σ=-0,10 |
|
-0,004 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
A1 |
8 |
0,739476357 |
0,91 |
|
0,024 |
|
|
-12287,85 |
325,225 |
|
|
4 |
B |
6 |
0,739353472 |
0,31 |
|
0,008 |
0,739476351 |
|
-16619,7 |
0,027 |
0,037 |
|
|
A2 |
7 |
0,739476344 |
-0,68 |
|
-0,018 |
|
|
2,8 |
325,198 |
|
|
|
|
|
К4=0,026 |
σ=-0,65 |
|
-0,017 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
A1 |
6 |
0,746344220 |
0,33 |
|
0,009 |
|
|
-12399,3 |
325,155 |
|
|
5 |
B |
6 |
0,746220209 |
0,33 |
|
0,009 |
0,746344202 |
|
-16616,1 |
0,027 |
-0,033 |
|
|
A2 |
6 |
0,746344184 |
0,47 |
|
0,012 |
|
|
2,8 |
325,128 |
|
|
|
|
|
К5=0,026 |
σ=-1,80 |
|
-0,048 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
gсер = 325,161 мГал M gсер = 0,031 мГал

10
Таблиця 3
Оцінка точності гравіметричного зв’язку
Но- |
mA1 , мГал |
mA2 , мГал |
σ, мГал |
m0 , мГал |
mT2 |
' , мГал |
μ, мГал |
mT , мГал |
m g , мГал |
|
мер |
P |
|||||||||
при- |
10-6, мГал2 |
10-6, мГал2 |
10-6, мГал2 |
10-6, мГал2 |
10-6, мГал2 |
10-6, мГал2 |
10-6, мГал2 |
10-6, мГал2 |
|
|
ладу |
|
|
|
|
|
|
|
|
|
|
1 |
0,012 |
0,023 |
0,016 |
0,021 |
|
0,019 |
0,028 |
0,034 |
0,040 |
|
|
144 |
529 |
256 |
424 |
|
361 |
784 |
1145 |
1569,25 |
1,18 |
2 |
0,028 |
0,020 |
-0,028 |
0,033 |
|
0,016 |
0,028 |
0,032 |
0,046 |
|
|
784 |
400 |
784 |
1080 |
|
256 |
784 |
1040 |
2120 |
0,87 |
3 |
0,021 |
0,013 |
-0,004 |
0,013 |
|
0,018 |
0,028 |
0,033 |
0,036 |
|
|
441 |
169 |
16 |
169 |
|
324 |
784 |
1108 |
1276,5 |
1,45 |
4 |
0,024 |
-0,018 |
-0,017 |
0,023 |
|
0,008 |
0,028 |
0,029 |
0,037 |
|
|
576 |
324 |
289 |
514 |
|
64 |
784 |
848 |
1362 |
1,36 |
5 |
0,009 |
0,012 |
-0,048 |
0,049 |
|
0,009 |
0,028 |
0,029 |
0,057 |
|
|
81 |
144 |
2304 |
2360,25 |
|
81 |
784 |
865 |
3225,25 |
0,57 |
|
|
|
|
4547 |
|
1086 |
3920 |
5006 |
9553 |
5,43 |
|
|
Сума квадратів |
|
|||||||
|
|
|
Середнє |
0,028 |
|
0,014 |
0,028 |
0,032 |
0,043 |
|
|
|
|
|
758 |
|
196 |
784 |
997 |
1850 |
|
|
|
|
|
|
|
|
|
|
|
|
gс.в. = 325,156 мГал M gсер = 0,058 мГал
10
