Б.1в1 Различные способы задания прямой.

1. Параметрическое уравнение прямой.

В пространстве дана аффинная система координат (О, , , ). Проведём прямую d: Md, || d.

Md <=> (1)

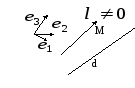
Формула (1) устанавливает взаимно однозначное соответствие между точками прямой d и значениями параметра t. Значения параметра t являются координатами точки M относительно аффинной системы (M, ). Точка M называется начальной точкой прямой d, - направляющий вектор прямой d. Положение прямой d в пространстве вполне определяется заданием точки M и вектором , т.е. d=[ M, ]. Выведем уравнение прямой d при этом способе задания: M(x, y, z), M (x, y, z). =l+l+l. Запишем равенство (1) в координатной форме: =t (l+l+l). Сравнивая одноимённые координаты векторов, стоящих в левой и правой частях последнего равенства, получим

(2)

Таким образом, из (1)=>(2). Обратно из (2)=>(1).

Исходя из справедливости прямого и обратного утверждений, заключаем, что уравнения (2) – есть уравнения прямой, которые называются параметрическими уравнениями прямой.

2. Каноническое уравнение прямой.

а) l∙ l∙l≠0; то исключая значения параметра t из (2), получаем

(3).

б) если одна из координат направляющего вектора l =0, например, l=0, тогда из (2)=>

(3').

В этом случае d||OXY. В частности dOXY.

в) две координаты направляющего вектора l равны нулю, например, l= l=0, тогда из (2) => y-y=0, z-z=0 (3''). В этом случае d||OX. В частности d=OX. Уравнения (3), (3'), (3'') называются каноническими уравнениями прямой.

3. Прямая d может быть задана двумя различными точками, например, M, M d. d=[M, M, M≠ M]. Пусть M (x, y, z), M (x, y, z).

Этот способ задания прямой сведём к первому способу задания прямой, взяв в качестве начальной точки любую из двух данных точек, например, M, а в качестве направляющего вектора . d=[ M, ]. Воспользуемся уравнением (3):

(4), где x-x≠0, y-y≠0, z-z≠0 – уравнение прямой, проходящей через две различные точки.

4. Прямая d может быть задана, как линия пересечения двух плоскостей:

П: Ax+By+Cz+D=0

(5)

П: Ax+By+Cz+D=0

ранг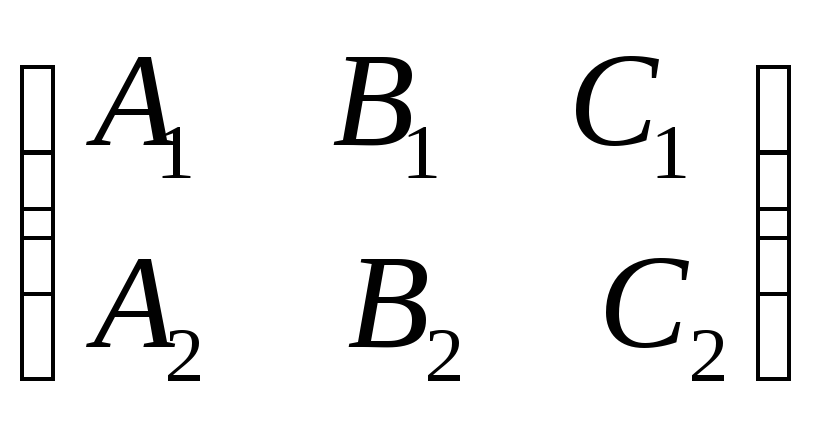=2 (*) – условия пересечения плоскостей Пи П, d = П∩ П.

Координаты x, y, z точки Md являются решением системы уравнений (5). M(x, y, z)d. Если x, y, z - какое - то решение системы уравнений (5), то эта система будет равносильна системе (5') A(x-x)+B(y-y)+C(z-z) = 0

A(x-x)+B(y-y)+C(z-z) = 0

Общее решение системы уравнений (5') имеет вид: x-x= t

y-y=t

=>z-z=t x=x+t

=> y=y+t (6). z=z+t

Уравнения (6) есть параметрические уравнения прямой d= П∩ П. В прямоугольной системе координат вектор .

Взаимное расположение прямой и плоскости

Пусть в пространстве задана аффинная система координат (О,) и пусть плоскость задана П: Ах+Ву+Сz+Д=0 (1) и прямая d: x=x₀+l₁t

y=y₀+l₂t (2)

z=z₀+l₃t

Нужно решить вопрос о взаимном расположении прямой d и плоскости П, т.е. нужно найти общие точки прямой и плоскости. Для этого нужно решить систему из (1) и (2): в ур-ние (1) вместо x,y,z подставим их знач-я, к-е следуют из равенств (2). Получим (Ах₀+Ву₀+Сz₀+Д)+(Al₁+Bl₂+Cl₃)t=0 (3).

Возможны следующие случаи:

1. система из (1) и (2) имеет единственное решение тогда и только тогда, когда уравнение (3) имеет единственное решение.

, ≠0 (4)- необходимое и достаточное

условие пересечения прямой d и плоскости П.

В прямоугольной с-еме координат это условие имеет простой геометрический смысл, оно означает, что , где (А,В,С) – вектор нормали пл-ти П, (l₁,l₂,l₃) – направляющий вектор прямой d. Т.к. , то эти вектора не перпендикулярны. В частности d  П  ,

А=, r(A)=1

2. система (1), (2) не имеет решения тогда и только тогда, когда

уравнение (3) не имеет решения. Это будет тогда и только тогда:

(5) – необходимое и достаточное условие того,

что d∩П=Ø. В прямоугольной системе координат – геометрический смысл: .

Т. М₀ (x₀, y₀, z₀)d, но М₀П.

3. Система имеет бесконечное мн-во решений тогда и только

тогда, когда (3) имеет бесчисленное мн-во решений:

(6) – необходимое и достаточное условие

принадлежности прямой d плоскости П. в прямоугольной системе

координат это означает, что . Т. М₀ (x₀, y₀, z₀)d, но М₀П.

Из условий (5) и (6) следует, что прямая d | | П  Аl₁+Bl₂+Cl₃=0