25. Решить задачу Коши

Решение: преобразуем это уравнение к каноническому виду:

Уравнение характеристик

Распадается на 2 уравнения

интегралами которых являются прямые

Вводя новые переменные

Уравнение колебаний струны преобразуем к виду

Где - функция только переменного. Интегрируя (2) попри фиксированном, получим

26. Решить первую краевую задачу для уравнения теплопроводности:

Решение:

Решение будем искать в виде

(4), где Х(х)- функция только первого х, T(t)- функция только t.

Подставляя (4) в (1) и производя деление обеих частей равенства на XT, получим

, где , так как левая часть равенства зависит только отt , а правая- только от х.

Отсюда следует, что

Граничные условия (3) дают

Таким образом для определения функции мы получи задачу о собственных значениях (задача Штурма-Ляувиля)

Только для значений параметра , равныхсуществуют нетривиальные решения уравнения (5), равные

Этим значениям соответствуют решения уравнения (6)

где - неопределенные пока коэффициенты.

Таким образом функции является частными уравнениями (1), удовлетворяющими нулевым граничным условием.

Требуя выполнения начальных условий, получаем

То есть С_п являются коэффициентами Фурье функции при разложении её в ряд по синусам на интервале (0,1)

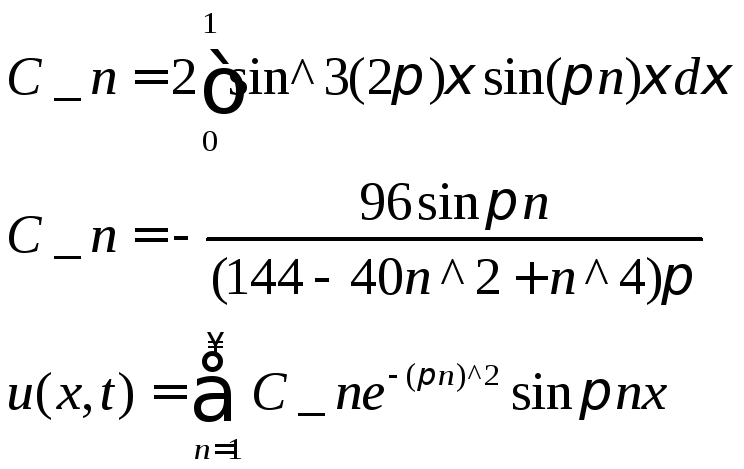
Таким образом искомое решение

27 разложить в ряд Лорана ф-ию 1/((z-2)(z-3)) в кольце 2<|z|3

Решение

Особые точки являются полюсами z=2, z=3

Разложим на простые дроби

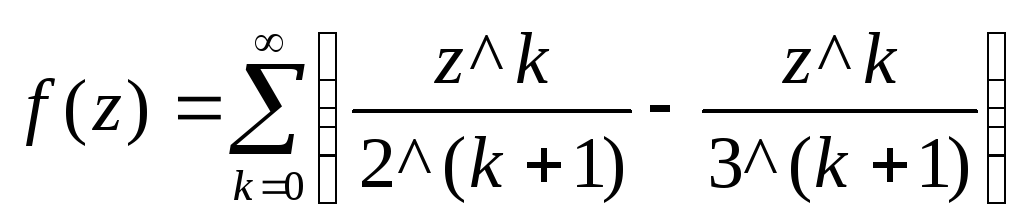
28.Найти изолированные особые точки аналитической функции и выяснить их характер:

А) , Б), В).

Решение:

А)

Особые точки

Очевидно, все точки изолированные и являются полюсами, так как

Б)

Запишем разложение в окрестностях особых точек.

Разложим дробь на элемент дроби

z=0: Первая дробь представляет собой слагаемое требуемого вида

- это разложение содержит только главную часть, состоящую из одного числа; это разложение имеет место в области . Для второй дроби точкаz=0 не является особой, то получаем ряд Тейлора в круге :

. Таким образом разложение содержит конечное число отриц степенейz (т=1) следовательно точка z=0- полюс первого порядка.

Аналогично

z=1:

- это разложение справедливо во всей плоскости с выколотой точкой , то есть в области. От первого слагаемого получим

Таким образом

Как видим разложение содержит конечное число отриц степеней (1-z), следовательно точка z=1- полюс функции f(z), так как т=1, то полюс простой.

В)

Особая точка z=0

Разложение f(z) в ряд Лорана по степеням z :

Разложение не содержит отриц степеней z, следовательно точка z=0 является устранимой точкой.

29. Найти вычеты функции

А) , Б), В).

****теория****

1) В случае когда z=a- устранимая точка

2) Если z=a – полюс функции f порядка р , то

(1)

В частности при р=1 (1) примет вид: (2)

3) Пусть функция f в окружности простого полюса z=a имеет вид: (3, где - аналитические в точкеz=a ф-ции, причем Имеем

(4)

4) Теорема Пусть 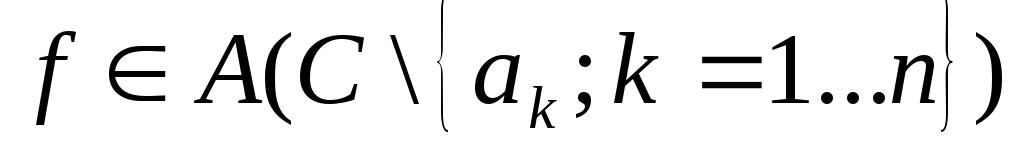, тогда сумма вычетов функцииf во всех ее конечных особых точках и вычета на бесконечности равна:

(5)

Решение: А)

Особыми точками данной функции являются . Данные точки являются простыми полюсами, поэтому применим формулу

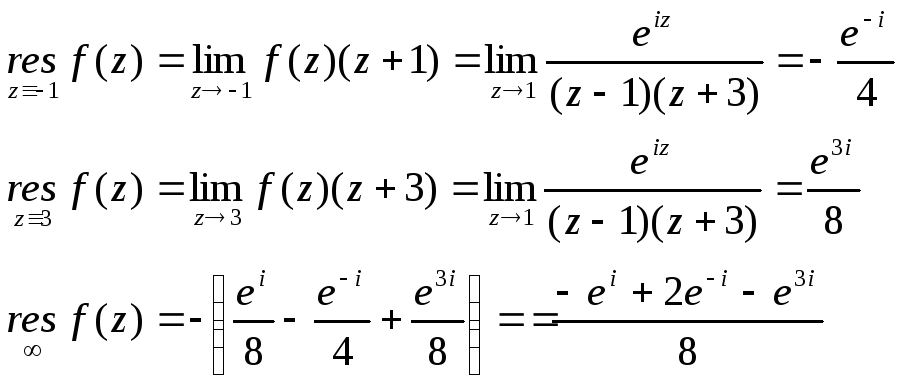
Б)

Особыми точками данной функции является .

Точка является полюсом первого порядка функцииf, поэтому для вычисления вычета в этой точке применим формулу , получим

Аналогично

Согласно формуле имеем

Следовательно

В) В точках данная функция имеет простые полюсы. Воспользуемся функцией, в которой.

Тогда

.

Бесконечно удаленная точка является предельной для особых точек.