- •Isbn 978-966-553-820-2
- •1.11. Виведення розрахункової формули поперечної похибки висячого
- •1.12. Виведення формули поперечної похибки полігонометричного ходу з попередньо
- •1.13. Полігонометричні знаки 130
- •1.14. Організація полігонометричних робіт 134
- •Лінійні вимірювання у траверсній полігонометрії 136
- •Прилади для вимірювання ліній у траверсній полігонометрії 136
- •Виконання лінійних вимірювань підвісними мірними приладами 138
- •Джерела похибок під час вимірювання ліній підвісними мірними приладами... 141
- •Розрахунок допусків на окреме джерело похибок лінійних вимірів 142
- •Кутові вимірювання у полігонометрії 148
- •Основні вимоги до кутомірних приладів у полігонометрії.
- •Відлікові пристрої оптичних кутомірних приладів. Їхнє призначення та
- •Принцип роботи автоматичних систем відліків електронних теодолітів
- •Будова оптичних та електронних теодолітів та тахеометрів 168
- •Перевірки теодолітів 173
- •Вимірювання горизонтальних кутів способом кругових прийомів 178
- •4. Знімання рельєфу та дешифрування фотопланів під час комбінованого методу
- •4.1. Встановлення мензули над точкою 493
- •4.2. Польове та камеральне дешифрування 494
- •IV.4.3. Послідовність роботи на станції під час рисування рельєфу й дешифрування
- •IV.4.4. Основні офіційні вимоги до точності зображення контурів та рельєфу 497
- •IV.4.5. Камеральні роботи під час знімання рельєфу на фотопланах (калька висот,
- •IV.4.6. Зведення за рамками суміжних топографічних планів 500
- •IV.4.7. Контроль робіт та приймально-здавальні роботи 501
- •IV.5. Стереоаерофотограмметричне знімання 503
- •IV.5.2. Технологічна схема стереофотограмметричного методу знімання 505
- •IV.5.3. Сучасні станції аналітичної фотограмметрії 506
- •6. Цифрове аерознімання 507
- •IV.6.2. Порівняння технічних можливостей фотограмметричної та цифрової камер.
- •6.3. Цифрові аерознімальні комплекси із лазерним скануванням 511
- •I. Автоматизація топографо-геодезичних робіт 516
- •1.1. Основні напрямки та технології автоматизації топографо-геодезичного
- •I.2. Автоматизація визначення висот 518
- •I.3. Автоматизація визначення планового положення точок 519
- •I.4. Автоматизація визначення просторового положення точок 521
- •I.5. Автоматизовані динамічні топографічні системи 524
- •I.6. Автоматизовані лазерно-паралактичні топографічні системи 525
- •I.7. Електронна тахеометрія 526
- •I.8. Автоматичні координатографи 528
- •I.9. Перетворювачі аналогової інформації на цифрову 528
- •1.10. Наземні лазерні сканери 530
- •2. Цифрові плани та карти 532
- •2.I. Загальні відомості про цифрові моделі місцевості 532
- •2.2. Вимоги до цифрових карт та планів 535
- •2.3. Поняття про кодування топографо-геодезичної інформації (тгі) 536
- •2.4. Алгоритми опрацювання польової інформації 538
- •2.5. Алгоритми формування моделі ситуації (мс) 540
- •2.6. Алгоритм формування моделі рельєфу (мр) 541
- •2.7. Диференційні перетворення або ортофототрансформування 544
- •2.8. Поняття про цифрову фотограмметрію та цифровий
- •2.9. Сканування фотознімків 552
- •2.10. Цифрові фотокамери 554
- •2.11. Цифрові фотограмметричні станції 555
- •Загальні відомості про геометричне нівелювання
- •III і IV класів
- •Призначення державної нівелірної мережі
- •Класифікація державної нівелірної мережі
- •II клас (200 км)
- •Складання проекту нівелірної мережі
- •Нівелірні знаки
- •Прилади, що використовують для геометричного нівелювання III, IV класів
- •Головні вимоги до нівелірів, що використовують для нівелювання III, IV класів
- •Головні вимоги до нівелірних рейок
- •/.2.5. Електронні цифрові нівеліри. Тотальні нівелірні станції
- •Перевірки та дослідження нівелірних рейок
- •2.8. Дослідження руху фокусувальної лінзи
- •Виконання нівелювання III та IV класів. Похибки та точність нівелювання
- •Послідовність роботи на станції під час нівелювання III класу
- •Послідовність роботи на станції під час нівелювання IV класу
- •Похибки нівелювання. Їхнє зменшення та усунення
- •Точність нівелювання III, IV класів
- •Зрівноваження нівелірних ходів та мереж
- •Зрівноваження висот окремого нівелірного ходу
- •Зрівноваження нівелірної мережі з однією вузловою точкою
- •Зрівноваження перевищень нівелірних мереж методом еквівалентної заміни
- •Зрівноваження нівелірних мереж способом послідовних наближень (спосіб вузлів)
- •Зрівноваження нівелірної мережі порівнянням нев’язок суміжних ходів
- •Методи створення планових мереж.
- •1.1. Сучасні методи створення планових мереж
- •1.2. Основні положення створення планових державних геодезичних мереж (дгм)
- •Астрономо-геодезична мережа 1 класу (агм-1)
- •1.4. Основні вимоги до державної мережі 2 класу
- •1.5. Основні вимоги до державної мережі згущення 3 класу
- •1.6. Розрядні мережі згущення
- •Класифікація полігонометрії
- •1.8. Формули для обчислення кутових та лінійних нев’язок у ходах полігонометрії
- •1.9. Поздовжні та поперечні похибки витягнутого полігонометричного ходу
- •1.11. Виведення розрахункової формули поперечної похибки висячого полігонометричного ходу
- •1.12. Виведення формули поперечної похибки полігонометричного ходу з попередньо ув’язаними кутами
- •1.13. Полігонометричні знаки
- •1 І 2 розрядів (тип 143)
- •1.14. Організація полігонометричних робіт
- •Лінійні вимірювання у траверсній полігонометрії
- •Прилади для вимірювання ліній у траверсній полігонометрії
- •І тип шкал
- •11 Тип шкал
- •Джерела похибок під час вимірювання ліній підвісними мірними приладами
- •Розрахунок допусків на окреме джерело похибок лінійних вимірів
- •М_1абогТ2_иЛ _ 1
- •Кутові вимірювання у полігонометрії
- •Основні вимоги до кутомірних приладів у полігонометрії. Класифікація теодолітів та тахеометрів
- •Відлікові пристрої оптичних кутомірних приладів, їхнє призначення та класифікація
- •Принцип роботи автоматичних систем відліків електронних теодолітів та тахеометрів
- •Будова оптичних та електронних теодолітів та тахеометрів
- •Перевірки теодолітів
- •Вимірювання горизонтальних кутів способом кругових прийомів
- •Вимірювання горизонтальних кутів способом повторень
- •Вимірювання горизонтальних кутів електронними теодолітами (тахеометрами)
- •I V вертикальний кут (0 у положенні “зеніт”)
- •V вертикальний кут (0 у положенні “горизонт” при кл)
- •Джерела похибок вимірювання горизонтальних кутів
- •Розрахунок допуску сумарної випадкової похибки вимірювання окремого горизонтального кута
- •Розрахунок допустимої систематичної похибки вимірювання окремого кута
- •11.3.12. Похибка редукції'
- •11.3.13. Похибки центрування теодоліта
- •Похибки вимірювання горизонтальних кутів
- •Інструментальні (приладні) похибки
- •Вплив зовнішнього середовища на вимірювання горизонтальних кутів
- •11.4. Попереднє опрацювання результатів польових вимірювань у полігонометрії
- •Попереднє опрацювання лінійних вимірів
- •Редукування довжин ліній на рівень моря і на площину Гаусса-Крюгера
- •2 ЛЛсер
- •Опрацювання результатів кутових вимірювань на окремому геодезичному пункті
- •Оцінка точності лінійних вимірювань за результатами польових робіт
- •Оцінка точності кутових вимірювань за результатами польових робіт
- •Прив’язувальні роботи у полігонометрії
- •Види та завдання прив’язувальних робіт. Способи прив’язування
- •Передавання координат із високих (недоступних) точок на Землю (знесення координат)
- •Пряма одноразова та багаторазова засічки
- •Обернена одноразова кутова засічка (задача Потенота)
- •Диференційні формули дирекційних кутів
- •11.5.6. Обернена багаторазова кутова засічка
- •Точність прямої та оберненої багаторазових кутових засічок
- •Точність прямої та оберненої одноразових кутових засічок
- •11.5.9. Лінійна геодезична засічка
- •11.5.10. Визначення координат двох точок за відомими координатами двох інших точок (задача Ганзена)
- •Прив'язування пунктів полігонометрії до постійних об'єктів місцевості. Відшукування полігонометричних пунктів
- •Світловіддалемірна полігонометрія.
- •Класифікація віддалемірної полігонометрії та віддалемірів
- •Принцип вимірювання віддалі визначенням часу поширення електромагнітних (світлових) хвиль
- •Основні відомості з теорії гармонічних коливань
- •Поняття про модулювання коливань
- •Принцип роботи фазових світловіддалемірів
- •Блок-схема візуального світловіддалеміра з визначенням різниці фаз за екстремумами світлового потоку
- •Блок-схема світловіддалеміра на фіксованих частотах із парафазним фотоелектронним визначенням різниці фаз
- •Світловіддалемір топографічний ст-5 (“Бпеск”). Будова. Імпульсний метод вимірювання віддалей
- •Перевірки світловіддалеміра ст-5
- •Вимірювання ліній світловіддалеміром ст-5
- •Вимірювання ліній та вертикальних кутів компактною тотальною станцією set-ge
- •Похибки світловіддалемірних вимірювань
- •Розрахунок точності ходів світловіддалемірної полігонометрії
- •11.7. Оптично-віддалемірна полігонометрія
- •//.7.2. Віддалемір із постійним базисом та змінним кутом
- •II. 7.3. Віддалеміри подвійного зображення
- •Суть паралактичної полігонометрії
- •Суть віддалемірно-базисної полігонометрії
- •II. 7. Б. Типи паралактичних і віддалемірно-базисних ланок
- •Строге зрівноваження полігонометричних ходів
- •Недоліки спрощених методів зрівноваження
- •Кількість вимірів та невідомих у полігонометричному ході. Необхідні та надлишкові виміри
- •Виведення умовних рівнянь, що виникають у полігонометричному ході, прокладеному між відомими пунктами
- •Строге зрівноваження витягнутого полігонометричного ходу корелатним методом
- •Строге зрівноваження витягнутого рівностороннього полігонометричного ходу
- •Приклад зрівноваження витягнутого полігонометричного ходу корелатним методом (способом найменших квадратів)
- •Суть параметричного методу зрівноваження геодезичних мереж
- •Зрівноваження полігонометричних мереж
- •Зрівноваження полігонометричної мережі, що збігаються в одну вузлову точку
- •Зрівноваження полігонометричної мережі способом послідовних наближень
- •Зрівноваження полігонометричної мережі методом еквівалентної заміни
- •Зрівноваження кутів полігонометричної мережі методом професора в. В. Попова
- •Зрівноваження приростів координат полігонометричних мереж методом професора в.В. Попова
- •Оцінка точності полігонометричних ходів та мереж за результатами зрівноваження
- •Будова та принцип роботи геодезичних супутникових систем
- •Принцип роботи систем визначення просторового положення точок
- •Вимірювальний пристрій
- •Найважливіші відомості про будову глобальних навігаційних систем
- •Основи теорії визначення положення пунктів глобальними супутниковими системами
- •Абсолютні та відносні методи супутникового вимірювання
- •Основні відомості про параметри орбіт супутників
- •1.6. Загальний принцип побудови супутникових передавачів системи gps
- •1.7. Структурна схема геодезичного супутникового приймача
- •Ill. 1.8. Короткі відомості про роботу системи керування та опрацювання вимірів приймачем gps
- •Супутникові методи визначення координат
- •Технології gps-вимірювання
- •111.2.2. Статичний метод визначення координат пунктів
- •111.2.4. Визначення координат методом “стій/йди” (“stop and go”)
- •Визначення координат методом “швидкоїстатики”
- •Технологія псевдостатична, псевдокінематична, реокупаційна (Reoccupation)
- •///.2.8. Робота у режимі “кінематика”
- •Робота у режимі “кінематика у польоті”
- •Технологія диференційного dgps-вимірювання (Differential gps)
- •Системи координат, що використовуються у космічній геодезії
- •///.3.3. Проектування та рекогностування просторових супутникових геодезичних мереж (сгм)
- •3.4. Складання робочого проекту
- •II 1.3.5. Підготування комплексу приладів до польового вимірювання
- •Будова та технічні характеристики компактного одночастотного приймача gps ProMark-2
- •Застосування режиму “стій/йди” для визначення просторових координат під час топографічного знімання місцевості
- •Рис III 3 32 Рамка ініціалізації
- •Загальні відомості про опрацювання gps-вимірів
- •Основні джерела похибок супутникових вимірювань і методи послаблення їхнього впливу
- •Класифікація джерел похибок супутникових вимірювань
- •Оцінка впливу зовнішнього середовища на результати супутникового вимірювання
- •Вплив іоносфери
- •II 1.4.5. Вплив тропосфери
- •Бвгатошляховість
- •Інструментальні джерела похибок
- •Геометричний фактор
- •1. Загальні відомості про великомасштабне топографічне знімання
- •1.1. Топографічні плани та карти
- •1.2. Мета та призначення топографічного знімання
- •1.3. Методи топографічного знімання. Їхня суть
- •1.4. Обґрунтування вибору перерізу рельєфу
- •Проміжок між осями горизонталей 0,2 мм
- •Ширина білого проміжку між горизонталями 0,1 мм
- •1.5. Обґрунтування масштабу знімання
- •1.6. Технічний проект топографо-геодезичних робіт
- •2. Робочі (знімальні) мережі великомасштабного топографічного знімання
- •2.1. Види геодезичної основи великомасштабного знімання. Розрахунок необхідної щільності робочої основи
- •2.2. Методи створення знімальної (робочої) основи. Закріплення пунктів мережі на місцевості
- •2.3. Аналітичні мережі (польові роботи)
- •2.4. Розрахунок точності ланки трикутників аналітичної мережі
- •2.5. Спрощені способи зрівноваження аналітичних мереж
- •2.6. Розрахунок планової точності та допустимої довжини мензульного ходу
- •2.7. Розрахунок точності та допустимої довжини теодолітного ходу
- •2.8. Розрахунок планової точності та допустимої довжини тахеометричного ходу
- •2.9. Технічне нівелювання для створення робочої основи топографічного знімання
- •2.10. Тригонометричне нівелювання для створення висотної знімальної основи
- •2.11. Вимірювання зенітних віддалей. Вертикальна рефракція
- •3. Комбіноване топографічне знімання
- •3.1. Виконання аерофотознімання
- •3.2. Складання накидного монтажу. Оцінка якості аерофотознімання
- •3.3. Технологічна схема комбінованого методу знімання
- •3.4. Прив’язування знімків
- •3.5. Польові роботи під час аеротопографічного знімання
- •3.6. Маркування розпізнавальних знаків
- •3.7. Планове підготування аерознімків
- •3.8. Висотне підготування аерознімків
- •3.9. Камеральне згущення планових та висотних ггзчок. Мета. Суть. Методи
- •3.10. Редукування фототріангуляційної мережі
- •3.11. Трансформування знімків
- •3.12. Складання фотопланів
- •3.13. Складання графічних планів
- •IV.4. Знімання рельєфу та дешифрування фотопланів під час комбінованого методу топознімання
- •IV.4.1. Встановлення мензули над точкою
- •IV. 4.2. Польове та камеральне дешифрування
- •IV. 4.3. Послідовність роботи на станції під час рисування рельєфу й дешифрування фотопланів
- •IV.4.4. Основні офіційні вимоги до точності зображення контурів та рельєфу
- •IV.4.5. Камеральні роботи під час знімання рельєфу на фотопланах (калька висот, викреслювання польового оригіналу, формуляр трапеції)
- •IV.4.6. Зведення за рамками суміжних топографічних планів
- •IV.4.7. Контроль робіт та приймально-здавальні роботи
- •IV.5. Стереоаерофотограмметричне знімання
- •IV.5.1. Загальні відомості про стереоаерофотограмметричне знімання
- •IV.5.2. Технологічна схема стереофотограмметричного методу знімання
- •IV. 5.3. Сучасні станції аналітичної фотограмметрії
- •IV.6. Цифрове аерознімання
- •IV. 6.1. Цифрова аерознімальна система
- •IV. 6.2. Порівняння технічних можливостей фотограмметричної та цифрової камер. Опрацювання цифрових знімків системою ads40
- •IV. 6.3. Цифрові аерознімальні комплекси із лазерним скануванням
- •1. Автоматизація топографо-геодезичних робіт
- •1.1. Основні напрямки та технології автоматизації топографо- геодезичного вимірювання
- •1.2. Автоматизація визначення висот
- •1.3. Автоматизація визначення планового положення точок
- •1.4. Автоматизація визначення просторового положення точок
- •1.5. Автоматизовані динамічні топографічні системи
- •1.7. Електронна тахеометрія
- •1.8. Автоматичні координатографи
- •1.9. Перетворювачі аналогової інформації на цифрову
- •1.10. Наземні лазерні сканери
- •2. Цифрові плани та карти
- •2.2. Вимоги до цифрових карт та планів
- •2.3. Поняття про кодування топографо-геодезичної інформації (тгі)
- •2.4. Алгоритми опрацювання польової інформації
- •2.5. Алгоритми формування моделі ситуації (мс)
- •2.6. Алгоритм формування моделі рельєфу (мр)
- •2.7. Диференційні перетворення або ортофототрансформування
- •2.8. Поняття про цифрову фотограмметрію та цифровий фотограмметричний знімок
- •2.9. Сканування фотознімків
- •2.10. Цифрові фотокамери
- •2.11. Цифрові фотограмметричні станції
Вимірювання горизонтальних кутів електронними
теодолітами (тахеометрами) 189
Джерела похибок вимірювання горизонтальних кутів 191
10. Розрахунок допуску сумарної випадкової похибки вимірювання окремого
горизонтального кута 193
11. Розрахунок допустимої величини систематичної похибки вимірювання
окремого кута 194
12. Похибка редукції 195
13. Похибки центрування теодоліта 198
14. Методи зменшення похибок редукції та центрування 200
15. Похибки вимірювання горизонтальних кутів 202
16. Інструментальні (приладні) похибки 205
17. Вплив зовнішнього середовища на вимірювання горизонтальних кутів 208
Попереднє опрацювання результатів польових вимірювань в полігонометрії 210
Попереднє опрацювання лінійних вимірів 210
Редукування довжин ліній на рівень моря і на площину Гаусса-Крюгера 211
Опрацювання результатів кутових вимірювань
на окремому геодезичному пункті 214
Оцінка точності лінійних вимірювань за результатами польових робіт 215
Оцінка точності кутових вимірювань за результатами польових робіт 217
Прив’язувальні роботи у полігонометрії 218
Види та завдання прив’язувальних робіт. Способи прив’язування 218
Передавання координат із високих (недоступних) точок на Землю
(знесення координат) 219
Пряма одноразова та багаторазова засічки 220
Обернена одноразова кутова засічка (задача Потенота) 222
И.5.5. Диференційні формули дирекційних кутів 224
Обернена багаторазова кутова засічка 226
Точність прямої та оберненої багаторазових кутових засічок 228
4
Точність
прямої та оберненої одноразових кутових
засічок 229
Лінійна
геодезична засічка 232
Визначення
координат двох точок за відомими
координатами
двох
інших точок (задача Ганзена) 234
Прив’язування
пунктів полігонометрії до постійних
об’єктів місцевості.
Відшукування
полігонометричних пунктів 235
Світловідцалемірна
полігонометрія. Основи теорії й
практики
світловіддалемірних
вимірювань 240
Класифікація
віддалемірної полігонометрії та
віддалемірів 240
Принцип
вимірювання віддалі визначенням часу
поширення
електромагнітних
(світлових) хвиль 240
Основні
відомості з теорії гармонічних
коливань 242
И.6.4.
Поняття про модулювання коливань 245
Принцип
роботи фазових світловіддалемірів 246
Блок-схема
візуального світловіддалеміра з
визначенням різниці фаз
за
екстремумами світлового потоку 248
Блок-схема
світловіддалеміра на фіксованих
частотах із парафазним
фотоелектронним
визначенням різниці фаз 250
Світловіддалемір
топографічний СТ-5 (“Блеск”). Будова.
Імпульсний
метод вимірювання віддалей 253
Перевірки
світловіддалеміра СТ-5 257
Вимірювання
ліній світловіддалеміром СТ-5 262
Вимірювання
ліній та вертикальних кутів компактною
тотальною
станцією
SET-GE 263
Похибки
світловіддалемірних вимірювань 265
Розрахунок
точності ходів світловіддалемірної
полігонометрії 269
Оптично-віддалемірна
полігонометрія 272
Принцип
роботи та класифікація оптичних
віддалемірів 272
Віддалемір
із постійним базисом та змінним
кутом 274
Віддалеміри
подвійного зображення 276
Суть
паралактичної полігонометрії 279
Суть
віддалемірно-базисної полігонометрії 281
Типи
паралактичних і віддалемірно-базисних
ланок 282
Строге
зрівноваження полігонометричних
ходів 283
Недоліки
спрощених методів зрівноваження 283
Кількість
вимірів та невідомих у полігонометричному
ході.
Необхідні
та надлишкові виміри 285
Виведення
формул, що зв’язують поздовжній та
поперечний зсуви ходу
з
нев’язками по осях координат 286
Виведення
умовних рівнянь, що виникають у
полігонометричному ході,
прокладеному
між відомими пунктами 288
Строге
зрівноваження довільного
полігонометричного ходу
корелатним
методом 293
Строге
зрівноваження витягнутого
полігонометричного ходу
корелатним
методом 296
Строге
зрівноваження витягнутого
рівностороннього
полігонометричного
ходу 298
Приклад
зрівноваження витягнутого
полігонометричного ходу корелатним
методом
(способом найменших квадратів) 300
Суть
параметричного методу зрівноваження
геодезичних мереж 305
Зрівноваження
полігонометричних мереж 309
Зрівноваження
полігонометричної мережі, що збігаються
в
одну вузлову точку 309
Зрівноваження
полігонометричної мережі способом
послідовних наближень...311
Зрівноваження
полігонометричної мережі методом
еквівалентної заміни 313
Зрівноваження
кутів полігонометричної мережі
методом професора
В.В.
Попова 316
И.9.5.
Зрівноваження приростів координат
полігонометричних мереж методом
професора
В.В. Попова 318
Оцінка
точності полігонометричних ходів та
мереж за результатами
зрівноваження 320
Розділ
III. ПРОСТОРОВІ СУПУТНИКОВІ МЕРЕЖІ
(ОСНОВИ
СУПУТНИКОВОЇ ГЕОДЕЗІЇ) 322
Будова
та принцип роботи геодезичних
супутникових систем 322
1.1.
Принцип роботи систем визначення
просторового положення точок 322
1.2.
Найважливіші відомості про будову
глобальних навігаційних систем 325
1.3.
Основи теорії визначення положення
пунктів глобальними
супутниковими
системами 332
1.4.
Абсолютні та відносні методи супутникового
вимірювання 338
1.5.
Основні відомості про параметри орбіт
супутників 342
1.6.
Загальний принцип побудови супутникових
передавачів системи GPS 345
1.7.
Структурна схема геодезичного
супутникового приймача 347
1.8.
Короткі відомості про роботу системи
керування та опрацювання вимірів
приймачем
GPS 350
Супутникові
методи визначення координат 352
Технології
GPS-вимірювання 352
Статичний
метод визначення координат пунктів 354
Параметри
місії, тривалість та довжини векторів
під час роботи
у
статичному режимі 356
Визначення
координат методом “стій/йди” (“stop
and go”) 357
ИІ.2.5.
Вибір проміжку часу та параметри місії
під час спостереження
у
режимі “стій/йди” (“stop
and go”) 358
Визначення
координат методом “швидкої статики” 359
Технологія
псевдостатична, псевдокінематична,
реокупаційна
(reoccupation) 360
Робота
у режимі “кінематика” 361
Робота
у режимі “кінематика у польоті” 361
Технологія
диференційного DGPS-вимірювання
(Differential
GPS) 363
Побудова
державних геодезичних мереж (ДГМ)
супутниковими методами 364
Загальні
відомості про побудову ДГМ супутниковими
методами 364
ПІ.3.2.
Системи координат, що використовуються
у космічній геодезії 367
Проектування
та рекогностування просторових
супутникових
геодезичних
мереж (СГМ) 372
Складання
робочого проекту 377
Підготування
комплексу приладів до польового
вимірювання 381
Будова
та технічні характеристики компактного
одночастотного
приймача
GPS
ProMark-2 383
Підготування
приймача Pro
Mark-2 до
роботи та виконання спостережень
на
геодезичному пункті 389
Застосування
режиму “стій/йди” для визначення
просторових координат
під
час топографічного знімання місцевості
397
Загальні
відомості про опрацювання GPS-вимірів 402
6
ІП.4.
Основні джерела похибок супутникових
вимірів
і
методи послаблення їхнього впливу 404
Класифікація
джерел похибок супутникових вимірів 404
Джерела
похибок, пов’язані з неточними
ефемеридами супутників
та
методи послаблення їх впливу 405
Оцінка
впливу зовнішнього середовища на
результати супутникового
вимірювання 408
Вплив
іоносфери 409
Вплив
тропосфери 413
Багатошляховість 415
Інструментальні
джерела похибок 417
Геометричний
фактор 420
Розділ
IV. ВЕЛИКОМАСШТАБНЕ ТОПОГРАФІЧНЕ
ЗНІМАННЯ 422
1.
Загальні відомості про великомасштабне
топографічне знімання 422
1.1.
Топографічні плани та карти 422
1.2.
Мета та призначення топографічного
знімання 425
1.3.
Методи топографічного знімання. їхня
суть 427
1.4.
Обґрунтування вибору перерізу
рельєфу 430
1.5.
Обґрунтування масштабу знімання 432
1.6.
Технічний проект топографо-геодезичних
робіт 440
2.
Робочі
(знімальні) мережі великомасштабного
топографічного знімання 441
2.1.
Види
геодезичної основи великомасштабного
знімання.
Розрахунок
необхідної щільності робочої основи 441
2.2.
Методи
створення знімальної (робочої) основи.
Закріплення
пунктів мережі на місцевості 445
2.3.
Аналітичні
мережі (польові роботи) 446
2.4.
Розрахунок
точності ланки трикутників аналітичної
мережі 448
2.5.
Спрощені
способи зрівноваження аналітичних
мереж 450
2.6.
Розрахунок
планової точності та допустимої довжини
мензульного ходу 453
2.7.
Розрахунок
точності та допустимої довжини
теодолітного ходу 455
2.8.
Розрахунок
планової точності та допустимої довжини
тахеометричного
ходу 1 456
2.9.
Технічне
нівелювання для створення робочої
основи
топографічного
знімання 458
2.10.
Тригонометричне
нівелювання для створення висотної
знімальної основи... 459
2.11.
Вимірювання зенітних віддалей.
Вертикальна рефракція 462
3.
Комбіноване
топографічне знімання 468
3.1.
Виконання
аерофотозніманн 468
3.2.
Складання
накидного монтажу. Оцінка якості
аерофотознімання 475
3.3.
Технологічна схема комбінованого
методу знімання 476
3.4.
Прив’язування
знімків 478
3.5.
Польові
роботи під час аеротопографічного
знімання 481
3.6.
Маркування
розпізнавальних знаків 481
3.7.
Планове
підготування аерознімків 482
3.8.
Висотне підготування аерознімків 483
3.9.
Камеральне
згущення планових та висотних точок.
Мета. Суть. Методи 485
3.10.
Редукування
фототріангуляційної мережі 489
3.11.
Трансформування знімків 491
3.12.
Складання
фотопланів 491
3.13.
Складання
графічних планів 492
топознімання 493
фотопланів 495
викреслювання
польового оригіналу, формуляр
трапеції) 499
ІУ.5.1.
Загальні відомості про
стереоаерофотограмметричне знімання 503
ІУ.6.Г.
Цифрова аерознімальна система 507
Опрацювання
цифрових знімків системою ADS40 509
Розділ
V. АВТОМАТИЗАЦІЯ НАЗЕМНИХ ТОПОГРАФО-ГЕОДЕЗИЧНИХ
РОБІТ.
ЦИФРОВІ
ПЛАНИ ТА КАРТИ 516
вимірювання 516
фотограмметричний
знімок 549
Список
літератури 559
84. Знімання рельєфу та дешифрування фотопланів під час комбінованого методу
4.1. Встановлення мензули над точкою 493
4.2. Польове та камеральне дешифрування 494
IV.4.3. Послідовність роботи на станції під час рисування рельєфу й дешифрування
IV.4.4. Основні офіційні вимоги до точності зображення контурів та рельєфу 497
IV.4.5. Камеральні роботи під час знімання рельєфу на фотопланах (калька висот,
IV.4.6. Зведення за рамками суміжних топографічних планів 500
IV.4.7. Контроль робіт та приймально-здавальні роботи 501
IV.5. Стереоаерофотограмметричне знімання 503
IV.5.2. Технологічна схема стереофотограмметричного методу знімання 505
IV.5.3. Сучасні станції аналітичної фотограмметрії 506
6. Цифрове аерознімання 507
IV.6.2. Порівняння технічних можливостей фотограмметричної та цифрової камер.
6.3. Цифрові аерознімальні комплекси із лазерним скануванням 511
I. Автоматизація топографо-геодезичних робіт 516
1.1. Основні напрямки та технології автоматизації топографо-геодезичного
I.2. Автоматизація визначення висот 518
I.3. Автоматизація визначення планового положення точок 519
I.4. Автоматизація визначення просторового положення точок 521
I.5. Автоматизовані динамічні топографічні системи 524
I.6. Автоматизовані лазерно-паралактичні топографічні системи 525
I.7. Електронна тахеометрія 526
I.8. Автоматичні координатографи 528
I.9. Перетворювачі аналогової інформації на цифрову 528
1.10. Наземні лазерні сканери 530
2. Цифрові плани та карти 532
2.I. Загальні відомості про цифрові моделі місцевості 532
2.2. Вимоги до цифрових карт та планів 535
2.3. Поняття про кодування топографо-геодезичної інформації (тгі) 536
2.4. Алгоритми опрацювання польової інформації 538
2.5. Алгоритми формування моделі ситуації (мс) 540
2.6. Алгоритм формування моделі рельєфу (мр) 541
2.7. Диференційні перетворення або ортофототрансформування 544
2.8. Поняття про цифрову фотограмметрію та цифровий
2.9. Сканування фотознімків 552
2.10. Цифрові фотокамери 554
2.11. Цифрові фотограмметричні станції 555
ПЕРЕДМОВА
Відповідно
до навчальних планів вищих геодезичних
закладів дисципліна “Геодезія”, що є
базовою для геодезичних спеціальностей,
вивчається протягом першого та другого
курсів. На першому курсі вивчається
перша частина курсу, яка достатньо
обґрунтовано називається “Топографією”,
на другому курсі - “Геодезія”. Відмінність
між топографією та геодезією буде
вісвітлена у підручнику.
У
курсі “Геодезія”, як і в курсі
“Топографія”, автори, з метою полегшення
засвоєння предмета студентами, окремо
розглядають питання висотних та планових
геодезичних мереж, а також просторових
(супутникових) мереж, і тільки потім
переходять до питань сумісного
використання цих мереж як математичної
основи створення графічних та цифрових
топографічних планів та карт. Саме
такої послідовності дотримувались
видатні вчені, педагоги, професори Н.Н.
Загрубський, М.В. В’яхірєв, А.Д. Моторний,
автори перших підручників з геодезії,
виданих українською мовою ще до Другої
світової війни.
У
другій частині геодезії вивчаються
питання:
створення
висотних мереж методами геометричного
нівелювання III, IV класів та технічного
нівелювання;
створення
геодезичних планових мереж методами
тріангуляції, полігонометрії,
трилатерації;
створення
просторових геодезичних мереж
глобальними супутни- ковими системами;
створення
знімальної (робочої) основи та виконання
топографічних аерофото та цифрових
аерознімань у масштабах 1:5000-1:500;
автоматизації
топографічних і геодезичних робіт,
створення цифрових карт та планів.
Зауважимо,
що на другому курсі вивчаються переважно
методи аерознімання, тоді як на
першому курсі головна увага акцентована
на наземному топографічному зніманні.
Відповідно до питань, які розглядає
друга частина геодезії, підручник має
п’ять розділів:
РОЗДІЛ
І. Висотні геодезичні мережі.
РОЗДІЛ
II. Планові геодезичні мережі.
РОЗДІЛ
III. Просторові супутникові мережі
(основи супутникової геодезії).
РОЗДІЛ
IV. Великомасштабне топографічне
знімання.
РОЗДІЛ
V. Автоматизація наземних топографо-геодезичних
робіт.
Цифрові
плани та карти.
Особливістю
цього підручника є поєднання методів
класичної наземної та супутникової
геодезії. Незважаючи на значні переваги
супутникової геодезії, її не можна
застосувати всередині споруд, у лісових
регіонах, важко використовувати між
висотними забудовами. Тому класична
геодезія не втрачає свого значення.
Окрім того, в недалекому майбутньому
можна очікувати поєднання методів
наземної та супутникової геодезії.
Такі поєднання в одному приладі уже
існують. Про це йтиметься в підручнику.
Геодезія
- наукова дисципліна, тісно пов’язана
з роботою на місцевості. Навчити студента
“оволодіти місцевістю” - одне з
найважливіших завдань викладання
геодезії. Кінцевим продуктом геодезичних
виробничих підприємств є плани та
карти. Тому геодезист передовсім повинен
уміти створювати карти та плани, які,
нарівні з писемністю, дають надзвичайно
широку й важливу інформацію, необхідну
для розв’язання різноманітних практичних
і наукових задач.
Цей
підручник не має на меті замінити
практикум з геодезії. Проте у ньому,
поряд з описом теоретичних питань,
відведено чимало місця на практичні
основи геодезії.
Студенти
геодезичних спеціальностей на II курсі
уже мають достатні знання з вищої
математики та вивчають математичну
обробку геодезичних вимірів, що дає
змогу викладати геодезію на II курсі на
ґрунтовній математичній основі. Саме
тому багато питань у підручнику викладено
значно ширше, ніж цього вимагає навчальна
програма.
Водночас
автори намагалися доступно описувати
прилади та методи виконання
вимірювання, пояснювати складні,
проміжні математичні перетворення під
час виведення формул, щоб полегшити
студентам освоєння курсу.
Проте
деякі розділи підручника, вивчення
яких передбачено на старших курсах як
спецдисциплін, для уникнення дублювання
та забезпечення міжпредметних зв’язків
викладені тільки в обсязі, достатньому
для розуміння суті. Звичайно, це полегшує
студентам навчання на старших курсах.
Автори
будуть вдячні читачам за пропозиції
та зауваження, спрямовані на покращання
підручника.
Заслужений
діяч науки і техніки України,
д-р
техн. наук, професор А.Л. Островський
10
ПРЕДМЕТ
ГЕОДЕЗІЇ
Геодезія
- прикладна математична наука, що вивчає
методи визначення:
форми
та розмірів планети Земля;
її
гравітаційного поля;
зміни
цих параметрів у просторі та часі;
а
також методи:
побудови
мереж пунктів з єдиною системою
просторових координат;
виконання,
на основі цих пунктів, топографічного
знімання, створення паперових та
цифрових планів та карт;
розв’язування
наукових та інженерних задач.
Студенти
уже знають, що дослівно з грецької мови
слово “геодезія” перекладається як
“землерозділення”. Проте точніше дає
змогу відтворити суть геодезичної
науки слово “землевимірювання”.
Нагадаємо, що “геометрія” дослівно
перекладається з грецької як
“землевимірювання”, а не як
“землерозділення”. Отже, слово
“землевимірювання” найкоротше,
найповніше і найкраще відтворює
зміст науки “геодезія”.
Під
дійсною поверхнею Землі розуміють її
фізичну поверхню, на якій виконуються
наземні вимірювання, тобто поверхню
суші і незбурену поверхню морів, океанів
та озер.
У
завдання вищої геодезії не входить
безперервне визначення фізичної
поверхні Землі, наприклад, у вигляді
карт. Цим займаються інші розділи
геодезії - топографія, аерознімання.
Основне завдання вищої геодезії
формулюють як визначення положення
деякої мережі опорних точок у єдиній
системі координат. На основі цієї мережі
і вивчаються форми й розміри планети
Земля, її гравітаційне поле, а за зміною
координат пунктів цієї мережі вивчається
зміна названих параметрів у просторі
та часі. Саме ці питання вивчає частина
геодезії, яку називають вищою геодезією.
Наведене
тут ширше визначення предмета геодезії
(не вищої геодезії) охоплює ще і методи
топографічного знімання, які вивчає
наука “геодезія”. І це небезпідставно,
оскільки “топографія” є частиною
“геодезії’”.
Отже,
доходимо висновку, що геодезія складається
з двох основних частин:
вищої
геодезії
та топографії.
Вища геодезія вивчає уявну поверхню,
так звану рівневу поверхню сили ваги
Землі, а топографія вивчає частинами
дійсну поверхню Землі. Дуже важливу
роль у геодезії відіграє поверхня
геоїда,
тобто рівнева поверхня поля сили тяжіння
(сили ваги), що проходить через початок
відліку
висот. Ця поверхня близька до незбуреного
середнього рівня океанів і з’єднаних
із ними морів. Тому часто на це вказують,
навіть даючи визначення геоїда. Через
різницю температур і солоності води в
різних частинах Світового океану і з
деяких інших причин поверхня геоїда
строго не збігається зі вказаною
рівневою поверхнею. За деякими оцінками,
такі відхилення можуть сягати 1 м. Ця
обставина змушує розрізняти поверхню
геоїда і так звану топографічну поверхню
океанів та морів.
Зауважимо
ще, що геодезія може бути розділена не
на дві, а на декілька наукових дисциплін:
Вища
геодезія.
Топографія.
Аерофотогеодезія
і фотограмметрія.
Прикладна
(інженерна) геодезія.
Г
еодезична гравіметрія.
Геодезична
астрономія.
Космічна
геодезія.
Картографія.
Г
еодезичне приладобудування.
Економіка
й організація геодезичних робіт.
Геодезія
спирається, передусім, на математичні
дисципліни. Крім того, для вивчення
геодезії важливо знати фізику, особливо
оптику і фізику атмосфери, геофізику,
геоморфологію. Геодезія тісно пов’язана
з астрономією. Геодезія необхідна
геології, геофізиці, приладознавству,
геоботаніці, інженерним наукам.
Будівництво залізниць, шосе, каналів,
метро вимагають знання геодезії.
Геодезія дуже потрібна військовій та
морській справі.
Історичний
аспект розвитку геодезії й уявлень
людства про форму й розміри Землі
висвітлено в топографії. Тут ми тільки
вкажемо, що в розвитку геодезії можна
виділити найважливіші етапи.
12
Перший
етап,
коли давні індуси, вавілоняни й греки
до Піфагора (VI ст. до н. е.) вважали Землю
плоскою,
або плоско-опуклою,
і такою, що тримається на підпірках.
Піфагор (580-500 рр. до н. е.) припустив, що
Земля, як “найдосконаліше тіло”,
має форму кулі, а його сучасник Парменід
пояснив, що ніяких підпірок у Землі
немає, усі тіла з різних боків падають
на Землю, а їй, виходить, падати немає
куди. Великий грецький учений Арістотель
(384-322 рр. до н. е.) довів кулеподібність
Землі за формою тіні на диску Місяця
під час місячних затемнень. Є відомості,
що ще до Арістотеля були спроби визначити
розміри земної кулі. Так, халдейські
вчені визначили довжину кола Землі у
24000 миль
(миля
дорівнювала 4000 крокам верблюда). Як це
було визначено - невідомо. Обґрунтував
розміри Землі як кулі Ератосфен (276-196
рр. до н. е.).
З цього
періоду і до кінця XVII віку -
Сьогодні
супутникові технології, які є могутнішими
засобами, ніж наземна геодезія, для
вивчення форми та розмірів Землі, її
гравітаційного поля, тобто поля сили
ваги. Технології космічної (супутникової)
геодезії дають також змогу визначати
взаємне положення точок земної поверхні,
будувати просторові опорні геодезичні
мережі і виконувати топографічне
знімання з метою складання планів та
карт.
Відзначимо
деякі особливості сучасної геодезичної
науки. Це:
Значне
підвищення точності вимірювань з
ІХІ0"6
до 1х10'7-1х10'8.
Можливість
вивчати не тільки координати другий
етап.
Землю вважали кулею. Останні століття
рабовласницького суспільства, тобто
період володарювання й розпаду Римської
імперії, не внесли нічого істотного в
історію розвитку геодезії. Під час
наступних семи століть центр наукової
думки перемістився до арабських країн.
У 829 р. арабські вчені визначили розміри
Землі. Результат цього визначення
виявився близьким до сучасних даних:
для дуги в 1° за меридіаном араби отримали
111,8 км. З епохи великих геофізичних
відкриттів починається період нового
природознавства. Від цього періоду,
пов’язаного з іменами голландського
математика та фізика Снелліула
(1580-1626), французького академіка Пікара
(1620-1682), англійського фізика й математика
Ньютона (1642-1727) бере початок і нова
геодезична наука.Третій
етап
- кінець XVII і до середини XIX століття,
коли Землю вважали приплюснутою
кулею,
тобто сфероїдом
(сфероїдальність Землі доведена
Ньютоном).Четвертий
етап,
коли наука дійшла висновку, що сфероїд
- тільки друге наближення до істинної
фігури Землі. Цій істинній фігурі у
1873 році німецький фізик І.В. Лістінг
дав спеціальну назву - геоїд
(землеподібний).П’ятий
- сучасний етап. Детально вивчається
геоїд, квазігеоїд, у різних країнах
визначаються відхилення геоїда від
деяких еліпсоїдів із певними розмірами
і у певний спосіб орієнтованими в тілі
Землі. Такі еліпсоїди, що мають мінімальні
відхилення від геоїда на території
певної країни, називають референц-
еліпсоїдами.
Еліпсоїд, що забезпечував би мінімальні
відхилення від геоїда по всій поверхні
Землі, називається загальноземним
еліпсоїдом.
Такий еліпсоїд практично вже знайдений
насамперед завдяки космічній геодезії,
яка започаткована 4 жовтня 1957 р. із
запуском першого у світі штучного
супутника Землі.
X,
Y,
Н
точок, але й їхні зміни АХ,
AY,
АН
у просторі й часі за повторними вимірами.
Перехід
від статичної тривимірної геодезії
до чотиривимірної кінематичної
геодезії, яка вивчає зміни положень
точок земної поверхні та елементів
земного гравітаційного поля, а далі -
до динамічної геодезії, яка не тільки
вивчає кінематику (рух точок), але й
сили, що є причиною цих рухів [12].
Небувала
автоматизація геодезичних робіт.
Перехід
від контактних методів вивчення Землі
до дистанційних.
Перехід
від аналогових (графічних) до цифрових
планів та карт.
Тільки
сучасну геодезію називають інформативною.
Насправді це не так.
Геодезія
завжди була інформативною, на будь-якій
стадії свого розвитку. Проте не можна
не погодитися з тим, що сучасна геодезія
стала інформативнішою.
14
РОЗДІЛ
І. ВИСОТНІ ГЕОДЕЗИЧНІ МЕРЕЖІ
Державна
геодезична мережа (скорочено ДГМ) - це
сукупність пунктів, рівномірно
розташованих на території країни й
закріплених на місцевості спеціальними
центрами, які забезпечують їхнє
збереження та стійкість у плановому
та висотному аспектах протягом тривалого
часу.
ДГМ
є носієм системи координат і висот
України.
Складовими
частинами ДГМ є
У
цьому розділі описуються висотні
мережі.
Відзначимо
три головні групи задач, розв’язання
яких неможливе без державної висотної
основи. А саме:
Будівництво,
меліорація
та інші задачі інженерно-технічного
характеру.
До
цієї самої групи задач можна зарахувати
й задачі оборони країни, якщо мати на
увазі будівництво захисних споруд. Для
розв’язання цих двох груп задач
використовують висоти точок, які
отримані за допомогою нівелювання І,
II, III та IV класів. Детальніше з використанням
висотної основи під час розв’язання
задач інженерно-технічного характеру
студенти ознайомляться під час вивчення
курсу “Інженерна геодезія”. Поки що
зазначимо, що, не знаючи висот, неможливо
збудувати навіть найпримітивнішу
споруду, наприклад, гараж для автомобіля,
так, щоб його не заливали дощові потоки.
Загальні відомості про геометричне нівелювання
III і IV класів
Призначення державної нівелірної мережі
планова
та висотна
геодезичні мережі. Між ними повинен
бути постійний зв’язок.
Топографічне
знімання.
Нівелірна мережа є висотною основою
під час складання планів та карт різних
масштабів і зображення на них рельєфу
місцевості в єдиній для всієї країни
системі висот.
Наукові
задачі.
Як зазначалось вище, сучасна геодезія
вивчає не тільки форму та розміри
Землі, але і їхні зміни у просторі та
часі. Глобальні, регіональні та локальні
зміни фігури та розмірів Землі стали
об’єктом між- предметних досліджень
астрономів, геодезистів, геофізиків,
сейсмологів, океанологів. На особливу
увагу заслуговує вивчення локальних
геодинамічних явищ на важливих
промислових об’єктах. Такі дослідження
вимагають побудови локальних
геодинамічних полігонів (ГДП). Кінцевою
метою створення ГДП є недопущення
катастрофічних ситуацій, аварій,
сприяння надійній експлуатації
промислових
та енергетичних об’єктів, реалізація
комплексних заходів із захисту довкілля.
На ГДП, передусім, виконують спостереження
за вертикальними та горизонтальними
рухами поверхні Землі й технологічного
обладнання. До появи космічної
геодезії та GPS-технологій,
геометричне нівелювання було
найточнішим методом дослідження
вертикальних рухів. І у наш час для
вивчення вертикальних рухів на локальних
ГДП геометричне нівелювання залишається
неперевершеним за точністю. Тільки під
час вивчення глобальних та регіональних
геодинамічних явищ перевагу мають
GPS-методи.
Під час розв’язання наукових задач
використовують нівелірні мережі тільки
І та II класів [20]. З їхньою допомогою
розв’язують такі наукові задачі:
визначення
фігури Землі та її зовнішнього
гравітаційного поля;
визначення
різниць висот морів та океанів, що
омивають територію країни;
визначення
ухилів середніх рівнів поверхонь морів
та океанів.
Обсяг
наукових задач розширяється, якщо
використовують результати повторного
нівелювання. З’являється можливість:
вивчати
та прогнозувати вертикальні рухи
земної кори та поверхні, а також
технологічного обладнання;
вивчати
техногенні (антропогенні) процеси,
тобто вплив виробництва на довкілля,
особливо під час видобування вугілля,
нафти, газу та інших корисних копалин.
Рухи
земної кори є передвісниками землетрусів,
тобто необхідними даними для їхнього
прогнозування.
Результати
повторного нівелювання використовують
для вивчення будови земної кори,
отримання даних про швидкості та
напрямки рухів окремих блоків, виявлення
діючих розломів у земній поверхні. Дані
про вертикальні рухи земної кори та
поверхні дають змогу цілеспрямованіше
виконувати пошуки корисних копалин,
прогнозувати майбутнє нашої планети.
Результати повторного нівелювання
також допомагають підтримувати висотні
державні мережі на сучасному рівні,
враховувати зміни висот пунктів мережі.
Отже,
нівелірна мережа має неабияке значення
в народному господарстві, у науці та
обороні країни.
Державна
нівелірна мережа України поділяється
на чотири класи: мережі I,
II,
III та IV класів. За початковий (вихідний)
рівень (нульову відмітку висот) в Україні
прийнято середній (за багато років
спостережень) рівень Балтійського
моря, точніше - нуль Кронштадтського
футштока - нуль особливої рейки на
станції вимірювання рівня води.
16
Класифікація державної нівелірної мережі
Клас нівелювання |
Граничні середні квадратичні похибки |
Допустимі нев’язки у полігонах та ходах /А,мм |
||
випадкові Т|, мм/км |
систематичні О, мм/км |
|||
І |
0,8 |
0,08 |
3 мм у/L |
|
п |
2,0 |
0,20 |
5 мм у[Е |
|
III |
5,0 |
- |
10 мм -JZ |
|
IV |
10,0 |
- |
20 мм л/L |
|
У
табл. 1.1.1:
Це
можна пояснити тим, що лінії нівелювання
цих класів значно коротші порівняно з
лініями І та II класів. А оскільки
систематичні похибки приблизно на
порядок менші за випадкові, то для
коротких ходів їхній вплив на результати
вимірювання вважають незначним і не
враховують.L-
периметр
(довжина) нівелірного полігона чи ходу
(лінії), км. Похибки Т| та а розраховують
за нев’язками f^.
у
полігонах або лініях. Розглядаючи табл.
1.1.1, зауважимо: по-перше, що для III та IV
класів нівелювання допустимі нев’язки
на один кілометр ходу приймають як
подвійні середні квадратичні випадкові
похибки; по-друге, що систематичні
похибки в III та IV класах нівелювання
Інструкцією не розглядаються.
Полігони
та лінії нівелювання І класу найдовші.
Такими полігонами (лініями) пов’язані
моря та океани, наприклад, Балтійське
та Чорне моря.
В
Україні, станом на 1997 рік, було 29 ліній
І класу, їхня загальна довжина - 11975 км
(максимальна - 1301 км, мінімальна - 70,7
км), 62 лінії II класу, їхня загальна
довжина - 11180 км (максимальна - 384 км,
мінімальна - 38 км), більше ніж 60000 км III
класу, близько 300000 км IV класу.
Рис.
1.1.1. Схема послідовного згущення
(заповнення) полігону It
класу
нівелірними
ходами:
-
лінія
І класу;
полігон
III
класу;
Q
-
репери
Нівелірні
лінії І класу прокладають ходами
завдовжки близько 1000 км.
Нівелірні
мережі II класу створюють всередині
полігонів І класу окремими
лініями
або системами з вузловими точками,
утворюючи полігони з периметром
до
400 км. Лінії нівелювання III класу
прокладають всередині полігонів II
класу
так, щоб утворювались полігони
з периметром 60-150 кілометрів.
Для
забезпечення топографічного знімання
у масштабі 1:5000 і більше
лінії
нівелювання III класу прокладають із
розрахунком створення полігонів
із
периметром до 60 км.
Нівелювання
IV класу є згущенням нівелірної мережі
III класу. Його
виконують ходами
завдовжки не більше за 50 км.
Лінії
нівелювання І та II класів прокладають
переважно вздовж шосейних
та
залізничних доріг, а за їхньої відсутності,
у важкодоступних районах - по
берегах
рік, стежках. Взагалі лінії нівелювання
будь-якого класу потрібно, за
полігон
II класу;
лінія
IV класу
18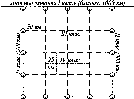
II клас (200 км)
можливістю,
прокладати на місцевості із твердим,
незаболоченим ґрунтом та з найменш
складним рельєфом (із малими ухилами).
Довжини
ліній (ходів) у полігонах повинні бути,
якщо можливо, однаковими. Нівелірну
мережу II класу створюють у межах полігона
І класу. Нівелірні мережі III та IV класів
відповідно прокладають, як правило, у
межах полігонів II класу, також окремими
лініями (ходами) або їхніми системами.
Схематично
послідовне заповнення деякої території
точками нівелірної мережі різних класів
можна уявити так, як це показано на рис.
1.1.1.
Насправді
реальні нівелірні мережі (оскільки їх
прокладають переважно вздовж доріг)
не є такими точними квадратами, як на
рис. 1.1.1.
Ходи
нівелювання молодших класів спираються
на ходи старших класів, тобто під час
прокладання нівелірних ходів, наприклад,
III класу, вихідними будуть висоти реперів
першого або другого класів.
Репери,
як відомо з курсу “Топографії*” - це
фундаментально закріплені на місцевості
точки, висоти яких знайдено у результаті
нівелювання.
Лінії
державної нівелірної мережі I,
II,
III та IV класів закріплюють реперами
через 5 км (вздовж траси).
У
важкодоступних районах на окремих
відрізках траси, де важко вибирати
місця для закладання реперів, віддаль
між ними може бути збільшена до 7 км. У
гірських районах лінії нівелювання
закріплюють скельними та стінними
реперами через 1-2 км, а ґрунтовими -
через 3-4 км.
На
геодинамічних полігонах, які призначені
для вивчення рухів земної поверхні,
поблизу геологічних розломів та меж
головних блоків, репери закладають
через 0,5-1,5 км. На кожній стороні блока
або розлому повинно бути закладено
принаймні два репери.
У
результаті виконання нівелірних робіт
уся територія країни покривається
нівелірними точками (реперами) із
відомими відмітками в одній системі
висот, що під час визначення висоти
будь-якої точки місцевості чи інженерної
споруди звільняє від необхідності
прокладати довгі нівелірні ходи (аж
від Кронштадтського футштока). Достатньо
прокласти хід від репера, який розташований
найближче стосовно точки, висоту якої
необхідно визначити.
Особливості
нівелірної мережі у містах,
населених
пунктах та на будівельних майданчиках
Нівелірна
мережа у містах, населених пунктах та
на будівельних майданчиках повинна
забезпечити всі потреби міського
господарства та будівельних робіт у
висотах. Перевищення між найвідцаленішими
реперами нівелірної мережі міста
повинні бути відомі з похибкою, що не
перевищує ЗО мм. Вимоги
Клас нівелювання |
Довжина ліній (ходів), км |
|||
між вузловими реперами |
між реперами старших класів |
|||
забудована територія |
незабудована територія |
забудована територія |
незабудована територія |
|
І |
15 |
20 |
25 |
25 |
п |
10 |
15 |
15 |
20 |
III |
1 |
2 |
2 |
4 |
Таблиця
1.1.3
Щільність
закладання реперів на лініях міської
нівелірної мережі нівелювання |
Щільність закладання реперів |
|
забудована територія |
незабудована територія |
|
і,п |
2 км |
3 км |
III, IV |
300-800 м* |
500-2000м |
*
Щільність зменшується з переходом від
суцільної до розрідженої забудови.
Як
бачимо, особливості міської нівелірної
мережі полягають у тому, що повторне
нівелювання в них виконують частіше
ніж у державних мережах, полігони та
лінії (ходи) - коротші, а репери закладають
значно щільніше.
20
Складання
проекту починають зі збирання та аналізу
всіх матеріалів про нівелірні роботи
на території, виконані раніше. Відомості
про ці роботи зберігають, як правило,
у територіальних інспекціях Держгеонагляду
або в організаціях, що виконували ці
роботи.
Проект
складається із трьох основних частин:
Під
час проектування ліній нівелювання
III та IV класів для великомасштабного
топографічного знімання в нівелірну
мережу включають наявні, а також
запроектовані пункти тріангуляції та
полігонометрії.
Запроектовані
нівелірні лінії повинні бути надійно
зв’язані з наявними лініями: по-перше,
з тими, до яких запроектовані лінії
прив’язуються, а по- друге, з тими, що
їх перетинають запроектовані лінії.
Прив’язувати лінії нівелювання
III—IV
класів до фундаментальних реперів не
дозволяється.
У
текстовій частині проекту вказують:
коротку характеристику фізико-
географічних та кліматичних умов
ділянок робіт; призначення проектних
робіт; інформацію про вихідні репери;
інформацію про раніше виконані нівелірні
роботи та способи зв’язку їх із
проектними лініями; інформацію про
гравіметричні роботи, якщо нівелювання
III класу буде прокладатись у гірських
районах; кількість запроектованих
реперів за типами; технологію закладання
реперів; прилади та способи нівелювання;
особливі випадки нівелювання; порядок
опрацювання результатів нівелювання.
Складений
на підставі топографічних карт попередній
(наближений) проект уточнюють на основі
рекогностування - геодезичної розвідки,
яку виконують безпосередньо в полі,
виконуючи огляд на місцевості помічених
на карті ліній нівелювання.
Головні
завдання рекогностування - це:
Остаточний
вибір ліній нівелювання.
Остаточний
вибір місць закладання реперів.
Остаточний
вибір типів нівелірних знаків, якими
закріплюють мережу.
Рівень
ґрунтових вод у місцях закладання
реперів повинен бути не ближче
ніж
3 м від поверхні землі.
Взагалі,
з метою забезпечення тривалого зберігання
реперів місця їхнього закладання
вибирають, за змогою, на підвищеннях
рельєфу із велико- зернистими, слабко
зволоженими ґрунтами.Складання проекту нівелірної мережі
Пояснювальна
записка
(текстова частина).Карти
масштабів 1:100000-1:200000 із нанесеними на
них запроектованими нівелірними
лініями та наявними реперами, пунктами
тріангуляції й полігонометрії, зокрема
й ті, які розміщені від запроектованих
ліній до 3 км.Кошторис
- грошова вартість запроектованих
робіт.
Рекомендують
закладати репери у скельні породи та
капітальні кам’яні, бетонні й
залізобетонні будови та споруди.
Пошуки
реперів, включених у попередній проект,
припиняють тільки з дозволу керівника
робіт, після чого складають акт утрати
знака. Репери, які не вдалося відшукати,
втраченими не вважають. Причинами
втрати можуть бути: знищення репера,
знесення споруди, у яку він був закладений,
втрата головки репера, деформація
трубчатого репера тощо.
Після
закінчення робіт рекогностувальник
здає такі головні документи: погоджену
схему ліній нівелювання, їхні довжини;
погоджені схеми зв’язку з наявними
лініями (прив’язування); описи місць
закладання реперів і зариси; типи
реперів, що будуть закладені; список
обстежених та відремонтованих реперів
і акти на втрачені й незнайдені репери;
результати геологічного обстеження;
пояснювальну записку.
Поданий
список документів дає читачу достатнє
уявлення про роботу, яку виконує
рекогностувальник.
На
підставі рекогностування попередній
проект уточнюють. Складають кошторис
на виконання робіт. Розрахунок коштів
виконують відповідно до обсягів
робіт, норм виробітку та категорій
складності виконання робіт. Зокрема,
у кошторисі подають загальну вартість
робіт, а також окремо вартість матеріалів,
виготовлення нівелірних знаків,
закладання знаків, власне нівелювання,
попередніх розрахунків та зрівноваження
мереж.
Чинна
Інструкція з геометричного нівелювання
рекомендує у випадках, коли проектують
тільки лінії нівелювання III та IV класів,
рекогностувальні роботи виконувати
одночасно із закладанням знаків.
Зрозуміло, що у такому разі попередньо
складений проект тільки наближено
визначає вартість запроектованих
робіт. Водночас це не має принципового
значення, оскільки завдяки сучасній
організації праці комплексна бригада,
що виконує закладання та рекогностування,
отримує заробітну платню за остаточний
результат. У такому разі - це кількість
закладених реперів.
Нівелірні
знаки - це репери (ґрунтові, скельні й
стінні) та марки (тільки стінні). Так
можна класифікувати знаки, якщо мати
на увазі об’єкти, в які вони закладаються.
Головною
відмінністю між репером і маркою є те
місце (точка), висота якого визначається.
У реперів такою точкою є верхній виступ
сферичної головки репера. Марка має
круглий отвір. Центр отвору і є тією
точкою, висота якої визначена.
22
Нівелірні знаки
Згідно
з фізико-географічними особливостями
окремих регіонів країни існують
різноманітні нівелірні знаки. Нараховують
більше ніж десять різних типів реперів.
Залежно від важливості та специфічних
призначень реперів їх можна поділити
на [6]:
Тимчасові.
Вікові
та фундаментальні репери закладають
тільки на лініях І та II класів (у місцях
перетину цих ліній та на геодинамічних
полігонах). Вікові репери дають змогу
вивчати вертикальні рухи земної кори,
оскільки їх закладають у корінні породи.
Фундаментальні репери забезпечують
багаторічне зберігання висотної основи
та дають змогу вивчати рухи земної
поверхні. їх закладають на лініях І та
II класів не рідше ніж через 60 км, а в
сейсмічних районах - через 40 км.
Фундаментальні репери закладають також
поблизу морських, основних річкових
та озерних рівневих постів.
Звичайні
репери закладають на лініях I,
II,
III та IV класів. Зазначимо, що називати
ці репери “звичайними” не прийнято.
їх просто називають ґрунтовими,
стінними. Це означає, що вони не вікові
і не фундаментальні.
Призначення
тимчасових реперів зрозуміле із самої
назви - вони дають змогу закріпити на
місцевості точки на короткий проміжок
часу (день, місяць тощо).
Ґрунтові
репери закладають такими способами:
Забиванням
безанкерних реперів
Загвинчуванням
Стінні
та скельні репери закладають, як правило,
бурінням із застосуванням свердел
та бурів.
Уся
територія України розміщена в зоні
сезонного промерзання ґрунтів. Тому
детальніше розглянемо будову ґрунтових
реперів для такої зони, а також стінного
репера, що закладають на лініях
нівелювання III та IV класів.
Ґрунтові
репери закладають у пробурені свердловини
діаметром 50 см. Ґрунтовий репер
складається із залізобетонного пілона
у формі
Вікові
(ґрунтові та скельні).Фундаментальні,
що, своєю чергою, поділяються на
ґрунтові, залізобетонні, азбестоцементні,
трубчаті (металеві) та скельні.Звичайні
(ґрунтові та стінні).
Котлованним.
Цей спосіб застосовують у місцях, де
неможливе використання механізмів.Свердловинним.
Для цього використовують бурові машини.палезабивними
механізмами.металевих
труб
у піщаних та заболочених районах.паралелепіпеда
(рис.
1.1.2, а) з поперечним розрізом 16x16
см
та бетонної плити (якоря) діаметром 48
см, які готують завчасно. Глибину
закладання репера щодо поверхні землі
та межі промерзання ґрунту показано
на рис. 1.1.2, а. Мінімальна глибина
закладання - 130 см (із висотою якоря).
Біля репера на віддалі 100 см
закладають
розпізнавальний стовп. У його верхній
частині прикріпляють охоронну пластину,
яка також показана на рис. 1.1.2, б.
Геодезичний
пункт
Охороняється
Державою
*
із *
Рис.
1.1.2, б. Охоронна
пластина
Рис.
1.1.2, а. Ґрунтовий репер
Охоронна
пластина повинна бути повернута в бік
репера. Дозволяють застосовувати
квадратні якорі розміром 50x50
см.
У верхню грань пілона повинна бути
зацементована марка (рис. 1.1.3). Всередині
бетонної плити (якоря) роблять виїмку
розміром 20x20x15
см,
у яку встановлюють залізобетонний
пілон. Пілон може бути замінений
азбестоцементною трубою із зовнішнім
діаметром не менше ніж 16 см, заповнену
бетоном та арматурою (рис. 1.1.4). У верхню
грань труби цементують марку. Для
зміцнення зв’язку труби з якорем на
віддалі 7-10 см від основи труби вкладають
два взаємно перпендикулярні стрижні,
товщина яких 1,0-1,2 см, довжина 25 см. Під
час встановлення труби у створ якоря
кінці стрижнів розміщують у кутах
виїмки.
У
південній частині зони промерзання
ґрунтів використовують якорі заввишки
20 см, у північній - 35 см. Межа між північною
та південною частинами зони проходить
по лінії Ужгород-Харків. Допускають
закладання реперів у свердловини
діаметром 35 см, але у такому разі висота
якоря повинна бути 50 см у південній, та
80 см - у північній частинах зони.
24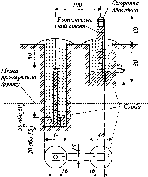
Рис.
1.1.4. Ґоунтовий репер
Рис.
1.1.3. Типи марок для ґрунтових реперів
Стінний
репер, який закладають на лініях
нівелювання III та IV класів, зображено
на рис. 1.1.5.
У
пісках, у заболочених районах реперами
слугують оцинковані труби, загвинчені
на глибину не менше за 4 м. Над поверхнею
землі така труба виступає на 0,8 м. На
частині репера, що виступає, приварюють
охоронну пластину, а на верхньому
зрізі - марку.
Усі
постійні геодезичні знаки, зокрема і
нівелірні репери, охороняються державою.
Догляд
за зберіганням геодезичних знаків
покладають на землях:
населених
пунктів та державних - на виконавчі
комітети районних та міських рад
народних депутатів;
якими
користуються підприємства, організації
та заклади - на ці підприємства,
організації та заклади.
Виконавець
робіт після закладання реперів здає
їх на зберігання місцевим органам влади
та підприємствам згідно з відповідним
актом.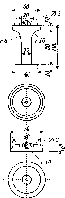

035
Рис.
1.1.5. Стінний репер
Найважливішими
показниками, якими оцінюють якість
нівелірів, є:
для
нівелірів fa
циліндричним
рівнем - збільшення зорової труби
для
нівелірів із компенсаторами - збільшення
зорової труби
Глухий
нівелір із рівнем та елеваційним гвинтом
придатний для нівелювання III класу,
якщо:
збільшення
труби
ціна
поділки циліндричного, контактного
рівня т (2 мм) не більша за ЗО".
26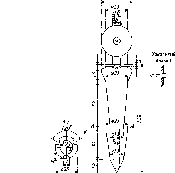
Прилади, що використовують для геометричного нівелювання III, IV класів
Головні вимоги до нівелірів, що використовують для нівелювання III, IV класів
Г
та ціна поділки рівня т;Г
та похибка самовстановлення лінії
візування в горизонтальний стан ту.
Г
(крат) не менше за 30х;
Нівелір
із компенсатором також придатний для
нівелювання III класу,
якщо:
збільшення
труби
похибка
самовстановлення лінії візування
Під
час нівелювання III класу застосовують
нівеліри з рівнем Н2, НА-1, Н- 3, НВ, Ni-ОЗО,
а також нівеліри з компенсатором Н-ЗК,
Ni-007,
NiB-3,4,5,6, НИК-2.
Ці нівеліри мають вищезгадані або вищі
показники точності. Варто зазначити,
що нівеліри Н2, НА-1, НВ (СРСР) та Ni-030,
Ni-007 фірми
“Karl
Zeiss” (Ієна),
NiB-3,4,5,6
(Угорщина)
уже не випускають, але ще широко
використовують на виробництві.
Глухий
нівелір із рівнем придатний для
нівелювання IV класу, якщо:
збільшення
труби
ціна
поділки циліндричного контактного
рівня т (2 мм) не більша за ЗО"
Нівелір
із компенсатором придатний для
нівелювання IV класу, якщо:
збільшення
труби
Під
час нівелювання IV класу застосовують
нівеліри з рівнем Н-3, НВ, Ni-
030, а
також нівеліри з компенсатором Н-ЗК,
НСЗ, НС4, NiB-3,4,5,6
(Угорщина)
і Ni-025
(фірма
“Karl
Zeiss”), НИК-2.
Зазначимо, що нівеліри НСЗ, НС4, Ni-025
також
уже не випускають. Характеристики
вказаних нівелірів достатні для того,
щоб використовувати їх для нівелювання
IV класу.
Нижче,
у табл. 1.2.1, наведено дані про сучасні
нівеліри, які випускають найвідоміші
у світі фірми-виробники. В Україні
сучасні нівеліри для нівелювання ПІ,
IV класів, які нічим не поступаються
закордонним, виготовляє Ізюмський
приладобудівний завод (Харківська
область).
У
наш час рівневі нівеліри заміняють
нівелірами з компенсаторами і
фірми-виробники називають їх автоматичними.
Насправді у таких нівелірах, завдяки
компенсаторам, автоматизоване тільки
встановлення візирної лінії в
горизонтальний стан. Найбільшим
досягненням у цій галузі є цифрові
(електронні) нівеліри. Ці прилади
практично повністю автоматизують
нівелювання, оскільки в них також
автоматизовано відлічування кодових
рейок. Найновіші нівеліри отримали
назву
Г
(крат) не менше за 30х;ту
(кутові секунди) не більша за 0,5".
Г
(крат) не менше за 25х;
Г
(крат) не менше за 25х
та похибка самовстановлення лінії
візування (кутові секунди) не більша
ніж 0,5".тотальні
станції
(total
-
загальний, сумарний). Вони дають змогу
з високою точністю визначати не тільки
перевищення та висоти, але і планове
розташування точок місцевості. Такі
сучасні цифрові нівеліри варто розглянути
детальніше.
Фірма, країна-виробник |
Назва нівеліра |
Збільшення труби, Гх |
Віддаль мінімального фокусування труби, м |
Точність роботи компенсатора |
Похибка на один кілометр подвійного ходу, мм |
Інші технічні дані |
Маса, кг |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ізюмський приладо будівний завод, Україна |
НИК-2 |
31,3 |
0,5 |
0,4" |
2 |
Пряме зображення |
2 |
Уральський оптично- механічний завод м. Єкате- ринбург, Росія |
Автоматичні нівеліри |
||||||
ЗНЗКЛ |
22 |
1,2 |
не подана |
3 |
діапазон роботи компенсатора ±15’ |
з футляром 2,6 |
|
ЗН2КЛ |
зо |
0,8 |
1,5" |
2/1 |
точність 3 насадним оптичним мікрометром -1 мм на км |
з футляром 2,5 |
|
ЗН5Л |
20 |
1,2 |
|
5 |
- |
з футляром 2,5 |
|
Лазерні нівеліри |
|||||||
НЛ-30 |
|
|
точність 30" |
1,5 |
|||
Sokkia, Японія |
Прецизійні нівеліри |
||||||
PL-1-39 |
42 |
2,0 |
рівневий 2 мм |
0,2 |
діапазон мікрометра - 10 км шкала мікрометра -0,1 мм |
4,8 |
|
Прецизійні автоматичні нівеліри |
|||||||
ВІС-31 |
32 |
2,3 |
0,3" |
0,8/0,5 |
компенсатор ±10’ з плоско- паралельною пластиною - 0,5 |
3,2 |
|
ВІС-41 |
32 |
2,3 |
0,3" |
0,8 |
- |
3,2 |
|
28
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Автоматичні нівеліри |
||||||
С41 |
20 |
0,9 |
0,5" |
2,5 |
діапазон роботи компенсатора ±12’ горизонтальний круг - 1° |
1,0 |
|
Karl Zeiss, сьогодні - Trimble (США) |
Цифрові нівеліри |
||||||
Dini 10 |
32 |
1,3-1,5 |
0,2" |
0,3/1,5 |
|
3,0 |
|
Dini 20 |
|
|
|
|
|
3,0 |
|
Автоматичні нівеліри |
|||||||
№ 10 |
25,32, 36,41, |
1,5 |
0,5" |
0,7 |
оптичний режим |
|
|
Ni ЗО |
32 |
1,5 |
0,5" |
0,7 |
оптичний режим |
|
|
Ni 40 |
25 |
1,5 |
0,5" |
0,7 |
оптичний режим |
|
|
№50 |
20 |
1,5 |
0,5" |
0,7 |
оптичний режим |
|
|
Тотальні нівелірні станції |
|||||||
Dini ЮТ |
32 |
1,5 |
0,2" |
0,3 1,0 1,5 |
інвар., електронний режим електронний режим оптичний режим |
3,5 |
|
Dini 11/1 IT |
32 |
1,3/1,5 |
0,2" |
0,3/1,0 |
подана точність для електр. і оптичного режиму |
3,1 |
|
Dini 21 |
26 |
1,3/1,5 |
0,5" |
0,7/1,7 |
3,0 |
||
Opton |
Ni 1 |
40 |
1,4 |
0,1" |
0,2 |
з плоско- паралельною пластиною |
5,2 |
№2 |
32 |
3,3 (1,8-1,0) |
0,2м |
0,3/0,7 |
змінні короткофокусні лінзи |
2,1 |
|
№ 22 |
32 |
3,3 (1,8;1,3;1,0) |
0,5" |
1,0 |
змінні короткофокусні лінзи |
1,9 |
|
Під
час нівелювання III класу використовують
дерев’яні шашкові або інварні штрихові
рейки. У гірських районах необхідно
використовувати тільки інварні рейки
та нівеліри із плоско-паралельною
пластинкою.
На
шашкові триметрові двосторонні рейки
нанесено сантиметрові поділки. На
чорних сторонах комплекту рейок нулі
збігаються з п’ятками рейок; наГоловні вимоги до нівелірних рейок
червоних
з п’ятками рейок збігаються відліки,
більші за 4000 мм; відлік на червоній
стороні однієї рейки відрізняється
від відліку на червоній стороні другої
на 100 мм (наприклад: на одній відлік
4687, на другій - 4787 мм). Під час прив’язування
до стінних марок використовують підвісні
рейки завдовжки 1,2 м із такими самими
поділками, як і на триметрових рейках.
Нуль на підвісній рейці повинен збігатися
із центром отвору для штифта, на якому
рейку підвішують до стінної марки.
Допускають й інші методи прив’язування
до таких марок, наприклад, заміною
підвісної рейки металевою лінійкою з
міліметровими поділками, або на стіні
відмічають проекції середньої та
віддалемірних ниток труби нівеліра, а
віддаль по вертикалі від центра отвору
марки до проекцій ниток вимірюють
перевіреною сталевою рулеткою або
лінійкою. Випадкові похибки дециметрових
і метрових інтервалів рейок, що
використовують для нівелювання ПІ
класу, не повинні перевищувати 0,5 мм.
Виняток становлять три нижні дециметри
рейок, оскільки проходження світлового
променя над поверхнею Землі нижче від
трьох дециметрів під час нівелювання
ІП класу не допускається.
Нівелювання
IV класу виконують тільки дерев’яними
шашковими рейками, такими, як і під час
нівелювання III класу, проте випадкові
похибки дециметрових та метрових
інтервалів цих рейок не повинні
перевищувати 1 мм. Рейки досліджують
за допомогою контрольної лінійки.
У
наш час широко застосовують (нарівні
з дерев’яними) металеві (переважно
алюмінієві), скляні і пластикові рейки.
До того ж, на рейки наносять не тільки
метричні поділки (1 см, 5 мм), але й кодові.
Саме кодові рейки використовують
під час роботи із цифровими (електронними)
нівелірами.
Будова,
перевірки
та дослідження нівелірів із рівнями
Будова
нівелірів із рівнями відома з курсу
“Топографія” та з цілої низки підручників
[3, 7, 8, 11, 29]. Проте, на нашу думку, корисно
нагадати, що існує відмінність між
Візирною
віссю будемо називати пряму, що проходить
через центр сітки ниток та центр
об’єктива (через задню головну точку
об’єктива).
Візирною
лінією будемо називати пряму, що
проходить через центр об’єктива (його
передню головну точку) та проекцію
центра сітки ниток на рейці. У нівелірах
із компенсаторами візирна вісь є також,
але вона дещо нахилена, якраз тоді,
коли візирна лінія встановлена
компенсатором у горизонтальний
стан.
На
рис. 1.2.1 подано загальний вигляд нівеліра
Н-3, найпоширенішого й найпридатнішого
для нівелювання III та IV класів.
ЗО
візирною
віссю нівелірів із рівнями
та візирною
лінією нівелірів із компенсаторами
[17].
Фокусувальний
Приціл
Циліндричні
рівень
Виправні
г цилтдриЧНОси
ріипн
Зорова
тру
гвинти
Рис.
1.2.1. Загальний вигляд нівеліра Н-3
Під
час отримання нівеліра та рейок
виконавець повинен детально їх оглянути
та впевнитись у відсутності будь-яких
пошкоджень. Перед початком польових
робіт нівеліри досліджують та перевіряють
у такій послідовності:
Визначення
коефіцієнта ниткового відцалеміра.
Перевірка
сферичного рівня.
Перевірка
відсутності коливання верхньої частини
нівеліра під час її обертання навколо
вертикальної осі.
Перевірка
правильності встановлення сітки ниток.
Перевірка
циліндричного рівня.
Розглянемо
детально ці перевірки та дослідження.
Визначення
коефіцієнта ниткового віддалеміра.
Під
час дослідження коефіцієнтів
Після
приведення нівеліра в робочий стан
беруть три пари відліків верхньої
(В) та нижньої (Н) віддалемірних ниток.
Кожну пару відліків беруть на різних
висотах нівеліра. Приклад визначення
коефіцієнта
Якщо
зорова труба має сталу віддалеміра С
(вибирають з паспорта), тоді коефіцієнт
віддалеміра обчислюють за формулою
D-c-
{Н-В)СЄр
(1.2.1)
К
ниткового віддалеміра у нівелірів Н-
3, Н-10 та інших вибирають рівну поверхню
і забивають два кілки на віддалі D
(приблизно
50 м один від одного), а у верхні зрізи
кілків забивають цвяхи з округлими
головками. Над одним із кілків встановлюють
(центрують) нівелір, над другим - рейку.
Віддаль між кілками вимірюють стрічкою
або рулеткою з точністю до 1 см.К
подано у табл. 1.2.2.
Нитки |
Відліки відцалемірних ниток |
Різниця відліків (Н-В), мм |
|
В |
1001 |
502 |
|
Н |
1503 |
||
в |
1143 |
504 |
|
н |
1647 |
||
в |
0930 |
503 |
|
н |
1433 |
||
К = 50400/503,0= 100,2 |
Середня різниця 503,0 |
||
Під
час обчислення довжини секції нівелірного
ходу, якщо стала відцалеміра С
не
дорівнює нулю, користуються формулою
L
=
KZ(l3
+Іп)
+ 2пС, (1.2.3)
де
Перевірка
сферичного рівня.
Вісь
сферичного рівня повинна бути паралельною
до вертикальної осі обертання нівеліра.
Цю перевірку виконують так: підіймальними
гвинтами приводять бульбашку сферичного
рівня в нуль-пункт. Повертають нівелір
навколо вертикальної осі на 180°. Якщо
бульбашка відхиляється від нуль- пункту
більше ніж на
Під
час двох-трьох таких дій бульбашка
рівня під час повороту нівеліра на 180°
залишається у нуль-пункті. Після цього
виправні гвинти рівня повинні бути
надійно закріплені.
3213
та Іп
- різниці відліків відцалемірних ниток
під час візування на задню та передню
рейки, мм; п-
кількість станцій у секції. Якщо відліки
взяті верхньою (В) та середньою (С)
нитками, то суму Х(1В
+1С)
подвоюють.
1А
радіуса кола, яким позначено нуль-пункт,
тоді бульбашку приводять у вихідний
стан: виправними гвинтами рівня на
половину дуги відхилення, а на другу
половину - підіймальними гвинтами.
Рис.
1.2.2. Схема перевірки правильності
обертання труби
навколо вертикальної
осі
Обертання
нівелірів навколо вертикальної осі
повинно бути легким, плавним, без зусиль,
в іншому разі необхідно почистити та
змазати вертикальну вісь.
33Перевірка
правильності обертання труби навколо
вертикальної осі. Перевіряють
відсутність коливання верхньої частини
нівеліра під час обертання його навколо
вертикальної осі за допомогою
циліндричного рівня. Досліджуючи
нівеліри Н-3, на корпус труби встановлюють
допоміжний циліндричний рівень з ціною
поділок 10-15" на 2 мм. Встановлюють
нівелір на кам’яному стовпі і ретельно
горизонтують за допомогою циліндричного
рівня. Приводять трубу в стан І-ІІ (рис.
1.2.2), роблять відліки на кінцях бульбашки
рівня. Поступово повертають верхню
частину приладу навколо вертикальної
осі на 720°; водночас через кожні 60°
відраховують кінці бульбашки рівня
(табл. 1.2.3). Перш ніж узяти відлік, рівню
дають можливість заспокоїтись. У
прямому ході обертають верхню частину
нівеліра за годинниковою стрілкою, у
зворотному - проти. Розходження між
відліками в прямому та зворотному
ходах для нівелірів Н-3 в одних і тих
самих положеннях не повинні перевищувати
40".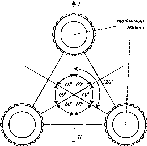
Встанов лення труби |
І |
II |
І-Н |
||||||
Прямий хід, поділки рівня |
Зворотний хід, поділки рівня |
||||||||
л |
п |
Л-П |
л |
п |
Л-П |
|
|||
0° |
11,0 |
11,5 |
-0,5 |
10,5 |
12,0 |
-1,5 |
+1,0 |
||
60° |
10,5 |
12,1 |
-1,6 |
10,8 |
11,6 |
-0,8 |
-0,8 |
||
120° |
10,2 |
12,0 |
-1,8 |
11,2 |
: п,з |
-0,1 |
; -і,7 |
||
180° |
10,0 |
12,2 |
-2,2 |
11,1 |
п,з |
-0,2 |
-2,0 |
||
240° |
10,4 |
11,7 |
-1,3 |
11,5 |
10,9 |
+0,6 |
-1,9 |
||
300° |
10,9 |
11,3 |
-0,4 |
11,3 |
11,1 |
+0,2 |
-0,6 |
||
360° |
11,0 |
11,2 |
-0,2 |
11,0 |
11,4 |
-0,4 |
+0,2 |
||
420° |
11,2 |
11,0 |
+0,2 |
10,5 |
11,9 |
-1,4 |
+1,6 |
||
480° |
11,4 |
П,І |
+0,3 |
10,6 |
11,7 |
1 -1,1 |
+1,4 |
||
540° |
11,2 |
10,9 |
+0,3 |
10,4 |
11,9 |
-1,5 |
+1,8 |
||
600° |
11,2 |
11,0 |
+0,2 |
10,3 |
12,0 |
-1,7 |
+1,9 |
||
660° |
11,5 |
10,8 |
+0,7 |
10,8 |
11,6 |
-0,8 |
! +1,5 |
||
720° |
11,4 |
10,7 |
+0,7 |
10,6 |
11,4 |
-0,8 |
+1,5 |
||
Ціна
поділок Т
дорівнює
10”. Максимальне коливання 3,9 поділки
рівня або
39”.
У
нівелірів Н-3, Н-10 цю перевірку виконують
так: встановивши нівелір за допомогою
сферичного рівня в горизонтальний
стан, наводять край середньої нитки на
добре видиму точку, яка розміщена від
нівеліра на віддалі близько 10 м, повільно
повертають трубу навідним гвинтом і
стежать, чи не відхилиться середня
нитка від цієї точки. Якщо відхилення
більше за 2 мм - сітку ниток виправляють.
Для цього необхідно відокремити окулярну
частину від корпусу зорової труби.
Потім, ослабивши закріпні гвинти
приблизно на один оберт, скляну пластинку
із сіткою ниток злегка обертають. Після
цього приєднують окулярну частину до
зорової труби і перевіряють розташування
горизонтальної нитки. Перевірку
виконують декількома наближеннями. На
закінчення, закріпивши гвинти, що
тримають сітку ниток, необхідно ще раз
переконатися, що розташування нитки є
правильним.
34Перевірка
правильності встановлення сітки ниток
Середня
нитка повинна бути горизонтальною, а
вертикальна - вертикальною. Досить
пересвідчитися у правильному розташуванні
горизонтальної нитки. Взаємну
перпендикулярність ниток гарантує
завод-виробник.
Цю
перевірку можна також виконувати
вертикальною ниткою (перевіряючи
її прямовисність), використовуючи
підвішений тягарець (надворі, коли
немає вітру, або у приміщенні).
Перевірка
циліндричного рівня.
Цю
перевірку поділяють на дві частини.
Вертикальна
площина, яка проходить через вісь
рівня, повинна бути паралельною до
вертикальної площини, що проходить
через візирну вісь зорової труби.
Або: візирна вісь та вісь циліндричного
рівня повинні розміщуватися у двох
взаємно паралельних вертикальних
площинах.
Величина
кута
Першу
половину перевірки виконують так:
встановлюють нівелір на віддалі близько
50 м від рейки у такий спосіб, щоб один
підіймальний гвинт був спрямований у
бік рейки. Ретельно приводять вертикальну
вісь нівеліра в прямовисний стан за
допомогою сферичного рівня. Приводять
елеваційним гвинтом зображення кінців
бульбашки в контакт і беруть відлік
рейки. Надають зоровій трубі бокового
нахилу, обертаючи підіймальні гвинти
у різні боки точно на два повні оберти.
Стежать, щоб точка перетину вертикальної
та середньої (горизонтальної) ниток
була наведена на ту саму точку, тобто
щоб відлік не змінився. Після цього
нахиляють нівелір в інший бік, повертаючи
ті самі гвинти в протилежному напрямку.
Якщо в обох випадках кінці бульбашки
не розходяться або зміщуються в одну
сторону, то встановлення рівня правильне.
Коли під час різних нахилів вони значно
розходяться у протилежні боки, тоді
виправляють розташування циліндричного
рівня за допомогою бокових виправних
гвинтів. Виправляють розташування,
поступово обертаючи один гвинт на
загвинчування, другий - на вигвинчування.
Правильного встановлення рівня досягають
методом наближень.
Другу
частину перевірки можна виконати так:
забивають два костилі (або кілки зі
цвяхами) на віддалі близько 50 м один
від одного (у точках
й
= а'-й'. (1.2.4)
У
(1.2.4)
35
і
повинна бути меншою за 10". Кутом і
називають кут, який утвориться на
вертикальній площині, якщо на неї
спроектувати вісь циліндричного рівня
та візирну вісь труби. Цю частину
перевірки можна ще сформулювати так:
візирна вісь та вісь циліндричного
рівня повинні бути розміщені у двох
взаємно паралельних горизонтальних
площинах.А
і В).
Встановлюють
нівелір точно посередині між костилями
і вимірюють перевищення h.
На основі рис. 1.2.3 запишемо:а'
та Ь'
-
правильні відліки, які були б узяті за
умови, якщо кут і
=
0. Оскільки і
Ф
0, то фактичні відліки будуть а
та Ь.
Враховуючи, що нівелір однаково
віддалений від задньої й передньої
рейок, відліки а
та b
помилкові
на однаковий відрізок х.
Рис.
1.2.3. Визначення перевищення нівелюванням
ізсередини
Тому
маємо рівняння:
a
=a—x;
b'
= b-x.
Відповідно
до (1.2.4) можна записати:
h
=
(а-х)-(Ь-х).
Розкриваючи
дужки, отримаємо:
Отже,
коли нівелір встановлений посередині
між рейками (прийнято говорити: рівні
плечі), то різниця помилкових відліків
дає правильне перевищення
Переносять
і встановлюють нівелір на віддалі
приблизно 10 м за одним із костилів (рис.
1.2.4). Беруть відліки близької та далекої
рейок
Відповідно
до рис. 1.2.4 правильне перевищення
знаходять за формулою
або
Отже,
Ь
= Б'-Д',
h
= Б
- a
-
(Д - a
-
х).
h
= Б
- Д + х.
(1.2.6)
(1.2.7)
(1.2.8)
36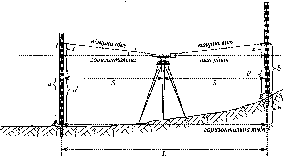
h-a-b. (1.2.5)h.-Б
та Д.
|
(1.2.9) |
Знаючи
.0 0 X ,=рг |
(1.2.10) |
де
L
-
віддаль між костилями.
Рис.
1.2.4. До визначення кута і
Щоб
позбутися кута/, необхідно спочатку
знайти правильний відлік
звідси
(*
+ <0=^, (,.2.11)
де
Отже,
Д'
= Д-(х
+ а).
(1.2.12)
37
Д'.
На
основі рис. 1.2.4 можна записати:х
+ a
_
L
+
/ х “і ’(L
+ 1)
-
віддаль від нівеліра до далекої рейки.
Знаючи
Деяким
слабким контролем правильності виконання
перевірки є те, що після виконаних дій
відлік близької рейки
Будова,
перевірки
та дослідження нівелірів з компенсаторами
Будова
нівелірів з компенсаторами, як і
нівелірів з рівнями, вже відома з курсу
“Топографія”. Головною відмінністю
між цими нівелірами є те, що в нівелірі
з компенсатором немає циліндричного
рівня. Цей рівень замінений на особливий
пристрій - компенсатор, що автоматично
встановлює візирну лінію в горизонтальний
стан.
На
рис. 1.2.5 подано загальний вигляд нівеліра
Н-ЗК, який застосовують для нівелювання
III та IV класів.
рівень гвинти гвинти
труби
Рис.
1.2.5. Нівелір Н-ЗК
Нівелір
Н-ЗК удосконалювали, й остання модель
4Н-2КЛ має цілу низку переваг порівняно
зі своїми попередниками: зорова труба
з прямим зображенням, збільшення
30х,
нівелір має горизонтальний круг з ціною
поділки 1°, середня квадратична похибка
вимірювання перевищення на 1 км подвійного
ходу не перевищує 2 мм, маса - 2 кг.
38Д\
елеваційним гвинтом встановлюють
візирну вісь так, щоб відлік далекої
рейки дорівнював Д'.
Зображення кінців бульбашки контактного
циліндричного рівня розійдуться.
Вертикальними виправними гвинтами
циліндричного рівня добиваються
контактування цих кінців. Одночасно
стежать, щоб відлік рейки залишався
таким, що дорівнює Д'.Б
практично не повинен змінитися. Проте
найнадійнішим контролем є повторне
виконання цієї самої перевірки.
Рис.
1.2.6. Нівелір 4Н-2КП
Для
нівелювання III,
IV
класів також використовують подібний
до попереднього нівелір НИК-2, який
показано на рис. 1.2.7. Нівелір має зорову
трубу з прямим зображенням, горизонтальний
круг, маса приладу - 2 кг.
гвинти
Рис.
і. 2.7. Нівелір НИК-2
Основні
технічні характеристики НИК-2:
Квадратична
похибка визначення:
•
перевищення
на 1 км ходу з рейками РН-3-3000СП - 1,5 мм;
•
горизонтальних
кутів - 8і.
Діапазон
роботи компенсатора - ±30’.
Найменша
відстань візування - 0,5 м.
Збільшення
труби - 31,3±1х.
Ціна
поділки сферичного рівня на 2 мм - 10±2’.
Перед
початком польових робіт нівеліри з
компенсатором досліджують та перевіряють
у такій послідовності:
39
Визначення
коефіцієнта віддалеміра.
Перевірка
сферичного рівня.
Перевірка
відсутності коливання верхньої частини
нівеліра під час її обертання навколо
вертикальної осі.
Перевірка
правильності встановлення сітки ниток.
Перевірка
правильності встановлення компенсатором
візирної лінії.
Визначення
середньої квадратичної похибки
встановлення компенсатором візирної
лінії та похибки недокомпенсації.
Перевірки
1, 2 та 3 виконують так само, як і для
нівелірів з рівнями. Зазначимо лише,
що у такому разі для виконання третьої
перевірки обов’язково необхідно
застосувати циліндричний рівень, що
накладається на зорову трубу нівеліра.
Перевірку 4 в цьому нівелірі формулюють
так: вертикальна нитка сітки під час
встановлення бульбашки сферичного
рівня в середнє положення (в нуль-пункт)
повинна зайняти вертикальний (прямовисний)
стан. Під час виконання цієї умови
і середня горизонтальна нитка сітки
буде горизонтальною. Цю перевірку у
нівелірах з компенсаторами доцільно
виконувати так: старанно привести
вертикальну вісь нівеліра за допомогою
сферичного рівня у прямовисний стан.
Навести вертикальну нитку сітки на
нитку виска (тягарця). Коли один кінець
вертикальної нитки сітки відхиляється
від нитки виска більш ніж на 0,5 мм, тоді
необхідно виправити розташування
сітки. Виправлення виконують так само,
як і в рівневих нівелірах.
П’яту
перевірку, тобто перевірку правильності
встановлення компенсатором візирної
лінії можна сформулювати так само, як
і перевірку 5.2 для рівневих нівелірів,
тобто: величина кута
Кут
Якщо
виникає необхідність виправлення кута
D'
= D-(x + a). (1.2.13)
Виправлення
виконують, переміщаючи сітку ниток у
вертикальній площині за допомогою
вертикальних виправних гвинтів. Один
виправний гвинт відгвинчують, а другий
загвинчують доти, поки відлік далекої
рейки не дорівнюватиме
40і
повинна бути меншою за 10". Але кут і
у такому разі є вертикальним кутом між
візирною лінією та горизонтальною
площиною. Цю перевірку необхідно
виконувати також так само, як перевірку
5.2 в рівневих нівелірах.і
можна визначити, скориставшись формулоюі,
то правильний відлік D'
знаходять
за (1.2.13):D'.
Як
бачимо, усі п’ять перевірок рівневих
нівелірів та нівелірів з компенсаторами
можна формулювати та виконувати
практично однаково, що полегшує засвоєння
матеріалу.
Дослідження
точності роботи компенсаторів нівелірів.
Дослідження
складається з двох частин:
Визначення
випадкової середньої квадратичної
похибки роботи компенсатора
Величина
(1.2.14)
деГ
=
кожній
із п’яти серій для різних станів
бульбашки, показаних на рис. 1.2.8. Можна
визначити п’ять значень
значення.
Визначення
недокомпенсації, тобто систематичної
похибки роботи компенсатора
Похибку
(1.2.15)
де
перевищення
в кожній із п’яти серій під час нахилу
вертикальної осі на кут V, (кут у мінутах
дуги).
Ці
два дослідження, якщо їх виконують у
польових умовах, можуть бути виконані
на основі вимірювання перевищень під
час різних станів бульбашки сферичного
рівня.
Нівелір
встановлюють у створі між двома рейками,
віддаленими одна від одної на 100 м (для
нівелювання III класу) або 200 м (для
нівелювання IV класу). Вимірювання
перевищення між точками, на яких
встановлені рейки, виконують серіями,
загальна кількість яких дорівнює п’яти.
У кожній серії бульбашка сферичного
рівня повинна займати п’ять різних
станів, показаних на рис. 1.2.8.
41тк..тк.
визначається за формулою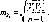
hcep
-
ht;
hcep
і
h{
-
відповідно середнє і окреме значення
перевищення утк.,
з яких знаходять найімовірніше, середнє
ок..Ок.
визначають за формулою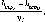
hcepo
-
середнє перевищення, коли бульбашка в
нуль-пункті; hcep,
-
середнє
Номер серії |
Сторони рейки |
Перевищення |
|||||||||||||||
Бульбашка у нуль-пункті |
Поздовжній нахил |
Поперечний нахил |
|||||||||||||||
0' |
V/ |
+10’ |
V/ |
-10' |
V/ |
+10' |
V,- |
-10' |
V/ -0,16 |
||||||||
1 |
чор. |
1575,4 |
-0,28 |
1575,4 |
-0,04 |
1575,6 |
-0,18 |
1575,4 |
-0,14 |
1575,7 |
|||||||
чер. |
1575,6 |
-0,08 |
1575,5 |
+0,06 |
1575,7 |
-0,08 |
1575,4 |
-0,14 |
1575,9 |
+0,04 |
|||||||
2 |
чор. |
1576,0 |
+0,32 |
1575,8 |
+0,36 |
1576,0 |
+0,22 |
1575,8 |
+0,26 |
1576,0 |
+0,14 |
||||||
чер. |
1575,8 |
+0,12 |
1575,7 |
+0,26 |
1575,6 |
-0,18 |
1575,6 |
+0,06 |
1575,8 |
-0,06 |
|||||||
3 |
чор. |
1575,5 |
-0,18 |
1575,3 |
-0,14 |
1575,6 |
-0,18 |
1575,4 |
-0,14 |
1575,8 |
-0,06 |
||||||
чер. |
1575,8 |
+0,12 |
1575,4 |
-0,04 |
1575,8 |
+0,02 |
1575,6 |
+0,06 |
1575,8 |
-0,06 |
|||||||
4 |
чор. |
1575,9 |
+0,22 |
1575,0 |
-0,44 |
1576,2 |
+0,42 |
1575,7 |
+0,16 |
1575,9 |
+0,04 |
||||||
чер. |
1575,9 |
+0,22 |
1575,4 |
-0,04 |
1575,9 |
+0,12 |
1575,7 |
+0,16 |
1576,1 |
+0,24 |
|||||||
5 |
чор. |
1575,4 |
-0,28 |
1575,5 |
+0,06 |
1575,6 |
-0,18 |
1575,2 |
-0,34 |
1575,8 |
-0,06 |
||||||
чер. |
1575,5 |
-0,18 |
1575,4 |
-0,04 |
1575,8 |
+0,02 |
1575,6 |
+0,06 |
1575,8 |
-0,06 |
|||||||
Середнє |
1575,68 |
|
1575,44 |
|
1575,78 |
|
1575,54 |
|
1575,86 |
|
|||||||
Знаходимо
Середнє
значення випадкової похибки роботи
компенсатора
42rnkl
=
0,23
мм; ткі
= 0,22 мм; Щ3=
0,20 мм; тц
= 0,18 мм; Шц
-
0,12 мм.щ
-
0,19 мм.
Значення
систематичних похибок у перевищеннях
під час нахилу вертикальної осі
нівеліра на кут v
=10'.
Отже,
під час нахилу вертикальної осі нівеліра
на кут V = 10’ систематична похибка
не перевищує -0,24 мм.
Відповідно
до чинної Інструкції для нівелірів, що
використовують під час нівелювання
III класу, систематична похибка
Ми
розглянули перевірки та дослідження
нівелірів, які виконують перед початком
польових робіт. У п. 1.2.1 вказано, що
якість нівелірів характеризує,
насамперед, збільшення зорової труби
Під
час польових робіт у нівелірів
перевіряють:
сферичний
рівень (кожний день перед початком
спостережень);
кут
Електронні
нівеліри дають змогу повністю
автоматизувати нівелювання, а відліки
рейок у цифровому вигляді відображаються
на дисплеї або, за бажанням, передаються
до внутрішнього (зовнішнього)
запам’ятовуючого пристрою для подальшого
опрацювання.
Виробники
досягли цього завдяки дуже важливим
конструктивним удосконаленням
нівелірів та рейок, а саме: вмонтували
в нівеліри цифрові камери з CCD-сенсорами
(Charge
Coupled Device) (українською
мовою: ПЗЗ - прилад зарядного зв’язку).
У таких камерах у площині знімка
встановлене плоске двовимірне поле
світлочутливих детекторів-сенсорів,
які дають елементи зображення предмета,
оскільки є деякою малою поверхнею, а
не точкою. Замість слів “елемент
зображення” вживають штучно утворене
слово Pixel
(від
43Мі
=(hcepj
-hcepQ)
=-0,24; +0,10; -0,14; +0,18.ак.
= ^- =-0,024; +0,010; -0,014; +0,018.ок
не повинна бути більшою за З мм; для IV
класу - 5 мм. Якщо ці умови не виконуються,
нівеліри необхідно віддати в майстерню
для ремонту компенсаторів.Г
та ціна поділки рівня т для рівневих
нівелірів або точність роботи компенсатора
тк
для нівелірів з компенсаторами.
Визначення параметрів Г
іт, якщо вони невідомі, необхідно
виконувати до початку польових робіт.
Методи визначення цих параметрів
нівелірів подані далі.
і
(перші сім днів роботи - кожний день, а
впевнившись у стабільності - один
раз на 15 днів)./.2.5. Електронні цифрові нівеліри. Тотальні нівелірні станції
Picture
x element) - піксел.
Пікселі -
це
носії інформації про ступінь почорніння
або колір. їхнє сприйняття різних
значень тону, які називають глибиною
зображення, значно перевищує здатність
людського ока. Сьогодні найвідоміші
пікселі з областю значень почорніння
від 0 до 255. Отже, такі пікселі дають
інформацію про 256 різних станів
зображень. На чорно-білих зображеннях
- це значення сірого тону (переважно
чорний колір має код 0, а білий 255). Розмір
піксела-7,5 рм2.
Відрізок
на рейці, який потрапляє на поле
детекторів, незначний - близько 15 см
вверх і вниз від середньої горизонтальної
нитки сітки зорової труби. Детектори
подають спочатку аналогові (неперервні)
сигнали, які зчитуються і потім
перетворюються на цифрові за допомогою
комп’ютера. У цьому контексті вживають
термін “комп’ютерне бачення” (англ.
Computer-Vision),
“розпізнавання
образу”, “розпізнавання знімка”.
Справді, око людини не здатне розрізняти
256 ступенів сірої шкали. Отже, певна
частина нівелірної рейки розглядається
комп’ютером, а не оком спостерігача.
Істотних конструктивних змін також
зазнали рейки. Традиційні рейки
замінюються кодовими рейками: з чорними
та білими смугами. Фірмами створений
ціла низка кодових рейок. Так, кодові
рейки фірми Leica-Wild
NA 2000,
Wild
NA 3000
мають довжину 4050 мм. На одному боці
рейки нанесено поділки у вигляді чорних
та білих смужок, що створюють двійковий
код; ширина (основної) смужки 2 мм. На
другому боці рейки нанесено поділки,
які призначені для візуального відліку.
Фірма Sokkia
для
електронного нівеліра SDL
30
створила рейки зі спеціальним кодом
(RAB-код),
який також є двійковим. Існують також
фібергласові рейки завдовжки 5 м. Цей
скловолокнистий матеріал (фіберглас)
використаний для виготовлення рейок
завдяки його перевагам порівняно з
іншими матеріалами за вагою та міцністю,
а також можливості застосування
найточніших технологій нанесення
штрихів.
Образ
кодової рейки, що розглядається камерою
(приладом зарядного зв’язку), автоматично
перетворюється (завдяки “комп’ютерному
баченню”) на цифровий відлік, який
відображається на дисплеї.
Зазвичай
у цифрових нівелірів є три режими
вимірювання: Single-Fine
(точний
одноразовий), Repeat-Fine
(точний
багаторазовий) і Tracking
(режим
слідкування). У точному одноразовому
режимі вимірювання виконуються кожні
три секунди, а в режимі слідкування -
кожну секунду. У багаторазовому режимі
на дисплеї відображається середнє
значення відліку.
Зауважимо,
що під час промислових вібрацій або
турбулентності атмосфери, коли поділки
рейки коливаються, похибки відліку
збільшуються. Ці похибки також можна
відображати на дисплеї.
Якщо
похибки перевищують діапазон найменших
поділок рейки, нівелір може зупинити
електронне нівелювання. Перевищення
відображається на
44
|
• з інварними кодовими рейками - |
1,5 мм. |
2. |
Діапазон вимірювання від далі - |
2 м-80 м. |
3. |
Точність вимірювання віддалі: |
|
|
• інварними кодовими рейками - |
10 мм. |
4. |
Межі дії компенсатора - |
± 10'. |
5. |
Чутливість сферичного рівня |
1072 мм. |
6. |
Збільшення зорової труби |
24х. |
45
Фірма
Zeiss
випускає
електронні нівеліри DiNi.
Нівелір
DiNi
10
має: Г = 32х,
точність 0,3/1,5 мм на км ходу - електронний
та оптичний режими. Загальний вигляд
електронного нівеліра третього покоління
DiNi
22
показаний на рис. 1.2.10.
Рис.
1.2.10. Електронний нівелір DiNi
22
Різні
програми вимірювань детально описані
в інструкції, що додається до приладу.
Основні технічні характеристики DiNi
22:
Середня
квадратична похибка визначення
перевищення на 1 км ходу:
з
інварними кодовими рейками - 0,7 мм;
із
кодовими рейками - 1,3 мм;
із
шашковими рейками - 2,0 мм;
Діапазон
вимірювання віддалі - 1,5-100 м.
Точність
вимірювання віддалі:
інварними
кодовими рейками - 25 мм;
кодовими
рейками - 30 мм;
шашковими
рейками (візуально) - 0,3 м.
Точність
відлічування кодової рейки:
висоти,
перевищення - 0,1 мм;
віддаль- 10
мм.
Тривалість
електронних вимірювань - 2 с.
Збільшення
труби - 26х.
Поле
зору електронних вимірювань на 100 м
- 0,3 м.
Межі
дії компенсатора - ± 15\
Точність
горизонтування лінії візування (кутові
секунди) - 0,5.
Ціна
поділки сферичного рівня - 8’.
На
рис. 1.2.11. показано панель керування з
описом функцій клавіш.
46
ON/OFF |
Клавіша вмикання приладу |
О |
Клавіша підсвічування дисплея |
3 |
Клавіша регулювання контрастності дисплея |
DIST |
Клавіша вимірювання віддалі |
MEAS |
Клавіша початку вимірювань |
MENU |
Клавіша головного меню |
INFO |
Клавіша відображення інформації про прилад |
DISP |
Клавіша відображення на дисплей вибраних даних |
PNr |
Клавіша введення номера точки |
REM |
Клавіша введення параметрів точки |
EDIT |
Клавіша редагування даних |
RPT |
Клавіша повторного вимірювання |
INV |
Клавіша режиму перевернутої рейки |
INP |
Клавіша введення даних |
0....9 |
Клавіша введення цифр |
j |
Клавіша десяткової коми |
+/- |
Клавіша введення знаків |
ТА |
Клавіша навігації курсора по пунктах меню |
Рис.
1.2.11. Панель
керування DiNi
22 та
опис функцій клавіш
Важливою
особливістю тотальних нівелірних
станцій є те, що ними можна визначати
як висотне, так і планове розміщення
точок, тобто, як і електронними
тахеометрами, виконувати топографічне
знімання, до того ж найбільших масштабів.
Крім того, тотальні станції дають змогу
визначати висоти або перевищення з
надзвичайно високою точністю. Наприклад,
тотальна станція DiNi
1
IT
(рис.
1.2.12) дає квадратичну похибку визначення
перевищення на 1 км
47Як
бачимо, за допомогою нівеліра можна
працювати ж в електронному, так і в
оптичному (візуальному) режимі. В останні
5-10 років з’явилися тотальні нівелірні
станції. Одна з таких станцій - Dini
ЮТ
- випущена до 150-річчя фірми “Karl
Zeiss”. Основні
характеристики тотальних станцій
подано у табл. 1.2.1.
ходу
- 0,3 мм; віддалі можна вимірювати з
точністю, що визначається за формулою
Рис.
1.2.12. Тотальна станція DiNi
11Т
Важливою
технічною новизною електронних, цифрових
нівелірів є те, що ними можна не тільки
визначати перевищення та висоти, але
й обчислювати похибки, з якими ці
параметри вимірюються.
Перевірки
та дослідження нівелірних рейок перед
початком польових робіт виконують за
такою програмою:
Дослідження
похибок дециметрових поділок (тільки
для нових рейок).
Визначення
середньої довжини одного метра пари
рейок (через 10-15 днів під час роботи в
гірських умовах та через місяць - у
рівнинних).
Визначення
різниці висот нулів рейок.
Визначення
збігання площин п’ятки рейки з віссю
нульової поділки рейки (на чорних
сторонах рейок).
Перевірки
3 та 4 виконують раз на рік перед початком
польових робіт.
Перевірка
встановлення сферичного рівня на
рейках (щодня).
Для
дослідження рейок застосовують
контрольну лінійку. Контрольна лінійка
(рис. 1.2.13) завдовжки 1 м має допоміжну
міліметрову шкалу та головну шкалу з
найменшою поділкою 0,2 мм.
Умонтований
термометр дає змогу визначати зміну
довжини лінійки залежно від температури.
На рис. 1.2.14 показано сотий сантиметр
лінійки в збільшеному вигляді. Лінійка
має дві лупи, які можна пересувати
вздовж ребра лінійки. Через ці лупи і
розглядають шкалу, коли беруть відліки.
Тому ми
48mD
=0,5
D
0,001
м, тобто для D
=
100 м похибка віддалі mD
=
0,05 м, а кути - з точністю 0,1°. Точність
роботи компенсатора 0,2".
Перевірки та дослідження нівелірних рейок
бачимо
поділки лінійки в збільшеному вигляді.
На лінійці нанесено сантиметрові
поділки (0, 1, 2, ..., 99, 100). Кожен сантиметр
лінійки поділено на міліметри
дев’ятьма штрихами однакової довжини
(окрім довшого п’ятого). Кожен
міліметр на п’ять частин (по 0,2 мм)
поділено чотирма штрихами різної
довжини. Під час відлічування найменшу
поділку 0,2 мм поділяють на око ще на 10
частин. Це означає, що відлік беруть з
точністю 0,02 мм.
Рис.
1.2.13. Контрольна лінійка
0 99 100
відліки 993,66 995,88 998,10
Рис.
1.2.14. Збільшене зображення останнього
сантиметра контрольної лінійки
та
приклади відліків
Для
того, щоб безпомилково брати відліки,
необхідно це робити так: спочатку
визначити цілу кількість міліметрів.
На рис. 1.2.14, це 993, 995, 998; після цього
відрахувати десяті та соті частки
поділки (0,33; 0,44; 0,05); оскільки найменша
поділка 0,2 мм, то, щоб перейти від поділки
до мм, необхідно значення десятих
та сотих подвоїти. Одержимо в мм: 0,66;
0,88; 0,10; отже, повні відліки в мм будуть:
993,66; 995,88; 998,10. Зауважимо, що відлік
обов’язково закінчується парною цифрою
(2, 4, 6, 8) або нулем. Користуючись контрольною
лінійкою, можна визначити, як цього
вимагає Інструкція, довжини кожного
нанесеного на рейці дециметра та метра
з точністю близько 0,01-0,02 мм.
Значення
довжини кожного дециметра рейки
необхідне для того, щоб впевнитися, чи
достатньо точно нанесені поділки на
рейці і чи похибки нане-сення поділок
не перевищують 0,5 мм для рейок, які
використовуються
49
для
III
класу,
та 1 мм для рейок, які використовуються
для IV класу нівелювання.
Перейдемо
до детальнішого розгляду окремих
досліджень рейок.
Дослідження
випадкових похибок дециметрових
поділок.
Для
дерев’яних рейок визначають похибки
дециметрових штрихів в інтервалі 1-29
на чорній і 47-76 на червоній сторонах
рейок, тобто нижній та верхній дециметри
не досліджують.
На
горизонтально розташовану рейку кладуть
контрольну лінійку так, щоб нуль лінійки
збігався з першим дециметровим штрихом
рейки, і роблять відліки лінійки у
місцях другого, третього та інших
дециметрових штрихів у межах першого
метра рейки. Потім лінійку трохи
пересувають так, щоб з першим дециметровим
штрихом рейки збігався відлік лінійки,
більший за нуль, і всі відліки повторюють.
Коливання різниць відліків у межах
кожного метра не повинні бути більшими
від 0,10 мм. Після цього лінійку встановлюють
на другий, а потім на третій метри рейки.
Потім розраховують середні відліки
одних і тих самих дециметрових штрихів.
Нехай, наприклад, середні відліки
лінійки по першому, другому та третьому
дециметрах відповідно дорівнюють: 0,14
мм; 100,28 мм; 200,36 мм. Тоді фактичні довжини
другого та третього дециметрів є: 100,14
мм; 100,08 мм. Похибки цих двох дециметрів
відповідно +0,14 мм; +0,08 мм.
Аналогічно
розраховують похибки усіх 26 дециметрів,
що залишилися. Проте ці похибки мають
випадкову та систематичну складові
частини. Виключимо систематичну частину.
Для цього отримані похибки всіх
дециметрів додамо, а одержану суму
поділимо на кількість досліджених
дециметрів. Нехай сума
Аналогічно
розраховують випадкові похибки інших
дециметрів. Повний приклад дослідження
однієї сторони рейки поданий у чинній
інструкції нівелювання [6].
Визначення
середньої довжини одного метра пари
рейок.
Спочатку
покажемо, що у нівелірних ходів з парною
кількістю штативів
половину
перевищення в ході вимірюють однією
рейкою, а половину - другою.
Нехай
маємо хід з чотирьох станцій (рис.
1.2.15). На непарних станціях задньою була
перша рейка, на парних - друга. Знайдемо
перевищення в ході.
X*/
=(<*, — ) + (л2
і
50
S
=
+0,56 мм. Тоді систематична похибка одного
дециметра становитиме: +0,56 мм / 28 = +0,02
мм. Отже, тільки випадкові похибки
другого та третього дециметрів
становитимуть +0,14 - 0,02 мм = +0,12 мм; 0,08 мм
- 0,02 мм = +0,06 мм.
-Ь2)
+ (аі-Ь3)
+ (аЛ-b4). (1.2.16)
1
Доданки
у правій частині рівняння (1.2.16) згрупуємо
у інший спосіб:
=(*2
-*і) +
(агз
1
Тепер
доданки є різницями відліків однієї і
тієї самої рейки, причому два доданки
- різниці відліків першої рейки, два -
другої. У разі рівних плечей, одноманітного
ухилу та однакових висот нівеліра на
станціях ми повинні дійти висновку, що
всі ці (чотири) різниці майже однакові.
Тому, поширюючи цей висновок на будь-який
хід з парною кількістю станцій, можна
говорити, що в ходах нівелювання в
середньому половину перевищення
вимірюють однією рейкою, а половину -
іншою. Цей факт, що перевищення вимірюють
по чорних та червоних сторонах рейок,
не має значення, оскільки за остаточні
беруть середні перевищення, що тільки
підтверджує необхідність знати середню
довжину одного метра пари рейок. Для
її визначення на горизонтально
розташовану рейку встановлюють
контрольну лінійку і визначають довжини
інтервалів 1-10 (0,9 м), 10-20 (1 м), 20-29 (0,9 м) на
чорній стороні та 48-57 (0,9 м), 57-67 (1 м), 67-76
(0,9 м) на червоній стороні. Отже, на одній
рейці комплекту вимірюють фактичну
довжину 5,6 м рейки, а для комплекту -
11,2 м.
Кожний
інтервал вимірюють у прямому, а потім
- у зворотному напрямках. Під час
зворотних вимірювань лінійку повертають
на 180°. Вимірювання окремого інтервалу
(наприклад, 1-10) складається з подвійних
відліків кінців лінійки. Спочатку
беруть відлік лівого кінця (Л), а потім
правого (П). Перед
51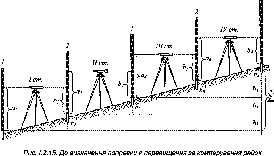
-Ь2)
+ (а4-Ьз)
+ (аі-b4). (1.2.17)
другим
вимірюванням кожного інтервалу
контрольну лінійку дещо зміщують.
Різниці подвійних вимірювань довжин
інтервалів не повинні перевищувати ОД
мм. Якщо отримано більші розходження,
тоді лінійку зміщують ще раз і повторюють
вимірювання. Грубі відліки викреслюють,
а з двох залишених беруть середнє. Перед
початком, а також у кінці вимірювання
на кожній стороні рейки беруть відліки
термометра і записують температуру
контрольної лінійки. У табл. 1.2.5 подано
приклад компарування чорної сторони
однієї дерев’яної рейки. Цифрами в
дужках показано послідовність відліків
та обчислень під час вимірювання
інтервалу 1-10. У виміряні довжини
інтервалів вводять поправки за довжину
лінійки та приведення довжини лінійки
до температури компарування рейки.
Нехай компарування рейки виконували
за середньої температури лінійки 8,65
°С. Тоді згідно з рівнянням лінійки
температурна поправка дорівнюватиме:
А/, =
0,01 + 0,018 мм • (t
-
16,8 °С) = 0,01 + 0,018 мм + (8,65 - 16,8 °С) =
=
0,01 мм-0,147 мм = -0,137 мм~-0,14 мм.
16,8
°С - це температура, під час якої визначали
довжину контрольної лінійки.
Ця
поправка (- 0,14 мм) припадає на 1 м. На
інтервалі 0,9 м поправка дорівнюватиме:
-
0,14 мм • 0,9 = - 0,126 мм 0,13 мм.
Коли
досліджують комплект рейок (дві рейки),
тоді таблиць, аналогічних до табл.
1.2.5, буде чотири.
Нехай
середня довжина одного метра комплекту
рейок дорівнює 1000,08 мм, а виміряне
перевищення в ході дорівнює +50,146 м.
Виникає запитання: як ввести у виміряне
перевищення поправку за компарування
рейок? Для вирішення цього питання
необхідно, по-перше, знайти знак поправки
(плюс чи мінус), а по-друге, її абсолютне
значення.
Для
визначення знака будемо міркувати так:
наш метр, яким ми вимірюємо перевищення,
довший за звичайний. Коли ж ми ним
вимірюємо перевищення, то вважаємо,
що він правильний, тобто має 1000 мм, і
виміряне перевищення знайдене саме
з такого розрахунку. Насправді у кожному
виміряному метрі перевищення становить
не 1000 мм, а 1000,08 мм. Тому фактичне
перевищення більше ніж виміряне.
52Висновок:
Поправка повинна бути додатною (зі
знаком плюс). Того самого висновку можна
дійти ще й з таких міркувань: наш метр,
оскільки він довший за звичайний, у
якомусь великому перевищенні вкладеться
меншу кількість разів, ніж звичайний,
і тому ним ми отримаємо занижений
результат. Щоб цей результат виправити,
потрібно поправку додати.
Інтервали рейки |
Відліки лінійки, мм |
П-Л, мм |
Середнє П-Л, мм |
Поправка за довжину лінійки та темп., мм |
Довжина інтервалі в рейки, мм |
||
л |
п |
||||||
поч. t = +8,6 °С (1) |
|||||||
1 10 |
0,00 (2) |
900,14(3) |
900,14(6) |
900,12(8) |
-0,13 (9) |
899,99 (10) |
|
0,44 (4) |
900,54 (5) |
900,10(7) |
|||||
10-20 |
0,10 |
1000,24 |
1000,14 |
1000,17 |
-0,14 |
1000,03 |
|
0,36 |
1000,56 |
1000,20 |
|||||
20 29 |
0,08 |
900,06 |
899,98 |
899,96 |
-0,13 |
899,83 |
|
0,30 |
900,24 |
899,94 |
|||||
t = +8,7 °С |
|||||||
29-20 |
0,14 |
900,10 |
899,96 |
899,93 |
-0,13 |
899,80 |
|
0,28 |
900,18 |
899,90 |
|||||
20-10 |
0,00 |
1000,10 |
1000,10 |
1000,12 |
-0,14 |
999,98 |
|
0,50 |
1000,64 |
1000,14 |
|||||
10-1 |
0,12 |
900,22 |
900,10 |
900,11 |
-0,13 |
899,98 |
|
1,36 |
901,48 |
900,12 |
|||||
£ |
3,68 |
11204,50 |
11200,82 |
5600,41 |
-0,80 |
5599,61 |
|
Середня
довжина метрового інтервалу рейки №
2342 чорної сторони дорівнює: 5599,61 / 5,6 =
999,93 мм.
Отже,
якщо середня довжина одного метра рейок
довша за номінал - поправка додатна,
коли ж середня довжина метра коротша
від номіналу - поправка від’ємна.
Вкажемо
ще на повну аналогію зі знаками поправок
за компарування нівелірних рейок та
мірних стрічок. Це й не дивно, оскільки
перевищення - не що інше, як віддаль,
але розташована вертикально.
53
CQ |
|
Відліки рейок |
Різниці відліків |
|||||||
•а .оі О |
«1 |
№ 2481 |
№ 2482 |
№ 2481 |
№ 2482 |
№2481-2482 |
||||
К Он й |
|
чорна |
червона |
чорна |
червона |
червона- чорна |
червона- чорна |
по чор. стороні |
по черв, стороні |
|
|
1 |
1363 |
6150 |
1362 |
6051 |
4787 |
4689 |
+1 |
+99 |
|
І |
2 |
1412 |
6200 |
1411 |
6099 |
4788 |
4688 |
+1 |
+101 |
|
|
3 |
1491 |
6276 |
і 1491 |
6178 |
4785 |
4687 |
0 |
+98 |
|
|
1 |
1409 |
6197 |
1410 |
6099 |
4788 |
4689 |
-1 |
+98 |
|
II |
2 |
1457 |
6246 |
1458 |
6147 |
4789 |
4689 |
-1 |
+99 |
|
|
3 |
1538 |
6325 |
1539 |
6227 |
4787 |
4688 |
-1 |
+98 |
|
|
1 |
1592 |
6379 |
1591 |
6279 |
4787 |
4688 |
+1 |
+100 |
|
III |
2 |
1638 |
6426 |
1636 |
6325 |
4788 |
4689 |
+2 |
+101 |
|
|
3 |
1718 |
6506 |
1717 |
6406 |
4788 |
4689 |
+1 |
+100 |
|
Сума |
13618 |
56705 |
13615 |
55811 |
43087 |
42196 |
+3 |
+894 |
||
Середнє |
1513,1 |
6300,6 |
1512,8 |
6201,2 |
4787,4 |
4688,4 |
+0,3 |
+99,3 |
||
Примітка:
на чорній стороні рейок різниця нулів
+ 0,3 мм, на червоній + 99,3 мм.
54
Для
непарної кількості штативів у ході
вводять поправку, якщо різниця висот
нулів більша за 1 мм. Для парної кількості
штативів ця похибка компенсується.
Крім того, необхідно визначити, чи
збігається площина п’ятки рейки з
початком нульової поділки чорної
сторони рейки. Це визначення виконують
за допомогою контрольної лінійки,
вимірюючи віддаль від площини п’ятки
(підкладини) рейки до першого дециметра
рейки. Для зручності відрахування до
п’ятки рейки прикладають лезо бритви.
Розходження не повинне перевищувати
0,5 мм.
/.2.7.
Визначення
ціни поділки циліндричного рівня та
збільшення зорової труби за допомогою
рейки
Перед
нівелюванням III або IV класів виконавець
повинен упевнитися, що вибраний нівелір
придатний для такого нівелювання. Для
цього необхідно визначити ціну поділки
циліндричного рівня та збільшення
зорової труби. Ці два параметри найкраще
характеризують точність нівелірів.
Найпростіші і достатньо точні визначення
цих параметрів нівеліра можуть бути
зроблені за допомогою рейки.
Встановимо
на майже горизонтальній площині нівелір
та рейку на віддалі ~ 50 м і виміряємо цю
віддаль з точністю 1-2 см.
Поділкам
рівня праворуч відносно нуль-пункту
допишемо знак “+”, а ліворуч - Елеваційним
гвинтом перемістимо бульбашку праворуч
на
максимально
можливу кількість поділок. Візирна
вісь труби відхилиться вверх від майже
горизонтального стану. Візьмемо відліки
шкали рівня лівого й правого країв
бульбашки. На рис. 1.2.16, а: +5,0 і +10,0. Середній
відлік +7,5 поділок. Відразу ж візьмемо
відлік рейки
Між
двома розташуваннями візирної осі
утворився вертикальний кут а (рис.
1.2.16, в), а середина бульбашки переміститься
на
Ціною
поділки циліндричного рівня т називають
вертикальний кут, на який нахилилася
візирна вісь приладу, якщо середина
бульбашки перемістилася на одну поділку
рівня.
55ах.
Тепер, повертаючи елеваційний гвинт у
протилежний бік, перемістимо бульбашку
максимально можливо ліворуч. Коли
бульбашка зупиниться, візьмемо відлік
рейки та відліки країв бульбашки. На
рис. 1.2.16, б: -5,0 і -10,0. Середній відлік:
-7,5. Візьмемо відлік рейки а2.п
поділок. У нашому прикладі п
=
15.
радіусом
|
|
|
Тому |
|
|
ЗВІДКИ |
||
|
|
(1.2.20) |
56
Підставимо
значення а' з (1.2.20) в (1.2.19). Отримаємо:
■ґЖ.
Sn
(1.2.21)
Якщо
залишити h
у
міліметрах, a
S
-
у метрах, то для збереження рівності
потрібно значення р* = 206265" зменшити
в 1000 разів. Матимемо: р* = 206,265" « 206".
Тоді формула (1.2.21) набуде робочого
вигляду:
. 206-А
т =
S
•
п
(1.2.22)
Як
видно з (1.2.22), для визначення необхідно
знати, що h
= ax
-а2,
п
- кількість поділок, на які перемістилась
середина бульбашки під час нахилу труби
та S
-
віддаль від нівеліра до рейки. Формула
(1.2.22) достатньо точна. Кутовим
збільшенням зорової труби Г
називають відношення:
Г = £*- = —, (1.2.23)
foK ®
де
fo6
-
фокусна віддаль об’єктива; fOK
-
фокусна віддаль окуляра; со' - кут, під
яким видно зображення предмета в трубі;
со- кут, під яким видно предмет неозброєним
оком, який розташований у головній
точці об’єктива (в задньому фокусі).
Оскільки
око спостерігача розташоване не в
головній точці об’єктива, а дещо позаду
окуляра, тоді предмет буде видно під
кутом щ
, іншим, ніж со.
Величину Гв називають видимим збільшенням зорової труби:
Гв=
— . (1.2.24)
“і
У геодезичній практиці найчастіше потрібно знати видиме збільшення труби. Метод визначення видимого збільшення труби запропонував Галілей. Суть методу полягає в тому, що одночасно розглядають рейку, одним оком у трубі, а другим - безпосередньо (без труби). У трубу бачимо збільшені поділки, а без труби - натуральні.
Рейку встановлюють на віддалі 5-10 м від нівеліра. Розглядають в трубу, наприклад, п’ять сантиметрових поділок рейки (див. рис. 1.2.17).
Уявно продовжимо верхній та нижній краї вибраного п’ятисантимет- рового відрізка на рейці, який бачимо лівим оком, тобто за межі поля зору труби, до перетину з рейкою, яку одночасно бачимо правим оком, і беремо два відліки рейки з точністю хоча б 0,5 см. Нехай нижній відлік рейки 50,0 см, а верхній - 200,5 см. Різниця відліків: 200,5 - 50,0 = 150,5 см.
57
Рис.
1.2.17. До визначення видимого
збільшення
зорової труби за допомогою
рейки
Тоді
видиме збільшення труби становитиме:
Гх
=1^ = 30,Iх
-30х.
5
Такий
метод визначення видимого збільшення
труби доволі простий, однак вимагає
від спостерігача деякого навику
одночасно розглядати одним оком рейку,
а другим - її зображення в полі зору
труби. Однак таким навиком спостерігач
оволодіє після декількох спроб.
Зорові
труби з внутрішнім фокусуванням мають
постійну довжину. Спостерігач під час
перефокусування повертає кремальєрний
гвинт. Фокусу- вальна лінза, що закріплена
в спеціальній трубочці, повинна рухатися
вздовж оптичної осі так, щоб лінія
візування залишалась незмінною.
Насправді завжди є деякий люфт трубочки,
що рухається разом із лінзою. У результаті
лінза буде мати поперечні переміщення
в трубі. Це викликатиме зміни відліків
рейки. Звернемось до рис. 1.2.18.
Нехай
під час фокусування труби на рейку, що
займає стан/, оптичні центри
58
2.8. Дослідження руху фокусувальної лінзи
Ох
і 02
об’єктива Ц
і фокусувальної лінзи L2,
а
також точка перетину ниток сітки К
розміщені на одній прямій. Тоді ми
зробимо правильний відлік, якому
відповідає точка N
на
рейці. Нехай рейка перемістилась вздовж
лінії
візування
в стан
Рейка,
роз.
І Рейка, роз. II
Безпосередньо
з рисунка, враховуючи подібність
трикутників ВКК'
t?lB02F2
,
можна записати:
е
У-ІЯ-е)
х
~/2
Тоді
Нехай
параметри труби 134,4 мм.
~Ji
59II
так, що точка N
залишилась
на ліні\КОх.
Зрозуміло, що відлік повинен залишитися
незмінним. Але зі зміною розташування
рейки ми повинні змінити стан лінзи 1^
для того, щоб знову сфокусувати трубу.
Якщо оптичний центр 02
лінзи залишиться на лінії КОх,
тоді відлік рейки справді не зміниться.
Але, якщо лінза переміститься у стан
0'2
так, що її оптичний центр відійде від
лінії КОх
на віддаль х, тоді промінь NOx
В,
що виходить з точки N
рейки,
заломиться в точці В
і відхилиться на кут 8, а в площині сітки
ниток точкам, яка є зображенням точки
N
рейки,
переміститься в точку АГ'. Зображення,
отже, зміститься на відрізок у. Відрізок
у
пропорційний до похибки відліку рейки
ВІД
поперечного
переміщення ЛІНЗИ
Iq
.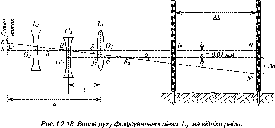
у
= ^-^х. (1.2.25)q
—
330 мм; Fx=
298
мм; F2=
-1000
мм;
Тоді
матимемо:
330-134,4 1
у
= х~
— х.
1000 5
Це
означає, що вплив поперечного переміщення
лінзи в такій зоровій трубі із внутрішнім
фокусуванням зменшиться у 5 разів. На
жаль,
Знайдемо
похибку відліку рейки, якщо для кута 8
віддаль до рейки змінилася на
рейці
точку
Aa
= ^-AS. (1.2.26)
Р
Розрахуємо
кут 8*. Задамося деяким незначним
поперечним зсувом фокусувальної лінзи.
Нехай
ВКК'
8'
= рд
У
(д-е)
(1.2.27)
Для
заданих значень параметрів:
у
_ 0,002-206265'_2
Тоді
за (1.2.26) для
А
2,1-10000
А1
206265
В
інженерній практиці, наприклад, для
передавання перевищень через широкі
ріки, різниця плечей може бути значною.
Для
Отже,
для визначення якості нівеліра необхідно
дослідити правильність руху фокусувальної
лінзи. Для дослідження вибирають рівну
ділянку площею ~ 60x60
м
з однорідною поверхнею і твердим
ґрунтом. На краю ділянки, у точці С,
забивають кілок. З точки
60х-
змінна величина і не може бути
прогнозована. Навіть в одному і тому
самому нівелірі, залежно від стану та
якості мастила, зношення деталей від
тертя, значення х
змінюється.AS.
Спроектуємо точку К'
на рейку, що займає розташування 11.
Для
цього продовжимо промінь K'BF2
до
перетину
з рейкою. Отримаємо наN'.
Відрізок А а
практично є цією похибкою (х< 0,1 мм).
Безпосередньо з рисунка видно, що:х
=0,01 мм. Тоді у
= 0,002 мм. З трикутникаґ
195-6AS
=
10 м знайдемо:Аа
= =
0,1 мм.AS
=
50 м, Аа
=
0,5 мм. Проте не виключено, що х
>
0,01 мм.С
(див. рис. 1.2.19) за допомогою троса описують
кола радіусом 25-50 м, починаючи від точки
А,
що також закріплюється. Радіуси вибирають
залежно від плечей нівелювання, які
будуть встановлюватися для цього
нівеліра. Використовуючи віддалемір
нівеліра й
рейку,
відкладають віддалі
Дослідження
необхідно виконувати в похмуру погоду,
під час незначного вітру, спокійних
або малопомітних коливань зображень,
попередньо позбувшись значного
значення кута
Нівелір
встановлюють у точці С, приводять його
в робочий стан, послідовно встановлюють
рейку (бажано користуватися однією
рейкою) у точках 7, 2, ..., 7 і беруть відліки
чорної та червоної сторін (І півприйом).
Потім йдуть із рейкою у зворотному
напрямку (II півприйом). Під час
спостереження з точки С фокусування
труби не змінюють. Це перший прийом.
Встановлюють нівелір у точці
Знову
встановлюють нівелір у точці С і
виконують другий прийом (два півприйоми).
В результаті по рейці, яку встановлюють
відповідно в точках 7, 2, ..., 7 під час
нівелювання, з точки С буде виконано
по 7 відліків. Так само 7 відліків кожної
рейки буде виконано під час нівелювання
з точки
10
м
7
50
метрів
Рис.
1.2.19. Схема розташування нівеліра -
. w •
і
рейок -
61Ах,
Л2,
Л3,...,
А7
, що відповідно дорівнюють 10, 20, ..., 70 м.
У точках 7,2,..., 7 забивають костилі або
кілки з цвяхами.і.
Проте деякий залишковий кут і
буде завжди.А,
а рейку в точках 7, 2, ..., 7, знову відраховують
обидві сторони рейок. Труба перефокусовується
зі зміною довжини плечей. Потрібно
виконати не менше від двох прийомів,
змінюючи горизонт нівеліра під час
кожного прийому.А.

№ точок |
Середні відліки, мм |
Назва перевищення |
Середні
перевищення |
1 |
2951,60 |
|
|
|
|
1-2 |
-8,20 |
2 |
2959,80 |
|
|
|
|
1-3 |
-39,65 |
3 |
2991,25 |
|
|
|
|
1-4 |
+10,25 |
4 |
2941,35 |
|
|
|
|
1-5 |
+87,75 |
5 |
2863,85 |
|
|
|
|
1-6 |
+95,95 |
6 |
2855,65 |
|
|
|
|
1-7 |
+53,10 |
7 |
2898,50 |
|
|
62
№ точок |
Середні відліки, мм |
Поправки
за кривину Землі та рефракцію |
Виправлені відліки, мм |
Назва переви щень |
Виправлені перевищен ня —А/, мм |
1 |
2912,55 |
+0,007 |
2912,557 |
|
|
|
|
|
|
1-2 |
-9,02 |
2 |
2921,55 |
, +0,027 |
2921,577 |
|
|
|
|
|
|
1-3 |
-40,85 |
3 |
2953,35 |
+0,061 |
2953,411 |
|
|
|
|
|
|
1-4 |
+8,30 |
4 |
2904,15 |
+0,106 |
2904,256 |
|
|
|
|
|
|
1-5 |
+85,09 |
5 |
2827,30 |
+0,166 |
2827,466 |
|
|
|
|
|
|
1-6 |
+92,52 |
6 |
2819,80 |
+0,242 |
2820,042 |
|
|
|
|
|
|
1-7 |
+49,13 |
7 |
2863,10 |
+0,324 |
2863,424 |
|
|
Звернемо
увагу читача на те, що під час спостереження
з точки С похибки відліків, які викликані
вищеназваними чотирма джерелами,
однаково впливають на всі відліки і
тому не впливають на перевищення.
Вважаємо за доцільне зазначити, що на
рівній ділянці у разі рівних плечей і
за однакового покриття поверхні впливи
рефракції на відліки під час похмурої
погоди також будуть однаковими за
проміжок часу до 1 години. Тому перевищення,
отримані нівелюванням із точки С ,
будуть достатньо точними. Вони подані
в колонці 4 табл. 1.2.7.
Під
час спостереження з точки
2
V
де
63А,
у зв’язку з нерівністю плечей, відліки
також будуть отримані з названими
похибками, але різними за величиною.
Тому їх потрібно виключити перед
обчисленням перевищень. Спочатку
виключимо вплив кривини Землі та
рефракції. Для виключення впливу кривини
Землі К
користуються формулоюК
= , (1.2.28)R3
-
радіус Землі; S-
довжина
плеча. Складніше виключити
рефракцію.
Оскільки спостереження
виконують під час нормального стану
атмосфери (за
Введемо позначення:
|
(1.2.32) |
р Тоді (1.2.31) набуде вигляду:
Д/г,-
= |
(1.2.33) |
Але ДА, =Л, -hf. |
(1.2.34) |
Тому рівняння похибок матимуть вигляд:
|
(1.2.35) |
Рівнянь
похибок буде стільки, скільки перевищень
(у нашому випадку шість).
Як
відомо з методу найменших квадратів,
розв’язання рівнянь похибок за
додаткової умови
64[VjVj]
=
min
приводить
до нормальних рівнянь, яких буде стільки,
скільки невідомих. Обчислення Ahj
та
коефіцієнтів нормальних рівнянь
подано у табл. 1.2.9.
Назва перевищення |
Точні
перевищення
|
Виправлені перевищення А/, мм |
ММ |
РІЗНИЦІ ДОВЖИН
плечей
|
д^ |
|
1-2 |
-8,20 |
-9,02 |
-0,82 |
10 |
100 |
-8,2 |
1-3 |
- 39,65 |
-40,85 |
-1,20 |
20 |
400 |
-24,0 |
1^1 |
+ 10,25 |
+ 8,30 |
-1,95 |
зо |
900 |
-58,5 |
1-5 |
+ 87,75 |
+ 85,09 |
-2,66 |
40 |
1600 |
-106,4 |
1-6 |
+ 95,95 |
+ 92,52 |
-3,43 |
50 |
2500 |
-171,5 |
1-7 |
+ 53,10 |
+ 49,13 |
-3,97 |
60 |
3600 |
-238,2 |
У
цьому випадку буде одне рівняння, яке
запишеться так:
[AS',A5i]/:
-
[Д5,.Д/% ] = 0. (1-2.36)
З рівняння
знайдемо невідомий коефіцієнт
к.
[ASjASj
]
Обчислимо
міліметрах,
а Д5, -у метрах, тоді значення
За
(1.2.32) знайдемо найімовірніше значення
кута
З’ясувалось,
що кут
допустимого
(
знайти
ці похибки
результати
вимірювання перевищень, оскільки інші
істотні похибки виключені.
65[AS?
]
= 9100,[Ahj
AS і
] =
-606,80.К
= ——=
-0,06668. Оскільки під час обчислення ДА,
у 9100 wК
збільшене у 1000 разів.і*
= Кр’
• 10_3.і*
= 13,75", тобто доволі значний, хоча й
близький доідоп-
Ю")- Залишається на підставі рівняння
похибок (1.2.35)Vt.
Вони характеризують вплив рухів
фокусувальної лінзи на
Назва переви щення |
Різниця довжин плечей AS, мм |
Aht, мм |
KASj |
У, |
Оцінка точності |
1-2 |
10 |
-0,82 |
-0,67 |
+ 0,15 |
}[Щ] тф~Іп-1 |
1-3 |
20 |
- 1,20 |
-1,33 |
-0,13 |
|
1^1 |
зо |
-1,95 |
-2,00 |
-0,05 |
|
1-5 |
40 |
-2,66 |
-2,67 |
-0,01 |
|
1-6 |
50 |
-3,43 |
-3,33 |
+ 0,10 |
Шф =0,10 miv |
1-7 |
60 |
-3,97 |
-4,00 |
-0,03 |
Зрозуміло,
що в окремих нівелірах похибки, пов’язані
з перефокусу- ванням труб, можуть досягти
значних величин (цілих мм), і вони будуть
збільшуватися залежно від збільшення
різниці довжин плечей нівелювання.
66
Під
час нівелювання III класу (а також IV)
нівелірні рейки встановлюють на репери
та перехідні точки. Як перехідні точки
зазвичай використовують так звані
“башмаки”. Башмак - це невелика металева
плита зі сферичним виступом. На цей
виступ і встановлюють рейку. Інколи
використовують башмаки із двома
виступами. Такі башмаки дають змогу
виконувати нівелювання односторонніми
рейками без зміни горизонту нівеліра.
Повна
бригада нівелювання складається із
семи осіб: виконавець - спостерігач;
помічник - заповнює польовий журнал;
два рейкарі; двоє робітників, що виконують
трасування - розмічають за допомогою
троса (стрічки) місця встановлення
нівеліра та башмаків; робітник, що
переносить і встановлює над нівеліром
топографічну парасолю. Бригада може
бути скорочена на 2-3 особи, якщо рейкарі,
користуючись “ковильком” (сажнем),
самі виконують трасування, а помічник
буде переносити і встановлювати
парасолю.
Нівелювання
виконують ізсередини, нормальну довжину
плечей (віддалі від нівеліра до рейки)
під час нівелювання III кл - 75 м; у разі
спокійних зображень поділок рейок
та збільшення
Розглянемо
послідовність роботи на окремій станції
нівелювання способом “трьох ниток”.
Приводять
нівелір у робочий стан, встановивши
бульбашку сферичного рівня за
допомогою підіймальних гвинтів у
нуль-пункт.
Наводять
трубу на чорну сторону задньої рейки
та елеваційним гвинтом контактують
зображення кінців бульбашки циліндричного
рівня, а після цього беруть три відліки
рейки, користуючись середньою, верхньою
та нижньою нитками сітки.
Наводять
трубу на чорну сторону передньої рейки
й виконують усі дії, вказані у п. 2.
Подають
команду рейковикам: “червоні”.
Рейковики повертають червоні сторони
рейок до нівеліра.
67Виконання нівелювання III та IV класів. Похибки та точність нівелювання
Послідовність роботи на станції під час нівелювання III класу
Гх
>
35 крат допускають 100 м. Обов’язковим
є захист
нівеліра парасолею
від прямих променів сонця, які неоднорідно
нагрівають різні частини нівеліра, що
викликає значні зміни кута і
за час роботи на станції.
Уточнюють
наведення труби на червону сторону
передньої рейки, контактують зображення
кінців бульбашки циліндричного рівня,
беруть відлік рейки, користуючись
тільки середньою ниткою.
Наводять
трубу на червону сторону задньої рейки
й виконують дії, вказані в п. 5.
Під
час роботи нівеліром із компенсатором
відліки беруть у наведеній вище
послідовності, одразу після приведення
нівеліра в робочий стан за допомогою
сферичного рівня. Результати спостережень
на станції записують у журнал установленої
форми або вводять у пам’ять
запам’ятовувального пристрою.
Приклад записів у журналі подано в
табл. 1.3.1.
Промінь
не повинен проходити над землею нижче
за ЗО см (мінімальний відлік рейки у
міліметрах - 0300). Рейки встановлюють
прямовисно за допомогою виска або
рівня, який кріпиться до них. Перевищення
вираховують тільки за відліками
середньої нитки. Відліки віддалемірних
ниток використовують для визначення
довжини ходу та нерівності плечей
нівелювання. На кожній станції отримують
два перевищення: за чорними і червоними
сторонами рейок. Розходження між
перевищеннями не повинні перевищувати
3 мм. Це перший контроль роботи на
станції. Другий контроль: половина суми
відліків, одержана відцалемірними
нитками, не повинна відрізнятися від
відліку середньою ниткою більше ніж
на 3 мм. Якщо ці контролі виконуються,
переходять на наступну станцію. Місця
встановлення нівеліра та башмаків
розмічають робітники, що виконують
трасування. Передній рейкар залишається
на своєму місці й стає заднім рейкарем;
нівелір переносять вперед за ходом;
задній рейкар іде до нової точки
встановлення нівеліра і проходить від
неї віддаль, яка дорівнює віддалі до
задньої рейки. Якщо бригада працює без
робітників, що виконують трасування,
тоді задній рейкар вимірює “ковильком”
кількість метрів від рейки, що стає
задньою, до точки нового встановлення
нівеліра й таку саму кількість метрів
відкладає “ковильком” вперед за ходом
від нівеліра та встановлює передній
башмак і рейку.
Нерівність
плечей допускають до двох метрів (20
поділок). У нашому прикладі, див. дія
(13) - дріб +14/+14, чисельник означає
нерівність плечей на цій станції - 1,4
м; знаменник - накопичення нерівностей.
Оскільки
в журналі подана перша станція, то й
накопичення нерівностей дорівнює +14
(1,4 м). Якщо, наприклад, на другій станції
нерівність плечей становитиме +8
поділок (0,8 м), дріб набуде вигляду
+8/+22. Якщо накопичення перевищує 5 м (50
поділок), тоді навмисне нівелір
установлюють дещо ближче до задньої
або передньої рейок так, щоб за декілька
станцій позбутися недопустимого
накопичення.
68
Номери штатива та рейок |
Зарис прив’язування |
Спостереження відцалемірних ниток |
Контрольні перевищення |
Спостереження по середній нитці |
Середнє перевищення, мм |
|||
задня рейка |
передня рейка |
задня рейка |
передня рейка |
переви щення |
||||
1 1-2 |
з*‘“" № vaxa z?r Ґрунт, pen. № 5540 |
1572 (2) 1904 (3) 352 (9) |
1812 (5) 2130 (6) 318(10) |
-240 (11) -226 (12) +14/14 (13) |
Чр 1739(1) Чв6430 (8) 4691 (16) |
1971 (4) 6761 (7) 4790(17) |
-232
(15) +99 (18) |
-231,5 (19) |
Примітка:
цифри в круглих дужках вказують на
послідовність відліків та обчислень
на станції; Чр - чорна, Чв - червона
сторона рейки.
Нівелювання
III класу виконують у прямому й зворотному
напрямах,
Після
перерви ще раз виконують нівелювання
на цих двох станціях. Якщо нові перевищення
не відрізняються від попередніх більше
ніж на 3 мм, обчислюють і приймають
середні перевищення й продовжують хід.
В іншому разі нівелювання повторяють,
починаючи від найближчого репера.
Нівелювання
за безхмарного неба виконують під час
спокійних і незначних коливань зображень
поділок рейок: вранці, через годину
після сходу Сонця, і до 9-10 години;
увечері, після 15-16 години, і закінчують
за годину до заходу Сонця. Під час
хмарного неба період нівелювання можна
розширити.
69секціями.
Секцією називають частину ходу між
суміжними нівелірними знаками.
Перерви в нівелюванні бажано робити,
пройшовши секцію (прямо та назад). Якщо
виникає необхідність перервати роботу
на деякий час, не дійшовши ходом до
репера, тоді замість башмаків забивають
у дно ям завглибшки 0,3 м три костилі або
кілки; в останні вбивають цвяхи зі
сферичними головками; знаходять
перевищення на двох станціях - між
першим і другим колом та між другим і
третім. Кілки маскують, прикривши
дерном.
Повна
бригада нівелювання IV класу - 5 осіб:
виконавець, його помічник, два рейковики,
робітник для перенесення й встановлення
парасолі над нівеліром. Мінімальна
бригада - 3 особи. Довжину плечей вимірюють
кроками. Нормальна довжина плечей 100
м. Якщо збільшення труби нівеліра більше
за 30х
та відсутні коливання зображень,
дозволено збільшувати довжину плечей
до 150 м; накопичення нерівностей - 10 м.
Довжину плечей можна вимірювати
віддалеміром.
Під
час нівелювання IV класу відліки червоних
і чорних сторін рейок роблять середньою
ниткою, а для визначення віддалі від
нівеліра до рейки беруть відлік ще й
верхньою віддалемірною ниткою. Висота
променя над підстилаючою поверхнею
повинна бути не меншою за 0,2
м.
Послідовність
спостережень на станції під час
нівелювання IV класу
Беруть
відлік середньої і верхньої віддалемірних
ниток чорної сторони задньої рейки
під час контактування зображення
кінців бульбашки циліндричного
рівня.
Дії
ті самі, що і в п. 1, але чорної сторони
передньої рейки.
Подають
команду рейковикам: “червоні”.
Відлік
тільки середньою ниткою червоної
сторони передньої рейки під час
контактування зображень кінців
бульбашки циліндричного рівня.
Дії
ті самі, що і в п. 4, але червоної сторони
задньої рейки.
Під
час роботи нівеліром із компенсатором
беруть відліки рейок одразу після
приведення приладу в робочий стан
сферичним рівнем у тій самій послідовності.
Контроль:
розходження перевищень, визначених по
чорній та червоній сторонах рейок,
допускають до 5 мм, з урахуванням різниці
висот нулів пари рейок.
Для
розходжень, більших за 5 мм, спостереження
повторюють, попередньо змінивши
висоту нівеліра не менше ніж на 3 см.
Під
час спостережень на станції нівелір
захищають від сонячних променів.
70Послідовність роботи на станції під час нівелювання IV класу
Номер штатива і рейок |
Віддалі до задньої та передньої рейок |
Відліки рейок |
Перевищення, мм |
Середні перевищення, мм |
||
Задня |
Передня |
|||||
і |
375 (7) 372 (8) |
1185 (1, верх.) 1560 (2, сер.) 6247 (6, сер.) 4687 (9) |
1058 (3, верх.) 1430 (4, сер.) 6217 (5, сер.) 4787 (10) |
+130(11) +30(12) +100(14) |
+130(13) |
|
ґрунт, репер №606 1-2 |
||||||
Примітка: цифри
в дужках пояснюють послідовність дій;
(1,
верх.), (З, верх.) - відліки верхньою
ниткою; (2 сер.), (4, сер.) - відліки середньою
ниткою;
=
(2, сер.)-(1, верх.);
=
(4, сер.) - (3, верх.).
Усі
похибки можна розділити на три групи:
Приладні
або інструментальні похибки.
Похибки,
викликані
зовнішнім середовищем.
Особисті
похибки спостерігача.
Розглянемо
окремо кожну групу цих похибок.
Приладні
або інструментальні похибки.
Неточне
виконання головної умови для нівелірів
(непаралельність візирної осі та осі
циліндричного рівня).
Як
видно з рис. 1.3.1, навіть за умови, що за
час роботи на станції кут
різні
х
Тому
помилкове
на Дх. Нехай:
Ах
= хх
- х2;
Дх
_ і*
~AS~p*‘
Дх
=
(1.3.1)
71
Похибки нівелювання. Їхнє зменшення та усунення
і
не змінюється, для нерівних плечей (S)
Ф
S2),
похибки у відліках рейки будутьі
Фх2,
а
перевищення AS
—-
*Sj
5*2
> тоді:AS
і*
Р*
Рис.
1.3.1. Вплив невиконання головної умови
нівеліра
на результати нівелювання
Інструкція
допускає
2000-10*
206265*
=
0,1
мм.
Це
в 15 разів менше за допустиме розходження
між перевищеннями на станції (±3 мм).
Отже, завдяки обмеженню інструкцією
нерівності плечей та кута /*, неточне
виконання головної умови нівелірами
не може внести в перевищення на станції
похибки, більшої за 0,2 мм. Ця похибка є
випадковою.
Нагадаємо,
що нерівність плечей викликає необхідність
перефокусування зорової труби та
урахування кривини Землі. Вплив цих
факторів на точність нівелювання
розглядався раніше.
Похибки
поділок рейки.
Як
відомо, максимальні похибки дециметрових
поділок рейок, які допускає інструкція,
не повинні перевищувати 0,5 мм і 1,0 мм
відповідно для рейок, які використовують
для нівелювання III та IV класів. Що
стосується різниці висот нулів рейок,
то цей недолік рейок компенсується
парною кількістю штативів у секції
нівелірного ходу.
Похибки
встановлення рейки у вертикальне
(прямовисне) положення.
На
рис. 1.3.2 показано, як непрямовисність
рейки впливає на відлік.
72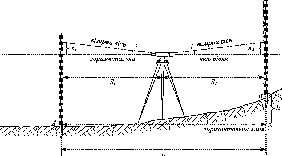
AS
=
2 м, а Ґ
=
10". Для цих значень на основі (1.3.1)
маємо:
Якщо
рейка прямовисна, відлік 60
буде мінімальним. Для нахилу рейки у
бік нівеліра на кут є або в протилежний
бік на такий самий кут є, відліки
збільшаться і дорівнюватимуть 6.
Похибка відліку Д6
= 6
- 60.
Безпосередньо з рисунка видно, що:
A
6
= 6-6-
cos
є
= 6(1 - cos
є)
= 26 • sin
2
£
2
(1.3.2)
Враховуючи,
що кут є - малий isiti—
=
—, отримаємо:
Д6
=
6.
(1.3.3)
Для
є = ЗО' 6
= 3000 мм, Д6
= 0,1 мм. Для Є
=
1° Д6
= 0,5 мм.
Отже,
рейку необхідно утримувати у прямовисному
положенні з похибкою, яка не більша
за 1°.
З такою точністю встановити рейку
вертикально, на око, не вдається. Тому
для зменшення цієї похибки до рейки
прикріпляють сферичний рівень із
ціною поділки 30' або висок на нитці
завдовжки близько 1
м.
Похибки,
викликані прогином
(викривленням!
рейки.
У
разі неправильного зберігання рейки
може виникнути викривлення, і вона
матиме стрілку прогину / (рис. 1.3.3). Нехай
рейка є дугою АСВ радіусом
73

R.
Довжина хорди - 2х.
А
Рис.
1.3.3. До визначення впливу викривлення
рейки
на зміну її довжини
Різниця
довжини дуги / і хорди
А/
= 7
-2х. (1.3.4)
Або
А/ = / -
розкладу:
Д/
= / -
о
7
і
Оскільки
з рисунка а =—, то, підставивши значення
виразу в попе-
2R
редній,
одержимо:
Отже,
Д/
= /
Д/
=
/
/3
^
2Л 48Л3
Р
24R
,2
‘
(1.3.5)
Виразимо
і? через стрілку прогину / . Із трикутника
Я/VO
запишемо:
Із
трикутника
R2
=х2
+(R-
/)2.
2 /.2
і
х2
+f
Т2
Додавши
два останні рівняння, виключимо х, і
після незначних перетворень отримаємо:
Д
= —. 8/
(1.3.6)
74
2х
становить:2R
sin а.
Розкладемо sin
а
в ряд, зберігши два члени2R(a
-
■%•).-2RCBN:
Підставивши
значення
о
f2
Д/
= --4^. (1.3.7)
З
/
Розв’язавши
(1.3.7) відносно /, отримаємо формулу, на
підставі якої визначимо допустиму
стрілку прогину
О-3-8)
Нехай
А
Похибка
встановлення візирної
осі в горизонтальний
стан. Встановлюють
середину бульбашки циліндричного
рівня в нуль-пункт із граничною помилкою
Ця
формула підтверджена багаторічним
досвідом.
Для
може
бути зменшена (якщо не мати на увазі
скорочення плечей). Тільки застосування
контактного рівня дещо зменшує цю
похибку. До вивчення впливу цієї похибки
на результати нівелювання ми ще
повернемося.
Похибки,
викликані зовнішнім середовищем.
Похибки,
викликані вертикальною рефракцією.
Скористаємося
відомою формулою поправки за вертикальну
рефракцію у відлік під час нестійкої
стратифікації повітря [27]:
г
= 0,962 10-3
~--52
-39,425 10-3
Перший
член у правій частині - нормальна частина
рефракції. Другий член - аномальна
рефракція. Зауважимо, що лінійна
рефракція під час гео-
2
Р
метричного
нівелювання пропорційна до
Т2
можна
вважати сталою
величиною,
яка для стандартної атмосфери (тиск
_Р
986
2882
=
0,0119.
75R
із
(1.3.6) в (1.3.5), матимемо:fdon
залежно
від допустимої зміни довжини рейки
ДІ:Ідо„
=0,1 мм. Для довжини рейки / = 3000 мм, одержимо:fdon
=
10>6
ММ-
т",
що визначається за формулоют'=
0,15-т'. (1.3.9)х”
= ЗО"; Шу
= 4,5". Похибка - випадкова, але одна з
найбільших, і не
—
S2
•
4aHje.cep\r
-умм).S
.
Дріб —Р
=
986 ГПа (740 мм рт. ст.), абсолютна температура
Т
= 288 °К (/= 15 °С) буде дорівнювати:Т2
Перехід
до сталого коефіцієнта не викличе
істотних похибок під час визначення
нівелірної рефракції, однак формули
значно спростяться:
Якщо
поправка за рефракцію у відлік задньої
рейки
Аг
= r3
Як
бачимо, на перевищення впливає
диференційна частина рефракції. Для
рівних плечей
вплив
аномальної рефракції на перевищення
буде компенсуватися. Проте, якщо на
станції нівелювання перевищення 0,2-0,3
м і більше (див. рис. 1.3.4), то
Треба
пам’ятати, що нормальна рефракція
завжди додатна, а аномальна для нестійкої
стратифікації - завжди від’ємна, тобто
зменшує абсолютне значення перевищення,
незалежно від знака перевищення. Тому
для нестійкої стратифікації атмосфери
поправка за аномальну рефракцію -
додатна, а поправка за нормальну
рефракцію - від’ємна.
Максимальні
градієнти на висоті 1 м над підстилаючою
поверхнею (асфальтом) досягають 2 град/м.
Максимальна різниця градієнтів для
різниці середніх висот променя на задню
і передню рейки 1,2
м може досягти
Аг
= 3,35 мм. Проте така різниця градієнтів
можлива тільки над асфальтом о 12-14
годині дня, у разі сильних коливань
зображень поділок рейки. У таких умовах
нівелювання не виконують. У разі
незначних коливань ця різниця становитиме
0,2- 0,4 град/м, тоді Аг = 0,53-1,05 мм. Але й
такий вплив буде максимальним і може
виникати тільки на станціях, де
перевищення 2,4—2,5
м, тобто практично максимальні, для
триметрових рейок. Справді, якщо
мінімальний відлік рейки 0,3 м, тоді для
перевищення в 2,5 м відлік іншої рейки
становитиме 2,8 м.
76г
= 1,141(Г552
- 46,87 • 10_552
• уанесер (1.3.10)г3
, а передньої гп,
то поправка в перевищення на станції
становитиме:-гп
. (1.3.11)S
вплив
нормальної рефракції на перевищення
дорівнюватиме нулеві. На рівнинній
місцевості з однорідною підстилаючою
поверхнею для рівних плечей промінь
на задню і передню рейки буде проходити
на однаковій висоті; тоді середні
вертикальні градієнти температури на
шляху променя на задню і передню рейки
будуть однаковими: Уан^сер3
= Уан.е.сер.п
• За
таких умовУан.е.сер.з
* Уан.е.сер.п
і поправка в перевищення за аномальну
рефракцію може бути обчислена за
формулоюДг
= 46,87 10-552
(уан.е.серз~Усш,.сер.п)- 0
3-12)АУан.е.сер.
=
1.27 град/м. Тоді для плечей завдовжки 75
м гранична похибка
Крім
того, для довжин плечей у 75 м можливий
ухил траси
=
10 мм/км). У наш час на основі турбулентності
атмосфери доведено [15], що для нестійкої
стратифікації градієнти температури
флуктують (коливаються) від
(поділки
рейки) rmax.
Такі максимальні коливання мають
частоту не менше за 1
Гц
(не менше від одного максимального
коливання на секунду).
Виконуючи
нівелювання під час коливань зображень,
спостерігач зауважує, що відлік увесь
час змінюється, оскільки середня нитка
сітки ниток, спроектована на рейку,
коливається. Спостерігач бере відлік
середнього стану нитки. Цьому стану
відповідає градієнт
1+Y*
/
ан.сер
(1.3.13)
Враховуючи,
що уан
тіп
= 0, отримаємо:
_
Удн.шах
І
ан.сер
(1.3.14)
77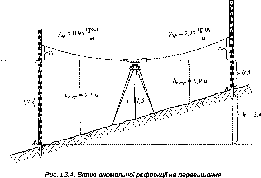
і
становить близько 17 проміле. Уже для
ухилу 2,5 проміле необхідно виконувати
нівелювання плечами завдовжки 50 м. Тоді
диференційна атмосферна рефракція Аг
= 0,23-0,47 мм. Враховуючи, що ця похибка
систематична, на хід завдовжки 1
км (10
таких станцій) накопичення похибок
тільки від цього джерела становитиме
майже половину допустимої нев’язки «
5 мм {fh
доп
Шкл
-Чан.min
~
0
ДО Уан.
max
>
Щ° викликає максимальний розмах коливань
візирної цілі
Цьому
стану відповідає рефракція
Тобто
відлік середнього стану нитки спотворений
середньою рефракцією.
Достатньо
брати відлік максимального верхнього
розташування середньої нитки, який
нитка займає за проміжок часу в 1
секунду не менше ніж один раз. Тоді
відлік буде вільний від аномальної
рефракції. Верхній стан нитки треба
відраховувати, якщо труба нівеліра дає
пряме зображення. Якщо ж труба нівеліра
дає обернене зображення, то треба
відраховувати максимально нижнє
розташування середньої нитки за такий
самий проміжок часу. Оскільки максимальні
амплітуди коливань доволі часті (кожну
секунду), то спостерігач витрачає
стільки само часу на відліки екстремальних
станів нитки, як і на відлік її середнього
положення.
Використовуючи
такий спосіб, можна не тільки позбутися
аномальної рефракції, підвищити точність
нівелювання, але й розширити час,
придатний для нівелювання. Не можна
виконувати нівелювання під час стійкої
стратифікації атмосфери (під час
інверсії), коли температура повітря в
приземних прошарках зростає з висотою.
Вертикальні градієнти температури під
час інверсії - додатні і на висоті 1
м можуть бути значно більшими за 2
град/м.
Інверсія діє вночі, зранку - приблизно
одну годину після сходу Сонця і ввечері,
починаючи, приблизно, за годину до
заходу Сонця. Інструкція нівелювання
забороняє виконувати нівелювання у ці
години зранку та ввечері. Під час
інверсії нормальна й аномальна рефракція
- додатні, їхній сумарний вплив - значний
і важко піддається урахуванню. До того
ж під час інверсії і за тихої (безвітряної)
погоди, коливання зображень рейки
відсутні, так само, як і під час нормальної
стратифікації повітря, коли нормальні
градієнти температури
Похибки,
викликані коливанням зображень поділок
рейки.
Неважко
зрозуміти, що спостерігач бере відліки
рейки під час спокійних зображень її
поділок точніше ніж під час коливання
цих поділок. Проте ці похибки випадкові
і не є такими загрозливими, як систематичні
похибки рефракції.
Численні
експериментальні дослідження показали,
що, наприклад, похибки відліків
інварної рейки мікрометром нівеліра
Н-1, труба якого має збільшення
78rcep=^f-- (1-3.15)унор
= 0,0098 град/м, а уан
= 0.
Г
= 45х,
для довжини плеча 75 м виконують із
середньою квадратичною похибкою: під
час спокійних зображень - 0,092 мм, а під
час максимальних розмахів коливань
rmax
=
2,84 мм (майже 3 мм) - 0,155 мм. Отже,
під
час значних розмахів коливань зображень
похибка відліку зростає у 1,7 раза.
Похибка, викликана коливаннями зображень
поділок рейки, становитиме на 1 км ходу
(10 станцій) ~ 0,5 мм. Одночасно, похибка
за рефракцію на порядок більша - 5 мм.
Саме тому необхідно враховувати
рефракцію, якщо виконується нівелювання
під час коливання зображень рейки.
Враховуючи
рефракцію будь-яким способом, ми, тим
самим, перетворюємо її вплив із
систематичного на випадковий. Якщо
навіть допустити, що випадкові похибки
урахування рефракції становлять 0,25 мм
(удвічі менші за систематичні похибки
рефракції) тоді її вплив буде на 1
км -
25>/Ї0«0,8
мм. Отже, вплив рефракції зменшився
приблизно в 6
разів і перестав бути загрозливим.
Тому можна виконувати нівелювання під
час коливань зображень, тільки якщо
будь-яким методом буде врахована
вертикальна рефракція.
Похибки,
викликані кривиною Землі.
Вплив
кривини Землі на відлік рейки можна
визначити за відомою нам формулою
2
Якщо
нівелювання виконувати з рівними
довжинами плечей, то вплив кривини
Землі на перевищення виключається.
Проте нівелювання виконують не строго
із середини. Наприклад, під час нівелювання
IV кл допускають нерівність довжин
плечей на станції -5 м, тобто
Розрахуємо
похибку перевищення, що виникає для
такої нерівності довжин плечей:
=
11^1
= 0,002
мм.
2
Отже,
вплив кривини Землі на відлік рейки у
разі нерівних довжин плечей до 5 метрів
є дуже малим, і його можна не враховувати.
Проте
не тільки кривина Землі обмежує
нерівність довжин плечей, а також зміни
із часом кута
Похибки,
викликані осіданням башмаків.
Експериментально
доведено, що кожне встановлення рейки
на башмак або костиль втискає їх у
землю. Досвід показує, що це джерело
похибок має переважно систематичний
характер, щоправда, на окремій станції
похибки не перевищують 0,02-0,03 мм. Вплив
осідання башмаків на середнє перевищення,
отримане із прямого та зворотного ходу,
значно ослаблене. Значна компенсація
впливу осідання башмаків, як і інших
чинників, наприклад, зміни кута
79
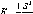
RAS
=
5 м.Rі
та необхідність перефокусування труби.
і
за час
роботи
на станції, забезпечується завдяки
виконанню відліків рейок в один фізичний
момент.
Розглянемо
це детальніше.
Нехай
відлік чорної сторони задньої рейки
середньою ниткою зроблено о 8
год
40 хв. (рис. 1.3.5). Відлік чорної сторони
цією самою ниткою передньої рейки - о
8
год 42 хв. Відлік червоної сторони
передньої рейки - о 8
год 43 хв. Відлік червоної сторони задньої
рейки - о 8
год 45 хв. Отже, у середньому відліки
задньої і передньої рейок зроблені в
один фізичний момент - 8
год 42,5 хв. Тобто передбачена інструкцією
послідовність відліків обґрунтована.
Недопустимо спочатку брати відліки
чорної і червоної сторін задньої рейки,
а потім - передньої. Тоді такої одночасності
відліків не буде. Є ще одна причина
недопустимості іншої послідовності
відліків. Якщо спостерігач, взявши
відліки двох сторін задньої рейки,
забув вивести бульбашку рівня в
нуль-пункт, а потім взяв відлік обох
сторін передньої рейки, то обчислені
перевищення за чорними та червоними
сторонами рейок будуть однакові або
відрізнятимуться не більше ніж на 3 мм.
Проте ці перевищення із грубою похибкою.
Якщо послідовність відліків така, як
рекомендує інструкція, імовірність
появи такої похибки дуже мала.
передня
рейка
Похибки,
викликані осіданням штатива.
Під
час роботи на станції спостерігач
переміщається навколо нівеліра і масою
свого тіла тисне на ґрунт. Внаслідок
цього, особливо на слабких та заболочених
ґрунтах, штатив осідає. Ці похибки мають
приблизно таку саму
80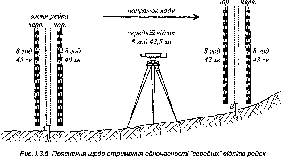
величину,
що й осідання башмаків, і не регламентують
точність нівелювання III та IV класів.
Особисті
похибки.
Похибки
відліків рейок.
Похибки
відліку (кутова похибка візування)
залежать від цілої низки чинників:
критичного кута зору спостерігача;
роздільної здатності труби
збільшення
труби
здатність
перелічених
факторів похибки візування є роздільна
здатність труби.
Під
час нівелювання III,
IV
класів спостерігач, беручи відлік,
розглядає сантиметрові поділки рейки
і ділить його на міліметри. Одні
спостерігачі відраховують на рейці
непарні частини сантиметра: 1, 3, 5, 7, 9
міліметрів, інші - парні частини: 2, 4, 6,
8
міліметрів.
Проте
ділення поділки на десять частин
окомірно виконують із точністю 0,15 від
цієї поділки. Від одного сантиметра
0,15 дорівнює 1,5 мм. Для довжин плечей 75
м похибка відліку в кутовій мірі
становитиме:
ж
1,5 мм 75000 мм
=
4,1*. Як бачимо, у нашому випадку кутова
похибка
візування
приблизно удвічі більша від роздільної
здатності труби. Це зрозуміло: з
роздільною здатністю
рейки
необхідно ще оцінити стан нитки (яка
має певну товщину) у проміжку між
видимими краями сантиметрової поділки.
Таку оцінку кожний спостерігач, залежно
від власного критичного кута зору,
виконує “особисто”, по-своєму. Тому
цю похибку і можна назвати особистою.
Отже, кутову похибку візування не можна
порівнювати з роздільною здатністю
труби. Похибка візування виявилась, у
цьому випадку, приблизно вдвічі більшою.
Загалом
у геодезичній практиці точність
візування може змінюватись на порядок
і більше: від десятка секунд до часток
секунди і дуже залежить від форми і
розмірів візирної цілі.
З
усіх розглянутих похибок найбільшими,
такими, що визначають точність
нівелювання III,
IV
класів, є похибки приведення візирної
осі в
81
тр;Гх
; форми і розмірів візирної цілі; віддалі
до візирної цілі; освітленості та
контрастності; товщини сітки ниток;
коливання візирної цілі. Однак похибку
візування часто порівнюють із роздільною
здатністю труби: бо'т
,
60" - критичний кут зору ока людини;
для Гх
= 30х,
роздільнатр
= 2". Насправді складовою частиною
серед інших, тільки щотв
= 2"
ми бачимо в трубу краї сантиметрової
поділки рейки (для S
=
75 м, лінійна похибка тр
=
0,73 мм), а під час відлічування
горизонтальний
стан та відліки рейок. Такий самий
порядок мають похибки нівелювання,
викликані рефракцією, до того ж похибки
рефракції є систематичними. Проте
похибки рефракції виключають, переважно,
завдяки спостереженням під час
нормальної стратифікації атмосфери.
Запропонований тут спосіб виключення
рефракції під час нестійкої стратифікації
ще не Набув широкого застосування у
виробництві.
Важливо
ще до початку робіт наперед (апріорно)
виконати оцінку очікуваної точності.
Під час таких оцінок вважають, що
систематичні похибки зведені до
мінімуму, а на точність вимірювань
впливають випадкові похибки, яких
неможливо позбутися. Подібні теоретичні
розрахунки виконують і укладачі
інструкцій, встановлюючи допустимі
похибки вимірів.
Будемо
враховувати сумісну дію двох найбільших
випадкових похибок,
які
пов’язані зі збільшенням зорової труби
нівеліра
похибки
відліку
похибки
установлення візирної осі в горизонтальний
стан
Під
час конструювання нівелірів конструктори
враховують, що збільшенню труби
повинна відповідати ціна поділки рівня.
Строго кажучи, кутова величина похибки
відліку
встановлення
візирної осі в горизонтальний стан
Розглянемо
простий спосіб визначення відповідності
збільшення труби і ціни поділки рівня.
Ставлять рейку на віддалі 50-70 м від
приладу, приводять середину бульбашки
в нуль-пункт і беруть відлік. Після
цього кількома обертами елеваційного,
або підіймального гвинта, переміщають
бульбашку і, не дивлячись на рейку,
встановлюють бульбашку на попереднє
місце. Знову беруть відлік. Якщо
відлік не змінився, то рівень достатньо,
а, можливо, навіть надлишково чутливий
і потрібно багато часу, щоб привести
середину бульбашки в нуль-пункт
(досягти контактування зображення
кінців бульбашки, якщо рівень контактний).
Щоб
виявити надлишкову чутливість рівня,
роблять так: приводять середину бульбашки
у нуль-пункт. Беруть відлік. Декілька
разів встановлюють середню нитку сітки
на цей самий відлік і кожний раз
визначають розташування
82
Точність нівелювання III, IV класів
Гх
та ціною поділки рівня т. Саме від цих
параметрів залежать:
тв;ту.т”в
повинна дорівнювати кутовій величині
похибкиту:т'
= ту. (1.3.17)
бульбашки.
Якщо розташування бульбашки змінюється,
то рівень надлишково чутливий. Для
точності роботи краще мати рівень із
трохи надлишковою чутливістю, але
надлишкова чутливість гальмує темп
роботи, якщо спостерігач буде добиватися
точного контактування.
Як
ми вже знаємо, ділення на око деякої
поділки на десять частин виконують
із точністю 0,15 від величини цієї поділки.
Тому
т'у
=0,15
т. (1.3.18)
Для
нами,
виявилась приблизно вдвічі більшою
від роздільної здатності труби та
дорівнює
загальна
величина становитиме:
Знайдемо
загальну лінійну похибку відліку
рейки
загальній кутовій (рис. 1.3.6):
т
_ т
~S~
Р
3_
. * >
т
= -
=
6*.
Рис.
1.3.6. До визначення лінійної похибки
т
за відомої кутової т”3
Для
III класу нормальна довжина плеча
75000
мм •
‘2мм.
Для
IV класу
_
100000
мм • 6"
206265'
=
3 мм.
Розрахуємо
похибку вимірювання перевищення на
станції (рис. 1.3.7). Перевищення h
= a
mh
=та
+тЬ’
де
та
та
ть
-
загальні похибки у відліках рейки.
83х
= ЗО"; їй"
= 4,5". Кутова похибка відліку, також
вже визначенаті
= 4,1". Як бачимо, рівність (1.3.17)
виконується доволі точно. їхнят3
= yjmj
+
ті
, т3
= л/4,5'2
+4, і'2
= 6',
т3т,
що відповідає (1.3.19)
S
=
75 м, тому:6мifiju
— —ш
206265S
=
100 м, тому:—
b.
Квадратична
похибка перевищення mh
буде
такою:
''С&'хх-'А
Рис.
1.3.7. До визначення похибки вимірювання
перевищення на станції Нехай:
та
=ть
= w,
що у разі рівних плечей обґрунтовано,
тоді
Проте
під час нівелювання визначають два
перевищення за відліками чорних і
червоних сторін рейок та обчислюють
середнє перевищення
З
(1.3.21) можна зробити важливий висновок:
похибка середнього перевищення на
станції нівелювання дорівнює похибці
відліку рейки. Отже, для III класу
середньому
на 1
км ходу припадає 10
станцій.
Тому
похибка 1 км ходу становитиме:
для
III класу
для
IV класу
Отримані
похибки можна вважати середніми
квадратичними похибками перевищень
на 1 км ходу III та IV класів.
mh
-
т\І2.
(1.3.20)
Середні
перевищення із двох будуть точніші в
(1.3.21)
84
hcep
:mhcep
ш
= 2 мм, а для IV класу Щсер
IV
=
3 мм. Досвід показує, що втш
ш
= 2
ммл/ЇО ~ 6
мм,тш
1V
=
3 ммл/ЇО ~ 10 мм.ті
= 2т2
, або
у/і
раза. Тому:
У
чинних інструкціях прийнято вважати
допустимими (граничними) похибками
подвійні середні квадратичні похибки.
Тому приймемо
mKMivdon
=2
mKMiv
=
2-10 = 20 мм.
Якщо
нівелірний хід має довжину
для
III класу
для
IV класу
Отримані
формули допустимих нев’язок збігаються
з допусками інструкції.
Розглянемо
спочатку зрівноваження окремого
нівелірного ходу, прокладеного між
двома реперами старших класів. У першій
частині курсу подано спосіб зрівноваження
перевищень такого ходу. Розглянемо
можливість безпосереднього зрівноваження
висот. Нехай маємо виміряні та обчислені
середні перевищення із прямих та
зворотних ходів між усіма сусідніми
реперами ходу, а відомі тільки висоти
кінцевих реперів. Необхідно визначити
висоти усіх новозакладених реперів.
Припустимо, ми, користуючись висотою
початкового репера
Різниця
fh=HEl-HEl. (1.4.1)
85ткмтдоп
=2
Щсш
=2-6
= 12
мм = 10
мм;L
(км),
то допустима нев’язка такого ходу
становитиме:fhdon
=Ю
ммл/і км ; (1.3.22)fhdm
=
20 ммкм
. (1.3.23)Зрівноваження нівелірних ходів та мереж
Зрівноваження висот окремого нівелірного ходу
Нп
та середніми перевищеннями, обчислимо
приблизні висоти всіх проміжних реперів,
зокрема й кінцевого репера, висота
якого Нк
- відома. Отримаємо нову висоту цього
репера Н'к.
А потім навпаки, користуючись висотою
Нк,
обчислимо ще раз наближені висоти всіх
інших реперів, зокрема й початкового
репера. Одержимо нову висоту цього
репера Н'п.
За результатами цих даних побудуємо
подвійний профіль, поданий на рис.
1.4.1.Н'к
-Нк
=+fh
являє
собою нев’язку ходу Rpn-RpK.
Одночасно
Н'И
- Нп
= -fh
-
теж нев’язка, але ходу RpK
-
Rpn.
Як це видно з подвійного профілю, для
всіх реперів отримано дві висоти.
Різниця висот цих реперів дає нев’язку.
Для репера Е
Рис.
1.4.1. Подвійний профіль нівелірного ходу
Знайдемо
найімовірнішу, тобто середньовагову
висоту цього репера
Р1+Р2
Нехай
кількість штативів у ході до репера
А
=-
1
к' п-к
Крім
того, на основі рис. 1.4.1, можемо записати:
HE2=HEx-fh.
(1.4.3)
Підставивши
значення
н
HExPx+HEx-P2-fh-P%
HEl
(Аі
+p2)-fh-Р2
Поділивши
почленно чисельник на суму (/J
Я£=Я£і-Л-^_. (1-4.4)
Рї
Перетворимо
дріб —-—:
3+3
1
1
З
_ п-к
_ п-к
_ п-к
_к{п~к)
_к
Рі+Р2
1 t
1
к
п-к к(п-к) к(п-к)
86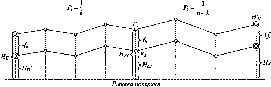
НЕ
:НЕл
+ #~ Р2н
=
_і! 1 h—2-. (1.4.2)Е
дорівнює к
. Якщо всього у ході п
штативів, тоді кількість штативів від
репера Е
до кінцевого репера дорівнює п
- к.
За ваги цих двох частин ходу приймемо
величини, обернені до кількості штативів
у цих частинах ходу, тобтоНЕі
із (1.4.3) у (1.4.2), отримаємо:Е 3+3 3+3+Р2),
одержимо:
п-к
+ к п
п(п-к)
п
Py
It
Підставивши
значення — = — у (1.4.4), матимемо кінцеву
формулу:
Рх
+ Р2
п
HE=HEl-fh~.
1 гп
(1.4.5)
Оскільки
репер Е
вибрано довільно, то ця формула придатна
для обчис-
лення найімовірнішої
висоти будь-якого репера. На підставі
формули можна
сформулювати правило
таких обчислень: зрівноважена
висота будь-якого
репера дорівнює
наближеній висоті, отриманій за середніми
перевищеннями
плюс поправка,
яка
дорівнює нев ’язці ходу,
взятій
з оберненим знаком,
поділеній
на
кількість станцій у всьому ході і
помноженій на кількість станцій до
цього
репера.
Під
час обчислення поправок у наближені
висоти доцільно нев’язку, взяту
f
з
оберненим знаком, розділити на
п
потім
цей коефіцієнт множити на змінну
Визначимо
найслабше місце ходу, тобто місце, де
висоти реперів визна-
чаються з
найбільшою похибкою. Висота кожного з
реперів обчислювалась два
рази: від
початкового та від кінцевого репера і
наприклад, для репера
Середнє
значення висоти
п
p=U.
1
(1.4.6)
к
п — к к(п — к)
Найбільшу
похибку у висоті буде мати репер, вага
якого
у
= к(п
- к)
= пк
- к2.
(1.4.7)
Візьмемо
першу похідну по
— =
2
Отже,
найслабше місце ходу - його середина.
87п,
тобто отримати постійний коефіцієнт
—, аk
-
кількість станцій до репера,
висоту
якого визначають.Е
, висоти
НЕї
та НЕг.Н,
отримане з вагою Р, що дорівнює сумі
ваг
Рг
таР2,
тобто: Р
= Р{
+ Р2,
або:Р
-
найменша.
Відповідно до (1.4.6) Р
буде мінімальним, якщо знаменник к(п
- к)
буде мак-
симальним. Отже, маємо
задачу на екстремум функції. Позначимо
знаменник:к
та прирівняємо її до нуля: dyп
- 2к
= 0. Звідси: dkк
= ~. (1.4.8)
Нехай
маємо мережу із трьох ходів, що сходяться
в одну вузлову точку (рис. 1.4.2). На рисунку
подані виміряні перевищення \, Й2,
Рис.
1.4.2. Нівелірна мережа із трьох ходів,
що
сходяться в одну вузлову точку
Визначимо
ваги ходів, як величини, обернені до
довжин ходів. Ваги також подано на
рисунку. Маємо можливість визначити
три значення висоти точки
Я,
=НА
+hl;H2=HB+h2iH3=Hc+hi.
Знайдемо
середнє вагове значення висоти точки
нЕ
=
Н\Р\
+Н2Р2
+
Я3Р3
Л
+Р2+^3
(1.4.9)
Далі,
знаючи зрівноважену висоту вузлової
точки НЕ,
знайдемо нев’язки
кожного
з ходів: /^ , /^, за формулами
Д
-нЕ,
а =н2-HEjh
=нг-нЕ.
Подальше
зрівноваження кожного із цих ходів
можна виконати описаним вище методом.
Залишається оцінити точність нівелювання
за результатами
88Зрівноваження нівелірної мережі з однією вузловою точкою
h3
та
довжини ходів Ц,
, Z3,
а
також висоти реперів А,
В, С -НА,
НВ,НС.
Стрілками показані напрямки збільшення
висот, тобто, напрямки додатних
перевищень.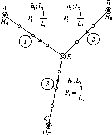
Е
: з першого, другого та третього ходів:Е
:
врівноваження.
Знайдемо середню квадратичну похибку
одиниці ваги - |і. для випадку, коли у
одну вузлову точку сходяться
Ц
=п
- ходів. Тоді, як відомо,
п-1 5
(1.4.10)
де
(л-1)- кількість надлишкових ходів; ваги
ходів;
Щоб
знайти висоту точки
С
Якщо
С
- довжина деякого ходу, км, то нівелювання
на одній станції
VC
= ;
якщо ж
л/іо Я,-
„л/ЇО.
Нарешті, якщо
\^км
хст
(і
- похибка ходу, що має
УІС
хибка
ходу, завдовжки в 1
км становитиме:
уіС
Похибку
визначення висоти вузлової точки
т
*
=
_
Ц
№
(1.4.11)
Візьмемо
нівелірну мережу, показану на рис.
1.4.3. Мережа має чотири вузлові точки
тобто
міру їхньої надійності
Введемо
поняття еквівалентного
нівелірного ходу. Еквівалентнім ходом
називають такий уявний хід, вага якого
дорівнює сумі ваг наявних ходів, які
замінені еквівалентним.
89Vx
—
поправки
ходу, отримані зі зрівноваження.Е,
достатньо прокласти один хід.
Pj
=
—, то |і - похибка ходу, завдовжки у 1 км;
якщо ж Pt-
—,
де\іст
■ нівелювання
на одній станції. Тоді,Р!
= —, то її - похибюPt
-
—, т<С
станцій; \іст
= -~=.
В останньому випадку по-=-^==\fl6.Е
знаходять за формулоюЗрівноваження перевищень нівелірних мереж методом еквівалентної заміни
А,
В,
С
,D.
Висоти
цих точок невідомі. Між вузловими
точками прокладено шість ходів. У ходах
виміряні перевищення h\,
h2,
...,
h6.
Відома кількість станцій ходів пх,
п2,
..., п6.
Це дає змогу обчислити ваги усіх ходів,Рх
= —.«і
Розглянемо
послідовність зрівноваження перевищень,
із використанням еквівалентних замін
дійсних, існуючих ходів.
h3
Д
=
1_
«з
С
h6
©
Рв=-
Рис.
1.4.3. Зрівноваження перевищень нівелірної
мережі
методом еквівалентної заміни
Замінимо
ходи 1 і 2 еквівалентними ходами є]2
та ходи 5 і 6
еквівалентним
ходом є5б.
Обчислимо
ваги еквівалентних ходів:
Р\2
-
Л +
^2 р56=р5+р6.
(1.4.12)
3.
Знайдемо кількість станцій еквівалентних
(уявних) ходів. Оскільки
„ 1 1
рі=—>
то «/ =7Г-
«,• ^
Оскільки
ми знаємо ваги еквівалентних ходів, то
можемо знайти кількість
станцій у
цих ходах:
1
«12
=-
Ріг
1
«56
=-
г56
4.
Визначимо перевищення еквівалентних
ходів як середні вагові:
г
_ Ь\Р\
+ ^2^2
.
«12
-
Рі+Рг
h
_h5P5+h6P6
(1.4.13)
(1.4.14)
(1.4.15)
90
Після
заміни ходів 1, 2 - еквівалентними ходами
є12,
та ходів 5, 6 - еквівалентним ходом є56,
мережа перетворилася на зімкнений хід
- полігон.
Знайдемо
нев’язку полігона /А
та кількість станцій полігона
fh=hl+h+h6+h4’ (1.4.16)
«
=
«12 +
«З +
«56 + «4 • (1.4.17)
Визначимо
нев’язки чотирьох ходів, що залишилися
після заміни: еквівалентних є12,
є56
та існуючих - 3,4:
fhn
-~пП>
Л56
~~п56
11
п 36
п
3
И
Л4
= —«4
4
и
(1.4.18)
Знаючи
нев’язки ходів 3 і 4, знайдемо їхні
зрівноважені перевищення
як поодинокі
ходи:
^4
Аналогічно
знайдемо зрівноважені перевищення
еквівалентних ходів:
^12
зв =^12
“Л, 2
]
^56
зв =
^56 “ /%б
J
Визначимо
нев’язки ходів 1 і 2 та 5 і 6:
fh,
-h~hi
зі
/*2
~h.~hh
(1.4.19)
(1.4.20)
(1.4.21)
Л5
_^5
~Ьбзв
fhf,
~h> ~
Ьб
зв
(1.4.22)
На
рисунку не показано, але в кожному із
шести ходів є репери. Тепер, коли ця
мережа розділилась на шість незалежних
ходів і відомі нев’язки цих ходів, то
надалі урівноважують перевищення між
цими реперами, пропорційно до ваг
частин ходів між суміжними реперами.
Ці ваги обернено пропорційні до
кількості станцій у секціях. Зрівноваження
закінчують оцінкою точності результатів.
Похибку одиниці ваги знаходять за
формулою
И
=
-п:
fh
з
~~«ЗІАЗзв=Лз-Л3fh4
п — к ’
(1.4.23)
де
91п
- кількість всіх ходів; к
-
кількість вузлових точок.
„ {НА +hl)Pl + (HB+h2)P2 її і о — Р1+Р2 |
(1.4.24) |
2. Знайдемо вагу та довжину еквівалентного ходу є12: |
|
Р\2 ~ Р\ + ^2 ’ |
(1.4.25) |
*.2=7- M2 |
(1.4.26) |
3. Визначимо висоту точки F з еквівалентного ходу є12 |
та ходу 3: |
#12,3 = #12 + *3 * |
(1.4.27) |
92
Тепер,
по суті, ми маємо мережу з однією вузловою
точкою
_
Аг,З
•
Аг,З
+
{Не
+
А ) А + (HD
+h5)P5
HF
=
Де
Аг,з
=
Аг + А >а
Аг,З
+ А + А
Аг,з
_
1
Аг,з
(1.4.28)
(1.4.29)
Знаючи
зрівноважене значення висоти точки
ходів,
що сходяться у цій точці:
Аг,з
=
Аг,з ~HF, (L4.30)
fb={Hc+hA)-HF, (1.4.31)
Розділимо
нев’язку fh[2
3
на нев’язки еквівалентного ходу є12
та ходу З, враховуючи довжини цих ходів:
, _
А
2,3 ,
fh[2
Аг + А 1,2
^
_ Аг,з г
/йз
—ї ГТ-^
(1.4.33)
Аг
+А
Тепер
є можливість розрахувати зрівноважену
висоту точки
HE=Hl2-fh2,
HE=HF-hi-fln.
Залишається
знайти нев’язку початкових ходів 1 та
2:
А
=(ил*\)-нЕ
A
(1.4.34)
(1.4.35)
(1.4.36)
Розглянемо
застосування цього способу для мережі,
що складається із шести ходів, які
створюють три вузлові точки (рис. 1.4.5).
Відомі перевищення та довжини ходів,
висоти трьох реперів, обчислені ваги
ходів.
93-F.
Знай-
демо найімовірніше значення
висоти цієї точки:F,
знайдемо
нев’язкиА=(Дп+М-*А. (І-4-32)
Е
-НЕ
з
контролем:
=(HB*h)-HE
Оцінку
точності виконують, як звичайно.Зрівноваження нівелірних мереж способом послідовних наближень (спосіб вузлів)
А
Рис.
1.4.5. Нівелірна мережа з трьома вузловими
точками
Припустимо,
що у якийсь спосіб знайдено висоти
вузлових точок
Врахуємо,
що кожен хід має певну вагу. Тому
припишемо цим рівнянням ваги ходів
(1.4.37)
X-{HA+hx)
= Vl\Pl'
X-{Y-h2)=V2\P2
X-{Z
+ hi)=F3|P3
Y-(HB+h4)
= V4\P4
Y-(Z-h5)=V5\P5
Z-(Hc+h6)
= V6\P6
Як
відомо з методу найменших квадратів,
якщо рівняння похибок розв’я-
зувати
згідно з умовою
[Paa]X+
[Pal] =
0
[Pbb]Y+
[Pbl] =
0
[Pcc]Z+
[Pcl] =
0
(1.4.38)
94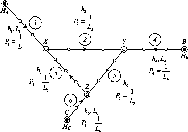
X,
Y,
Z.
Але, якщо визначено висоти цих точок,
то для кожного ходу можна скласти
рівняння похибок.—Рі:[PW]
=
min,
то
приходимо до нормальних рівнянь,
яких
буде стільки, скільки невідомих.
Невідомими фактично є висоти вузлових
точок
X,
Y,
Z.
Загалом нормальні рівняння для нашої
мережі запишуться так:
У
нормальних рівняннях прийнято позначати:
аі
=Ьі
=с, =1;
li=-{HA+hі);
h=-(Y-fh)
;...i6=-(Hc+h6).
Перше
нормальне рівняння системи (1.4.38) у
розгорнутому вигляді
запишеться
так:
РхХ
+ Р2Х
+ Р3Х
~(НА
+
hx)Px-{Y-h2)P2
~{Z
+ hi)P2
=
0. (1.4.39)
Розв’яжемо
це рівняння відносно невідомого
(^+a,)p1+(f-a2)p2+(z+a3)p3
Х
= -
(1.4.40)
Рі+Рі+Рз
Аналізуючи
(1.4.40), зауважимо, що невідоме
(X
+ h2)P2+(HB+h4)P4+(Z-h5)P5
_
Рг
+
А +
^5
Z
=
{X-h)Pz
+{Y + h5)P5+(Hc
+h6)P6
(1.4.41)
(1.4.42)
рг
+P5
+P6
Оскільки
у (1.4.40),
(1.4.41), (1.4.42) є
невідомі, як у лівій, так і в правій
частині,
то безпосереднє розв’язання цих рівнянь
неможливе. Справді,
наприклад, у
(1.4.40), в лівій частині невідоме -
У
рівняння (1.4.40) підставимо наближені
значення
Визначаючи
Z
з
(1.4.42), будемо підставляти не
пр
'■
а
знайдемо
з першого наближення
95ах
-
коефіцієнти у рів-
няннях похибок
при першому невідомому (перше невідоме
-X),
Ьх
- відповідні
коефіцієнти при другому
невідомому - Y
;Cj-
при
третьому невідомому - Z.
Як
видно з (1.4.37), коефіцієнти при X,
Y,
Z
-
одиниці, тобто:Іх
- вільні члени, відомі частини рівнянь:X:X
визначається як середнє
вагове з
трьох ходів, що сходяться у вузлову
точку. Тепер, не записуючи інші
два
нормальні рівняння в розгорнутому
вигляді, можемо, за аналогією з
(1.4.40),
записати формули для знаходження
невідомих Y
та
Z:Y
=
-X,
а в правій - невідомі Y
та
Z.
Те
саме у двох інших рівняннях. Але ці
рівняння можна розв’язувати
способом
послідовних наближень, тобто способом
ітерацій. Для цього спочатку
знайдемо
наближені значення невідомих висот
вузлових точок, викорис-
товуючи
відомі репери, що розташовані найближче
до шуканих:Xпр
~ а
»^пр
~
в
^4
> = Hq
+
Ag.Ynp
та
Znp.
Знайдемо
Хх
із першого наближення. Далі, під час
розв’язування рівняння (1.4.41),
підставляємо
не Хпр,
а значення Хх
-
із першого наближення. Знайдемо lj.Хпр,
YrХх
та Yx.
ТодіZx.
Переходимо
до другого наближення: визнаючи
Зазвичай
достатньо 3-4 наближень. Ітерацію
закінчують, якщо в останньому й
передостанньому наближенні значення
невідомих однакові. Зрозуміло, що такий
метод придатний для мережі зі значною
кількістю ходів та вузлових точок.
Рівняння для визначення невідомих
висот реперів складають безпосередньо
зі схеми нівелірної мережі. Тому цей
спосіб широко застосовується у
виробництві. Обчислення виконують на
персональних комп’ютерах.
Цей
простий, наближений метод розглянемо
на мережі з восьми ходів, що створюють
чотири полігони і п’ять вузлових точок
(рис. 1.4.6).
в
Рис.
1.4.6. Нівелірна мережа з чотирьох полігонів
У
прямокутниках подані нев’язки полігонів
у мм, у кружках - довжини ходів між
вузловими точками у км.
Нехай
у ході
96X,
підставляємо у (1.4.40) значення Yx,
Zx
і
так далі.
Зрівноваження нівелірної мережі порівнянням нев’язок суміжних ходів
BE
полігона
І перевищення з плюсом, тоді в ході ЕВ
II полігона перевищення з мінусом.
Нев’язки в цих двох полігонах із
протилежними знаками. У першому полігоні,
щоб позбутися нев’язки, потрібно в
окремі ходи, наприклад, на хід BE,
вводити додатні поправки, оскільки
перевищення між точками BE
й
ЕВ
за абсолютною величиною повинні бути
однакові, тоді поправки на хід ЕВ
повинні бути такої самої величини, але
від’ємні. Оскільки
пов’язка
у полігоні II - додатна, то від’ємна
поправка на хід
Тому
у цей хід доцільно вводити поправки.
Розглянемо
два суміжні полігони, нев’язки яких
мають однакові знаки. Візьмемо хід
Це
означає, що у такому разі похибки
вимірювання перевищень у цьому суміжному
ході не є причиною нев’язок. Тому в цей
хід вводити поправки не треба. Зі
сказаного випливають такі правила
розподілу нев’язок:
Якщо
у двох суміжних полігонах нев’язки з
протилежними знаками, то в суміжний
хід необхідно вводити однакові поправки
з протилежними знаками і зменшити
нев’язки цих полігонів.
Якщо
у двох суміжних полігонах нев’язки з
однаковими знаками, то в суміжні ходи
не можна вводити поправки.
Абсолютні
значення поправок повинні бути прямо
пропорційні до довжини ходів, що
створюють полігон.
Користуючись
цими правилами, зрівноважимо мережу,
подану на рис. 1.4.6. Почнемо з полігона
І. У хід
Перейдемо
до полігона П. Полігон отримав поправку
(-4). Залишилась нев’язка (+11). Поправки
на два інші ходи цього полігона будуть
(-4) та (-7).
Перейдемо
до полігона III. Тут залишилась нев’язка
(-8).
У хід
Нарешті,
розглядаємо полігон IV. Два ходи цього
полігона отримали нульові поправки.
Це означає, що всю нев’язку треба ввести
в зовнішній хід
Спосіб
простий, оскільки зрівноваження
виконують безпосередньо на схемі
мережі, практично без обчислень і, за
певного досвіду, спосіб дає результати,
що часто задовольняють інженерну
практику.
97ЕВ
зменшить пов’язку полігона II. Це
означає, що похибка в суміжному ході
цих полігонів є до певної міри причиною
нев’язок.ЕА
полігона І та хід АЕ
полігона IV. У хід ЕА
цього полігона треба вводити додатну
поправку, щоб зменшити нев’язку полігона
І. Тоді хід АЕ
отримає від’ємну поправку такої самої
величини. Оскільки нев’язка полігона
IV - від’ємна, тоді ця нев’язка збільшиться.
ЕА
вводити поправку не треба. Тому поправки
в цей суміжний хід дорівнюють нулеві.
Нев’язка (-11) мм припадає на два ходи.
Хід АВ
-
довший порівняно з ходом BE.
Тому розподілимо нев’язку так: на хід
BE
-
(+4); на хід АВ
- (+7). Поправки на рисунку взяті у круглі
дужки. Перший полігон ув’язано.DE
вводити
поправки не можна, залишок нев’язки
необхідно ввести в зовнішній хід CD
-(+8).DA
-
(+8).
Мережа ув’язана.
/.4.7.
Зрівноваження
нівелірної мережі методом В. В. Попова
146
0.25
0.42
(~У(
-6
А
6- |
і |
|
-3 |
|
-11 |
-1 |
|
-10 |
0 |
|
-2 |
0
30
IV
-10 (+5) , <°> |
Г —■* (-5) ,Е (-V , |
(0) |
|
(0) |
(0) |
0,26 S |
k 0,26 |
III
0J1
+з
0.33
0.43
Рис.
1.4.7. Зрівноваження нівелірної мережі
способом полігонів
Професор
В.В. Попов удосконалив розглянутий нами
спосіб порівняння
нев’язок так
вдало, що він став точним. Розглянемо
суть цього способу на тій
самій
мережі, яка подана на рис. 1.4.6. Мережа
зображена у збільшеному вигляді
на
рис. 1.4.7. Спосіб, названий автором
способом полігонів, зводиться
до
послідовного розподілення нев’язок
у кожному полігоні пропорційно до
ваг
окремих ходів, приведених до
одиниці. Ці ваги називаються червоними
чис-
лами, оскільки на схемах мереж
їх виписують червоним кольором.
Розглянемо,
як обчислюють червоні числа (приведені
ваги) на прикладі
полігона І. Периметр
полігона 1-15,2 км, а хід АВ
має
довжину 7,0 км.
15,2 7
Складемо
пропорцію: ходу АВ.
1
X
-,
ХАВ=
0,46;
0,46 і є приведена вага
АВ
15
2 3 7
Для
ходу BE
відповідно
знайдемо: —= —-—, ХВЕ=0,24.
1
1ВЕ
Аналогічно
знайдемо вагу ходу ЕА.
Вона становить ХЕА
-
0,30. Контроль: сума приведених ваг
полігона повинна дорівнювати одиниці:
0,46 + 0,24 + 0,30= 1,00.
98
Обчислюють
ваги всіх ходів і записують зовні
полігона, біля відповідних ходів. Під
кожним червоним числом заготовлена
рамочка, у яку вписують поправки, що
припадають на відповідний хід. Ці числа
на рис. 1.4.7 наведено нахиленими,
підкресленими цифрами.
Розпочати
розподілення нев’язки можна з будь-якого
полігона, але краще з полігона з
найбільшою абсолютною нев’язкою.
Помноживши +15 відповідно на червоні
числа II полігона 0,42; 0,33; 0,25, записуємо
результати, округлені до цілих міліметрів
у відповідні рамки зовні полігона з
тим самим знаком, що і нев’язка полігона.
Це будуть поправки, які припадають на
ті ходи в суміжних полігонах, біля яких
ці червоні числа записані. Так: +4
(записані під 0,25); +5 (записані під 0,33);
+6
(записані під 0,42) будуть стосуватися
відповідно ходів
Потім
переходимо до III полігона, тобто йдемо
за годинниковою стрілкою. У ньому хід
Нарешті,
переходимо до І полігона. У ньому
поправки мають два ходи: хід
Переходимо
до другого кола, все повторяючи у тій
самій послідовності і починаючи з
полігона II. У цьому полігоні нев’язку
ми вже розподілили, але потім ходи
99BE
(І
полігон), EC(lII
полігон), ВС~
зовнішній хід. Сума прправок повинна
даватинев’язку: 4 + 5 + 6=15.ЕС
отримав поправку +5. Одержану залишкову
нев’язку (-7) записують у рамку під
числом (-12). Цю залишкову нев’язку
множимо на червоні числа полігона III і
результати (-2), (-2), (-3) записуємо у
відповідні рамки полігона III, що
розташовані зовні нього. Далі переходимо
до четвертого полігона. У ньому була
нев’язка (-8),
але хід ED
отримав
поправку (-2). Тому сумарну нев’язку
(-10) записують під початковою нев’язкою
(-8).
Нев’язку (-10) множать на червоні числа
полігона IV і записують у рамки зовні
цього полігона (-5), (-3), (-2).BE
(+4)
та хід ЕА
(-3). Тому нев’язку (-11) виправимо на суму
цих поправок. Отримаємо (-10), які записуємо
під (-11). Нев’язку (-10) множимо на червоні
числа І полігона, записуючи відповідні
поправки (-5), (-3), (-2) у відповідні рамки.
На цьому закінчується перше коло
розподілення нев’язок.СЕ
й ЕВ
отримали нові поправки (-2) і (-2). Додавши
їх, одержимо нову нев’язку - (-4) цього
полігона. Нову нев’язку розподіляємо
так само, як описано вище, вписуючи
вторинні поправки ходів у відповідні
рамки. Аналогічно розподіляємо вторинні
нев’язки в усіх полігонах і переходимо
до наступного кола. У нашому випадку
необхідно було зробити три кола. Тепер
залишається в кожній рамці під червоними
числами розрахувати алгебраїчну суму
поправок. Для периферійних ходів
потрібно в алгебраїчній сумі поміняти
знаки на обернені й отримані у такий
спосіб числа записати всередині
відповідного полігона біля відповідного
ходу. Наприклад, для ходу АВ
маємо
зовні
- 6,
тоді ми повинні записати (+6).
Для розпізнавання поправок у ходи
записуємо їх у круглі дужки.
Для
внутрішніх ходів кожної пари суміжних
полігонів є по дві рамки, розміщені по
різні сторони ходу. Так, для ходу
Зазначимо,
що якщо розподіл нев’язок виконувався
б із заокругленням до десятих часток
мм, то поправки деяких ходів змінились
би тільки на 1
мм, однак потрібно було б шість кіл, що
не виправдовує витрат потрібного для
цього майже вдвічі більшого часу.
Порівнюючи
рис. 1.4.6 і рис. 1.4.7, бачимо, що в деяких
ходах поправки, отримані двома способами,
відрізняються. Спосіб порівняння
нев’язок, як уже відзначалось, наближений
і застосовували ми його спрощено, не
дотримуючись точної пропорційності
поправок і довжин ходів. Проте на цьому
прикладі ми бачимо, що розподіл нев’язок
наближеним способом виконується
приблизно так, як і строгим способом.
Нульові поправки одержали ті самі ходи
під час зрівноваження обома способами.
Зрівноважування закінчують складанням
каталогу висот реперів та оцінкою
точності отриманих результатів.
100СЕ
рамка всередині II полігона дає поправку
(-3), а для ходу ЕС
-
рамка всередині полігона III дає поправку
(+4), що під час переводу на хід СЕ
дає (-4)* Додавши (-3) і (-4), знайдемо загальну
поправку ходу СЕ, яка дорівнює (-7). Для
ходу ЕС
поправка дорівнюватиме (+7). Ці дві
величини ми і вписуємо біля цього ходу,
кожну всередині відповідного полігона.
Контролем знайдених поправок є те, що
їхня сума має давати початкову нев’язку
з оберненим знаком.
Розділ
II. ПЛАНОВІ ГЕОДЕЗИЧНІ МЕРЕЖІ
Основні
вимоги. Формули
Планові
опорні геодезичні мережі - це точки з
відомими координатами (
Залежно
від геометричної форми та безпосередньо
виміряних елементів розрізняють чотири
основні методи створення планових
мереж:
Тріангуляція.
Полігонометрія.
Трилатерація.
Супутниковий
метод.
Розглянемо
суть кожного із цих методів.
Тріангуляція
- це мережа трикутників, що межують один
з одним, у яких вимірюють усі кути й
хоча би одну сторону. На рис. II. 1.1 подано
ланку тріангуляції, що складається із
восьми трикутників. Довжини сторін
трикутників у ланках тріангуляції
можуть сягати 20-25 км.
Чотирикутник
101Методи створення планових мереж.
1.1. Сучасні методи створення планових мереж
Xt,
Yt),
які фундаментально закріплені на земній
поверхні або на спорудах і визначені
на основі лінійних та кутових вимірювань.
AMBN
-
базисна мережа. Базисні мережі будувались
для визначення довжини сторони
трикутника. Сторона АВ
безпосередньо не вимірювалась.
Вимірювався базис - лінія MN
та
вісім кутів чотирикутника - ромба, що
отримав назву геодезичного чотирикутника.
У цьому чотирикутнику більша діагональ
АВ,
що визначалась, одночасно є стороною
першого трикутника ланки. Базис
вимірювався підвісними мірними
приладами. Такі сторони, як АВ,
називають вихідними. Базисні мережі
будувалися до появи світловіддалемірів.
Світловіддалемірами можна вимірювати
довжини сторін трикутників, не будуючи
базисних мереж. Сторони, безпосередньо
виміряні світловіддалемірами, називають
базисними.
Ланки тріангуляції зазвичай складаються
з 10-12 трикутників. Віддалі між кінцевими
пунктами ланки можуть сягати 200-250 км.
Ланки, як правило, прокладають уздовж
меридіанів та паралелей. Чотири такі
ланки (дві - уздовж паралелей, дві -
уздовж меридіанів) створюють полігон
периметром 800-1000 км. Усередині полігон
заповнюють суцільною мережею трикутників
тріангуляції такого самого класу або
нижчого за точністю. Вершини трикутників,
закріплені на місцевості, називають
пунктами тріангуляції. Координати
початкових (вихідних) пунктів
" ~~ _ ^ Класи Характеристики |
і |
2 |
3 |
4 |
Довжини сторін трикутників, км |
20-25 |
7-20 |
5-8 |
2-5 |
Відносні похибки визначення базисних сторін |
1:400000 |
1:300000 |
1:200000 |
1:100000 |
Середня квадратична похибка вимірювання кутів, " |
±0,7 |
±1,0 |
±1,5 |
±2,0 |
102Трилатерація
-
це також ланки трикутників, як і в
тріангуляції, що межують один з одним,
але з виміряними сторонами, а не кутами.
Вершини трикутників мережі трилатерації
називають пунктами трилатерації.
Кінцева мета створення трилатерації,
як і створення тріангуляції - визначення
планових координат пунктів.
^ Класи Характеристик^— |
і |
2 |
3 |
4 |
Довжина сторін, км |
20-25 |
7-20 |
5-8 |
2-5 |
Відносна похибка вимірювання сторін |
1:300000 |
1:250000 |
1:200000* (1:150000) |
1:150000* (1:100000) |
Середня квадратична похибка вимірювання кутів, " |
0,4 |
1,0 |
1,5 |
2,0 |
*
Для сторін полігонометрії 3 та 4 класів,
близьких до мінімальних, допускають
відносні похибки 1:150000 та 1:100000 відповідно.
103
Рис.
II. 1.3. До пояснення принципу роботи
системи GPS
104
Рис.
II. 1.4. До пояснення принципу
визначення
приростів координат
системою GPS
Проте
до появи світловіддалемірів
(світловідцалеміри у геодезичному
виробництві з’явились тільки після
Другої світової війни) тріангуляція
займала провідне місце як метод створення
державних геодезичних мереж. Метод
полігонометрії застосовувався значно
менше, переважно через складність
вимірювання ліній.
«2
=V(X2
f- (II.l.
1)
*3
= V№-Xpf
+(Y3-YPf
+(Z3-Zpf
R,
=V(^/ ~xpf
+(Yi~Ypf
+(zi-zPf
У
системі (II.
1.1) три
невідомі
GPS-приймачі
пристосовані до визначення прямокутних
геодезичних координат
Якщо
один GPS-приймач
розміщений на пункті з відомими
координатами, а другий - на невідомому
(рис. II. 1.4), тоді можна отримати прирости
координат
105Супутниковий
метод створення мереж.
У наш час поширена система GPS
-
Global
Positioning System (глобальна
пошукова система). Розглянемо принцип
визначення розміщення наземних пунктів
системою GPS.
GPS-
приймач, що встановлюють на пункті,
координати якого визначають (пункт Р
на
рис. II. 1.3), приймає радіосигнали від
штучних супутників Землі, що мають
відомі миттєві координати; приймач
вимірює віддалі ЯЇ9
Т?2,
/?3,
..., Rt
до
супутників (не менше від чотирьох).
Координати супутників передаються на
GPS-приймач.
Відповідно до рис. II. 1.4 можна записати
чотири такі рівняння:«і -XPf
+0Ї-YPf
+(Z, -Z,)2-Xpf
+(Г2-rpf
+ (Z2-Zpf
ХР,
YP,
ZP.
Насправді
є чотири невідомі: крім ХР,
YP,
ZP,
ще невідома асинхронність 8Х
(різниця похибок показів хронометрів
супутника та приймача). Саме тому
потрібно спостерігати мінімум чотири
супутники. Розв’язавши ці рівняння,
знайдемо шукані координати точки Р.
Електронно-обчислювальна система
GPS-приймача
розв’язує ці рівняння і відображає на
дисплеї координати ХР,
YP,
Zp.X,
Y,
Z
(з
початком у центрі мас Землі), топоцентричних
прямокутних координат X,
7, Н
(із початком координат на топографічній
поверхні Землі) та геодезичних координат
В,
L,
Н
(широт, довгот та висот). Визначають
геоцентричні координати з точністю до
5 м. Така точність не задовольняє вимог
геодезії.АХ,
А7, AZ.
Такі
відносні,
а не абсолютні
визначення координат значно (приблизно
в 100 разів) точніші. Похибка визначення
координат близько 5 см може бути зменшена
збільшенням часу спостереження.
Як
це зрозуміло з рисунка, GPS-технології
дають змогу одночасно визначати як
планове, так і висотне положення наземних
пунктів. У геодезії широко застосовується
відносний метод визначення координат.
Основні
положення затверджені Постановою
Кабінету Міністрів України від 8
червня 1998 р. № 844.
Планова
геодезична мережа складається з:
астрономо-геодезичної
мережі 1
класу;
геодезичної
мережі 2
класу;
геодезичної
мережі згущення 3 класу.
Для
знімання масштабів 1:5000, 1:2000, 1:1000, 1:500
створюють розрядні мережі згущення,
які поділяють на:
мережі
полігонометрії, трилатерації і
тріангуляції 4 класу;
мережі
полігонометрії, трилатерації і
тріангуляції І і II розрядів.
ДГМ
створюють для вирішення таких основних
завдань в інтересах господарської
діяльності, науки та оборони країни:
встановлення
єдиної геодезичної системи координат
країни;
забезпечення
вихідними геодезичними даними засобів
наземної, морської й аерокосмічної
навігації;
вивчення
фігури і гравітаційного поля Землі та
їхніх змін у часі;
дослідження
геодинамічних явищ та рухів земної
поверхні;
обґрунтування
регіонів пошуку корисних копалин;
вивчення
руху полюсів та нерівномірності
обертання Землі;
інші
задачі.
Положення
пунктів ДГМ визначають у двох системах
координат - загальноземній та референцній;
між ними встановлюється однозначний
зв’язок, який визначають параметрами
взаємного переходу. За загальноземну
систему приймають геодезичну референцну
систему 1980 року (GRS
1980)
з такими параметрами еліпсоїда:
велика
піввісь
а-Ь
а
1
298,257
піввісь).
На
перехідний період (до введення системи
GRS)
залишається
система координат 1942 року (СК-42) з
вихідними даними:
1061.2. Основні положення створення планових державних геодезичних мереж (дгм)
a
=
6378137 м, стиснення е-(Ь
-
мала
референц-еліпсоїд
Красовського (велика піввісь
стиснення
1:298,3;
висота
геоїда в Пулково над референц-еліпсоїдом
дорівнює нулю.
Астрономо-геодезичну
мережу будують у вигляді однорідної
за точністю просторової геодезичної
мережі, яка складається із системи
рівномірно розташованих геодезичних
пунктів, віддалених один від одного на
50-150 км. АГМ-1 є геодезичною основою для
побудови нових мереж і забезпечення
подальшого підвищення точності наявної
мережі.
Частина
пунктів АГМ-1 являє собою постійно діючі
станції GPS-спостережень
та астрономо-геодезичні обсерваторії,
на яких виконують комплекс безперервних
супутникових астрономо-геодезичних,
гравіметричних та геофізичних
спостережень за змінами форми і розмірів
Землі, її гравітаційного поля, викликаними
геодинамічними процесами.
Решта
пунктів АГМ-1 - це фундаментально
закріплені на місцевості пункти,
положення яких періодично визначають
за довгостроковою програмою їхнього
функціонування.
Систему
координат АГМ-1 узгоджують з науковими
проектами міжнародної співпраці.
Просторове положення пунктів АГМ-1
визначають методами супутникової
геодезії у загальноземній системі з
відносною похибкою А
Пункти
АГМ-1 повинні бути зв’язані з мережами
високоточного нівелювання, що дає змогу
визначити перевищення нормальних висот
між сусідніми пунктами АГМ-1 з
середньоквадратичними похибками, не
більшими за 0,05 метра. На кожному пункті
АГМ-1 періодично повторяють визначення
відхилення прямовисних ліній із
середньоквадратичною похибкою - 0,5”.
Геодезичну
мережу 2 класу будують у вигляді
однорідної за точністю просторової
мережі, яка складається з рівномірно
розташованих пунктів мережі 1
та
2 класів, побудованих згідно з вимогами
до такої мережі у СРСР та нових пунктів,
що визначаються відповідно до вимог
сучасних основних положень. Нові пункти
геодезичної мережі 2 класу розташовуються
на відстані 8-12 км, і
107а
= 6378245 м);
Астрономо-геодезична мережа 1 класу (агм-1)
р/р
= = 1
• 10'8
(Ар- середня квадратична похибка
визначення геоцентричного радіуса
р
пункту). Кожен пункт АГМ-1 повинен бути
зв’язаний GPS
вимірюваннями
не менш як з трьома пунктами мережі, що
межують з ним.
1.4. Основні вимоги до державної мережі 2 класу
Параметри мережі |
GPS |
тріангуляція |
полігонометрія |
трилатерація |
|
Довжини сторін, км |
найбільша |
20 |
20 |
12 |
12 |
найменша |
5 |
7 |
5 |
5 |
|
Середня квадратична похибка вимірювання кута, не більше за, " |
- |
1 |
1 |
- |
|
Відносна
похибка вимірювання сторін (базису),
|
1:300000 |
1:300000 |
1:300000 |
1:300000 |
|
Середня квадратична похибка вимірювання сторони, не більше за, м |
0,03 |
- |
0,03 |
0,03 |
|
Геодезичну
мережу згущення 3 класу будують з метою
збільшення кількості пунктів до
щільності, яка забезпечує створення
знімальної основи великомасштабного
топографічного та кадастрового знімання.
Вона об’єднує геодезичні мережі
згущення 3 та 4 класів, побудованих
згідно з вимогами положення про державну
геодезичну мережу СРСР 1954-1961 років, та
нові мережі згущення, що будують згідно
із сучасними основними положеннями.
Нові
пункти геодезичної мережі згущення 3
класу визначають одним із чотирьох
раніше перерахованих методів. Вихідними
слугують пункти АГМ-1 та геодезичні
мережі 2 класу (ГМ-2).
Якщо
мережі згущення 3 класу будують методом
полігонометрії, то прокладають поодинокі
ходи або ходи з вузловими точками, які
спираються на
1081.5. Основні вимоги до державної мережі згущення 3 класу
Параметри мережі |
Методи побудови |
||||
GPS |
тріангуляція |
полігонометрія |
трилатерація |
||
Довжини сторін, км |
найбільша |
10 |
8 |
8 |
8 |
найменша |
2 |
5 |
2 |
2 |
|
Кількість сторін у ході, не більше за |
|
|
6 |
|
|
Середня квадратична похибка взаємного положення пунктів, м |
0,05 |
0,05 |
0,05 |
0,05 |
|
Середня квадратична похибка вимірювання кута, не більше ніж, " |
- |
1,5 |
1,5 |
- |
|
Найбільша нев’язка трикутника, " |
|
6,0 |
|
|
|
Кутова нев’язка ходу |
|
|
|
|
|
Відносна
похибка вимірювання сторін (базису),
не більше за, |
1:200000 |
1:200000 |
1:200000 |
1:200000 |
|
Середня квадратична похибка вимірювання сторони, не більше за, м |
0,04 |
0,04 |
0,04 |
0,04 |
|
Таблиця
II. 1.5
Основні
вимоги до побудови мережі згущення,
що
створюють методом полігонометрії 4
класу та І і II розрядів Показники """" |
4 клас |
І розряд |
II розряд |
|
і |
2 |
3 |
4 |
|
Довжини ходу, км |
окремого |
14,0 |
7,0 |
4,0 |
між вихідною та вузловою точками |
9,0 |
5,0 |
3,0 |
|
між вузловими точками |
7,0 |
4,0 |
2,0 |
|
Граничний периметр полігона, км |
40 |
20 |
12 |
|
109
1 |
2 |
3 |
|
|||
Довжина сторін ходу, м |
найбільша |
3000 |
800 |
500 |
||
найменша |
250 |
120 |
80 |
|||
оптимальна |
500 |
300 |
200 |
|||
Кількість сторін у ході, не більше ніж |
15 |
15 |
15 |
|||
Відносна
похибка вимірювання сторін (базису),
не більше ніж, |
1:25000 |
1:10000 |
1:5000 |
|||
Середня квадратична похибка ходу, не більше ніж, м |
0,05 |
0,05 |
0,05 |
|||
Середня квадратична похибка вимірювання кутів за нев’язками, не більше ніж, " |
3 |
5 |
10 |
|||
Найбільша нев’язка трикутника, " |
|
6,0 |
|
|||
Допустима
кутова нев’язка у ході або полігоні,
(для |
5
|
|
20
|
|||
пункти
вищого класу. Периметри полігонів
полігонометрії 70-90 км; найбільша довжина
ходу становить ЗО км. Якщо відстані між
пунктами, що належать до різних ходів,
менші за 2
км, ці ходи обов’язково з’єднують
додатковими ходами. За змогою, повинна
забезпечуватися видимість (земля-земля)
між суміжними пунктами мережі. За
відсутності видимості закладають два
орієнтирні пункти.
Основні
вимоги до побудови мережі згущення 3
класу (МЗ-З) подані у табл. II. 1.4.
Як
уже відзначалося, для знімання у
масштабах 1:5000, 1:2000, 1:1000, 1:500 створюють
розрядні мережі згущення методами
полігонометрії, трила- терації і
тріангуляції. Розглянемо окремо вимоги
до побудови таких мереж цими трьома
методами 4 класу та І і II розрядів. У
табл. II. 1.5 подано вимоги до мереж
згущення, що створюють методом
полігонометрії 4 класу та І і II розрядів
[5].
Типові
схеми побудови полігонометричних мереж
4 класу, І та II розрядів показано на рис.
II. 1.5.
На
рис. II. 1.5, а зображено поодинокий хід,
на рис. П.1.5, б - система ходів з однією
вузловою точкою, на рис. ІІ.1.5, в - складна
система ходів. Використані умовні
позначення подані на рисунку.
1101.6. Розрядні мережі згущення
-1*1—'■
І
\
/
• /
/
Умовні
позначення:
=3= -
полігонометрія
вищих класів
—/С\
- вихідний пункт тріангуляції та
вихідний
дирекційний напрямок
Рис.
II. 1.5. Схеми побудови полігонометричних
мереж 4 класу, І та II розрядів
Ланка
геодезичних чотирикутників
Умовні
позначення:
/\ -
вихідний геодезичний пункт
—— -
вихідна сторона
О -
пункт, який визначається
Поєднані
центральні системи - сторони трилатерації
Рис.
11.1.6. Схеми побудови трилатерації
Перейдемо
до вимог стосовно побудови мереж
трилатерації 4 класу та І і II розрядів.
Трилатераційні мережі будують у вигляді
ланок трикутників,
111



Показники |
4 клас |
І розряд |
II розряд |
Довжина сторони трикутника, км |
2-5 |
0,5-5 |
0,25-3 |
Мінімальна допустима величина кута трикутника, ° |
зо |
20 |
20 |
Гранична довжина ланки трикутника між вихідними сторонами або між вихідним пунктом і вихідною стороною, км |
14,0 |
7,0 |
4,0 |
Максимальна довжина вихідної сторони, км |
2,0 |
1,0 |
1,0 |
Відносна середня квадратична похибка вимірювання сторони мережі |
1:120000 |
1:80000 |
1:40000 |
Нам
залишилося розглянути основні вимоги
до побудови тріангуляційних мереж 4
класу та І і II розрядів. За геометричною
формою мережі тріангуляції такі самі,
як і мережі трилатерації, але у
трилатерації вимірюють тільки довжини
сторін, а в тріангуляції - кути і хоча
б одну (дві для контролю) сторони.
Мережі
побудови тріангуляції 4 класу та І і II
розрядів подано на рис. II. 1.7.
Ланка
трикутників повинна спиратися на два
вихідні геодезичні пункти (бажано на
початку і у кінці ланки) і на дві сторони,
що прилягають до цих пунктів.
Суцільна
мережа тріангуляції повинна спиратися
не менш ніж на три вихідні пункти і на
дві вихідні сторони. Вихідними можуть
бути сторони полігонометрії, трилатерації
або тріангуляції вищих класів, а також
сторони
112
Показники |
4 клас |
І розряд |
II розряд |
|
Довжина сторони трикутника, не більше за, км |
5 |
5 |
3 |
|
Мінімальна допустима величина кута, ° |
у суцільній мережі |
20 |
20 |
20 |
сполучного кута в ланці трикутників |
ЗО |
зо |
зо |
|
у вставці |
ЗО |
ЗО |
зо |
|
Кількість трикутників між вихідними сторонами або між вихідними пунктами і стороною, не більше за |
10 |
10 |
10 |
|
Мінімальна довжина вихідної сторони, км |
2 |
1 |
1 |
|
Граничне значення середньої квадратичної похибки кута (обчисленого за нев’язками трикутників), " |
2 |
5 |
10 |
|
Допустима нев’язка у трикутнику, " |
8 |
20 |
40 |
|
Відносна похибка вихідної базисної сторони, не більше за |
1:200000 |
1:50000 |
1:20000 |
|
Відносна похибка визначення сторони у найслабшому місці, не більше ніж |
1:50000 |
1:20000 |
1:10000 |
|
113
розрядної
тріангуляції, якщо її довжина не коротша
за 1
км, а точність її вимірювання не нижча
від зазначеної у табл. II. 1.7. У цій самій
таблиці подано основні вимоги до
побудови мереж тріангуляції 4 класу та
І і II розрядів.
Розрядні
мережі полігонометрії, трилатерації,
тріангуляції 4 класу та І і II розрядів
будують з метою згущення геодезичних
мереж до щільності, що забезпечує
знімальну основу великомасштабного
знімання. Проте найпоширенішим із
цих трьох методів є полігонометрія.
Тріангуляцію застосовують тільки на
відкритій і гірській місцевості або
якщо (з будь-яких причин) застосування
полігонометрії неможливе. Своєю чергою,
трилатерацію застосовують тоді,
коли (з будь-яких причин) неможливі
кутові вимірювання. Крім того, оскільки
в полігонометрії виконують як лінійні,
так і кутові вимірювання, а в трилатерації
- тільки лінійні, у тріангуляції - тільки
кутові, тоді з методичного погляду
достатньо детально розглянути технологію
створення полігонометричних мереж,
щоб навчити майбутнього інженера
виконувати побудову мереж тріангуляції
та трилатерації. Зауважимо, що метод
полігонометрії, відповідно до
основних положень створення ДГМ України,
не використовується для побудови
астрономо-геодезичних мереж 1 класу
(АГМ-1), на відміну від основних положень,
прийнятих у СРСР.
Проте
цей факт не говорить про зменшення
інтересу геодезистів до полігонометрії.
З появою світловіддалемірів можливості
продуктивності та точності полігонометрії
значно зросли. Відмова в основних
положеннях України від полігонометрії
під час створення державних геодезичних
мереж 1 класу обґрунтована появою
супутникового методу створення
високоточних мереж, який значно
досконаліший за полігонометрію, особливо
під час вимірювання значних довжин
ліній в сотні кілометрів. Проте
полігонометрія залишається ефективною
під час створення
просторові
геодезичні мережі на геодинамічних
полігонах;
спеціальні
мережі геодезичного забезпечення
будівництва та виконання спостережень
за деформаціями, насамперед унікальних
споруд, таких, наприклад, як прискорювачі
елементарних частинок;
спеціальні
мережі вивчення рухів земної кори у
регіонах видобування корисних копалин;
спеціальні
мережі в сейсмоактивних регіонах для
прогнозування землетрусів, запобігання
природним та техногенним катастрофам.
Такі
мережі відіграють важливу роль у
прогнозуванні майбутнього планети
Земля, у збереженні чистоти довкілля
та у житті людства.
Вищенаведені
параметри побудови мереж згущення
такі, як вимагає цього чинна інструкція
[5]. Проте враховуючи, що сьогодні
зростають обсяги
114геодезичних
мереж спеціального призначення.
До таких мереж належать:
топографічного
знімання у масштабах 1:2000, 1:1000, 1:500, а
інколи (1:200, 1:100),
мережі згущення потребують кардинальної
реконструкції, оскільки вони не
забезпечують вимог великомасштабного
топографічного знімання.
Наприклад,
хід полігонометрії 4 класу завдовжки
14 км, якщо кількість
Шо
сторін
я=15, а —=- = 1:25000 та =5”, матиме максимальну
похибку всередині
ходу
або нев’язку, що дорівнює
1:500
відповідно 0,4 м, 0,2 м, 0,1 м. Сучасні методи
вимірювання кутів, а особливо ліній,
дають змогу підвищити точність
полігонометрії 4 класу до Mdo/J=0,l
м
з довжинами ходів до 8
км. Такі ходи можна будувати на основі
ДГМ згущення 3 класу (середня довжина
сторін ДГМ 3 класу - 6
км). Тоді немає потреби у мережах І та
II розрядів, оскільки їх замінять
теодолітні та тахеометричні ходи
лінійними вимірюваннями, виконаними
електронними методами.
Полігонометрію
класифікують за такими трьома ознаками:
Призначення.
Точність.
Спосіб
вимірювання ліній.
Покажемо
класифікацію на схемах.
Під
115SМ
=0,44 м за допустимих похибок координат
пунктів Мдопкоорд,
якщо знімання виконується в масштабах
1:2000,
1:1000,Класифікація полігонометрії
траверсною
полігонометрією розуміють таку, у якій
прилади для вимірювання довжин
безпосередньо вкладають у створі лінії,
що вимірюється. Такими приладами в
полігонометрії є підвісні мірні дроти
та рулетки. У віддалемірній
полігонометрії прилади для вимірювання
довжин безпосередньо в створі ліній
не вкладають. Лінії вимірюють посередніми
методами. У віддалемірній полігонометрії,
позначеній на схемі цифрами 1,
2,
3 визначають довжини сторін
полігонометричного ходу посередньо;
у віддалемірній полігонометрії,
позначеній цифрами 4, 5, 6
створюють допоміжні геометричні
побудови, у яких вимірюють не сторони
ходу, а коротші відрізки-базиси; потім
довжини сторін обчислюють аналітично.
Геометричні побудови для визначення
довжин сторін ходу називають
полігонометричними
ланками.
У полігонометричних ланках базиси
завжди розташовувалися перпендикулярно
до сторін ходу. Тільки в ланках,
запропонованих професором А.Д. Моторним
[13], базиси є частинами ліній сторін
ходу. Такі ланки названі новими
ланками
і віднесені до інших видів полігонометрії.
У нових ланках до сторін ходу
встановлюють
перпендикуляри значної довжини (довжини
перпендикулярів не вимірюють). Це дає
змогу позбутися гострих кутів у ланках
полігонометрії без довгих базисів, що
значно підвищує точність визначення
сторін ходу. Зауважимо, що з появою
електронних відцалемірів види
полігонометрії 4, 5, 6
значно
втратили актуальність. Це стосується
і траверсної полігонометрії.
Ознаки
Призначення
Точність
Спосіб
вимірювання ліній
-
світловідцалемірна;
-
радіовідцалемірна;
-
оптично-віддалемірна;
-
паралактична;
-
відцалемірно-базисна;
-
інші види
Рис.
11.1.8. Схеми класифікації полігонометрії
Полігонометричні
ходи, як і теодолітні, є кутомірними, у
них вимірюють кути та лінії. Тому
принципово полігонометричні та
теодолітні ходи нічим не відрізняються.
Різниця тільки в точності вимірювання
як кутів, так і ліній. У полігонометрії
ці вимірювання у десятки, а інколи в
сотні разів точніші. Але формули для
визначення нев’язок у полігонометричних
і теодолітних ходах однакові. Виведемо
ці формули, хоча вони вже виводились в
курсі “Топографія”.
Нехай
на місцевості прокладено довільний
полігонометричний хід (рис. II. 1.8).
Пункти
116

1.8. Формули для обчислення кутових та лінійних нев’язок у ходах полігонометрії
Тп
та Тк
є одночасно початковим та кінцевим
пунктами полігонометричного ходу Рх
та Рп+1;
зрозуміло, що ці пункти відповідно
мають
однакові
координати;
Рис.
11.1.9. Полігонометричний хід, прокладений
між початковим Тп
та кінцевим Тк
тріангуляційними
пунктами з відомими координатами Xп,
Уп ІХК,
ук
Як
відомо, кутова нев’язка /р - це різниця
між практичною сумою кутів, тобто між
сумою виміряних кутів полігонометричного
ходу (правих або лівих)
И+1 И+1
X
Ряряш
* те°Ретичною
(безпомилковою) сумою цих кутів £ $тП(Л)
> тобто:
і (
’ і
(
’
И+1 И+1
/р
= X Ря/>Я(Л)
“X
РтЩЛ)
Виникає
запитання: як знайти теоретичну суму
кутів? Користуючись відомою залежністю
між дирекційними кутами а, та кутами
повороту (3,, можемо записати для
виміряних
и+1
лівих
кутів:
і
И+1
правих
кутів: =
ап
+ 180°(п +1)
-
ХРгя- (И.1.4)
1
117п-
кількість сторін ходу; (и + 1)-
кількість кутів цього самого ходу.
Відомі також дирекційний кути ліній
А-Тп
і Тк
—В,
які показані на рисунку відповідно ап
таак.
Будемо вважати відомі координати та
дирекційні кути такими, що не мають
похибок. Хід прокладено для визначення
координат пунктів полігонометрії Р2,
Р3,
...,РП.
Допустимо, у ході виміряні усі ліві
кути (3Z-,
зокрема межуючі та pw+1,
та довжини сторін St
(і
= 1,
2,...,
п).
■ (п-1
-2)aK
=ctn
+
ХР тл
-180°(w
+ l); (II.
1.3)
Формули
(II. 1.3) і (II. 1.4) справедливі тільки за
умови, що суми кутів без похибок, тобто
є теоретичними сумами.
Розв’яжемо
ці формули стосовно теоретичних сум
кутів. Одержимо:
71+1
ІРг*
= «* -«я +180°(и +1); (ІІ.1.5)
1
72+1
І Ргя
= «я - +180
1
Підставивши
значення теоретичних сум кутів з формул
(II. 1.5) та (II. 1.6) у формулу (II. 1.2), отримаємо
кінцеві формули для визначення кутових
нев’язок, як у разі вимірювання лівих,
так і правих кутів.
72+1
і
71+1
і
Знаючи
нев’язки, введемо у виміряні кути Pz
поправки,
а також знайдемо дирекційні кути усіх
ліній ходу. Потім, використовуючи
виміряні значення ліній
1=7! 2=72
приростів
координат Ax//zp
та]Г
A
2=1 2=1
кінцевої
точки ходу
'
2
=72 2
=72 2
=72 2
=72
/*
= X Ьхіщ,
-
X ^ІТ
і fy
=
X дЛлр
- X АКіг •
2=1
2=1 2=1 2=1
2
=72 2
=72
Враховуючи,
що £ Дхг/г
= % - •% І X 4>V
=
Ук~Уп>
зможемо записати 2=1 2=1
кінцеві
формули для визначення
118°{п
+1). (II.
1.6)Нл
=ХРярл
-а* +ося
-180°(и + 1); (П.1.7)/Ря=ХРлря
-а/7 -180°(Л
+ 1). (II. 1.8)Sj,
обчислимо прирости координат Axt
та
Ayt
і
знайдемо практичні сумиyt ,
а також координати Х'к
та Y'KР'+1.
На рис. II. 1.8 точка Р'+1
не збігається з точкою Рп+1
• Отже, обчислені координати кінцевої
точки Р'+\
виявляться не такими, як відомі координати
точки Рп+Х
-XK,YK.
Відрізок
Рп+Х
- К*
1
позначимо fs.
Це абсолютна нев’язка ходу. Спроектуємо
fs
на
координатні осі X
та У. Отримаємо нев’язку по осях: fx
та
f
.
Отже, рис. П.1.8 дає геометричну інтерпретацію
нев’язки: виявляється, /хта
f
є
катетами прямокутного трикутника Pn+l
P'+l
N.
Гіпотенуза цього трикутника - fs.
Абсолютні нев’язки по осях fx
та
fy
полігонометричного
ходу можна знайти за різницями практичних
та теоретичних сум приростів координатfx
та
.
(II.
1.9)
fx
= yLAxinP
-(%-%);
/y=X4>V-ІУк-Уп)-
(II.
1.10)
Нехай
маємо висячий, рівносторонній, витягнутий
хід (кути повороту Р, витягнутого ходу
близькі до 180°), див. рис. II. 1.10.
Висячим
називають хід, що має тільки одну точку
з відомими координатами, зазвичай
на початку ходу.
Рис.
II. 1.10. До пояснення причин поздовжніх
t
та
поперечних и похибок висячого,
витягнутого,
рівностороннього полігонометричного
ходу
Нехай
безпомилкове положення кінцевої точки
ходу
Своєю
чергою, як це видно з попереднього рис.
II. 1.8:
1191.9. Поздовжні та поперечні похибки витягнутого полігонометричного ходу
-Рп+\.
Якщо потім на плані графічно побудувати
хід за виміряними лініями та кутами,
то в результаті похибок вимірювань
(результатами похибок графічних побудов
нехтуємо) кінцева точка ходу займе
деяке інше положення -Р'+\;
f$~
абсолютна
нев’язка ходу. Проте, оскільки хід
витягнутий, то похибки вимірювання
ліній можуть викликати зсув кінцевої
точки Рп+1
тільки вздовж ходу [18,21] (праворуч або
ліворуч). На рис. II. 1.9 цей зсув позначимо
t.
Своєю чергою, похибки вимірювання кутів
здатні викликати тільки поперечний
зсув кінцевої точки ходу (вверх або
вниз). На рис. II. 1.9 цей зсув позначимо
и.
З прямокутного трикутника Pn+l
N Р'+ї
можемо записати:
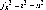

|
(II. 1.12) |
|
|
|
(II. 1.13) |
Знайдемо и: |
|
«
= —. |
(II. 1.14) |
Тоді можемо записати |
|
2
2
^ |
(П. 1.15) |
120
або
yfs
(II.
1.16)
T-r mh
Позначимо
уГі
коефіцієнт
випадкового впливу (випадкова похибка
на
одиницю довжини). Справді, приймаючи /
= 1, маємо
ms
=\l4s .
(II.
1.17)
Для
ходу завдовжки
mLb
=|WI. (II.
1.18)
Далі,
припустимо, що під час вимірювання тієї
самої лінії завдовжки
Запишемо:
Позначимо
(II.
1.19)
З цим
позначенням формула (II. 1.19) набуде
вигляду:
mSc=XS. (II.
1.21)
Для
ходу завдовжки L
матимемо:
mLc=\L. (II.
1.22)
Фактично
під час вимірювання одночасно діють
випадкові та систематичні похибки, і
ми можемо записати, враховуючи, що
поздовжній зсув витягнутого
полігонометричного ходу t
= mL:
t2
=mL2
=ц2-L
+ X2
L. (II.
1.23)
Для
підвісних мірних приладів відомі
коефіцієнти |і та
121—=г
= іі\і
= ть
,
З цим позначенням формула (II. 1.16)
набуває вигляду:L,
за аналогією, запишемо:S
діють
тільки систематичні похибки тс
(такі похибки не змінюють знака).S
=
п
■ І.
Тодіms
=п
тс,
або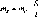
^
= Х, (II.
1.20)X-
коефіцієнт систематичного впливу
(систематична похибка на одиницю
довжини). Справді, якщо І
=1, то тс
= А,.X.
Тому на основі формули (II. 1.23) ще до
вимірювання, наперед (апріорно) можна
розрахувати очікуваний поздовжній
зсув /.
Далі
виведемо формули очікуваних поздовжніх
похибок відцалемірної полігонометрії.
У геодезичній практиці найпоширеніша
світловіддалемірна полігонометрія,
менше - радіовіддалемірна.
Вимірювання
ліній світло- та радіовіддалемірами
має одну важливу відмінність від
вимірювання ліній підвісними приладами
у траверсній полігонометрії. У траверсній
полігонометрії мірний прилад, який має
постійну довжину (температурними
впливами на зміну довжини приладу
будемо тут нехтувати), вкладається в
лінії
У
світло- і радіополігонометрії вимірюють
не частини, а цілі лінії, що мають різні
довжини. Зміняться і похибки, що виникають
під час вимірювання. Тому для апріорних
розрахунків точності таких вимірювань
потрібно знати не тільки характер
впливів (випадковий чи систематичний),
але й залежність або незалежність
джерел похибок від довжини лінії
Проте
усі ці похибки залежні від довжини ходу
ms2
=\l23-S
+ \l2H+X23S2+Х2Н. (II.
1.24)
mL2
=\l\ L + \l2h-L
+ Xj L2
+X2H
L2. (II.
1.25)
Надалі,
у п. “Світловіддалемірна полігонометрія”
буде показано, що існує сім основних
джерел похибок, які діють на вимірювання
електронними (світло та радіо)
віддалемірами:
Похибка
приведення ліній до горизонту (
залежить
переважно від характеру рельєфу (більша
- у горбистій місцевості, менша - у
рівнинній). Значно менше залежить від
довжини лінії.
122п
разів і похибки кожного відкладання
можна вважати однаковими.іS'.
Отже,
усі похибки у світлорадіовіддалемірних
вимірах поділяють на чотири групи:
L
(від
кількості сторін ходу я). Випадкові
пропорційні до -Jb
(пропорційні
до yfn),
а
систематичні пропорційні до L
(пропорційні
до п).
Тому загальну формулу для окремих ліній
ms
та
ходу mL
можна
записати так:
mSh).
Похибка випадкова,
Похибка
вимірювання різниці фаз
Похибка
визначення сталої віддалеміра (лі5
). Похибка діє під час
вимірювання,
як систематична, безпосередньо не
залежить від довжини лінії, накопичується
прямо пропорційно до кількості ліній
ходу, а отже, посередньо Залежить від
довжини ходу.
Похибка
визначення циклічної поправки фазометра
(
цієї
поправки залежить від тієї частини
різниці фаз, що компенсується
фазообертачем, тобто від значення
відліку фазометра. Отже, поправка -
змінна величина. Похибка визначення
цієї поправки -
залежить
від
Похибка
відхилення основної частоти віддал
еміра від заданої номінальної
частоти (
Похибки
центрування приймача та редукції
відбивача для світловід- далемірної
полігонометрії (
одну.
Ця сумісна похибка випадкова і не
залежить від
Похибка
робочої швидкості ЕМХ (світлова хвиля
- для світло- відцалемірів, радіохвиля
для радіовіддалемірів) (
і має
переважно систематичний характер. Це
тому, що хвиля зазвичай проходить
над поверхнею землі вище ніж середнє
значення висоти, на якій виконують
вимірювання метеопараметрів: біля
випромінювача та приймача ЕМХ, а густина
повітря (показник заломлення повітря)
змінюється з висотою.
Отже,
розділивши усі сім похибок за їхнім
характером на чотири групи, можемо
записати:
Враховуючи
формули (II. 1.26), можемо (II. 1.24) та (II. 1.25)
записати в розгорнутому вигляді: +
(II.
1.26)
іSf2.S2+mSc2.S
+ mSk2.
(II.
1.27)
Ф
-1
+ тч,р2
'L
+
(II.
1.28)
123(msA^)-
Похибка
випадкова, незалежна від S.
ms
).
Величинаms^
. Ця похибка випадкова, неS.
ms
).
Похибка систематична, залежить від S.тц
). Ці похибки діють сумісно і тому
об’єднані вS.
mSc
).
Похибка залежить від S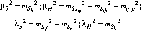

Формули
(II. 1.27) та (II. 1.28) є строгими, але неприйнятними
для попередніх розрахунків, оскільки
в них усі сім похибок невідомі. Проте,
як бачимо, три похибки
Отже,
практично усі чотири випадкові похибки
не залежать від
V2
=msh2
+ msJ +mSs2
+тц,р2’^2
=msf2
+ms2
+m
Sk
Отже,
для деякої лінії
ms2=ii2+k2-SKM2. (II.
1.29)
Відповідно
для ходу будемо мати:
mL2
=
\і2
-L
+ X2
І2. (П.1.30)
Порівнюючи
(II. 1.23) для ходу завдовжки
Проте
фірми, що виготовляють прилади, та
інструкція [5] рекомендують визначати
очікувані похибки вимірювання ліній
електронними відцалемірами, використовуючи
рівняння прямої регресії
т^ц
+ Х-^КГ6. (II.
1.31)
У
(II. 1.31) рта
Для
ходу чинна інструкція пропонує формулу
Як
бачимо (II. 1.31), не враховує, що деякі
джерела випадкових і систематичних
похибок можуть мати протилежні знаки
і компенсуватися. Формула додає похибки
незалежно від їхніх знаків. Тому формула
буде прогнозувати більші похибки в
лінії, ніж насправді. Навпаки (II. 1.32),
для ходу допускає, що усі похибки
накопичуються як випадкові. Тому ця
формула буде прогнозувати змінні
похибки для ходів однакової довжини з
різною кількістю сторін. Покажемо це
на конкретному прикладі. Для сучасних
віддалемірів |Х змінюється у межах 5-30
мм, а
ms2
=
202
+ 52
=
20,6 мм.
124ms^,
т3ф
, тц
р
є випадковими та не залежать від S,
аms
також
випадкова й істотно залежить від рельєфу
і мало залежить від S.S.
Усі три систематичні похибки залежні
від довжини лінії або довжини ходу.
Тому з незначними неточностями можемо
усі похибки об’єднати в дві групи:
випадкові, суму яких позначимо |і, та
систематичні, суму яких позначимо X.
Тоді:S
знайдемо
очікувану похибку за формулоюL
траверсної
полігонометрії з (ІІ.1.30) для
світловіддалемірної полігонометрії
такої самої довжини L,
зауважимо,
що вони ідентичні.X
у міліметрах, S
у
кілометрах.mL~ms
' • (II.
1.32)X
- у межах 2-10 мм на 1 км. Нехай довжина
лінії S
=
1 км, а |і = 20 мм, Х=
5 мм. Тоді за (II. 1.29):
За
формулою регресії (II. 1.31) маємо:
Як
бачимо, різниця незначна, а оскільки
застосування формули регресії дещо
збільшує, а не зменшує очікувану похибку,
то для попередніх розрахунків такий
спрощений метод можна використовувати.
Дослідимо, як зміниться суть для
конкретного ходу. Нехай полігонометричний
хід складається з
Тоді,
за точнішою формулою (II. 1.30) маємо:
За
(II. 1.32) матимемо:
Результат
справді дещо менший, хоча й незначно.
Проте під час зміни довжини ліній цей
результат буде змінною величиною.
Справді, нехай
За
формулою (II. 1.32) матимемо:
Як
бачимо, похибка на 1/3 більша від
очікуваної.
Отже,
для розрахунків похибок ходів краще
користуватися формулою (II. 1.30). Проте
для оптимальної довжини сторін
a
Необхідно
зробити ще два зауваження. По-перше,
подані вище розрахунки очікуваних
похибок враховують тільки похибки
вимірювання довжин, але не враховують
похибки вихідних даних (похибки відомих
координат початкової та кінцевої точок
ходу). Ці похибки можуть змінити апріорно
розраховані нев’язки. По-друге, отримані
похибки
Для
спрощення виведення знову будемо
розглядати витягнутий, рівно- сторонній
хід.
Нехай,
під час вимірювання кута зроблена
похибка , а усі інші кути - безпомилкові.
Тоді хід повернеться на кут і кінцева
точка ходу
125ms
=
20
+ 5 = 25 мм.п
= 14 ліній, S=
1
км, L=14
км - максимальна допустима довжина
ходу.mL2
= 202
• 14 + 52
• 142;
mL
=
102,5 мм.mL
=
25 мм • л/Ї4 = 93,5 мм.S
=
250 м, тоді для L
=
14 км, п=
56. Тому відповідно матимемо для лінії:
за точною формулою (ІІ.1.29) ms
=
20,04 мм; за формулою регресії (П.1.31) ms
=
21,25 мм. Для ходу за точною формулою (II.
1.30) результат не зміниться, mL
=
102,5 м.ть
= 21,25 мм >/56 = 159,02 ММ.S
=
500 м, матимемо п
= 28,mL
=
22,5
мм • V28
=119,06
мм. Тепер результат завищений тільки
на 16 %.ms
та
ть
є середніми квадратичними. Допустимі
похибки приймаються як подвійні середні
квадратичні.
1.11. Виведення розрахункової формули поперечної похибки висячого полігонометричного ходу
зсунеться
знаки.
Зсуви wz
також
будуть з різними знаками. Тому для
визначення загального поперечного
зсуву необхідно додавати квадрати
окремих зсувів.
Рис.
II. 1.12. До розрахунку поперечного зсуву
кінцевої точки
висячого полігонометричного
ходу
Будемо
розглядати
Тому
щ
_ Wp
Ul=^Sn. (II.
1.34)
Р
Ж Ж
то та
За
аналогією:
Р Р
Відповідно
до (II. 1.33) матимемо:
*2
У
(II. 1.35) у квадратних дужках сума квадратів
натурального ряду чисел
.
,
від
1
до
126Hat/j.
Насправді,
похибки можливі і в усіх інших кутах
і,
відповідно,
матимемо зсуви и2,
и3,
... ип.
На рис. ІІ.1.12 зображено випадок, коли
усі виміряні кути більші від безпомилкових
на щ,
тобто коли діють однакові систематичні
кутові похибки; насправді похибки тр
випадкові, змінюють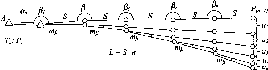
и2
= и,2
+ и22
+... + и2. (П.
1.33)щ
як дугу, описану радіусом L
= S п.S
n~
р'
’и2
=—у
• S
•
(и -1) ...м„ = —у
• S.и2
=^-S2[n2
+(и-1)2
+... + 12]. (II.
1.35)п(п
+ 1)(2и
+1)п,
яка дорівнює: — .
.2 _ Т2 п + 5 1 — . ' L р'2 3 |
(II. 1.39) |
іп+і,5 р' \ з |
(II. 1.40) |
Перейдемо
до загальної похибки М
у положенні кінцевої точки ходу:
Але
поздовжній зсув відповідно до формули
(II. 1.30) складається із випадкових та
систематичних похибок:
t2
=mL2
=\і2
-L
+ X2
-L2. (II.
1.42)
Технологія
вимірювання ліній забезпечує зменшення
систематичних похибок до мінімуму.
Тоді, нехтуючи систематичними похибками,
загальну похибку
M2=R2.z
+ ^.i2«
+ l,5
*2
Перейдемо
до відносної похибки
М)2
(II.
1.43)
(II.
1.44)
127M2=t2+u2. (П.1.41)М
можна описати формулою=у2_
П$
и + 1,5
L)
L+p'2
З
Виразимо
коефіцієнт випадкового впливу |і через
похибки лінійних вимірів. На підставі
(II. 1.17) запишемо:
Звідси:
Ц2=^-
(II.
1.46)
Підставимо,значення
ц2
з (II. 1.46) у (II. 1.44) і отримаємо:
ms2
(S
{т&2
п +1,5
[і
J
(II.
1.47)
або
п
+ 1>5
L
) ~п{ S
) +
р”2
З
(II.
1.48)
Формулу
(II. 1.48) широко використовують під час
апріорних розрахунків очікуваних
похибок, оскільки для розрахунків
необхідно знати тільки відносну
тч
похибку
вимірювання ліній —— та похибку
вимірювання кутів
Якщо
полігонометричний хід прокладено між
пунктами з відомими координатами та
дирекційними кутами, то максимальний
поперечний зсув ходу буде всередині
ходу. Для парної кількості сторін
-+і
2
ходу,
що має помилкове положення, будемо
мати, відповідно, зсуви
якщо
рухатися від початку ходу до середини
та навпаки, від кінця ходу до середини,
як показано на рис. П. 1.13.
Виведення
відповідної формули спроститься, якщо
цей хід розглядати як два незалежні,
висячі ходи, оскільки формулу для
висячих ходів ми вже маємо.
Для
парної кількості сторін будемо мати
сторін
першого та другого висячих ходів.
Логічно записати, що
128ms=\i-Js. (II.
1.45)nS
р'2
З.1.12. Виведення формули поперечної похибки полігонометричного ходу з попередньо ув’язаними кутами
п,
для точки Р
всерединіщ
та и2,щ
= п2
= ^, де щ
та п2
-
кількістьщ=и2.
Загальний
зсув становитиме:и2
= и2
+ и2
= 2mj2
=
2 и2. (II.
1.49)
Рис.
II. 1.13. Поперечний зсув середньої точки
ходу
На
рисунку:
-+і
2
-+і
2
початкової
точки ходу
-+і
2
точки
ходу
На
основі (II. 1.35) можемо записати:
и
= 2-
Ші
*2
р
s2
ЩІЩ
+1)(2Щ
+1)
*2
(II.
1.50)
Оскільки
п
*2
U>=2
9-
(II.
1.51)
Спростимо
(II. 1.51), помноживши та розділивши праву
частину на 2:
Г2 б
2
U
=-
•S‘
(II.
1.52)
Якщо
помножимо та розділимо праву частину
на и, то одержимо:
.2
и
=-
*2
12
(II.
1.53)
129
Рп
-
безпомилкове розміщення середньої
точки;Р„ -
розміщення точки, якщо її координати
обчислювались відТп;Р*
-
розміщення точки, якщо її координати
обчислювались від кінцевоїТк.m
=
—, то:
1
2*2_mV
,52
и(и + 2)(и
+ 1)_и
або
2
_nf
Т2(П
+ 1)(П
+ 2)
19
и
(II.
1.54)
Перетворимо
праву частину чисельника рівняння
(II. 1.54), нехтуючи двійкою (це майже не
спотворить результату. Справді, для
(п
Підставивши
отриманий результат, будемо мати:
Отже, ' — _ 1 JL/ • р'2 12 |
(II. 1.55) |
р V 12 |
(II. 1.56) |
Порівняємо
поперечні зсуви висячого ходу та ходу
такої самої довжини, прокладеного між
точками з відомими координатами. Для
цього достатньо порівняти формули (II.
1.40) та (II. 1.56), вони відрізняються тільки
підкорінним дробом. Не будемо звертати
увагу на різницю в чисельниках. Знаменник
12 формули (II. 1.56) розкладемо на 4 і 3 і
запишемо:
..іа-ь
2
Р
и
+ 3
(II.
1.57)
Отже,
поперечний зсув такого ходу практично
зменшується вдвічі.
Кінцевий
проект геодезичної мережі пунктів
затверджують після рекогностування.
Головними завданнями рекогностування
є:
уточнення
проекту мережі;
остаточний
вибір трас полігонометричних ходів;
остаточний
вибір місць закладання пунктів;
остаточний
вибір типів знаків, якими закріплюють
геодезичні пункти мереж тріангуляції,
трилатерації, полігонометрії.
Під
час рекогностування вибрані місця для
закладання пунктів закріплюють
тимчасовими знаками (кілками, металевими
штирями, обкопуванням тощо), і на них
складають абриси з прив’язуванням до
постійних місцевих предметів не менш
ніж трьома промірами. Під час закладання
знаків проміри уточнюють. Оскільки уся
територія України розміщена в зоні
сезонного
1301.13. Полігонометричні знаки
Рівень покриття *\ 1 “ |
|
|||
< Тверде покриття |
і |
с f |
|
|
|
«4 |
|||
|
«~20-н |
|
||
Рис.
II. 1.15. Центр пункту
полігонометрії,
тріангуляціУ,
трилатерації4 класу
1 і 2 розрядів для
міст Києва, Севастополя
і обласних
центрів (тип У15к)
Рис.
II. 1.16. Центр пункту
полігонометрії,
тріангуляції,
трилатерації4 класу
1 і 2 розрядів для
забудованих
територій, райцентрів,
міст, селищ,
сільських населених пунктів
(тип
У15)
131
Часто
застосовують видозмінений знак, що має
тільки один центр. Такий центр закладають
нижче від рівня землі, а зверху закривають
чавунним ковпаком із кришкою. Кришка
розташована нарівні з асфальтом або
землею зі знятим дерном. Такий знак
показано на рис. II. 1.15.
Ці
знаки закладають у великих містах та
обласних центрах. Для забудованих
територій, райцентрів, міст, селищ,
сільських населених пунктів застосовують
дещо інший тип знака, показаний нарис.
II. 1.16.
У
місцях суцільних забудов широко
застосовують настінні знаки
полігонометрії. Такий знак показано
на рис. II. 1.17.
Рис.
II. 1.17. Стінний знак пункту полігонометрії
4 класу,
Настінні
знаки полігонометрії закладають по
одному (одинарні), а також по два
(подвійні) та по три (потрійні). Стінні
знаки (за статистичними даними)
зберігаються на порядок більше років,
ніж ґрунтові.
На
пунктах мереж тріангуляції, трилатерації,
інколи полігонометрії, що створюються
як основа великомасштабного знімання,
для забезпечення видимості між сусідніми
центрами установлюють зовнішні
геодезичні знаки таких типів: металеві
піраміди-штативи з візирними цілями,
що знімаються, чотиригранні металеві
піраміди (див. рис. II. 1.18, II. 1.19, II. 1.20).
132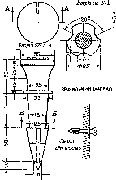
1 І 2 розрядів (тип 143)
Рис.
II. 1.18. Чотиригранна піраміда Рис. II.
1.19. Піраміда-штатив з кутової (з кутової
сталі) сталі (50x50x5
або
35x35x4)
з
малофазною
візирною ціллю, що
знімається,
з
висотою
до інструмен-
тального столика
від
1,2 до 4,0 м
Рис.
II. 1.20. Металевий переносний Рис. II. 1.21.
Г-подібна віха (дерев’яна або
майданчик
для спостереження з пірамід- металева)
штативів
виготовляється з кутової
сталі
(50x50x5
і
35x35x4)
Використовують
також Г-подібну віху (рис. II. 1.21).
133
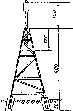

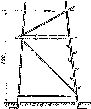
Візирні
цілі геодезичних знаків повинні бути
малофазними та мати такі розміри: висота
візирного циліндра - 0,5 м, діаметр - 0,25
м. Віддаль від інструментального столика
до нижнього диска візирного циліндра
повинна бути не меншою за 0,8 м. Малофазна
циліндрична поверхня створюється
краями радіально розташованих планок,
що прикріплені до дисків. Відхилення
проекцій центрів візирного циліндра
і столика для приладу від центрів пункту
повинні бути не більшими за 5 см.
Назвемо,
насамперед, основні види робіт під час
створення полігонометричних мереж
у послідовності їхнього виконання:
Складання
проекту.
Рекогностування,
вибір місця закладання та типів знаків.
Закладання
знаків.
Дослідження
та перевірки приладів.
Прив’язування
пунктів майбутньої (запроектованої)
мережі до пунктів державної мережі.
Лінійні
вимірювання.
Кутові
вимірювання.
Лінійні
і кутові вимірювання можуть виконуватися
окремо або одночасно.
Попередні
обчислення. Обчислення робочих
координат.
Виконання
зрівноваження.
Оцінка
точності виміряних та зрівноважених
величин.
Складання
каталогу координат.
Складання
технічного звіту.
Під
час проектування ходів потрібно,
відповідно до умов на місцевості,
прокладати їх, якщо можливо, прямолінійно.
Якщо виникає необхідність, допускають
викривлення ходу, проте з метою досягнення
більшої точності треба дотримуватися
правила, щоб хід якомога менше відхилявся
від основного напрямку. Хід
Як
видно з (II. 1.48), зі збільшенням довжини
ходу настає момент, коли другий член у
правій частині формули перевищить
перший і буде вирішальним щодо точності.
Зрозуміле бажання знайти спосіб зменшити
вплив похибок кутових вимірювань. Для
досягнення цієї мети вибирають через
декілька точок повороту ходу пункти з
розрахунком забезпечення їхньої
взаємної видимості.
134
1.14. Організація полігонометричних робіт
ABCDE,
пункти якого ближче до основного
напрямку АЕ,
за інших однакових умов, наприклад, за
однакового периметра, необхідно вважати
точнішим, порівняно з ходом GHK,
який має тільки один згин (див. рис. II.
1.22), а точка значно віддалена від напрямку
KG.
Наприклад,
на рис. II. 1.23 між пунктами тріангуляції
Е К
A G
Рис.
11.1.22. Урахування форми ходу
Рис.
II. 1.23. Підвищення точності передавання
дирекційних кутів
Під
час прокладання полігонометричного
ходу доцільно визначати по обидві
сторони ходу положення пунктів
1.24.
Ці пункти називають
135Тп
і Тк
вибрано пункти Е
і F
так,
щоб з точки Е
було видно точку Тп*
і навпаки, з точки F
-
точку
Тк
. Такі пункти (тут пункти Е
і F
)
називають головними
пунктами ходу або полігона. Для
забезпечення взаємної видимості в
таких пунктах, за необхідності,
встановлюють піраміди або піраміди-штативи,
а кути повороту між створеними лініями
Тп
Е
та іншими вимірюють найстаранніше;
окрім звичайних кутів повороту, вимірюють
ще й кути Вх,
В2,
В3
та В4.
Це дає змогу передати дирекційні кути
на лінії, використовуючи менше кутів
повороту і цим зменшити кутову нев’язку.
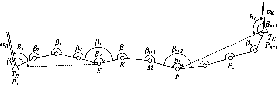
А,
В,
С, D,
Е,
показаних на рис.
боковими
пунктами.
Е
Рис.
II. 1.24. Визначення місцезнаходження
бокових пунктів
Під
час створення полігонометричної мережі
треба, за змогою, уникати різної довжини
сторін. Необхідно пам’ятати, що
найслабшим місцем ходу, що спирається
на дві відомі точки, є його середина.
Тому, коли два ходи близько сходяться
(менше за 2,0 км), середні точки
Рис.
II. 1.25. Приклад перетворення двох ходів
А-В
таС -D
на
мережу з п’яти ходів
Завдяки
ходу
У
траверсній полігонометрії лінії
вимірюють підвісними мірними приладами.
У
комплект таких приладів входять:
Сталеві
або інварні дроти завдовжки 24 м або 48
м - не менше від двох.
Верстати
із блоками для підвішування дротів -
2 шт.
136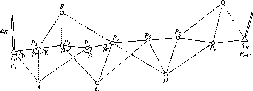
Q
та
R
цих
ходів необхідно зв’язувати додатковими
ходами. Так окремі ходи перетворюються
на мережу ходів, як це показано на рис.
II. 1.25.
Q-R
створена
мережа з п’яти ходів з двома вузловими
точками.
Лінійні вимірювання у траверсній полігонометрії
Прилади для вимірювання ліній у траверсній полігонометрії
Гирі
по 10 кг для натягування дротів - 2 пгг.
Тросики
з карабінами для з’єднання гир із
дротами - 2 шт. Тросики пропускають
через блоки.
Штативи
з оптичними центрирами - не менше від
двох. Штативи центрують над кінцями
лінії.
Штативи
із ціликами, які встановлюють у створі
ліній, що вимірюють, - 8-10
шт.
Візирні
марки - 1-2 шт.
Теодоліт
зі штативом (точність не менша за ЗО")
для встановлення штативів із ціликами
у створ лінії.
Нівелір
Н-3, Н-ЗК або інший зі штативом для
визначення перевищень між сусідніми
ціликами.
Двостороння
нівелірна рейка - 1-2 шт.
Термометр-пращ
для вимірювання температури дротів.
цілик цілик
1=10+(п-з)
8 7 6 5 4 3 2 1 0
І І І І І І І І
_'Y"~
З
задній
цілик
k
7
М0+(з+п)
0
1 2 3 4 5 6 7 8
І І
І
І
І І І 1
І
переб
цілик
Рис.
11.2.1. Найпоширеніші типи шкал мірних
дротів: і та II типи
Підставки
до теодоліта, оптичних центрирів та
візирних марок повинні бути універсальними
(тобто такими, щоб на них можна було
почергово встановлювати всі три названі
прилади). На кінцях мірних дротів
прикріплені пікали завдовжки 8-10
см із міліметровими поділками. Існують
три типи шкал. На рис. ІІ.2.1 зображено
шкали І та II типів. На цьому самому
рисунку показано,
137І тип шкал

11 Тип шкал
як
визначають віддалі (відрізок лінії
полігонометрії) між сусідніми ціликами.
Цілики схематично показані стрілками
(насправді, на верхньому зрізі цілика
нанесено два взаємно перпендикулярні
штрихи). Перетин штрихів на сусідніх
ціликах означає початок та кінець
кожного відрізка лінії.
Під
час вимірювання ліній дротами з І типом
шкал дріт має бути розташований так*
щоб поділки на шкалах зростали в напрямку
вимірювання лінії. Для дротів зі шкалами
II типу будь-яка шкала може бути як
задньою, так і передньою. У шкалах
ІП типу нульові поділки - посередині
шкал, а поділкам ліворуч і праворуч
від нуля присвоюють знаки. Такі шкали
не набули поширення.
На
рисунку відліки шкал позначені:
задній
відлік -
На
рис. ІІ.2.1 також подано формули, за якими
визначають довжину відрізка / між
сусідніми ціликами, залежно від типу
шкал.
//.2.2.
Виконання
лінійних вимірювань підвісними мірними
приладами
Нехай
вимірний дріт, натягнутий гирями за
гачки, що на кінцях шкал, завдяки
тросикам, які пропущені через блоки
спеціальних верстатів і шкали підняті
на однакову висоту (рис. ІІ.2.2).
.
kM
Рис.
11.2.2. Мірний дріт, підвішений на блочних
верстатах і натягнутий гирями
Висоту
дроту регулюють, змінюючи нахил блочних
верстатів. Висота дроту має бути такою,
щоб шкали доторкалися до ціликів і
можна було вимірювати довжину / між
сусідніми ціликами. Підвішений дріт
завжди буде мати прогин, який залежить
насамперед від сили натягу. Вимірювання
підвісними приладами, запропоновані
шведським геодезистом Едеріним,
ґрунтуються на тій властивості, що під
час постійного натягування дроту або
мірної рулетки
138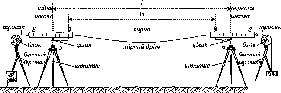
з,
передній -я, /0
- віддаль (по хорді) між нулями шкал, / -
довжина відрізка лінії (похила) між
сусідніми ціликами.
довжина
хорди /0
(між нулями шкал) - практично стала. Цю
хорду /0
і приймають за довжину мірного приладу.
Бригада
лінійних вимірювань поділяється на
три ланки:
Ланка
провішування - чотири особи. Завдання
ланки - зцентрувати оптичні центрири
над кінцями лінії, а також розташувати
створні штативи в створі лінії
(застосовуючи теодоліт) і на віддалях
приблизно 24 або 48 м (залежно від довжини
дроту), користуючись спеціальним дротом
або тросом відповідної довжини. Керівник
ланки, навівши трубу теодоліта на
візирну марку, що на протилежному від
теодоліта кіїїці лінії, повертає трубу
тільки у вертикальній площині, задаючи
створ. Два виконавці в створі розмічають
відрізки по 24 м (48 м), натягнувши трос.
Четверта особа ланки встановлює штативи
так, щоб цілики були в створі лінії.
Віддалі між суміжними ціликами також
контролюються дротом або тросом.
Ланка
вимірювання ліній - вісім осіб. Керівник
робіт; два техніки, які одночасно, за
командою керівника, беруть відліки
задньої та передньої шкал; двоє
робітників - тримають блочні верстати;
двоє - підвішують, знімають та переносять
гирі; старший технік - записує в журнал
результати вимірювань, вимірює
температуру повітря термометром-пращом.
На окремому відрізку лінії вимірювання
виконують так: подають команду:
“підвісити дріт”, техніки, що переносять
дріт у натягнутому стані (дріт під час
переходів до наступного відрізка не
повинен торкатися землі) з’єднують
дріт із тросиками та підтримують шкали
так, щоб вони не бились об цілики. Далі
команда: “приготувати гирі”, потім
через декілька секунд “гирі опустити”.
Коливання дроту під час натягування
можна загасити легкими дотиками біля
середини дроту. Під час вимірювань
тільки техніки, що беруть відліки,
злегка притримують шкали над ціликами
без зусиль уздовж лінії, дріт повинен
вільно провисати під своєю вагою. Далі
подають команду: “Увага! Відлік!”
Передній і задній техніки одночасно
беруть відліки з точністю до 0,1 мм.
Потім передній голосно називає свій
відлік. Записувач записує в журнал
139
Щ;
тільки після цього задній технік, що
запам’ятав свій відлік 31;
голосно називає його. Візьмемо шкали
І типу. Записувач розраховує: А1
= П1
- Зу.
Дріт дещо (на 1-3 см) зміїцують уздовж
лінії, щоб змінити відліки шкал. Це
робить передній технік. Далі відліки
повторяють. Знаходять Д2
=
П2
- 32,
А3
= Щ
- З3.
Зрозуміло, відліки змінюються, а різниці
відліків Aj,
Д2,
Д3
повинні
бути майже однаковими. Допускають
максимальне розходження між найменшими
та найбільшими значеннями А 0,5 мм для
/0
~ 24 м, та 1,0 мм для /0
~ 48 м. Якщо
ця
умова не виконується, беруть три пари
нових відліків. Якщо умова досягнута,
подають команду: “гирі зняти”, “дроти
відчепити”, “вперед”. Ланка переходить
до наступного відрізка лінії. На кожному
відрізку виконують вимірювання
температури одночасно з лінійними
вимірюваннями.
Ланка
нівелювання - 3 особи (нівелювальник,
записувач, рейковик), методом геометричного
нівелювання визначає перевищення
Отже,
бригада вимірювання ліній у траверсній
полігонометрії складається не менше
ніж з 15 осіб (8
інженерно-технічних робітників і 7
робітників). Зауважимо, що цей вид
геодезичних робіт вимагає найбільшої
бригади серед усіх інших видів геодезичних
робіт. Якщо послідовно встановлювати
штативи у створі, виконувати лінійні
вимірювання та нівелювання ціликів,
тоді можна обмежитися мінімальною
бригадою з 7 осіб. Але тоді час виконання
вимірювань збільшиться майже втричі.
Тому доцільною є описана організація
робіт. Зауважимо, що встановлення
штативів у створі інколи доцільно
замінити кілками (товщина не менше за
5 см, висота - не менше ніж 1 м), які
забивають у ґрунт. Тоді у верхні зрізи
кілків забивають особливі металеві
цілики, загострені в нижній частині.
У
полігонометрії 4 класу виконують
вимірювання одним інварним або сталевим
дротом у прямому та зворотному напрямах,
або двома такими дротами в одному
напрямі. Кожний відрізок (без переходів)
вимірюють одним і одразу ж іншим дротом.
Це значно економить час, хоча необхідно
ще двоє додаткових робітників, які
тримають другий дріт напоготові
розмотаним.
У
полігонометрії І розряду вимірювання
виконують одним інварним або сталевим
дротом тільки у прямому напрямку. У
полігонометрії II розряду - також одним
сталевим дротом, тільки у прямому
напрямку. Можна не брати відліки шкал,
а фіксувати під час натягування
розташування нульових поділок шкал
(наприклад, цвяхами).
Під
час вимірювання, як правило, дріт не
вкладається в лінію цілу кількість
разів. Є ще залишок, який називають
140
ht
між
сусідніми ціликами з контролем (по
чорній та червоній стороні рейки).
Допускають розходження до 5 мм, як і
під час виконання технічного нівелювання;
з однієї станції можна визначити 4
перевищення, якщо дріт 48 м, та 8
перевищень, якщо дріт 24 м. Максимальна
довжина плеча становитиме - 100 м. Створні
штативи можна знімати з місць тільки
після закінчення нівелювання.доміром.
Доміри вимірюють металевою рулеткою
з міліметровими поділками, яку натягують
так, що вона майже не провисає. Тому не
допускають, щоб домір був довший за Уг
довжини дроту. Якщо домір виявляється
довшим, тоді на продовженні створу
лінії встановлюють ще один штатив,
виміряють цей відрізок, який наближено
дорівнює
довжині дроту. У такому разі домір буде
від’ємним. Отже, під час лінійних
вимірювань бувають додатні і від’ємні
доміри. Домір також приводять до
горизонту. Для цього визначають
перевищення між кінцями доміру.
Будемо
вважати, що діє тільки десять джерел
похибок, а саме:
Компарування.
Компарування виконують для встановлення
фактичної довжини мірного дроту. Під
час компарування неминуче буде деяка
похибка, що має випадковий характер
(знак похибки невідомий). Припустимо,
що в результаті компарування знайшли
рівняння дроту: /0
= 24 м + 5,5 мм, якщо
Провішування.
Неточне встановлення ціликів у створ
лінії приводить до вимірювання лінії,
довшої від прямої. Похибка
Натяг.
Під час польових робіт масло, яким
змащують осі блоків, забруднюється
пилом, згущується: тертя блока з віссю
збільшується. У результаті, навіть для
тих самих гир, натяг зменшується, дріт
провисає більше. Похибка а3
систематична, подовжує лінію.
Вітер.
Вітер, особливо боковий (діє під деяким
кутом до напрямку лінії), додає дроту
деякої ваги, збільшує провисання дроту.
Похибка а4
систематична,
подовжує лінію.
Нахил
місцевості. Викликає нахил дроту.
Виміряне перевищення
Температура.
Під час вимірювання необхідно знати
температуру дроту. Фактично вимірюють
температуру повітря. Похибка ± Д6
випадкова.
Нестійкість
створних штативів. Приводить до
випадкової похибки ± Д7.
Похибка
відліку шкал. Похибка
Похибка
вихідних даних (координат). Впливає на
величину нев’язки. Похибка ±Д9
випадкова.
Інші
похибки. У цю групу ми зараховуємо
сумарну (спільну) дію неврахованих
джерел (наприклад, нахил шкал, похибка
ланцюгової лінії, тобто зміїіа довжини
від нахилу дроту тощо). Похибки ± Д10
випадкові.
141
Джерела похибок під час вимірювання ліній підвісними мірними приладами
t
°
= 15 °С. Нехай допустили випадкову похибку
0,2 мм, тобто насправді довжина дроту
/0
= 24 м + 5,7 мм, t°
=
15 °С. Похибка ох
0,2 мм під час вимірювання ліній стає
систематичною, діє для кожного
відкладання дроту з одним знаком
(скорочує довжину дроту у наведеному
прикладі).о2
систематична (подовжує лінію).h
між
сусідніми ціликами має випадкову
похибку ± Д5.±
Д8
випадкова.
Як
ми вже знаємо, похибки лінійних вимірів
витягнутого ходу приводять до поздовжнього
зсуву кінцевої точки.
Тому
запишемо:
t2
=
о,2
+
с22
+ <т32
+ с42
+ Д52
+
Д62
+
Д72
+
Д82
+
Д92
+
Д102.
(ІІ.2.1) Припустимо, що всі похибки мають
однакову абсолютну величину аі
=
/
= 4о = 4Д. (ІІ.2.2)
Сумарну
похибку
М2
=Г2
+и2.
Продовжуючи
принцип рівних впливів, приймемо:
М2
=212
=2и2,
М = іЛ,М = иЛ.
Перейдемо
до відносної похибки:
L
~Ta
°
L
~
L
~
Т
або
Отже,
t
_
и
_ 1
L
~
L
тЛ
'
Враховуючи
(ІІ.2.2), запишемо:
4Д
_ 4о _ 1
Т-Т-тч72
’
А
1
о 1
L~
Т-4-Л’
L~
Т-4-Л
'
(П.2.3)
(ІІ.2.4)
Беручи
до уваги, що 4 •
Д
__1_ o=J_
L
~
6Т ’ L
”
вТ
'
Отже,
допуск на окреме відкладання мірного
приладу завдовжки /, становитиме:
Д/
1 о,
І /
/
6Т
1 6
Т 1 1
6Т
142а2
=
аі
= Az
=
а = А (тобто діє так званий принцип
однакових впливів); врахуємо також, що
похибки 2, 3, 4 діють з одним знаком: і2
= а2
+
(Зо)2
+ 6Д2
= 16о2
= 16Д2.Розрахунок допусків на окреме джерело похибок лінійних вимірів
М
в місцеположенні кінцевої точки ходу
вираховують за формулоюt
=
и,
тоді:М_1абогТ2_иЛ _ 1
Л
=
5,66
= 6,
отримаємо:
Для
одного відкладання мірного дроту
допустимі похибки однакові: A/
= o,.
Для
полігонометрії 4 класу
А
/= О/ = ±0,16 мм.
Для
ходу, що має
_ A
для
випадкових похибок —
пк
6Т
Gj
к-п
1
1-п
к
_6Т'
Отже,
граничні випадкова та систематична
похибки ходу становитимуть:
/л/w
• к І
гранА
хгіу
= ,
гран
сходу
=
—.
Максимальна
допустима довжина ходу полігонометрії
4 класу - 14 км, для
Л
24000^28-20 гРанАходу
~ 6.25000
=
3,79 мм, грано^ф, =
24000
6-25000
=
0,16 мм.
Отже
(для граничного ходу), допуск на окреме
джерело систематичних похибок майже
в 24 рази менший, ніж на джерело випадкових
похибок. Це вказує на значну загрозу
систематичних похибок.
Далі
розглянемо, які похибки можуть викликати
окремі джерела під час виконання
вимірювання, та чи можливо виконувати
вимірювання так, щоб окремі джерела
похибок не перевищували допуск 0,16 мм
для / = 24 м та 0,32 мм для / = 48 м.
Похибка
компарування мірного приладу Як
уже відзначалося, компарування підвісних
мірних приладів виконують для встановлення
дійсної довжини приладу (мірного дроту)
/0
. Компарування виконують на стаціонарних
або польових компараторах.
Стаціонарні
компаратори створюють у закритих (як
правило, підвальних) приміщеннях, де
майже не змінюється температура. Базовою
мірою компарування є триметровий
еталон довжини. Якщо відкласти 8
довжин еталону, то створимо базис
завдовжки приблизно 24 м (саме тому
довжина дротів ~ 24 м). Довжина цього
базису відома з точністю до 1 мікрона
(0,001 мм)
143Т
= 25000, при І
= 24000 ммп
ліній, а в кожній лінії к
відкладень, запишемо:jyjn-k 1 _ =
—, для систематичних похибок -
S
=
500 м, п=
28, к
=
20, / = 24 м. Для Т
= 25000 матимемо:1Б
= 24 м + Аіб
мм
.
Далі цей базис вимірюють дротом (дріт
натягують гирями). Спочатку вважають,
що довжина дроту /0
= 24 м.
Нехай
для такого допуску отримали:
НеобхІДНО
ВИМІРЯТИ Температуру Приладу (вважаЄТЬСЯ
t
дроту
~ t
повітрі-
Наприклад,
На
стаціонарних компараторах зазвичай
компарують інварні дроти. Маючи
прокомпаровані інварні дроти, створюють
польові компаратори, на яких компарують
сталеві дроти. Під час створення польових
компараторів закладають у ґрунт на
рівній місцевості два фундаментальні
центри на віддалі ~ 240 м (10 відрізків по
24 м, або 5 по 48 м). Через деякий час, коли
ґрунт осяде, горизонтальну віддаль між
центрами вимірюють (як описано вище)
інварними, прокомпарованими дротами
6-8
разів (якщо один дріт, роблять три прямі
і три зворотні ходи, якщо два дроти -
кожним дротом два прямі, два зворотні).
У
результаті знаходять довжину компаратора
де
A
Вважають,
що довжина польового компаратора не
залежить від температури земної
поверхні. Далі цю довжину вимірюють
некомпарованими дротами (не менше ніж
чотири рази). Так само, як на стаціонарних
компараторах, спочатку вважають, що /0
= 24 м і знаходять деяку довжину компаратора
якщо
о *
Lk-L
Величина
поправки о = ———.
Рівняння
дроту: /0
= 24 м ± 5 мм для
Розрахуємо,
з якою точністю необхідно компарувати
дроти. Скористаємося формулою
°/_
=
JL
/ 6
Отримаємо:
а7=
0,16 мм (для / = 24 м), G/=
0,32
мм (для / = 48 м). Компарування з такою
точністю не викликає особливих проблем.
1441Б
=24м + Д/0
мм. Якщо справді А1Б
=
А/0,
тоді дріт має насправді 24 м. Якщо А/0
> А1Б
(результат вимірювання більший), то
дріт коротший на 8
= Д/0
- АІБ.
Під час компарування обов’язковоtnoeimpH
=
15 °С. Тоді для останнього рівняння
приладу запишеться так: /0
= 24 м - 5 мм .Lk
=
240м ± АЬк,Lk
відома
з точністю 0,1-0,15 мм.L,
для середньої температури tcep
.
Якщо L>Lk,
дріт
коротший,L
<
Ьк
- довший. Так знаходять знак поправки.tcep
=
15 °С.Т'
Похибка
укладання мірного приладу в створ лінії
Безпосередньо
з рис. II.2.3
можемо
записати формулу для похибки нестворності
А/:
А/
= / — jc
= / —s//2
—
4є2
.
створ
Рис.
11.2.3. Вплив неточного укладання мірного
приладу І у створ
(нестворність
кінців приладу-
Є) на
вимірювання лінії
Після
деяких перетворень матимемо:
А/
=
2е_
І
Знайдемо
допустиме значення є :
А/
_ 2е2
_ 1
звідси:
е
= /.
1
е
= 24000.
1
12Г
=
44 мм «4см.
(ІІ.2.5)
(ІІ.2.6)
(ІІ.2.7)
[12-25000
З
такою похибкою встановити у створ
цілики можливо, але потрібно виконувати
візування не окомірно, а зоровою трубою
теодоліта.
Похибка
за нахил мірного приладу
Рис.
11.2.4. Вплив нахилу h
мірного
приладу завдовжки І
на вимірювання
лінії
З
рис. ІІ.2.4 маємо:
Alh
=1-х.
(ІІ.2.8)
145
І
~ І2
~6Т
Після
перетворення отримаємо:
Alh
=
21
(ІІ.2.9)
Визначимо,
які малі перевищення
Д/*
/
— =
~, /г = \Р~
6
Т 212 V3
Т
Проте
точність визначення
Диференціюючи
(ІІ.2.9) за
прирівнюючи
ц до—, матимемо:
І2
гран
h-6T
Для
/ = 24 м, Л = 2 м, гран
Інструкція
допускає 2 мм для Л від 1 до 3 м.
Похибки
від неточного визначення температури
мірного приладу Під час зміни температури
мірного приладу змінюється його довжина,
тому можна записати:
Д/,
де
компарування
приладу.
Диференціюючи
(ІІ.2.11) за
Розв’язавши
(ІІ.2.12) відносно
(ІІ.2.13)
Для
сталі
Отже,
для сталі,
Вимірювати
з такою точністю температуру повітря
нескладно. Проте температура дроту
може значно відрізнятися від температури
повітря (на 10 °С і більше), тому із цією
похибкою боротися важко. Найкращий
спосіб - заміна
146h
можна
не враховувати під час вимірювання
ліній:h=
8,8
см для / = 24 м, h=
17,5
см для / = 48 м.h
повинна
зростати під час збільшення h,
оскільки відповідно до (ІІ.2.9) Д/А
пропорційна до И2.h
та
переходячи до відносної похибки і 1dh
= . (ІІ.2.10)dh
=
1,92
~ 2 мм.=a-l(t-t0), (ІІ.2.11)а
-
коефіцієнт лінійного розширення сталі
або інвару; І
-
довжина приладу; t-
температура
під час вимірювання ліній; t0-
температура
під часt,
матимемо:d(Al,)
= aldt. (ІІ.2.12)dt
і
перейшовши до допустимої відносної
похибки, отримаємо:dAl,
_
1
J_
а/
а 6Тас
= 0,0000124, для інвару аІН
= 1/40 ас.dt=
0,54
~ 0,5 °С.
сталевих
дротів інварними, для яких
Похибки
від зміни натягування мірного приладу
Відповідно
до закону Гука зміна довжини приладу
від зміни натягування
dAlP
=
EF‘
У
(ІІ.2.14)£- модуль еластичності, для сталі
Розв’язавши
(ІІ.2.15) відносно
EF
6
Т
20000-2
150
=
270 грам.
(ІІ.2.14)
20000
кг/мм2;
(ІІ.2.15)
(ІІ.2.16)
Отже,
вага гирі може відрізнятися від
номінальної ваги на
Похибки,
викликані впливом вітру
Вітер
має поривчастий характер, тому вплив
вітру різний у різні миті часу. Проте
доведено, що боковий вітер зі швидкістю
7,6 м/с може викликати додаткову вагу
дроту
Похибки
вимірювання, вихідних даних та інші
Найменша
поділка шкал дротів - 1 мм. Відлік шкал
виконують із точністю до 0,1 мм. Проте
розділити на 10 частин міліметр із такою
точністю важко. Будемо вважати, що
похибки відліків дорівнюють 0,2 мм. Тоді
похибка відрізка
пари
відліків, тоді середня похибка А
0,2-72
=
0,16 мм.
Допуск
випадкової похибки на окремий відрізок
також становить 0,16 мм. Отже, три пари
відліків - обґрунтовані.
Особливо
необхідно звертати увагу на похибки
центрування ціликів оптичними висками
над кінцями лінії, що вимірюють, та на
стійке встановлення створних штативів.
Загрозливими можуть бути похибки
вихідних даних.
147аін
приблизно в 40 разів менше ніж у сталі.
Не можна допускати, щоб дроти під час
вимірювання торкалися нагрітої земної
поверхні.dP
описується
формулоюIdPЕ
F
-
площа поперечного перетину дроту, F
~
2 мм2.
Перейдемо
до допустимої відносної похибкиdAIP
dP
_
1
/ ~EF~6T‘dP,
отримаємо:Ул
кг.dP
=
270 грам. Отже, під час вітру зі швидкістю
більше ніж 7 м/с вимірювання дротами не
можна виконувати.АІ
становитиме А/ = 0,2
мм ■ л/2
. Оскільки під час вимірювання беруть
триІсер
До
теодолітів, що використовуються для
кутових вимірювань у полігонометрії,
ставлять дві головні вимоги, практично
протилежні за своєю суттю. А саме,
теодоліти повинні:
Бути
легкими, переносними.
Забезпечувати
високу точність вимірювань горизонтальних
кутів.
Виявилося,
що ці дві вимоги найповніше задовольняють
оптичні
теодоліти.
Такі теодоліти мають не металеві, а
скляні круги із градусними поділками
для вимірювання горизонтальних та
вертикальних кутів. Останнім часом
оптичні теодоліти замінюють електронними
теодолітами, у яких скляні круги із
градусними поділками замінюють також
скляними кругами, але з умовними
позначками. Ці умовні позначки дають
змогу автоматизувати вимірювання.
Існують три системи автоматизації
відліків: кодова, імпульсна, динамічна.
Названими системами відліки кругів у
градусах (або в гонах) відображаються
на дисплеї теодолітів або тахеометрів.
Відповідно
до ДЕСТ теодоліти за точністю класифікують
на:
Високоточні
- Т 02, Т 05, Т 1 та багато інших.
Точні-Т2,ТБ,ОТБ.
Технічні
Т ЗО, 2Т ЗО.
Тут
перераховано тільки теодоліти,
найпоширеніші на виробництві. У табл.
ІІ.3.1 подані теодоліти та тахеометри,
що виготовляються сучасними, найвідомішими
у світі провідними фірмами.
Ще
на початку XX століття теодоліти
виготовляли тільки з горизонтальними
кругами, оскільки вони призначалися
для вимірювання горизонтальних
кутів. З розвитком геодезичного
приладобудування відбувалась
універсалізація теодолітів. У наш час
фірми вже не виготовляють теодоліти
без вертикальних кругів. Отже, теодоліти
перетворились на тахеометри, якими
можна вимірювати горизонтальні та
вертикальні кути, а також віддалі,
спочатку нахилені, за допомогою
ниткових віддалемірів, пізніше -
горизонтальні, особливими номограмами.
У
наш час випускають теодоліти обов’язково
з вертикальними кругами - не тільки
оптичні, але й електронні, які автоматично
відображають на дисплеї відліки кругів.
Ці теодоліти ще називають
148Кутові вимірювання у полігонометрії
Основні вимоги до кутомірних приладів у полігонометрії. Класифікація теодолітів та тахеометрів
цифровими.
У деякі теодоліти (фактично тахеометри)
умонтовано лазери для створних
спостережень та лазерні виски для
центрування. Такі прилади продовжують
називати теодолітами.
Тільки
після заміни в теодолітах оптичних
відцалемірів на електронні світловіддалеміри
фірми, що виготовляють геодезичні
прилади, назву приладу “теодоліт”
змінюють на “тахеометр”.
Насправді
усі сучасні теодоліти, оскільки ними
можна вимірювати одні й ті самі величини,
що й за допомогою тахеометра, можна
було б назвати тахеометрами. У таблиці
збережено назви “теодоліти” та
“тахеометри”, як це роблять
фірми-виробники.
Високоточні
та точні електронні тахеометри, в які
вмонтовані внутрішні комп’ютери,
здатні відображати на дисплеї не тільки
кути та довжини, але й просторові
координати пунктів і розв’язувати
цілу низку інженерно- геодезичних
задач, отримали назву тотальні станції
(total
station).
В
останні роки з’явилися електронні
тахеометри, що не потребують відбивачів.
Теодоліти та тахеометри, у яких під час
вимірювання повертаються круги (які
мають динамічні системи відліків),
називають моторизованими - (М). Крім
того, виготовляють також тахеометри з
автоматичним наведенням візирної осі
на ціль. Наприклад, ТС А - 1000 (L)
(тотальна
станція з автоматичним наведенням та
лазером (L),
серії
1000). Тахеометри найпоширеніше
застосовують у сучасному геодезичному
виробництві й тому фірми, що виготовляють
тахеометри, випускають їх у багатьох
модифікаціях. Така різноманітність
цих приладів зумовлює необхідність
класифікувати теодоліти не тільки за
точністю, але й за конструктивними
особливостями та вимірювальними
можливостями.
У
табл. ІІ.3.2 подана класифікація теодолітів
та тахеометрів.
У
табл. ІІ.3.1 подано прилади, що виробляють
тільки чотири фірми. До лідерів, що
також виробляють геодезичні прилади,
належать й інші фірми, такі, як Торсоп
(Японія), Trimble
(США).
Фірма Торсоп випускає, наприклад,
електронні тахеометри серії GTS
720
(GTS-721,
722,
723, 725) з точністю вимірювання кутів 1”,
2”, 3”, 5” відповідно, а також електронні
тахеометри серії GPT
-
3000 (GPT-3002,
3003,
3005, 3007) з точністю вимірювання кутів
2”, З”, 5”, 7” відповідно та вимірювання
ліній до 250 м без відбивача з точністю
до 10 мм; з однією призмою - до 3000 м з
точністю 3 мм + 2 ppm.
Фірма
Trimble
випускає
електронні тахеометри без відбивача
серії 3600 DR
(3601
DR,
3602
DR,
3603
DR,
3605
DR)
з
точністю вимірювання кутів 1,5”, 2”, 3”,
5” відповідно, та ліній до 120 м без
відбивача з точністю 3 мм.
Особливий
інтерес становить названа у табл. ІІ.3.1
трикоординатна мобільна вимірювальна
станція фірми Sokkia,
що
забезпечує (як вважає фірма) найбільшу
у світі точність вимірювання довжини
149±
(0,8 + 1 * 10"6)
мм. Станція швидко вираховує просторові
координати з розв’язком до 0,1
мм.
Фірма, країна |
Назва приладу |
Труба |
Ціна поділки шкали мікрометра |
Середня квадратична похибка одного прийому |
Електронний віддалемір |
Вага без футляра, кг |
|||||||||||||||
світловий діаметр об’єктива, мм |
збільшення труби,х |
поле зору |
мінімальна віддаль фокусування, м |
коеф. ниткового віддалеміра |
гориз. |
верт. |
Діапазон роботи компенсатора |
Макс в/д |
Точність |
||||||||||||
віддаль з одною призмою |
без відбивача |
|
|||||||||||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|||||||
Уральський оптично- механічний завод, Росія |
Теодоліти серії ЗТ |
ЗТ2КП |
40 |
ЗО |
1°35' |
0,9 |
100 |
1" |
2м |
2,4м |
4і |
- |
- |
- |
4,7 |
||||||
ЗТ5КП |
40 |
ЗО |
1°35* |
0,9 |
100 |
Iм |
5м |
5м |
5' |
- |
- |
- |
4,3 |
||||||||
Теодоліти серії Т4 |
тзоп- 10 |
38 |
20 |
2°00’ |
1,2 |
100 |
Iм |
20й |
30м |
- |
- |
- |
- |
3,5 |
|||||||
4Т15П |
ЗО |
20 |
2°00' |
1,2 |
100 |
10м |
15" |
30м |
- |
- |
- |
- |
2,4 |
||||||||
Теодоліт електронний Т10Е (зображення пряме) |
ЗО |
20 |
2°00' |
1,2 |
100 |
10м |
10м |
10м |
- |
- |
- |
- |
2,5 |
||||||||
Тахеометр електронний ЗТА5Р (два дисплеї) |
ЗО |
зо |
1°30' |
1,5 |
- |
5м |
5м 1,5 мгон |
7м 2,2 мгон |
5' |
2000 м |
- |
5 + 3 lO^D |
|
||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
Тахеометр електронний (total station) ЗТА5РМ |
30 |
30 |
1°30’ |
1,5 |
- |
5” |
5" 1,5 мгон |
7” 2,2 мгон |
5' |
2000 м |
- |
5 + З.Ю-^Т) |
5,4 |
|
Karl Zaiss, Німеччина |
Тахеометр електронний ELTA50R (дисплей) |
40 |
26 |
1°25’ |
1,5 |
- |
5" |
5” 1,5 мгон |
5” 1,5 мгон |
2040' |
1000 |
- |
5 ММ + 3 ppm |
3,5 |
|
ELTA40R (дисплей) |
40 |
26 |
1°25’ |
1,5 |
- |
3" |
3” 1,0 мгон |
3" 1,0 мгон |
2040' |
1200 |
- |
3 мм + 3 ppm |
3,5 |
||
Теодоліт електронний (високоточний) TTh 2 (дисплей) |
45 |
30 |
Г25' |
1,0 |
- |
0,6" 0,2 МГОН |
0,6” 0,2 мгон |
0,6" ОДмгон |
Компл. рідинни й |
- |
- |
- |
4,7 |
||
Тахеометр електронний (total station) Rek Elta 13 Cm S (динамічний) |
45 |
30 |
1°25' |
1,2 |
- |
0,6H 0,2 mgrad |
1,5" 0,5 mgrad |
1,5" 0,5 mgrad |
2040' |
2000 |
- |
3 мм + 2 ppm |
6,0 |
||
SOKKIA, Японія |
Електронні (цифрові) теодоліти |
DT 2Е |
45 |
30 |
1°30’ |
0,9 |
100 |
r ол МГОН |
2" 0,6 мгон |
2" 0,6 мгон |
3’ |
- |
- |
- |
4,8 |
DT 4E DT4F |
45 |
30 |
1°30' |
0,9 |
100 |
5" 1 МГОН |
10” 2 мгон |
10” 2 мгон |
3’ |
- |
- |
- |
4,8 |
||
Електронний цифровий лазерний теодоліт LDT 50 (кодовий) Діаметр лазерного кола: 10 м - 1 мм, 200 м - 20,7 мм, 400 м - 443 мм |
42 |
30 |
1°30' |
1,3 |
- |
Iм 0,2 МГОН |
5" 1,0 мгон |
5” 1,0 мгон |
3’ |
- |
- |
- |
5,7 |
||
SOKKIA, Японія |
Електронні тахеометри серії Power SET |
SET 1010 |
45 |
30 |
1°30’ |
1,0 |
- |
0,5” 0,1 МГОН |
1" ОДмгон |
1" 0,3 мгон |
3’ |
2400 м |
плівка 120м |
на призму |
5,4 |
SET 2010 |
45 |
30 |
1°30’ |
1,0 |
- |
0,5” 0,1 МГОН |
2” ОДмгон |
2" ОД мгон |
3’ |
2400 м |
120м |
2+ 2 10Л) |
5,4 |
||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
||||||||||||||
|
|
SET ЗОЮ |
45 |
30 |
1°30' |
1,0 |
- |
Iй 0,2 МГОН |
3м 0,1мгон |
3м 0,1 мгон |
3' |
2200 м |
100 м |
на плівку |
5,4 |
|||||||||||||
SET 4010 |
45 |
30 |
1°30' |
1,0 |
- |
5й 1,0 МГОН |
5м 1,5мгон |
5м 1,5 мгон |
3' |
1600 м |
80 м |
4+ 5 ЮЛ) |
5,4 |
|||||||||||||||
Електронні тахеометри серії 30R (без відбивачів) |
SET 330R |
45 |
30 |
1°30' |
1,3 |
- |
Iй 0,2 МГОН |
3м 1 МГОН |
3м 1 мгон |
3’ |
4000 м |
без відб, 100 м |
3+ 2 lff^D |
5,3 |
||||||||||||||
SET 530R |
45 |
30 |
Г30' |
1,3 |
- |
Iм 0,2 МГОН |
3” 1 МГОН |
3м 1 мгон |
3' |
4000 м |
плівка 500 м |
на призму |
5,3 |
|||||||||||||||
SET 63 OR |
45 |
26 |
1°30' |
1,3 |
- |
|
|
|
3’ |
3000 м |
|
|
5,3 |
|||||||||||||||
Електронні тахеометри серії 10 |
SET 310 |
45 |
30 |
1°30’ |
1,0 |
- |
Iм 0,2 МГОН |
3„ 1 МГОН |
3м 1 мгон |
3’ |
2400 м |
плівка 120 м |
на призму 2+ 2 10-6D |
5,2 |
||||||||||||||
SET 510 |
45 |
30 |
Г30’ |
1,0 |
- |
Iм 0,2 МГОН |
5м 1,5 мгон |
5м 1,5 мгон |
3' |
2400 м |
120 м |
на плівку |
5,1 |
|||||||||||||||
SET 610 |
45 |
30 |
1°30’ |
1,0 |
- |
Iм 0,2 МГОН |
6" 1,9 мгон |
6м 1,9 мгон |
3’ |
2400 м |
120 м |
4+ 3 10^D |
5,1 |
|||||||||||||||
трикоординатна автономна мобільна станція MONMOS (кодова) |
49 |
30 |
1°30' |
20 |
- |
Iм 0,2 МГОН |
2" 0,4 мгон |
2м 0,4 мгон |
3’ |
призма 50 м- 1000 м |
2м- 100 м |
найм, ціна поділки мм 0,8 + 1 10Л) |
5,7 з акумулятором |
|||||||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
||
Leica Швейцарія |
Прецизійні електронні теодоліти ТЗООО/ТЗОООА |
52 |
59 |
1°20' |
0,6 |
- |
0,1” 0,01 МГОН |
0,5" 0,15 МГОН |
0,5м 0,15 мгон |
3’ |
- |
- |
- |
5,5 |
||
ТМ5000/ TDM5000 динамічні, пряме зображення |
42 |
42 |
1°30’ |
1,7 |
- |
0,1" 0,01мг oh |
0,6м 0,2 мгон |
0,6м 0,2 мгон |
3’ |
1200 м ТОМ 500 |
- |
1 мм+2 ррш± 0,5 мм на 120 м |
6,5 |
|||
Електронні тахеометри (total station) серія TPS 400 |
TPS 403 |
42 |
30 |
1°30' |
1,7 |
- |
Iй 0,5 МГОН |
3м 1 мгон |
3м 1 мгон |
4' |
3500 м |
250 м |
2 мм+2 ррш |
4,2 |
||
TPS 405 |
42 |
30 |
1°30' |
1,7 |
- |
Iй 0,5 МГОН |
5м 1,5 мгон |
5м 1,5 мгон |
4’ |
3500 м |
250 м |
2 мм+2 ррш |
4,2 |
|||
TPS 407 |
42 |
30 |
1°30’ |
1,7 |
- |
1" 0,5 МГОН |
1" 2 мгон |
7м 2 мгон |
4' |
3500 м |
250 м |
2 мм+2 ррш |
4,2 |
|||
TPS 410 лазерний висок |
42 |
30- 42 |
1°30' |
1,7 |
- |
Iм 0,5 МГОН |
10м |
10м |
4' |
3500 м |
250 м |
2 мм+2 РРт |
4,2 |
|||
Серія TPS 800 |
TPS 802 |
42 |
30- 42 |
Г30' |
1,7 |
- |
Iй 0,1 МГОН |
2м 0,6 мгон |
2м 0,6 мгон |
4’ |
3500 м |
250 м |
2 мм+2 ррш |
5,4 (3 призмою GPR-1- 10000 м |
||
TPS 803 |
42 |
30- 42 |
1°30’ |
1,7 |
- |
Iм 0,1 МГОН |
3м 1 мгон |
3м 1 мгон |
4' |
3500 м |
250 м |
2 мм+2 ррш |
||||
TPS 805 лазерний |
42 |
30- 42 |
1°30' |
1,7 |
- |
1” 0,1 МГОН |
5м 1 мгон |
5м 1 мгон |
4’ |
3500 м |
250 м |
2 мм+2 ррш |
||||
Leica Швейцарія |
Серія TPS 1000 |
T1100 |
42 |
30 |
1°30' |
1,7 |
- |
Iм 0,5 МГОН |
3м 1 мгон |
3м 1 мгон |
4’ |
3500 м |
250 м |
2 мм+2 ррш |
5,5 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
|
Т 1800 |
42 |
зо |
Г30' |
1,7 |
- |
Iм ОД мгон |
1” 0,3 мгон |
Г 0,3 мгон |
4' |
3500 м |
250 м |
2мм+2 РРШ |
5,8 |
Теодоліти динамічні |
ТМ 1100 |
42 |
зо |
Г30' |
1,7 |
- |
Г 0,5 мгон |
3" 1 мгон |
3” 1 мгон |
4' |
3500 м |
250 м |
2 мм+2 ppm |
5,6 |
|
ТМ 1800 |
42 |
зо |
1°30' |
1,7 |
- |
Г 0,1 мгон |
Iм 0,3 мгон |
Г 0,3 мгон |
4' |
3500 м |
250 м |
2 мм+2 ppm |
5,9 |
||
Тотальні станції ТС |
ТС110 0(L) |
42 |
зо |
1°30' |
1,7 |
- |
1" 0,5 мгон |
3" 1 мгон |
3„ 1 мгон |
4’ |
2,5/3,5 км |
250 м |
2 мм+2 ppm |
6,1 |
|
ТС 1800 |
42 |
зо |
1°30' |
1,7 |
- |
Г ОД мгон |
Iй 0,1 мгон |
1” 0,1 мгон |
4’ |
2,5/3,5 км |
250 м |
2 мм+2 ppm |
6,4 |
||
Тотальні станції динамічні тем 1100 |
42 |
зо |
1°30’ |
1,7 |
- |
Iм 0,5 мгон |
3" 1 мгон |
3" 1 мгон |
4' |
2,5/3,5 км |
250 м |
2 мм+2 ppm |
6,2 |
||
ТСМ 1800 з автоматичним наведенням |
42 |
зо |
1°30' |
1,7 |
- |
1” 0,1 мгон |
1" 0,3 мгон |
Iй 0,3 мгон |
4’ |
2,5/3,5 км |
250 м |
2 мм+2 ppm |
6,5 |
||
ТСА1100 (Ь)-лазер |
42 |
зо |
1°30' |
1,7 |
- |
1" 0,5 мгон |
3й 1 мгон |
3м 1 мгон |
4f |
2,5/3,5 км |
250 м |
2 мм+2 ppm |
6,8 |
||
Назва приладу |
Конструктивні особливості |
Оптичні теодоліти |
Скляні круги з градусними або градовими поділками |
Електронні теодоліти (цифрові) |
Скляні круги з умовними позначками та автоматизованими відліками |
Електронні теодоліти (цифрові) моторизовані |
Динамічна автоматизована система відліків. Круги під час вимірювання обертаються |
Електронні теодоліти (цифрові) лазерні |
Автоматизована система відліків; вмонтовані лазери - цілевказівники для створних спостережень, іноді - лазерні виски |
Електронні тахеометри (цифрові) |
Автоматизована система відліків, вмонтовані електронні світловіддалеміри (с/в), працюють з відбивачем |
Електронні тахеометри (цифрові) моторизовані |
Динамічна автоматизована система відліків, вмонтовані с/в; працюють з відбивачами |
Електронні тахеометри (цифрові) лазерні |
Автоматизована система відліків, умонтовані с/в та лазерні цілевказівники, іноді-лазерні виски; працюють з відбивачами |
Електронні тахеометри (без відбивача) |
Автоматизована система відліків, с/в, працюють без відбивачів |
Тотальні станції |
Високоточні та точні електронні тахеометри з програмним забезпеченням розв’язання багатьох інженерно-геодезичних задач, внутрішнім комп’ютером |
Тотальні станції моторизовані |
Високоточні та точні електронні тахеометри із програмним забезпеченням; розв’язання багатьох інженерно- геодезичних задач. Круги під час вимірювання обертаються (динамічна автоматизована система відліків) |
Тотальні станції з автоматизованим візуванням |
Аналогічні до попередніх тотальних станцій з автоматизованою системою відліків та автоматизованим наведенням візирної осі труби на ціль |
Тотальні електронні тахеометри з інтегрованим GPS- приймачем |
Нова революційна геодезична станція фірми “Leica”, в якій вперше у світі об’єднані високоточний тотальний тахеометр з потужним GPS-приймачем |
155
На
ще більшу увагу заслуговує запропонований
фірмою Leica
згаданий
у табл. ІІ.3.2 тотальний електронний
тахеометр з інтегрованим GPS-приймачем.
Використовуючи його, не потрібно
створювати геодезичну основу у вигляді
ходів. Координати точки встановлення
визначають GPS-технологією
за декілька секунд із сантиметровою
точністю для віддалей до 50 км від базової
GPS-станції.
Визначивши координати пункту спостережень
за допомогою GPS,
далі
виконують тахеометричне знімання.
Тахеометр орієнтують на другу точку
встановлення. Координати цієї другої
точки встановлення визначають також
методом GPS,
перейшовши
на цю точку.
Відлікові
пристрої створені виробниками з метою
підвищення точності відліків передусім
для точного відлічування найменшої
поділки круга. Пояснимо це детальніше.
Нехай маємо шкалу, показану на рис.
ІІ.3.1.
Відліковий
індекс
0° 5°
І і
і і і _| і У?'
і і і
Рис.
II. 3.1. До пояснення призначення відлікових
пристроїв
Найменша
поділка шкали А, = Ґ. Взяти відлік шкали
означає визначити
відрізок
шкали від 0°
до відлікового індексу, що дотикається
до шкали або проектується на неї. Якщо
стрілка індексу збігається з деякими
градусними поділками, то точний відлік
становитиме
Відлікові
пристрої оптичних теодолітів та
тахеометрів можна класифікувати
на:
Штрихові
мікроскопи.
Шкалові
мікроскопи.
Мікроскопи
із гвинтовими мікрометрами.
Односторонні
оптичні мікрометри.
Двосторонні
оптичні мікрометри.
156
Відлікові пристрої оптичних кутомірних приладів, їхнє призначення та класифікація
І 10°S
=
N
-X,
де N
-
кількість градусних поділок, що утворюють
відлік. Але здебільшого відліковий
індекс не збігається з поділками шкали,
як це показано на рис. ІІ.3.1. Тому відлік
становитиме S
=
NX
+
х.
Величина х
- невідома. Саме для підвищення точності
визначення х
призначені всі відлікові пристрої.
С Я=Г 1 0° і° * |
2° Частина круга |
І 1 1 і 1 рп 1 1 1 10 5 ( |
Шкала ) мікроскопа |
і* m-ji * |
Рис.
11.3.2. Приклад відліку шкаловим мікроскопом
На
рис. ІІ.3.2 подано приклад відліку шкаловим
мікроскопом
поділки
шкали р = — = — = 0,1° =6’.
становитиме:
Якщо
відліковий пристрій має шкалу, одразу
виникає питання рена. Реном
r
= X-m\l. (ІІ.3.2)
157X
= 1°. Ціна X
Гх
=
0,7 (визначають окомірно). Відлік т
10S
=
М° + 4 • 6'+
0,7 • 6’;
S
=
1°
+ 24’+ 4,2’ = 1°28,2’.г
називають різницю між номінальним
значенням найменшої поділки круга X
та значенням цієї поділки, виміряним
шкалою мікроскопа, тобто
Річ
у тім, що насправді
де
т
На
підставі рівняння (II.3.3) запишемо:
Підставимо
значення
X X
ц=-
т-г
-(-і)'
(ІІ.3.6)
Розкладемо
значення правої частини останньої
формули у степеневий
ряд і, обмежившись
членами першого степеня, отримаємо:
\(
И
= -
т
1-
т
У_Л
А, г
J
т
т т
(ІІ.3.7)
Позначимо
ц0
= ціна поділки шкали за задумом виробника.
Введемо
т
|Х0
У (ІІ.3.7):
Ц
=
т
або
|Х
= ц0
г
де
А(і = Цо поправка за рен ціни поділки
шкали мікрометра. Якщо деякий
т
відлік
шкали містить
S
= £p0
158X
Ф т\і
і, як підтверджує (ІІ.3.2), виникає рен.
Ця нерівність виникає тому, що ми бачимо
в окулярі мікроскопа не самі поділки
круга, а їхні зображення, збільшені
мікроскопом. За визначенням, рен треба
було б описувати формулоюr-m-m\ (II.3.3)т
—
кількість поділок шкали, яка (за задумом
конструктора) повинна поміститися в
одній найменшій поділці лімба; т'-
фактична кількість поділок зображення
шкали, яка вміщується в цій самій
поділці. Зрозуміло також, що змінюючи
збільшення мікроскопа, можна позбутися
рена або мінімізувати його вплив. На
практиці у відліки вводять поправки
за рен. Враховуючи наявність рена,
дійсна ціна поділки шкали мікроскопа11
= —'. (ІІ.3.4)my
— m-r. (II.
3.5)т'
з (ІІ.3.5) в (ІІ.3.4):Ш>+М<г
— • (П.3.8)+Ац, (ІІ.3.9)к
поділок, то:+£Др. (ІІ.3.10)
Перший
член правої частини рівняння (ІІ.3.10) -
є наближеним відліком, другий - поправкою
у відлік шкали за рен. Якщо
S
=
NX
+
k\l
+
41.
В
окулярах мікрометрів зображення поділок
горизонтального та вертикального
кругів видно одночасно, що доволі зручно
під час відлічування. На рис. П.3.3 показано
поле зору мікроскопа теодоліта ТІ фірми
Wild.
Бісектори
Рис.
І 1.3.3. Поле зору одностороннього оптичного
мікрометра теодоліта Т1
фірми
Wild
(327°59'36")
На
рис. ІІ.З.З бісектується штрих 327
горизонтального круга. Тому в розташуванні,
показаному на рис. ІІ.З.З, можна відлічити
тільки горизонтальний круг. Щоб
отримати відлік вертикального круга,
потрібно барабаном мікрометра повертати
плоско-паралельну пластинку й бісектувати
штрих 92°. На шкалі мікрометра з’являться
кутові мінути та секунди відліку.
159т>т'
- рен додатний, в іншому разі він
від’ємний. Такі самі знаки поправок
за рен.Односторонній
оптичний мікрометр.
В оптичних мікрометрах на шляху променя,
що спрямований від лімба до окуляра
мікроскопа, ставлять плоско- паралельну
пластинку. Під час повороту цієї
пластинки спостерігачу здається, що
поділки лімба рухаються. Із
плоско-паралельною пластинкою пов’язана
шкала мікрометра. Якщо “рухати”
(поворотом пластинки) поділки лімба й
сумістити з відліковим штрихом (або
бісектувати) найближчу до штриха
(бісектора) молодшу поділку лімба, то
в такому розташуванні відлік мікрометра
дає + х(Х; повний відлік (відповідно до
(ІІ.3.1):
Двосторонній
оптичний мікрометр.
Такий мікрометр має дві плоско- паралельні
пластинки, й у полі зору окуляра
мікроскопа видно діаметрально протилежні
штрихи лімба: зверху пряме зображення,
знизу - перевернуте.
г |
7 V |
"оо |
со |
||||||
6< |
|
|
|
|
|
||||
ІЄ |
со |
ІЄ |
І***- |
і£ |
|
||||
тг=т
О-г-2
о-і-з
Рис.
11.3.4. Приклад відліку двостороннього
оптичного мікрометра
теодоліта 2Т2:
177°50,22"
Це
зменшує похибки суміщення штрихів,
тобто підвищує точність відліків.
Детально будову оптичних мікрометрів
та методи їхнього відлічування описано
в [17]. Оскільки під час відлічування
двосторонніх оптичних мікрометрів
діаметрально протилежні штрихи,
пройшовши шлях Х/2,
суміщаються, то
160реном
двостороннього оптичного мікрометра
називають різницю між номінальною
величиною найменшої півподілки круга
та його величиною,
виміряною
мікрометром.
Автоматизовані
системи відліків кутомірних приладів
(теодолітів та тахеометрів) звільнили
від необхідності запису в польових
журналах відліків кругів. До того часу
заповнення польового журналу під час
кутових вимірювань здавалося
неминучим.
Як
вже зазначалося, це уможливилось завдяки
заміні горизонтальних та вертикальних
кругів (лімбів) - скляних кругів із
градусними поділками, на такі самі
скляні круги (диски), але з нанесеними
умовними позначками, що створюють
доріжки прозорих і непрозорих полів.
Такі
диски з умовними позначками розташовуються
між джерелом світла та фотодетектором.
Фотодетектор працює як ФЕП (фотоелектронний
помножувач - перетворює світловий
сигнал на електричний струм). Диски
виконують роль модуляторів світла.
Пройшовши диски (із прозорими та
непрозорими частинками), світло, що
потрапляє на фотодетектори, буде
модульованим. Зняті з фотодетектора
електричнг імпульси, збуджені
модульованими світловими променями,
дають змогу встановити значення відліку,
відобразити його на електронному
дисплеї, автоматично зареєструвати
цей відлік в електронній пам’яті
теодоліта або переслати його до
комп’ютера, що співпрацює з електронним
теодолітом, для виконання подальших
обчислень. Такий прилад названо
За
останні роки створено три системи
автоматичних відліків електронних
теодолітів:
Проста
ілюстрація кодової системи відліку
наведена на рис. ІІ.3.5. На рис. ІІ.3.5
зображено кодовий диск з концентрично
нанесеними доріжками - коду двійкової
системи відлічування. Теоретично
можливо реалізувати автоматичний
зчитувальний пристрій також із десятковою
системою цифр, до якої ми звикли під
час візуальних відлічувань. Проте
електронний пристрій буде набагато
простішим, якщо користуватися двійковою
системою. Це пояснюється тим, що двійкові
цифри 0
і 1
можна дуже просто реалізувати фізично:
темно - ясно, напруга є - немає, реле
ввімкнено - вимкнено. На жаль, двійковий
код вимагає від ЕОМ ємності, у 3,3 раза
більшої, ніж десятковий код. Тому інколи
застосовують двійково-десяткові та
інші коди. Доріжки відраховують від
центра круга. Перша складається із двох
полів: затемненого й світлого півкола,
а в кожній наступній - кількість полів
подвоюється, почергово наносяться
прозорі й непрозорі поля.
161Принцип роботи автоматичних систем відліків електронних теодолітів та тахеометрів
електронним
теодолітом.
Електронний теодоліт відрізняється
від електронного тахеометра передусім
тим, що не має електрооптичного
відцалеміра [31].кодові,
імпульсні
та динамічні.
Всі вони ґрунтуються на загальному
принципі: автоматизованому підрахунку
світлових (електричних) імпульсів за
допомогою мікропроцесорів і перетворення
імпульсів на відлік у числовому вигляді.
Далі розглянемо ці три системи
автоматичних відліків детальніше.
Рис.
11.3.5. Вид диска зверху
На
рис. ІІ.3.5 показано три доріжки. Остання
має 23
= 8
полів. У практиці
їх може бути,
наприклад, дванадцять. Тоді остання
доріжка буде мати 212
=
4096 інтервалів.
Зауважимо,
якщо необхідно визначити розташування
алідади з точністю
1 сс для градових
поділок: круг поділено на 400 g;
1
g
=
100 с; 1с = 100 сс, тоді
на крузі радіусом
2
а
= -
400
100 100 400 100 100
=
0,0000942 мм.
(113.11)
Отже,
закодувати повністю відлік неможливо.
Найменшою величиною, що ще кодується,
буде 0,1 g.
Тоді
дуги а
становитимуть
0,094 мм, приблизно а = 0,1 мм. Для визначення
частини поділки, меншої від 0,1 g,
необхідно
якесь інше рішення.
Не
вдаючись у подробиці цього важливого
питання, скажемо тільки, що нині
використовують аналогову (безперервну)
систему, яка в першому наближенні
відповідає способу відлічування секунд
у класичних теодолітах, тобто частини,
менші від одного інтервалу, оцінюють
окремо. Уточнення відліку (напрямку)
виконують електронною інтерполяцією
відрізку: від останньої дециградової
поділки (0,1 g)
до
індексу. Точність інтерполяції має
становити 0,0001 g,
тоді
точність відліку становитиме 1 сс. Якщо
виконавця задовольняє відлік 10
сс, то достатня інтерполяція 0,001
g.
Перейдемо
до принципової суті
162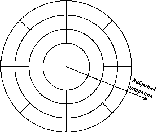
г
= 60 мм потрібно було б мати дуги a,
розміромпг 6,28
• 60 ммкодової
системи відліку, яка зображена на рис.
ІІ.3.6. Над скляним диском розташовано
джерело світла. Промені світла, пройшовши
щілинну заслінку, перетворюються на
“площину світла”,
спрямовану
паралельно до осі обертання теодоліта.
Промені “площини світла”, пройшовши
кодовий диск, потрапляють на фотодетектор
FD.
Промінь,
який пройшов через прозоре поле кодового
диска, збуджує у діодах фотодетектора
сигнал, що відповідає двійковій цифрі
- 0,
а відсутність такого сигналу дає цифру
1. Отже, відповідно до рис. И.3.5 (три
доріжки), фотодетектор подає відлік
101. Потім цифрові відліки надходять на
мікропроцесор МР, який відображає їх
на дисплеї.
Світлодетектор
Частина
кодового диска
Фотодетектор
FD
Мікропроцесор
МР
Рис.
11.3.6. Переріз диска за вибраним напрямком
Далі
розглянемо
400
g
N
(ІІ.3.12)
Один
прозорий і сусідній непрозорий штрихи
диска утворюють один квант кута. Доріжку
прозорих та непрозорих штрихів називають
a
= CL. (ІІ.3.13)
Знайдемо
необхідну кількість імпульсів, щоб
отримати відліки з точністю 1 сс (до
однієї градової секунди). Розв’язуючи
(П.3.12) відносно
ft
_
400
8'100'100
_
^ 106
1
сс
163
імпульсний
принцип автоматизації відліку кодового
диска. Принцип зчитування (відліку) за
допомогою імпульсних систем ґрунтується
на тому, що деякий постійний кут повороту
алідади прирівнюють до одного імпульсу.
Це означає, що будь-яка зміна в розташуванні
алідади може бути прирівняна до певної
кількості імпульсів. Якщо N
-
кількість імпульсів, що подаються за
одним повним обертом круга, розділеного
на 400 g,
то
одному імпульсу буде відповідати кут
С, який називається квантом
і визначається за формулоюрастром.
Ціна елемента квантування С
для N
=
4000 становитиме 0,1 g
(0,1
града), тобто, С = 0,1 g.
Лічильник
рахує кількість імпульсів L,
які виникли під час обертання круга
від одного напряму до другого. Тоді кут
становитиме:N,
знайдемо:
Як
ми вже знаємо, таку кількість імпульсів
отримати на крузі радіусом 60 мм або
дещо більшому неможливо. Кількість
імпульсів можна зменшити певними
конструктивними рішеннями. Отже,
кількісне значення кута буде визначено,
якщо підрахувати кількість поданих
імпульсів, що відповідають зміні
розташування візирної осі труби,
скріпленої з алідадою під час візування
(наведення труби) за напрямками, що
створюють цей кут. Частота імпульсів
(не кількість) буде змінною величиною,
що залежить від швидкості обертання
алідади виконавцем.
Використовуються
світлові імпульси, які перетворюються
на електричні або на імпульси, викликані
електричною індукцією. Тому можна
говорити про
Вісь
Опишемо
використання
Світло
від джерела
164фотоелектричні
та електроіндуктивні
(індуктивні) імпульсні методи.
фотоелектричних
імпульсів. В імпульсному методі центром
приладу також є скляний круг (лімб)
(рис. ІІ.3.7, а), що має одну доріжку рисок.
Ширина рисок така сама, як і проміжків,
що їх розділяють. Цей круг називають
вимірювальним (вимірювальною сіткою).
Напроти цієї сітки (шкали), на, можливо,
найкоротшій віддалі від неї, розташована
зчитувальна (відоікова) сітка А/, яку
називають маскою. Риски та проміжки
цієї сітки (маски) такі самі, як і у
вимірювальної сітки. Риски та проміжки
маски створюють ряд прозорих та
непрозорих полів.S
(люмінесцентного
діода) перетворюється конденсатором
К
на паралельний пучок, проходить
вимірювальну, а потім зчитувальну
(відлікову) сітку. Скерований об’єктивом
Об,
він потрапляє на
S II 45? |
(ІІ.3.15) |
2те |
|
а
=— |
(ІІ.3.16) |
Нехай
відома кількість обертів круга за
хвилину
60се*
_ тсек
„_60
л 9 1
^оберт
* оберт ^
/;
(ІІ.3.17)
165п.
Тоді період обертання Т
в секундах або частоту знайдемо за
формулою
Підставивши
значення
а
= 2%—і.
60
(ІІ.3.18)
Оскільки
2
Як
бачимо, справді мірою кута може бути
час. Тому динамічний метод може ще бути
названий
Рис.
11.3.7, б. Принципова схема динамічної
системи автоматизації відліків
Розглянутий
вище імпульсний метод також є динамічним,
але в імпульсному методі обертання
круга не обов’язково повинні бути
рівномірними. У такому разі динамічний
метод вимагає строго рівномірних
обертань круга зі сталою частотою.
Такий метод ґрунтується на застосуванні
імпульсного диска (лімба), тобто такого
самого диска, як і для імпульсного
методу, та чотирьох зчитувальних
фотоелектричних пристроїв, які під час
вимірювання розташовують у площинах
166Т
з (ІІ.3.17) у рівняння (ІІ.3.16), отримаємо:п—
= const
—
с,
то 60a
= ct. (ІІ.3.19)часовим.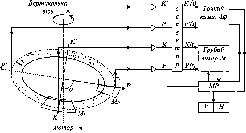
РР'
та КК'
(рис. ІІ.3.7, б). Два з них - Р
та К,
утворюють
кут а. Перед вимірюваннями круг
(горизонтальний та вертикальний)
приводять в обертовий рух навколо його
осі зі сталою частотою /, контрольованою
мікропроцесором. Доріжка диска Р,
пересуваючись під щілинами масок Мр
і Мк
зчитувачів Р
і К,
виконує функції модулятора світла
та створює дві смужки світлових сигналів
в інтервалах, що відповідають розташуванню
зчитувачів над доріжкою диска.
Світлові
сигнали над напрямками
Під
час вимірювання кутів нульовий діаметр
лімба, над яким розташована одна
пара фотодіодів, встановлюють за одним
із напрямків кута, а трубу спрямовують
за другим напрямком цього кута. З цим
напрямком збігається розташування
другої пари діодів. Під час зміни
напрямку обертання круга, навпаки,
трубу спрямовують на перший, а нульовий
діаметр - на другий напрямок кута.
Завдяки
діаметральному розташуванню зчитувачів
Рис.
11.3.8. Теодоліт Т2000 (фірми Wild)
167Р
і К
та збуджені ними електричні імпульси
надходять у мікропроцесор МР
неодночасно. Ця неодночасність
трансформується лічильниками та МР
у часову міру кута t
та
числове значення кута а. За даними
зчитувачів Р
та К
отримують наближене (грубе) значення
кута (як функцію часу/)- Потім, використовуючи
дані всіх чотирьох зчитувачів Р,
К, Р', К',
одержують точне значення кута а. Увесь
процес автоматизований.Р
і Р'
та К
і К'
та обертанням круга під час вимірювань
у двох протилежних напрямках виключаються
ексцентричні похибки, викликані
розташуванням кругів та зчитувачів.
Значення горизонтального (г) і
вертикального (в) кутів та їхніх похибок
відображаються на центральному
мікропроцесорі СМР. Прилад має додаткові
вмонтовані системи, що автоматично
компенсують вплив нахилу вертикальної
осі теодоліта (неточного горизонтування
приладу) на значення горизонтальних
та вертикальних кутів. Ці системи також
електричні і ґрунтуються на компенсаторах.
Зафіксовані фотодетектором зміни
нахилу приладу, перелічені на поправки,
вводяться у виміряні горизонтальні та
вертикальні кути автоматично.
Реалізовані
на практиці динамічні системи дали
змогу отримати високу
точність
кутових вимірювань. Для теодоліта Т2000
(фірми Wild)
точність
характеризується
середньою похибкою 0,5 сс. Цей теодоліт,
показаний на рис.
ІІ.3.8, має дві таблиці
операційної клавіатури для введення
даних, виконання
потрібних операцій
і відображення результатів. Окреме
гніздо дає змогу
під’єднати реєстратор
інформації GRE
(модуль
пам’яті), який співпрацює з
теодолітом
Т2000. Найновіші типи реєстраторів дають
змогу вводити і
виводити додаткові
дані, наприклад, про нумерацію пунктів,
знайти та випра-
вити записані дані
чи закодувати їх. Використовуючи
нескладну програму,
можна обчислити
координати пунктів, що спостерігаються,
або визначити рухи
цих пунктів у
тривимірному просторі.
Оптичні
та електронні теодоліти, які, по суті,
є тахеометрами, оскільки
мають не
тільки горизонтальні, але й вертикальні
круги та оптичні віддалеміри,
складаються
здебільшого з тих самих вузлів та
деталей, що й оптично-
механічні
теодоліти. Основна відмінність оптичних
теодолітів, як вже
зазначалось,
тільки в тому, що в них вмонтовані не
металеві, а скляні круги.
Перехід до
скляних кругів дав змогу створити нові
відлікові пристрої, а саме
розглянуті
вище штрихові та шкалові мікроскопи,
оптичні односторонні та
двосторонні
мікрометри. На рис ІІ.3.9 показаний
оптичний теодоліт серії ЗТ
Уральського
оптично-механічного заводу (Росія). У
серію входять ЗТ2КП (К -
компенсатор,
П - пряме зображення труби), ЗТ2КА (з
автоколіматором),
ЗТ5КП. Точність
вимірювання горизонтальних кутів одним
прийомом -
відповідно 2й
та 5”, ціна поділки шкали відлікового
пристрою Iм,
похибка
відліку 0,1”. Збільшення
труби 30х.
1
2
3
4
5
6
7
8
Рис.
11.3.9. Теодоліт серії ЗТ
168
Будова оптичних та електронних теодолітів та тахеометрів
Назва
частин ЗТ
Ручка
для перенесення.
Підставки
труби.
Навідний
гвинт труби.
Закріпний
гвинт труби.
Навідний
гвинт алідади.
Підставка
теодоліта.
Гвинти
горизонтування приладу (підіймальні
гвинти).
Трегер
- носій приладу.
Закріпний
гвинт лімба.
Циліндричний
рівень.
Дзеркало
підсвічування.
Лінза
об’єктива труби.
Головними
частинами оптичних теодолітів є лімб
та алідада, вертикальні осі обертання
лімба та алідади, підставки труби
(горизонтальна вісь обертання труби,
на яку встановлюють вертикальний круг,
зорова труба, рівні сферичні та
циліндричні, компенсатор нахилу,
закріпний гвинт лімба на підставці).
Подальше
вдосконалення відлікових пристроїв,
їхня автоматизація завдяки заміні
градусних поділок кругів на кодові
позначки перетворили оптичні
теодоліти на електронні (цифрові, які
відображають відліки на електронному
дисплеї). Як вже відзначалося, приймаючи
термінологію, запроваджену
фірмами-лідерами виробництва геодезичного
обладнання, будемо також називати такі
прилади електронними тахеометрами, а
не теодолітами, тільки тоді, коли у них
вмонтовані електронні світловідцалеміри.
Використовують
два способи поєднання електронних
теодолітів з електронними
світловідцалемірами. Перший з них
полягає в поєднанні відцалемірної і
кутомірної частин в одну систему
вимірювань, що має спільну будову і
багато спільних елементів (спільна
зорова труба, мікропроцесор, фазометр,
клавіатура, реєстратор, до складу якого
входить також зовнішній комп’ютер).
Такі системи називають
Другий
спосіб полягає у поєднанні окремо
сконструйованих світловід- далеміра
та теодоліта (оптичного або електронного).
У такому поєднанні теодоліт є одним
елементом (модулем), а світловіддалемір
- другим. Тоді це
Ці
два модулі поєднуються із зовнішнім
реєстратором або комп’ютером. В обох
цих модулях спільним є відбивач, візирні
марки та інші дрібні деталі. Модулі
можуть працювати незалежно як теодоліт
та світловіддалемір.
169
інтегрованими
тахеометрами.модульний
тахеометр.
У
нових інтегрованих тахеометрах
застосовуються тільки фазові світло-
відцалеміри, а для кутових вимірювань
- один з методів електронного вимірювання
кута: кодовий, імпульсний або (найчастіше)
- динамічний. Саме у інтегровані
тахеометри вмонтовано потужні внутрішні
комп’ютери, які здатні відображати на
дисплеї не тільки кути та довжини, але
й просторові координати пунктів і
розв’язувати цілу низку інженерно-геодезичних
задач. їх називають тотальними станціями.
На рис. ІІ.3.10 зображено компактну
тотальну станцію SET-GE
фірми
Sokkia.
Рис.
11.3.10. Тотальна станція SET-GE
фірми
Sokkia
Назва
частин SET-GE
Позначка
середини приладу.
Ручка
для перенесення.
Позначка
висоти приладу.
Гвинт
горизонтування приладу (підіймальний).
Підставка
(трегер).
Гвинт
регулювання сферичного рівня.
Сферичний
рівень.
Окуляр
оптичного виска.
Лінза
об’єктива.
Г
ніздо орієнтир-бусол і.
Гвинт
кріплення ручки для перенесення.
Батарея
BDC
25.
Увімкнення
напруги.
170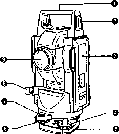
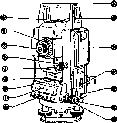
Гніздо
відбирання даних.
Закріпний
гвинт алідади.
Навідний
(мікрометричний) гвинт алідади.
Клавіатура.
Дисплей.
Циліндричний
рівень алідади.
Гвинт
регулювання (виправний) циліндричного
рівня.
Закріпний
гвинт труби.
Навідний
(мікрометричний) гвинт труби.
Окуляр
труби.
Кільце
фокусування труби по предмету.
Оптичний
візир.
На
рис. ІІ.3.11 показана клавіатура у
збільшеному вигляді. Тахеометр SET-GE
приваблює
простотою клавіатури. Він має тільки
шість клавіш. Нижче на рис. ІІ.3.12 подана
система основних функцій клавіатури.
Керівна
клавіша має п’ять робочих клавіш.
Робочі клавіші доступні (здатні
виконувати функції) тільки після
натиснення клавіші shift,
скорочено
SHFT.
Цій
клавіші дамо номер 6.
Отже,
керівна клавіша SHFT
має
п’ять головних функцій:
Встановлення
величин, що будуть вимірюватися.
Контроль
відбитого (зворотного) сигналу та
запуску/зупинки вимірювань.
Встановлення
виду вимірювання (М або Т) (М - поодинокий,
багаторазовий; Т - до рухомого об’єкта).
Зміни
розмірності величин.
Освітлення
дисплея і сітки ниток (вмикає/вимикає)
та затримання відображення горизонтального
кута на дисплеї.
Кожна
з п’яти робочих клавіш виконує дві-три
функції. Нижче подано перелік функцій
робочих клавіш (табл. ІІ.З.З).
JH.
,.рршА.
&
У
V
J2L
-Q.SEL
У
V
<2і
іа.
SHFT
Рис.
11.3.11. Клавіатура тахеометра SET-GE
171
У
ч.У
V.
№1 |
Клавіша послідовного вибору розташування вимірюваної віддалі (горизонтальної, похилої, вертикальної); три функції |
№2 |
Клавіша вибору виду (характеру) вимірювання; М - поодинокий, багатократний, Т - до рухомого об’єкта; три функції |
№3 |
Клавіша запуску/зупинки вимірювань та контролю відбитого сигналу; три функції |
№4 |
Клавіша встановлення горизонтального кута на “0”, (лівого, правого); дві функції |
№5 |
Клавіша освітлення дисплея та сітки ниток (вмикає/вимикає світло послідовно); затримання відображення горизонтального кута на дисплеї; три функції |
Кодові
малюнки, зображені на робочих клавішах,
сприяють запам’ятовуванню їхніх
функцій і відрізняють їх від керівної
клавіші Shift.
172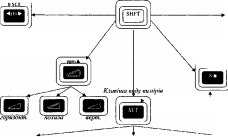
Назвемо
шість основних перевірок теодолітів:
Перевірка
циліндричного рівня.
Перевірка
круглого (сферичного) рівня.
Перевірка
сітки ниток.
Перевірка
колімаційної похибки та ексцентриситету
осей (алідади відносно лімба).
Перевірка
горизонтальності осі обертання зорової
труби.
Перевірка
оптичного виска.
До
цих шести перевірок теодолітів необхідно
додати перевірку місця нуля вертикального
круга (фактично перевірку тахеометра),
враховуючи, що у наш час не випускають
теодолітів без вертикальних кругів.
Усі інші перевірки сучасних теодолітів
та тахеометрів стосуються перевірок
електронного обладнання, зокрема,
передусім, перевірок світловіддалемірів.
Ці перевірки будуть розглянуті під час
вивчення світловіддалемірів. Перевірки
1-5 детально викладені в курсі “Топографія”.
Тому тут ми сформулюємо тільки вимоги
до взаємного розташування осей теодоліта,
які повинні виконуватися.
Друга
перевірка. Вісь сферичного (круглого)
рівня повинна бути паралельною до
вертикальної осі обертання теодоліта.
Віссю сферичного рівня називають
нормаль до сферичної поверхні у центрі
сферичного рівня. Центром
173Перевірки теодолітів
Перша
перевірка. Вісь циліндричного рівня
повинна бути перпендикулярною до
вертикальної осі обертання теодоліта.
Віссю циліндричного рівня називають
дотичну в нуль-пункті шкали рівня. Ця
дотична горизонтальна тільки тоді,
коли середина бульбашки розміщена в
нуль-пункті. За вертикальну вісь
теодоліта прийнято вважати вертикальну
вісь обертання алідади, а не лімба.
Зауважимо, що ці дві вертикальні осі
повинні бути паралельними, оскільки
вони, як правило не збігаються через
наявність деякої лінійної величини -
ексцентриситету алідади відносно
лімба. Під час виконання першої перевірки
рівень встановлюють приблизно паралельно
до лінії, що з’єднує будь-які два
підіймальні гвинти. Виводять середину
бульбашки у нуль-пункт шкали рівня, а
потім повертають алідаду на 180°. Під
час виконання сформульованої вимоги
середина бульбашки повинна залишатися
в нуль- пункті. Якщо середина бульбашки
зміщується від нуль-пункту, тоді
виправними гвинтами рівня переміщують
бульбашку на половину дуги відхилення.
Якщо, наприклад, відхилення становить
чотири поділки шкали рівня, тоді
бульбашку переміщують на дві поділки
шкали. У результаті змінюється
розташування осі рівня у вертикальній
площині, так, що вона стає перпендикулярною
до вертикальної осі обертання теодоліта.
сферичного
рівня є центр малого кола (радіусом
1,0-1,5 мм). Для перевірки виконання умови
найпростіше привести вертикальну вісь
теодоліта у прямовисний стан за
допомогою перевіреного циліндричного
рівня. Тоді у разі виконання умови
паралельності осі сферичного рівня та
вертикальної осі обертання теодоліта
центр бульбашки сферичного рівня
повинен збігатися з центром сферичного
рівня. Під час юстування бульбашку
переміщують за допомогою трьох виправних
гвинтів сферичного рівня, розташованих
у нижній частині рівня.
а-(6
±180°)
2
(ІІ.3.20)
У
(ІІ.3.20) с- колімаційна похибка;
я
+ (6
±180°)
(ІІ.3.21)
174Третя
перевірка. Сітка ниток має бути
встановлена правильно: вертикальна
нитка повинна бути прямовисною,
а
горизонтальна нитка - горизонтальною.
У теодолітах перевіряють вертикальну
нитку (бісектор). Для цього спочатку
алідаду та лімб за допомогою циліндричного
рівня встановлюють у робочий стан
(горизонтально). Потім на віддалі 20-50 м
від теодоліта підвішують тягарець
(висок) на довгій нитці. Трубу наводять
на нитку так, щоб верхній кінець
вертикальної нитки сітки ниток збігався
з якоюсь точкою нитки з тягарцем. Тоді
по всій довжині вертикальна нитка сітки
повинна збігатися з ниткою з тягарцем*
Достатньо перевірити вертикальну
нитку, оскільки заводи, що виготовляють
теодоліти, забезпечують взаємну
перпендикулярність ниток сітки.
Юстування виконують відповідним
повертанням сітки ниток так, щоб нитка
сітки та прямовисна нитка з тягарцем
збігались по усій довжині.Четверта
перевірка. Візирна вісь зорової труби
повинна бути перпендикулярною до
горизонтальної осі обертання труби.
Візирна вісь - уявна лінія, що проходить
через центр сітки ниток та центр
об’єктива. Величину неперпендикулярності
цих осей називають колімаційною
похибкою. Наявність колімаційної
похибки визначають наведенням зорової
труби на одну і ту саму далеку точку
(приблизно в горизонті приладу) при
крузі праворуч (КП) та ліворуч (КЛ). Кожне
наведення труби супроводжують відліками
горизонтального круга. За відсутності
колімаційної похибки різниця відліків
повинна становити 180°. Значення
колімаційної похибки визначають за
формулоюа
та b
-
відліки горизонтального круга відповідно
при КП та КЛ. Якщо колімаційна похибка
с> 10', її мінімізують. Для цього
знаходять середній відлік (с. в.), який
дорівнює
Повертають
алідаду навідним гвинтом і встановлюють
середній відлік (с. в). Центр сітки ниток
виявиться не наведеним на вибрану
точку. Виправними боковими гвинтами
сітки ниток переміщають сітку так, щоб
центр сітки був наведений на точку.
Необхідно стежити, щоб не порушити
правильність встановлення сітки
ниток. Для технічних теодолітів з
односторонньою системою відліків
необхідно одночасно з визначенням
колімаційної похибки виконувати
перевірку ексцентриситету алідади
відносно лімба (ексцентриситету
осей). Виконання цієї перевірки детально
описано в курсі “Топографія”.
Яквиднозрис.
ІІ.3.13,—
ар"
1
h
О А
З
цього самого рисунка можемо записати—
=
S
h
= S tgv.
(ІІ.3.22)
(ІІ.3.23)
175П’ята
перевірка. Горизонтальна вісь обертання
зорової труби повинна бути горизонтальною
- перпендикулярною до вертикальної осі
теодоліта.
За відсутності колімаційної похибки
і горизонтальності осі обертання труби
візирна вісь труби (під час обертання)
описує вертикальну площину, яку і
повинна створювати зорова труба
теодоліта. Якщо вісь обертання труби
не горизонтальна, то труба, точніше,
візирна вісь (під час обертання) буде
описувати нахилену площину, що під час
вимірювання горизонтальних кутів буде
вносити значні різниці у значення
кутів, виміряних при КЛ та КП.
Негоризонтальність (кут нахилу осі і)
можна визначити так. На горизонтальній
ділянці земної поверхні встановлюють
теодоліт на віддалі S
=
20-30 м (віддаль, що вимірюється) від
вертикальної стіни будинку Н. На рис
11.3.135 = /- А'.
Вибирають
на стіні довільну, помітну точку Я.
Приводять теодоліт у робочий стан,
наводять трубу на точку А
та, повертаючи трубу у вертикальній
площині, проектують точку А
на горизонт теодоліта (на таку саму
висоту, що і центр вертикального круга
теодоліта, точка /) при двох розташуваннях
круга - КЛ та КП. Відмічають на стіні
дві точки А{
та Аг
(це робить помічник спостерігача
олівцем). Якщо точки Ах
та А2
збігаються, умова виконується. Під час
нахилу осі обертання труби на кут Ґ,
візирна вісь описуватиме нахилені
площини, слідами яких на рис. ІІ.3.13
є лінії АА{
та АА2.
Визначають половину горизонтальної
віддалі між точками Ах
та А2,
тобто а
= АіА',
а також вимірюють вертикальний кут v.=
tg і-—;-
Томуh рtgv,
отже,
Рис.
11.3.13. До визначення негоризонтальності
осі обертання труби теодоліта
Підставивши
А з рівняння (ІІ.3.23) в (ІІ.3.22), отримаємо
кінцеву формулу для визначення кута
нахилу осі
ар"
S
tg V
(ІІ.3.24)
Виправити
розташування осі обертання труби, щоб
позбутися кута
Цю
перевірку виконують по-різному, залежно
від того, де розташований (де вмонтовано)
оптичний висок - на підставці теодоліта
чи на його алідадній частині. Якщо висок
на алідадній частині, тоді перевірку
виконують так: виском центрують теодоліт
над цим геодезичним пунктом
176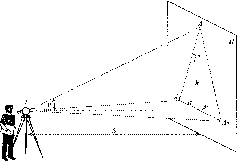
і".і"
для оптичних та електронних теодолітів,
можливо тільки в оптичній майстерні.Шоста
перевірка. Візирна вісь оптичного виска
повинна збігатися з вертикальною віссю
обертання теодоліта.
Оптичний висок - це ламана труба, схема
якої показана на рис. II.3.14. Точка Ох
- центр окуляра, С
-
сітка ниток, М-
точка на заломлюваній поверхні призми,
02-
центр об’єктива, Т-
центр геодезичного знака, над яким
необхідно зцентрувати теодоліт.
Виконуючи перевірку, встановлюють, чи
збігається лінія М-02
з вертикальною віссю обертання алідадної,
верхньої частини теодоліта.Т
або над будь- якою точкою так, щоб під
час горизонтального розташування
алідади центр
сітки
виска С проектувався на точку
Якщо
оптичний висок вмонтовано в підставку
теодоліта, то перевірку виконують іншим
способом, який можна також застосувати
і для теодолітів, у яких висок вмонтовано
в алідадну частину. Тому цей метод можна
вважати універсальним, до того ж він
точніший. На зоровій трубі зверху є
мітка, яка у разі горизонтального
розташування труби розміщена на
продовженні вертикальної осі
обертання теодоліта. Як відомо, ця вісь
проходить і через центр лімба, а саме
центр лімба повинен бути на одній
висковій лінії, що є вершиною
горизонтального кута, який необхідно
виміряти. Для виконання перевірки
необхідно мати ще один теодоліт. Цим
додатковим теодолітом проектують мітку
на трубі на горизонтальну поверхню.
Для цього під досліджуваним теодолітом,
який встановлено на штативі, кладуть
горизонтально на поверхню землі
квадратну частину дошки (можна
використовувати мензульну дошку). На
дошку прикріпляють аркуш паперу. Мітку
на трубі проектують на папір допоміжним
теодолітом з трьох розташувань, вибраних
так, щоб спроектовані вертикальні
площини перетиналися під кутами у 120°.
Рис.
11.3.14. Схема оптичного виска (центрира)
177Т
(рис. ІІ.3.14). Далі, відкріпивши закріпний
гвинт алідади, повертають алідаду і
спостерігають, чи не зміщується проекція
центра сітки ниток С з точки Т.
Якщо не зміщується - умова виконується.
Якщо ж проекція центра сітки С зміщується
і під час повороту алідади на 360° описує
коло деякого радіуса, то виправними
гвинтами сітки ниток потрібно переміщати
сітку ниток так, щоб центр сітки ниток
проектувався на центр цього кола. Після
переміщення сітки ниток ще раз ретельно
горизонтують алідаду за допомогою
циліндричного рівня, уточнюють
центрування над точкою Т
, переміщуючи теодоліт на головці
штатива. Далі ще раз повертають алідаду
на 360° і спостерігають, чи не зміщується
центр сітки С з точки Т
. За необхідності повторяють дії, описані
вище.

Рис.
11.3.15. Визначення розташування проекції
центра лімба (осі обертання лімба) С'
У
разі першого розташування теодоліта
спостерігач наводить трубу на вертикально
встановлену помічником голку, вістря
якої суміщено з центром мітки на трубі.
Далі трубу повертають тільки у
вертикальній площині так, щоб було
видно папір на дошці. У створі вертикальної
площини помічник, яким керує спостерігач,
наносить на папір дві точки. Нехай при
КЛ це будуть точки 1 та 2, з’єднані
штрих-пунктиром. Відповідно при КП
отримано точки Г та 2', які також з’єднані
штрих-пунктиром. Проведена суцільна
середня лінія. На цій лінії розміщена
шукана точка - проекція центра лімба
Найвживанішим
і найточнішим способом вимірювання
горизонтальних кутів є спосіб кругових
прийомів. Спосіб особливо ефективний,
якщо з деякої точки (вершини кутів)
виходять декілька напрямків. Нехай
маємо чотири напрямки на точки 1, 2, 3,4
(рис. ІІ.3.16). Один з них вибирають за
початковий; це напрямок на візирну
ціль, яку найкраще видно. Візирними
цілями слугують
178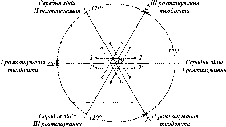
С'.
Щоб знайти цю точку з контролем, необхідно
поставити допоміжний теодоліт ще в
двох точках і аналогічно визначити
розташування ще двох середніх ліній.
У результаті, як це показано на рис.
ІІ.3.15, одержано проекцію точки С'.
У цю точку повинен проектуватися центр
сітки ниток оптичного центрира С.
Якщо ця умова не виконується, то
виправними гвинтами сітки ниток центрира
переміщають сітку так, щоб проекція
точки С
збігалася з С'.
Вимірювання горизонтальних кутів способом кругових прийомів
спеціальні
візирні марки, в які вмонтовані оптичні
виски для центрування марок над точками
1, 2, 3, 4. Теодоліт центрують над точкою
Розглянемо
ці дії детальніше:
При
КЛ трубу наводить на марку 1 (початковий
напрямок) і встановлюють відлік, менший
за одну мінуту. Для цього на шкалі
мікрометра встановлюють відлік,
наприклад, О'ЗО" або 0?40".
Потім поворотом головки гвинта
переставляння лімба суміщають верхнє
(пряме) зображення нульової поділки
лімба (поділки, підписаної 0°)
із зображенням діаметрально протилежної
(перевернутої) поділки лімба (підписаної
180°). У результаті встановлюють бажаний
відлік, менший за одну мінуту.
Відкріпивши
закріпний гвинт алідади, повертають
алідаду 2-3 рази тільки за годинниковою
стрілкою, і трубу знову навідним гвинтом
точно наводять на марку 1.
Беруть
початковий відлік. Повертаючи головку
гвинта оптичного мікрометра,
домагаються точного суміщення зображення
діаметрально протилежних штрихів
0° і 180°. Останній рух гвинта мікрометра
повинен бути за годинниковою стрілкою
(на загвинчування). Відлік записують
у журнал.
Позначимо
відлік
другий
відлік
Відліки
Відкріплюють
закріпний гвинт алідади й алідаду
разом з трубою повертають тільки за
годинниковою стрілкою. Трубу послідовно
точно наводять на марки 2, 3, 4 і знову
на марку 1. Під час кожного такого
наведення виконують дії, описані в
пункті 3. У результаті отримані відліки:
під час
наведення
на марку 2
179Т.
Лімб та алідаду приводять у горизонтальний
стан. Трубу фокусують по оку та по
предмету. Припустимо, початковий
напрямок - 1. За методом кругових прийомів
алідаду спочатку при крузі ліворуч
(КЛ) повертають за годинниковою стрілкою,
а трубу послідовно наводять на усі
марки, а потім, у другому півприйомі,
навпаки, при крузі праворуч (КП) алідаду
повертають проти годинникової стрілки
і трубу знову наводять на всі марки.
а1.
Потім головку гвинта мікрометра трохи
повертають проти годинникової
стрілки. Поділки 0° і 180° розійдуться.
Знову повертають гвинт за годинниковою
стрілкою і ще раз суміщають поділки 0°
і 180°. Берутьа11.
З двох відліків виводять середній.
Позначимо його ах.а1,
а11,
ах
записують в журнал, а відлік ах
(для наочності) показаний і на рис.
И.3.16.
-Ь1,
Ь11,
середній \
і на марку 3 -с1,
с11,
середній сх;
на марку 4 -d1,
d11,
середній^. Під час нового наведення на
марку 1: а111,
alv,
середній а2.
Розходження середніх відліків під час
наведення труби на
марку
1 Дл
= Oj
-
Трубу
переводять через зеніт, і вертикальний
круг виявиться праворуч від труби
(КП). Трубу знову наводять на марку 1.
Беруть відліки, як вказано в пункті 3.
Тепер пряме зображення ділень лімба
- 180°, обернене - 0°.
Відліки
позначимо
Відкріпляють
алідаду і повертають разом з трубою
тільки проти годинникової стрілки, а
трубу послідовно наводять на марки 4,
3, 2 і знову на марку 1. Відліки записують
в журнал знизу-вверх. Матимемо:
під
час наведення на марку 4:
під
час наведення на марку 3:
під
час наведення на марку 2:
під
час нового наведення на марку 1:
Нове
незамикання горизонту (у другому
півприйомі) А„ =
Рис.
11.3.16. Розташування теодоліта (Т ) і
візирних марок
180а2,
значення Ал
називають незамиканням горизонту, яке
наявне, незважаючи на те, що труба
зробила 360°, тобто повний оберт; значення
Дл
регламентується інструкціями щодо
виконання кутових вимірювань. Допустимі
розходження залежать, передусім, від
найменшої поділки шкали мікрометра
цього теодоліта. Якщо найменша поділка
мікрометра 1" або 2", то допуск Д„,
відповідно, 6"
та 8".
Описані дії є одним півприйомом. Далі
виконують другий півприйом.av,
aV!,
середній а3.
dm,
dIV,
середній d2;сш,
сІ¥,
середній с2
;Ьш
, bIV
,
середній Ь2
;aVH,
ауш,
середній а4.аг
- а4.
Допуск на замикання - такий самий. Усі
ці дії становлять один круговий прийом.

Подальші
прийоми виконують так само, як і перший,
але початковий
.
180°
відлік
встановлюють, повертаючи лімб на кут
ос, який дорівнює а = + а,
п
де
9.
Під час спостережень у будь-якому
прийомі необхідно виконувати такі
правила:
а) ретельно
відфокусувати трубу, бажано не змінювати
фокусування протягом усіх прийомів;
б) не
затискати сильно закріпні гвинти
алідади та труби, не спиратися на
в) коливання
подвійної колімаційної похибки не
повинні бути більшими за 20”;
г) відхилення
від нуль-пункту середини бульбашки
циліндричного рівня не повинно
перевищувати двох поділок шкали рівня;
д) наводити
трубу на візирну марку необхідно одним
і тим самим місцем вертикальної нитки
або бісектора, біля горизонтальної
нитки, як показано на
[
рис. ІІ.3.17. Якщо уявно продовжити
вертикальну нитку вверх, тоді її
продовження повинно поділити марку
на дві рівні частини; одночасно, для
контролю, краї марки повинні бути
рівновіддалені від вертикальних ниток
бісектора;
є)
як вже зазначалося, точне наведення
труби навідним гвинтом повинно
закінчуватись на загвинчуванні. Якщо
вертикальна нитка або бісектор пройшли
візирну марку, потрібно трохи вигвинтити
навідний гвинт, а потім знову останній
рух гвинта повинен бути на загвинчування;
Бісектор
Горизонтальна
р . нитка
/
Центр
сітки ниток наведений на Вертикальна
візирну
марку
Рис.
11.3.17. Приклад наведення труби на візирну
марку
181п
- кількість прийомів (регламентує
інструкція); а'= 10'або а'= 5'. Наприклад,
для п
= 6
встановлення лімба в другому прийомі
повинно бути <Х2
= 30° 10’ або 30°05’; в третьому прийомі а3
= 60° 10' або 60°05' тощо. f
8.
При двох напрямках горизонт можна не
замикати. Тоді спосіб кругових прийомів
перетворюється на спосіб прийомів,
відомий з курсу “Топографія”.\
штатив; Г нитка
ж)
необхідно працювати середньою частиною
навідного гвинта. Підводити від руки
нитки сітки найближче до візирної
марки, щоб унеможливити значні повороти
алідади навідним гвинтом.
Точне
вимірювання горизонтальних кутів -
дуже складна і тонка робота, яка
прирівнюється до наукової.
Методи
опрацювання результатів спостережень
Методи
та послідовність опрацювання результатів
спостережень, що виконуються в польовому
журналі, стануть зрозумілішими, якщо
показати їх спочатку в буквеному
вигляді.
Можна
запропонувати два методи оброблення
результатів кутових спостережень на
деякому геодезичному пункті, залежно
від причини незамикання горизонту.
Існують дві можливі причини незамикання.
Перша причина: спільний вплив випадкових
похибок відліків шкали мікрометра та
наведення зорової труби на візирні
цілі. Всі відліки - рівноточні, а
найімовірніші з них - середні арифметичні
найімовірніші
кути (3, становитимуть: Р, =
Рз
=
чотирьох
(фактично з восьми) відліків, і всі інші
двох
відліків (фактично з чотирьох). Отже,
якщо діють тільки випадкові похибки
вимірювань, тоді опрацювання результатів
спостережень є простим обчисленням
середніх значень відліків та різниць
між середніми значеннями відліків у
напрямках 2, 3 та 4 та середнім відліком
у напрямку 1.
Таке опрацювання показано в табл.
ІІ.3.4.
Найімовірніший
середній відлік у напрямку дорівнює
-_ах+ал
^
асер„ 2 ’
а<:ер«
а2
а3 а‘:еРп ^сеРк ^1
а2
«З а4
'
де
відліків
необхідно
відняти від усіх напрямків. Тоді перший
напрямок стане нульовим, а всі інші -
приведені до нуля (відраховані від
нульового напрямку). Тому це метод
вимірювання напрямків, а не кутів. Таке
опрацювання показано у табл. И.3.5, а
також частково на рис. ІІ.3.16.
Друга
причина: “затягування” лімба алідадою.
Незамикання горизонту можливе тому,
що алідада під час поворотів “затягує”,
тобто дещо повертає лімб силою тертя
між осями лімба та алідади, тоді як лімб
під час вимірювання
182асер
, 6 ,
с , dcep
.
У такому разіЬсер
- асер;
(32
= ссер
- асер;dcep
~
асер
(див. рис. ІІ.3.16). Зауважимо тільки, що
асер
є середнім зbcep,
ссер
, dcep
є
середніми з
асер
= 2 = 4
Гасерп
-
середній початковий та асерк
-
середній кінцевий відліки. Кожний заІ9
а2,
а3,
а4
також є середнім з двох. Тому середній
відлік асер
№ напрямків |
КЛ |
КП |
|
Приведені напрямки |
Робочі формули |
1 |
«1 |
а4 |
асер асер.„ |
0°00'00” |
а. +а4
dj + G* а — — — cePk 2 асер„ +acepk сер ~ 2 а\ + а2 + а3 + а4 асер - 4 |
2 |
Ьх |
ь2 |
Ьсер |
^сер ~ асер |
|
3 |
|
с2 |
^сер |
^сер “сер |
|
4 |
4 |
|
^сер |
^сер ~~ Ясер |
|
1 |
а2 |
аг |
асерк |
0°00’00" |
Отримуємо
два незамикання горизонту при КЛ та КП
(у першому та
другому півприйомах):
Ал
= а2
В
одному прийомі матимемо середнє
незамикання горизонту, що
дорівнює
Дл+Д„
(а2-ах)
+ {аг-аА)
Асер
' 2 2 Такі
самі значення можна ще одержати за
формулою
Асер
®ССрк Ясер„
•
(II.
3.26) (ІІ.3.27)
Справді
(а2
+ ) {а\
+ а4
) _
(а2
~ а\
+ (а3
- аЛ
))
Асер
асерк
асер„ 2 2
Поправки
у напрямки вводяться за формулою
8„=-Д5Ц*-1).
(ІІ.3.28)
183
~ а\
і К
= аг
~ а4
• (Ії.3.25)
№ марки |
Круги |
Відліки штрихів лімба |
Відліки мікрометра |
/ + Я 2 |
2 с |
кл+кп 2 |
Приведені напрямки |
|
І |
II |
|||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
КЛ |
0°00' |
25” |
23" |
24,0" |
|
0°00'36,3" |
|
1 |
|
|
|
|
|
-23,0 |
0°00'35,5" |
0°00’00,0” |
|
кп |
180°00' |
48м |
46" |
47,0" |
|
|
|
|
|
|
|
|
|
|
|
|
|
КЛ |
68° 15' |
34й |
36" |
35,0" |
|
|
|
2 |
|
|
|
|
|
-23,5 |
68° 1546,7" |
68° 15’10,4” |
|
кп |
248° 15' |
58” |
59" |
58,5" |
|
|
|
|
|
|
|
|
|
|
|
|
|
КЛ |
129°18’ |
43" |
46" |
44,5" |
|
|
|
3 |
|
|
|
|
|
-29,0 |
129°18’59,0" |
129°18’22,7” |
|
кп |
309° 19’ |
14" |
13" |
13,5" |
|
|
|
|
|
|
|
|
|
|
|
|
|
КЛ |
0°00' |
24" |
25" |
24,5" |
|
|
|
1 |
|
|
|
|
|
-25,5 |
0°00'37,2" |
0°00’00,0” |
|
кп |
180°00’ |
50" |
50" |
С-Л О О |
|
|
|
КТТ
4-
кп
Зауваження:
для обчислення найпростіше
2
зультат
додати до меншого значення відліку.
Наприклад,
1842с
розділити на 2 і ре-2с-
-23,0”. Половина - 11,5”. Половину 11,5”
додаємо до меншого відліку 24”. Маємо
результат - 35,5”.
№> марки |
Круги |
Відліки штрихів лімба |
Відліки мікрометра |
/ + Я |
2 с |
кл + кп 2 |
Поправки 8к |
Виправ лені напрямки |
Приве-дені напрямки |
|
2 |
||||||||||
І |
II |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
КЛ |
0°00' |
25” |
23" |
24,0" |
|
|
|
0°00’36,3” |
|
|
1 |
|
|
|
|
|
-23,0 |
0°00’35,5" |
о о |
0°00’35,5” |
О^О’ОО^” |
|
КП |
180°00’ |
48" |
46" |
47,0" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
КЛ |
68°15' |
34” |
36" |
35,0" |
|
|
|
|
|
2 |
|
|
|
|
|
-23,5 |
68°15’46,7" |
-0,6 |
6S°1546,r |
68°\5'10,6” |
|
КП |
248° 15' |
58" |
59" |
00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
КЛ |
129° 18’ |
43" |
46" |
44,5" |
|
|
|
|
|
3 |
|
|
|
|
|
-29,0 |
129°18'59,0" |
-1,2 |
129°18’57,8” |
129°18’22,3” |
|
КП |
309° 19’ |
14" |
13" |
13,5" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
КЛ |
0°00' |
24" |
25" |
24,5" |
|
|
|
|
|
1 |
|
|
|
|
|
-25,5 |
0°00,37,2" |
-1,7 |
0°00’35,5” |
0°00’00,0” |
|
КП |
180°00’ |
50" |
50" |
о o' LT) |
|
|
|
|
|
Незамикання:
Дл=
0,5й;
похибка
у напрямки;
Зауважимо,
що заздалегідь справжня причина
незамикання горизонту невідома. Про
наявність “затягування” лімба алідадою
в тому чи іншому теодоліті можна
робити висновок за дослідженнями цього
теодоліта на основі пробних кутових
вимірювань: якщо Д ,
1852с
- подвійна колімаційна похибка; 2с
= КЛ
- {КП
± 180°)Ап
= 3,0"; Асер
= 1,1" 5k
= —(£-1)
; 6*.
-k
-
номер напрямку; п-кількість
напрямків.Ащ,
Асер.
не змінюють знака, то це
вказує
на наявність затягування. З іншого
погляду: враховуючи, що алідаду при КЛ
повертають за годинниковою стрілкою,
а при КП - проти, можна впевнено говорити
про значну компенсацію “затягування”.
Водночас є велика ймовірність, що ці
дві названі причини діють одночасно,
важливо, яка причина переважає. Проте
різні оброблення спостережень не
викликають розходжень у напрямках та
кутах, більших, ніж 1-3". Тому для
полігонометрії 3, 4 класів можна надати
перевагу першому методу опрацювання
результатів спостережень на пункті,
як простішому. У табл. ІІ.3.4, ІІ.3.5 подано
числові приклади опрацювання результатів
спостережень відповідно першим та
другим методами. Необхідні пояснення
наведені під таблицями та в тексті.
Повторювальні
теодоліти, як ми вже знаємо, мають
закріпні та навідні гвинти окремо для
лімба та алідади. Якщо відпустити
закріпний гвинт лімба такого теодоліта
і повертати трубу в горизонтальній
площині, то лімб і алідада будуть
повертатися одночасно і відліки лімба
не будуть змінюватися. Якщо ж відпустити
гвинт алідади і повертати трубу в
горизонтальній площині, то відліки
будуть змінюватися, оскільки під час
цього повертається тільки алідада, а
розташування лімба незмінне (і
“затягування” лімба поки що не будемо
враховувати). Використовуючи описану
конструктивну особливість таких
теодолітів, було запропоновано
вимірювання кутів методом повторень.
Розглянемо суть цього методу. Цим
способом вимірюють кожний окремий
горизонтальний кут. Встановивши
теодоліт у вершині кута
Після
цього відкріпляють лімб, повертають
трубу проти годинникової стрілки і
навідним гвинтом лімба знову наводять
трубу на точку 1.
Контрольний відлік не зміниться. Потім
відкріпляють алідаду, повертають за
годинниковою стрілкою і наводять трубу
повторно на точку 2. Відлік не беруть
(відлік дорівнюватиме приблизно 2(3 ).
Візування
на ліву точку 1 поворотами лімба, а на
праву точку 2 поворотами алідади
виконують декілька разів. Останнє
візування повинно бути на точку 2; після
чого роблять кінцевий відлік (при КЛ
186
Вимірювання горизонтальних кутів способом повторень
Т
(рис. ІІ.3.18), який необхідно виміряти
та, привівши теодоліт у робочий стан,
наводять трубу при КЛ на точку 1,
попередньо встановивши відлік, дещо
більший за нуль, або нуль. Позначимо
цей відлік ал.
Після цього відпускають алідаду,
повертають за годинниковою стрілкою
трубу, і наводять на точку 2. Беруть
контрольний відлік вх.
Зрозуміло, що відлік наближено буде
дорівнювати куту, який вимірюють.-вл
). Величина кута, який вимірюють,
становитиме:
(ІІ.З.ЗО)
де
З кутів
та рл
виводять середній. Числовий приклад
вимірювання показано у табл. ІІ.3.7, яка
є сторінкою польового журналу. Контрольний
відлік 126°33’ - підкреслений. Інші дані
журналу не потребують окремих пояснень.
Р
(ІІ.3.31)
‘о
Рис.
11.3.18. До пояснення способу повторень
187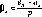
Р
-
кількість повторень. Якщо під час
вимірювання нульова поділка лімба
декілька разів пройшла через напрямок
на точку 1, тоді в чисельнику (ІІ.З.ЗО)
потрібно додати 360°, повторене таку
кількість разів, скільки було переходів
нульової поділки через цей напрямок.
Щоб не стежити за переходами нульової
поділки лімба, робиться контрольний
відлік вл
. Формула (ІІ.З.ЗО) дає значення кута при
КЛ. Далі, перевівши трубу через зеніт
і при КП, відкріпивши алідаду, наводять
трубу на праву точку 2. Беруть відлік,
який позначимо вп
. Відлік вп
є кінцевим при КП. Потім відкріпляють
алідаду, повертають трубу проти
годинникової стрілки і наводять навідним
гвинтом алідади на точку 1. Далі
відкріпляють лімб і повертають трубу
за годинниковою стрілкою, наводять на
точку 2 навідним гвинтом лімба. Ці дії
повторяють. Під час таких дій відлік
на лімбі буде прямувати до початкового,
точніше до (ал
+ 180°). Для такої самої кількості повторень
Р
буде наближено дорівнювати (ял
+ 180°). Труба буде наведена на точку 1.
Беруть відлік ап,
який буде початковим при КП. Вимірюваний
кут при КП знаходять за формулою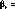
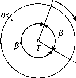
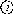
Спостереження |
Відліки |
Р -кратний кут |
Кути р |
Середнє з кутів $сер |
|||||||||||||
к-ть |
пункти |
КЛ |
КП |
КЛ |
КП |
КЛ |
КП |
|
|||||||||
3 |
КЛ |
1 |
126°33'00” 0°00’30м |
|
379о40'28" |
|
126°33'29' |
|
|
||||||||
2 |
19°40'58" |
|
|
|
|
|
126°33'32” |
||||||||||
КП |
2 |
|
199°4Г27" |
|
379°40’45м |
|
126°33’35" |
|
|||||||||
1 |
|
180°00'42" |
|
|
|
|
|
||||||||||
Проте
цей спосіб може застосовуватися та
виявитись корисним у разі необхідності
точного вимірювання кутів і за наявності
у виконавця тільки технічних теодолітів.
188
Якщо
під час побудови полігонометричних
мереж працюють спеціалізовані
бригади, які виконують окремо кутові
та лінійні вимірювання, то тільки кутові
вимірювання можуть виконуватися не
тільки електронними теодолітами, але
й електронними тахеометрами. Тому в
цьому параграфі розглянемо тільки
вимірювання кутів електронними
теодолітами (тахеометрами). Наперед
зауважимо, що процеси вимірювання
горизонтальних (та й вертикальних)
кутів такими приладами значно спрощуються,
а цілий ряд похибок, залежних від
спостерігача (насамперед похибки
відлічування) просто виключаються.
Основні дії, які виконує спостерігач,
- це встановлення приладу над точкою,
приведення приладу у робочий стан та
наведення труби на ціль. Як вже
зазначалось, наведення труби (в деяких
приладах) також автоматизовано.
Підготування
до вимірювання кутів
Підготування
приладу до вимірювань складається з
таких кроків:
Центрують
та горизонтують прилад над точкою
Встановлюють
батареї. Напругу дає батарея BDC
25.
Для вмикання напруги тумблер повертають
вверх. Після вмикання напруги прилад
подає звуковий сигнал і відображає
всі можливі символи, одночасно виконує
автоматичне тестування. Ці символи
подано на рис. ІІ.3.19. Після закінчення
самоконтролю на три секунди
відображається напруга батареї у
декількох кодових символах. Символ
ded
вказує
на те, що напруга батареї недостатня
для вимірювання. Такий самий символ
відображається також під час вимірювань,
якщо напруга батареї є низькою, під
час інших - кути можна вимірювати.
Висвітлені символи “VO/HO.SET”
вказують
на те, що прилад підготований до
індексування. Якщо кут нахилу
(компенсатора) перевищує 3', на екрані
з’явиться код Е 115 або Е 117. Досягають
горизонтальності циліндричним рівнем.
Індексують
круги. Для індексування вертикального
круга відпускають закріплювальний
гвинт труби і трубу повертають у
вертикальній площині на 360°. Індексація
(встановлення місця “нуля” або
“зеніту”) відбувається у момент
проходження об’єктивом лінії горизонту
в розташуванні КЛ. Підтвердженням
виконання індексації є звуковий сигнал
ТС встановлення на дисплеї значення
вертикального кута, наприклад, 91°04,30".
Аналогічно індексують горизонтальний
круг, але трубу повертають на 360° в
горизонтальній площині. Індексування
відбудеться, коли нуль-пункт алідади
перетне поділку “нуль” горизонтального
круга. Підтвердженням виконання
індексації є також звуковий сигнал і
висвітлення горизонтального кута
189Вимірювання горизонтальних кутів електронними теодолітами (тахеометрами)
Т
(рис. ІІ.3.18). Фокусують трубу по оку та
по предмету. Виконують ці дії так само,
як і для оптичних теодолітів.Н.
SHIFT\
Режиму
відслідковування
(I
V
вертикальний кут (0
у положенні “горизонт” ±90є)
Xf
5 ; ^7—^Куг
відкоригований
*"°
■ н"18888888
zl.-нахил
лінії в %
л
SHFT
Т8К
ФЧ-і898МВВ
|^ф-|—Напруга
віддалеміра ув.
“• J
^ ^-Одиниці
вимірювання
%
_
г,ООП'
^ОдиниШ
вимірювання кута
Значення
кутів або віддалей
відстані
Горизонтальний
кут правий
Горизонтальний кут лівий
Н
Затримання гор. кута
^
Віддаль похила Л
Відцаль горизонтальна Перевищення
Рис.
І 1.3.19. Символи, що відображаються на
дисплеї
Увага:
1) під час кожного вмикання приладу
індексацію повторяють;
за
бажанням змінити розмірність кутових
одиниць, наприклад, градусів (360°) на
гради (гони) 400 або змінити кутову
роздільність - (найменша поділка): 20"
(5 mgon/0,lmil)
Остаточна
перевірка готовності приладу до
вимірювання. Для цього:
необхідно
встановити рефлектор (будь-яку виразну
ціль) на відстані ~ 100
м;
увімкнути
напругу; 3) навести трубу на ціль при
КЛ. Відлічити значення кутів, наприклад,
Н: 18°34,00",
V: 90°30’20". 4) навести трубу на ту саму
ціль при КП і знову зробити відліки
кутів: Н: 198°34'20", V: 269°30’30". Крім
цього, значок на екрані означає, що
корекція вертикального кута виконана
автоматично. Якщо ні, користуватися
клавішею 4.
Вимірювання
кутів
Навести
трубу на лівий сигнал (пункт А), див.
рис. П.3.20.
Натиснути
головну клавішу 6
- SHFT,
а
потім клавішу 4 - 0SET,
щоб
встановити
“нульове” значення кута (правого або
лівого). Горизонтальні кути позначаються
кодами: Н, Н правий, Н лівий, лівий-правий.
Відпустити
закріплювальний гвинт алідади і навести
трубу на правий сигнал (пункт В).
Відображений на дисплеї горизонтальний
кут і буде кутом
190I V вертикальний кут (0 у положенні “зеніт”)
V вертикальний кут (0 у положенні “горизонт” при кл)
-F0;
кутову
роздільність: 10" (2mgon/0,05mil)
-
F{,
треба натискати одночасно на клавіші
№ 1 і № 2, N{
-
зміна розмірності параметра;N2-
перехід
до наступного параметра. Нумерація
шести клавіш на клавіатурі приладу
відраховується зліва направо. Номери
клавіш подано у п. И.3.4. Можна встановити
градуси F0
-
360°; Fx
-
400 gon;
400
grad;
F2 - 6400 mil - тисячні.
між
пунктами А та В. Аналогічно вимірюють
кут при КП. Перевівши трубу через зеніт,
наводять її спочатку на лівий пункт А.
Далі наводять трубу на правий пункт В.
Відображається значення кута при КП.
Щоб почав змінюватися відлік на дисплеї
або відображений кут, необхідно натиснути
на клавіші 6
та 5.
Щоб
розпочати вимірювання на інших поділках,
наприклад, на 60°00'20", потрібно: 1)
відпустити закріпний гвинт алідади
і, повертаючи трубу в горизонтальній
площині, встановити грубо відлік, що
дорівнює 60°, а точно навідним гвинтом
- 60°00'20"; 2)
зафіксувати на дисплеї цей відлік; для
цього натиснути клавіші 6
та 5. Закріплений кут має код: На. Навести
трубу на пункт, якому відповідає цей
відлік, наприклад, на лівий пункт А,
якщо будемо виконувати вимірювання
кутів на різних поділках круга. Для
підвищення точності вимірювання кутів
можна вимірювати ліві та праві кути,
як і під час способу повторень. Потрібно
встановлювати коди: Н (лівий кут) а
потім Н ■ ►(правий кут), клавіша 5.
Рис.
11.3.20. До вимірювання горизонтальних
кутів
електронним теодолітом
Як
відомо, похибки кутових вимірювань
викликають поперечні зсуви в
полігонометричних ходах. Ці зсуви ми
позначали літерою
Редукція
візирної цілі
над
геодезичним пунктом.
Центрування
теодоліта (
Інструментальні
похибки (м,), тобто похибки викликані
недоліками приладу, з якими виконують
вимірювання кута.
Зовнішнє
середовище
191

Джерела похибок вимірювання горизонтальних кутів
и.
Джерелами похибок вимірювання
горизонтальних кутів є:
(ир)
- неточне встановлення візирної марки
иц
) - неточне встановлення центра лімба
над вершиною кута, що вимірюється.(и3).
До них належать похибки, викликані
неоднорідністю за густиною атмосфери,
в якій проходить промінь світла від
візирної
цілі до приладу, неабсолютна прозорість
атмосфери, коливання зображення візирної
цілі, викликана турбулентністю атмосфери
(рухомість її елементарних частинок
та вихорів).
Вимірювання
кута (
Вихідні
дані (
Як
координати, так і обчислені за ними
дирекційні кути містять певні похибки.
Це викликає додаткові величини нев’язок
у кутомірних ходах, що прокладені між
цими відомими дирекційними кутами.
Виникнення цих додаткових нев’язок
необхідно передбачати і вимірювати
кути з деяким запасом точності. Зрозуміло,
що ці додаткові похибки пов’язані не
з цими вимірюваннями, а з вимірюваннями,
які виконувалися під час створення
геодезичної мережі вищого класу.
Вважаючи, що всі ці похибки виражені
поки що в лінійній мірі і є випадковими,
можна записати:
и2
= и2
+ и2
+и2
+и2
+и2л
+и2их. (ІІ.З.ЗЗ)
Приймаючи,
що всі ці похибки за величинами однаково
впливають на кутові виміри, матимемо:
ир=иц=иі..=ивих=т.
Запишемо:
М
= тл/б. (ІІ.3.34)
Як
відомо, допустима відносна похибка
поперечного зсуву ходу зав-
довжки
и
1
L
Т-Л’
(для
полігонометрії 4 класу
Враховуючи
(ІІ.3.34), (ІІ.3.35) можемо записати так:
m-yj6 1
(ІІ.3.35)
(ІІ.3.36)
L Г-V2'
Відносну
допустиму похибку на окреме джерело
похибок одержимо,
розділивши (ІІ.3.36)
нал/б, тобто:
m
_ 1 _ 1
L~
T-y[2-j6~ Т-УІЇ2
’
192
ив
к
), тобто вплив дій, які виникають під
час вимірювання кута, а саме: похибки
наведення труби на візирну ціль (марку)
та похибки відліків кругів.ивих).
Під час математичного опрацювання
кутових вимірів використовуються
відомі, наперед задані величини. Це
координати пунктів та дирекційні кути
напрямків.L
виражається
формулоюТ
= 25000).
або
Для
ходу з параметрами
за формулою
(ІІ.3.37):
т
1
1
3,5
(ІІ.3.37)
10
км;
/я
= 12
см.
Отже,
окреме джерело похибок повинно викликати
похибку в положенні кінцевої точки
такого ходу не більше за 12 см. У кутовій
мірі da."
це
становитиме:
12
м
10000
м”
р'
’ “
" 10000 “
’
Ці
прості розрахунки вже вказують на те,
що похибка в положенні кінцевої точки
ходу, викликана окремим джерелом
похибок, не повинна перевищувати 2,5".
Для
ходу з попередньо ув’язаними кутами
у п. II. 1.12 ми отримали формулу
и
_т$
Іп +
З
\~Ї2~
(ІІ.3.38)
Розв’яжемо
цю формулу відносно
Т
12
п
+
З
Враховуючи
формулу (ІІ.3.35), матимемо:
(Ії.3.39)
(п-3-40)
Оптимальні
довжини ліній в полігонометрії 4 класу
За
(ІІ.3.40) матимемо:
т 25000
V2
і—
=4,2". 23
Теоретичні
розрахунки дають допустиму сумарну
похибку кута - 4,2". Часто, особливо в
міських умовах, лінії полігонометрії
менші за 500 м. Як
193L
=ТТ
= 25000; Т
■
%/Ї2 = 86600 отримаємо_da* 0,12-206265Розрахунок допуску сумарної випадкової похибки вимірювання окремого горизонтального кута
:S
=
500 м; для L
=
= 10000
м, кількість сторін ходу п
=
20.щ
=206265 ^
видно
з (ІІ.3.1.38), навіть для однакової довжини
ходу у разі збільшення кількості сторін
поперечний зсув
[5]
допускає = 5". Для однакового впливу
кожного з шести джерел випадкових
похибок на результати вимірювання
окремого кута можна записати формулу
для розрахунку допустимої величини
похибки на окреме джерело
™окр.дж. ^г
(ІІ.3.41)
Це
гранична похибка. Середня квадратична
похибка буде дорівнювати 1,2".
Нехай
у витягнутому, рівносторонньому ході,
показаному на рис. II.3.21,
/
и
Р Р Р Р
(ІІ.3.42)
або
и
=
т$
сист
S[n
+
(и — 1) + (и —
2)
+... + lj.
(ІІ.3.43)
Рис.
11.3.21. Дія на витягнутий, рівносторонній
полігонометричний хід однакової
систематичної похибки сист
вимірювання кутів
У
квадратних дужках формули (ІІ.3.43) маємо
суму натурального ряду
чисел від
и(и
+ і)
І
=
1
(ІІ.3.44)
194и
зростає, і /Яр буде змінюватися. Інструкціягп"окр
дж
.
Розрахунок допустимої систематичної похибки вимірювання окремого кута
п
сторін. Для такого ходу з однаковими
систематичними похибками сист
поперечний
зсув и
знайдемо на основі рисунка за формулою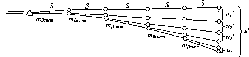
п
до 1. Як відомо, сума такого ряду чисел
дорівнює
Тому
(II.3.43) надамо вигляду:
г_™$сист
0
н(и + і) її
— —
* о
(ІІ.3.45)
^ «
Оскільки
L
Т-л/2
(ІІ.3.45)
відносно
або
U
_
тр
сист
(я + 1)
сист
_U 2 _ 1 2
р'
гран
сист
J2_'
п
+1
Для
w
=
20 матимемо:
гран
206265
л/2 25000 21
(П.3.46)
Як
бачимо, систематичні похибки майже на
порядок небезпечніші, ніж випадкові.
Допуск на сумарний вплив випадкових
похибок на один кут становить 5".
Відповідний допуск на сумарну систематичну
похибку - 0,6", тобто, у вісім разів
менший. Допуск на сумарну систематичну
похибку майже в чотири рази менший
навіть від допуску на одне джерело
випадкових похибок. Знешкоджувати такі
малі систематичні похибки - доволі
складне завдання.
Припустимо,
що у напрямку
а
=р
• esin
(ІІ.3.47)
Точка
195и
1 ,L
= S п,
а — = ——у=,
то, враховуючи це, розв яжемо рівняннятрсист:L
~ р'
2 ’L
(w + 1) Т-yfl
(и
+ 1)5
11.3.12. Похибка редукції'
АВ
(рис. ІІ.3.22) візирна марка встановлена
не в точці В
(не над центром геодезичного знака), а
помилково в точці В'.
Лінійна величина редукції - е.
Кутова похибка редукції - малий кут а.
Сторони та S[
трикутника
АВВ'
практично рівні. З цього трикутника,
оскільки кут а малий, можемо записати:В',
рухаючись по колу радіуса е,
може займати різні положення. Кут х
буде змінюватися разом з кутом а'. Для
х
=
0° та х
=
180°, о.”
= 0. Для
п
п
=
—
dx
(ІІ.3.48)
Рис.
11.3.22. Редукція одного напрямку
Кожному
положенню точки
Квадрат
середньої квадратичної похибки редукції
в напрямку
p'V
sin2
May
=■
S[_
2
n
(II.
3.49)
або
dx
Sy
•
2
к
o
2
n
Можна
довести, що інтеграл J
sin2
o
де
вигляду:
may
=
2
2
pV
2
Si
(II.3.51)
196х
=
90° та х
= 270° а* набуває максимального значення.
Нехай точка переміщається з постійними
кутами dx;
тоді п
-
кількість положень точки В'
знайдемо
за такою формулою: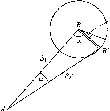
В'
буде відповідати похибка редукції в
деякому напрямку і.і
становитиме:Xml
= -
f sin2
xdx. (II.3.50)xdx
= n.
Тому
формула (II.3.50)
набу-
Для
другого напрямку кута з вершиною в
точці
2
_р2-е2
Ш<х2 „
о2
2Sj
Сумарна
квадратична похибка редукції:
J2
2
2 2 2 0
• Є
тр
~~ тщ
та2
~ 2
1_
L^i2
+
Для
„2
2
2
р * в L "
р Є
(ІІ.3.52)
(ІІ.3.53)
(ІІ.3.54)
Як
бачимо з (ІІ.3.54), похибка редукції прямо
пропорційна до лінійної редукції і
обернено пропорційна до довжини ліній
5і,
що створюють кут.
Для
полігонометрії
4 класу
0,01м-
206265" _
250
=
8";
таке значення
недопустиме.
За нашими розрахунками за (ІІ.3.41)
допустиме значення окремого джерела
кутової похибки (у такому випадку
похибка редукції)
2,4".
Знайдемо допустиму лінійну похибку
центрування візирної марки, розв’язавши
формулу (ІІ.3.54) відносно
®доп
(ІІ.3.55)
Мінімальна
сторона
®доп
2,4*-250
м
206265
=
2,9 мм.
Оптимальна
довжина сторони ходу
На
підставі розрахунків можна зробити
два висновки:
Для
коротких сторін центрування марки
необхідно виконувати значно точніше
ніж для довгих сторін.
Забезпечити
точність центрування марки, встановленої
на штативі, З мм нитковим виском - важко.
Необхідно застосовувати оптичний
висок.
197А
(для довжини S2)
похибка:si.S{=S2=S
матимемо:то=^- ,
або т0е
=
10 мм та за мінімальної допустимої
довжини сторони ходуS
=
250 м, т'
=т"=е:
S
полігонометрії
4 класу за інструкцією [5] становить
250 м. Тоді:S
=
500 м. едоп
= 5,8 ~ 6
мм.
Припустимо,
що під час вимірювання кута теодоліт
встановлено поза центром знака, тобто
в точці
В
Рис.
11.3.23. Встановлення теодоліта поза
центром
Розглянемо
трикутник
£>
+ р = Л + а (ІІ.3.56)
або
D-A
= a-$ = z. (И.3.57)
З трикутника
sin
a sin
е'
S{
Оскільки
кут а малий і
(П.3.58)
(Н.3.59)
Своєю
чергою, з трикутника
р,
ep*sin(x
+ £>)
(П.3.60)
19811.3.13. Похибки центрування теодоліта
А,
а не в точці В.
Тоді буде виміряний кут А,
а не кут D
(рис.
ІІ.3.23). Нехай точка А
переміщається по колу радіуса е
. Звернемо
увагу на те, що на відміну від впливу
редукції, вплив центрування теодоліта
завжди впливає на кут, що вимірюється,
де б не була розміщена на колі точка А.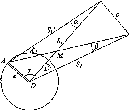
АМВ
та DMC.
Кути в точці М
в них однакові.
Тому кутиABD
знайдемо:хS{
~
Sx,
тоді запишемо:„
e'-p'sinx
а
=— .ACD
знаходимо:
Якщо
точка
n
то
кількість встановлень теодоліта
становитиме и = —, тому для кожного
dc
положення
точки
2
2
2
2
тц
=mz
=та+тр
(ІІ.3.61)
За
аналогією з похибкою редукції запишемо
в розгорнутому вигляді:
т:
2
_9'2
■ Є'2
2?
2д
о
sin2
X
t
Sin2
>i
dx.
Після
інтегрування та деяких перетворень
матимемо:
„2А
також переміщається по колу радіуса е
з інтервалами dx,
А,
враховуючи (ІІ.3.57), можемо записати:(x
+ D)
гї»ї
2 Є Р
тч = 9—Т’с
4 ^ г<2 о2
Sf-S:
(ІІ.3.62)
(ІІ.3.63)
де
с
-
віддаль між точками А
та С
(див. рис. ІІ.3.23).
Для
гострих кутів A
=D,
значення
с
мале. Для витягнутого ходу
А
= D
=
180°, с
= 5і!
+ ^. Якщо ^ = S2
=
S,
тоді с
=2
S,
ас2
=4 - S2.
У* такому разі (ІІ.3.63) набуде вигляду:
w2=£_j?—4S2 (ІІ.3.64)
ц 2 S4
або
тч=Цг-'12. (ІІ.3.65)
Порівнюючи
формули (ІІ.3.54) та (ІІ.3.65), бачимо, що
вплив похибок центрування на виміряний
кут в %/2
більший, ніж вплив редукції візирних
цілей. Поставимо вимогу, щоб тц
= тр,
тобто:
Отже,
е
• уі2
= е,
або
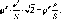
е
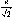
(11,3.66)
Якщо
е
відповідно 3 мм і 6
мм, тоді е
=2
мм, е
= 4
мм.
Отже: 1) теодоліт необхідно центрувати точніше ніж візирні марки;
обов’язково використовувати оптичні виски або якісь інші методи знешкодження впливу похибок центрування на кутові вимірювання.
199
//.3.14.
Методи зменшення похибок редукції та
центрування
Розглянемо
спочатку
Використовують
віхотримачі. Це металеве кільце, до
якого шарнірно прикріплені металеві
стрижні - ніжки віхотримача (рис.
ІІ.3.24). Віху встановлюють в кільце,
ставлять вертикально так, щоб вістря
віхи було над центром знака. Вертикальність
віхи перевіряють за допомогою виска
на нитці. Корегуючи розташування верху
віхи, ніжки віхотримача встромляють
в землю на різні глибини.
Рис.
11.3.24. Віхотримач Рис. 11.3.25. Види оптичних
центрирів
Віхи
(для коротких ліній) заміняють шпильками;
головне призначення шпильок - фіксувати
кінці вимірювальної стрічки для
лінійних вимірювань.
Шпильку
можна замінити звичайним стрижнем.
Застосування
оптичних центрирів (рис. ІІ.3.25).
Способи
підвищення точності центрування
теодоліта
Важкий
висок. Нитка такого виска менше
відхилятиметься вітром від вертикального
стану.
Жорсткий
висок. Це висок не на нитці, а на тонкій
металевій штанзі із загостреним кінцем.
Довжину штанги можна змінювати. Така
штанга, прикріплена шарніром до
станового гвинта, під своєю вагою
займає вертикальне положення.
200можливі
методи зменшення похибок редукції.
Нагадаємо, що під час вимірювання
горизонтальних кутів у теодолітних
ходах як візирні цілі зазвичай
використовують віхи. Інколи, щоб не
тримати віху в руках вістрям над центром
знака, робітник встромляє віху в землю
поруч з центром знака. У полігонометрії
це недопустимо. Тому:
Оптичний
центрир теодоліта.
Лазерний
центрир. Дуже зручний.
Проте
найефективнішим способом, яким практично
повністю можна знешкодити як вплив
редукції, так і центрування, є так звана
триштативна система. Основою такої
системи є три універсальні підставки
теодоліта. Універсальність підставок
полягає в тому, що на них можна
встановлювати не тільки теодоліт, але
й візирну марку, знявши теодоліт з
підставки. Вертикальна вісь обертання
теодоліта на підставці повинна збігатися
з вертикальною віссю марки. У підставки
вмонтовують оптичні виски. На рис.
ІІ.3.26 підставки показано трикутниками,
кружками показані місця, в які вставляють
теодоліт або візирну марку, крапками
- точки, через які проходить вертикальна
вісь теодоліта або марки.
Рис.
II. 3.26. До пояснення суті триштативної
системи знешкодження
впливу похибок
центрування та редукції
Встановлену
на штатив підставку з оптичним центриром
центрують над центром геодезичного
знака і її розташування не f
змінюють,
на підставку встановлюють теодоліт,
знявши оптичний центр, або, знявши
теодоліт, встановлюють візирну марку.
Штатив та підставку залишають в
незмінному стані. Наприклад, вимірюють
кут р2
на
точці 2, а на точках 1 та 3 встановлено
візирні марки. Теодоліт та марки
попередньо встановлені за допомогою
оптичних центрирів. Після вимірювань
теодоліт (без підставки) знімають з
точки 2
і на цю підставку, що залишилася на
штативі, встановлюють задню візирну
марку. Теодоліт переносять на точку 3,
знімають передню марку (без підставки).
Теодоліт встановлюють точно над тією
самою точкою, над якою тільки що була
встановлена передня візирна марка.
Передню візирну марку встановлюють
над точкою 4. Використовують штатив
(що'звільнився), на якому була встановлена
задня візирна марка (можна мати ще один
штатив). Потім вимірюють кут Р3
і так далі. Теодоліт та візирні марки
ніби “відриваються” від центрів
знаків, розташованих на земній поверхні,
і створюється (якщо полігонометричний
хід замкнутий) багатокутник у “повітрі”
(фактично в точках, де встановлюють
теодоліт та марки). Саме в цьому
“повітряному
201
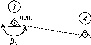
багатокутнику”
виконують вимірювання кутів, і на
значення кутів практично не впливають
ні похибки центрування, ні редукції.
Кутові нев’язки, викликані цими
факторами, виключаються, хоча зрозуміло,
що діяли похибки центрування підставок
оптичними висками.
Як
ми вже знаємо, до цих похибок належать
похибки наведення труби на візирну
ціль та похибки відліків лімба
(горизонтального кута). Розглянемо
окремо, як впливають ці похибки на
вимірювання кутів методом кругових
прийомів та методом повторень, якщо
кут виміряний одним повним прийомом
або одним повторенням, а також якщо кут
виміряний
Спосіб
кругових прийомів
Нехай
вимірюють кут Р, утворений двома
напрямками (див. рис. ІІ.3.27). Як відомо,
під час вимірювання, після наведення
труби на ціль беруть два відліки і з
них виводять середнє значення.
Рис.
11.3.27. До розрахунку похибок вимірювання
горизонтального кута
методом кругових
прийомів
Нехай
труба наведена на ліву ціль та взято
відлік . Похибка відліку
Аналогічно,
під час наведення труби на праву ціль
взято відлік
найімовірніші
похибки також
за
ходом годинникової стрілки, то кут р
знайдемо з виразу
Р
= *-а. (ІІ.3.67)
202
Похибки вимірювання горизонтальних кутів
п
прийомами або Р
повтореннями.
тв,
похибка середнього відліку, якщо діють
тільки випадкові похибки, становитиме
; випадкову похибку наведення труби
позначимо тн.
V2в;—=
та тн
. Оскільки поділки на лімбі зростають
З виразу
(ІІ.3.67), що є різницею двох змінних
величин, можемо (на основі теорії похибок
вимірювань) записати для півприйому
(при КЛ або КП) квадрат середньої
квадратичної похибки:
2
тя
т„ 2 2
тїп/п=-^
+ -^ + тн
+%-
або
r4r,in=ml+2m2H-
Квадрат
похибки одного прийому становитиме:
2 п/п
т$п=—1Г~’
або
2
_тв
, 2
т^„-
— + тн.
Квадрат
похибки кута, виміряного
2
1
Щ
=-
п
2
тн+
— н
2
2
Л
Отже,
2
Л
2
тв
"
2
(11.3.68)
(11.3.69)
(11.3.70)
(11.3.71)
(11.3.72)
(11.3.73)
Спосіб
повторень
Як
і раніше, нехай кут (3 виміряний методом
повторень. Наводимо трубу на
ліву
ціль. Беремо два відліки. Будемо мати
похибки середнього відліку та
V2
наведення
кінцеві
відліки. Похибка середнього з них
V2
Р,
виміряного за одного розташування
вертикального круга, становитиме:
2
2
т,
т. 2
т» 2
=^+-^+р-ти+Ртн>
л
або
/ир
t
- ml
+2Р • ml,
кр
(11.3.74)
(11.3.75)
203п
прийомами, становитиме:та
=ті
+ —тн.
Далі наведемо трубу на праву ціль.
Відлік не беремо. Буде тільки похибка
наведення тн.
Потім здійснюємо тільки наведення
труби р
разів, на лівий і на правий предмети.
Кінцеве наведення труби на праву ціль.
Беруть два.
Квадрат похибки Р
кратного кута
Р
разів
тн;тн;тн;тн
Р
разів
л
тп
^ тн>т„>тн\тн'^
Рис.
11.3.28. До розрахунку похибок
вимірювання
горизонтального кута
способом повторень
Квадрат
похибки
<<Р=ЇТ+Рт”■
Допустимо,
однократний кут Р, а
1
(ІІ.3.76)
Р
=
--А.
Р
(ІІ.3.77)
Це
найпростіша функція добутку постійної
величини 1
Тому:
.,2
__ І „2
щ=
— -т-А.
(ІІ.3.78)
Оскільки
'
«р
2
1
fti2 2
-P+p™1
Вираз
(ІІ.3.79) можна ще записати так:
2
1
^
2
^
2 тв
н 2
Р
або
/ир
2
2
тв
ті
+ — н
2Р
(ІІ.3.79)
(ІІ.3.80)
(ІІ.3.81)
Порівнюючи
формули (ІІ.3.73) та (ІІ.3.81), зауважимо, що
коли
204
т0
t л >>Р
-кратного кута, виміряного за двох
розташувань вертикального круга,
становитиме:Р
-кратний кут —А.
Тоді:/Р
на змінну Л.Р2т2Л
= т^р
, тоді:тп
Н n
=
Р
(кількість
прийомів дорівнює кількості повторень),
похибка відліку під час
вимірювання
методом повторень в
Ці
похибки детально вивчаються у курсі
“Геодезичні прилади” [17, 29]. Тут ми
тільки перерахуємо ці похибки, відзначимо
величини їхніх можливих впливів на
точність вимірювання кутів, а також
способи мінімізації або виключення
цих похибок.
кута
нахилу осі обертання труби
x'
= i'-tgx>°. (ІІ.3.82)
Проаналізуємо
цю формулу. Для
і) =
45°, tg
45°
= 1, тоді
205Р
разів менша за похибку відліку, ніж під
час вимірювання способом кругових
прийомів. Саме через це спосіб повторень
був основним способом вимірювання
кутів, коли не було високоточних
відлікових пристроїв. Сьогодні спосіб
втратив колишню популярність.
Інструментальні (приладні) похибки
Похибки
поділок лімба.
Точність кругових шкал характеризується
похибками нанесення штрихів. Похибки
поділяють на довгоперіодичні, які
поступово змінюються на всьому кругу
лімба, та короткоперіодичні (у межах
окремого градуса з періодом 15’... 1°).
Розрізняють також випадкові та
систематичні похибки, а їхні суми
називають повними похибками. Випадкові
похибки у декілька разів менші за
систематичні. У сучасних теодолітах
похибки діаметрів, тобто середня
арифметична похибка двох діаметрально
протилежних штрихів лімба, не перевищують
1,5”, короткоперіодичні - 1", а випадкові
0,1-0,3". Мінімізують ці похибки
вимірюванням кутів на різних поділках
лімба, тобто завдяки перевстановленню
лімба під час вимірювання.Ексцентриситет
лімба,
алідади
та осей.
Ці похибки також повністю компенсуються
завдяки двостороннім відліковим
системам, а для односторонніх
відлікових систем - завдяки вимірюванням
кутів при двох розташуваннях
вертикального круга КЛ та КП.Нахил
осі обертання труби.
У курсі “Топографія” виведена формула,
за якою можна визначити похибку напрямку
в секунді х,
залежно від значенняі
та нахилу візирної осі труби v°.V
= 0°, х*
= 0. Це означає, що коли сторони, які
створюють кут, який вимірюють -
горизонтальні, тоді нахил осі обертання
труби не впливає на вимірювання цього
горизонтального кута. Якщох”
= Ґ
9
тобто похибка в напрямку х*
дорівнює кутові нахилу труби і*.
Ця похибка компенсується, якщо
горизонтальні кути вимірюють при двох
розташуваннях вертикального круга КЛ
та КП, якщо під час вимірювання і
незмінна.
кута
нахилу візирної осі труби і)°, що
описується формулою
м
*
С
cos
О
(ІІ.3.83)
Якщо
і)° = 0°, cos
впливає
на середнє значення кута, якщо під час
вимірювання кута
о/Г
о
р'
де
1
є'2
8'
=
р'
Насправді
таких нахилів лімба не буває. Ціна
поділки циліндричного рівня при алідаді
точних теодолітів не більша за ЗО".
Під час відхилення такого рівня на дві
поділки лімб нахилиться тільки на Г,
8'=
0,004". Отже, нахил лімба можна не
враховувати, якщо вертикальна вісь
теодоліта прямовисна. Якщо вісь рівня
не перпендикулярна до вертикальної
осі обертання теодоліта (не зроблена
перевірка циліндричного рівня) або
недбало виконано горизонтування
приладу, тоді нахилиться і вісь обертання
труби і похибка у відліку буде значна
- визначатиметься за (II.3.82).
206Колімаційна
похибка.
У курсі “Топографія” також виведена
формула впливу колімаційної похибки
с
на окремий напрямок кута у”
залежно відУ
=-d°
=
1, то у*
= с*, тобто якщо полігонометрію прокладають
на рівнинній місцевості - похибка в
напрямку дорівнює колімаційній
похибці. Якщо V
>
0, COS
\)°
< 1, то у*
>с".
З цього зрозуміло, що в горбистій
місцевості вплив колімаційної похибки
може бути значним. Проте під час
вимірювання кутів при КЛ та КП, у*
змінює знак і тому колімація нес
незмінна.
Нахил
лімба.
У [17] виведена формула похибки відліку
лімба, якщо лімб нахилений:/ 1
Є . ^-а
-а- -sm2tf,
а
-
відлік горизонтального лімба;а'- відлік
нахиленого лімба;є- кут нахилу лімба.
Якщо лімб буде значно нахилений,
наприклад є' = ЗО’, тоді максимальне
значення похибки відліку 8*
для а
= 45° та а
=
135° становитиме:—”-1
= 3,93'= 4'.
Рен
оптичного мікрометра.
Питання впливу рена на вимірювання
кутів розглянуто у п. ІІ.3.2. Рен
мінімізується зміною збільшення
мікроскопа оптичного мікрометра, через
який розглядається зображення поділок
лімба. Якщо збільшення мікроскопа
надлишкове, рен додатний; якщо недостатнє,
рен від’ємний. Для юстування рена,
якщо збільшення мікроскопа надлишкове,
необхідно об’єктив мікроскопа віддалити
від лімба. Для недостатнього збіль
шення
необхідно, навпаки, наблизити об’єктив
до лімба. Якщо виконано дослідження
рена і відомо точне значення рена
де
Під
час нормальної роботи мікрометра окремі
різниці “загвинчування” мінус
“вигвинчування”, для високоточних
теодолітів, повинні лежати у межах - 1"
... + 1".
Вплив “мертвого” ходу на відліки
знешкоджують тим, що останній рух
барабана мікрометра перед відліком
повинен бути на загвинчування.
(ІІ.3.84)
(ІІ.3.85)
207г,
то можна майже повністю звільнитися
від впливу рена введенням поправки у
відліки 5т} за формулоюX
-
ціна найменшої поділки лімба; с, - відлік
оптичного мікрометра у мінутах дуги.
Під час вимірювання рен г
зазвичай не враховують, якщо його
значення під час точного вимірювання
кута менше за 0,5”.
“Мертвий
хід” оптичного мікрометра.
Під “мертвим” ходом мікрометра
розуміють нерухомість шкали мікрометра,
коли на малі кути повертають барабан
(ручка гвинта), хоча зміщується зображення
діаметрально протилежних штрихів
лімба. Особливо “мертвий” хід
проявляється під час зміни напрямку
руху із загвинчування на вигвинчування
(під час рухів за та проти ходу
годинникової стрілки). Тому дослідження
“мертвого” ходу рекомендують
виконувати, повертаючи алідаду на 15°
(всього буде 24 встановлення алідади).
Під час кожного встановлення алідади
суміщають штрихи лімба два рази:
повертаючи барабан за годинниковою
стрілкою та проти ходу годинникової
стрілки. Кожне суміщення штрихів
супроводжують відліками. Всього буде
48 відліків та 24 їхні різниці -Д, .
Знаходять середню різницю. Точність
визначення середньої різниці оцінюють
за відхиленнями окремих різниць від
середньої за формулою
Систематичні
похибки поділок гикали мікрометра.
Якщо малий кут Р вимірювати в поділках
мікрометра на різних частинах шкали,
тоді, у разі відсутності систематичних
похибок мікрометра, значення кута Р
повинно залишатися однаковим. За
наявності систематичних похибок
значення кута буде різним. Це справедливо,
якщо не діють інші похибки вимірювання.
Тому кут Р повинен бути стабільним і
малим. Наприклад, шкала мікрометра
теодоліта Т2 має 0-10’. Якщо візьмемо
малий кут, що дорівнює 2’, то його можна
виміряти на різних п’яти частинах
шкали: 0-2’; 2'-4’; 4'-6’; 6-8';
8’-10’.
Виконують
прямий та зворотний хід. Для підвищення
точності вимірювання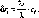

можна
на кожній з п’яти частин шкали кут
виміряти чотири рази (два прямі та два
зворотні ходи). Оцінюють наявність
систематичних похибок за помітними
систематичними змінами кута. Якщо,
наприклад, під час переходу від першої
частини шкали 0-2’
до п’ятої частини 8-10’
кут Р увесь час збільшується або
зменшується, то вважають, що систематичні
похибки мікрометра існують. Якщо ж
такої закономірності в ряді вимірювань
кута р, немає, тоді немає підстави
говорити, що систематичні похибки
поділок шкали більші за точність
вимірювання.
Неповна
прозорість атмосфери та коливання
зображень візирних цілей викликають
випадкові похибки вимірювання кутів,
хоча коливання зображень візирної цілі
в горизонтальній площині є короткотривалим
явищем бокової рефракції - викривленнями
світлового променя в горизонтальній
площині, викликаними миттєвими змінами
горизонтальних градієнтів температури
на всьому шляху променя від візирної
цілі до теодоліта. Ці впливи не є
загрозливими і не перевищують допуску
на одне джерело кутових похибок - 2,4”.
Проте в атмосфері часто існують
довготривалі, спрямовані середні
горизонтальні градієнти температури,
які не змінюють знака: зменшення чи
зростання температури в одному напрямку
протягом годин. Так, наприклад,
208
Зміна
розташування візирної осі під час
перефокусування труби.
Під час перефокусування труби в її
корпусі переміщується двоввігнута
фокусувальна лінза. Зміна розташування
цієї лінзи (частини складного об’єктива
труби) викликає зміну розташування
візирної осі. Це виникає тоді, коли
спостерігач за кожним напрямком
(залежно від довжини сторони кута)
перефокусовує трубу. Вплив перефокусування
практично неможливо виключити, якщо
сторони, що утворюють кут, значно
відрізняються за довжиною. Величину
такого впливу можна знайти, виконуючи
визначення колімаційної похибки
декілька разів на близькі та далекі
візирні цілі. Нагадаємо, що мінімальні
сторони полігонометрії (відповідно
до інструкції) для 4 класу - 250 м, 1 розряду
- 120 м, 2 розряду - 80 м. Приблизно на цих
віддалях мають бути близькі цілі;
далекі цілі - на віддалях, більших за
кілометр. Цілі мають бути приблизно
на одній висоті (у горизонті приладу).
Потрібно також виконувати вимірювання
приблизно на одних діаметрах
горизонтального круга, тільки, наприклад,
на 0°
і 180°, особливо це важливо для теодолітів
з односторонньою системою відліків,
щоб виключити вплив на зміну колімації
ексцентриситету осей.
Вплив зовнішнього середовища на вимірювання горизонтальних кутів
якщо
на вулиці стіни будинку нагріті сонцем,
то від стін нагріваються близькі до
стін прошарки повітря. У результаті,
якщо на віддалі 10 см від стіни середня
температура, наприклад, становить 25
°С, то в напрямку до середини вулиці,
на такій самій висоті на віддалі 110
см від стіни температура нижча і може
становити 24,5 °С. Тобто горизонтальний
градієнт температури
S
найкоротшим
шляхом: = мінімум; и,— показник заломлення
на відрізку
І
A
Рис.
11.3.29. Вплив бокової рефракції
на
вимірювання горизонтальних кутів
Припустимо,
в точці 2 потрібно виміряти горизонтальний
кут р. Візирні марки розташовані у
точках 1 та 3. Промені світла від точок
1 та 3 до точки 2 поширюються криволінійно,
до того ж ці криві повернуті опуклістю
у бік стін. Якщо навести трубу на точку
1 або на точку 3, спостерігачу буде
здаватися, що труба наведена на точку
1
або 3, коли труба буде спрямована по
дотичній до кривих у точці 2.
Справді,
наприклад, від точки 1 йде промінь світла
по кривій і зображення точки 1
потрапить в об’єктив труби, якщо її
візирна вісь буде спрямована по дотичній
до кривої в точці 2,
оскільки в цій точці крива збігається
з дотичною. Отже, будемо вимірювати не
кут р, а кут pj.
Малі горизонтальні кути між хордами
Ці
кути можна визначити за формулами [27]
Р
dT
r;=8,13-^~*S, (ІІ.3.86)
Т
dx
209dT
/
dx
=
*= 0,5 град/м. Градієнти можуть сягати 1°.
З віддаленням від стін градієнти
зменшуються. Біля стін густина повітря
буде менша, ніж далі від стін. Світловий
промінь, що йде від візирної цілі до
теодоліта, викривиться (за законом
Ферма) опуклістю у бік будинку. Промінь
поширюється за оптичноSi.
У результаті матимемо картину, показану
на рис. П.3.29.
гГ,
показані на рисунку пунктирами та
дотичними, називають кутами бокової
рефракції.
де
Посереднім
критерієм м&лих градієнтів є відсутність
коливань зображень візирної цілі у
горизонтальній та вертикальній площинах
та за наявності хоча б незначного вітру
швидкістю 0,5 м/с. Це так звані періоди
У
похмуру погоду вони значно довші. Можна
знешкоджувати бокову рефракцію введенням
поправок, але це потребує вимірювання
додаткових параметрів.
Загальна
формула обчислення довжини ліній
траверсної полігонометрії має вигляд:
-
де
210Р
-
тиск повітря, мб (Г-Паскалі);Т-
абсолютна температура (Т=
273° + + t°C);
dT
!
dx-
горизонтальний
градієнт температури; S
-
довжина лінії. Для Т
= 298°, Р
= 980 мб, S=
500
м, dT/dx-
0,5
град/м, г/= 22,4”. Але, для градієнта dT
/
dx
=
0,025 град/м, гг=
1,12”, 2г/ = 2,24". Отже, тільки за малих
градієнтів температури можна виконувати
вимірювання кутів вздовж стін будинків.
Значна бокова рефракція існує також,
коли полігонометричний хід прокладають
вздовж рік, озер, шосейних доріг та
залізниць, вздовж меж поверхонь з різним
альбедо (наприклад, луки-рілля), вздовж
крутих схилів. Зрозуміло, що в таких
умовах необхідно виконувати вимірювання
кутів у такі періоди доби, коли
горизонтальні градієнти температури
малі.спокійних
зображень,
які також називають періодами
видимості.
Вони настають вранці, приблизно за
півтори години після сходу та увечері
за годину до заходу сонця. На жаль, під
час ясної, антициклонної погоди ці
періоди короткі: 20-30 хвилин зранку та
ввечері.11.4. Попереднє опрацювання результатів польових вимірювань у полігонометрії
Попереднє опрацювання лінійних вимірів
S =
п
• /q
+ (Пі
— 3j)
+ ASfc
—
ASh
+
ASt
+
d
+ Дd^
—Adh
+ Adt
+ ASH
+ ASr_K
, (П.4.1)n
-
кількість
укладень мірного дроту в лінію, що
вимірювалась; /0
- довжина дроту між нулями шкал; щ,
з,- - передній та задній відліки шкал;
ASk
-
поправка за компарування дроту; ASh
-
поправка за перевищення між задньою
та передньою шкалами дроту (під час
кожного його вкладання); ASt
-
поправка за різницю температур дроту
під час вимірювання та компарування;
d
-
домір,
частина
лінії
Якщо
лінія виміряна світловіддалеміром, то
загальна формула її довжини має вигляд:
S
= St
-ASh
+AS„ +ASf
+AS4-ASH
+ASr_K, (П.4.2)
де
(ІІ.4.1)
- поправки за редукцію лінії
Відповідно
до рис. ІІ.4.1 лінія
тт
__ 11
сер
(ПАЗ)
Виконаємо
просте, але достатньо точне розв'язання
цієї задачі. Проведемо через точку
Трикутники
Нсер
R3+Hcep
’
(ІІ.4.5)
ЗВІДКИ
^н=нсер
s
R3+Hcep
(ІІ.4.6)
211(d<10),
виміряна рулеткою; Дdk-
поправка
за компарування рулетки; Adh
-
поправка за перевищення між кінцями
доміру; Adt
-
поправка за різницю температур рулетки
під час вимірювання та компарування;
ASн
- поправка за редукування (приведення)
лінії до рівня моря; ASr_K
-
поправка за редукування на площину
проекції Гаусса-Крюгера.St
-
середнє
арифметичне значення відліків у режимі
“точно” із урахуванням відомої
кількості кілометрів; ASh
-
поправка за приведення нахиленої лінії
до горизонту; AS„-
поправка
за середні температуру Тср
та тиск повітря Рср
вздовж
лінії; ASj--
поправка
за дрейф частоти кварцового генератора
від номінальної частоти; ASy
-
поправка за циклічну похибку; ASH
та
ASr_K,
як і уS
на
рівень моря та на площину проекції Г
аусса-Крюгера.Редукування довжин ліній на рівень моря і на площину Гаусса-Крюгера
S
між
точками А
та В
розташована на земній поверхні. Середня
висота лінії:я,+я2Sa
-
проекція цієї самої лінії на рівні
моря; О
-
центр Землі; R3
-
радіус Землі. Необхідно знайти ASH
-різницю
між S
таSa:ASH=S-Sg. (ІІ.4.4)Вх
пряму, паралельну до ААІ.
Тоді відрізок В'В
=ASH.АБО
та В'ВВ{
-
подібні. З їхньої подібності можемо
записати:ASH
_
S
Враховуючи,
що
к3
Рис.
11.4.1. Редукування лінії S
на
рівень моря
Отже,
Розглянемо,
з якою точністю необхідно знати
ЗКГ*.
'
8<я»)
"
RsJ
'
Квадрат
середньої квадратичної похибки поправки
становитиме:
т
д%
2
_
— т
ГГ
2
гг2
2
, 11
сер
* ° _ 2
'ли,
+
n
тЯз
•
V
"ap
(ІІ.4.9)
Нехай
Smax
-
3000 м,
212R3
у
багато разів більший за Нсер
.тобто R3
»Нсер,
отже, Нсер
можна знехтувати, тоді:^н=Неер~. (ІІ.4.7)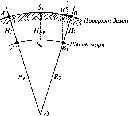
Sa=S-ASH. (ІІ.4.8)Нсер
та R3.
Продиферен- ціюємо (ІІ.4.7) за змінними
Нсер
та R3:д(ASff
)_S
d(AS’fj)
^_HcepS2 ЛЛсер
mRj
=
300 м, Нсер=
3000 м, тНсер~
1 м. Тоді отримаємо mAsH
=
0,47 мм. Другий член формули (ІІ.4.9) дає
0,066 мм. Отже, радіус Землі можна знати
з похибкою 300 м, але Нсер
потрібно знати з точністю 0,5 м, тоді
похибка поправки т^н
становитиме 0,24 мм при величині поправки
ASH
=-1,4126
м.
*
де
_ Є .
2 r; |
(ІІ.4.10) |
|
(ІІ.4.11) |
213
Рис.
11.4.2. До пояснення геометричної
суті
проекціїГаусса-Крюгера
Зауважимо,
що поправки за редукування ліній на
рівень моря на території України завжди
від’ємні; навпаки, поправки редукування
ліній на площину Гаусса-Крюгера завжди
додатні. Завжди від’ємними є також
поправки за приведення нахилених ліній
до горизонту.
Нехай
на деякому пункті кути вимірювали
способом кругових прийомів. Припустимо,
на цьому пункті було
Можемо
записати матрицю виміряних кутів:
к—\
Pl2>Pl3>Pl4"Plfc
Р22
’ P23
’
р24***р2£
Рз2>РзЗ>Рз4-Рз*
►П
Рл2
> РлЗ > Рл4 -"P/ifc
214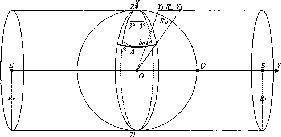
Опрацювання результатів кутових вимірювань на окремому геодезичному пункті
k
напрямків,
а під час вимірювання виконано п
прийомів. Завданням попереднього
опрацювання результатів вимірювань
є встановити точність вимірювань.
Визначимо середню квадратичну похибку
вимірювання кутів на цьому пункті.
Звернемося до рис. ІІ.4.3.
$12 = Рі2 ~$сер2 |
|
8іЗ = Різ - Рсерз |
•81* =pl* “Р* |
$22 = р22 $сер2 |
|
^23 = Р23 “ Рсерз |
"•82* =Рг* -Р* |
4 $32 = Рз2 ~ $сер2 |
|
833 = РзЗ “ Рсерз |
"•83* =Рз* -Р* |
$«2 _ Р«2 _ ^сеР2 |
|
$/13 “ Рл3 Рсе/73 |
=Ри* "Рі |
Матриця
похибок також матиме
ш
І
[88]
(ІІ.4.12)
Припустимо,
що під час польових робіт створена
мережа поліго- нометричних ходів, які
за формою близькі до витягнутих та
мають поздовжні зсуви
215п-(к
— \)
похибок. Проте виміряти всі кути одним
прийомом необхідно. Тому надлишкових
прийомів буде (я-1), а надлишкових
вимірювань (я - \)(к
-1).
Тому формула (формула Бесселя) середньої
квадратичної похибки, обчислена за
найімовірнішими похибками вимірювання
8у,
матиме вигляд:Оцінка точності лінійних вимірювань за результатами польових робіт
t'j.
Кількість ходів N,
їхні довжини Ц.
Тоді маємо:
ХОДИ |
1, |
2, |
3, |
N; |
поздовжні зсуви, м |
|
*г> |
'з> |
..., tN; |
довжини ходів, м |
|
к. > |
к> |
..., ln |
Поздовжні
зсуви
Х
=
(ІІ.4.13)
Тепер
знайдемо поздовжні зсуви, викликані
тільки випадковими похибками:
ti=t;~X-L. (ІІ.4.14)
Будемо
мати ряд таких (випадкових) похибок
Для
кожного з ходів характерний певний
коефіцієнт випадкового впливу ц,, тобто
випадкова похибка на одиницю довжини.
Можемо записати:
h
=
Ці'4к
’■>h
=
М-2 '4к
>
-4*n
=
M-jv 'лДл~
■
Випадкові
похибки
піднесемо
останні рівняння до квадратів:
Л .2 Л
2 м 2 12 2 ‘/V
цг
=— ;Цг =—; ...;ці =—.
1 Ц 2 L2 ™ L
Якщо
ходи прокладають однаковими за точністю
приладами, а лінії вимірюють однаковими
методами, тоді значення ц2
можна вважати рівно-
точними.
Знайдемо найімовірніше значення ц2:
..2
(ІІ.4.15)
Тепер
ми знаємо коефіцієнти випадкових ц та
систематичних
т\
—
ц2
•
+
X2
• S?
т\
=\іг
-Ц+Х1
-L]
(ІІ.4.16)
216t'j
викликані
як випадковими, так і систематичними
похибками. Виключимо систематичні
похибки. Дйя цього спочатку визначимо
коефіцієнт систематичного впливу
X,
тобто систематичну похибку на одиницю
довжини:
tx,
t2,
/3 .tt
матимуть
різні знаки. Щоб позбутися різних
знаків,_Ц?+Ц2+Цз+-
+ ЦлгЦ
" Nабо
X
впливів на результати лінійних
вимірювань. Це дає змогу розрахувати
сумарну похибку ms
будь-якої
лінії St
або
похибку mL
будь-якого
ходу Z,,:
Зауважимо:
ми виконали оцінку точності за
результатами польових робіт, так звану
постеріорну оцінку. Для підвісних
мірних приладів та для евітловіддалемірів
заздалегідь (до виконання вимірювань)
відомі значення коефіцієнтів р. та А
Оцінку
точності кутових вимірювань виконаємо
аналогічно, як і оцінку лінійних
вимірювань. Нехай маємо
запишемо:
ходи: 1, 2, 3, ...,
N;
нев’язки: /Рі, /р2, /р3, /pw;
кількість
кутів у ході:
Будемо
вважати, що кути містять переважно
випадкові похибки, а систематичні
похибки зведені до мінімуму. Позначимо
сумарну випадкову похибку окремого
кута в ході . Тоді можемо записати
формули
або
/Рі
=/Яр1
■ л/и[ +1; /р2
=Wp2
-V«2 +1
;/р3
=wp3
-фц+l;
-i/p* +1.
2
_
f&\ 2
_ fh
.
„,2
_
f£
. .
2
_
fin
Знайдемо
квадрат найімовірнішої похибки
вимірювання кута, вважаючи, що кути
вимірювались рівноточно:
2
/ир
=
mh+mb+mb"
+
mfiN
N
(ІІ.4.17)
Або:
А.
и,
+ 1
N
(ІІ.4.18)
217..
Це дає змогу наперед, до вимірювань,
підрахувати очікувані похибки, тобто
виконати апріорну оцінку. Останнє,
своєю чергою, дає Змогу підібрати такі
прилади та методи для виконання
вимірювань, щоб мати мінімальні
матеріальні затрати й задовольнити
всі вимоги замовника робіт.Оцінка точності кутових вимірювань за результатами польових робіт
N
полігонометричних
ходів, кутові не- в’язки яких /р., а
кількість кутів у ході (иг
+1),
де и,- - кількість ліній. Тоді(п{
+1
), (и2
+1)
, («3
+1),
..(nN
+1).^і-гтт’^-гтт’^з-гту’-’щ
+1'
n
n2
+1
нз
«з +1 '
VN
nN
+1
Для
теодолітів (тахеометрів) також відомі
середні квадратичні похибки вимірювання
куга одним прийомом. Тому можна виконувати
апріорну та постеріорну оцінки точності
вимірювань. Проте зауважимо, що остаточну
оцінку точності вимірювання кутів та
ліній здійснюють на основі зрівноваження
мереж.
Розрізняють
два види прив’язувальних робіт:
Прив’язування
пунктів полігонометрії до пунктів
тріангуляції, трила- терації, космічних
мереж або до пунктів полігонометрії
старших класів.
Прив’язування
пунктів полії'онометрії до постійних
предметів на місцевості.
Задача
І виду прив’язування - передати
координати та напрямки з уже наявних,
раніше закладених геодезичних пунктів,
на пункти полігонометричних мереж, що
створюються.
Задача
II виду прив’язування - відшукування
полігонометричних пунктів на місцевості.
Існує багато способів прив’язування
І та II видів. Проте найтиповіїпими
прив’язуваннями І виду є:
Безпосереднє
поєднання пунктів полігонометрії з
раніше закладеними пунктами
тріангуляційних мереж або старших
пунктів полігонометрії. Центри знаків
наявних пунктів одночасно стають і
центрами знаків нових полігонометричних
мереж. Зрозуміло, що координати цих
нових пунктів такі самі, як і координати
раніше закладених.
Прив’язування
до близьких пунктів, але недоступних
або важко- доступних пунктів тріангуляції.
Такі пункти зазвичай розташовані на
високих спорудах. Наприклад, основи
хрестів на церквах є такими пунктами
(мають відомі координати). Прив’язування
до таких пунктів називають “знесенням
координат”.
Прив’язування
до далеких пунктів тріангуляції
(виконуються прямими, оберненими та
комбінованими засічками).
Прив’язування
II виду виконуються в кожному конкретному
випадку різними способами, залежно від
наявності постійних (фундаментальніших,
ніж пункти полігонометрії) предметів
та споруд на місцевості. Від стабільних
споруд вимірюють віддалі до пунктів
так, щоб за цими вимірюваннями можна
218
Прив’язувальні роботи у полігонометрії
Види та завдання прив’язувальних робіт. Способи прив’язування
було
з контролем знайти ту точку на місцевості,
де закладався полігоно- метричний знак.
У забудованих територіях такими
місцевими предметами є будинки,
перехрестя вулиць, опори дротів тощо;
отже, прив’язування не викликає
ускладнень. У малоконтурній місцевості
таке прив’язування ускладнюється,
доводиться виконувати прив’язування
до значно віддаленіших предметів.
Щоб
виконати таке прив’язування, необхідно,
щоб для точки, координати якої
визначаються, було видно не тільки
високу (близьку) точку з відомими
координатами, але, як мінімум, ще одну
точку (зазвичай пункт тріангуляції,
також з відомими координатами).
Рис.
11.5.1. Знесення координат із недоступної
(високо)) точки
7]
на
пункт полігонометрії Рх
Задачу
знесення координат поділимо на три
частини:
Визначення
горизонтальної віддалі
Виміряємо
горизонтальні кути а, р, у, \|/
S 6, S і>2
sin
у
sin[l
80°
- (а + у)] ’ sin
у
sin[l
80°
- (р + \|/)]
(ІІ.5.1)
На
підставі (ІІ.5.1) знаходять два значення
5) та
Визначення
дирекційного кута аГі_^
лінії
219
Передавання координат із високих (недоступних) точок на Землю (знесення координат)

S
(рис.
П.5.1) між точками 7] та Рх.
Виміряємо
два базиси вх
та в2.
Базиси є сторонами трикутників 7]/} 1,
Щ2.таф.
Для вищеназваних трикутників за
теоремою синусів можемо записати:S2.
Виводять
середнє значення S.Tj-Tj.
Для
трикутника
в
S
(И.5.2)
]
(ІІ.5.3)
Із
цього самого трикутника визначимо кут
А,
= 180° -(р. + ф).
Далі
знаходимо дирекційний кут аГ]_^
:
(II.
5.4)
(ІІ.5.5)
Визначення
координат
Знаючи
координати точки 7]
координати
точки ,
Нехай
для визначення координат точки
Маючи
координати всіх чотирьох точок, чотири
дирекційні кути та чотири виміряні
кути, можна визначити по шість значень
АХ
= S
■
cosa^_p^
А
У
= S
■
sina^r]_P|j
(ІІ.5.6)
(П-5.7)
2
20ТХТ2РХ
запишемо теорему синусів: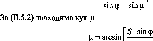
X:
Х^, .(Xx,Yx),
довжину лінії S
та
її дирекційний кут і> розв’язавши
пряму геодезичну задачу, знайдемо
шуканіY^
.Р
(рис. ІІ.5.2) з кожного з відомих пунктів
7]
, Т2,
Тг,...,
TN
(координати
всіх цих пунктів відомі) було зроблено
візування на шукану точку Р
та виміряні кути Pj,
Р2
>
Рз
>
—> Р/лініями
з відомими дирекційними кутами аА,
<хв,
<хс,ocv
та
напрямками на точку Р.ХР
та YP,
комбінуючи
точки з відомими координатами по дві:
1,2; 1,3; 1,4; 2,3; 2,4; 3,4. Визначення
найімовірніших координат точки Р(хр,ур)
за
Цими вимірюванняминазивають
прямою багаторазовою засічкою.
Проте, як зрозуміло з тільки що сказаного,
достатньо мати дві відомі точки,
наприклад, 7]
та Т2,
щоб знайти координати шуканої точки
ХР
та YP.
Справді,
розглянемо рис. ІІ.5.3. УХрх
= ХТі
+S
-cosa^^
Yn
=YTi
+S-
sina(7i_fl)Пряма одноразова та багаторазова засічки
трикутнику
7j
S{ в
sinp2
sm[180°-(p, +Р2)]
S2
в
sin
р! sin[180°-(p1+p2)]
(ІІ.5.8)
Рис.
11.5.2.
Пояснення
суті прямої багаторазової засічки
Р(ХР,
Yp)
Рис.
11.5.3.
До
пояснення суті прямої одноразової
засічки
З (II.5.8)
знайдемо довжини ліній
а(тх-Р)
=а(Ті-т2)
“Рі> а(т2-Р)
~а(т2-тх)
+ 02 • (ІІ.5.9)
Координати
точки
раз
- користуючись точкою 7J,
а другий раз - точкою
(II.5.10)
x’p+x'p.y
_ур+у;
- ,
(II.5.11)
221Т2
Р
відомі три елементи. Це означає, що
трикутник можна розв’язати та знайти
інші три елементи.
S{
та
S2.
Далі визначимо дирекційні
кути цих
ліній:Р(хрур)
можна визначити два рази (із контролем):
одинТ2
.Xр
31
Хрі
+ Sj
cos ос^7^_1
Xр
=
Хр^
+ S2
cos ос^р^-р^Yp
=УГі
+ sin
oc^jj_p^ J Yp
=Yp2
+ S2
sin oc^-p)ip
-
—-—
Xp=X0+5x;Yp=Y0+5y. (И.5.12)
Зрозуміло,
що таке розв’язання задач позбавляє
необхідності декілька разів розв’язувати
пряму одноразову засічку.
Розглянемо
суть цієї задачі. Нехай маємо три точки
7J,
Рис.
11.5.4 Обернена одноразова засічка (задача
Потенота)
Розв’яжемо
цю задачу. Припустимо, що координати
точки
дені.
Тоді для визначення дирекційного кута
а напрямку
Гі-Г
Хх-Х
(ІІ.5.13)
222Визначення
координат точки Р за двома відомими
точками та виміряними в цих точках
кутами
Pj
та
р2
називають
одноразовою прямою кутовою засічкою.
Якщо виконані польові вимірювання
необхідні для прямої багаторазової
засічки, тоді ця задача розв’язується
так. Вибирають дві точки з відомими
координатами, бажано так, щоб лінії
візування на шукану точку Р
перетиналися
під кутом, близьким до прямого. Розв’язують
одноразову пряму засічку й знаходять
наближені координати точки Р
-X0t&Y0.
Потім
за
способом найменших квадратів
визначають найімовірніші поправки 8^
та 8Г
до наближених координат, тобто знаходять
Обернена одноразова кутова засічка (задача Потенота)
Т2
та Г3
з відомими координатами (рис. II.5.4), а
координати четвертої точки необхідно
визначити. Теодоліт встановлюють тільки
в шуканій точці Р
і вимірюють два кути між напрямками на
відомі точки, тобто кути та р2
• Така задача називається оберненою
одноразовою кутовою засічкою.
P(X,Y)
знайР—7]
можемо записати формулу
Далі
знайдемо дирекційні кути двох інших
напрямків (рис. ІІ.5.4):
а2=а
+ Р2- (ІІ.5.15)
запишемо
дещо в іншому вигляді для кожного із
трьох напрямків:
Yx-Y
= {Xx-X)tga
Y2-Y
= {X2-X)tg(*
+ h)'
Y,-Y
= (X,-X)tg(a + $2)
(ІІ.5.16)
Маємо
систему із трьох рівнянь. У цій системі
три невідомі координати
_
(Y2-Yl)ctg^-{Y3-Y1)ctgfi2+(X3-X2)
(Х2-Xx)ctgh
~{Хг
- Хх)
ctg$2-(У3
-У2)
‘
^
=
х
, {X2-Xx)
tga-(Y2-Yx)
2 Jg(a
+ p,)-'ga
(II.
5.18)
Знаючи
Обернена
одноразова засічка (задача Потенота)
дуже широко застосовується у
геодезичній практиці, оскільки для
визначення координат точки достатньо
виміряти 2-3 кути на одній точці, на що
витрачається не більше від 10
хвилин. Існує більш ніж сто методів
аналітичного та графічного розв’язання
цієї задачі. Студентам відомі з курсу
“Топографії*” графічні методи
розв’язання цієї задачі, запропоновані
Бесселем, Леманом. Відомо також, що ця
задача не має розв’язку, якщо шукана
точка розташована на колі, на якому
розміщені також три точки з відомими
координатами. Уже цей факт вимагає
візувати з шуканої точки не на три, а
мінімум на чотири відомі точки. Одноразова
обернена засічка перетворюється на
багаторазову обернену засічку. Така
засічка, як і багаторазова пряма засічка,
уможливлює кількаразове визначення
координат шуканої точки, тобто також
постає питання визначення найімовірніших
поправок 8^
та 8Г
до наближених координат^,
223а1=а
+ Р1. (ІІ.5.14)
X,
Y
та
дирекційним кута.
Отже, система рівнянь може бути розв’язана
і визначені невідомі X,
Y
та
а. Не вдаючись у подробиці перетворень
рівнянь системи (II.5.16),
подамо
тільки кінцеві формули для обчислення
дирекційного кута а та координат X,
Y.Знаючиа,
визначимо дирекційні кути ах
та а2
за (И.5.14) та (ІІ.5.15). Формула визначення
X
має вигляд:X,
знайдемо Y,
скориставшись одним з рівнянь системи
(ІІ.5.16). Візьмемо друге рівняння цієї
системи і запишемо його так:Y
= Y2+(X-X2)-tg{
a + Pi). (ІІ.5.19)Y0
.
Визначають 8^
та
8Г
за методом найменших квадратів, і широко
застосовують диференційні формули
дирекційних кутів. Ці формули виведені
в наступному параграфі. Зауваження: у
попередніх параграфах розглядалися
кутові засічки, характерні для методу
тріангуляції. Аналогічно можуть
виконуватися лінійні засічки, характерні
для трилатерації, коли вимірюються не
кути, а лінії.
Допустимо,
що лінія
також
змінить своє значення на
координат
та змінами дирекційних кутів. Формули,
що виражають такий зв’язок, називаються
Можливий
інший випадок, коли, навпаки, точка
I II III
пряма
засічка обернена засічка мережа точок,
що визначається
А
відома
(Ха,
Ya)
“тверда
”
відома
В B(Xb,Yb)
gf
Рис.
11.5.5. До пояснення суті диференційних
формул дирекційних кутів
Нарешті,
загальний випадок, коли змінюються,
уточнюються координати як точки
224Диференційні формули дирекційних кутів
АВ
має координати її кінців А(ХЛ,
YA
)
, В(Хв,
YB
)
, а її дирекційний кут - а. Нехай точка
А
не змінює свого розміщення (“тверда”
точка). У цій точці стоїть теодоліт. На
“твердих” точках стоїть теодоліт,
коли виконується пряма засічка.
Припустимо далі, що точка В
дещо змінила своє положення, а її
координати стали Хв
+ dXB;
YB
+dYB.
Тоді
дирекційний кутda.
Потрібно знайти зв’язок між змінамидиференційними
формулами дирекційних кутів.А
дещо змінила координати. Нехай ця
точка “шукана” (шукаємо її найімовірніші
координати). Точка В
-
відома (“тверда”). Теодоліт встановлено
в точці А.
Цей випадок відповідає оберненій
засічці.
А,
так і точки В
або усієї мережі точок. Теодоліт може
встановлюватись у будь-якій із цих
точок. Нам потрібно вивести формули
для двох
випадків
(пряма та обернена засічки), а також
загальну формулу. Скористаємося
відомою формулою, аналогічною до
(ІІ.5.13):
tga
=
yb-ya
Хв-Ха
(ІІ.5.20)
Продиференціюємо
цю формулу, вважаючи, що змінними є
координати тільки точки
1
da\
{Хв-Хл\dYB-(YB-Ys)dXB
cos2
а
р' (Хв-Хл)2
Оскільки:^
-
запишемо
так:
1
da’
cos
a
S2
cos2
a
Помноживши
рівняння (II.5.22)
на
cos2
a, матимемо
для
d
=P
~J~dYB~p
~s~dXe-
Введемо
позначення:
(a)
= -p"sin al
(ft) = p'cosa j
З
урахуванням цих позначень (II.5.23)
набуде
кінцевого вигляду:
da
= — dXB
+ — dY,
Ів
■
(ІІ.5.22)
(ІІ.5.23)
(II.
5.24)
(ІІ.5.25)
S
D
S
Для
другого випадку, коли змінюються
координати точки
da
= -^-dXA
~ — dYA.
S S
Відповідно
для загального випадку матимемо формулу
da
= -—dXj dYA
A-^-dXn
dYB.
(II.5.26)
(II.5.27)
Як
бачимо з цих формул, щоб знайти малі
зміни дирекційних кутів
225В
(випадок І):XА
— S
cosa;
YB
— YA
=S
sin а,
то, враховуючи це (И.5.21),S
cos a d
Ig-Ssina dXBda':,
„ »
cosa »sina
,vА,
якщо розглядати (ІІ.5.20), неважко зауважити,
що координати точки А
у цій формулі відрізняються від координат
точки В
знаками. Тому для другого випадку
кінцеву формулу можна записати за
аналогією до (ІІ.5.25):da,
необхідно, крім зміни координат точок,
ще знати довжини ліній S,-
та
коефіцієнти (а);
і (ft)..
Суть
оберненої багаторазової кутової засічки
пояснена у п. ІІ.5.4. Для складання рівнянь,
на основі яких можна буде знайти поправки
На
підставі рис. ІІ.5.6 можемо записати
очевидні, наведені нижче рівняння.
Віднімемо від першого рівняння друге:
Рі=
«,■+!-«/ (1)
РО,
=«0/+і
~аоі (2). (ІІ.5.28)
Р»
—
Рої —
®/+1 — —
®оі+1 ®ог
Рис.
11.5.6. Зміни дирекційних кутів та
координат
під час елементарного
переміщення шуканої точки Р
Рівнянь
(ІІ.5.28) можна записати стільки, скільки
виміряних кутів (і,. З цього самого
рисунка, своєю чергою, можна записати:
а;+і
=
ао(+і
+
^а/+і (3)
ai=aoi+da, (4)'
У
(II.5.28)
а/+1
та ос, замінимо їхніми значеннями,
відповідно до (3) та (4) отримаємо:
Pi
~~
Ро/ “ ^о/+1 ^^/+1 «о/ d(Xj
—
ос0/+і
+ аоі,
або,
після скорочення, матимемо:
р
i-$oi=daM-dai. (ІІ.5.29)
22611.5.6. Обернена багаторазова кутова засічка
8Х
та 5У
у наближені координати точки, скористаємось
рис. II.5.6, на якому зображено дві вихідні
(“тверді”) точки 7} та Тм
; точка Р0,
наближені координати якої Х0
та Y0,
та точка Р,
найімовірніші координати якої X
та Y
поки
що невідомі.
Це
рівняння можна було б записати також
на основі рисунка, оскільки під час
переміщення точка
Р,
- р; + р; - Ро,- = daM
-
da,j. (II.5.ЗО)
Позначимо
відому різницю ро/
- Р- = , а невідому різницю р,- - Р*
=
V,-,
тоді
(ІІ.5.30) набуде вигляду рівняння похибок:
v,
=
Замінимо
у (ІІ.5.31) зміни дирекційних кутів
v^^-dX
+ ^-dY-
Soi
Soi
^^-dX-^lldY
+ li,
>оі+1
sn.
ОІ+1
(II.5.32)
або
Щ«+№
dY
+ lt
(ІІ.5.33)
Позначимо
;Д[
(М (У.)
^о/+1
І І ^оі+1
(ІІ.5.34)
Тоді
отримаємо скорочений, остаточний вигляд
рівнянь похибок:
у,- =
Таких
рівнянь можна записати стільки, скільки
виміряних кутів:
Vj
=
(II.5.35)
(II.5.36)
vn=Andx
+ Bndy
+ ln
Нормальних
рівнянь буде стільки, скільки невідомих.
У нас невідомі
та
[AA] dx
+ [AB]dy + [Al] = b
[AB] dx
+ [BB]dy+
[S/] = 0
(ІІ.5.37)
227Р0
в точку Р
кут Роі
перетвориться
на Р;,
а різниця зміни дирекційних кутів da.j
та
doсі+1
перетвориться на нуль. У (ІІ.5.28) роі
знаходять
як різницю відомих дирекційних кутів
ао/+1
та аоі;
р, поки що невідома величина. У рівнянні
(ІІ.5.29) немає виміряного кута. Позначимо
виміряний кут р- і введемо його у
(ІІ.5.29), віднявши і додавши його. Одержимо:dai+l
-
daf
+
lt. (ІІ.5.31)daM
та
dat
змінами
координат відповідно до отриманої
диференційної формули (ІІ.5.26) (обернена
засічка): під час зміни координат
точки Р0
змінюються дирекційні кути oloM
та
аоі:ІаЛ
(6.)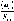
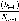
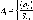
Ajdx
+
Bjdy
+
lj.Aidx
+
Bxdy
+
Zj
v2
= A2dx
+ B2dy
+ Z2
v3
= A3dx
+ B2dy
+ Z3
•.dxdy
.
Тому буде два рівняння:
Знайдемо
невідомі
[AA] [ВВ\-[АВ\
[АВ]
[AB] [АІ]-[АА]
[5/]
[АА]
[ВВ]-[АВ] [АВ]
(ІІ.5.38)
Оскільки
Для
оцінки точності таких засічок необхідно
знайти середні квадратичні похибки
вимірювання кутів та середні квадратичні
похибки
визначення
координат точки
Похибки
V, = (і, - (З- (Р, - виправлені, р-- виміряні
кути) знаходять за системою рівнянь
похибок (ІІ.5.36). У знаменнику формули
(II.5.40) («- 2)- кількість надлишкових
виміряних кутів (два необхідні).
Квадратичні похибки
(ІІ.5.39)
(ІІ.5.40)
т
Щ _
(ІІ.5.41)
*Х
де
або
[АА]
[ВВ]-[АВ] [АВ]
Щ
(ІІ.5.42)
228dx
T&dy
.[АВ]
[5/] -[55] [Al]Sj
у
км, а р' приймемо таким, що дорівнює 20
6265, тоді dx
та
dy
буде
виражено в десятих частках метра (у
дециметрах). Тому:Точність прямої та оберненої багаторазових кутових засічок
тх
та туР.
Як відомо, з теорії похибок, обчислюється
за формулоютх
та ту
визначаться за формулами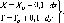
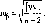
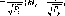
Рх
та Ру
-
ваги вимірів. Як відомо,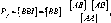
Як
бачимо, чисельник (II.5.42) дорівнює
знаменникам системи рівнянь
(ІІ.5.38).
Позначимо:
D
=
[AA}[BB]-[AB}[AB\. (П.5.43)
Тоді
формула ваги Ру
скорочено
запишеться так:
D
P’"WY
(II.
5.44)
D-
вже
відома величина, і її не потрібно
розраховувати, як і суму [АА].
Своєю чергою, вагу Рх
знаходять
за формулою
[АА]
Р
= -—-
Р .
х
[ВВ] у
З
урахуванням (II.5.44) для Рх
маємо:
Р
=——
*
[ВВ]
(ІІ.5.45)
(П.5.46)
У
табл. II.5.1
подано
приклад розв’язання оберненої
багаторазової засічки з оцінкою точності
обчислення найімовірніших координат.
Для
кожної з таких засічок вимірюються два
кути: для прямої - по одному куту на двох
точках, а для оберненої - два кути на
одній точці (див. рис. ІІ.5.7).
Рис.
11.5.7.
Визначення
точності одноразових засічок: а
- прямої;
б
- оберненої
Для
таких засічок можна скласти тільки по
два рівняння похибок виду (ІІ.5.35).
229Точність прямої та оберненої одноразових кутових засічок
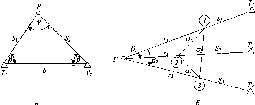
Відповідно
до (II.5.41) можемо записати формулу похибки
у визначенні координат точки
або
М1
р= т2
+т2у,
ГХ
Гу
(ІІ.5.47)
Підставляючи
в (ІІ.5.47) значення обернених ваг, будемо
мати після
деяких перетворень:
з
yjs2
+
S%
Мр=-
р
sin
у
Якщо
(ІІ.5.48)
(ІІ.5.49)
Як
бачимо, похибка координат точки
10
м. Для оберненої одноразової засічки
оцінити точність визначення коор-
динат
значно складніше. Професором О.С.
Чеботарьовим запропонований
такий
метод [28]. Будують так званий “зворотний”
трикутник (рис. ІІ.5.7). Для
цього
обчислюється
_Р#
гі
=
S,
(ІІ.5.50)
Значення
,
^ (ІІ.5.51)
Мр=^((Т?+еї+<ТІ)-
напр'
де
тнапр
^
’
(ІІ.5.52)
230Р:Sl=S2=S
,а
у =
90°, то (ІІ.5.48) набере вигляду:Р
прямо пропорційна до довжини
ліній
та похибки вимірювання кутів. Якщо mj,
=
5", S
=
3000 м, тоді Мр
=
г(
відкладають у напрямках від точки Р.
Отримують на лініях
S2,
S3
точки
1,
2,
3,
що є вершинами “зворотного” трикутника.
Довжини
сторін цього трикутника
<7,, <У2,
(73
вимірюють графічно. Вираховують
площу
трикутника F
також
графічно, або за формулою Герона.
Похибка Мр
у поло-
женні точки Р
визначається за формулоюЩр
-
похибка вимірювання кутів; тнапр
- похибка вимірювання напрямків.
р9 |
У, |
|
tana, |
с _ |
S,= |
|
л |
|
|
|
|
|
•*<> |
|
Ду, coscca, |
Ах* seed, |
|
р |
Ч; 1 £ II $ |
1 £ й jr |
аі |
1.
По приблизних координатах |
37169,000 36257,483 |
36379,900 38235,034 |
-0,4913484 |
2066,975 |
2066.975 |
153°49'58,36" |
|||||
+911.517 |
- 1855,134 |
||||
* |
35000,000 36257,483 |
35000,000 38235,034 |
+0,3887078 |
3470,837 |
3470,837 |
201°1429,36“ |
|||||
- 1257,483 |
- 3235,034 |
||||
|
34925,240 36257,483 |
37752,960 38235,034 |
*2,763565 |
1416,780 |
1416,780 |
250&0б,26,16" |
|||||
- 1332.243 |
-482,074 |
||||
2*4 |
32354,300 36257,483 |
41027,700 38235,034 |
-1,3976548 |
4799,356 |
4799,356 |
305°34'59,24" |
|||||
-3903,183 |
+2792,666 |
2
По врівноважених координатах |
37169,000 36257,632 |
36379,900 38234,997 |
-0,4912778 |
2066,876 |
2066,876 |
ІЗЗ^ОЧО.Ю" |
|||||
+911.368 |
- 1855,097 |
||||
|
35000.000 36257,632 |
35000,000 38234,997 |
+0,3887583 |
3470,856 |
3470,856 |
201°14,38,42н |
|||||
-1257,632 |
-3234,997 |
||||
А |
34925,240 36257,632 |
37752,960 38234,997 |
+2,764087 |
1416,908 |
1416,908 |
25о°об,38,б2" |
|||||
-1332,392 |
- 482,037 |
||||
А |
32354,300 36257,632 |
41027,700 38234,997 |
- 1,3976896 |
4799,499 |
4799,499 |
305°34'56,82" |
|||||
- 3903,332 |
+2792,703 |
Кінцеві
координати точки Р
+0,15,
~ 38235,034 + (-0,037)- 38234,997 у=у0
+ 0,16, = 36257,483 + 0,149 - 36257,632
Оцінка
точності
2,0'
~іаД’"іоЛїбї*
«v=r^=I^»°,°22M
Мf,
= ^mx2
+
/иу2
*0,026 м
X
ж
38234,997 ± 0,014 Г = 36257,632 ±0,022
Схема
заачхи
Пїі
Обчислення
вільних члени початкових рівнянь lt з/и |
Дані точки г, |
Приблизні дирекціоні кути («о), |
Обчислені кути (приблизні) (ft>), =(ao)i-(ao)i |
Виміряні кути ft |
А = (ft»)/-ft |
АА |
|||||||||||||||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|||||||||||||||||||||||
1 |
А |
153°49'58,36" |
|
|
|
|
|||||||||||||||||||||||
2 |
А |
20 Р 1479.36" |
47°24*31.00" |
47°24'31,0" |
0,00" |
0.00" |
|||||||||||||||||||||||
3 |
А |
гзітібдб" |
96°1677,80" |
96° 1627,8й |
0,00" |
0,00" |
|||||||||||||||||||||||
4 |
А |
305°34'59,24" |
151°45ЧЮ,88" |
151044’46,2" |
+14,68“ |
215,50" |
|||||||||||||||||||||||
гааі= |
215,50" |
||||||||||||||||||||||||||||
№ з/п |
«0 |
(а) |
Ф) |
|
а |
Ь |
А |
В |
1 |
6* |
АА |
АВ |
AL |
AS |
ВВ |
BL |
BS |
||||||||||||
1 |
153°49' |
+9,10 |
+18,51 |
2,07 |
+4,40 |
+894 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
201°14' |
-7,47 |
+19ДЗ |
3,47 |
-2,15 |
■*•5,54 |
-6,55 |
-3,40 |
0,00 |
-9,95 |
42,90 |
+22Д7 |
0,00 |
+65,17 |
1136 |
0,00 |
+33,83 |
||||||||||||
3 |
250°06’ |
-19,40 |
+7,02 |
1,42 |
-13,66 |
+4,94 |
-18,06 |
-4,00 |
0,00 |
-22,06 |
326,16 |
+7224 |
0,00 |
+398,40 |
16,00 |
0,00 |
+8824 |
||||||||||||
4 |
305°35’ |
-16,78 |
-12,00 |
4,80 |
-3,50 |
-2,50 |
-7,90 |
-11,44 |
+ 14,68 |
-4,66 |
62,41 |
+9038 |
-115,97 |
+36,81 |
130,87 |
-167,94 |
+5331 |
||||||||||||
І |
-32,51 |
-18.84 |
+14,68 |
-36,67 |
431,48 |
+184,89 |
-115,97 |
+50039 |
158,43 |
-167,94 |
+175,38 |
||||||||||||||||||
ЖжнорштьткрШаш* +[и^
+№,;о |
+68359 |
[<B}[BL] |
-31050 [AB\AL] |
-21442 |
бх - -0,371 |
Рх =216 |
[АВ\[АВ] |
+34184 |
[BB][AL] |
-18373' [ЛА][ВЦ |
-72463 |
5? = +1,493 |
> її 'О |
D |
+34175 |
Dt |
-12677 D} |
+51021 |
|
|
Обчислення
поправок
V,
<
дирекціиних
кутів
а з/п |
Обчислені V, |
Виправлені кути fi>fi,+K |
Кінцево обчислені дирекцій ні кути а( |
Кінцево обчислені кути Д' = а, -а, |
vy |
|||||||||
А8Х |
BS, |
А |
Vt |
|||||||||||
1 |
|
|
|
|
|
153o50'10.i0" |
|
|
||||||
2 |
+2,43" |
- 5,08" |
0,00" |
-2,65" |
47°24’28,35" |
2ori438,42" |
47°242832" |
7,02 |
||||||
3 |
+6,70" |
-5,97" |
0,00" |
+0,73" |
%°16'28,53": 250°06'38.62" |
96°16’28,52" |
0,53 |
|||||||
4 |
-t-2,93" |
- 17,08" |
+14.68" |
L0,53" |
151°44*46,73"і 305°34'56,82" |
151°44,46 72" |
028 |
|||||||
гта= |
7,83 |
|||||||||||||
ГАА1 |
[/(од |
[вія |
IKK] |
|||||||||||
+215,50 |
-*-43,02 |
-250,73 |
7,79 |
|||||||||||
Визначення
координат точки
Розв’язавши
обернену геодезичну задачу, за
координатами точок
в
Рис.
11.5.8. Лінійна геодезична засічка
За
формулами тригонометричних функцій
косинусів (або тангенсів) половинних
кутів обчислимо кути трикутника:
d
+ d{+d2
де
Знаючи
всі шість елементів трикутника
(ІІ.5.53)
(ІІ.5.54)
(ІІ.5.55)
23211.5.9. Лінійна геодезична засічка
Р
за координатами двох вихідних (відомих)
пунктів А
і В та.
двома виміряними віддалями d{
та
d2
від
іруканої точки до вихідних пунктів
називають лінійною
геодезичною засічкою.А
(XА,
Ya
)
та В
(Хв,
YB),
знайдемо довжину сторони АВ
=d9
та
її дирекційним кут ССА_В.
Тоді в трикутнику АВР
будуть відомі усі три сторони. Трикутник
розв’язується.р
=
- півпериметр трикутника АВР.АВР,
за формулами прямої та оберненої засічок
можна обчислити координати точки Р
два рази: за координатами точки А
та за координатами точки В.
Контролюють обчислення за збігом
координат. Проте, якщо зроблено похибку
під час польового вимірю-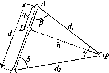

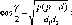
|
(II.5.56) |
Якщо
кут |
|
|
(II.5.57) |
У
нас |
|
|
(II.5.58) |
3
прямокутного трикутника |
|
|
(II. 5.59) |
Оскільки
|
|
*
.
|
(II.5.60) |
Дирекційний
кут |
|
|
(II.5.61) |
Знак
кута |
праворуч розта- |
шована
точка |
|
випадку - ліворуч. |
|
Прирости
координат точки |
|
|
(II.5.62) |
|
(ІІ.5.63) |
233
Допустимо,
координати точок полігонометрії
Суть
цього методу полягає в тому, що довжину
лінії
s[ K
sin
& sin\iw
-fa+p2+p3)]’
S'2 _ K
sin(03+04)
sin[l80°
- (02
+ 03 + 04)]
% ... K
sin(0,
+ 02)
sin[l80°
-(0, +02
+ 03)]’
K -■ K
sin
02 sin[l 80° - (02 + 03 + 04 )]
23411.5.10. Визначення координат двох точок за відомими координатами двох інших точок (задача Ганзена)
Рх
та Р2
необхідно одночасно визначити щодо
координат пунктів Тх
та Т2
тріангуляції. Існує багато розв’язків
такої задачі. Одним із найдоцільніших
серед них є розв’язок, який можна
назвати методом умовного базису.Рх-Р2
умовно приймають за одиницю. Потім,
за виміряними кутами Д, Д, Д, Д та, вважаючи
лінію Рх-Р2
відомою, такою, що дорівнює 60,
розв’язуванням трикутників Тх
Р2
Рх
та Т2
Р2
Рх
визначають сторони S[,
S2,
S'3,
S'4.
Оскільки
у кожному з двох трикутників Тх
Т2
Рх
та
Тх
Т2
Р2
відомі
дві сторони та кути між ними Д та Д,, то
ці трикутники розв’язуються. Можна
знайти третю сторону та два інші кути.
Знайдемо також кути
Ь'
_ S'
ь'
_ s'4
sin
Д
sin
Я
’ sin
Д
sin
<р
(ІІ.5.65)
Отже,
справді
З
відношення b
до
Ь'
ми
знайдемо дійсну довжину лінії Рх—Р2.
Позначимо
цю довжину
S
= jf. (И.5.66)
Тепер
у нас є всі необхідні дані, щоб знайти
дирекційні кути і фактичну довжину
усіх чотирьох ліній:
Sl=S'l
S; S2=S'2
S; S3=S'3
S; S4=S4S.
Залишається
за довжинами ліній та дирекційними
кутами визначити прирости координат,
а потім і координати точок Рх
та
Р2.
Координати кожної з цих точок будуть
обчислені двічі, що і буде їхнім кінцевим
контролем.
Розглянутий
спосіб є дуже простим та природним.
Найдоцільнішим випадком визначення
координат двох точок буде той, коли
форма, створена двома заданими та двома
шуканими точками, близька до квадрата.
Потрібно уникати дуже гострих кутів у
чотирикутнику.
Від
прокладення полігонометричної мережі
до її використання для топознімання
може пройти декілька років, і, як би
фундаментально не закріплювались
пункти, все ж знайти їх на місцевості
буває дуже важко. Головна мета
прив’язування пунктів до постійних
предметів, як вже
235(р
та Я. Тепер у нас є можливість два рази,
з контролем, знайти довжину b
в
цій умовній одиниці довжин. Позначимо
цю умовну довжину Ь'.
З трикутників Тх
Т2
Рх
та
Тх
Т2
Р2
відповідно
маємо:Ь'
визначено з контролем (двічі). Два
результати Ь'
повинні
сходитися у межах точності обчислень.
Але фактичну довжину цієї лінії b
та
її дирекційний кут ми можемо визначити
за координатами пунктів Тх
та
Т2.S:Прив'язування пунктів полігонометрії до постійних об'єктів місцевості. Відшукування полігонометричних пунктів
відзначалося
- забезпечити їх знаходження. Способи
такого прив’язування різноманітні.
Суть їх стане зрозумілою після
ознайомлення з типовими прикладами
прив’язування.
Прив’язування
до фасадів будинків
Pi РіН Рі+2
Рис.
11.5.10. Прив'язування до фасаду будинку
Якщо
полігонометричний хід проходить біля
постійних предметів, то прив’язування
виконують переважно лінійними
вимірюваннями - рулетками. Наприклад,
якщо маємо
Прив’язування
до кута будинку
Якщо
хід проходить біля кута будинку, то
прив’язування можна виконати методом
створів, а саме: продовження стіни
Крім
того, потрібно з точки
236
LMNS
-
цегляну або кам’яну споруду (будинок),
а точка ходу Рі+Х
розташована біля стіни MN,
тоді доцільно опустити на лініюMN
фасаду
перпендикуляр з точки та виміряти
довжину перпендикуляра a.
Крім того, доцільно виміряти віддалі
b
і
с
від основи перпендикуляра, тобто від
точки К,
до кутів будинку. Цих вимірів достатньо,
щоб знайти точку Рп+1,
але безконтрольно. Прив’язування
необхідно виконувати так, щоб обов’язково
був контроль. Тому необхідно ще виміряти
віддалі d
та
е
від кутів будинку М
та N
до
точки Рі+1.
Тепер точку Рі+Х
можна знайти з контролем лінійними
засічками, використовуючи довжини a,
d
та
е.AN
дає
на стороні ходу точку L,
а продовження стіни BN
-
точку М
.N
опустити,
за допомогою екера, перпендикуляр
на цю саму лінію ходу. Точки М
, R
та
L
необхідно
зафіксувати. Для цього необхідно
виміряти відрізки с,
а,
Ь9
а також частини S{
та
S2
сторони
ходу Р.-Рі+1.
Цих даних достатньо, щоб з контролем,
якщо необхідно, відновити положення
точок М
у L
та
R
.
Якщо ж продовжити створ відрізка ML
,
то
зможемо
знайти точки
Рис.
11.5.11. Прив’язування двох пунктів Pt
та
Рм
до
кута будинку
Прив’язування
до залізниці
Рис.
11.5.12. Прив’язування до залізниці
237Рі
та Рі+1.
Для точнішого встановлення напрямку
сторони полігонометричного ходу
корисно виміряти на одній з точок М,
R
або
L
кут
є
між напрямком сторони ходу та напрямком
на віддалений, стійкий предмет Q.
Оскільки
дирекційний кут лінії Pt
та
Рі+Х
відомий, тоді буде відомий і дирекційний
кут ліній RQ
та
RN.
Отже, у результаті прив’язу- вальних
вимірювань можна отримати на місцевості
координати додаткових точок R
та
N.
Це може виявитись корисним, наприклад,
під час поновлення пунктів Р{
та Рм.
Якщо
полігонометричний хід перетинає
залізницю, необхідно на осі дороги
визначити точку
Контролями
прив’язувальних вимірювань у такому
разі є те, що сума Д +
Прив’язування
до далеких предметів
У
малонаселених районах близькі стійкі
предмети місцевості просто відсутні.
Одночасно часто трапляються випадки,
коли з полігонометричних пунктів видно
далекі предмети місцевості: поодинокі
дерева, перехрестя доріг, чіткий край
лісу тощо. У такому разі необхідно
виміряти кути Д і Д (рис. ІІ.5.13), як це
робиться в задачі Потенота та, крім
того, виміряти кути 7]
та
Є
для
орієнтування сторін ходу. Під час пошуку
пункту
Під
час прив’язування необхідно дотримуватися
одного загального правила: кількість
елементів прив’язування повинна бути
необхідною і достатньою для того, щоб
поновити хоча б два сусідні пункти
полігонометричного ходу.
Зрозуміло,
що для відшукування пунктів можна
використовувати не тільки прив’язування
цих пунктів до предметів місцевості,
але й прив’язування до пунктів
тріангуляції, трилатерації чи
полігонометрії старших класів.
Рис.
11.5.13. Прив’язування до далеких предметів
238А
- перетин осі з лінією ходу; виміряти
віддалі Д та S2
від
цієї точки до початку та кінця лінії,
а також виміряти кут Є
між
напрямком лінії та осі залізниці та
виміряти віддаль від точки А
до найближчого кілометрового стовпа,
ліворуч чи праворуч, відносно лінії
Р.-Рм.S2
повинна
дорівнювати довжині сторони ходу
Р.-Рі+1.
Відома також віддаль до наступного
кілометрового стовпа.Pt
треба
встановлювати теодоліт послідовно в
такі точки, щоб вимірювані кути
наближалися до відомих Д і Д. Контролем
будуть кути 7]
та
Є.
Доволі корисно для такого прив’язування
використовувати метод створів.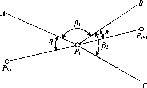
Відшукування
пунктів за прив’язками до інших пунктів
геодезичних мереж застосовують
найчастіше для поновлення пунктів
полігонометрії. Якщо, наприклад, було
виконане прив’язування пункту
Тепер,
знаючи координати точки
V
~ &(мр)
~ ^(мт3)
•
Рис.
11.5.14. Відшукування пункту
полігонометрії,
прив’язаного до
пункту тріангуляції
Додамо
кут
239Р
до пунктів тріангуляції Тх,
Т2
та Т3
(рис. ІІ.5.14) розв’язанням задачі про
четверту точку (задачі Потенота), то
для відшукування втраченого пункту
потрібно, ставши на місцевості там, де
передбачається, розмістити цей пункт
(наприклад, у точці М), визначити
координати точки М
, користуючись пунктами тріангуляції
7j,
Т2,
Г3.М
і координати точки Р,
ми можемо поновити точку Р.
Для цього за координатами обчислюється
довжина та напрямок лінії МР.
Далі, знаючи дирекційний кут лінії
(МГ3),
знаходять кут Tj
за
формулою: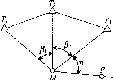
Г/
до відліку лімба теодоліта, який
встановлено в точці М
і труба якого наведена на точку Т3,
отримаємо новий відлік, який необхідно
встановити на лімбі, відкріпивши
алідаду і повертаючи трубу в горизонтальній
площині. Далі, користуючись вертикальною
ниткою сітки, виставляють віху у напрямку
візирної осі труби. Залишається за цим
напрямком відкласти довжину обчисленої
лінії МР,
і місце точки Р
на місцевості буде знайдено.
Основи
теорії й практики світловіддалемірних
вимірювань
У
віддалемірній полігонометрії довжини
сторін полігонометричних ходів
вимірюються посередніми методами. Під
посередніми методами вимірювання
ліній, як уже зазначалось, розуміють
такі вимірювання довжин, під час яких
вимірювальний прилад (одиниця довжини)
не відкладається послідовно в створі
лінії, що вимірюється. Тому віддалемірну
полігонометрію можна було б ще назвати
полігонометрією з посереднім вимірюванням
довжин.
У
віддалемірній полігонометрії виділяють:
1) світловіддалемірну; 2) ра- діовіддалемірну;
3) короткобазисну; 4) паралактичну; 5)
віддалемірно-базисну;
інші
види полігонометрії.
До
інших видів полігонометрії можна
зарахувати, наприклад, полігонометрію,
що прокладається ланками професора
А.Д. Моторного [17]. Два перші види такої
полігонометрії становлять власне
віддалемірну (посередню) полігонометрію,
тобто віддалемірну полігонометрію у
“чистому вигляді”, у якій вимірювальний
прилад, як реальний відрізок довжини,
відсутній. Чотири подальші види
віддалемірної полігонометрії такі, що
мірний прилад (відрізок довжини) усе ж
використовується, але для вимірювання
не усієї довжини лінії, а її частини
або базису. Знаючи ці відрізки та маючи
ще додатково кутові виміри, можна
обчислити усю довжину тієї чи іншої
лінії полігонометричного ходу. Усі
віддалеміри можна поділити на: 1)
світловіддалеміри; 2)
радіовіддалеміри; 3) оптичні віддалеміри.
Найпростіше
пояснити цей принцип на прикладі з
імпульсними світловими сигналами.
Нехай у деякий момент часу
Якщо
віддаль між приймачем-передавачем та
відбивачем
240
Світловіддалемірна полігонометрія.
Класифікація віддалемірної полігонометрії та віддалемірів
Принцип вимірювання віддалі визначенням часу поширення електромагнітних (світлових) хвиль
tx
приймач-передавач
(п/п), розташований у точці А,
посилає світловий імпульс (спалах
світла). Припустимо, що цей імпульс
поширюється прямолінійно й рівномірно
зі швидкістю с,
доходить до відбивача (наприклад,
дзеркала), розташованого в точці В,
відбивається й повертається до п/п
(як це показано на рис. ІІ.6.1)
у момент часу t2.Sl9
то
за час т =
h
“
h
імпульс
пройде шлях 2Sx.
Тому:S,=f- (ІІ.6.1)
|
|
(ІІ.6.2) |
Тому |
|
(ІІ.6.3) |
Позначимо |
|
(ІІ.6.4) |
будемо
називати |
сталою світловідцалеміра. Звідси маємо кінцеву формулу: |
|
|
|
(ІІ.6.5) |
Визначимо, з |
якою точністю необхідно знати час |
т, щоб віддалемір був |
придатний для геодезичних цілей. Для цього продиференціюємо (ІІ.6.5) за т. |
||
|
|
(ІІ.6.6) |
Звідки |
|
(ІІ.6.7) |
Швидкість
світла с
~ 300000 км/с. Необхідно, щоб лінія S
(наприклад,
1
км) вимірювалась з похибкою, не більшою
за 15 см. На підставі (ІІ.6.7) маємо:
2
* 15 см
-
=
30000000000
см/с
Точність
вимірювання часу повинна бути надзвичайно
високою. Заува-
жимо, що 1*10~9
(одна міліардна частка секунди)
називається наносекундою,
скорочено
не.
241d
т
= -11(Г9с.
Порівняно
недавно вимірювання часу з такою
точністю було неможливим. Тому
імпульсні віддалеміри почали з’являтися
тільки в наш час. Ширше застосовуються
світловіддалеміри (с/в), у яких час
поширення електромагнітних хвиль
світлового діапазону вимірюють
посереднім методом, що ґрунтується на
визначенні різниці фаз двох синусоїдальних
коливань. Для розуміння суті фазового
методу необхідно згадати деякі відомості
з теорії гармонічних коливань.
Коливні
процеси, наприклад, зміни яскравості
світла, можна зобразити графічно,
проекцією на вісь
Рис.
11.6.2. Гоафічне зображення гармонічного
коливання
Проекція
У
= Л sin
ер. (ІІ.6.8)
Швидкість
зміни
242
(ІІ.6.9)
Основні відомості з теорії гармонічних коливань
Y
вектора
ОВ,
що повертається навколо точки О.
Розташування
вектора ОВ
у який завгодно момент часу t
визначається
кутом між віссю X
та розташуванням вектора. Цей кут ер
називається фазою (рис. 2.6.2)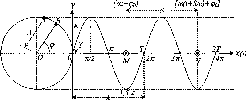
ОВ
на вісь Y
-
змінна величина. Для зміни фази ер від
0° до 90° (від 0 радіан до тс/2
радіан) проекція ОВ
змінюється від 0 до А.
Максимальне значення Y
-
А -
амплітуда коливань. Наприклад, яскравість
світла змінюється від нуля до деякого
максимального значення. Отже, коливання
будь-якої величини описується рівняннямY
залежить
від швидкості обертання вектора ОВ
навколо точки О
.
Введемо поняття кутової швидкості або
кругової частоти. Кутовою швидкістю
або круговою частотою ео називається
швидкість зміни фази із часом, тобто: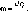
1 /’ |
(ІІ.6.12) |
1 т' |
(ІІ.6.13) |
Отже,
період і частота коливань є взаємно
оберненими величинами. Частота коливань
вимірюється у герцах. Якщо за секунду
відбувається одне коливання, то частота
/ дорівнює одному герцу. Якщо за 1 секунду
проходить 1000
коливань, то частота / = 1000
герц (Гц), або / = 1
кілогерц, скорочено
кГц.
Коли за секунду відбувається 1000000
коливань то / = 1000000 Гц або / = 1 мегагерц,
скорочено МГц. У світловіддалемірах
використовуються частоти коливань
яскравості світла (масштабні або
вимірювальні частоти) від 10-30 МГц до
150 МГц і більше.
Перетворимо
формулу (ІІ.6.8).
Для цього у (ІІ.6.11) підставимо значення
1__2п
г
~ 5
/
ю
ЗВІДКИ
<в=2ті
/. (ІІ.6.14)
Як
бачимо, кутова швидкість (кругова
частота) дорівнює добуткові
Ф
= 2л
Формула
(ІІ.6.15) - нова залежність фази від частоти
коливань та часу.
243Т
із (ІІ.6.12).
Отримаємо:2%
на / . На підставі (ІІ.6.14) формула (ІІ.6.10)
набуває вигляду:ft. (II.6.15)
Тепер,
підставляючи у (ІІ.6.8) значення ф з
(ІІ.6.10) та (ІІ.6.15) одержимо
відповідно:
У
= Я • sin
ш
• /. (ІІ.6.16)
Y
= A sin2n f t. (ІІ.6.17)
На
рис. ІІ.6.2 для
Для
У
практиці найчастіше буває так, що в
момент початку відліку часу (/ = 0) фаза
ф не дорівнює нулеві, а має деяке
початкове значення ф0.
Тоді (ІІ.6.16) та (ІІ.6.17) набувають вигляду:
У
=
^sin(oo
y
= ^sin(2Ti
Рівняння
(ІІ.6.18), (И.6.19) є рівняннями гармонічних
коливань.
Поширення
у просторі коливань того чи іншого роду
називаються хвилями. Якщо хвиля
поширюється вздовж деякої прямої з
кінцевою швидкістю
У
= A
sin
(ІІ.6.20)
Вираз
(ІІ.6.20) називається рівнянням плоскої
хвилі гармонічних коливань. За
проміжок часу
Х
= Т с,
(П.6.21)
де
Замінюючи
в (ІІ.6.21)
X
/
(ІІ.6.22)
Віддаль
244t
=
0 фаза ф також дорівнює нулю.t
=
0,5 Т
фаза дорівнюєте; для t
=
Т
фаза дорівнює 2 те; для t
=
1,5 Т
фаза дорівнює 3 те; для t
=2Т
фаза дорівнює 4те тощо.t
+
ф0). (ІІ.6.18)ft
+
ф0). (ІІ.6.19)с,
то фази коливань в різних точках цієї
прямої будуть також різними. Якщо в
точці М
(рис. ІІ.6.2) коливання описується рівнянням
У = A
sin (со
t
+
ф0),
то в точціN,
віддаленій від М
на віддаль S,
коливання
будуть відбуватися із запізненням
на проміжок часу %
= S/c.
Тому
рівняння гармонічних коливань для
точки N
має
вигляд: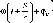
Т
коливання поширюються на віддаль X.,
тодіс
- швидкість.Т
на / , одержимо:X
називають довжиною хвилі. Як бачимо з
(ІІ.6.22), для постійної швидкості світла
с
довжина хвилі залежить тільки від
частоти коливань.
У
геодезичних фазових віддалемірах поряд
із гармонічними коливаннями використовують
також модульовані коливання, які є
складнішими коливаннями. Модулювання
коливань виникає у разі зміни одного
з параметрів гармонічних коливань.
Такими параметрами є, як видно з (ІІ.6.18)
та (ІІ.6.19), амплітуда
Зміну
цих параметрів називають
Розглянемо,
як графічно виглядають коливання, що
модульовані за амплітудою
Коефіцієнт
\А
називається
245
Поняття про модулювання коливань
А,
частота / (або кругова частота оо) та
початкова фаза ф0
.модуляцією.
Модулювальні пристрої отримали назву
модуляторів.
Модулювання коливань виконується
переважно для того, щоб за допомогою
високочастотних коливань, що називаються
передавальними
коливаннями, передати на віддаль інші
коливання, низькочас- тотніші, у яких
закладена та чи інша інформація. Ці,
низькочастотніші коливання, називають
масштабними,
або вимірювальними
коливаннями (частотами).А.™
= (ІІ.6.23)коефіцієнтом
глибини модуляції.
Він може змінюватися від 0 до 1. Для того,
щоб передати інформацію на віддаль із
мінімальним спотворенням, повинна
виконуватися умова: частота модуляції
повинна бути значно нижчою від
передавальної частоти, тобто ю0
«со.
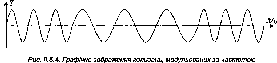
Для
частотної модуляції із часом змінюють
частоту передавальних коливань. Графічно
це показано на рис. П.6.4.
Нехай
ю - кругова частота немодульованих
передавальних коливань, яка називається
са,
(ІІ.6.24)
що
дорівнює відношенню девіації до частоти
модулювальних коливань, називається
У
деяких світловіддалемірах використовується
фазова модуляція (ф. м.), під час якої
фаза гармонічних коливань періодично
змінюється на 180° (на
Частота
зміни фази значно менша за частоту
передавальних коливань.
Принцип
дії фазових віддалемірів ґрунтується
на використанні залежності поточної
фази від віддалі. Нехай п/п розміщений
у точці
Ф,
=ow,
+ф0. (ІІ.6.25)
За
час, поки коливання пройдуть віддаль
ф2
= (0^, + ^
j+
ф0. (ІІ.6.26)
Визначимо
різницю фаз випромінюваних та прийнятих
коливань:
S
Дф
= ф2
-ф1
= со—. (ІІ.6.27)
с
246центральною
частотою; Дсо- максимальне відхилення
кругової частоти під впливом модулювальних
коливань. Це відхилення називається
девіацією
частоти. Нехай ю0
- кругова частота модулювальних коливань.
Тоді коефіцієнт
індексом
частотної модуляції.п).
Графічно
це показано на рис. ІІ.6.5.
Принцип роботи фазових світловіддалемірів
А
(рис. II.6.1) і випромінює гармонічні
коливання з поточною фазою фі:S,
відіб’ються
і повернуться в точку А,
поточна фаза випроміїїюваних передавачем
коливань становитиме:
Підставляючи
у формулу (ІІ.6.27) значення со з (ІІ.6.14),
отримаємо:
Аср=2тс
с
Зазначимо,
що коливання, які потрапляють від
передавача на вхід приймача найкоротшим
шляхом, не проходячи дистанції,
називаються
Розв’язавши
(ІІ.6.28) відносно
2ті
2
У
Отже,
коли швидкість
Будь-які
фазовимірювальні пристрої вимірюють
різницю фаз тільки в межах одного
періоду, тобто від 0 до
Дф
= ф + Дф, (ІІ.6.30)
де
ф -різниця фаз, кратна
с
2/
(ІІ.6.31)
ч2тс
2 л;
У
(ІІ.6.31) ф/2тс=У ціле число (кількість
коливань); Дф/2л=AV
-
правильний дріб. Тепер (П.6.31) запишемо
ще так:
S
= (N + AN)^j. (ІІ.6.32)
Нарешті,
ураховуючи (ІІ.6.22), запишемо (ІІ.6.32) у
такому вигляді:
S
= (N + AN)^. (ІІ.6.33)
Розглянемо
фізичний зміст двох складових правої
частини (ІІ.6.33). А/2-
половина довжини хвилі, це особливий
“метр”, особлива (нереальна) “одиниця
довжини”, яку ніби відкладають
247•/—. (ІІ.6.28)опорними.
По суті, Дер є різницею фаз між опорними
коливаннями та коливаннями, що повернулись
з дистанції.S,
одержимо загальну формулу фазових
відцалемірів:S
= ^-—. (ІІ.6.29)с
і частота коливань / відомі, а різниця
фаз Дф виміряна, то за (ІІ.6.29) можна
знайти віддаль. Такий метод визначення
віддалей називається фазовим.
Різниця фаз Дф може набувати різні
значення, які часто в багато разів
більші за 2
к.2п.
Зважаючи на це, подамо Дф у вигляді:2к;
Дф - різниця фаз у межах одного періоду,
тобто Дф < 2к.
Враховуючи (ІІ.6.30), запишемо (ІІ.6.29) в
дещо іншому вигляді:N
разів
у лінію, яку вимірюють. Добуток AN
■
А/2
- частина “метра”, що доповнює цілу
кількість “метрів” до віддалі, що
вимірюється. Нагадаємо, що AN
=
Дф/2тс, де Дф - різниця фаз, яка
вимірюється.
Отже, у (ІІ.6.33) два невідомі:
S
= (N + AN)^ + K. (II.
6.34)
Стала
світловіддалеміра
Типовим
представником такого віддалеміра є
світловіддалемір СВВ-1 (світловіддалемір
Васильєва-Величко), у якому індикатором
різниці фаз слугує око спостерігача.
Блок-схема візуального світоловіддалеміра
показана на рис. ІІ.6.6.
м/с
Рис.
11.6.6. Блок-схема візуального світловіддалеміра
Модулятор
і демодулятор світла (м/с і д/с)
конструктивно аналогічні (це конденсатори
Кера) і працюють синхронно, керовані
за допомогою змінної синусоїдальної
напруги, що подається на конденсатори
від генератора масштабної частоти
(ГМЧ). Коли напруга подана на пластинки
конденсатора,
248SiaN.
Для того, щоб знайти N,
або, як прийнято говорити, розв’язати
неоднозначність,
вимірювання фазовими відцалемірами
виконують на декількох частотах.
Нагадаємо, що п/п та відбивач центруються
так, що Sx
неточно
дорівнює S
(див.
рис. ІІ.6.1), тоді (ІІ.6.33) повинна бути
доповнена сталою відцалеміра К.
Тому остаточна формула віддалеміра
має вигляд:К
є “сталою” умовно. Вона змінюється із
часом і залежить від температури та
зовнішнього середовища. В останні роки
у с/в використовують довші хвилі
(червоні, інфрачервоні), які менше
поглинаються атмосферою. Навпаки, у
радіовіддалемірах використовують
коротші хвилі, які менше відбиваються
від підстилаючої поверхні та легко
концентруються у промінь.
Блок-схема візуального світловіддалеміра з визначенням різниці фаз за екстремумами світлового потоку
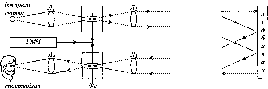
світло
проходить, коли напруга знята - світло
не проходить між пластинками.
Рис.
11.6.7. Зміна світлового потоку на виході
демодулятора світла (д/с)
залежно
від різниці фаз
Це
означає, що для того, щоб на виході д/с
мати Фтіп
(мінімум відбитого сигналу), необхідно,
щоб різниця фаз була кратною до 2
пристроями
для поступової зміни частоти (без
стрибків). Так, у с/в СВВ-1 частоту можна
плавно змінювати у межах від 9,6 до 10,4
МГц. Якщо різниця фаз кратна до 2л;, тоді
ДА/ = 0 і (ІІ.6.33) набуває вигляду:
S=N-+K.
2
(ІІ.6.35)
Для
розв’язання неоднозначності (у (ІІ.6.35)
невідомі
хвилі
s=nx
.h.+K.
(11.636)
Будемо
поступово змінювати частоту, наприклад,
збільшуючи її. Тоді око спостерігача
буде спочатку бачити збільшення
яскравості світла, вона досягне
249Лінзи
ЛІ9
Л2,
Л3,
Л4
збирають промені, що розходяться, в
пучки, або перетворюють розбіжні
пучки на майже паралельні. Величина
потоку світла Ф на виході д/с залежить
від різниці фаз між відправленою на
дистанцію та прийнятою з дистанції
хвилями світла. Око спостерігача здатне
фіксувати тільки екстремальні значення
світлової енергії; впевненіше око
фіксує мінімум світлової енергії Фтіп
. Як видно з рис. ІІ.6.7, мінімум світлового
потоку Ф настає під час різниці фаз,
кратної до 2л,
а максимум - під час різниці фаз, кратної
до п.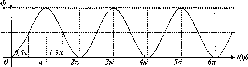
к.
Цього можна досягти, якщо поступово
змінювати масштабну частоту і, цим
самим, змінювати довжину своєрідного
“метра” А/2 = С/2 . Візуальні с/в оснащеніS
та
АГ) вимірювання виконують не менше
ніж на двох частотах. Нехай для деякої
довжини . у
лінії, що вимірюється, вкладається Nx
циклів:
• • • • rp. ^2 • •••
максимуму,
а потім знову настане мінімум світла.
Тому в лінії, що
вимірюється,
вкладається
збільшувати
частоту й розраховують кількість
мінімумів, що спостерігалися.
= .
Тепер
2
fn
запишемо
друге рівняння, аналогічне до (ІІ.6.36):
X
S
= (N + n)^- + K. (ІІ.6.37)
Нехай
усього їх буде
У
(И.6.36) та (ІІ.6.37) невідомі
віддалеміром
характеризується відносною похибкою
-^Г -
візуальні
відцалеміри мають деякі недоліки. Це:
Спостереження
дуже втомлюють око.
Низька
точність реєстрації різниці фаз.
Необхідність
мати в польовому комплекті віддалеміра
частотомір для вимірювання частоти /
, що значно збільшує масу віддалеміра.
Усувають
ці недоліки використанням віддал емірів
зі стабільними, наперед заданими
частотами та заміною візуального
визначення різниці фаз на фотоелектронне.
Одразу
зазначимо, що в сучасних світловіддалемірах
використовують лазери. Це не тільки
сильніші джерела світла, що поліпшує
вимірювальні якості с/в, точніше, дає
змогу вимірювати довгі сторони, але,
водночас, ці джерела є модуляторами
світла: частота модуляції залежить від
частоти генератора вимірювальних
(масштабних) частот.
Нехай
лазер
Демодулятор
- фотоелектронний помножувач (ФЕП)
перетворює світловий сигнал на
електричний струм, який подається на
індикатор. З генератора масштабної
частоти (ГМЧ) подається на ФЕП ще й
опорний
250N2
циклів,
до того ж N2
= +1.
Продовжують«.Тоді
Nn
=(NX
+
«),
а довжина хвиліS
та
Nx.
Одночасне розв’язання цих рівнянь дає
значення двох невідомих. Точність
вимірювання ліній цим^^qqq
•
На жаль>
Блок-схема світловіддалеміра на фіксованих частотах із парафазним фотоелектронним визначенням різниці фаз
Л
- джерело та модулятор світла (рис.
ІІ.6.8)
посилає імпульс світла, колімований
лінзою Кх
у майже паралельний пучок. Світло
досягає відбивача, повертається й
потрапляє на лінзу К2,
яка збирає світловий сигнал у фокусі
і спрямовує його на демодулятор.
електричний
сигнал, який також надходить на індикатор.
Подальше завдання - шайти різницю фаз
опорного сигналу та сигналу, який
повернувся з дистанції. Розглянутий
раніше віддалемір дає змогу порівнювати
не яку завгодно різницю фаз, а тільки
кратну до 2я
або я; ця різниця фаз створювалась
поступовою зміною частоти модуляції
світла. У віддалемірі з фіксованими
частотами така можливість відсутня.
Тому в опорному тракті встановлюється
особливий пристрій, що затримує в часі
електричний сигнал. Цей пристрій отримав
назву
Рис.
11.6.8. Блок-схема с/в із фотоелектронною
реєстрацією різниці фаз
Величина
струму /, що надходить на індикатор із
демодулятора, залежить від тільки що
названої різниці фаз. Нехай, якщо
відімкнено пристрій для зміни фази на
180°, на індикатор надходить з демодулятора
сигнал
Рис.
11.6.9. Синусоїдальні струми Іх
таІ2,
що подаються з демодулятора
на
індикатор
Якщо
увімкнути пристрій і змінити фазу на
180°, то і на індикатор надійде сигнал/2,
зсунутий по фазі відносно сигналу
251фазообертач.
Отже, фазообертач дає змогу встановити
бажану різницю фаз без зміни частоти
модуляції світла.
Іх,
який має вигляд синусоїди (рис. ІІ.6.9).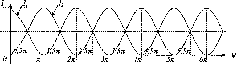
Іх
на 180°. Оскільки за цим
методом
порівняння різниці фаз виконується за
допомогою двох груп сигналів із фазами,
що відрізняються на 180°, то метод названий
Дср
=
на
нуль), потрібно внести додатковий
фазовий зсув за допомогою фазообертача.
Нехай цей додатковий зсув становить
0. Тоді повна різниця фаз становитиме:
2
Використаємо
загальну формулу світловіддалеміра
(ІІ.6.29):
s=4E.-£-+jc.
2л
2/
Підставимо
значення Дер з формули (11.6.38). Отримаємо:
5
= ^ —
+ к,
(ІІ.6.38)
або
2
п
4/
■ +
К.
Останню
формулу можемо записати так:
с
(ІІ.6.39)
(П.6.40)
4/ 8
/ я 4/
Врахуємо,
що
N
= — ,&6oN' = 2N.
2
Замінимо
у (2.6.40)
м
8
/
Q
с
я
4/
252парафазним.
Електричні сигнали Іх
та /2
(фотоструми) не тільки зміщені по фазі
на 180°, але і рухаються один назустріч
одному (потоки електронів протилежно
спрямовані). Зміна (перекид) фази на
180° проходить автоматично із частотою
80-100 Гц. Як бачимо з рисунка, рівність
сигналів Іх
і /2
настає тоді (стрілка індикатора
встановиться на нуль), коли різниця фаз
між сигналом з дистанції та опорним
сигналом буде дорівнювати 0,5я,
1,5я, 2,5я, 3,5я
тощо. ЗагаломN'n
+
— я. Щоб досягти саме такої різниці фаз
(вивести стрілку індикатораДф=.АҐ-я
+ —+
0.N'n
+
— + 02п
2/N'-c
1
с 0 с „ S
= + + +
К.N'
дорівнює
кількості к
у цій лінії, а N
дорівнює
кількості
2л;,
тому:N'
на
2N,
а також позначимо:
т
1
сЬ
= стала
величина;L-,
= змінна
величина.
Крім
того, приймемо, що
(ІІ.6.41)
Крім
того, позначимо
(II.
6.42)
Тоді
матимемо кінцеву формулу:
S
= N-X + L + K.
(II.
6.43)
У
системі рівнянь (ІІ.6.44) чотири невідомі
Вимірювання
імпульсним методом виконуються із
застосуванням посилання двох частот
випромінюваних імпульсів: yj=
14985,5
кГц та /2
= 149,855 кГц. Тривалість імпульсів 10 не.
Джерелом випромінювання є напівпровідниковий
лазерний діод з довжиною хвилі
випромінювання 0,80 мкм; приймачем -
фотоелектронний помножувач (ФЕП).
Світловіддалемір
СТ-5 є одним з найкращих віддалемірів
і першим з виготовлених у СРСР. Він
працює на імпульсному методі вимірювання
ліній.
S
= NiXi +Ц +К
S
=
N2X2
+1^
+ к
►
S
— N3X3
+
Zg
+
К
(ІІ.6.44)
253L
= Ll
+
L2
також
змінна величина. Враховуючи все це,
(ІІ.6.40) зміниться так: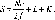
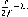
L
відлічується
на шкалі фазометра (фазообертача).
Віддалемір працює на трьох постійних
частотах X.}, Х2
та Х3;
тому можна записати три рівняння виду
(ІІ.6.43):S,
Nx,
N2,
N3.
Для
розв’язання неоднозначності
прийнято: Х.,= 0,998004 м; Х2
= 1,052631 м; Х3
= 1,000000
м. Для таких довжин Xj
на
1/500 коротше Х3,
а Х3
на 1/20
коротше Х2.
Тому для ліній до 500 м N{=N3;
для
граничної довжини S
=
500 м, N\
=
N3
+1.
Крім того, для S
=
20 м N3
=
N2
+1.
Оскільки віддалемір призначений
для вимірювання ліній до 700 м, то такі
довжини А.;
дають змогу розв’язувати неоднозначність.
Світловіддалемір топографічний ст-5 (“Бпеск”). Будова. Імпульсний метод вимірювання віддалей
Рис.
II6 10. Світловіддалемір СТ-5
Рис.
II 6.11. Світловіддалемір СТ-5
Основні
частини с/в (рис И.6.10): 4 - головний корпус,
в якому розміщена приймально-передавальна
оптична система, джерело випромінювання,
фотоприймальний пристрій, друкуючі
вузли з елементами електричної системи.
Цей корпус має кришки 1 та 14, які можна
зняти; на кришці 1 закріплена зорова
труба; стояки 6,
13 скріплені зверху ручкою 3, знизу
гвинтами 7 скріплені з основою 11. В
основі 11 та стояка 13 розташовані навідні
та закріпні гвинти, якими світловіддалемір
наводиться на відбивач у горизонтальній
та вертикальній площинах. На рис. ІІ.6.11
показано головки навідних гвинтів 5,
10 та рукоятки закріпних гвинтів 6,
9. На основі також кріпиться циліндричний
рівень 12
з юстувальними гвинтами 13 та окуляр
оптичного центрира 11.
Лицьова панель - 2; на ній розташовані:
8
- головка гвинта “сигнал”; 7 - перемикач
І - “точно”-“контроль”-“грубо”; 4 -
перемикач II - “виключ”- “навед”-“счет”;
1
- прилад зі стрілкою (мікроамперметр);
3 - цифровий дисплей, 16 - головка гвинта
встановлення контрольного відліку.
Під кришкою 15 встановлено гнізда для
під’єднання частотоміра (частота
1498,55 кГц); резистор / - підстроювання
частоти кварцового генератора, резистори
Д і О - початкового встановлення рівня
вимірюваних сигналів; резистор Н -
початкового встановлення сигналу
“наведення”. Розташування Д і О
встановлює підприємство-виробник.
Регулювання цих резисторів не
дозволяється, оскільки це може призвести
до непрацездатності приладу. На стояку
13 (рис. II.6.10)
встановлено гніздо 12
для під’єднання реєструвального
пристрою; на стояку 6
гніздо
5 для під’єднання кабелю від джерела
напруги; 14 - мікротелефон (рис. ІІ.6.11).
254
Кількість призм відбивача |
Максимальна віддаль, що вимірюється, м |
і |
1500 |
3 |
2200 |
6 |
3000 |
12 |
4000 |
18 |
5000 |
255
у цій віддалі |
|
І! |
(ІІ.6.45) |
2
|
(ІІ.6.46) |
II oj! |
256
Оскільки
період коливань Т
та
частота коливань / - взаємно обернені
величини, то
(ІІ.6.47)
Підставляючи
у (ІІ.6.45) значення т та Т
з
(ІІ.6.46) та (ІІ.6.47), матимемо:
(ІІ.6.48)
Виробники
прийняли частоту / такою, що дорівнює
половині швидкості світла, тобто:
Тоді
с
2
Як
бачимо, для такої частоти кількість
імпульсів заповнення дорівнює довжині
вимірюваної лінії 5. Тому достатньо
мати лічильник, який розраховує кількість
імпульсів -N
та
частину хвилі AN
(менше
за2тс), щоб точно знайти
Ми
будемо розглядати тільки перевірки,
що стосуються віддалемірного модуля
приладу. Перевірки кутомірного модуля
розглянуто раніше.
Перевірка
функціонування приладу.
Перевірку
виконують з метою підтвердження
нормальної роботи електронних вузлів
світловіддалеміра. Якщо ці вузли
працюють неналежно - прилад підлягає
ремонту. Під час цього контролюються:
257

/то™
=| = 14,9855МГц. (ІІ.6.49)N-—
— = S. (ІІ.6.50)S.
У світловіддалемір СТ-5 вмонтовано
такий лічильник, який працює переходом
з високих частот до низьких гетеродинним
діленням частот. У комплект світловіддалеміра
входять дві батареї живлення Б-5-29 з
напругою 6,0 В. Якщо показ мікроамперметра
менше за 6,0 мкА, батарею необхідно
замінити. Атенюатор - прилад, що оберігає
об’єктив від потрапляння на с/в яскравого
світла. Атенюатор встановлюється на
об’єктив с/в і є, по суті, “ситом”, що
розсіює та послаблює світлові промені.
Блок контрольного відліку - прилад,
який дає змогу контролювати незмінність
сталої віддалеміра К
.Перевірки світловіддалеміра ст-5
а)
б)
в)
г)
д)
Перевірка
оптичного центрира світловіддалеміра
та відбивача.
Перевірка
виконується так само, як і оптичного
центрира теодоліта.
Зміщення
центра сітки ниток з центра знака на
радіус малого кола, яким є форма сітки
ниток центрира (для висоти штатива 1,3
м), дає похибку центрування 0,7 мм.
Перевірка
сітки ниток зорової
труби
світловіплалеміра.
Виготовити
з картону або твердого паперу спеціальну
марку відповідно
до
рис. П.6.17. Центр перехрестя марки повинен
бути розташований вище від центра
призми однопризмового відбивача на 63
± 1 мм. Встановити відбивач на віддалі
100-150 м від с/в. Увімкнути світловіддалемір
у режим “наведення”. Навести с/в на
відбивач, добитись максимуму відбитого
сигналу. Встановити заготовлену марку,
як показано на рис. ІІ.6.17. Оцінити
розбіжність центрира сітки ниток з
перехрестям марки. Якщо розбіжність
значна (більша від радіуса кола),
відкрутити захисний ковпачок, що
закриває юстувальні гвинти сітки ниток.
Повертаючи послідовно протилежні
юстувальні гвинти, ввести центр сітки
ниток (центр кола) у перехрестя марки.
Затягти юстувальні гвинти. Повторити
перевірку. Встановити захисний ковпачок.
258схема
контролю джерела напруги.
Встановити перемикач І в положення
“контр.”, перемикач II в положення
“викл.” Оцінити покази мікроам-
перметра. Покази приладу мають бути в
межах 60...9 мкА, якщо джерело струму
заряджене;індикатори
дисплея.
Увімкнути с/в у режим “счет”, “точно”.
Спостерігати за показами дисплея: на
всіх індикаторах протягом 1-4 секунд
після встановлення перемикача II в
положення “счет” повинна відображатися
цифра 8;схема
вимірювання температури кварцового
генератора.
Увімкнути відцалемір у режим “счет”,
“контроль” і взяти декілька відліків
на дисплеї. Кожний наступний відлік не
повинен відрізнятися від попереднього
більше ніж на 5 одиниць;схема
встановлення контрольного відліку.
Зняти з об’єктива атенюатор.
Встановити на об’єктив с/в блок
контрольного відліку. Увімкнути
відцалемір у режим “счет”, “точно”,
встановити рівень “сиглалу” всередині
робочої зони. Перевірити можливість
зміни відліку поворотами головки
встановлення контрольного відліку;мікроамперметр.
Перевірка виконується вимірюванням
сили струму двома приладами незалежно.
Мікроамперметром сила струму вимірюється
так. Встановлюють перемикач І в положення
“контр”, а перемикач II - у положення
“викл”, під’єднують до с/в джерело
енергії і встановлюють на його виході
напругу, за якої показ приладу с/в зі
стрілкою становить 60 мкА. Потім іншим
приладом вимірюють напругу, що дає
батарея. Напруга має бути 60 ± 0,5 В.
Рис.
11.6.17. Марка для перевірки зорової труби
Перевірка
відхилення частоти кварцового генератора
від номіналу.
Перевірка виконується частотоміром
з частотою 1498,55 кГц. Спочатку
потрібно
зняти кришку 15. Під’єднати частотомір
до гнізда / плати в стояку 6
(рис.
ІІ.6.11). Перемикач частотоміра “время
счета” встановити в положення
ДГ
=
(ю/сер
-&ft)-fH0MiH, (ІІ.6.51)
де
A/J
-
поправка за температурну зміну частоти,
Гц, яка визначається за графіком,
наведеним у паспорті світловіддалеміра;
fH0MiH=
14985500 Гц. Значення Д/-
не має бути більшим за 60 Гц для часу у
межах 6
місяців (півроку). Підстроювати частоту
кварцового генератора резистором / до
розходження з номіналом, не більшого
за 15 Гц. Опломбовують підстроювальні
резистори та закривають кришку 15.
Перевірка
відхилення контрольного
відліку під час
зміни напруги живлення.
Встановлюють
на об’єктив с/в блок контрольного
відліку. Встановлюють напругу джерела
струму (8,5 ± 0,2) В. Вмикають с/в в режим
“счет”, “точно” і
259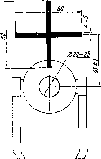
Iq4»j5
увімкнути
світловіддалемір у режим “счет”,
“контр”. Взяти декілька відліків за
частотоміром та обчислити їхнє середнє
арифметичне fcep
у
Гц та десятих частках Гц. Обчислити
відхилення (дрейф) частоти Af
за
формулою
встановлюють
контрольний відлік, вказаний у паспорті
світловіддалеміра. Зменшують напругу
до значення, під час якого спрацьовує
схема звукової індикації розряджання
акумуляторів (5,8-6,2
В). Зміна контрольного відліку не повинна
бути більшою за 3 мм.
Перевірка
(визначення) циклічної похибки світлові
ллалеміра.
По
суті, це вже не перевірка, а дослідження
світловіддалеміра. Розмічають на
місцевості 11
точок на відстанях від світловіддалеміра,
що визначаються за формулою
де
АК
= Дтк-Док, (ІІ.6.53)
де
Рис.
11.6.18. Гоафік поправки АДЦ,
побудований за отриманими значеннями
АДЦК
260
Дк
= А + К
± 0,1 (метри), (ІІ.6.52)А
-
будь-яке число у межах від 5 до 25 м, К
= 0, 1, 2, 3...9, 10. Вимірюють отримані відстані
рулеткою. Похибки вимірювань не повинні
перевищувати 1,5 мм. Вимірюють ці самі
відстані світловіддалеміром. Вимірювання
виконують з атенюатором (оскільки всі
відстані до 400 м вимірюють з атенюатором)
з рівнем відбитого сигналу всередині
робочої зони. Під час вимірювання кожної
відстані визначають значення контрольного
відліку. Відхилення значення контрольного
відліку від паспортного враховують
під час обчислення результатів
вимірювань. Далі обчислюють значення
ДК
для кожної з точок за формулоюДтк
- середнє арифметичне значення відліку
в режимі “точно”; Док~
результат
вимірювання рулеткою, мм. Для різниці
значень АК
у двох сусідніх точках більше ніж 5 мм
розмічають проміжні (додаткові) точки
і для них також знаходять значення АК.
Розмах циклічної похибки (різниця
максимального та мінімального значення
АК)
не повинен перевищувати 10 мм. Приклад
результатів вимірювань для визначення
циклічної похибки подано у табл. ІІ.6.1,
а приклад побудови графіка циклічної
поправки наведено на рис. ІІ.6.18.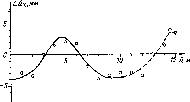
Відстань
|
Результат
вимірювання світловіддалеміром |
АЦцк — ~^К - (Док Дтк ) > мм |
5099 |
5097 |
+2 |
6089 |
6087,5 |
+1,5 |
7035 |
7037 |
-2 |
8037 |
8041 |
-4 |
9004 |
9007,5 |
-3,5 |
10088 |
10091 |
-3 |
11080 |
11083 |
-3 |
12001 |
12004,5 |
-3,5 |
12997 |
12997 |
0 |
14010 |
14008,5 |
+1,5 |
15023 |
15019,5 |
+3,5 |
14503 |
14499 |
+4 |
Визначення
середньої квадратичної похибки
вимірювання віддалей світоовіддалеміром
СТ-5.
Визначення
фактичної точності світловіддалеміра
також належить не до перевірок, а до
дослідження світловіддалеміра. Кожна
контрольна лінія має бути виміряна не
менше ніж шістьма прийомами у режимі
“точно”. Прийом - одне наведення на
відбивач та три відліки на дисплеї.
Рекомендується лінії завдовжки 100, 300,
500 м вимірювати з 3-призмовим відбивачем;
лінії 1000, 2000 м - з 6-призмовим;
лінії 3000, 5000 м - з 18-призмовим. Разом не
менше ніж 7 ліній. Рекомендується
виконувати вимірювання під час похмурої,
безвітряної погоди, незначних турбулентних
перемішувань в атмосфері. Похибка
вимірювання температури вздовж
контрольних ліній не повинна перевищувати
1 °С, атмосферного тиску - 2 гПа (1,5 мм рт.
ст.). Контрольні лінії повинні мати
точність, хоча б у 5 разів вищу за точність
світловіддалеміра
СТ
5, тобто
-і
тд.г
=
£Дг
і
.•2
(її.6.54)
261ms
= 2 + 110~6S\
Виробник
вважає, що точність СТ-5 дорівнюєms
=10
+ 5-10 6
S.
Значення середньої квадратичної похибки
вимірювання к
-ї контрольної лінії одним прийомом
обчислюють за формулою
де
A;
-
різниця між результатами вимірювання
Попереднє
підготування до вимірювання.
Перерахуємо
основні процеси підготування.
Центрування
с/в та відбивача над кінцями лінії, що
вимірюється. Вимірювання висоти
приймача
Живлення
вмикати тільки тоді, коли перемикач
II "вимкнено” і встановлено атенюатор,
щоб уникнути засвічення.
Увімкнути
живлення. Поставити перемикач І у
положення "контроль”. Стрілка
мікроамперметра (мкА) повинна показувати
однакову напругу незалежно від
положення перемикача II: чи "вимкнено”,
чи "наведення”, чи "счет”.
Якщо
для положення "счет” напруга 6
В (60 мкА), а для "наведення” менше
або більше на 20-40 мкА, тоді виконується
регулювання. Необхідно зняти кришку
15, викруткою повертати шліц резистора
Н через отвір у планці резистора.
Встановити
контрольний відлік на дисплеї, вказаний
у паспорті приладу (зазвичай, 100-105). Для
цього:
а) встановити
положення "вимкнено”, поміняти
атенюатор на блок контрольного відліку;
б) поставити
"точно”, "счет”. Взяти кілька
відліків на дисплеї;
в) за
необхідності головкою встановлення
контрольного відліку поставити вказаний
у паспорті відлік. Встановити атенюатор.
Наведення
с/в на відбивач
Трубу
з атенюатором навести на відбивач.
Поставити
головку гвинта "сигнал” до обмеження,
а у разі яскравого сонячного світла
та за великого засвітлювання - до
відліку не більше за 20 мкА.
Навідними
гвинтами змінювати наведення у
горизонтальній та вертикальній площинах
до максимуму сигналу й одночасно
утримувати головкою "сигнал” рівень
сигналу всередині робочої зони шкали.
Вимірювання
Перемикач
II поставити в положення "счет”, а
перемикач І залишити в положенні
"точно”. Почнуться вимірювання.
Дочекатися звукового сигналу і
послідовно взяти три відліки з дисплея,
записати їх у журнал. Це один прийом.
262к
-ї лінії, /-м прийомом та довжиною цієї
контрольної лінії, мм, ті—
кількістю прийомів,п>
6.
Значення тд
к
-
не повинно перевищувати 10
+ 5
• 1СГ6
• S.
Вимірювання ліній світловіддалеміром ст-5
і
та відбивача /.
Вимірювання (режим “точно”) |
Обчислення |
||
наведення 1 983,573 |
наведення 2 |
наведення 3 |
|
983,573 |
983,571 |
*„ = -0,9; */ = +0,3; Д#„ = -5мм
|
|
983,575 |
983,575 |
983,574 |
|
983,573 |
983,580 |
983,568 |
|
Будова
цієї тотальної станції та вимірювання
нею горизонтальних кутів розглянуто
у п. ІІ.З.
Перед
вимірюванням ліній необхідно впевнитися,
що:
Станція
та рефлектор (відбивач) встановлені
над кінцями лінії, приведені в робочий
стан, тобто виконане їхнє центрування
та нівелювання.
Напруга
батареї достатня.
263Вимірювання ліній та вертикальних кутів компактною тотальною станцією set-ge
|
похила віддаль |
|
|
горизонтальна віддаль |
Послідовно натискати першу клавішу |
|
перевищення |
|
Натиснути
клавішу 3 (start/stop)
і
розпочнуться вимірювання. Мерехтіння
екрана інформує про те, що вимірювання
виконуються.
264
Вибрані
значення віддалі і кута будуть
відображені після закінчення вимірювань.
їх необхідно записати в журнал.
Щоб
зупинити вимірювання, потрібно ще раз
натиснути на клавішу З (stop),
якщо
вимірювання багаторазове, або “TRK”.
У
методі “вимірювання поодиноке”
клавішу “стоп” натискати не потрібно.
Описані
дії становлять один прийом. З кожним
новим прийомом уточнюється наведення
на рефлектор.
Нараховується
сім основних джерел похибок
світловіддалемірних вимірювань, якщо
не враховувати похибки вихідних даних.
Похибка
вимірювання різниці фаз Дф.
Скористаємося
формулою фазового віддалеміра:
S
= ^l.^ + K, (ІІ.6.57)
2п
2/ '
у
(ІІ.6.57)
с„=2-, (ІІ.6.58)
п
де
Продиференціюємо
(ІІ.6.57) по Дф. Переходячи від диференціалів
до квадратичних похибок, отримаємо:
о
=^-'%>60 (ІІ.6.59)
де
4л/
Прийнявши
/ = 15000000 Гц;
тДф
= 0,5°
265
Похибки світловіддалемірних вимірювань
ср
- робоча швидкість світла, яка дорівнюєс0
-
швидкість світла у вакуумі; п-
інтегральний показник заломлення
світла на шляху поширення ЕМХ.к0=-^-. (П.6.60)с
= 299700000 м; 4л= 12,56; К0
=
1,59233, для цих віддалемірів матимемо:
2СМ2 для тДф°
=1°
ms&<f
=
27,8 мм; СТ-5 дляms&sf
-
13,9 мм. Сучасні можливості вимірювання
тДфтіп°
= 0,1°. Для двох прийомів відповідно:
для
2СМ2/Ис
°ф
сер
для
СТ-5
°ф
сер
27,8
=
72
13,9
V2
=
19,7 = 20мм;
=
9,8 мм = 10мм.
Похибка
вимірювання фаз випадкова і не залежить
від
Похибка
приведення ліній до горизонту.
Скористаємося
відомою формулою та продиференціюємо
її за змінною А (перевищенням).
2
hdh
2
S
Матимемо:
msh
(ІІ.6.61)
Оскільки
— =
вигляду:
Нехай
для горбистої місцевості
перевищення:
500
м і для v
=
2°, перевищення А = 16,7 м,
технічного
нівелювання
=
— • 5 мм • 77 = 0,44 мм. Ця похибка, 30
як
і похибка нівелювання, має випадковий
характер, залежить від рельєфу і менше
залежить від довжини лінії 5. Для
однакових довжин
Циклічна
похибка фазометра.
У
світловіддалемірів із сталими частотами
модуляції частина різниці фаз, менша
від ті або 2ті, набирається на фазометр
або фазообертач. Ця похибка встановлюється
для кожного світловіддалеміра на основі
спеціальних досліджень, описаних у п.
ІІ.6.8.
Позначимо цю похибку
лічний
характер, тобто змінюється залежно від
значення набраної на фазообер-
266то =S.
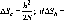
tgM,
а для кута нахилу ц = 6°
tgv
=
0,1 (ІІ.6.61) набуде Smsh
=0,l-mA. (ІІ.6.62)S
=
500 м, А = 50 м. З однієї станції технічного
нівелювання можна виміряти перевищення
А = 2,5 м. Тоді для А = 50 м кількість станцій
п
-
50/2,5 = 20 станцій. Похибка вимірюванняmh—
5
мм • 720=22,4 мм. Відповідно до (ІІ.6.62)
знайдемо похибку mSh
в
лінії S.
mSh
=
2,24 мм. На рівнині для тієї самої довжини
S
=h/S
=
1/30. Кількість станційп
=
7. Тоді: mShS
у
горбистому районі похибка у 5 разів
більша, ніж на рівнині.
т5ф
.
Похибка має цик
і ач
різниці фаз. Для 2СМ-2
випадкова,
не залежить від S'.
Центрування
світловідцалеміра, редукція відбивача.
Похибки
Гранична
похибка візування на віддалі 1 = 1,5 м
(середня висота центрира над точкою
ходу) для збільшення труби центрира
Гранична
похибка приведення осі оптичного
центрира у прямовисний стан за допомогою
рівня з ціною поділки не більше за 60м
дорівнює
Повна
похибка центрування становитиме:
Тому
сумарна похибка у довжині лінії, оскільки
вплив центрування і редукції впливають
однаково, становить:
Розрахована
тут похибка є середньою квадратичною.
Гранична похибка становитиме:
тц,р.гр.
=3'тц.р.
=0,65-3
= 1,92*2мм.
Похибка
центрування та редукції випадкова, не
залежить від S.
Дрейф
генератора частоти.
Похибка
Знову
скористаємося основною формулою
фазового світловідцалеміра (ІІ.6.57):
S
=
2л
If
Диференціюючи
(ІІ.6.57) по / і переходячи до відносної
похибки, отримаємо:
msf
nif
~S~
=
T'
267ms
=
3 мм, для СТ-5 = 1 мм. Ця похибка
ms^
^
- похибки фіксації кінців лінії. Похибка
центрування кожного з приладів, як
світловідцалемірів, так і рефлектора,
складається з похибки візування тв
та похибки приведення осі центрира у
прямовисний стан тпр.г
= 4х
становитме:т 1
= ——-1500
= 0,11мм.rp
4-206103тпп
=^— 1 =
———-1500 = 0,44мм .Р
Р 206 103тц
=\Jme
+тІР
=л/(°Л І)2
+ (0,44)2
=0,45 мм.тц
р
= тц
• у/ї
= 0,45 • 1,41 = 0,65 мм.
mSj.
у
лінії викликана відхиленням основної
частоти від заданої.
Тому
(ІІ.6.63)
Як
бачимо, ця похибка залежить від
15000000;
Похибка
швидкості
світла.
Скористаємося
формулою:
Формула
(ІІ.6.64) - інший запис (ІІ.6.57), з урахуванням
того, що робоча
швидкість виражена
формулою (ІІ.6.58). Диференціюючи (ІІ.6.64)
по
mSr
ш-
переходячи
до відносної похибки, отримаємо ——
= , або
Як
бачимо,
Нехай
1,5
мм. Ця похибка систематична, оскільки
висота
ij
-
висота світловіддалеміра; г\ - висота
відбивача. Вимірювання метеопа- раметрів
виконують на висоті
Похибка
визначення сталої світловіддалеміра.
Скористаємося
формулою
45
Wo,
= —
• 500000 = 1,5 мм.
S
п
(ІІ.6.65)
(ІІ.6.66)
268
S
(пропорційна
до S)
і
має систематичний характер. Досвід
показує, що ту
не перевищує 45 Гц. Для / =S=
500
м на підставі (ІІ.6.63) матимемот$с
у довжині викликана похибками визначення
робочоїп
іms
пропорційна
до S.п
= 1,00, т^=
З 1 O'6,
а
довжина лінії S
=
500 м. Одержуємо: mSc
=h
вимірювання
метео- параметрів, як правило, менша
від hcp
-
середньої висоти променя над землеюh.
Крім
того, оскільки лінії вимірюються у
світлий період доби, коли температура
повітря падає з висотою, то значення
довжин S
завищене.
Sf
15-1О6

де
похибка,
за інструкцією, допускається 2 мм. Базис
вимірюється світловід- далеміром з
деякою похибкою
прийомами.
Припустимо, що діють тільки фазові
похибки, а всі інші похибки не розсіюють
результатів вимірювань. Таке припущення
має зміст, коли всі 54 прийоми виконуються
за 1-1,5 години і під час похмурої погоди.
Щ
=
V6
•
На
підставі (ІІ.6.67) маємо:
для
2СМ2
для
СТ-5
(ІІ.6.67)
Визначимо
Відповідно:
/?2г
>%,
=;/=-• (ІІ.6.68)
Обчислення
за (ІІ.6.68)
дають: для 2СМ2
ср
1хср
кількості
ліній
Похибка
вихідних даних. Ця похибка, по суті, не
є похибкою с/в, проте впливає на нев’язки
ходів.
Похибка
прийнята, як середня із семи інших. Для
2СМ2 - 2,76 мм; для СТ-5-1,79 мм.
У
попередньому параграфі вісім похибок
світловіддалемірних вимірювань поділені
на:
систематичні
та випадкові;
залежні
та незалежні від довжини ліній
залежні
від інших факторів (кількості сторін,
рельєфу).
269mSo
-
середня квадратична похибка довжини
контрольного базису. Цяms..
Всього вимірюється 9 базисів, кожний 6ms.
=
27,8/2,44 = 11,4 мм;т.
= 13,9/2,44 = 5,7 мм.тк.
за(П.6.66):для2СМ2аиа-і
=-у/22
+11,42
=11,6
мм;
для СТ-5 тк.
= д/22
+ 5,72
= 6,0
мм .тк
-
3,9 мм; для СТ-5тк
= 2 мм. Ця похибка систематична і не
залежить від S,
залежить відп,
посередньо залежить від довжини ходу
L.
Розрахунок точності ходів світловіддалемірної полігонометрії
S;
Такий
поділ дає змогу вирішити питання
розрахунку точності ходів. Що стосується
рельєфу, то для розрахунків прийнято
умови горбистої місцевості, з максимальними
кутами нахилу v
=
6°.
Усі інші похибки приймають такими, що
дорівнюють розрахованим за формулами.
Для наочності всі похибки зведено у
табл. (ІІ.6.3), в якій вказані вищеназвані
характеристики, а також очікувані
значення цих похибок у мм, якщо виконується
вимірювання однієї лінії. Для похибок,
залежних від довжини, прийнято
Відповідно
до теорії похибок можемо записати для
одночасної дії випадкових похибок:
V-2=msAv+ml
+
т
с +ті
"ср иЦ.р•
Для
дії систематичних похибок, залежних
від
=
msf
+ msn
■
+
ПІС
(11.6.69)
(11.6.70)
Для
дії систематичної похибки, залежної
від кількості сторін:
Поздовжній
зсув
t2
=
р2
• п
+ Х2Ь2
+Х\-п2. (ІІ.6.72)
Інструкція
[5] допускає окремі ходи полігонометрії
4 класу до 14 км. Для середньої довжини
сторін
Знайдемо
числові значення кожної з трьох складових
(П.6.72). Отримаємо: р2
=(9,8)2
+ (2,24)2
+(1,0)2
+(2,0)2
+(2,0)2;
=
(2)2
= 4;
Як
бачимо, три складові вносять майже
однакові похибки у поздовжній
зсув
270S
=
500 м. їхній вплив на S
=
1 км подвоїться.S:Xl=m2SK. (ІІ.6.71)t
кінцевої
точки полігонометричного ходу виразиться
формулоюScep
=
500 м кількість сторін у ході становитиме
п
= 28.ц2
=
110,058;р = 10,49 м;р-л/й = 55,51 мм;Xj
=(3,0)
+{3,0)
-,х\
=18;A.J
=4,24
jA,!
-1
= 59,40 мм ;Х2
= 2
мм; Х2
• п
= 56,00 мм.t.
Знайдемо: t2=
9745,72;
t=
98,72
мм. Такий зсув можна очікувати під час
вимірювання ліній світловіддалеміром
СТ-5 або іншими віддалемірами такого
самого класу. Проте, як вже зазначалося,
прийнято під час оцінки точності
світловіддалемірних вимірювань
використовувати не строгу формулу
теорії похибок (ІІ.6.72), а рівняння прямої
регресії. Для окремої лінії це рівняння
запишеться так:ms
=
р + X
■
10-6
• SKU
мм. (ІІ.6.73)
№ з/п |
Позначення похибок |
Джерела похибок |
Числові значення, мм |
Властивості похибок |
|
2СМ-2 |
СТ-5 |
||||
і |
"Ч, |
Вимірювання різниці фаз Дф |
19,7 |
9,8 |
Випадкові,
незалежні від |
2 |
|
Приведення ліній до горизонту |
2,24 |
2,24 |
Випадкові,
незалежні від |
3 |
|
Циклічна похибка фазометра |
3,00 |
1,00 |
Випадкові,
незалежні від |
4 |
|
Центрування світловідцал еміра, редукція рефлектора |
2,00 |
2,00 |
Випадкові,
незалежні від |
5 |
|
Дрейф частоти ГВЧ |
1,50 |
1,50 |
Систематичні,
залежні від |
6 |
|
Неточне
значення інтегрального показника
заломлення |
1,50 |
1,50 |
Систематичні,
залежні від |
7 |
|
Похибки
визначення сталої |
3,90 |
2,00 |
Систематичні,
незалежні від |
8 |
|
Похибки координат вихідних пунктів |
2,00 |
2,00 |
Випадкові,
незалежні від |
Рівняння
регресії розрізняє тільки випадкові
похибки, незалежні від
А
числове значення:
X2
= 18 + 4 = 22
Згідно
з нашими розрахунками рівняння (ІІ.6.73)
для світловідцалемірів СТ-5 набуває
числового вигляду:
Формула
(ІІ.6.75) добре узгоджується з формулою,
запропонованою фірмою-виробником:
271S,
та систематичні. Усі систематичні
вважаються залежними від S.
Насправді, як це показано вищеД2
=/(«).
Проте зі збільшенням кількості сторін
п
зростає і довжина ходу. Тому можна
записатиХ2=Х2х+Х\. (ІІ.6.74)мм;Х
= 4,69.ms
=
10,49 + 4,69 • КГ6
• S. (ІІ.6.75)ms
=10,0
+ 51(Г6
S.
У
чинній інструкції [5] прийнято для
поздовжнього зсуву ходу
Для
допуск,
майже на 38 % більший від одержаного за
строгими формулами.
Поперечний
зсув ходу світловіддалемірної
полігонометрії визначається за тією
самою формулою, що й траверсної
полігонометрії. Для висячого ходу
поперечний зсув кінцевої точки ходу
визначається за формулою
U2
и
+ 1,5
З
(ІІ.6.77)
Для
ходу, прокладеного між точками з відомими
координатами, матимемо
максимальний
поперечний зсув всередині ходу, який
знаходять за формулою
"
+
3 (ІІ.6.78)
2
U2
=—У-т-L-
»2
р-
12
Загальна
похибка
#2
»2
и
+ 1,5
(ІІ.6.79)
II.
7.1.
Принцип роботи та класифікація оптичних
віддалемірів
Вимірювання
довжин оптичними віддалемірами
ґрунтується на розв’язанні дуже
витягнутого, так званого паралактичного
трикутника за кутом (р та базисом
Із
трикутника
Оскільки
кут ф малий, то
«З
2
(ІІ.7.1)
272t
= ms
■
-Jn
. (ІІ.6.76)S
=
500 м = 0,5 км, tns
=
12,84 мм. Тоді, відповідно до ((ІІ.6.76), для
ходу з п
= 28 отримаємо t
=
67,94 мм. Цю похибку інструкція рекомендує
вважати середньою квадратичною. Гранична
похибка приймається вдвічі більшою
ігр
=
135,88 мм. Як бачимо, інструкція дозволяє
доволі вільний
М
у положенні кінцевої точки висячого
ходу визначається для світловіддалемірної
полігонометрії за строгою формулоюМ2
=
ц2
• п
+ X2
• L
+ •
п2
+11.7. Оптично-віддалемірна полігонометрія
b
(рис.
ІІ.7.1), перпендикулярним до лінії.АВМ
маємо:S=—2-
Рис.
II. 1.1. Паралактичний трикутник AMN
для
визначення довжини AB=S
Тому
<Р
У
цій формулі кут ф у радіанах. Відношення
відцалеміра.
Оскільки ф = ^ і р' = 3438', то для ф' = 34,38'
(кутових мінут),
Р
к=
100.
Отже,
Оптичні
віддалеміри, залежно від положення
базису
віддалеміри
з базисом, відокремленим від кутомірного
приладу;
віддалеміри
з базисами, поєднаними з кутомірним
приладом (віддалеміри внутрішньобазисні).
Останні
віддалеміри використовуються для
вимірювання віддалей до недоступних
та важкодоступних предметів.
За
способом визначення елементів
паралактичного трикутника оптичні
віддалеміри можна класифікувати так:
віддалеміри
одинарного зображення;
віддалеміри
подвійного зображення.
Конструктивно
оптичні віддалеміри поділяються на:
віддалеміри
з постійним (відомим) базисом
віддалеміри
зі змінним базисом
273
S
= ~. (II.
7.2)S
1—
= — -к
- коефіцієнтb
фS
=
1006. (ІІ.7.3)b,
поділяються на:
b
та
змінним кутом ф, що вимірюється;Ь,
що вимірюється та постійним (відомим)
кутом ф.
Відцалеміри
одноразового зображення з постійним
кутом ер та змінним базисом b
-
це вже відомі з першого курсу ниткові
відцалеміри. Відносні похибки вимірювання
ліній нитковими відцалемірами наближено
дорівнюють 1/300-1/400. Така точність
недостатня для полігонометрії навіть
2 розряду.
Вищу
точність мають відцалеміри одноразового
зображення з постійним базисом b
та
точно виміряним змінним кутом ер, а
також відцалеміри подвійного зображення,
які і будуть розглянуті далі.
У
комплект такого віддалеміра входить
точний або високоточний оптичний
теодоліт та горизонтальна рейка (базис),
яка встановлюється на штативі. Рейка
без поділок, з марками на кінцях. Довжина
рейки 2-3 м.
Для
такого віддалеміра справедлива формула
(ІІ.7.2). Розрахуємо його точність. Для
цього спочатку прологарифмуємо (ІІ.7.2):
1п£
= 1п6-1пер.
(ІІ.7.4)
Тепер,
диференціюючи (ІІ.7.4) за обома параметрами,
матимемо:
dS
_
db
d
ф
S
b
cp
(П.7.5)
>b
Рис.
11.7.2. До пояснення принципу роботи
віддалеміра з постійним базисом
Перейдемо
від диференціалів до середніх квадратичних
похибок:
(П.7.6)
274//.7.2. Віддалемір із постійним базисом та змінним кутом
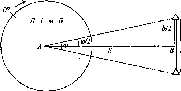

Довжина
базису
Визначимо
ер з (ІІ.7.2):
т§
ь
S
Підставляючи
у (П.7.7) значення ф з (ІІ.7.8), отримаємо:
S2
-от„
ТИс
=-
(ІІ.7.7)
(ІІ.7.8)
(ІІ.7.9)
Переходячи
від тф
у радіанній мірі до кутової міри
остаточно
маємо:
т
-
s2-m;
р'Ь
(ІІ.7.10)
Як
бачимо, похибка такого віддалеміра
прямо пропорційна до квадрата вимірюваної
довжини та похибки вимірювання кута
до
довжини базису
вимірювати
кут ф з мінімально можливою похибкою;
застосовувати
якомога довші базиси
основне:
виконувати вимірювання ліній короткими
відрізками, встановлюючи відцалемір
та рейку у створі лінії, яка підлягає
визначенню (див. рис. ІІ.7.3).
Рис.
11.7.3. Принцип створної короткобазисної
полігонометрії
Такий
метод вимірювання ліній називають
методом
створної короткобазисної полігонометрії.
Нехай
таким віддалеміром вимірюється лінія
завдовжки
275Ь
може бути визначена як завгодно точно,
якщо прийняти ть
=
0. На підставі (ІІ.7.6) матимемо:S
фф=—.т"
(у секундах)т*
і обернено пропорційнаЬ.
Це означає, що для підвищення точності
роботи віддалеміра необхідно:
b;S
=
iSj
+
$2
+ S3
+ S4
+
S5
+ .
S
=
200 м. Розрахуємо відносну похибку
вимірювання цієї лінії, якщо довжина
базису
1 /Иф
5000
~ р |
(ІІ.7.13) |
5-
|
(ІІ.7.14) |
Для
тих самих значень |
|
206265'-2
Ґ•5000
=
80 м.
Якщо
кути <р будуть вимірюватися з абсолютною
похибкою = 2", що ймовірніше, тоді,
відповідно:
Отже,
можливості використання в полігонометрії
віддалеміра одноразового зображення
з постійним базисом доволі обмежені.
Але, все-таки, точність такого віддалеміра
майже на порядок вища, ніж ниткового
віддалеміра, і ним можна прокладати
полігонометрію 2
розряду.
Оптичні
віддалеміри подвійного зображення
поширеніші у виробництві, ніж віддалеміри
одноразового зображення. У таких
віддалемірах, створених у кінці XIX
століття, промені світла, що йдуть через
об’єктив зорової труби,
276S
=
40 м.II. 7.3. Віддалеміри подвійного зображення
розділяються
на два пучки. Це досягається завдяки
тому, що перед об’єктивом
ставлять
оптичний клин, який перекриває половину
поля зору труби
(рис. ІІ.7.4).
Рис.
II. 7.4. Оптичний клин: а - загальний вигляд;
6
- оптичний клин перекриває половину
об’єктива зорової труби
Вертикальний
розріз зорової труби з оптичним клином,
встановленим на об’єктив, показано на
рис. ІІ.7.5.
Горизонтальна
вісь обертання труби проходить через
точку О. Точка
3 4
1
5
Sj
N
„ш
Рис.
ІІ.7.5.Вертикальний розріз зорової труби
з оптичним клином та принцип
роботи
віддалеміра подвійного
зображення: 1
- окуляр;
2
- фокусувальна
лінза;
З -
об'єктив; 4 - оптичний клин
Якщо
на рейці між точками
Розглядаючи
трикутник
S
-
k
= S\ = na ctg(f>, (ІІ.7.15)
277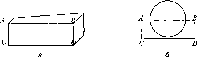
Р
- так звана аналатична (вимірювальна)
точка. Якраз у цій точці відбувається
розділення (заломлення тієї частини
променів світла, що проходить через
об’єктив і клин). Та частина променів,
яка проходить тільки через об’єктив,
не заломлюється. У результаті в полі
зору труби видно дві рейки, зміщені по
вертикалі одна відносно одної, тобто
видно подвійне зображення рейки. Інакше
кажучи, точка Р
проектується на рейку подвійно: у точці
М
та в точці N.

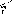
М
та N
є
п
поділок рейки, а одна поділка завширшки
a,
тоді відрізок MN
=an.PMN,
запишемо:
|
(ІІ.7.16) |
Оскільки
кут ф незмінний, то й ctg
ф
- стала величина. Позначимо ^ф |
|
|
(II. 7.17) |
Введемо нове позначення: |
|
|
(П.7.18) |
отримаємо: |
|
|
(ІІ.7.19) |
Формула
(ІІ.7.19) така сама, як і формула ниткового
відцалеміра. Проте завдяки подвійному
зображенню відрізок на рейці
Розглянутий
тільки що віддалемір подвійного
зображення з постійним кутом ф та
змінним базисом
Оптичні
віддалеміри, як правило, є віддалемірами
подвійного зображення.
Відповідно
до ДЕСТу в СРСР випускали оптичні
відцалеміри трьох типів. Всі вони
подвійного зображення.
ДН8
(віддалемірна насадка, 8
см - похибка на 100 м довжини). За допомогою
ДН8
вимірюються нахилені (не редуковані
на горизонтальну площину) віддалі. Це
віддалемір з постійним базисом
ДНР5
(віддалемірна насадка, редукційна, 5 см
- похибка на 100 м довжини). Дає змогу (для
кутів нахилу до 12°) автоматично редукувати
й одержувати горизонтальні прокладення
ліній з відносною похибкою 1:1000—
1:2000 завдовжки 20-120 м. Рейка двостороння,
вертикальна. Це віддалемір з постійним
кутом ф та змінним базисом
278п
• а
може бути виміряний значно точніше ніж
нитковим віддалеміром. У цьому перевага
віддалеміра подвійного зображення
порівняно з нитковим віддалеміром.
Завдяки саме цій перевазі відцалеміри
подвійного зображення значно точніші
від віддалемірів одноразового зображення.Ь
= ап.
Інколи замість оптичного клина перед
об’єктивом труби розташовують лінзові
компенсатори, які дають змогу не тільки
змінювати, але й вимірювати змінний
кут ф між двома пучками променів.
Тоді ми маємо віддалемір з постійним
базисом b
(горизонтальним
або вертикальним) та змінним кутом ф.b
та
змінним кутом ф. Рейка встановлюється
на штативі горизонтально. Можна
вимірювати довжини від 50 до 700 м з
відносною похибкою 1:1000. Використовується
для вимірювання ліній у теодолітних
ходах. Може бути застосована в
полігонометрії, якщо виконувати
вимірювання ліній створним методом
короткими відрізками.b.
Використовується так само, як і ДН8.
Д-2
(віддалемір, 2 см - похибка на 100 м довжини).
Це удосконалений віддалемір ДН8;
також з постійним базисом
Траверсна
полігонометрія з вимірюванням ліній
підвісними мірними приладами потребує
значних затрат праці. Тому, коли ще не
було світло- віддалемірів, пошуки нових,
посередніх методів вимірювання ліній
були дуже актуальною науковою проблемою.
Як
відомо, оптимальна довжина ліній
полігонометрії 4 класу 500 м, а максимальна
- 3 км. Враховуючи, що допустима довжина
ходу 14 км, то для довжини ліній 1000 метрів
у ході буде 14 сторін. Розрахуємо необхідну
точність вимірювання ліній ходу з
такими сторонами. Скористаємося відомою
розрахунковою формулою для висячого
ходу:
У
правій частині (ІІ.7.20) перший та другий
члени є складовими відносної
похибки
— висячого ходу, викликаними відповідно
похибками вимірювання
ліній
та кутів. За умови рівності цих двох
членів можна записати:
(ІІ.7.20)
або
Розв’яжемо
(ІІ.7.21)
(П.7.22)
279Ь
та змінним кутом ф. Рейку можна
встановлювати на штативі горизонтально
або вертикально. Дає змогу вимірювати
похилі (не редуковані) віддалі 40-400 м з
відносною похибкою 1:5000. Можна вимірювати
віддалі до 700 м, тільки тоді точність
1:1000. Використовується для вимірювання
ліній у полігонометрії 2 розряду та в
теодолітних ходах.LСуть паралактичної полігонометрії
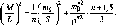



Оскільки
для 4 класу полігонометрії
М
1
25000
то
для
ms
1
отримаємо:
—1—
~ .
Жодний
оптичний відцалемір не дає такої
точності для
Розрахуємо
спочатку необхідну величину паралактичного
кута. Оскільки
(ІІ.7.23)
якщо
1
_ 2°
10000
ф'
(ІІ.7.24)
А
тому ф'= 20000", або ф°= 5,6°. Залишається
знайти необхідну довжину базису
3L
Ф°
Р°
або
Ь
=
(ІІ.7.25)
280п
=
14S
10000S
=
1000 м. У 1836 р. проблема швидкого визначення
була успішно вирішена В.Я. Струве, який
запропонував паралактичну ланку
полігонометрії. Головна відмінність
відомої вже полігонометричної ланки
з коротким базисом (з горизонтальною
рейкою, завдовжки 2-3 м) і паралактичною
ланкою в тому, що в цій ланці застосовують
значно довший базис, виміряний мірними
дротами. Така ланка показана на рис.
П.7.6.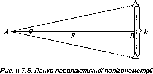
1Г~’т'=
2",
можна записати:b.
Відповідно до (ІІ.7.2):S
ф°
Тоді
для *? = 1000 м, ср°= 5,6°, р° = 57,3° матимемо:
L
1000
57,3°
Отже,
для довжини мірного дроту
Як
очевидно з розрахунків, точність
полігонометричної ланки В.Я. Струве
залежить від величини кута ер. Проте
для збільшення кута ер необхідно
збільшувати довжину базису. У зв’язку
з цим професор А.Д. Моторний запропонував
[17] ланку полігонометрії, у якій базис
розташовано не перпендикулярно до
лінії, а вздовж лінії, тобто базис є
частиною лінії, що визначається. Для
однакових довжин базисів, але довших
перпендикулярів (які не вимірюються),
така ланка дає змогу збільшити кути ер
і отримати значно вищу точність
визначення*?. Для однакових за довжиною
базисів та величин кутів ер, навпаки,
точність ланки Струве дещо вища.
Віддалемірно-базисна
полігонометрія - це поєднання віддалемірних
визначень базисів з паралактичними
ланками. Такий метод дуже еластичний
і може застосовуватись у найважчих
топографічних умовах. Як видно з рис.
ІІ.7.7, базис
Виникає
питання про найвигідніше співвідношення
між
d
= yfb~S. (П.7.26)
При
цьому повинні бути наближено однакові
кути ер! ~ ер2.
281мм-5,6°
1ЛЛ
о
= ~100м.10
= 24 м достатньо буде відкласти чотири
мірні дроти. Під час вимірювання ліній
завдовжки 1000 м у траверсній полігонометрії
необхідно буде відкласти у створі
більше ніж 40 дротів. Звідси зрозуміло,
як істотно зменшаться затрати часу,
якщо використовувати паралактичні
ланки навіть при тому, що ще потрібно
в кожній ланці точно вимірювати кути.
Суть віддалемірно-базисної полігонометрії
b
може
бути виміряний мірним дротом, якщо
лінії ходу Sx,
*?2,
S3
-
довгі, більші за 1
км або частіше, методом короткобазисної
полігонометрії (Ь=
2-3 м), якщо лінії *?,•
- короткі (50-100 м). Знайшовши з паралактичної
ланки довжину BN
= d,
далі, розв’язуючи трикутники ANB,
BNC,
визначають довжини сторін ходу*?!, *?2
тощо.b,
d
та
*?. Теоретичними дослідженнями
доведено, що найвигіднішими, тобто
найточнішими будуть ланки, коли
виконується рівність
A Sl В S2 С S3 S4
Рис.
11.7.7. Ланка
віддалемірно-базисної полігонометрії
Паралактичні
ланки поділяються на прості та складні.
Подамо деякі типи ланок, що можуть бути
застосовані у разі відсутності у
виконавця робіт світа овіддал емірів.
В
б
- тип І-б
S
= di +d2
=| +
^gyj
»S|
— d^
+ > 5*2 — d\
^2
Рис.
11.7.8. Прості
типи паралактичних ланок
282
II. 7. Б. Типи паралактичних і віддалемірно-базисних ланок
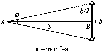

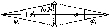
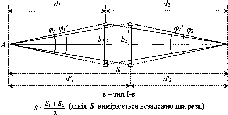
Рис.
11.7.9. Складні ланки віддалемірно-базисної
полігонометрії
Згадаємо,
як ми виконували обчислення координат
теодолітного ходу, прокладеного між
точками з відомими координатами, а
також відомими початковим і кінцевим
дирекційними кутами.
Аналогічно
можна виконувати обчислення координат
полігонометричного ходу. У теодолітному
ході ми спочатку знаходили кутову
нев’язку за формулою
W+l W+1
/р
= Х (П.8.1)
1
1
W+l W+1
ДЄ
SP*.
і
ZP-
-
відповідно практична і теоретична сума
кутів ходу. Потім
і і
вводили
поправки у виміряні кути. Сума поправок
у кути J
повинна
дорівнювати нев’язці з оберненим
знаком:
IЧ, ]
= -/?• (П.8.2)
Це
перша умова, яку має задовольняти
виправлення кутів.
Потім
за виправленими (зрівноваженими) кутами
ми знаходили дирек- ційні кути а,-,
а, маючи ще і виміряні довжини
Ахі
= Sj
■
cos
а,-;
Ау,- = St
•
sin
а,-. (ІІ.8.3)
283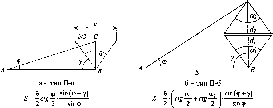
Строге зрівноваження полігонометричних ходів
Недоліки спрощених методів зрівноваження
St,
визначали прирости координат
Далі
окремо (незалежно від кутів) зрівноважували
прирости координат. Спочатку знаходили
нев’язки за відомими формулами
Л
= Xfa
-
(** - ); (п.8.4)
1
Л=І^/-(Л-Л). (ІІ.8.5)
і
Нев’язки
розподіляли в прирости координат,
виконуючи ще дві умови:
суми поправок
у прирости абсцис та ординат [rfAxz
] та
[ЛЦ]
= -/Х; (ІІ.8.6)
[dAyi]
= -fy. (И-8.7)
За
виправленими (ув’язаними) приростами
знаходили координати вершин ходу
п+1
умова
дирекційних кутів
П
умова
абсцис Хк
=Хп
+
lL*Xy.:>
і
п
(ІІ.8.8)
умова
ординат YK~Yn+'L
АУув.
і
У
(ІІ.8.8)
прийняті позначення: (Зл>,8
- ліві (стосовно напрямку ходу),
ув’язані
кути повороту;
Але
ці три умови (рівняння) розв’язувалися
окремо.
Спочатку
виконана умова [<5?{3,
] = -/р, а потім, тільки після
обчислення
приростів координат,
виконано умови: [с/Дх, ] =
284[<ЗАуі
]
повинні дорів-
нювати нев’язкам
fxify3
оберненим
знаком:Xt
і
Yt.
Здається, ніби три геометричні умови,
що виникають у такому ході, виконані
введенням поправок d$t
в
кути TadAxi9
dAyi
-
у прирости координат. Ось ці три умови,
записані у вигляді рівнянь:ак
= ап
+ ХРлув. -180(и + і);Ахув
,
Ауув
-
ув’язані прирости координат; а„,
ак-
задані
початковий і кінцевий дирекційні кути;
Хп,
Yn-
задані
координати
початкової точки ходу;
Хк,
^-координати кінцевої точки.-fx,
[dAyt
]
= —fy.
Ці три геомет-
ричні умови взаємозалежні.
Справді, зміна р, кутів ходу викличе
зміну довжин
сторін ходу Sj.
А
це не враховано. Три рівняння потрібно
розв’язувати разом.
Тому, фактично,
три геометричні умови, що виникають у
ході, не задовольняються.
Щоб
впевнитися в цьому, будемо за розрахованими
нами координатами розв’язувати обернені
геодезичні задачі, тобто знаходити
довжини ліній
У
цьому і полягають недоліки спрощених
методів зрівноваження. Вказані недоліки
виникають через те, що ми не враховували
залежностей між лініями та кутами.
Потрібно поправки в кути та лінії шукати
з одночасного розв’язання трьох
геометричних умов, що виникають у ході.
Такі
зрівноваження, коли знаходять поправки
у кути та лінії з одночасного розв’язання
умовних рівнянь, називаються
Існують
два методи строгого зрівноваження
(вирівнювання) геодезичних ходів та
мереж:
Нехай
маємо полігонометричний хід, прокладений
між “твердими” (відомими) пунктами,
показаний на рис. П.8.1.
Рис.
11.8.1. Полігонометричний хід, прокладений
між відомими пунктами
та дирекційними
кутами
У
ході виміряно
285S',
а також дирекційні куга а,', а потім куга
повороту (3-. Тоді виявиться, що а'
ї
а,, Р' Ф
$іув
; S'
ї
S(,
тобто
ні ув’язані куга Р,-
ув
не
будуть такими, як виправлені поправками
( ) куга Р •; ні обчислені за координатами
довжини лінійS'
не
будуть такими, як виміряні St.
Це означає, що знайдені координати не
є такими, що задовольняють геометричні
умови ходу, не є найімовірнішими.строгими
(точними).
Накладається додаткова умова: сума
квадратів поправок у кути та лінії
повинна дорівнювати мінімуму [W]
=
min.
До
того ж обґрунтовано вибираються ваги
вимірів кутів та ліній.корелатний
та параметричний.
Ці методи детально розглядаються в
теорії ймовірностей. Практичне
застосування названих методів у
геодезії, передусім у полігонометрії,
буде висвітлено далі.
Кількість вимірів та невідомих у полігонометричному ході. Необхідні та надлишкові виміри
п
ліній та (и +1) кутів. Кутів у ході завжди
на один більше ніж ліній, якщо виміряні
також і кути та (Зп+1,
що межують з лініями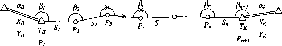
тріангуляції.
Отже, усього вимірів: (и + 1) + и = 2я + 1.
Невідомими є
координати
пунктів ходу, показаних кружками. їх у
ході завжди на одиницю менше ніж ліній.
Невідомих абсцис
Знайдемо
кількість надлишкових вимірів: {2л +
полігонометричному
ході, який прокладений між відомими
пунктами, завжди є три
Знайдемо
у наведеному ході “надлишкові” виміри,
тобто такі виміри, які можна було б не
робити, а всі невідомі координати
пунктів знайти. Якщо обчислювати
координати точок від початкової точки
Нарешті,
можна частину точок обчислити від
початку ходу, а частину - від кінця ходу.
Тоді надлишковими будуть, наприклад,
два кути й одна лінія, позначені на рис.
II.. 1 хрестиками.
Надлишкові
вимірювання спонукають до контролю
вимірів і можливості зрівноваження
ходів або мереж. За відсутності
“надлишкових” вимірів хід перетворюється
на “висячий” (спирається тільки на
один відомий пункт), унеможливлюється
контроль вимірів та зрівноваження
ходів. Зрозуміло, що зникають і геометричні
умови, що виникають у ході чи мережі.
Тому
надлишкові виміри є дуже важливими.
Виведення
формул,
що
зв'язують поздовжній та поперечний
зсуви ходу з нев’язками по осях
координат
На
рис. II.8.2 показано витягнутий
полігонометричний хід, прокладений
між відомими точками
Але
координати усіх точок ходу, зокрема
точки
286Xt
-
(л -1).
Невідомих ординат Yi:
- (п
-1).
Усього
невідомих (п
-1)
+ (п
-1)
= 2п
-
2.і}-(2и-2)
= 3.
Отже, внадлишкові
виміри. Вони не є “непотрібними”. Саме
надлишкові виміри приводять до того,
що в ході виникають геометричні умови,
про які йшлося вище. Завжди в ході або
мережі кількість умов дорівнює кількості
надлишкових вимірів.Тпоч,
тоді знайдемо координати всіх точок,
зокрема Хп,
Yn
точки
Рп
без вимірів кутів (3„, (3„+1
та лінії Sn.
Якщо, навпаки, обчислювати координати
точок від кінцевої точки Ткін,
тоді знайдемо координати всіх точок,
зокрема Х2,
Y2
точки
Р2
без вимірів кутів РІ5
р2
та
ліній S.
А
та В.В,
обчислювались не за зрівноваженими, а
за виміряними лініями і кутами, починаючи
від точки А.
У результаті кінцева точка ходу зайняла
положення 5'. Отже, відрізок BfB
=
fs
-
це
лінійна нев’язка ходу. З’єднаємо точки
А
та 5' прямою (замикаючою) і
дещо
продовжимо її. Дирекційний кут замикаючої
а. Дирекційний кут нев’язки є. Довжина
замикаючої
Безпосередньо
з рисунка маємо:
х
х
[ДХ]<
А
Рі
[AY]
Рис.
11.8.2. До виведення залежності між зсувами
t
і
и
та нев’язками по осях координат
fx
та
fy
(ІІ.8.9)
З рисунка
також можемо записати:
(II.
8.10)
287АВ'
=L.
Спроектуємо
точку В
на координатні осі X
та Y
і
на замикаючу. Отримаємо точки В1,
В2,В3.Як
видно з рисунка, відрізки: В'ВХ
= ВВ2
=
fx;
В'В2
= ВВ{
—fy.
Ці
відрізки дорівнюють нев’язкам fx
та
fy.
Відрізок
В'В3
= t
-
поздовжній зсув; а ВВг
= и
-
поперечний зсув. Проектуючи хід на осі
X
та Y,
одержимо суми приростів координат [Ах]
та [Ау].


Розкладаючи
cos
|
(II.8.11) |
|
(П.8.12) |
Враховуючи (II.8.10), маємо:
|
(П.8.13) |
|
(II.8.14) |
Оскільки з цього самого рисунка
[Ах]
cosa
= -—
|
(II.8.15) |
м
|
(П.8.16) |
,=/ ^1+/[Ау]
|
ai.8.i7) |
|
(II.8.18) |
L.Jlbcf. |
(II.8.19) |
Формули
(ІІ.8.17), (ІІ.8.18) пов’язують зсуви ходу
t,
и
з нев’язками по осях координат fx,fy.
Скористаємось
розглянутими в п. П.8.1 відомими вимогами
рівності суми поправок у кути та у
прирости координат відповідним
нев’язкам, взятим з оберненим знаком.
Ці
рівності запишемо так:
Ж=-/р;
[db.y]
= fy
(ІІ.8.20)
288Виведення умовних рівнянь, що виникають у полігонометричному ході, прокладеному між відомими пунктами
Припустимо,
ЩО
МИ нев’язку
/р7
порівну
розподілили в усі виміряні кути.
Нехай
виникла необхідність у виправлені кути
ввести ще якісь вторинні поправки. Тоді
сума цих поправок повинна дорівнювати
нулеві. У протилежному випадку в
ході з’явиться нова нев’язка. Але,
якщо ми замінили виміряні кути (З,
первинними поправками, то зміняться і
дирекційні кути, а, отже, зміняться
нев’язки
поправки
у прирости абсцис і ординат.
У
зв’язку з цим рівняння (ІІ.8.20) змінюються,
і їх запишемо так:
И*]
= 0;
[dAx]
= -fx;
-.
IdAy]
= -fy
(ІІ.8.21)
Як
відомо, прирости абсцис та ординат
знаходять за формулами
Ax
= 5'cosa;l
Ч. (ІІ.8.22)
Продиференціюємо
ці формули:
da
P
(II.
8.23)
Значення
Отримаємо:
№=0;
[cosoci/51]
-
—[Ду</а] +
(ІІ.8.24)
Перейдемо
від поправок у дирекційні кути
«/
=аі+ХР/
—180
(і + 1). (11-8.25)
і
289fx
та
fy.
Одночасно
виникне необхідність змінитиAy
= S
sin ос.
JdAx
=
cos
осdS
-
S
sin a-dAy
= sin a dS
+ S
cos a—.dAx
та
dAy
із
рівнянь (II.8.23)
підставимо
у початкові рівняння (ІІ.8.21),
враховуючи (ІІ.8.22).fx
=0;
••
[sinou/5]+—[Дхс/а]
+ fy=
0dai
до
поправок у виміряні кути . Для цього
скористаємося залежністю між дирекційними
кутами та кутами повороту. Припустимо,
вимірялись ліві по ходу кути. Тоді
можемо записати:
№=0 |
|
|
[coso^C] - — Р |
г 1 со. -н- £ 1 1 |
О II + |
[sin 0^5] + - р |
д*Х</р і |
|
|
1 |
|
|
Дх£а?Р і |
|
Запишемо
суму А
у розгорнутому вигляді:
А
=
+...
+
Згрупуємо
члени з^/Pj,
с/р2,
<ірз,
...,<5?Р„
:
+ofp3
(Ду3
+ Ду4...
+ Ду„) +... + ^Р„Ду„.
Замінимо
суми приростів ординат різницями
координат відповідних
точок:
А
=
^Рі (л+і -Уі)
+ ^Рг (Уп+і
~Уг)
+ ^Рз {Уп+і
~Уз)
+- + dVn
ІУп+1
~
У*)•
В
останній сумі відсутній кут рп+1
і поправка dp„+1.
Введемо цю поп-
равку, скориставшись
виразом, що дорівнює нулеві: с?Р„+1
(у„+1
-
(IL8-29)
Введемо
в рівняння (ІІ.8.29) ординату центра ваги
ходу:
ш:
1/7+1
(ІІ.8.30)
290А<7pj
=
Аух
df>\
+
Ау2
(<5?Р|
+ <7(32
) + Ау3
(c/j3j
+
d$2
+
^Рз) +Ауп
(с?р, + rfp2
+
fi?p3
+...
+ с/р„).А
= <7Р, (Ду! + Ауг
+
Ау3
+... + Ау„)
+ с/Р2
(Ау2
+
Ду3
+... + Ду„)
+уп+1).
Цей ви-
раз додамо до А.
Тоді останній вираз можемо записати
скорочено:
Це
можна зробити, враховуючи, що [</р,] =
0. Отже, (ІІ.8.29) можна записати так:
л=[УРі
(у
Позначивши
в (ІІ..31) різниці
И-Г„=Л,, (ІІ.8.32)
де
Л
= -МР,]. (ІІ.8.33)
Позначивши
де
- абсциси точок ходу відносно центра ваги,
можемо за аналогією
записати:
В
= -[%,<ф,]. (П.8.35)
Отже,
умовні рівняння набувають вигляду:
[<*Р]=0;
[cos
Р
[sin
осей]
- - - [^Р] +
(ІІ.8.36)
Оскільки
у рівняннях (ІІ.8.36) поправки в кути t/p
та
в лінії
[V]
= 0;
[cos
аса]+
—[т|Г] +
fx=®’>
[sin
aco]--^F] + />,
=0.
Це
і є умовні рівняння в кінцевому вигляді.
(ІІ.8.37)
291т
- у,
)]"*'+
№ 1
гч
=№]>»*і - -№л]+№]і; =-[(л-ц)<ф,]. (пазі)j\t
-
ординати точок ходу відносно центра
ваги ходу. Матимемо:х,-Хч=Ь> (ІІ.8.34)adS
]
+—[л^Р] + Л =
0;fy
-
0.
РdS
записані
двома літерами, доцільно ввести
позначення: е?Р = V;
dS
=
(о, тобто позначити однією літерою
поправки в кути V,
а поправки в лінії со. Тоді записи
(ІІ.8.36) спростяться:
Для простоти скористаємось |
витягнутим рівностороннім полігономет- |
ричним ходом із шести точок, п’яти сторін, показаного на рис. ІІ.8.3: |
|
, Wf. |
V
|
I
|
|
|
~£>2~х2~хц ; |
-Лз = 73-Уч; |
|
+ II £ 1 |
+
^4 — ДС4
|
+ <-* II 1 |
+^5
=
*5
|
+Лб
= Л |
+£б
=
|
[Лі]= 0. |
&]=о. |
292
И = 0; |
(/) |
[cos
аса]+
—[r|v]
+
|
|
[sin аш] “ [£v] + /; =0. |
|
4-
де
|Х - коефіцієнт випадкового впливу
лінійних вимірів; /ир- похибка
вимірювання
кута;
Користуючись
довільністю
Р=_^
= ІІІ
=
І.Р =!•
'
\i2S
112S
S’ Si
s’
o
_ c
_
[І2 ц2
•
Mp2
Отже,
ваги виміру ліній - змінні величини й
обернено пропорційні до довжини ліній,
а кути мають однакові ваги, оскільки
вимірюються приладами однієї точності
і за однаковою програмою вимірювань.
293с
—
довільний коефіцієнт пропорційності.с,
приймемо: с
=|Х2.
Тоді отримаємо:
№ рівнянь |
Для поправок у куги |
Для поправок у лінії |
І |
|
11 £ н н н о |
II |
|
|
III |
Сі = (і =1,2,..., и+1) Р |
|
Розглянемо,
як змінюються нормальні рівняння
корелат, якщо замість коефіцієнтів
а,-,
для
кутів: для ліній:
294Ьі,
с;
підставити їхні фактичні значення:
|
II о |
© |
|
[у]*2 +Л =0; |
(П) |
|
|
(Ш) |
|
|
|
|
|
(ІІ.8.40)
Сума
Отже,
завдяки тому, що [г|,] = 0 та [£,] = 0, у
системі (ІІ.8.40) залишається тільки
два рівняння, які необхідно розв’язувати
одночасно.
Позначимо =
набудуть
вигляду:
Ак2
+ Вк2
+ fx
=
0;
Вк2
+ Ск3
+ fy—
0.
Розв’яжемо
ці два рівняння:
Bfy~Cfx
(ІІ.8.41)
АС-В2
h
=
(11.8.42)
(11.8.43)
Загальна
формула переходу від корелат до
шуканих поправок при трьох умовних
рівняннях має вигляд:
Враховуючи,
що |
(ІІ.8.44) |
v,
=тг(6Л
|
(И.8.45) |
Поправки в кути визначаються за формулою з)- лзР |
(ІІ.8.46) |
Відповідно поправки в лінії знайдемо, аналогічно:
<%
= (cos
|
(ІІ.8.47) |
295
Оскільки
Si
то—
=
Ps>
CO,-
=
Виправивши
виміряні куги вторинними поправками
V,- та лінії поправками
Нехай
маємо витягнутий полігонометричний
хід, координати точок якого обчислені
за виміряними кутами та лініями і, в
результаті, кінцева точка ходу
Повернемо
координатну вісь
мальні
рівняння:
*1=0
(І)
[?]*2+[7]*3+,=0(ІІ)
'
Н*!+Ніз+“=о
<ш)
(ІІ.8.49)
Оскільки
дирекційний кут замикаючої a
=
0° (cosос
= 1; sin
a =
0; t|,
= 0), то
рівняння (ІІ.8.37) набудуть вигляду:
М=о
[ш]
(ІІ.8.50)
[£v]
+ « =
0
Р
Складемо
на підставі (ІІ.8.50) таблицю коефіцієнтів
нормальних рівнянь.
296Ps.
=St,
тосо, =
(Sf
cos a,
k2
+ St
sin a,&3),Axfa
+ Ay(^3. (II.8.48)щ,
задовольнимо усі геометричні умови,
що виникають у полігоно- метричному
ході, і знайдемо ймовірніші координати
пунктів ходу.Строге зрівноваження витягнутого полігонометричного ходу корелатним методом
В'
не збігатиметься з фактичною кінцевою
точкою ходу В,
координати якої відомі. Тоді відрізок
В'В
= fs
-
це лінійна нев’язка ходу (рис. ІІ.8.4).X
системи координат і спрямуємо її вздовж
замикаючої ходу. Новий напрямок осі
абсцис позначимо X',
а вісь ординат Y'.
Спроектуємо
точку В
на вісь X'.
Як
видно з рисунка, після повороту
координатної системи нев’язка fx
дорівнюватиме
поздовжньому зсуву t,
а нев’язка fy
-
поперечному зсуву и.
Враховуючи це, запишемо скорочені нор+1
=
0
№ рівнянь |
Для поправок у куги |
Для поправок у лінії |
І |
її £ її аР + II |
0 II II II оГ II 01 II 6" |
п |
2>,
= 0 |
|
ш |
1 ^
с,-
= — |
с,
= 0(г'=
1,2,
|
Надамо
нормальним рівнянням відповідного
вигляду, враховуючи значення
коефіцієнтів табл. ІІ.8.2 і те, що ——
PSi
kx
=0
[S,]^+/
= 0
Розв’яжемо
систему (И.8.51) відносно невідомих
корелат:
(ІІ.8.51)
297=
Si9
a[St]
= L:
^2
““
*3
=-'РрР
[$Г
2
U
[c?]'
(II.8.52)
(П.8.53)
Залишається
знайти шукані поправки в кути V, та в
лінії to,-.
Скористаємося
уже відомою формулою (ІІ.8.45):
Значення
коефіцієнтів
• для
ліній:
• для
кутів:
V/
=
Рь
Р '
^ 2
W
-^рр
•
[;?]
=
Р
И
і,-
(П.8.54)
(11-8-55)
Виправивши
лінії та кути відповідними поправками,
знайдемо ймовірніші координати пунктів
ходу. Приклад зрівноваження витягнутого
полігономет- ричного ходу буде подано
в п. ІІ.8.8.
Поправки
в лінії обчислюють за простою формулою:
со
L
Оскільки
~ =
в
лінії будуть однаковими:
ю,
Проте
для обчислення поправок vz-
в
кути необхідно знати абсциси точок
ходу
відносно центра ваги ходу та суму їхніх
квадратів J.
Розглянемо,
як зміниться формула (ІІ.8.55) для
рівностороннього ходу. Візьмемо для
простоти хід із парною кількістю сторін
298у/=^г(^2+с/£з)-Ь;
і с;
візьмемо з табл. ІІ.8.2. Отримаємо:'_L.it'Строге зрівноваження витягнутого рівностороннього полігонометричного ходу
i=--S.. (ІІ.8.56)с
- стала величина для цього ходу, а лінії
рівні, то поправки L=-cSr (ІІ.8.57)п.
Це буде справедливим
і для
непарної кількості сторін. Спрямуємо
вісь
Тоді:
Х[= 0;
(ІІ.8.58)
Центральну
абсцису знайдемо за формулою
X
=-S.
4
2
Визначимо
абсцису точок ходу відносно центра
ваги:
або:
(II.
8.59) (ІІ.8.60)
В(Рп+І)
ФЛ,
S
S
S
^+1
V4
\Ps
?
Р2
Д*
90е
А(Рі)
Рис.
11.8.5. До зрівноваження
витягнутого
рівностороннього
ходу
полігонометрії
(П.8.61)
Розглянемо
далі, як зміниться [С? ] • Спочатку
знайдемо
на основі (II.8.61)
значення
усіх £z-.
Маємо:
t,-і*
<--(Н
НН
2
=
о
(ІІ.8.62)
Такими
самими за абсолютним значенням бу-
дуть
абсциси для другої половини точок ходу,
тільки
зі
знаком “плюс”. Тому J
можна
подати так:
\2
/ \2
/ \2
.
(ІІ.8.63)
299X
уздовж ходу і за початок координат
приймемо першу точку (рис. ІІ.8.5).X2-S;
Х3
= 2S.
Отже, для будь-якої точки і
маємо:^+і
У
квадратних дужках сума квадратів
натурального ряду чисел від — до 1. Як
відомо, для такого ряду з
£
.2
_ я(л
+ і)(2и
+ і)
і 6
Для
/ = -^ маємо (помноживши
[Cf
]
= 25-
Після
перетворень
-(-+1Y2-+11
212
А 2
)2п
2
п
[Є]-
Отже,
и\2п
2
(ІІ.8.64)
(11.8.65)
(11.8.66)
Враховуючи,
що
отримаємо
для поправок у кути просту формулу
U
L
Зауважимо,
що
Отже,
зрівноваження витягнутого рівностороннього
ходу (майже рівно-
стороннього) значно
спрощується.
(П.8.67)
(11-8.68)
Для
кращого розуміння зрівноваження
витягнутого полігонометричного ходу,
описаного у п. ІІ.8.6,
наведемо приклад такого зрівноваження.
Використовується відомість обчислення
координат, в останньому стовпчику якої
подано робочі формули та виконано
допоміжні обчислення.
300п
чисел справедлива формулаі
поділивши на 2п):(п
+ і)(п + 2)
т2
12
пS
n = L,
а
також позначивши:І'=(»
+
1)(п
+ 2)('“2_1}v'=p
іь'-bt
є
функцією тільки кількості сторін ходу
п
та номера
сторони ходу і.
Професором А.С. Чеботарьовим складено
таблиці bt
=
/(и, і)
.
Під
час обчислення поправок у кути значення
bt
вибирають
з цих таблиць.Приклад зрівноваження витягнутого полігонометричного ходу корелатним методом (способом найменших квадратів)
У
вертикальній графі 1 виписані номери
відомих та тільки що закладених пунктів,
координати яких треба визначити.
У
графі 2 записані виміряні кути, зокрема
і прилеглі. Нев’язка в ході виявилась
такою, що дорівнює^
майже
порівну розподілена у виміряні кути з
оберненим знаком. Поправки величиною
2", або 3" записані зверху над
виміряними кутами. Внизу, під виміряними
кутами, записані вторинні поправки,
поки що невідомі. Щоб позбутися двох
поправок на кожний кут, можна у графу
2
записати кути, уже виправлені первинними
поправками, або доповнити відомість
ще одною вертикальною графою.
Далі
переходимо до обчислення дирекційних
кутів, використовуючи кути, виправлені
первинними поправками. Дирекційні кути
записуємо у графу 3. Початковий дирекційний
кут
*38=
212,421; У38=
7835,154;
Контролем
правильності обчислень дирекційних
кутів є формула
і
Тобто,
послідовно обчислюючи дирекційні кути
усіх ліній, використовуючи спочатку
У
графу 4 записують виміряні лінії. Графу
5 поки що пропускаємо. А далі виконуються
обчислення наближених приростів
координат за виміряними лініями
Обчислені
значення
нев’язки
fx=t^-{XK~Xn)-
fy=tby-(YK-Yn).
1
1
Далі
графи 8
і 9 та 10 і 11 поки що не заповнюються.
301=20',
за допустимої f$don
=±24'.
Ця нев’язкаа„
= 101°38'46" і кінцевий ак
=
329°36'29", як задані, уже повинні бути
записані у відомість (у графу 3). Так
само в графах 10 та 11 повинні бути записані
координати початкової (№ 38) та кінцевої
(№ 40) точок:Х40
= 2069,639; У40
= 8722,717.ак=ап
+ ІРлв„
-180(л + 1).<х„
- початковий дирекційний кут а37_28
= 101°38'46" (наприклад, а38_98=
101°38'46" + 104°12'43" - 180° = 25°5Г29") і,
дійшовши до кінцевого дирекційного
кута ак
(0140-41=
329°36'29’’), ми повинні отримати точно
кінцевий дирекційний кут ак,
тому що кутова нев’язка вже врахована.S
та
дирекційними кутами, що подані у графі
3.Ах
та Ду
записують у графах 6
та 7. Розраховуютьсяfx
та
fy
і
записують їх унизу відомості.
Використовують, зазвичай, формули
Заповнюють
далі графу 12, в якій обчислюються
наближені абсциси
*1
=
та
п+1
+11356
=
+1262.
У
графі 13 обчислюють абсциси точок ходу
відносно центра ваги:
Z,=x;-x;.
У
графі 14 обчислюють квадрати цих абсцис
Далі
у допоміжній графі 15 обчислюють:
1.
Поздовжній і поперечний зсуви
Поправки
в лінії. Робоча формула: оо,
L
ється
з точністю до сьомого знака після коми).
Поправки у лінії у міліметрах записані
у графі 4 над виміряними лініями.
Для
отримання зрівноважених довжин
додаються
до виміряних ліній. Зрівноважені лінії
подано у графі 5.
3.
Поправки в кути. Робоча формула: V* = о/
• , десо' =
Значення
со* також обчислюється з точністю до
сьомого знака після коми. Поправки v'
записані
під виміряними кутами у графі 2. Контроль
поправок у кути:
Поправки
в дирекційні кути v*. .
Ці поправки записані над
приблизними
дирекційними кутами у графі 3.
Щоб
знайти зрівноважені дирекційні кути,
ці поправки алгебраїчно додають до
наближених значень дирекційних кутів.
Зрівноважені дирекційні кути у відомості
не записані. За бажанням їх можна
записати в графу 3 під наближеними
дирекційними кутами, взявши їх у дужки.
Обчислення закінчуються заповненням
граф 8
і 9 та 10 і 11. У графах 8
і 9 записуються ув’язані прирости
координат, обчислені за зрівноваженими
дирекційними кутами та довжинами ліній
302X'.
Абсциса
X'
початкової точки Х'г%
= 0. Абсциса наступної точки Х98
дорівнює довжині лінії S38_98
=
423,678 м, округленій до цілих метрів: +424.
Для точки № 99 Х99
= 5,38_98
+ S98_99
=
+790 і так далі. Для кінцевої точки № 40
Х'40
= +2060. Далі знаходять абсцису центра
ваги ходу :п
+1 9Q
та
їхню суму j.t
і
и.
Необхідні формули виписані у цій графі.=-e-Si9
де
е = — (е
визнача-S3p
поправки
алгебраїчнор*[с?]'[v*]
=
0. Кути округляються до Iм.S3pe.
№ точок |
Куги повороту (ліві) (З |
Дирекцій- ні куги (X |
Виміряні довжини S, м |
Зрівноважені
довжини |
Прирости координат (наближені) |
Зрівноважені прирости координат |
||
О 1 и |
О 1 II |
Ах = S cos а |
S sin а |
= S„ cos а. |
АУзе = sin а„ |
|||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
37 |
|
|
|
|
|
|
|
|
|
|
101 38 46 |
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
38 |
104 12 45 |
|
|
|
|
|
|
|
|
+6,5 |
+6,5 |
-2,8 |
|
|
|
|
|
|
-2 |
25 51 29 |
423,678 |
423,6752 |
+381,258 |
+184,784 |
+381,249 |
+184,795 |
98 |
181 32 13 |
|
|
|
|
|
|
|
|
-чз |
+10,8 |
2,5 |
|
|
|
|
|
|
-2 |
27 23 40 |
366,123 |
366,1205 |
+325,066 |
+168,458 |
+325,055 |
+168,474 |
99 |
174 18 00 |
|
|
|
|
|
|
|
|
-♦2,4 |
М3,2 |
-2.8 |
|
|
|
|
|
|
-2 |
21 41 38 |
412,725 |
412,7222 |
+383,493 |
+152,563 |
+383,481 |
+152,586 |
100 |
188 17 49 |
|
|
|
|
|
|
|
|
+0,3 |
і 13.5 |
-1,7 |
|
|
|
|
|
|
-2 |
29 59 25 |
248,645 |
248,6433 |
+215,354 |
+124,286 |
+215,344 |
+124,299 |
101 |
173 28 42 |
|
|
|
|
|
|
|
|
-1,0 |
+ 12,5 |
-1.4 |
|
|
|
|
|
|
-2 |
23 28 05 |
207,548 |
207,5466 |
+190,380 |
+82,653 |
+190,374 |
+82,664 |
102 |
180 02 40 |
|
|
|
|
|
|
|
|
-2,0 |
+10,5 |
-U |
|
|
|
|
|
|
-2 |
23 30 43 |
156,267 |
156,2659 |
+143,293 |
+62,341 |
+143,289 |
+62,348 |
303
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
||||
103 |
184 15 11 |
|
|
|
|
|
|
|
||||
|
2.8 |
*7,7 |
-1,0 |
|
|
|
|
|
||||
|
-3 |
27 45 52 |
138,117 |
138,1160 |
+122,216 |
+64,478 |
+122,213 |
+64,482 |
||||
104 |
178 42 31 |
|
|
|
|
|
|
|
||||
|
-3,6 |
-41 |
0,7 |
|
|
|
|
|
||||
|
-3 |
26 28 20 |
107,485 |
107,4843 |
+96,215 |
+47,913 |
+96,213 |
+47,915 |
||||
40 |
123 08 12 |
|
|
|
|
|
|
|
||||
|
4,1 |
0,0 |
|
|
|
|
|
|
||||
|
|
329 36 29 |
|
|
|
|
|
|
||||
41 |
|
|
|
|
|
|
|
|
||||
|
1487 58 03 |
[S]= 2060,58 |
|
|
||||||||
|
+20 |
Дх,у= |
+1857,275 |
+887,476 |
||||||||
fp ДОП |
24 |
її |
+0,057 |
-0,087 |
||||||||
fs=+0,104
k_
= 1
S 20000 |
X' |
|
% |
Формули допоміжного обчислення |
|
хт |
YT |
||||
10 |
11 |
12 |
13 |
14 |
15 |
|
|
|
|
|
, ЛМ+ЛІДу]. t » L /Л^Ь/Лау] и L t _ 0,057 • 1857 + 0,087 - 887 _ г 2061 -a087.1857-a057.887 2061 Контроль обчислення t Taw . fs2=t2+u2, /5 =0,1038. Поправки в лінії t — = е =0,0000068; CD, = -е ■ St L Поправки у лінії записані в колонці 4 Контроль поправок виконується за формулою |
|
|
|
|
|
|
|
|
|
|
|
|
+212,421 |
+7835,154 |
0 |
-1262 |
1592644 |
|
|
|
|
|
|
|
|
|
|
|
|
|
+593,670 |
+8109,949 |
+424 |
-838 |
702244 |
|
|
|
|
|
|
|
|
|
|
|
|
|
+908,725 |
+8188,423 |
+790 |
-468 |
219024 |
|
|
|
|
|
|
|
|
|
|
|
|
|
+1302,206 |
+8341,099 |
+1203 |
-59 |
3481 |
|
|
|
|
|
|
|
|
|
|
|
|
|
+1517,550 |
+8465,308 |
+1451 |
+189 |
35721 |
|
|
|
|
|
|
|
|
|
|
|
|
|
+1707,924 |
+8547,972 |
+1659 |
+397 |
157609 |
|
|
|
|
|
|
|
|
|
|
|
|
|
+1851,213 |
+8610,320 |
+1815 |
+553 |
305809 |
|
304
10 |
11 |
12 |
13 |
14 |
15 |
+1973,426 |
+8674,802 |
+1953 |
+691 |
477481 |
Поправки в куги 0 0 W у. v,"pkHv Позначимо m'-o'JL; (o'=0,0051360. &] V* = ^ . Контроль: [V*] = 0. Поправки в диоекіїійні куги Контроль: кінцевий дирекційний кут не повинен отримати поправок. |
|
|
|
|
|
|
|
|
|
|
|
|
+2069,639 |
+8722,717 |
+2060 |
+799 |
638401 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2= +11356 +2
Х\= 1262
[£%]= 4132414
Суть
такого зрівноваження розглянемо на
прикладі багаторазової лінійної засічки
(рис. П.8.6).
Нехай 1, 2, 3 та 4 - вихідні пункти, тобто
пункти з відомими координатами
Рис.
11.8.6. До пояснення суті зрівноваження
лінійної
засічки параметричним
методом
305
Суть параметричного методу зрівноваження геодезичних мереж
Хі,
Yt.
Ці пункти не отримають поправок у
результаті зрівноваження. Для визначення
координат точки Р
виміряні довжини ліній dx,
d2,
d3,d4.
Відомі
також середні квадратичні похибки
вимірів цих ліній ті
(/=
1, 2, 3, 4). Кінцеве завдання - визначити
найімовірніші значення координат
пункту Р
(Xp,YP).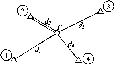
Під
час параметричного зрівноваження
параметрами зазвичай приймають саме
координати пунктів, які потрібно
визначити. Отже, у нас це
Зв’язок
виміряних віддалей з координатами
пункту
Таких
рівнянь відповідно до рис. ІІ.8.6
можна записати чотири. Оскільки невідомих
величин тільки дві
Потім
достатньо визначити середнє вагове з
них. Проте зрівноваження виконується
іншим способом: за двома довільними
лініями знаходять наближене значення
координат
У
загальному вигляді (під час зрівноваження
деякої кількості
де
Рівняння
системи (ІІ.8.70) називають
Далі
із системи (П.8.70) та (ІІ.8.71) знайдемо
формули для визначення поправок V,-:
d^KXi-Xpf+tf-Ypff2.
(ІІ.8.69)
^=ВД,72,...,^)
d2=F2(Tl,T2,...,Tt)
►
(ІІ.8.70)
(П.8.71)
(П.8.72)
306ХР
та Yp.
Проте
для визначення координат пункту Р
достатньо виміряти дві віддалі,
наприклад, di
та
d2.
Отже, в нашому прикладі два надлишкові
виміри d3
та
d4.Р
можна записати в такому вигляді:-ХР
та YP,
то задача має шість розв’язків. Справді,
можливі шість комбінацій по дві лінії.
Тому отримаємо по шість значень ХР
та YP.ХР
та YP,
а
потім визначають найімовірніші поправки
до наближених координат. Розглянемо
цей метод детальніше.t
параметрів)
вираз (ІІ.8.69) запишеться так:Tt
-
зрівноважені значення шуканих параметрів
(координат); dt-
зрівноважені
значення виміряних величин (у нашому
випадку ліній).параметричними
рівняннями зв’язку. Замінивши
зрівноважені значення dt
на
виміряні dt
з
шуканими поправками V,-,
матимемо: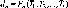
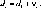
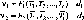
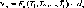
Рівняння
(П.8.72) називають
Для
розв’язання системи (ІІ.8.72) приведемо
функції
Тоді:
дЕ
дЕ
дЕ
Е{ТХ,Т2,...,Т()
= Е{Т{,Т^+ -87]
+
—LbT2
+
... + -*-87]. (ІІ.8.73)
37]
З
г,
37]
Позначимо
часткові похідні
Щ=п.Щ_
=
ь.
.&L
=
f 37]
"зг2
'’"’зт,
''
Тоді
отримаємо систему (ІІ.8.72) в лінійному
вигляді:
V,
=«/5Т] + 6,8Г2
Оскільки
відомі значення виміряних величин
параметрів
7)°, тобто відомі функції 7<](7]0,7^0,...,7]0)
то, останні два члени рівняння (ІІ.8.74)
приймемо як вільні члени:
/,.
=
Підставивши
вирази (П.8.74) та (П.8.75) в (П.8.72), одержимо
параметричні рівняння поправок у
лінійному вигляді:
Vj
=
aj87]
+
(П.8.76)
v„
=
а„87] +
307рівняннями
поправок у загальному вигляді. Задача
зрівноваження складається із знаходження
поправок V,-
(/
= 1, 2,...,п)
та параметрів Tj
(у'
= 1,2,Ft
до
лінійного вигляду, розклавши їх у ряд
Тейлора, обмежившись першими членами
розкладу. Це можливо, якщо попередньо
відомі наближені значення параметрівTj°.
У нашому прикладі, як уже відзначалося,
за наближені значення параметрів
ХР°,
Ур° можна прийняти значення координат,
визначені за однією парою виміряних
віддалей.
+ ... + ґ;87]
+ Fj
(7]°
,Т2°7]°
)-dt. (ІІ.8.74)dj
та
наближені значенняFj
(7]°,
Т2,
-, 7]° )-dt. (П.8.75)1\ЬТ2
+... + ґ,87] + /j
з
вагою 7]
v2
=
о287]
Ь2ЬТ2
+... + f287]
+
/2
з вагою Р2Ьп5Т2
+... + tnbTt
+
Іп
з вагою Рп
Як
відомо, істинна похибка вимірювання
Af
характеризується
тією самою вагою, що й результат
вимірювання, тільки поправка vf
=
-Д;,
тому можна вважати, що будь-яка
поправка V,-
в
системі рівнянь (П.8.76) має вагу, яка
дорівнює вазі відповідного виміру <7,,
який знаходять за формулою
де
(X
- середня
квадратична похибка одиниці ваги;
Проте
система (ІІ.8.76) має нескінченну множину
розв’язків, оскільки маємо
ф
= [А^2]
= Х^.(а,87’1
/=1
Для
визначення мінімуму функції Ф необхідно
знайти похідні цієї функції за всіма
аргументами V,-,
тобто за 8Гу,
та прирівняти їх до нуля.
Часткова
похідна функції Ф за першим параметром
дФ
3(87і)
м
1 (ІІ.8.79)
=
2 t(Piaia№
+РіаМТ2
+-..
+ PiaitibTl+Piaili)
= 0.
/=і
Звідси
отримаємо
t&PiWM
+
(£^А)8Г2
+.-
+ (iw,)87; +Іад,
=0. (ІІ.8.80)
і=1 /=1 і=1 /=1
Далі
визначимо часткову похідну функції Ф
за другим параметром ЬТ2
:
Дф п п п п
^гт
= (І^Л)87і +&РіЬіЬі)ЬТг
+... + (£РМЩ
+XW/
=0.(11-8-81)
0(0^2/ 1=1 м м /=і
За
аналогією знайдемо часткові похідні
за всіма параметрами 87),
та,
ввівши
позначення Гаусса, запишемо:
.D
[Раг^бТ^+[Pab]ST2
+...+1РаіЩ
+ [Pal]
=
О'
[РаЬЩ+[РЬЬ\ЗТ2
+ ...+[Pbt]ST,
+
[РЬІ]
= О
'-є
[Pat]8Tt
+[Pbt]8T2
+...+№1$
+[Ptl]
=
О
D'
(II.
8.82)
Система
(II.8.82) є системою нормальних рівнянь
розміром
308Pi=V?lm?
, (II.8.77)ті-
середня квадратична похибка результатів
вимірювання.п
рівнянь та («+/)
невідомих. Тому застосуємо принцип
найменших квадратів і позначимо+ЬІЬТ2
+ ... + (87; + ()2
. (11-8-78)ЬТХ
буде мати вигляд:=
^2РМЩ +ЬІЬТ2
+... + (8
Tt
+
/>,. =
txt,
симетричною
щодо діагоналі D
D'.
На цій діагоналі розташовані квадратичні
коефіцієнти, які завжди додатні.
Неквадратичні коефіцієнти розміщені
симетрично відносно головної діагоналі.
Розв’язавши
систему нормальних рівнянь (II.8.82),
знайдемо поправки 87) до попередніх
(наближених) значень шуканих параметрів
та отримаємо
зрівноважені
значення параметрів (координат). Потім
знайдені значення 87) підставимо в
систему рівнянь поправок (П.8.76). Визначимо
поправки у виміряні величини
Найпростішою
полігонометричною мережею є мережа із
трьох ходів, що сходяться в одну вузлову
точку. Раніше була розглянута висотна
мережа, яка також складалася із трьох
нівелірних ходів, що збігались в одну
вузлову точку. Проте раніше ми визначали
зрівноважене значення висоти вузлової
точки. У цьому випадку ми повинні
визначити зрівноважені значення
координат вузлової точки.
В
основу такого зрівноваження, як у разі
визначення висот, так і у разі визначення
координат вузлової точки чи дирекційних
кутів ліній, що виходять із цієї точки,
покладено ваги ходів. Проте зрівноваження
полігонометричних мереж має певні
особливості, й ми детально його
розглянемо.
Рис.
11.9.1. Схема полігонометричної мережі
із трьох ходів,
що збігаються в одну
вузлову точку
309dj
і,
нарешті, знайдемо зрівноважені значення
довжин di
за
(ІІ.8.71).Зрівноваження полігонометричних мереж
Зрівноваження полігонометричної мережі, що збігаються в одну вузлову точку

До
того ж зауважимо, що на виробництві
зрівноважують полігоно- метричні мережі
окремо (окремо кути, окремо прирости
координат), тобто використовують
наближені методи. Тільки для зрівноваження
окремих ходів застосовують строгі
методи. Якоюсь мірою це правильно,
оскільки координати вузлових точок
визначають як середні вагові, тобто як
зрівноважені.
Нехай
маємо полігонометричну мережу, зображену
на рис. ІІ.9.1. Формули для визначення
ваг дирекційних кутів та приростів
координат записані на рисунку.
Зрівноваження будемо виконувати у
такій послідовності:
Спочатку
визначимо середнє вагове значення
дирекційного кута однієї з ліній, що
виходить із вузлової точки
її
дирекційний кута^-^.
Ваги дирекційних кутів обернено
пропорційні
до
кількості кутів (у ході). Врахуємо, що
в ходах вимірювались ліві кути, і крім
того, для ходу 1
кількість кутів дорівнює
межуючий
кут цього ходу pj.
Для ходу 2 визначається не , a
(обернений
дирекційний кут); під час визначення останнім
вико
ристовується
кут Рз, ДЛЯ
ХОДУ 2
КІЛЬКІСТЬ
кутів
дорівнює КІЛЬКОСТІ
ЛІНІЙ «2
ЦЬОГО
ходу.
Для ходу 3 межуючим Є
сумарний
кут, ЩО
дорівнює
Рі + Р2
. Отже,
середнє
вагове значення дирекційного кута
а
(M-N)
+Ph
+%
Знайдемо
кутові нев’язки ходів
4-«("-*)
%
(ІІ.9.1)
(П.9.2)
Виміряні
кути Pf.
виправляються
поправками. Суми поправок у кути
будь-якого ходу повинні дорівнювати
нев’язці цього ходу, взятій з оберненим
знаком:
310
М.
Візьмемо лінію MN
і
визначатимемощ
+1
(пх
- кількість ліній цього ходу);cSM~N^
визначимо
за формулоюш-т
аім~',)Л+к2(м-">А+а3
Переходимо
до зрівноваження координат. Розглянемо
зрівноваження тільки абсцис. Зрівноваження
ординат виконується аналогічно.
Знайдемо середнє вагове значення
абсциси точки
Р1+Р2+
Р3
(ІІ.9.3)
Після
визначення
Розглянемо
такий спосіб на конкретному прикладі.
Припустимо, ми маємо мережу з п’яти
ходів, що створюють дві вузлові точки
Рис.
11.9.2. Полігонометрична мережа з п’яти
ходів,
що створюють дві вузлові точки
311М.
Ваги ходів обернено пропорційні до
довжини ходів.Хм
та YM
вузлової
точки мережа розділяється на три
незалежні ходи, які врівноважуються
окремо строгим або спрощеним методом.Зрівноваження полігонометричної мережі способом послідовних наближень
М
та N
(див.
рис. ІІ.9.2). Необхідно знайти ймовірні
координати точок М
та N
способом
послідовних наближень. Для стислості
будемо виконувати визначення тільки
*м
та XN
.
Ординати YM
та
Yn
знаходять
аналогічно. Припустимо, що Хм
та XN
вже
знайдені. Тоді для кожного ходу можна
скласти рівняння похибок. Цим рівнянням
припишемо ваги як величини, обернені
до довжини ходів.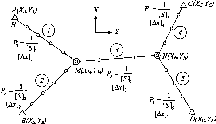
(ІІ.9.4)
XM-(xA-[bX\)
= V,
XM-(xB+[bX}2)
= V2
XM-{XN-[XX\)
=
V2P2.
xn-(xc-[ax]4)
= v4
xn-(xd+[ax]5)
= v5
Як
відомо, коли ці рівняння розв’язувати
за додаткової умови
[Раа\Хм
+{Раі} =
0
[.Pbb]XN
+[РЬІ]
=
0
(ІІ.9.5)
У
(ІІ.9.5) а, - коефіцієнти при першому
невідомому (при
Підставимо
в перше нормальне рівняння системи
(ІІ.9.5) значення а, та /(-
і запишемо це рівняння в розгорнутому
вигляді. Отримаємо:
РхХм-{ха-[ьх\)р,+р2хм-(хв+[ьх]2)р2
+ .
f
Розв’яжемо
(И.9.6) відносно невідомого
{*а
Рі+Р2+Рг
(ІІ.9.7)
Аналізуючи
(ІІ.9.7), зауважимо, що
XN
-
(Хс
-
(ДАТІ,) • Р,
+ {xD
+
[ддг]5)
• Ps
+
(+ [ДДГ],) ■ Р,
Рг+Р4+
Р5
(П.9.8)
312\PW\
= min,
то це приведе до нормальних рівнянь,
які у скороченому вигляді
при двох
невідомих (Xw
таXN)
запишуться так:Хм);
у рівняннях похибок (И.9.4), тобто at
=
1; своєю чергою, bt-
коефіцієнт
при другому невідомому (при XN);
у цих самих рівняннях похибок (ІІ.9.4) bt
=
1.
Відомі частини рівнянь похибок, взяті
в круглі дужки, позначені /,. Наприклад,
[хА
-
[АХ]х
) = lx,
Pt
-
ваги ходів.РгХм
-
(х^ - [ДХ]3)
• Р3
=
0. (ІІ.9.6)Xм.
Матимемо:~
[АХ],) • Рх
+ (Хв
+
[ДХ]2)
• Р2
+ (X* - [ДХ]3)
• />3Хм
знаходять як середнє вагове з трьох
ходів, які збігаються в одну вузлову
точку. Аналогічне рівняння ми вже
отримали раніше під час зрівноваження
мережі з однією вузловою точкою (рівняння
ІІ.9.3). Тому для знаходження ймовірної
абсциси точки N
-
XN
запишемо
аналогічно:
Розглядаючи
(ІІ.9.7) та (ІІ.9.8), бачимо, що в цих рівняннях
невідомі (тобто
Тоді,
розв’язавши (ІІ.9.7), знайдемо
Далі,
у рівняння (ІІ.9.8) підставимо
значення
абсцис в останньому
Аналогічно
знаходять кінцеві ординати цих точок
Розглянемо,
як урівноважуються цим методом
горизонтальні кути. Прирости координат
врівноважуються аналогічно.
Нехай
маємо мережу з п’яти ходів із двома
вузловими точками, показану на рис.
ІІ.9.3. Дужками на рисунку показано
горизонтальні кути.
На
вузлових точках
шукані
дирекційні кути яких позначені ос^ та
ос^.
В
усіх ходах мережі виміряні ліві кути,
якщо рухатися від вихідних тріангуляційних
пунктів (показаних на рисунку трикутниками)
у напрямку до вузлових точок
х«~ь=хс-\
*4,-
(ІІ.9.9)
(ІІ.9.10)
313Хм
та XN)
є
в лівій та у правій частинах. Тому ікне
безпосереднє розв’язання неможливе.
Але ці рівняння можна розв’язати
методом наближень (ітерації). Щоб знайти
значення абсциси цієї точки з першого
наближенняХт,
підставимо у (ІІ.9.7) замість невідомого
X
N
наближену
абсцису цієї точки, знайдену з ходу 4
(можна з ходу 5):Хш
-
значення абсциси точки М
з першого наближення.Хмх,
знайдемо Хт,
тобто визначимо Хт
з першого наближення. Маємо Хм{
та XNl
з
першого наближення. Переходимо до
другого наближення. Для обчислення Хм2
в (ІІ.9.7) підставляємо значення Хт,
а для обчислення XN2
підставляємо
в (И.9.8)Хд/2
• Достатньо 3-4 наближень. КолнХм.
=ХМ,
,, aXN.=XN/
тобто
колиі
-му наближенні такі самі, як і в
попередньому (/ -1)
наближенні, ітерацію зупиняють.YM
та
YN.
Після цього мережа розпадається на
п’ять незалежних ходів, кожний з яких
врівноважується, як звичайно.М
та N
вибрані
напрямки (М-М')
та (N-N'),М
або N.
Ваги ходів обчислені як величини,
обернені до кількості кутів у ходах:Зрівноваження полігонометричної мережі методом еквівалентної заміни
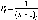
Рис.
11.9.3. До зрівноваження кутів мережі з
п'яти полігонометричних ходів,
що
сходяться у дві вузлові точки
Суми
виміряних кутів [р] також показані на
рисунку. Замінимо ходи 1 та
еквівалентним
ходом. За визначенням вага еквівалентного
ходу дорівнює сумі ваг ходів, які
замінені еквівалентним ходом:
Ри2=Рі+Р2. (П.9.11)
Під
час зрівноваження далі будемо
дотримуватися такої послідовності:
Визначимо
дирекційний кут лінії (
ходу
1,2:
а{м)
=-
а1,2
а
(м)
Рі+<АМ)
Р2
Рі+Р2
(ІІ.9.12)
У
(ІІ.9.12), оскільки виміряні ліві кути
(див. рисунок), то:
а\М)
=а, + [р], -180° (и
+1),;
а[М)
=<х2
+
[р]2
-180° (п
+1)2.
Знайдемо
кількість кутів в еквівалентному ході
1,2. Відповідно до (Н.9.10) маємо:
("+1)і2=тг- <п'913)
Знайдемо
значення дирекційного кута лінії
«!ЇЇ
=о$)
+[Р3]-180°
(я + 1)з . (П.9.14)
314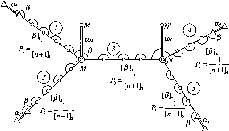
М-М')
з еквівалентного
(N
-
N')
з
трьох ходів, тобто з першого, другого
(точніше, з еквівалентного) та третього
ходу:
I % II |
(И.9.17) |
4 =4"» -«<*>. |
(ІІ.9.18) |
Підрахуємо
сумарну кутову нев’язку, що припадає
на еквівалентний
та третій ходи:
/ри,
Розділимо
цю нев’язку і підрахуємо окремо
нев’язки, що припадають на
еквівалентний
та третій ходи. Нев’язка /р123
припадає на кількість кутів
(я
+ l)j
2
+ (я +1)3.
Звідки неважко здогадатися, що:
/Ь=(„
+
,)і4"(„
+
і)з'("
+
1)и
•^Рі.2,3
4
“
(И
+ 1)і,2+("
+
1)3
(11.9.20)
(11.9.21)
Формула
(ІІ.9.21) визначає нев’язку у третьому
ході. Знаючи /р3,
кути
третього
ходу, можна зрівноважувати, вводячи
поправки у виміряні кути, як в окремому,
незалежному ході. Формула (ІІ.9.20) визначає
нев’язку еквівалентного ходу 1,
2.
Оскільки
завжди кутову нев’язку можна знайти,
як різницю між попереднім (наближеним)
значенням й остаточним (кінцевим)
значенням дирекційного кута, то для
еквівалентного ходу 1,
2
запишемо:
4
,2
-а<м)—(и)
1,2
ОТ
(ІІ.9.22)
315з=а,)2>3(л0-а(Л°. (ІІ.9.19)
(н
+ 1)
Розв’язуючи
рівняння (ІІ.9.22) щодо невідомого
(М-М')~
а(м):
Значення
визначаємо за (ІІ.9.20), а значення - за
формулою
(ІІ.9.12).
Праві члени формули (П.9.23) відомі. Отже,
за (П.9.23) знайдемо
Знайдемо,
нарешті, нев’язки в початкових ходах
1 та 2:
/р,
=а[м)-а{м). (ІІ.9.24)
=а2
У
результаті виконання дій задана мережа
розділена на п’ять незалежних ходів
з відомими кутовими нев’язками, кожний
з ходів врівноважується як незалежний.
Як
вже відзначалося, професор В.В. Попов
удосконалив наближений метод зрівноваження
порівнянням нев’язок суміжних полігонів.
Зрозуміло, що такий метод (метод порівняння
нев’язок) придатний як для зрівноваження
висотних, нівелірних мереж,
так і для зрівноваження теодолітних
та
полігонометричних
мереж. Удосконалення В.В. Попова привели
до створення ним строгих методів
зрівноваження геодезичних мереж. Метод
В.В. Попова дає змогу, насамперед,
підрахувати кількість кутів у ходах
межуючих полігонів. На рис. ІІ.9.4 показана
мережа з трьох полігонів. Хід
Справді,
два напрямки
316cSM\
отримаємо
формулу для обчислення кінцевого
значення дирекційного кута лініїaW=aW_/pi2. (ІІ.9.23)аім)
_ кіНцеве
значення дирекційного кута лінії М
— М'.
М)-«(М)- (ІІ.9.25)
Зрівноваження кутів полігонометричної мережі методом професора в. В. Попова
А-D
є
суміжним з першим та третім полігонами.
Виникає запитання: скільки у цьому ході
кутів? В.В. Попов міркував приблизно
так: кут створюється двома напрямками;
але кожна лінія ходу також має два
напрямки: прямий та зворотний. Кут при
точці А
в першому полігоні двома напрямками
входить в полігон І і, одночасно, одним
напрямком (напрямок AN)
в полігон III. Напрямок NA
-
другий напрямок цієї лінії. Отже,
напрямки AN
та
NA
також
можна розглядати як кут. Тому у суміжних
ходах стільки кутів, скільки ліній.AN
та
NA
створюють
один кут, а інші два напрямки -ND
та
DN
-
другий кут. Отже, в ході AD
два
суміжні кути, в ході BD
(абоDB)
один
- суміжний кут. У ході CD
(абоDC)
два
суміжні кути. Це,
вдавалося
б, просте міркування, дає змогу складати
нормальні рівняння корелат безпосередньо
на основі схеми мережі і виконати строге
зрівноваження кутів.
Рис.
11.9.4. Зрівноваження кутів мережі полігонів
полігонометріїметодом професора В. В.
Попова
Позначимо
+7
-Кг
+ 6К2-2К3-12'
= 0
►. (И.9.26)
Розв’язавши
цю систему, знайдемо корелати
1
2
3
Кут
Аналогічно,
у точці
1
2
2
2
2
1
317
корелати
- поправки в один кут першого полігона
Кх,
в один кут другого полігона К2,
третього полігона . Тоді можемо записати:Кх
- К2-
2К3
-30' = 0 '-2КХ
- 2К2
+ 6К3
+ 24' = 0Кх
= (+4М),
К2
= (+2), К3
= (-2). Зовнішні ходи отримають поправки,
відповідно, в першому полігоні (+4), у
другому - (+2), у третьому - (-2). Кут А
в полігоні І (два напрямки кута входять
в полігон І, одночасно один із цих
напрямків входить в полігон III) одержить
поправкуК,
--К,
=+4' + Ґ = +5'.А
у полігоні III:В.
Полігон І:
Полігон II:Кз
--Кг
=-2'-2'
= -4'. 3
2
1К,--К2=4'-1'
= +3'.К2 =+2'-2'
= 0'.
Так
само у точці С, полігон II:
К2--Кг=+2'
+ 1' = +3'.
Полігон
III:
2
Знайдемо
поправки у куги в точці
На
ланку
На
ланку DA
: К3-Кх
=-2'-4’ =
-6'.
Визначимо
поправки у куги при точці
На
ланку CD:
На
ланку
Залишається
знайти поправки на три кути при точці
D.
Кут
у точці D
у
полігоні І:
Кут
у точці D
у
полігоні II:
Кут
у точці D
у
полігоні III:
Контроль
правильності обчислення поправок: ] =
Нехай
маємо ту саму мережу з трьох полігонів.
У прямокутних рамках подано нев’язки
полігонів
Позначимо
,
ходу
відповідно для першого, другого та
третього полігонів. Аналогічно
(7)
4К(Х)
- к[Х)
-
0,%К(Х)
-
0,80 = 0
-к\Х)
+3,5К(Х)
-0,9к\Х)
+0,66 = 0
-0,8К{Х)
- 0,9
(ІІ.9.27)
318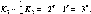
N.AD
: Кх-К3
= +4' + 2' = +6'.М.Кг-К2=-2'-2'
= -4'.DC: К2-К3=
+2' + 2"
= +4'.Кх
- ^К2
- ^Кг
=+4'-1'+1'=+4#.К2
-^К2
=
+2”-2*
+
Y =
+\”.К2
— Кх
-
-
jК2
= -2' — 2' -1' = -5#.-f^..
Зрівноваження приростів координат полігонометричних мереж методом професора в.В. Попова
fx
та
fY
у
метрах. У кружках подано довжини ходів
у кілометрах.К2Х^, -
поправки у прирости абсцис АХ
на 1 кмКх
’,(У)Щ
, Щ
-
поправки у прирости ординат Д7 також
на 1 км ходу. Складемо нормальні рівняння
корелат для зрівноваження приростів
АХК.[Х)
+ З, ОЛ:^ - 0,29 = 0
2,2
Рис.
11.9.5. Зрівноваження приростів координат
мережі полігонів
полігонометрії
способом професора В. В. Попова
Нормальні
рівняння корелат для зрівноваження
приростів A
4tffy)
- k[Y)
-
0,8K{Y)
+0,22
= 0
-k\Y)
+3,5К{¥)
-0,9K{Y)
-0,53 = 0
-0,8xjy)
- 0,9K{Y)
+
3,+ 0,32 = 0
(II.9.28)
Розв’язавши
системи рівнянь (ІІ.9.27) та (II.9.28), знайдемо
поправки
зовнішніх
ходів мережі. Поправки у прирости
координат на окремі ходи обчислюють у
відомості (табл. ІІ.9.1). У цій відомості
подані буквені вирази для визначення
поправок на окремі ланки (ходи), з яких
складаються полігони.
У
відомості позначено відповідно
(ланок)
Контроль
правильності введення поправок у
прирости координат виконується за
сумами поправок в окремі ходи, що
створюють полігони: суми цих поправок
повинні дорівнювати відповідним
нев’язкам fx
та
цих
полігонів,
взятих з оберненими знаками.
319
Y
будуть
відрізнятися тільки вільними членами
та позначеннями корелатк\Х^, ,
К^
та , К^у
прирости абсцис та ординат на 1
кмщ
, п2,
пг
-
довжини зовнішніх ходівАВ,
ВС
та СА
у кілометрах; nx>3,
n21,
щ
2
~
довжини суміжних ланокAD,
BD,
CD
в
кілометрах. У стовпчики 2 і 3 вписують
числові значення поправок у метрах.
Назва ланок |
Поправки на |
Буквені вирази поправок |
||
ХДАГ |
ХА
|
на ХАХ |
на
|
|
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
"з, |
|
Раніше,
під час попереднього опрацювання
результатів польових вимірювань,
ми виконували оцінку точності лінійних
та кутових вимірювань полігонометрії
за нев’язками, тобто за результатами
польових робіт. Проте достовірнішою є
оцінка точності кутових та лінійних
вимірювань за результатами
зрівноваження на основі поправок у
кути Fp.
та
лінії
Для
оцінки точності зрівноважених кутів
та ліній скористаємося узагальненою
формулою Бесселя. Для кутів:
Для
ліній:
тир
=1
v*v*
n-k
PsvsySi
n-k
(II.9.29)
(II.9.30)
де
320Оцінка точності полігонометричних ходів та мереж за результатами зрівноваження
Vs.n
— кількість
усіх ходів; k-
кількість
вузлових точок. Різниця (п-к)
дає кількість надлишкових вимірювань
у мережі. При цьому, як відомо, кути
вважаються
рівноточними, а лінії - нерівноточними.
Ваги ліній можна визначити за формулою
якщо
похибки
Оцінку
точності результатів вимірювань за
результатами зрівноваження вважають
надійнішою, тому що на таку оцінку
впливають як випадкові, так і систематичні
похибки вимірювань, тоді як на нев’язки,
отримані за результатами польових
вимірювань, часто не впливають або
менше впливають деякі систематичні
похибки, характерні для усього масиву
кутових та лінійних вимірювань.
Р
=
с
ms
(ІІ.9.31)
321ms
відомі.
В іншому разі для визначення ваг
оцінюваних величин необхідно кожну
з них подавати у вигляді функції
результатів вимірюванняT
= f(dl,d2,...,dn).
Тоді
вагу Р(
знайдемо за відомою формулою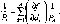
РОЗДІЛ
III.
ПРОСТОРОВІ
СУПУТНИКОВІ МЕРЕЖІ
(ОСНОВИ СУПУТНИКОВОЇ
ГЕОДЕЗІЇ)
Більшість
високоточних приладів наземної геодезії
(теодоліти, нівеліри, світловіддалеміри,
тахеометри тощо) удосконалені завдяки
вдалим технічним рішенням та продуманим
технологіям їхнього використання.
Проте майже всі вони використовують
оптичний діапазон електромагнітних
хвиль.
Це,
по-перше, спричинило певні недоліки,
наприклад: необхідність під час
вимірювання не тільки прямої
(геометричної), але й оптичної видимості
між пунктами; певні складності цілодобових
спостережень; неможливість безперервних
моніторингових спостережень та багато
інших.
Другою
особливістю традиційного геодезичного
вимірювання є значне поширення
вимірювання кутів, хоча сучасні
світловіддалеміри забезпечують вищий
рівень точності. Крім того, наземне
вимірювання виконується у прошарках
високодинамічної атмосфери, що істотно
ускладнює вимірювання і знижує
потенціальний рівень точності.
Альтернативний
підхід до геодезичного вимірювання на
принципово іншій основі проявився у
застосуванні просторових методів
вимірювань із використанням миттєвого
положення штучних супутників Землі як
точок із відомими координатами. Засновані
на такому принципі вимірювальні
комплекси отримали назву
Проте
подальші дослідження показали, що
завдяки приладному та програмному
забезпеченню такі системи можуть бути
використані для розв’язання широкого
кола геодезичних задач та різко підвищити
продуктивність та точність вимірювань.
Під
час вибору найефективнішого діапазону
електромагнітних хвиль враховувалось
те, що ці системи повинні забезпечити
виконання вимірювання під час будь-яких
погодних умов. Дослідженнями встановлено,
що саме таким є ультракороткий діапазон
радіохвиль.
Ще
одна особливість супутникових
віддалемірних систем - те, що вони
повинні уможливити одночасне забезпечення
вимірювання віддалі між незнач-
322Будова та принцип роботи геодезичних супутникових систем
Принцип роботи систем визначення просторового положення точок
глобальних
систем позиціонування,
початковим призначенням яких було
розв’язання навігаційних задач.
> |
|
Приймач |
|
ж
т ; ~
Місцевий
високочастотний генератор
Рис.
III.
1.1.
Спрощена функціональна схема
віддалеміра,
що працює на односторонньому
принципі
Формула
(III. 1.1) аналогічна до відомої нам формули
імпульсних наземних світловіддалемірів:
Множник
у (ІІІЛ. 1) відсутній, оскільки сигнал
проходить віддаль
323Вимірювальний пристрій
S
= ^c-т. (III.
1.2)S
один
раз. Оскільки ЕМХ за одну наносекунду
(1нс = 110-9с)
проходять
віддаль
близько ЗО см, то для забезпечення
сантиметрового рівня точності необхідно
синхронізувати годинники на супутнику
та на приймачу до сотих часток наносекунди.
Але сучасний рівень техніки поки що не
дає змоги цього зробити. Тому необхідно
враховувати асинхронність цих годинників,
що ускладнює розв’язання задачі і
вимагає одночасного вимірювання
віддалей від точки на поверхні Землі
(координати якої визначаються) до
чотирьох супутників, як мінімум.
Зауважимо, що
Вимірювання
супутникової геодезії ґрунтується
переважно на використанні глобальної
позиційної системи GPS
(Global Positioning System), що
останнім часом широко застосовується
в усіх видах геодезичних робіт. Менш
відомою є система ГЛОНАСС, запропонована
Росією.
Супутникова
геодезія зарекомендувала себе цілою
низкою кардинальних переваг перед
наземною геодезією. Найважливіші з
них:
зникла
необхідність будувати зовнішні
геодезичні знаки;
з’явилася
можливість об’єднати планові і висотні
пункти геодезичних мереж, оскільки
система GPS
дає
одночасно просторове положення цих
пунктів;
значно
коротший час, необхідний для отримання
кінцевих результатів;
можливість
повнішої автоматизації вимірювання;
значне
зменшення вартості робіт.
GPS-вимірювання
використовують не тільки для встановлення
положення пунктів геодезичної основи,
топографічного та кадастрового знімання,
інженерної геодезії, але й в геодинамічних
дослідженнях, для визначення таких
важливих параметрів геодинаміки, як
рухи полюсів нашої планети, стабільності
обертових рухів Землі та інших параметрів.
Усе
вищесказане та, особливо, висока точність
GPS-вимірювання
є причиною того, що “Основні положення
створення державної геодезичної
мережі”, затверджені Постановою
Кабінету Міністрів України від 8
червня 1998 р. № 8441, передбачають створення
нових та оновлення наявних мереж
сучасними радіонавії'аційними системами
(GPS)
та
комп’ютерними технологіями. Допускається
застосування традиційних геодезичних
методів. Проте традиційні методи вже
нездатні конкурувати з методами
космічної геодезії. Щоправда, поки що
таку конкуренцію витримує високоточне
геометричне нівелювання, яке, до того
ж, ще необхідне для визначення геоїда.
324віддалі,
виміряні
без урахування синхронізації
годинників, називають псевдовіддалями.
Глобальна
позиційна система GPS
спроектована
і сконструйована міністерством оборони
США. Уряд США витратив понад 12 мільярдів
доларів на створення системи і продовжує
витрачати кошти на її розвиток і
підтримання в робочому стані. Повна
назва системи - Navigation
System with Time and Raining, Global Position System. Виділені
потовщенням літери утворюють скорочену
назву системи NAVSTAR/GPS.
У
перекладі ця назва означає: навігаційна
система часу і віддалей, глобальна
система визначення місцезнаходження.
У Радянському Союзі була створена
система ГЛОНАСС (глобальна навігаційна
система супутників), початкова назва
проекту “Ураган”. Саме ці дві системи
уже застосовуються в геодезії. Крім
цього, Європейське співтовариство
створює свою навігаційну систему
GALLILEO.
Оскільки
GPS-система
створювалась передусім як військова,
вона стійка, надійна і несприйнятлива
до природних та штучних перешкод. До
складу системи входять:
Навігаційні
супутники.
Наземний
комплекс керування.
Апаратура
користувачів.
Отже,
GPS
поділяється
на три блоки, які найчастіше називають
Космічний
сегмент.
Повністю розвинутий космічний сегмент
спроможний забезпечити у глобальному
масштабі можливість одночасного
спостереження від чотирьох до восьми
супутників для кутів відсікання понад
15 градусів. Якщо цей мінімальний
вертикальний кут між горизонтом і
напрямком на супутник зменшити до
10
градусів, тоді час від часу в полі зору
буде до 10
супутників,
а за умови зменшення цього кута далі
до 5 градусів кількість видимих супутників
інколи може сягати 12. Для цього космічні
апарати розташовуються на орбітах,
близьких до кругових, з висотою над
поверхнею Землі близько 20200 км та
періодом обертання приблизно 12 зоряних
(сидеричних) годин. Спочатку було
заплановано здійснити запуск 24
супутників, які б обертались в трьох
орбітальних площинах, нахилених під
кутом 63° до екватора.
Пізніше
космічний сегмент був скорочений до
18 супутників, які розташовувались
по три на кожній із шести орбітальних
площин. Згодом довелось відмовитись
від цієї скороченої конфігурації,
оскільки вона не забезпечувала можливості
цілодобового неперервного використання
системи в будь-якій точці на поверхні
Землі. Приблизно в 1986 р. кількість ШСЗ
була збільшена до 21,
325Найважливіші відомості про будову глобальних навігаційних систем
сегментами.
також
по три супутники на кожній із шести
орбітальних площин та три запасні
супутники. Запасні супутники призначені
для заміни зіпсованих “неактивних”
супутників. Сьогодні планується
конфігурація, що складатиметься з 24
діючих супутників, розташованих на
шести орбітальних площинах, нахилених
до площини екватора під кутом 55°, по
чотири в кожній. Крім того, для оперативної
заміни ще чотири запасні супутники є
на Землі. Супутники виводяться дуже
точно на свої орбіти відповідно до
генерального цлану розгортання системи
і, оскільки на висоті 20200
кілометрів атмосферне гальмування
практично відсутнє, залишаються на них
протягом тривалого часу. Орбіти відомі
заздалегідь, а у пам’яті комп’ютера
кожного приймача є “альманах”,
тобто своєрідний довідник, що постійно
оновлюється, з якого видно, де буде
кожний супутник у будь-який момент
часу.
Космічні
апарати GPS
фактично
слугують платформами для встановлення
транссенсорів (приймачів-передавачів),
атомного годинника, комп’ютера та
іншого устаткування, необхідного для
роботи системи. Це електронне обладнання
дає користувачу змогу своїм приймачем
вимірювати відстань до супутника. Крім
того, кожен спостерігач, завдяки
інформаційному повідомленню про
орбіти, яке кодується в сигналі із
супутника, може визначити просторові
координати
Допоміжне
обладнання кожного супутника складається
із двох сонячних батарей площею 7 м2,
які забезпечують електричне живлення,
та системи реактивних двигунів, потрібних
для корекції орбіти та керування
орієнтацією космічного апарата у
просторі.
Супутники
мають різноманітні системи ідентифікації,
а саме: за номером запуску, за присвоєним
кожному апарату окремим псевдошумовим
кодом (PRN),
за
номером позиції на орбіті, за номером
у каталозі НАСА, за міжнародною
класифікацією. Для того, щоб уникнути
можливих непорозумінь та зберегти
відповідність змісту навігаційного
повідомлення із супутника, ми
використовуємо, як правило, Номер PRN.
Нині
створено п’ять типів супутників GPS.
їх
розділяють на класи: Block
I, Block II,
Block
ПА,
Block
IIR, та
Block
IIF. Конфігурація
супутників типу Block
І
дещо відрізняється від конфігурації
супутників Block
II,
оскільки кут нахилу їхньої орбітальної
площини до екваторіальної дорівнює
55°, тоді як до попереднього покоління
він становив 63°. Крім кута нахилу орбіти,
існує ще одна істотна відмінність між
супутниками Block
І
та Block
II,
пов’язана з національною безпекою
СІЛА. Сигнали супутників Block
І
могли вільно
326ps
супутника
у довільний момент часу. Спираючись на
ці дві можливості та на метод просторових
засічок, користувачі можуть визначити
свої координати на поверхні або поблизу
Землі.
реєструватись
цивільними користувачами, а доступ до
інформації з ШСЗ наступного покоління
Block
II
став обмеженим.
Супутники
типу Block
II
були призначені для забезпечення першої
версії повної уніфікованої системи
GPS
(тобто
21 активного та трьох запасних супутників).
Перший із супутників типу Block
II
коштував приблизно 50 млн. доларів США
і важив більше ніж 1500 кг. Його запуск
здійснено 14 лютого 1989 р за допомогою
ракети “Дельта II” яка стартувала з
космодрому ім. Кеннеді, що на мисі
Канаверал у штаті Флорида. Сьогодні
середня тривалість функціональної
здатності супутників цього типу
становить шість років, хоча метою
проекту було досягти семи з половиною
років. Деякі із супутників можуть
справно працювати навіть до десяти
років, тому що їхні основні модулі
функціонують упродовж такого часу.
Супутники
наступного покоління, які названо Block
IIF (від
слова follow
on -
наступний), будуть запускатись у період
від 2001 до 2010 р. Ці супутники обладнуються
удосконаленим устаткуванням для
автономної навігації, наприклад,
інерціальними системами навігації.
Планується
збільшити термін роботи супутника
Block
IIF до
14-15 років, а також увести в склад сигналів
додаткову частоту L5,
яка
дорівнює 1176,45 МГц, що істотно полегшить
визначення неоднозначності, характерне
для фазового вимірювання.
Розгортання
Російської системи ГЛОНАСС також
проходить поетапно. Перший супутник
системи (із назвою Космос 1413) був
запущений 12 жовтня 1982 р. До кінця 1998 р.
було запущено 74 супутники, більшість
з яких уже виведені з експлуатації. У
лютому 2000 р. залишилось 8
супутників.
За
проектними даними у сузір’я супутників
ГЛОНАСС повинні також входити 24
супутники, розташовані на трьох
орбітальних площинах, нахил яких щодо
площини екватора дорівнює 64,8°. Номінальна
висота кругової орбіти над земною
поверхнею становить 19100 км, період
обертання навколо Землі 11 год 15 хв 44 с.
Загальна маса супутника 1415 кг. Планується
підвищити стабільність частоти
генераторів, точність визначення
ефемерид супутників та їхній прогноз,
а також продовжити термін функціонування
супутників. Проект запуску 24 супутників
системи ГЛОНАСС здійснено в Росії
важкими ракетами “Протон”.
Технічні
параметри системи NAVSTAR/GPS
та
ГЛОНАСС є різними. Істотною відмінністю
цих систем є те, що в системі GPS
усі
супутники випромінюють коливання
однакових частот, а в системі ГЛОНАСС
кожен супутник випромінює свою частоту.
Вивчається можливість одночасного
використання обох систем для визначення
положення наземних пунктів. Такі
дослідження дуже важливі, оскільки
дають змогу використати для визначення
327
пунктів
більшу кількість супутників (в обох
системах понад сорок ШСЗ), не кажучи
вже про те, що сигнали ГЛОНАСС не
спотворюються і тому ця система дає
змогу отримувати вишу точність.
Країни
Європейського Союзу, як уже зазначалось,
планують створити свою, незалежну від
США, глобальну навігаційну систему.
Принцип
визначення положення наземних пунктів
за допомогою глобальних систем описано
у п. II. 1.1.
У
США для заміни супутників, які припинили
функціонувати, починаючи з 1995 р. виводять
на орбіти нові супутники кораблями
“Шатл”. Хронометрами (основними
генераторами) таких супутників є водневі
лазери, стабілізація частот яких на
порядок вища, ніж генераторів попередніх
супутників, і становить 10‘13.
До того ж ці супутники мають засоби
міжсупутникового зв’язку, які, завдяки
обміну даними між супутниками та
вимірюванню віддалей між ними, здійснюють
автономне уточнення параметрів орбіт
та автономну синхронізацію годинників.
Передавачі
всіх супутників безперервно випромінюють
коливання двох частот. Частоти модельовані
кодами. Крім вимірювальних сигналів,
передавачі передають інформацію про
свою орбіту, а також про стан інших
супутників системи і параметри їхніх
орбіт. Супутники мають також приймачі,
які приймають сигнали від основної
станції сегмента керування. Ці сигнали
містять інформацію про орбіту супутників.
Траєкторії супутників можна коригувати
з основної наземної станції керування.
Сегмент
керування.
Сегмент являє собою мережу наземних
станцій спостереження за ШСЗ і центрів
оброблення інформації. Головним
завданням сегмента є стеження за
супутниками з метою визначення траєкторій
ШСЗ та похибок годинників на їхньому
борту. Крім того, через систему керування
здійснюється синхронізація годинників
та оновлення даних.
Цей
сегмент складається з:
головного
центра керування MCS
(Master Control Station), розміщеного
у місті Colorado
Springs;
основної
станції керування GPS
(Ground Control Station), що
розташована на Г авайських островах;
трьох
стаціонарних станцій контролю (Monitor
Station). Вони
розміщені на островах Вознесіння
(Ascension)
у
північній частині Атлантичного океану,
Дієго-Гарсія в Індійському океані та
Кваджалейн у північній частині Тихого
океану;
рухомих
контрольних станцій.
328
Як
бачимо, станції сегмента керування
розташовані на великих віддалях одна
від одної. Вони безперервно приймають
коливання, які випромінюють супутники,
що розміщені в одній півкулі зі станцією.
Віддалі від станцій до супутників
визначають через півтора секундні
інтервали часу. Віддалі усереднюються
для інтервалів часу 15 хв. Крім того, на
станціях керування виконуються
метеорологічні зондування атмосфери
по вертикалі з метою визначення поправок
за тропосферу. Результати опрацювання
сигналів супутників та вертикального
зондування із контрольних станцій
передаються до головного центра
керування. Тут обчислюють ефемериди
орбіт супутників та рівняння їхніх
хронометрів (генераторів ШСЗ) на 12 годин
наперед. Ці дані передаються на ШСЗ, а
вони, своєю чергою, пересилають їх
користувачам, точніше - на наземні
приймачі користувачів системи GPS.
Військово-
картографічному агентству США
підпорядковано ще п’ять станцій
стеження, дані яких використовують для
обчислення високоточних ефемерид
супутників. Крім вищеописаних станцій,
на Землі ще працюють приватні станції
стеження за ШСЗ. Ці станції не керують
роботою супутників, а виконують уточнення
параметрів їхніх орбіт та рівнянь
хронометрів (генераторів) супутників.
Сегмент
користувача.
Це власники приймачів сигналів ШСЗ,
програмного забезпечення та комп’ютерів.
Кількість приймачів системи є необмеженою,
оскільки вони пасивні.
Для
геодезичних вимірювань кожний споживач
повинен мати мінімум два приймачі з
антенами, комп’ютер та програмне
забезпечення для відповідних геодезичних
робіт.
Приймачі,
які використовують геодезисти,
виготовляють декілька фірм. Найвідоміші
з них: Trimble,
Ashtech (США),
Leica
(Швейцарія),
Sercel
(Франція),
Sokkia
(Японія).
Кожна з фірм виготовляє декілька
моделей, різних за точністю та ціною.
Усі приймачі за кількістю частот, на
яких вони здатні працювати, поділяють
на дві великі групи:
одночастотні;
двочастотні.
Із
назв цих приймачів зрозуміло, що перші
приймають від супутників тільки одну
частоту, а другі - дві частоти. Останні
забезпечують більшу точність, тому
що приймання двох частот дає змогу
враховувати вплив іоносфери.
Будова
приймачів, методика спостережень та
опрацювання результатів спостережень
увесь час удосконалюються, а точність
визначення положення пунктів на поверхні
Землі підвищується. Найточніші способи
визначення положення спочатку були
призначені тільки для військових цілей.
329
Сегмент
користувача являє собою множину
GPS-приймачів.
За способом вимірювання віддалей
GPS-приймачі
радіосигналів із супутника можна
розділити на такі групи:
С/А-кодові
з використанням псевдовіддалей;
С/А-кодові
з вимірюванням фази передавальної
хвилі;
Р-кодові
з вимірюванням фази передавальної
хвилі;
Y-кодові
з вимірюванням фази передавальної
хвилі.
За
великої різноманітності приймачів на
сучасному ринку доцільно описати
їхні основні типи, а також принципи
побудови, переваги і недоліки.
За
можливостями одночасного приймання
сигналів приймачі можна також розділити
на дві великі групи.
До
першої входять приймачі, які працюють
за принципом послідовного, тобто
почергового стеження за супутниками
робочого сузір’я.
У
другій - ті, які відстежують чотири або
більше супутників одночасно, тобто
паралельно. Усередині кожної із цих
груп є велика різноманітність приймачів
різного призначення.
Одночастотні
приймачі з малим енергоспоживанням.
Ці пристрої проектуються як портативні
і тому зазвичай працюють на батарейках.
Для обмеження споживання енергії вони
виконують визначення координат один
раз на хвилину і потім самостійно
вимикаються до наступного визначення.
Для
індивідуального використання туристами
або під час плавання на невеликих суднах
такі приймачі є найкращим компасом.
їхня точність здебільшого вища, ніж
точність системи Loran,
і
працюють вони в будь-якій точці земної
кулі.
їхні
основні недоліки - це низька, порівняно
з іншими приймачами, точність,
обмежені інтерфейсні можливості і
грубе вимірювання швидкості руху.
Одночастотні
приймачі.
Ці пристрої також використовують один
канал для вимірювання віддалей до всіх
супутників робочого сузір’я, але вони
не обмежені за енергоспоживанням.
Звичайний одноканальний приймач може
залишатися увімкненим постійно і, отже,
бути точнішим, а також вимірювати
швидкість із достатньою точністю
принаймні доти, доки немає значних
прискорень або різких змін курсу.
Оскільки єдиний канал використовується
і для приймання сигналів декількох
супутників, і для обчислень віддалей,
такі приймачі не можуть застосовуватися
для безперервного визначення
місцеположення.
Швидкодіючі
мультиплексні одночастотні приймачі.
Цей варіант дуже подібний на звичайні
одночастотні приймачі, але в них
перемикання від супутника до супутника
відбувається набагато швидше. Настільки,
що виявляється можливим практично
одночасно і виконувати вимірювання
віддалей, і
330
стежити
за сигналами супутників, тобто працювати
у безперервному режимі. Приймачі цього
варіанта менш чутливі до неточності
ходу годинника.
Двочастотні
приймачі послідовного типу.
Наявність другого каналу значно розширяє
можливості GPS-приймача.
По-перше, вдвічі покращується відношення
сигнал/шум системи. Своєю чергою, це
означає, що з’являється можливість
уловлювати супутникові сигнали під
час несприятливіших умов і відстежувати
супутники, що розміщені ближче до
горизонту. Оскільки один канал може
бути використаний тільки для опрацювання
інформації про координати положення,
а другий - тільки для пошуку і приймання
сигналів чергового супутника,
двоканальний приймач не перериває
вимірювань та обчислень.
Самі
визначення координат і швидкості можуть
бути точнішими, оскільки у доброму
двоканальному приймачі використовуються
обчислювальні алгоритми, що виключають
вплив неточності ходу його годинника.
Недоліком
двоканального варіанта є те, що його
використання є дорожчим і приймач буде
споживати велику потужність.
Приймачі
паралельного (безперервного) стеження.
Приймачі, які відсте- жують чотири або
більше супутників одночасно, можуть
відображати миттєве положення і
швидкість. Це дуже цінно у разі
застосування на високодинамічних
об’єктах і під час високоточних
вимірювань. Ці пристрої часто
використовуються в геодезії і для
наукових цілей. Вони можуть мати від 4
до 10, 12 і навіть до 24 каналів стеження.
Крім
очевидної переваги - безперервного
вимірювання координат положення і
швидкості, ці багатоканальні приймачі
можуть також спростити проблему з
Для
чотириканального приймача відношення
сигнал/шум удвічі вище, ніж для
двоканального, і в чотири рази вище ніж
для одноканального. Крім того, здійснюючи
взаємну відносну синхронізацію каналів,
можна усунути будь-які міжканальні
тимчасові зсуви, які могли б вплинути
на точність визначення місцеположення.
Недоліком
цього типу систем є збільшення їхніх
розмірів, вартості і споживаної
потужності.
Сучасні,
довершеніші приймачі, обробляючи
основні супутникові дані складними
методами, видають значно більшу кількість
інформації і подають її наочнішим
відображенням на дисплеях із високою
роздільною здатністю, наприклад,
накладаючи на електронні цифрові карти.
331GDOP.
Замість того, щоб виконувати обчислення
на основі сигналів чотирьох у найкращий
спосіб розташованих супутників, деякі
із цих систем обробляють спільно сигнали
всіх видимих у певний момент супутників.
Застосування до цієї надлишкової
інформації відповідних алгоритмів
оброблення дає змогу мінімізувати
помилки визначення місцезнаходження
GDOP.
Отже,
хоча усі приймачі і сприймають одні і
ті самі дані GPS,
використовують
вони їх по-різному.
Успішний
запуск перших штучних супутників Землі
та спостереження за супутниками виявили
високу стабільність параметрів орбіт
супутників, що дає змогу доволі точно
обчислити положення супутника на
будь-який момент часу.
Саме
цей факт підштовхнув учених до
незвичайної, революційної ідеї:
використати
штучні супутники як носії вихідних
координат, за якими визначаються
положення точок на поверхні Землі.
Досі
було навпаки: такими носіями відомих
(вихідних) координат слугували тільки
пункти, жорстко закріплені на земній
поверхні або на спорудах, жорстко
скріплених із земною поверхнею, а
положення супутників визначалось
системою координат із початком на
поверхні Землі або в центрі її мас.
Якщо
згадати, що планета Земля також перебуває
в безперервному русі в космічному
просторі, то ідея передавання функції
носіїв координат супутником стає
правомірною.
Ідея
передавання ролі носіїв координат
супутникам докорінно змінила засади
космічної геодезії. За цією ідеєю,
названою революційною, положення
пунктів на земній поверхні стосовно
рухомих супутників можна визначити
методами просторових кутових або
лінійних засічок. Тому потрібно точно
знати моменти часу, в які виконуються
вимірювання. Тільки конкретний момент
часу положення супутників є однозначним.
Тому однозначним у цю мить є і розташування
наземних пунктів стосовно супутників.
Як
відомо з II. 1.1, GPS-визначення
ґрунтуються на вимірюванні відстані
від супутникового приймача, розташованого
на поверхні Землі, до супутника. ШСЗ
безперервно випромінюють радіохвилі.
Приймачі, встановлені на земній поверхні,
приймають ці коливання і вимірюють
такі параметри, які дають змогу однозначно
встановити напрямки на супутники або
віддалі до них. Проте віддалі вимірюються
точніше, тому сучасні супутникові
системи є відцалемір- ними. Вимірювання
віддалей виконується одночасно кодовим
та фазовим методами.
Кодові
визначення.
Під час вимірювань за допомогою
супутникових систем на передавальному
кінці вимірюваної лінії (на супутнику)
формується відповідний кодовий сигнал,
а на приймальному кінці лінії (у наземному
приймачі) має бути сформований опорний
сигнал відгуку, який обов’язково є
332
Основи теорії визначення положення пунктів глобальними супутниковими системами
аналогічним
до кодового сигналу. Ці коди в
передавальному та приймальному пристроях
повинні бути створені синхронно.
Код,
що із сигналами супутника досягає
приймача, є зсунутим у часі відносно
коду, створеного приймачем. Це так звана
Знаючи
SMai=c-xMM. (ІП.1.3)
Проте
(ІІІ.1.3) потребує уточнення. Річ у тім,
що супутник і наземний приймач повинні
створювати коди в еталонний для GPS
системи
час. Позначимо зсув показу годинника
передавача (супутника) відносно
еталонного часу
час
поширення ЕМХ може бути описано таким
співвідношенням:
де
ронністю
ходу годинників на супутнику та наземному
приймачі. Якщо ми будемо користуватись
виміряним часом
^вим
~ с
‘ ^вим
” С іст Sіст ^
де
Поправковий
член
333репліка
коду.
Цей зсув хвим
є
мірою часу, за який сигнал із супутника
досягає антени приймача і є пропорційним
до віддалі супутник-Земля. У приймачі
відбувається порівняння двох кодів, а
точніше, виконується кореляційний
аналіз, на основі якого визначається
час хвим
проходження сигналу від супутника до
приймача.хвим
, можна знайти виміряну довжину SeuM
за
формулоюЬ,пер
,
а відповідний зсув показу годинника
приймача 5,^ . Зареєстрований%им
= (t„p
+
Ь1пр
) - (tnep
+
Ь'пер
) = хіст
+ 6т, (III.
1.4)хвим
- час проходження сигналу за годинниками
передавача та приймача; tnep
та
tnp
-
моменти часу випромінювання та приймання
інформаційного сигналу щодо показу
еталонного годинника GPS;
хіст
=tnp
-tnep-
істинний
час проходження сигналом віддалі; 8Т
= 8, -
8, -
поправка, викликана несинх-хвим,
тоді значення виміряної віддалі SeuM
визначиться
з виразуSicm
-
геометрична (істинна) віддаль, яка нас
цікавить, дійсна віддаль між супутником
та приймачем. Цю віддаль Sicm
ми
зможемо визначити тільки якщо будемо
знати 8Т
- несинхронність ходу годинників на
супутнику та приймальній станції.cbx
(III.
1.5) залежить від стабільності ходу
годинників на віддалених у просторі
пунктах і може сягати значних величин
- декілька сотень метрів і більше. Така
істотна відмінність між SeUM
та
Sicm
зумовила
введення
поняття
Розглянемо
визначення
1,6
109
/
SeuM=N-X;N
= ^-;N
= f-
хвим.
За
1 секунду кількість коливань / = 1,6 ГГц,
а за 0,07 с кількість коливань становитиме
Як
бачимо, кількість коливань
Кожний
супутник формує свій псевдовипадковий
двійковий код (0; 1), один зразок якого
має тривалість (відрізок часу від
початку випромінювання коду до кінця),
дещо більшу від 0,07 с, тобто більший за
час подолання радіохвилями віддалі
від супутника до наземного приймача.
Цей зразок безперервно повторюється
і змішується з коливаннями, які випромінює
супутник.
Код
має значно меншу частоту, ніж коливання,
які випромінює передавач ШСЗ. Але код
і коливання є синхронними, тому що і
код, і коливання формуються з коливань,
які випромійює основний гейератор
супутника. У приймачі створюється код,
аналогічний до того, що створюється в
супутнику; це так звана
Частоту
коду вибирають такою, щоб час
334псевдовіддалі.
Це поняття найчастіше асоціюється саме
з кодовими методами відцалемірного
вимірювання.івим
та SeuM
-
псевдовіддалей кодовим методом
детальніше. Оскільки швидкість світла
у вакуумі с
= 299792458 м/с, а супутники літають на висоті
= 20000
км, то час проходження коливань %
приблизно
дорівнює 0,07 с. Частота коливань, які
випромінює супутник, дорівнює наближено
/ = 1,6 Гц, отже, період Т
становить:Т
= —^Ц-
;7’ = 6,25 10~10сД
= 18,7 си;Х
= — = сТ;N
-
кількість хвиль, що вкладається у
віддаль SeUM
.N=
/
0,07 =1,6ГТц 0,07 = 0,1-Ю8.N
значна,
перевищує 100 мільйонів. Саме для
наближеного визначення N
використовують
кодові вимірювання.репліка
коду.
Порівнюючи між собою код, прийнятий
від супутника, з кодом, створеним у
приймачі (точніше, виконуючи їхній
кореляційний аналіз), як це показано
на рис. III. 1.2,
визначають проміжок часу тв1ш,
за який коливання долають віддаль SeuM
.твим,
визначений з порівняння кодів, дав
змогу визначити віддаль SeUM
з
точністю до 1 м, що достатньо для
наближеного визначення У. Точне значення
N
отримують
фазовим методом, коли опрацьовують
результати вимірювання статичними
методами, що вимагає збільшення часу
спостережень. Отже, кодовий метод за
своїми показниками точності істотно
поступається перед фазовим. Цьому
методу відводять лише
допоміжну
роль (наприклад, наближене визначення
координат точок встановлення
приймача).
"пл_пги І_Л І—U—UU
"ПІІ—шл_п
І~І
П П П _Г\Г]
'
!« Ттм »
Рис.
111.1.2. Визначення Хвим
кодовим методом
Фазові
визначення.
У геодезичному використанні супутникових
систем найбільший інтерес викликають
фазові методи, що ґрунтуються на
застосуванні (як інформаційних сигналів)
передавальних, гармонічних коливань
дециметрового діапазону радіохвиль.
Як ми вже знаємо з розділу II (с/в
вимірювання), такі коливання описуються
в загальному вигляді аналітичним
співвідношенням такого вигляду:
де
Головним
параметром, що використовується для
фазового віддалемірного вимірювання,
у (III. 1.6)
є вираз, що стоїть під знаком
тригонометричної функції і має назву
поточної фази ф^:
Ф(/)
= со / + Фо. (III. 1.7)
Як
відомо, фаза ср = со
період
коливань, або со=2л/г,
де / - частота коливань. Фаза ср, як
правило, вимірюється у кутових одиницях
(у градусах або радіанах). Але під час
супутникового вимірювання для спрощення
обчислювальних процесів фазу виражають
у відносних одиницях (у частинах фазового
циклу), тобто визначають, скільки разів
у фазі ср вкладається 2
л.
Фазу
у відносних одиницях позначають
(,)
2л 2л 2л
(III.
1.8)
Найбільшим
недоліком фазового вимірювання є те,
що фазометр дає змогу визначати різницю
фаз тільки у межах одного фазового
циклу (в межах
335у
= А
sin
(а>Н-ф0), (III.
1.6)А
- амплітуда коливань; со- кутова частота;
t-
еталонний
час системи GPS
(тобто
синхронний час для супутника та
приймача); ф0-
початкова фаза.t,
де со - кругова частота, при цьому (£>=
— ,
а Т
—Ф:
0{t)=N
+ АФ, (III.
1.9)
де
Повернемося
до (III. 1.7). Ця формула з урахуванням
формули (III. 1.8) може бути подана у вигляді:
Ф{()=/(
+ Ф0. (III.
1.10)
Зауважимо,
що під час супутникових спостережень
початкову фазу
ф0
де
8Х
- асинхронність годинників супутника
та приймача.
У
такому розумінні початковий фазовий
зсув може перевищувати величину, що
відповідає одному циклу. З урахуванням
цього такий зсув розглядають одночасно
з величиною
З урахуванням
цих зауважень поточна фаза передавальних
коливань може бути записана в такій
аналітичній формі:
^(,)=/('-T.««)
+
/5v
де
йдуть
від передавача супутника на вхід
приймача; / - номінальне значення
£
передавальної
частоти;
с
коливаннями
шуканої віддалі; 8, -
зсув у показах годинника передавача,
встановленого
на супутнику, викликаний нестабільністю
його роботи на момент виконання
вимірювання. Знак оскільки випромінювання
з супутника
випереджують
на т збурення коливань у приймачі.
Відповідно
для поточної фази збурених у приймачі
опорних коливань будемо мати:
KP(t)=ft+f^np- Сш.і.13)
Різницю
фаз
ДФ=Ф^(,)
-*„(,) =-Л» +/(s.„
-».,)• (ІІП.14)
3362к).
Насправді величина Ф
багаторазово перевищує 2п.
Зважаючи на це, параметр Ф(/)
записують так:N
-
кількість циклів; АФ
= AN
-
частина циклу.Ф0
прийнято
розглядати як зміну фази за час 8Х
= §, - 5,^ . Тому:=/А, (іп.1.11)N,
яка також є зсувом поточної фази
коливань, що надійшла від супутника на
вхід наземного приймача.
(ШІЛ2)Ф'пер^
- поточна фаза передавальних коливань
(у мить випромінювання), щотвим
=-— -
час проходження передавальнимиАФ,
на основі якої обчислюється шукана
віддаль до супутника, знаходять із
співвідношення
Знак
перед першим членом у правій частині
рівняння (ІІІ.1.14) викликаний тим, що у
супутникових системах як “стартові”
сигнали під час цифрового фазового
вимірювання найчастіше використовують
сигнали, що надходять від супутника і
які через запізнення мають від’ємний
фазовий зсув. Сигналом “стій” є сигнал,
що формується місцевим генератором
приймача.
Оскільки
8Т
= 8, -
8, ,
то -8Т
=8, -
8,
. Тому (III. 1.14) можна запи-
1
Іпр
Іпер 1
lnep
lnp J '
сати
ще так:
Остаточно
ця формула матиме вигляд:
ДФ
= ~/ '
З урахуванням
знака (III. 1.9) запишемо так:
Комбінуючи
(III.
1.15)
та (III.
1.16)
та попередньо позначивши через АФ,
отримаємо:
ДФ
= /^+^ + /8х, (III.
1.17)
де
поправка,
викликана несинхронністю ходу годинників
на супутнику та приймачі.
$
Враховуючи
те, що
с
фаз
А
АФ
=—SM
+N +
/5Т.
(III.
1.18)
Формула
(III. 1.18) є основною формулою для
односторонніх супут-
с
никових
віддалемірних систем. Враховуючи, що
/ = —, цій формулі можна ще
X»
надати
дещо іншого вигляду:
ДФ
= ^+^8г+ЛГ. (III.
1.19)
Рівняння
(III. 1.18), (III. 1.19) називають
337^вим
~
/бх. (III.
1.15)<P(t)=N-A<P. (III.
1.16)АФ
- виміряне значення зміни фази; / -
номінальне значення масштабної
(передавальної) частоти; N-
ціла
кількість періодів зміни фази за час
проходження радіосигналом віддалі
від супутника до приймача; 8Т
= 8^
- 8^
-твим
= ——-,
рівняння, яке зв’язує виміряну різницюФ
з величиною шуканої від далі SeUM
,
запишемо в такому вигляді:рівняннями
псевдовіддалей.
Як
видно із попереднього, головним
параметром координатних вимірів є
віддаль між супутником та приймачем.
Залежно
від мети задач, що розв’язуються,
розрізняють
Кожну
виміряну псевдовіддаль від приймача
до супутника можна вважати радіусом
сфери, у центрі якої супутник, а приймач
- на поверхні цієї сфери. Побудуємо
другу сферу, радіус якої дорівнює другій
псевдовіддалі, тоді у центрі цієї другої
сфери буде другий супутник. Тоді приймач
буде на перетині кривих поверхонь двох
сфер. Для визначення просторового
положення приймача потрібно виміряти
ще одну псевдовіддаль до третього
супутника і побудувати третю сферу.
Точка, в якій перетнуться поверхні
трьох сфер, і буде точкою положення
приймача. Отже, для визначення просторового
положення приймача потрібно разом
розв’язати три рівняння сфер:
SiguM
=yj{x,
-xf +(уі
-yf
+(zj-zf
, (ІІІ.1.20)
де
супутника,
Фактично,
оскільки наявна асинхронність
хронометрів, запишемо:
Sim
=І*,-х?+(Уі-у)2+(г,-г)2+с
(5V
-5,J. (III.1.21)
Величини
6,
та 8, -
відхилення годинників наземного
приймача та
Іпр 1пер
супутникового
передавача від еталонного часу GPS.
Значення
8,
для кожного
супутника
визначається станціями спостережень
за супутниками, які входять в сектор
керування і контролю та передаються у
складі навігаційних даних кожному
користувачу. Будемо поки що вважати
величини 8,
відомими. Але
невідомими
залишаються 8, -
зсуви годинника приймача. Тому у рівнянні
(III.
1.21)
чотири невідомих -х,
Саме
тому для розв’язання задачі координування
потрібно спостерігати, як мінімум,
чотири супутники.
338Абсолютні та відносні методи супутникового вимірювання
абсолютні
і відносні
(диференційні) методи координатних
визначень. У першому випадку поставлена
задача може бути розв’язана на основі
використання одного супутникового
приймача, що працює незалежно. У другому
випадку, за ди- ференційним методом,
використовуються два або більше
приймачі, що одночасно працюють,
встановлені на віддалених пунктах
місцевості, координати яких визначаються.SiguM
-
віддаль до і-то
супутника xt,
yt,
z, -
відомі координати і-тоі
= 1,2,
3, х,
у, z
-
шукані координати приймача.y,z
та
St
.
№ з/п |
Джерело похибок |
Значення похибок С/А коду, м |
і |
Іоносфера |
7,0 |
2 |
Тропосфера |
0,7 |
3 |
Багатошляховість |
1,2 |
4 |
Шуми приймача |
1,5 |
5 |
Координатно-часове забезпечення супутників |
3,6 |
Сумарна похибка |
8,1 |
|
Така
точність для геодезичного вимірювання
вочевидь недостатня. Тому в геодезії
використовуються
1 с
—
^
відносні
методи. Розглянемо один з варіантів
таких методів. Припустимо, що одночасно
працюють два віддалені на місцевості
приймачі 1 та 2, які приймають сигнали
від супутника а
(рис. ПІ. 1.3). Згідно з (ПІ. 1.19) в момент t
віддалям
від супутника до приймача відповідає
різниця фаз:
1 с
^^2 _ ^вим а2 «2 ^а2
(III. 1.22)
339
Індекси
ах
та
а2
відповідають
віддалям між супутником а
та
приймачами 1
та 2.
«.ч-К-А)’
(III.
1.23)
5х
о, “ 8ха2
= \
- К - К
+ 8Г„
= \
- 5,.
X
02
Рис.
III.
1.3.
До пояснення відносних методів
визначення
просторових координат
точок місцевості системами GPS
Створимо
перші різниці фаз:
АФ„
=ДФ„
-Д
Ураховуючи
(III. 1.23), зсув 8,а
виключається:
АФа
=і(мв1Ша)
+ ^(8<1
-8,2)
+ АNa. (III.
1.24)
Якщо
з цих самих точок 1 та 2 приймають сигнали
від супутника
ДФв + -8,2)
+ ДУє. (III.
1.25)
Якщо
створити другі різниці фаз, то виключиться
асинхронність приймачів. Отже, приймаючи
сигнали від двох та більше супутників,
по-перше, виключають похибки несинхронності;
по-друге, різниці
менші
за значення
різниці
фаз у (III.1.22)—(III. 1.25) є функцією віддалі
між приймачами. Якщо ж положення одного
з приймачів точно відоме, тоді можна
знайти розміщення другого приймача,
до того ж доволі точно, оскільки ряд
похибок, характерних для абсолютного
методу, вилучений. Координати другого
приймача є відносними координатами
щодо першого.
340
-S^
)+f (б,,
-5,ч
) + (*, - АГ,).в,
то за аналогією з (III. 1.24), можемо записати
такі самі різниці:ANa
та
ANe
значноNai,
Nai,
Nei,
Nei
і
тому легше визначаються; по-третє,
У
геодезії застосовують відносні методи
спостережень. Для таких спостережень
потрібно мати щонайменше два приймачі,
які встановлюють на різних пунктах.
Координати одного з них мають бути
відомі з необхідною точністю. Кожен
приймач вимірює псевдовіддаль не менше
ніж до чотирьох супутників. З восьми
псевдовіддалей створюють чотири
різниці. Відповідно до (III. 1.21),
враховуючи, що в різницях 8^
скоротяться, можна записати чотири
рівняння
виду:
$вим
і
в
~ $вим і
н
=
>/(х;
~хв)
+{Уі~~Ув)
+
(zi
~
ze)
~
, (111.
1.26)
-
У(ХІ
~хн)2+
(Уі
-Ун? + (*і
-zHf
+С
(б([
-
6<2)
де
У
цих рівняннях чотири невідомих:
несинхронності
хронометрів приймачів.
Як
бачимо, за відносним методом вимірювання
деякі похибки виключаються, а деякі
значно ослаблюються, оскільки для
незначних віддалей між приймачами ЕМХ
поширюються майже в однакових умовах.
Як показує досвід, відносний метод
визначення координат приблизно в 100
разів точніший за абсолютний і порівняно
легко можна досягти сантиметрової
точності. Спостереження абсолютними
та відносними методами можна виконувати
нерухомими приймачами, або приймачами,
встановленими на рухомих об’єктах. У
першому випадку спостереження називають
Супутникова
система використовується також для
точного керування транспортним засобом
вздовж наперед запроектованого маршруту,
а також для уточнення цього маршруту.
У геодезії використовують відносний
кінематичний метод, якщо достатня
метрова точність. Один приймач, який
встановлено нерухомо на точці з відомими
координатами і який безперервно приймає
сигнали від супутників, а другий приймач
переміщується, зупиняється на короткі
проміжки часу на пунктах, координати
яких необхідно визначити.
Недоліком
відносного кінематичного методу є
необхідність
341і
=
1, 2, 3,4.хн,
ун,
zH
та
8Т
= (8^
- 8t2)
- різницястатичними,
в другому - кінематичними.
У геодезії під час побудови мереж
частіше використовують відносний
статичний метод. Кінематичні спостереження
виконують приймачами, які безперервно
рухаються. Тому під час таких спостережень
можна не тільки визначити миттєві
положення об’єктів, але й швидкість
їхнього руху.ініціалізації,
тобто початкового прив’язування
приймачів перед початком спостережень
на інших пунктах або на рухомих об’єктах.
Ініціалізація дає змогу виключити
початкову
багатозначність результату вимірювань
(визначити кількість циклів#). Оскільки
координати початкового пункту відомі
і по інформаційних каналах приймач
отримує координати супутника на момент
/, то у цей момент, знаючи від даль між
початковим пунктом та супутником,
визначають
Ч'
Виконавши
прив’язування, мобільний приймач
постійно реєструє
зміни
У
супутникових системах, як ми вже знаємо,
носіями координат є ШСЗ, які рухаються
своїми орбітами. Тому точки орбіти, на
яких перебувають супутники, і є
координатами супутників. Необхідно
пам’ятати, що ці координати супутники
мають тільки у визначені миті часу.
Тому параметри орбіти і параметри
роботи хронометрів повинні бути точно
узгоджені. Ці параметри увесь час
контролюють наземні станції сегмента
керування. Значення Параметрів з
наземних станцій керування періодично
передають на ШСЗ, а супутники, своєю
чергою, пересилають їх кожному приймачу.
Важливо знати закони руху ШСЗ, значення
основних параметрів орбіт та роботи
хронометрів.
Якщо
Землю вважати однорідним тілом, тоді
рух супутників навколо неї описується
законами Кеплера. Для супутників Землі
ці закони можна сформулювати так:
орбітою
супутника є еліпс, в одному з центрів
якого розміщена Земля;
радіус-вектор
супутника (лінія, яка з’єднує центр
Землі з супутником) за однакові
проміжки часу описує рівні площі;
відношення
квадратів періодів обертання двох
супутників дорівнює відношенню кубів
великих півосей орбіт супутників.
Рівняння
руху супутників отримують із закону
всесвітнього тяжіння Ньютона. Воно є
векторним рівнянням другого порядку
з шістьма сталими інтегрування. Рух
супутників відносно Землі має шість
степенів свободи, і тому його визначає
шість основних параметрів орбіти.
Для
точного визначення місцезнаходження
реального супутника використовується
орбітальна система координат, яка є
інерціальною - не обертається разом
із Землею (рис. ПІ. 1.4).
342N:N
та
інших вимірюваних величин, тому потрібний
безперервний зв’язок приймача з
супутником.Основні відомості про параметри орбіт супутників
Рис.
111.1.4.
Орбітальна система координат
Основними
елементами орбіти супутника є:
лінія
перетину площини орбіти з площиною
екватора, лінія
точка
точка
Подамо
шість основних параметрів орбіти:
е
- ексцентриситет: е
=
£2-
довгота висхідного вузла, яка
відраховується у площині екватора на
схід від напрямку на точку весняного
рівнодення у;
со-
довгота перигею (кут у площині орбіти
між напрямками на висхідний вузол та
перигей);
Перші
два параметри визначають форму еліпса
орбіти супутника. Два наступні описують
орієнтування орбіти відносно екватора.
Останні два параметри дають змогу
визначити положення супутника на
орбіті. Оскільки
343
АА',
яку називають лінією
вузлів;А
- висхідний
вузол.
У цій точці супутник перетинає площину
екватора, переходячи з південної
півсфери в північну;А'
- несхідний
вузол.
У цій точці, навпаки, супутник переходить
з північної на південну півсферу;перигей
- найближча до Землі точка орбіти
супутника;апогей
- найвіддаленіша від Землі точка орбіти
супутника.
а,
b
-
велика і мала півосі еліпса орбіти;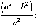
і
-
нахил площини орбіти до площини
екватора;ь-
дійсна аномалія, визначає положення
супутника на орбіті. Суму довготи
перигею та істинної аномалії називають
аргументом широти и.
дійсна
аномалія і) є незамкнутою функцією
часу, то замість неї часто використовують
середню аномалію
де
Відхилення
форми Землі від кулі, неоднорідність
розподілу мас у тілі Землі, інші зовнішні
чинники, що впливають на супутник,
викликають появу збурень в орбіті
супутника. Тому еліпси, за якими мають
рухатися супутники відповідно до
законів Кеплера, перетворюються на
незамкнуту, приблизно еліптичну
просторову криву, яка описує Землю.
Параметри цієї орбіти змінюються з
часом і подаються незамкнутими формулами
у вигляді рядів. Найбільше збурення
орбіти дає еліпсоїдальність форми
Землі, яка викликає зміни довготи
висхідного вузла £2 та довготи перигею
со. Положення супутника спочатку
визначається на його орбіті, а потім,
трансформуванням за
Систему
часу супутників:
Параметри
орбіт Кеплера:
й0-
пряме сходження висхідного вузла до
часу відносності;
(0-
аргумент перигею;
Параметри
збурення орбіт:
AQ
-
зміна прямого сходження;
Д
344М
= 2п-~, (III.
1.27)t
-
поточний час; U
-
час, за який супутник здійснює один
оберт навколо Землі; Т
-
момент часу проходження супутника
через перигей.і
та Q,
на
екватор, а в кінці ще виконується
трансформування, яке враховує рух
полюсів Землі і власне обертання Землі.
Додатково, під час обчислень, враховується
збурення орбіти на основі параметрів
збурення. Станції супутників пересилають
наземним приймачам ефемериди супутників,
тобто інформацію про траєкторію
супутників. До ефемерид входять дані
про:
t0e
-
відносного часу для ефемерид;t0c
-
відносного часу для параметрір
хронометра;а0,
аІ9
а2
- коефіцієнти полінома рівняння
годинника (відхилення, дрейф тощо).
а
-
корінь квадратний із значення великої
півосі;е
- ексцентриситет;і0
-
нахил до часу відносності;М0-
середня аномалія до часу відносності.
An-
різниця
середнього зміщення та обчисленого
значення;і
- зміна нахилу;
•
По
суті, супутники являють собою платформи,
на яких кріпиться апаратура, необхідна
для роботи системи. До цього обладнання
входять:
дві
сонячні батареї площею 7 м2
для живлення вузлів обладнання;
системи
реактивних двигунів, за допомогою яких
коригують положення супутника на
орбіті;
передавач
супутника, який безперервно випромінює
коливання двох частот
Ці
коливання одночасно є передавальними
і вимірювальними. Як передавальні
ці коливання використовуються для
передавання кодів на наземні станції;
одночасно коливання є вимірювальними,
оскільки їх застосовують для точних
фазових вимірювань. Головним вузлом
передавача, який синхронізує роботу
інших вузлів, є
дециметровому
діапазону хвиль (X,Ll
=
19,0 см і
Коди,
які випромінюють передавачі, є
послідовностями двійкових сигналів.
Усіх кодів чотири: код
Код
параметри
орбіти супутника;
час
системи супутника;
скорочена
інформація про інші супутники системи.
У
цьому коді за 1 с передається 50 двійкових
знаків, тобто щільність інформації -
50 біт/с. Ця інформація сформована у
блоки тривалістю по 30 с.
345Сш»
Cue»
Cis,
C/c,
Cr5,
Crc
-
параметри
для коригування збурень орбіти. Ці дані
передає на наземні приймачі кожний
супутник на коді D.
1.6. Загальний принцип побудови супутникових передавачів системи gps
1^
таї^ •основний
високостабільний атомний генератор.
Його також коротко називають хронометром.
Він випромінює частоту / 0
= 10,23 МГц, стабільність якої досягає
10'12,
тобто є дуже високою. Довжина хвилі цих
коливань дорівнює 29,31 м. Ці коливання
і їхню частоту називають стандартними.
Передавальні частоти Ц
та формуються завдяки множенню частоти
атомного генератора відповідно на 154
і на 120 (див. рис. III. 1.5). Отримують частоти
fL{
=
1575,42 МГц і fLl
=
1227,60 МГц, які відповідаютьXLl
=
24,4 см).D,
код СІ
А,
код Р
і код V.D
(Daten Code) -
це закодована у двійковій формі така
цифрова інформація:
Ac
j sinfi}j/
Змішувач
Код
С/А
fc/A=fo/10
=
1,023
МГц
С/
A(t)
Модулятор
90°
Ag
COSCtJ^
JfCodD
50
Гц
КодР
fp
=/о
=
10,23
Гц
D(t)
Л'>
Модулятор
D[t)P(t) |
|
Змішувач |
|
|
D(t)C! A(t) |
|
|
Змішувач
AcXD(t)C
/
A(t)
cos a\t
AplD(t)P(t)
sin Щі
Передавач
Ap
2
sin^
AP2D(t)P(t)
sin co2t
Рис.
III. 1.5. Спрощена
функціональна схема супутникового
передавача
U 1500
біт (ЗО с) >і |
1 |
2 |
3 |
4 |
||
|
||||||
0 1 |
2 3 |
4 5 |
6 7 |
8 9 |
||
k— |
|
|||||
|
8 |
8 |
||||
Рис.
III.
1.6.
Схема одного блока двійкового коду D
тривалістю
ЗО с
Один
блок поділяється на п’ять підблоків
по 300
бітів,
а підблок складається із 10
тридцятибітових
слів; 24
біти
інформаційні та 6
паритетних
[9].
У
першому підблоці є дані для корекції
хронометра та для визначення атмосферної
поправки.
У
підблоках 2 та 3 наводяться значення
ефемерид орбіти супутника. Підблок 4
призначений для спеціальних повідомлень.
У підблоці 0 - дані про ефемериди та
рівняння хронометрів інших супутників.
Ці дані прийнято називати
346альманахом.
Вони дають приймачеві змогу вибирати
для спостережень оптимальні супутники.
Це супутники, на які напрямки з приймача
утворюють кути з горизонтальною
площиною, не менші, ніж 15°.
Коди
Ці
коди використовують для визначення
часу проходження коливаннями шляху
від ШСЗ до приймача. Код
Код
Код
Код
Отже,
коди накладають на коливання, а вони
переносять коди із супутників до
наземних приймачів. Коливання Zj
з
незмінною фазою змішуються з
модульованим кодом
що
і з кодом
Апаратура
різних фірм, що виробляють геодезичні
супутникові приймачі, різноманітна,
але відмінності їхньої будови, як
правило, незначні. Тому можна описати
узагальнену структурну схему GPS-приймача,
яка дає змогу розглянути необхідність
використання поданих на схемі основних
складових приймача, пояснити їхні
функції та взаємозв’язок.
347Р,
СІ
А і V
є випадковими послідовностями 0 і 1
(рис. III.
1.2).Р
(Precise
Code) -
точний код. Кожний супутник у проміжок
часу у сім діб формує із загального
коду свій зразок, який складається з
послідовності відрізків різної
тривалості загального коду. Тривалість
одного зразка коду більша від часу
проходження сигналу від супутника до
наземного приймача. Кожної суботи
опівночі змінюються коди всіх супутників.
З цього моменту і починається відлік
часу. Для кожного супутника створено
38 зразків коду. Тому через кожні 38 тижнів
(266 днів) коди, які випромінюються
супутником, повторюються. Код Р
має стандартну частоту / 0
= 10,23 МГц; за одну секунду в цьому коді
формується 10230000 двійкових знаків.V
має характеристики, близькі до коду Р.
Він призначений переважно для військових
потреб.С!A
(Coarse Accuracy Code) -
менш точний двійковий код. Його частота
в 10 разів менша від стандартної, тобто
1,023 МГц. Він призначений для грубого
визначення віддалей. Кожний супутник
формує свій зразок коду СІ
А
за таким самим принципом, як і код Р.D
модулює
коди Р
і СІ
А.
Після цього модульовані коди змішують
з коливаннями 2^
таі^.Р.
На рис. III. 1.5 цей складний сигнал
позначений D(t)
Р(/).
З кодом СІ
А,
позначеним D(t)
СІ
A(t),
відбувається
те саме,Р,
але після зміни фази коливання Ц
на 90°. Коливання змішуються з
немодульованим кодом СІ
А
і Р
і з модульованим кодом Р.
У результаті на першому коливанні можна
прийняти три коди, а на другому - тільки
код СІЛ
або тільки код Р,
або коди Р
і D.
Коливання із змішувачів подаються на
передавальний пристрій з антеною.
1.7. Структурна схема геодезичного супутникового приймача
Рис.
111.1.7.
Узагальнена структурна схема GPS-приймача
Вхідною
частиною приймача є його антена, яка
забезпечує приймання радіосигналів
від супутників, що перебувають у полі
зору приймача. Вибраний тип антени та
режим її роботи істотно впливають не
тільки на можливість прийняття сигналів
від супутників, але й на точність
супутникових спостережень. Основними
характеристиками антен є: показник
перетворення сигналів (коефіцієнт
підсилення), яке повинно відбуватися
з мінімальними енергетичними
втратами, та показник напрямленості
антен (коефіцієнт напрямленої дії).
Ідеальною формою фазової діаграми
напрямленості (як і амплітудної) є
півсфера, яка забезпечує однакову
величину запізнень сигналу, незалежно
від напрямку їхнього надходження.
Завдяки такій формі ці запізнення
вдається виключити.
Другим,
не менш важливим, показником антен є
поняття фазового центра, його положення
і стабільність в часовому аспекті. Під
фазовим центром розуміють таку точку
антени, яка не піддається геометричному
вимірюванню, від якої відраховуються
усі віддалі до супутників, а положення
цієї точки “прив’язується” до
положення відповідної точки відносності
на пункті спостережень (до геодезичного
центра знака). У разі використання у
приймачі антени, симетричної відносно
своєї вертикальної осі, положення
фазового центра в горизонтальній
площині збігається, як правило, з
положенням згаданої тільки що осі
симетрії. Але, що стосується зсуву цього
центра по вертикалі, то такий зсув
визначається на основі спеціальних
досліджень (найчастіше під час
налагодження та калібрування антени).
Ще
однією специфікою супутникових антен
є їхнє ігнорування щодо сигналів,
відбитих від підстилаючих поверхонь
(тобто до багатошляховості). Як додаткові
заходи використовують спеціальні
екранувальні металеві диски.
348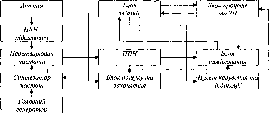
Оскільки
радіосигнали від супутника до приймача
проходять великі віддалі (близько
20
тисяч км), а потужність встановленого
на супутнику передавача порівняно
невелика (близько 10 Вт), то на вході
антени сигнал має надзвичайно малу
величину. Тому виникає необхідність
його попереднього підсилення за
допомогою підсилювача надвисокої
частоти НВЧ, який розташовується
біля антени. Часто антенний пристрій
та НВЧ збирають окремим блоком, який
з’єднується з основним блоком приймача
порівняно довгим коаксіальним кабелем.
Оскільки
багаторазове підсилення коливань НВЧ
пов’язане з істотними технічними
ускладненнями, то в супутникових
приймачах застосовують супергетеродинний
принцип, під час реалізації якого
коливання, що приймаються після
попереднього підсилення, піддаються
перетворенням, у результаті яких істотно
знижується частота передавальних
коливань до декількох десятків мегагерц.
Створену проміжну частоту ще називають
частотою биття. Роль гетеродина виконує
високостабільний головний генератор,
що входить до складу приймача. Необхідна
для роботи приймача сітка частот
формується синтезатором частот, який
використовує як вихідні коливання
сигналів головного генератора. Основне
підсилення сигналів, що приймаються,
виконується підсилювачем проміжної
частоти (ППЧ), який під’єднано до виходу
перетворювача частот. Безпосередньо
з виходом ППЧ з’єднаний блок пошуку
та захоплення, а також вимірювальний
блок. Принцип дії системи пошуку сигналів
від потрібного нам супутника оснований
в системі GPS
на
так званій структурній селекції. При
цьому методі передавання сигналів від
різних супутників виконується на одній
і тій самій передавальній частоті, а
розрізняють їх за структурою кодових
сигналів. Тому такий метод ще називають
кодовим.
Важливою
особливістю приймача є те, що на вхід
приймача одночасно надходять радіосигнали
від декількох супутників. Завдання
приймача - прийняти та виконати
селекцію (розділення) сигналів. У
геодезичних GPS-
приймачах ця задача розв’язується
введенням у схему приймача певної
кількості каналів, залежно від
кількості супутників, що одночасно
приймаються. Кожен канал повинен
опрацьовувати інформацію тільки від
одного супутника. Після закінчення
пошуку відбувається захоплення сигналів,
яке дає змогу стежити за відповідним
сигналом упродовж усього сеансу
спостережень, в якому бере участь
“захоплений” супутник. У розділювальному
блоці відбувається розділення сигналів
на кодові та суто гармонічні. Від
останніх відрізняють також навігаційні
повідомлення, що надходять від супутника.
Два перші сигнали використовуються у
блоці процесора для обчислення шуканих
349
віддалей
до супутника. На основі отриманих
значень псевдовіддалей виконується
грубе визначення координат. Фазові
вимірювання в приймачі опрацьовуються
тільки попередньо. Вони згладжуються
та групуються і передаються у
запам’ятовувальний пристрій ЗП.
Кінцеве
опрацювання фазових вимірів виконується
на стадії “посто- працювання” в
камеральних умовах. Блок процесорів,
що входить до приймача, крім попередніх
обчислень, керує роботою приймача в
автоматичному режимі на основі
закладеного в ньому програмного
забезпечення.
Пульт
керування та індикації, показаний на
структурній схемі, містить клавіатуру
та індикаторний дисплей, на якому, за
бажанням оператора, можна відображати
величини, що визначаються приймачем,
а також іншу допоміжну інформацію.
Клавіатура дає змогу оператору вводити
необхідну інформацію, а також різні
команди.
Описаний
вище принцип роботи GPS-приймача
показує, що під час підготування та
виконання спостережень виникає
необхідність виконання багатьох
операцій, пов’язаних з оперативним
керуванням роботою різних вузлів
приймача. Крім того, у приймачі виконується
попереднє опрацювання отриманої
інформації. Для реалізації опрацювання
у складі приймача є спеціалізована
мікро-ЕОМ, яка має процесори, таймер,
різні запам’ятовувальні пристрої та
інші вузли, характерні для обчислювальної
техніки. Керують роботою обчислювального
комплексу пультом керування та індикації
за допомогою програми, що введена у
приймач. Розглянемо блок-схему, яка
ілюструє принцип послідовної зміни
станів GPS-приймача,
характерних для пошуку, захоплення та
відстежування супутникових сигналів.
Після
розміщення приймача на пункті
встановлюється режим очікування
сиґналів. Якщо сигнали надходять і в
пам’яті приймача є альманах супутників,
тоді виконується попереднє обчислення
положення вибраного супутника. Якщо
альманах в пам’яті відсутній, тоді
витрачається додатковий час на режим
збирання даних про супутник (близько
12,5 хвилини).
Наступний
етап - синхронізація режиму роботи
генератора кодових сигналів та
генератора фазових, гармонічних коливань
приймача із супутниковими сигналами.
У результаті такої синхронізації
виконується захоплення сигналів від
відповідних супутників і подальше
збирання та реєстрація даних. Надалі
у приймачі підтримується режим
відстеження захоплених сигналів та
періодичний набір відліків, що
використовуються для обчислення
віддалей до супутників та реєстрації
точного часу.
350Ill. 1.8. Короткі відомості про роботу системи керування та опрацювання вимірів приймачем gps
Рис.
III.
1.8. Бпок-схема
послідовності режимів роботи приймача
GPS
Як
уже зазначалось, одна із функцій
GPS-приймача
полягає в первинному визначенні
результатів вимірювання, які ґрунтуються
на використанні часових запізнень
кодових сигналів, що передаються із
супутника, та фазових зсувів, що надходять
на вхід приймача передавальних коливань.
Відповідно
до (III. 1.4) на основі кодових сигналів
визначається час проходження
електромагнітним випромінюванням
віддалі між супутником та приймачем,
що дає змогу знайти псевдовіддалі (ПІЛ
.5), до яких входять істинна віддаль та
поправковий член, викликаний різницею
величин показів годинників на супутнику
та у приймачі. Одночасне вимірювання
псевдовіддалей до чотирьох супутників
та наявних у приймачі даних про координати
цих супутників на момент вимірювання
дає змогу обчислювальному комплексу
приймача на основі просторової лінійної
засічки визначити координати пункту
спостережень з урахуванням вищезгаданої
поправки за рахунок розходження у
показах годинників супутника та
приймача. Точність такого позиціювання
з використанням
Первинною
інформацією під час фазового вимірювання
є зареєстрований за допомогою цифрового
фазовимірювального пристрою зсув фаз
між коливаннями, прийнятими від
супутника і сформованими у приймачі
головним генератором.
Через
безперервну зміну від далі до супутника,
що пов’язано з його рухом, дані, що
реєструються, порівняно швидко
змінюються, тому відліки реєструються
доволі часто (як правило, через 0,1 с). Ці
дані в приймачі ущільнюються; в
результаті створюються вибірки, інтервал
між якими може
351
С/А-коду
оцінюється з похибкою у межах від 5 до
10 м. Для геодезії найбільший інтерес
становить попереднє опрацювання фазових
вимірювань, на основі яких під час
“постопрацювання” забезпечується
можливість отримання високої точності
вимірювання (сантиметрової, міліметрової).
змінюватися
за бажанням оператора (діапазон змін,
зазвичай, від 1 до 60 с). Під час ущільнення
відбувається згладжування значень
отриманих даних у межах наявної вибірки
(зазвичай обмежуються поліномами
другого степеня). Поряд зі згладжуванням
у багатьох типах GPS-приймачів
передбачена процедура, що отримала
назву фільтрації Кальмана. Суть такої
процедури, характерної, як правило, для
динамічних систем, у систематичному
порівнянні одержаних результатів
спостережень з наперед розрахованими
їхніми значеннями на основі закономірностей
їхньої зміни з часом. У разі відхилення
реальних даних від наперед розрахованих
вищевстановлених норм виконується
їхнє відбракування.
Зауважимо,
що під час спостережень, що виконуються
за допомогою одного приймача, не вдається
виключити з результатів фазового
вимірювання цілу низку похибок
систематичного характеру і, тим самим,
надійно компенсувати притаманну
фазовим вимірюванням неоднозначність.
Саме тому не роблять спроб обчислення
в одному приймачі кінцевих значень
віддалей до супутників на основі
фазового вимірювання передавальних
коливань.
Тому
після відповідних процедур згладжування
та фільтрації дані передаються у
передбачені в приймачі пристрої пам’яті
з метою їхнього використання під час
остаточного опрацювання. Використовується
аналогічна інформація від інших
приймачів, що одночасно працюють. Окрім
опрацювання кодових фазових даних, в
обчислювальних комплексах виконується
опрацювання іншої інформації, яка
передається із супутника у складі
навігаційної інформації, а також тієї,
що подається з клавіатури безпосередньо
від оператора.
Як
уже зазначалося, існують абсолютні та
відносні методи спостережень за
допомогою GPS-приймачів.
У геодезії використовують тільки
відносні методи, які є в десятки разів
точнішими, ніж абсолютні. Тому надалі
будемо розглядати тільки відносні
(relative)
методи.
Спочатку
було створено тільки дві відносні
технології GPS-
вимірювання:
статичну та кінематичну. Здавалось, ці
дві технології задовольняють як
цивільні, так і військові організації.
Проте
користувачі вимагали підвищення
точності результатів вимірювання
з одночасним скороченням часу на
виконання вимірювання. Це вимагало
поліпшення системи GPS,
конструювання
компактніших, легших, переносних
приймачів з удосконаленим програмним
забезпеченням. Останнє, своєю чер-
352
Супутникові методи визначення координат
Технології gps-вимірювання
гою,
привело до того, що на основі вищеназваних
технологій вимірювання було створено
ще декілька, а саме:
Статичні
відносні технології вимірювання
(Static
relative positioning).
Кінематичні
відносні технології вимірювання
(Cinematic
relative positioning).
Напівкінематична
відносна технологія (semi-cinematic
relative positioning) (технологія
“стій/йди” - technology:
“stop and go”).
Технологія
псевдостатична, псевдокінематична,
відносна реокупа- ційна (pseudo-static,
pseudo-cinematic relative positioning, intermittent static
positioning, reoccupation).
Технологія
швидка статична відносна (fast/rapid
static relative positioning).
Диференційні
GPS-технології
(differential
GPS-DGPS).
Одним
із найважливіших параметрів, які
визначають режим роботи приймача,
є файл конфігурації місії. Він може
бути різним залежно від особливостей
шести вищеназваних технологій
вимірювання. Для побудови супутникових
геодезичних мереж (далі СГМ) та
топографічного знімання існують
відповідно два основні режими роботи:
статичний режим - для СГМ та режим
знімання “стій/йди” - для знімання.
Назва “статичний” походить від
статичного збирання інформації на
пункті упродовж певного проміжку часу.
Мінімально два приймачі виконують
спостереження тих самих супутників
упродовж однієї або декількох сесій
спостережень (по декілька годин щодня)
і залишаються стаціонарно на тих самих
пунктах.
Для
відносних кінематичних технологій
один приймач установлюють стаціонарно,
на точці з відомими координатами, а
другий - на рухомому об’єкті. Це типова
навігаційна технологія. У ній
застосовується так зване положення
об’єкта в “реальному часі”. Суть цієї
технології в тому, що базова (нерухома)
станція передає до рухомого приймача
поправки, які використовуються ним
для уточнення координат рухомої станції.
Детальніше технологію “реального
часу” буде описано далі.
Технологія
дає змогу визначити дискретно (із
перервами 1-5 с) координати рухомого
об’єкта щодо приймача, встановленого
стаціонарно. Такий режим застосовується,
наприклад, під час аерознімання.
Технологію “стій/йди” називають ще
напів-кінематичною. Головна відмінність
цієї технології від кінематичної у
тому, що під час визначення положення
рухомий приймач (роверний) не рухається,
як у кінематичній технології, а
зупиняється (стоїть) деякий короткий
проміжок часу на точці, координати якої
визначаються.
Далі
розглянемо всі вищезгадані технології
супутникових методів визначення
координат детальніше.
353
Статичний
метод є основним під час побудови СГМ
і застосовується найчастіше. Для
статичної технології всі приймачі за
весь час спостережень розміщені на
одних і тих самих пунктах. Час виконання
спостережень залежить переважно від
заданої точності та від віддалі між
пунктами (довжин векторів) [22].
З багаторічного
досвіду різних організацій відомо, що
достатньо:
30-90
хвилин для локальних сесій.
1-2
дні для пунктів, зарахованих до
державної, геодинамічної сесії.
4-6
днів для сесій континентальних й
основних геодинамічних.
Наприклад:
для вимірювання геодезичної локальної
сесії для довжин
сторін
до 15-20 км достатньо виконати спостереження
впродовж 1 години, для сесії типу EUREF
(European Reference Frame), коли
якась країна виконує вимірювання до
найвищого закладу Західної Європи -
сесія проходить 5 днів. Стільки само
часу потрібно, коли виконується компанія
геодинамічного вимірювання CERGOP
(Central Europe Regional Geodynamics Project).
На
практиці точність такої технології
становить 5 мм
Важливим
для супутникових спостережень є так
званий геометричний фактор. Точність
лінійної просторової засічки залежить
не тільки від точності лінійного
вимірювання, але й від геометрії
розташування супутників: від кутів,
під якими перетинаються у шуканій точці
напрямки із супутників. Величину
геометричного фактора часто пов’язують
з об’ємом багатогранної фігури, вершини
якої збігаються із розташуванням
супутників та точками спостережень.
Установлено: чим більший об’єм
багатогранної фігури, тим менше
проявляється вплив геометрії
розташування супутників на результативну
точність визначення координат пункту.
Під час взаємного зближення супутників
об’єм цієї фігури зменшується, а вплив
геометричного фактора зростає [23].
Параметр,
який оцінює зростання похибок вимірювання
через геометрію розташування супутників,
отримав назву геометричного фактора,
який у сучасних публікаціях прийнято
позначати абревіатурою
354111.2.2. Статичний метод визначення координат пунктів
±
1 мм на 1 км довжини вектора, що визначається.
Під час вимірювання статичними методами
важливим є підбір відповідних приймачів.
Для відстаней між пунктами, більших за
100
км, потрібно використовувати приймачі
із частотами 1^
таї^. На коротких лініях, коли є достатня
кількість супутників, за умови доброї
геометрії розташування супутників
можна отримати високу точність за
порівняно невеликої тривалості
спостережень. Швидкість вимірювання
та підвищена продуктивність підтримуються
достатньо досконалими алгоритмами
оброблення у програмному забезпеченні
SKI.DOP
(Dilution of
Precision
- зниження
точності). Цей параметр використовується
як коефіцієнт між точністю визначення
координат
супутників
Найуніверсальнішим
показником є параметр
Для
переважної більшості пунктів умови
щодо
Другим
чинником, що може викликати значне
зниження точності, є іоносферне збурення.
Іоносферне збурення змінюється в часі
і залежить від положення пункту на
земній поверхні. У нічний період доби
іоносферні збурення значно менші, ніж
у світлий період доби. Тому в нічний
період можна зменшити час спостережень
наполовину або вдвічі збільшити довжину
вектора.
Під
час вимірювання, яке вимагає найвищої
точності, використовують двочастотні
приймачі SR-9500
(фірми
Leica);
SNR-8000 або
SNR-8100
(фірми
Alen
Osborne); Z-XII (фірми
Ashtech);
4000 SSI (фірми
Trimble).
mpe3
= DOP
■ m0.
(III.2.1)
GDOP
=
(III.2.2)
355трез
та точністю вимірювання віддалі дощ.GDOP
-
геометричний фактор зниження точності,
який характеризує одночасно як точність
тривимірного позиціювання, так і часу.
Він виражається формулоюдетх,
ту,
mh
-
середні квадратичні похибки визначення
по осях координат; mt
-
середня квадратична похибка визначення
часу; с
- швидкість ЕМХ. Отже, GDOPдає
змогу оцінити геометрію супутникового
“сузір’я”. Маленьке значення GDOP
(<
8)
свідчить про добру геометрію. Високе
значення GDOP
означає,
що супутникове “сузір’я” погане. Чим
менше GDOP,
тим більша ймовірність отримати добрі
результати. Значення GDOP,
менше за шість, вважається допустимим,
а більше за шість - завеликим. Коефіцієнти
GDOP
відображають
лише миттєву геометрію для окремої
точки. Ці коефіцієнти обчислюють самі
приймачі. Вони ж автоматично вибирають
оптимальну конфігурацію супутників.
Одночасно з GDOP
використовують
також PDOP
-
фактор, що враховує тільки фактор
тривимірного позиціювання, без похибок
визначення часу, і HDOP
-
аналогічний фактор, але тільки для
зниження точності розташування у
горизонтальній площині; VDOP-
у
вертикальній.GDOP
виконуються,
якщо в полі зору доступні п’ять або
більше супутників. Найкраще “вікно”
спостережень для “статики” повинно
містити чотири і більше супутників з
GDOP
<
8
під
час кута відсікання, що дорівнює 15°
(вертикальний кут між горизонтом і
напрямком на супутник).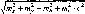
Кількість супутників
|
Наближена довжина базисних ліній |
Приблизний час спостережень |
|
вдень |
вночі |
||
4 і більше |
15-20 км |
1-2 години |
1 година |
4 і більше |
більше за ЗО км |
2-3 години |
2 години |
356
Метод
“стій/йди” створений на основі
статичного методу. Він є найшвидшим
для детального топографічного знімання.
Застосовується, коли між базовою та
мобільною станціями невеликі віддалі.
Під час вимірювання технологією
“стій/йди” беруть участь щонайменше
два приймачі GPS.
Найви-
гіднішим у цій технології є те, що
рухомий приймач виконує вимірювання
на рядових пунктах (наприклад, пікетах)
тільки 1-2 хвилини. Час витрачається
переважно тільки на переміщення з
пункту на пункт, а на пункті - “затримуємось”
і зразу ж ідемо далі.
Робота
в режимі “стій/йди” складається із
двох частин: 1 -
Головний
недолік такої технології в тому, що
протягом спостережень усієї мережі
пунктів (під час вимірювання на пункті
і навіть під час транспортування чи
перенесення приладу з пункту на пункт)
обов’язковим є зв’язок хоча б із
чотирма супутниками GPS.
Тому
цю технологію неможливо застосувати
на територіях із високими забудовами,
у лісі. Рух під деревами, мостами
Ініціалізацію
можна виконувати одним із трьох способів:
Приблизно
25-хвилинне статичне вимірювання
довільної бази. Це виконується до
початку вимірювання. Мінімум два
приймачі ведуть статичне вимірювання
на двох довільних пунктах, а далі
рухомий приймач виконує мобільну
частину. Такий спосіб ініціалізації
називають ще режимом “швидкої статики”.
Установлення
станції на точці з відомими координатами
або відомим вектором між двома точками.
Виконується вимірювання статично
протягом 5-10 хв.
Статичне
вимірювання із заміною антен. Обидва
приймачі виконують вимірювання
статично упродовж 5 хв, а далі в приймачах
замінюються антени і продовжуються
спостереження ще близько 5 хв. Точність
визначення координат точок у режимі
“стій/йди” дорівнює 1-2
см ± 1
ррм.
QC7111.2.4. Визначення координат методом “стій/йди” (“stop and go”)
частина
ініціалізації,
яка необхідна для того, щоб розв’язати
початкову неоднозначність під час
постопрацювання за допомогою програмного
забезпечення SKI;
2
- мобільна
частина,
у межах якої розв’язання неоднозначності
вносяться в програмне забезпечення
SKI.
Ініціалізація
та наступна за нею мобільна частина
називаються лайкою режиму
“стій/йди”.перериває
вимірювання.
Якщо з’являється повідомлення про
втрату захоплення сигналів і, у
результаті, захоплення менше ніж
чотирьох супутників, потрібно заново
почати ланку спостережень. Тому цей
метод можна застосувати тільки на
відкритій місцевості, незарослій і
незабудованій.
Вікно |
Кількість
супутників, їх висота над горизонтом,
|
Добре вікно |
5
або більше супутників, висота >20°,
|
Використовувати можна, але не рекомендується |
4
супутники, вище за 15°, |
Не варто використовувати |
4
супутники, |
Використовувати неможливо |
3 супутники або менше |
Під
час роботи у режимі “стій/йди” можна
використовувати статичну місію STS
Default (Місія
статичного знімання за замовчуванням).
Проте можна створити спеціальну місію
для роботи в режимі “стій/йди” для
референцної станції і для мобільної
станції. У референцному приймачі повинен
бути встановлений режим роботи “статика”
(STS),
а
у мобільному - “стій/йди” (SGS).
В
обох приймачах повинен бути встановлений
ущільнений режим збирання даних
(“COMPACTED”).
Дискретність
записування даних повинна бути однакова
на обох приймачах. Під час вибору
дискретності запису даних варто
враховувати ємність записувальних
пристроїв на референцній станції, а
також тривалість перебування на точці,
де встановлений мобільний приймач.
Здебільшого дискретність запису даних
вибирають такою, що дорівнює 3, 4 або 5
секунд (див. табл. ІП.2.3).
358
Параметри |
Референцна станція |
Мобільна станція |
Працездатність/частота |
AUTO |
AUTO |
Мінімальна висота супутника над горизонтом |
15° |
15° |
Режим роботи |
“статика” (STS) |
“стій/йди” (SGS) |
Ущільнений, вибірковий режим запису даних |
ущільнений |
ущільнений |
Дискретність реєстрації даних |
5 секунд |
5 секунд |
Статичний
метод - це класичний метод GPS-знімання,
який використовується на довгих
лініях. Спостереження можуть тривати
декілька годин.
На
коротких лініях, за нормальних умов
для роботи, час спостережень може бути
значно зменшеним - до 5-Ю хвилин. Звідси
термін “швидка статика”. Отже, для
“швидкої статики” час спостережень
скорочується до проміжків часу, близьких
до методу “стій/йди”.
Проте
під час “швидкої статики” мобільна
станція залишається на пункті 5-10 хвилин.
Потім вона вимикається і переміщується
на наступну точку. Під час знімання в
режимі “стій/йди” мобільна станція
залишається увімкненою, а захоплення
супутників обов’язково зберігається
також під час переміщення приймача з
точки на точку. У цьому істотна відмінність
між “швидкою статикою” та методикою
“стій/йди”.
З іншого
погляду, “швидка статика” є різновидом
статичного методу. Для “швидкої статики”
особливо необхідно, щоб іоносферні
збурення були більш- менш ідентичними
для двох точок встановлення. Для всіх
GPS-вимірювань
і, особливо, для “швидкої статики”
пртрібно намагатися мінімізувати
довжини базисних ліній. Для надто
короткого часу спостережень, поганого
геометричного фактора (
359Визначення координат методом “швидкоїстатики”
GDOP)
або інтенсивних іоносферних збурень
можлива така ситуація, коли програмне
забезпечення під час постоброблення
розв’яже неоднозначність, але результати
будуть спотворені й істотно відрізнятимуться
від технічних характеристик приймачів.
Під час вимірювання “швидкою статикою”,
як і в попередніх технологіях, працюють
щонайменше два приймачі. Один -
встановлений на пункті відносності,
другий переміщується з пункту на пункт.
Технологія вимагає одноразового
вимірювання на кожному визна-
Кількість
супутників |
Наближена довжина базисних ліній, км |
Приблизний час спостережень |
|
вдень, хв |
Вночі, хв |
||
4 і більше |
до 5 |
5-10 |
5 |
4 і більше |
5-10 |
10-20 |
5-10 |
5 і більше |
10-15 |
більше за 20 |
5-20 |
Ця
технологія позбавлена недоліків
методики “стій/йди”. Вона ґрунтується
на подвійному GPS-вимірюванні
на кожному пункті, що визначається, не
вимагає, як технологія “стій/йди”,
постійного безперервного зв’язку із
супутниками під час транспортування
приймачів із пункту на пункт.
У
вимірюванні беруть участь щонайменше
два приймачі. Можуть одночасно
працювати декілька рухомих приймачів.
Тоді потрібно розраховувати маршрути
так, щоб усі приймачі переміщались
приблизно одночасно, тому що всі рухомі
приймачі повинні починати спостереження
на нових пунктах (після переміщення)
одночасно. Увесь маршрут кожний рухомий
приймач повинен пройти за 2 години.
Вимірювання на кожному пункті триває
близько 10-15 хвилин. На останньому пункті
маршруту, що визначається, чекаємо 1-2
години на зміну конфігурації супутників
і заново виконуємо спостереження GPS
на
кожному визначуваному пункті (реокупація)
у зворотній послідовності. Це подвійне
вимірювання на кожному пункті замінює
ініціалізацію. Точність визначення
вектора завдовжки до 10
км цим методом із застосуванням
високоточних, двочастотних приймачів
є такою: довжина вектора 3 см ± 2
х 10
6S,
перевищення кінців вектора 4 см ± 2 х
lO^S.
360Технологія псевдостатична, псевдокінематична, реокупаційна (Reoccupation)
Перевага
цієї технології в тому, що вона не
потребує зв’язку із супутниками
під час транспортування приладів;
недоліки - необхідність подвійного
встановлення приймачів на тих самих
пунктах та необхідність одночасного
спостереження не менше ніж п’яти
супутників.
Робота
у режимі “кінематика” аналогічна до
режиму “стій/йди”. Вона складається
із двох частин:
Частини
ініціалізації, яка необхідна для того,
щоб розв’язати початкові
неоднозначності під час постпольового
оброблення, виконаного за допомогою
програмного забезпечення SKI.
Мобільної
частини, у межах якої розв’язання
неоднозначності вносяться у програмне
забезпечення SKI.
Розбіжностями
між режимами “кінематика” і “стій/йди”,
по-перше, є те, що під час мобільної
частини в режимі “стій/йди” вимірювання
стосуються тільки реальних точок на
місцевості, а під час мобільної частини
в режимі “кінематика” вимірювання
стосуються визначених моментів часу;
по-друге, як уже зазначалось, у режимі
“кінематика” мобільний приймач
рухається безперервно, а в режимі
“стій/йди” мобільний приймач зупиняється.
Ініціалізація
та наступна за нею мобільна частина
називаються
Ініціалізація
- необхідний процес. Неоднозначності
повинні бути розв’язані під час
постопрацювання за допомогою програмного
забезпечення SKI.
Тільки
після цього значення знайдених
неоднозначностей будуть послідовно
передаватися вперед за допомогою SKI
у
мобільну частину ланки.
Ініціалізація
може бути виконана з використанням:
Режиму
“швидка статика”.
Встановлення
станції на точці з відомими координатами.
На
мобільній ділянці ланки повинно
спостерігатися не менше від чотирьох
супутників. Якщо супутників менше ніж
чотири, через втрату захоплення сигналу
або розташування супутників SKI
не
може передавати вперед значення
неоднозначностей, і ланка буде перервана.
Значення
Щоб
досягти високоточних результатів
визначень координат у режимі “кінематика”,
необхідно виконувати вимірювання у
максимально сприятливих вікнах
розміщення супутників.
361///.2.8. Робота у режимі “кінематика”
ланками
режиму “кінематика”.
GDOP
не
повинне перевищувати 8,
якщо результати за точністю мають
досягати значень, зазначених у технічних
характеристиках. Бажано, щоб значення
GDOP
дорівнювало
або було менше за 5.
Вікно |
Кількість
супутників, їхня висота над горизонтом,
|
Добре вікно |
5 і більше супутників,
висота
за можливістю більше ніж 20°,
|
Можна використовувати, але не рекомендується |
4
супутники, супутники вище ніж 15°,
|
Не рекомендується використовувати |
4
супутники, |
Використовувати не можна |
3 супутники або менше |
Визначення
координат у режимі “Кінематика у
польоті” (КВП) забезпечують отримання
траєкторії руху сенсора без необхідності
виконання статичної ініціалізації.
Сенсор може безперервно рухатись,
починаючи з першої епохи спостережень.
Ланка
вимірювання в режимі КВП складається
тільки з мобільної (рухомої) частини.
У цьому режимі може бути досягнутий
такий самий рівень точності визначення
координат, як і в режимі “кінематика”.
Для цього необхідно:
під
час першої епохи спостережень захопити
не менше від п’яти супутників;
повинно
бути невеликим значення коефіцієнта
відсутність
пропуску циклів або зникнення сигналу
під час перших 200
секунд спостережень у ланці;
максимальна
відстань між референцною і мобільною
станціями повинна зберігатись на рівні
не менше ніж 5 км.
Значення
неоднозначностей будуть передаватись
вперед по ланці КВП доти, доки будуть
спостерігатись не менше від чотирьох
супутників без втрати. Як тільки
кількість супутників стане меншою від
чотирьох, необхідно буде ще 200
секунд спостережень не менше ніж п’яти
супутників без їхньої втрати.
Програма
для опрацювання GPS-вимірів
буде опрацьовувати результати у два
етапи:
На
першому етапі неоднозначність буде
розв’язуватися після перших 200 секунд
реєстрації даних. Після цього розв’язані
неоднозначності передаються вперед
протягом часу спостереження не менше
ніж чотирьох супутників.
362Робота у режимі “кінематика у польоті”
GDOP;
На
другому етапі розв’язані неоднозначності
передаються назад на початок ланки, що
забезпечує отримання високоточних
результатів визначення координат для
першої епохи під час руху вперед.
Метод
КВП рекомендується застосовувати, якщо
ініціалізацію в статичних умовах
важко виконати або під час визначення
координат із рухомих об’єктів.
Щоб
досягти високоточних результатів
визначень координат у режимі “Кінематика
у польоті”, необхідно виконувати
вимірювання у максимально добрих вікнах
розташування супутників, поданих у
табл. ІІІ.2.5.
Ця
технологія спочатку спиралась тільки
на навігаційні кодові вимірювання
псевдовіддалей, які виконувалися з
розривами в часі. В останні роки в цій
технології почали застосовувати також
фазові вимірювання й опрацювання
вимірів типу “past-processing”.
Істотним
у цій новітній технології є те, що базова
станція передає до рухомого приймача
поправки, які використовує цей приймач
для уточнення свого положення (координат).
Сучасна
диференційна технологія передбачає
наявність базової станції, яка
стаціонарно, цілодобово працює на
пункті з високоточно визначеними
координатами і визначає певні
систематичні похибки. Якраз такі дані,
як поправки, передаються до рухомих
приймачів. Це дає змогу в реальному
часі визначати точні результати
(координати) рухомого приймача.
Зауважимо,
що під час цього методу користувач може
мати тільки один приймач, оскільки роль
другого приймача виконує базова,
стаціонарна станція.
Для
диференційних технологій використовують
спеціально обладнані приймачі, які
повинні підтримувати безперервний
зв’язок із базовою станцією. Деякі із
цих приймачів, що забезпечують метрову
точність визначення координат, мають
масу менше ніж 1
кг, а їхні розміри такі, що вони поміщаються
на долоні.
Точність
вимірювання DGPS,
що
ґрунтуються тільки на кодових
вимірюваннях, становить 1-2 м. Така
точність достатня для навігаційних
цілей, а також для виклику міліції
(поліції), швидкої допомоги, пожежників,
автотранспорту тощо. На цих засадах
працюють також морські та авіаційні
системи.
363
Технологія диференційного dgps-вимірювання (Differential gps)
ІІІ.З. Побудова
державних геодезичних мереж (ДГМ)
супутниковими методами
ІІІ.З. 1.
Загальні відомості про побудову ДГМ
супутниковими методами
Керівний
технічний документ (КТД) побудови
державної геодезичної мережі (ДГМ)
супутниковими методами створений
відповідно до чинних “Основних положень
створення ДГМ України”. ДГМ - це
сукупність пунктів, рівномірно
розташованих на території країни й
закріплених на місцевості спеціальними
центрами, які забезпечують їхнє
збереження та стійкість у плановому
та висотному аспектах протягом тривалого
часу.
Складовими
частинами ДГМ є планова й висотна
геодезичні мережі, пункти яких повинні
бути суміщені або мати надійний
геодезичний зв’язок.
Державні
геодезичні планові та висотні мережі
створювались окремо класичними, до
того ж принципово різними методами.
Просторові
ДГМ також створюються в інтересах
господарської діяльності, науки та
оборони країни для розв’язання таких
основних задач:
встановлення
єдиної системи координат на території
усієї країни;
забезпечення
картографування країни, акваторій
морів та внутрішніх водойм;
вивчення
природних ресурсів та ведення державних
кадастрів;
забезпечення
вихідними даними засобів наземної,
морської й аерокосмічної навігації,
аерокосмічного моніторингу довкілля;
вивчення
фігури й гравітаційного поля Землі та
їхніх змін у часі;
вивчення
геодинамічних явищ та рухів земної
поверхні;
вивчення
зон деформацій земної поверхні для
складання карт загального сейсмічного
районування;
вивчення
руху полюсів та нерівномірності
обертання Землі;
метрологічне
забезпечення високоточних технічних
засобів визначення розташування й
орієнтування.
У
світовій практиці супутникові просторові
мережі прийнято поділяти на:
глобальні;
364
Супутникові
методи дають змогу створювати просторові
(планові та висотні) мережі одночасно.
Надалі будемо розглядати тільки
просторові мережі, що створюються
супутниковими методами [25, 26].
континентальні;
національні;
регіональні;
локальні.
Зрозуміло,
що національні мережі є державними
геодезичними мережами. Інші - регіональні,
локальні є мережами, що створюються на
певних частинах країни, регіональні -
на значних за площею територіях, а
локальні - на значно менших.
Далі
будуть розглядатися національні,
регіональні та локальні мережі.
Розглянемо
мережі, що створюються з використанням
методів супут- никової геодезії.
Просторове
положення пунктів АГМ-1 визначається
методом супут-
никової
геодезії з відносною похибкою
Пункти
АГМ-1 повинні бути вставлені у мережі
нівелювання 1 та 2 класів, що дає змогу
визначити перевищення нормальних висот
між суміжними пунктами із с. к. п., не
більшою за 0,05 м.
На
кожному пункті АГМ-1 виконуються й
періодично повторюються визначення
відхилень вискових ліній із середньою
квадратичною похибкою, що дорівнює
0,5".
Пункти
2 класу також мають бути суміщені з
геометричним нівелюванням 1,
2,
або 3 класу, яке забезпечить точність
взаємного положення пунктів за висотою
із с. к. п., не більшою за 0,05 м на рівнині,
а в гірських районах - 0,2 м.
365Астрономо-геодезичні
мережі 1 класу
(АГМ-1) будуються у вигляді однорідної
за точністю мережі, що складається з
рівномірно розміщених пунктів, віддалених
один від одного на 50-150 км. Частина
пунктів АГМ-1 являє собою постійно діючі
(перманентні) станції супутникових
спостережень та астрономо-геодезичні
обсерваторії, на яких виконується
комплекс супутникових,
астрономо-геодезичних, гравіметричних
та геофізичних спостережень, що
забезпечить редукування координатних
визначень на єдину епоху з урахуванням
релятивістських ефектів, приливних та
інших рухів земної кори.Др/р
= 1:108
(де Ар - с. к, п. визначення геоцентричного
радіуса р - певного пункту). Кожний пункт
АГМ-1 має бути пов’язаний супутниковими
вимірами не менше як із трьома суміжними
пунктами мережі.Геодезична
мережа 2 класу.
Пункти розташовуються на відстані 8-12
км один від одного, а на територіях
міст, великих промислових об’єктів -
5-8 км і визначаються, як правило,
супутниковими методами (допускається
визначення традиційними методами) із
відносною похибкою 1/300000. Найбільша
довжина сторін 20 км, найменша - 5 км.
Нові
просторові мережі згущення 3 класу
будуються тільки відносними методами
супутникової геодезії. Відносне
визначення взаємного положення пунктів
повинно бути забезпечене з похибкою
1:200000,
а середня квадратична похибка - 0,05 м.
Вихідними пунктами побудови є пункти
старших класів.
Пункти
просторової мережі 3 класу (як і 2 класу)
повинні бути суміщені з мережами
нівелювання 1,
2
або 3 класів, які забезпечать точність
висотного положення пунктів із с. к.
п., не більшу за 0,05 м, а у гірській і
важкодоступній місцевості нормальні
висоти можуть визначатися, як і мережі
2 класу, GPS-
нівелюванням, яке виконується відносними
супутниковими методами. У такому разі
середня квадратична похибка пунктів
за висотою також не повинна перевищувати
0,2
м, як і для мереж 2
класу.
Просторові
геодезичні
Виробничий
цикл побудови ДГМ складається з таких
основних циклів
робіт:
проектування
мереж;
рекогностування
й побудова геодезичних пунктів;
спостереження
методами супутникової геодезії;
математичне
опрацювання вимірів;
складання
каталогів просторових координат.
Для
забезпечення топографічного знімання
встановлюють такі норми щільності
пунктів та реперів ДГМ:
для
знімання у масштабі 1:25000 і 1:10000 - 1 пункт
на 30 км2
і 1 репер на трапецію масштабу 1:10000;
для
знімання у масштабі 1:5000 - 1 пункт на
20-30 км2
і 1 репер на 10- 15 км2;
для
знімання у масштабі 1:2000 і більше - 1
пункт на 5-15 км2
і 1 репер на 5-7 км2.
366Геодезична
мережа згущення 3 класу
будується з метою збільшення кількості
пунктів до щільності, яка забезпечує
створення знімальної (робочої) основи
великомасштабного топографічного та
кадастрового знімання.мережі
спеціального призначення,
які, по суті, є регіональними та
локальними, здійснюються методами
супутникової геодезії або традиційними
геодезичними методами. Усі геодезичні,
астрономо-граві- метричні вимірювання
та супутникові спостереження на таких
мережах зазвичай виконуються з
підвищеною точністю й приводяться до
єдиної геодезичної системи координат
для використання їх під час зрівноваження
ДГМ.
Положення
пунктів ДГМ визначається у двох системах
координат: за- гальноземній та референцній.
Між обома системами встановлюється
однозначний зв’язок, який визначається
параметрами взаємного переходу
(елементами орієнтування).
За
загальноземну систему координат
приймається Європейська геоцентрична
система координат ETRF-89
із
початком координат у центрі мас Землі
та з відліковим еліпсоїдом GRS-80,
що
має такі параметри:
велика
піввісь
стиснення
еліпсоїда 1:298,2572220101;
мала
піввісь
середній
радіус
значення нормального гравітаційного поля на екваторі
значення нормального гравітаційного поля
на полюсі
перший
ексцентриситет
Референцною
системою координат залишається система
координат 1942 року (СК-42) із вихідними
даними референц-еліпсоїда Красовського:
велика
піввісь
мала
піввісь
стиснення
еліпсоїда 1:298,3;
висота
геоїда в Пулково над референц-еліпсоїдом
дорівнює нулю;
геодезичні
координати Пулковської обсерваторії
(центр сигналу
широта
довгота
від Гринвіча
геодезичний
азимут на пункт Бугри 121°06'42,305";
середній
радіус Землі 6371117,6729 м;
перший
ексцентриситет е2
= 0,006693420623.
Положення
пунктів у прийнятих системах задаються:
просторовими
прямокутними координатами
367Системи координат, що використовуються у космічній геодезії
a
=
6378137 м;b
=
6356752 м;Rx
=
6371008,7714 м;ge
=
9,7803267715 мс'2;
gp
=
9,8321863685 мс2;
е2
= 0,00669438002290.
a
=
6378245 м;b
=
6356863 м;А
);В
= 59°46'15,359";L
=
28°19'28,318";
X,
У ,Z.
Вісь X
лежить у площині нульового меридіана,
вісь У-у площині екватора і спрямована
праворуч від площини нульового
меридіана, а напрямок осі Z
збігається
з віссю обертання відлікового еліпсоїда;
геодезичними
еліпсоїдальними координатами
плоскими
прямокутними координатами
Рис.
І І 1.3.1. Прямокутні геоцентричні
координати, координати X, Y,
Z
та
геодезичні еліпсоїдальні координати
В, L;
АО
- прямовисна
лінія;
АК
- нормаль
до еліпсоїда в точці А; АА' = Н - геодезична
висота точки А
Нагадаємо:
геодезична широта
Плоскі
прямокутні координати, відомі з курсу
топографії, обчислюються на площині у
комфорній проекції Гаусса-Крюгера у
шестиградусних зонах, а під час знімання
у масштабах 1:5000 і більше - у триградусних
зонах.
Осьові
меридіани шестиградусних зон на
території України - 21°, 27°, 33°, 39°, а
триградусних зон - 21°, 24°, 27°, 30°, 33°, 36°,
39°.
Геодезичні
висоти пунктів ДГМ визначаються
безпосередньо або обчислюються як
сума нормальної висоти й висоти
квазігеоїда над еліпсоїдом:
Н
= Ннор+М, (ПІ.3.1)
368В,
Ь,Н
;X,
Y
.
В
точки А
- це кут, створений нормаллю до поверхні
еліпсоїда із площиною екватора;
геодезична довгота L
точкй
А
- це
двогранний кут, створений площиною
початкового меридіана та площиною
геодезичного меридіана. Геодезичний
меридіан проходить через нормаль до
еліпсоїда АК
і паралельний до полярної осі РР'.
Геодезична висота - відрізок по нормалі
до еліпсоїда від поверхні еліпсоїда
до пункту на фізичній поверхні Землі.
де
відліковим
еліпсоїдом. Нормальні висоти пунктів
ДГМ визначаються у Балтійській системі
висот, вихідним пунктом якої є нуль
Кронштадтського футштока. Нижче подано
формули переходу від еліпсоїдальних
геодезичних координат до просторових
прямокутних координаті,
І
= (і' + Я) cos5
•
cosZ,;
\
z
=
f
h2
KrN'
+ H
Vа
sin
5,
(III.3.2)
де
Va2
cos2
Обернений
перехід від
tgB
=
Z
уіХ2
+Y2
+
—■■
(ІІІ.3.2)
Формули
(ІІІ.З.З) дають змогу організувати цикл
наближень. Для першого наближення
приймається
значенням
Н
= уіХ2
+Y2
■
sec
В
- N';
N'
=
а
(ІІІ.3.4)
Зазвичай
для досягнення розбіжності між наступним
і попереднім наближеннями
Астрономічні
широти й довготи, які визначаються на
пунктах ATM,
обчислюються
в екваторіальній астрономічній системі
координат (рис. ІІІ.3.2).
369Н
- геодезична висота; Ннор
-
нормальна висота; N
-
висота квазігеоїда надY,
Z, які
широко застосовують у космічній
геодезії:Y
= (N' + H)
cos 5 • sin Z,;N'
= . :: — r—
- радіус
першого вертикала; a
, b-
велика
таB
+ b2
sin2
В
мала
півосі відлікового еліпсоїда.X,
Y,
Z неминуче
пов’язаний з ітераційним процесом
обчислення широти В
і висоти Н.
Зручні для обчислення на комп’ютері
формули можна отримати із системи
рівнянь (ІІІ.3.2):
e—tgB
= C
+
a
tgB. N' + H
S 5tgB
=
С.
Для другого та наступних наближень заВ
з попереднього наближення розраховують
значення:е
sin
ВВ
= 0,03" достатньо трьох наближень.
Перехід від еліпсоїдальних геодезичних
координаті?, L,
Н
до плоских координат X,
Y
студенти
виконують під час розрахунків координат
кутів рамки трапеції плану масштабу
1:2000.
т
Рис.
III.
3.2. Екваторіальні астрономічні системи
координат
(екліптика не показана)
Z
-
точка зеніту,
Як
відомо, часовий кут точки весняного
рівнодення
зоряному
часу у момент спостережень у певній
точці
Екваторіальна
система координат відповідає
фундаментальному зоряному каталогу
на епоху загального врівноваження ДГМ
і приводиться до міжнародного
умовного початку й системи астрономічних
довгот
370NS
-
горизонт; z
-
зенітна віддаль супутника (дуга Zo);QQ
-
екватор; h
-
висота супутника (дуга сК);Р
- полюс; 8
- схилення супутника (дуга сМ);N
-
точка
півночі; а
- пряме
сходження супутника (дуга уМ);S
-
точка півдня; t
-
часовий кут супутника;a
-
азимут супутника;Ґ
-
точка надиру; ty
-
часовий кут точки весняного рівнодення
(ty
=
t
+
а);
а
-
світило-супутник; ф
-
широта у
-
точка весняного рівнодення;ty
числово
дорівнюєА,
а різниця довгот ДА, у двох точках
дорівнює різниці у часі в цих точках.X
Міжнародного бюро часу.
Для
побудови ДГМ використовується атомний
час, який задається шкалою Державного
еталона часу й частоти (з урахуванням
поправок за перехід до системи
міжнародного координатного часу).
Масштаб ДГМ задається державним еталоном
довжини - метром, за довжину якого
приймається відстань, яку проходить
світло у вакуумі за 1:299792458 частку
секунди.
Метрологічне
забезпечення геодезичних робіт
здійснюється із використанням
метрологічної бази Держстандарту
створенням мережі відомчих взірцевих
базисів, основних довготних пунктів
та еталонних азимутів.
Нагадаємо,
що у геодезії використовуються не
абсолютні, а відносні супутникові
спостереження і, по суті, застосовується
топоцентрична система координат.
Прямокутні координати в цій системі
будуть дорівнювати різниці координат
двох точок кінців базисної лінії 1
та 2.
Сферичні
координати у топоцентричній системі
можуть бути визначені за довжиною
сторони Z)12
та
кутами
Зауважимо,
що коли за основну площину
Кути
Кути
можна знайти за формулами
(ІІІ.3.5)
Ф
=
УІАХ2+АГ
(ІП.3.6)
Зворотний
перехід можна виконати за формулами
гАїЛ I^cos
Ф-со*/7;\
AY
=D
совФ-віп.#;
> AZ sin
Ф.
(ІІІ.3.7)
Детальніше
це описано у [2].
371Л
і Ф, аналогічними кутам а і 8
в зоряній системі координат (рис.
III.3.2).XOY
прийнято
площину, яка паралельна до екватора,
то кут Лп
відраховується від меридіана Гринвіча
до проекції Dn
на
цю площину. Кут Ф12
характеризує нахил лінії Dn
до
екватора.Л
і Ф в екваторіальній топоцентричній
системі називають орієнтуючими
кутами сторони Dl2.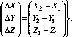

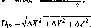
arctg
—=========
Основним
завданням технічного проектування СГМ
є оптимальне положення пунктів на
місцевості, яке залежить від вартості
робіт, дотримання заданої точності та
щільності, однорідності та правильної
геометрії, тривалого збереження центрів.
Для
складання проекту, передусім, необхідно
зібрати дані про фізико- географічні,
економічні особливості та раніше
виконані геодезичні роботи на території.
Інформацію про геодезичні роботи,
виконані раніше, надає інспекція
Державного геодезичного нагляду. Такі
матеріали містять:
загальний
список усіх звітів раніше виконаних
робіт, роки виконання, назви
організації виконання робіт;
виписки
з каталогів координат та висот пунктів,
їхні класи;
картки
закладання центрів;
схеми
геодезичних побудов;
дані
про системи координат та висот.
Проект
мережі створюють на топографічних
картах масштабів 1:200000- 1:10000. На карту
наносять всі наявні пункти. Нові пункти
необхідно розташовувати у вершинах
рівносторонніх трикутників. Рекомендуються
два найпоширеніші методи побудови
супутникових мереж:
радіальний,
коли всі пункти мережі координуються
з однієї рефе- ренцної або перманентної
станцій (рис. ІІІ.З.З);
мережевий
метод (метод замкнутих геометричних
фігур) - вимірювання виконуються на
кожній лінії або на кожному пункті
мережі (рис. ІІІ.З.З).
372
Рис.
ІІІ.З.З. Радіальний метод побудови
мереж: А-
референцний
пункт;
□-///.3.3. Проектування та рекогностування просторових супутникових геодезичних мереж (сгм)

1
2
Рис.
111.3.4.
Мережевий метод побудови
(однорангова
мережа):
А
-
референцний
пункт;
[7]
- пункти,
що визначаються
Недоліками
радіального методу є неминуче виникнення
довгих векторів та відсутність
контрольних вимірів. Перевагою є те,
що можна виконувати побудову одним
приймачем і те, що побудована мережа
однорідна за точністю.
Контролем
у такій мережі можуть бути тільки
незалежні вимірювання іншими приладами
та від інших відомих точок. Критерій
точності і надійності вимірів
підвищується, якщо організуються
мережеві вимірювання. На практиці
застосовують дві технології мережевих
побудов:
повторного
вимірювання на пунктах, для яких
задається кількість обов’язкового
повторного вимірювання на кожній
мережі;
обов’язкового
вимірювання кожної лінії мережі.
Щоб
позбутися довгих векторів, необхідно
мати декілька референцних пунктів. На
жаль, виникають різнотонні (багаторангові)
мережі (рис. III.3.5). Крім того, необхідно
мати декілька приймачів.
1
2
Рис.
111.3.5. Мережевий метод побудови
(багаторангова
мережа):
А
- референцні
пункти;
[•]-
пункти,
що визначаються
373
Мінімальна
кількість сесій (сеансів) спостережень
(ІИ.3.8)
R
а
для другої технології (вимірювання
кожної лінії) за формулою
R-O
Друга
технологія (вимірювання усіх векторів)
поширеніша.
На
рис. ІІІ.3.6 подано схему, яка пояснює
послідовність вимірювання і перенесення
станцій для другої технології. На схемі
подано 20 пунктів, назви яких складаються
з букви та цифри. Наприклад, лівий
верхній пункт А-1, нижній правий пункт
D-5
і
т. д. Усіх приймачів шість. Використовувались
три приймачі, які залишалися на тих
самих пунктах у попередній та наступній
сесіях.
Рис.
III.
3.6.
Схема вимірювання за другою технологією
Тому
кількість сесій
У
першій сесії приймачі встановлені на
пунктах А-1, В-1, С-1, А-2, В-2, С-
Були
виміряні сім векторів. Далі, для
виконання другої сесії приймачі з
пунктів А-1, В-1, С-1 були перенесені на
пункти A-З,
В-3, С-3. Знову в другій
374N
для
мережі, якщо кількість пунктів S
і
використовується R
приймачів
для кількості повторних вимірювань М
та кількості приймачів, які використовувались
у попередній та наступній сесіях О,
визначається для першої технології
(спостереження на кожному пункті) за
формулоюN
= ——. (ІП.3.9)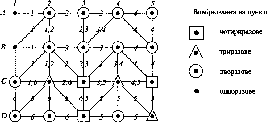
N- = =
5,67 «6
сесій.R-O
6-3
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
3 |
6 |
10 |
15 |
21 |
28 |
36 |
45 |
55 |
66 |
78 |
Під
час проектування СГМ з метою висотного
прив’язування необхідно передбачити
включення в мережу Мінімум чотирьох
висотних реперів відповідного класу.
З метою підвищення надійності та
контролю визначення параметрів переходу
між ETRF-89
і
СК-42 рекомендується включати в СГМ уже
існуючі пункти того самого або вищого
класу, розташовані на території робіт
і визначені тільки в системі координат
СК-42.
375Польове
рекогностування
пунктів мережі здійснюється на підставі
затвердженого технічного проекту.
Рекогностування
розпочинається з відшукування на
місцевості та обстеження стану наявної
геодезичної основи, до якої планується
прив’язування нових пунктів. Оцінюється
стан пункту; його збереженість; порушення
зовнішнього оформлення; стан споруд,
у які закладені стінні знаки; наявність
і розмір тріщин у стінах; видимі зміщення
фундаменту. Репери, закладені в зруйновані
споруди або споруди з видимими
деформаціями, розташовані біля
залізничних шляхів, вважають нестійкими.
До нестійких належать також репери,
закладено в споруди, навколо яких є
значна вологість або які закладені в
місцевість зі штучним або природним
зволоженням ґрунту, у торф’яниках
тощо.
Рекогностувальна
бригада виконує відновлювальні роботи:
бетонує відколений кут пілона, наносить
протиерозійну суміш на марку, верхню
частину репера, відновлює розпізнавальний
знак та стовп із охоронним написом,
зовнішнє оформлення.
Важливим
завданням рекогностування є уточнення
на місцевості місць закладання нових
реперів.
Вважають
за доцільне поєднувати рекогностування
із закладанням нових пунктів. Пункти
для супутникових спостережень вибирають
з дотриманням таких вимог:
відсутність
на висоті 15° над горизонтом перешкод
для проходження радіосигналів;
відсутність
поблизу пункту відбивних поверхонь
(металеві дахи, водні поверхні, рекламні
щити, металеві огорожі);
відсутність
поблизу джерел електромагнітного та
радіовипромінювання;
віддаленість
від доріг (з погляду безпеки та впливів
вібрації під час спостережень).
Окрім
пунктів мережі, на відстані 500-1000 м
закладаються два орієнтирні пункти,
на які забезпечується видимість
(земля-земля). У разі неможливості
виконання супутникових спостережень
над центром знака допускається
встановлення антени приймача поза
центром, але елементи приведення повинні
бути мінімальними, а під час висотного
прив’язування повинна бути можливість
передавання висоти на антену приймача
геометричним нівелюванням.
У
результаті виконання рекогностування,
будівельних робіт подаються такі
документи:
остаточна
схема мережі;
уточнені
схеми прив’язувальних ліній, передавання
висот через водні перешкоди;
376
акти
обстеження та оновлення пунктів;
карти
рекогностування, обстеження, оновлення
та побудови геодезичних пунктів;
акти
втрати пунктів;
акти
перезакладання центрів;
акти
здачі пунктів на зберігання.
За
результатами рекогностування складають
кінцевий проект мережі і загальну
програму виконання робіт із зазначенням
супутникових технологій, якими будуть
виконуватися вимірювання. Ці дані
подаються в технічному звіті про
результати рекогностування та закладання
знаків. Графік виконання й закінчення
робіт створюється відповідно до обсягів
робіт та можливостей виконавця.
Кошторис
на виконання робіт складають згідно з
нормативними документами, затвердженими
Державною геодезичною службою України.
Перед
виїздом на польові роботи для створення
СГМ на основі технічного завдання і
технічного звіту складають робочий
проект спостереження мереж, який
затверджується в робочому порядку.
У
робочому проекті детально висвітлюються
розділи: “Організація робіт” і “Польові
роботи”. Вихідними даними для складання
робочого проекту, крім технічного
завдання проекту, звіту про рекогностування
та закладення пунктів, є максимальна
кількість приймачів, їхні типи, відповідно
- кількість виконавців-спостерігачів
та кількість одиниць транспорту.
Під
час складання графічної частини робочого
проекту на картах вищого масштабу, ніж
у технічному проекті, наносять пункти
супутникової мережі, вибрані як основні
та резервні. На тих самих картах вибирають
оптимальні шляхи переміщення між
пунктами і на їхній основі складають
схему переміщень на об’єкті робіт із
відзначенням місць і часу зустрічі для
концентрації інформації, місць переправ
через водні перешкоди, схеми радіозв’язку
тощо.
За
допомогою програм, що входять у
супутникові приймачі, уточнюються
методи побудови і будуються графіки
пониження геометричного фактора
Оскільки
період обертання супутника навколо
Землі становить близько 12 годин, ці
графіки повторяються з такою самою
періодичністю. Тому графіки складають
із розрахунку один графік на 7-10 днів.
Взагалі увімкнення приймачів доцільно
проектувати на нічний період доби,
найсприятливіший для спостережень.
Тоді світлий період доби можна
використовувати для переміщення по
об’єкту.
377
3.4. Складання робочого проекту
GDOP.
Широта:
56°15‘N,
Довгота:
43°45'Е. Дата: 03/28/02, Вікно: 10.40-21.00.
12 14
U
Вікна,
сприятливі для вимірювань
16
18 20
П
Вікна,
несприятливі для вимірювань
Рис.
ІІІ.3.7. Гоафік зниження геометричного
фактора на пункті
Попередньо
з’ясовують інтервали часу зі сприятливими
За
наявності великомасштабних карт
складають таблиці або зарис перешкод
на пункті.
Послідовність
роботи під час камерального визначення
перешкод навколо пункту спостережень
така: на плані масштабу 1:5000-1:500
транспортиром визначають азимути
з пункту на ближні точки перешкод з
урахуванням зближення ліній сітки та
схилення магнітної стрілки. Точність
азимута - не грубіле за 20'. Вертикальний
кут визначають за формулою
h
V
= arctg
—,
де
5
- віддаль до перешкоди, що визначається
за допомогою вимірника та поперечного
масштабу; висоту перешкоди h
знаходять,
використовуючи інформаційне навантаження
плану (кількість поверхів у споруді,
висоту дерев, рельєф тощо).
Якщо
великомасштабних планів на район робіт
немає, зариси складають під час
рекогностування.
Розробляється
програма спостережень на окремих
пунктах або програма спостереження на
кожний день. У табл. НІ.3.1 подано план
організації сесії на один день.
Програмою
заплановано п’ять сесій. Усіх приймачів
та відповідно виконавців п’ять.
378
DOP
на
кожну добу на період спостережень. Ці
інтервали уточнюються з отриманням
нового альманаху ефемерид.
№ сесій І |
Час спостере жень |
Приймачі |
і |
II |
III |
IV |
V |
Спосте рігачі |
і |
2 |
3 |
4 |
5 |
||
|
Номери пунктів |
1573 |
1574 |
1575 |
1019 |
1706 |
|
2 |
11ш-124и |
1256 |
1261 |
1576 |
1019 |
1012 |
|
3 |
13‘>-1415 |
1672 |
1670 |
1671 |
1019 |
1708 |
|
4 |
14"-15JU |
1674 |
1654 |
1801 |
1019 |
1673 |
|
5 |
15и-16зи |
1800 |
1702 |
1907 |
1019 |
1704 |
Діаграма
перешкод
і секторів видимостей по горизонту
пункту
180°
Вказати
перешкоди і а їхню віддаленість від
цупкі у
Вшоїа
над поверхнею землі, з якої Склав
зарисовано
горизонт м посада шдщк.даїа
Рис.
111.3.8. Діаграми перешкод по горизонту
на пункті ДГМ
379
Діаграма
перешкод по горизонту на пункті ДГМ
Північ
Висота,
з якої зарисований горизонт: 2 м
Назва
пункту; пункт ДГМ І класу
Шацьк,,.4-симвЛденшфікатор:8НАТ.>&
пункту:010
Місцеположення:с.Світять Місто:
Шацьк Країна: Україна......
Напис
на марці моиоліту:ГУПС 1512 Склав:
Сідоров Л.С.. 1
Рис.
111.3.8. Діаграми перешкод по горизонту
на пункті ДГМ (продовження)
Мережа,
що спостерігається, має один референцний
пункт. На цьому пункті (№ 1019) приймач
IV виконує спостереження без переїздів.
Інші 20 пунктів - роверні: приймачі
змінюють положення між сесіями. Час
виконання першої сесії вибирають,
враховуючи необхідність одночасного
виконання умови видимості і геометричної
конфігурації сузір’я супутників на
всіх пунктах, які задіяні в сесії. Тому
тривалість цього інтервалу спостережень
сесії повинна перевищувати тривалість
вимірювання будь-якого вектора. Загальна
тривалість вимірювання будь-якого
вектора складається з часу, необхідного
для виконання таких операцій:
380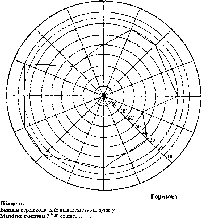
Клас дгм |
Відстані між пунктами, км |
Тривалість |
Примітка |
1 |
150-300 |
5-6 діб |
Фундаментальна мережа |
50-150 |
1-3 діб |
Пропорційно до довжини вектора |
|
2 |
10-20 |
2,5 год |
Двочастотний приймач |
5-10 |
30 хв-1 год |
Двочастотний приймач (пропор. довж. вект.) |
|
5-10 |
1-1,5 год |
Одночастотний приймач (пропор. довж. вект.) |
|
3 |
2-10 |
15-ЗОхв |
Двочастотний приймач (пропор. довж. вект.) |
2-Ю |
20 хв-1 год |
Одночастотний приймач (пропор. довж. вект.) |
Пояснювальна
записка до робочого проекту повинна
містити такі матеріали:
проектні
роботи із зазначенням усіх пунктів та
реперів, які задіяні у спостереженнях
і всіх векторів, що підлягають
вимірюванню;
програма
робіт на об’єкті з відображенням
періоду та часу роботи на пункті,
маршрутів переміщення на об’єкті;
роздруковані
графіки зниження геометричного фактора
та графіки- зариси на пунктах, де є
перешкоди;
технологія
виконання робіт з обґрунтуванням
вибору методу вимірювання та часу
спостереження на пунктах.
Перед
виїздом на польові роботи керівник
робіт проводить інструктаж з усіма
керівниками бригад і видає кожній
бригаді робочий проект або відповідні
витяги з нього.
381
II 1.3.5. Підготування комплексу приладів до польового вимірювання
Кожна
бригада укомплектовується приладами,
необхідними для виконання польових
робіт, обладнанням та матеріалами.
Подамо
детальний список усього необхідного
обладнання:
автомобіль
(бажано підвищеної прохідності);
приймач
із комплектом допоміжного обладнання;
додатковий
запам’ятовувальний пристрій;
2
комплекти кабелів;
2
акумулятори (із комплекту приймача
або автомобільні);
зарядний
пристрій для акумуляторів;
переговорний
пристрій з 2
акумуляторами (один запасний із зарядним
пристроєм до нього);
штатив;
оптичний
центрир;
комплекс
метеорологічних приладів (еталонований
психрометр із “сухим” та “мокрим”
термометрами), а також баромегр-анероїд;
оптичний
теодоліт (ЗО") для знімання елементів
приведення під час встановлення антени
приймача поза центром;
нівелір
із рівнем або компенсатором;
складна
шашкова рейка з рівнем;
ліхтарики;
бусоль;
рулетка
20
м;
інструменти
для дрібного ремонту та юстування
приладів;
комплект
карт масштабу 1:50000-1:25000 на район
вимірювання;
робочий
проект мережі (або витяг з нього) зі
схемами та списком пунктів, на яких
будуть виконуватися спостереження та
прив’язування, графіки виконання
вимірювання та зазначатися інформація
про доїзди до них;
картка
рекогностування, обстеження, оновлення
та побудови геодезичних пунктів
(реперів);
журнали
супутникових спостережень;
лист
графічного та аналітичного визначення
елементів центрування антени
супутникового приймача;
медична
аптечка для надання першої допомоги.
Перед
початком польового сезону супутникові
приймачі повинні пройти еталонування
на взірцевих базисах або метрологічних
полігонах. Повторно еталонування
виконується після кожного сильного
струсу або ремонту антен і радіочастотних
блоків приймача. Під час транспортування
та перенесення
382
приймач
потрібно оберігати від ударів та
пошкодження. Запам’ятовуввальні
пристрої, які входять до комплекту
приймача, необхідно зберігати в сухому
місці та оберігати від температурних
впливів, ударів, згинів, стежити, щоб
поверхня роз’ємів була чистою і
незапиленою.
У
цьому параграфі та у двох наступних
буде детально розглянуто питання будови
та можливостей застосування компактного
приймача РгоМагк-2 фірми Ashtech
(США)
для побудови геодезичних мереж та
топографічного знімання. Деталізація
цього питання можлива тільки під час
вивчення конкретного приймача, хоча
всі приймачі GPS
мають
багато спільних загальних систем,
вузлів та деталей. РгоМагк-2 -
повнофункціональна GPS
система,
що розв’язує задачі точного геодезичного
вимірювання та навігації. Комплект
системи РгоМагк-2 складається із двох
або більше приймачів з антенами та
допоміжними компонентами.
Приймач,
завдяки своїй компактності, менший за
вартістю порівняно з іншими приймачами,
а також доволі високий за точністю
вимірювання, широко застосовується у
геодезичному виробництві. Крім фірми
Ashtech,
аналогічний
приймач виготовляє фірма Magellan
Corporation, названий
ProMark
Х-СМ,
а фірма Ashtech
почала
випускати модифікований приймач
РгоМагк-3. Приймач РгоМагк-2 отримує та
зберігає неопрацьовані дані з
GPS-супутників
про кожну точку знімання. Дані із
приймача пізніше піддаються
пост-опрацюванню з метою визначення
положення точок знімання. Зовнішній
вигляд приймача показано на рис. ІІІ.3.9.
Рис.
111.3.9. GPS-приймач
ProMark-2 Рис.
ІІІ.3.10. Зовнішня GPS-антена
383
Будова та технічні характеристики компактного одночастотного приймача gps ProMark-2
Якщо
для навігації достатньо вмонтованої
у приймач антени, то для
отримання
даних точного геодезичного знімання
необхідна
Зовнішня
антена має точку, у якій фізично
збираються дані з GPS-
супутників
про положення (просторові координати)
саме цієї точки. Тому ця
точка антени
повинна прямовисною лінією проектуватися
на центр геоде-
зичного знака або
точки місцевості, положення якої
визначається. Антена
центрується
за допомогою оптичного центрира та
стандартного штатива або
GPS-штатива.
До
комплекту приймача входить
висоти
антени над центром знака (рис. ІІІ.3.13).
рч
І
Рис.
ІП.3.11. Зовнішній Рис. 111.3.12.
Вертикальний
антенний кабель подовжувач
антени
Початок
рулетки фіксується у виїмці, розташованій
збоку на корпусі
антени. Витягується
рулетка вниз у напрямку до центра знака
так, щоб
загострений штир, розташований
на корпусі рулетки, торкнувся знака. У
цю
мить береться відлік шкали рулетки.
Відлік дає не вертикальну, а похилу
висоту
антени над центром знака. Ця
висота може бути приведена до
вертикальної
висоти. Достатньо знати
радіус антени.
Рис.
Ні. 3.13. Вимірювальна
рулетка
384зовнішня
антена
(рис.
ІІІ.3.10)Зовнішній
антенний кабель
(рис. ІП.3.11) поєднується до РгоМагк-2
через
задню частину польового утримувача
приймача. Маленький роз’єм
під’єднується
до приймача, великий роз’єм - до антени.Вертикальний
подовжувач антени
(рис. ІІІ.3.12) забезпечує можливість
під’єднання
антени, коли вона встановлена на штатив.
Його довжина 76,2 мм.вимірювальна
рулетка
для вимірюванняОфісний
утримувач приймача з кабелем завантаження.
Цей тримач дає
змогу під’єднати
приймач РгоМагк-2 до офісного комп’ютера
з метою
завантаження в комп’ютер
даних GPS-знімання.
Як тільки приймач
установлюється
на тримач, кабель завантаження автоматично
поєднується до
приймача через
контакти, що розміщені на задній частині
приймача. Офісний
утримувач із
кабелем показано на рис. ІІІ.3.14.
Адаптер антени |
Трегер |
|
Бульбашка |
1 і |
рівня |
Підставка |
|
адаптера |
Оптичний Підішшльн, це гвинти |
Адаптер
та трегер
б
Рис.
ІІІ.3.16:
а
- антена,
адаптер,
трегер
та штатив; б - трегер та адаптер антени
окремо
та в зібраному вигляді
До
комплекту приладу входить
Програма
має модулі, які забезпечують завантаження
та опрацювання супутникових даних із
кожного приймача РгоМагк-2. Програмне
забезпечення записане на компакт-диск.
Ashech
Solutions User’s Guide - інструкція
з використання офісного програмного
забезпечення з метою планування
завантаження і постопрацювання даних.
385
програма
постопрацювання
(Ashtech
Solutions) (рис.
ІІІ.3.15).
До
комплекту приймача ще входить польова
сумка для транспортування приладу, а
також компакт-диск (Map
Send Streets). Компакт-диск
має тільки карти на територію США. Диск
не входить до комплекту системи приймача,
який продається за кордоном США.
Крім
того, під час роботи з приймачем необхідно
додаткові предмети, які не входять до
стандартного комплекту. Серед таких
предметів є штатив, підставка
(трегер-носій) та адаптер антени. На
рис. ІІІ.3.16, б показано ці три предмети
окремо та в зібраному вигляді разом з
антеною та штативом (рис. ІІІ.3.16, а).
У
трегер антени вмонтовано оптичний
центрир та підіймальні гвинти для
приведення антени в робочий стан.
Під
час роботи у псевдокінематичному та
кінематичному режимах для кріплення
РгоМагк-2 може бути використана
Рис.
III.
3.17.
GPS-eixa Рис.
Ill
3.18.
Клавіші приймача
На
рис. ІІІ.3.9 показаний загальний вигляд
приймача.
На
рис. ІІІ.3.18 показана панель керування
приймачем - керівні клавіші.
У
таблиці ІІІ.3.2 описано функції кожної
клавіші.
На
рис. ІІІ.3.19 показано три вікна, які дають
змогу виконувати редагування, описування
(ідентифікацію) пунктів, вводити або
змінювати деякі параметри Site
ID, Site description і
Receiver
ID.
Подамо
далі деякі дані про термін роботи джерел
електроенергії. Живлення приймача Pro
Mark-2 здійснюється
за допомогою двох стандартних батарей
типу АА. Також можна використовувати
будь-які батареї цього типу як одноразові
(лужні, літієві), так і перезарядні
(нікель-кадмієві, нікель-метал- гідридні,
лужні). Найдовше працюють літієві
батареї, потім лужні. Термін
386віха,
показана на рис. III.3.17.
Клавіші |
Опис дії |
ENTER, Введення |
Використовується під час виконання вибраної функції, редагування вибраних параметрів або введення вибраних значень, які наведені у вікні survey menu (меню в режимі “знімання”). Наприклад: серед них функція “Point Attribute” вибирається за допомогою стрілок “вверх” і “вниз”. Для виконання цієї функції потрібно натиснути клавішу ENTER і т. д. |
MENU, Меню |
Призначена для доступу до пункту Servey Menu в будь-який момент, навіть під час збирання даних (тобто під час спостережень) |
IN |
Ввійти у вибраний пункт меню |
OUT |
Вийти із вибраного пункту меню |
Червона кнопка on/off ув/вимкн |
Якщо клавішу швидко натиснути і відпустити, вмикається або вимикається приймач. Якщо утримувати клавішу 2 секунди, коли приймач уже ввімкнений, тоді дисплей підсвітиться. Якщо її знову утримувати 2 с, підсвічення вимкнеться |
Mark/GOTO |
Дає змогу отримати доступ до пункту Point Attribute (дані про пункт спостережень) у будь-який момент збирання даних |
ESC |
Використовується для закриття поточного і повернення до попереднього пункту меню. Відредаговані, попередньо не збережені параметри, закриті за допомогою цієї клавіші, не збережуться |
Овальна кнопка із чотирма стрілками |
Дає змогу виділити функцію, яку ви хочете виконати, або виділити величини, які потрібно ввести. Пункт “Mode” дає змогу працювати в режимах Survey або Navigate. Стрілки “вверх” та “вниз” призначені для перемикання між режимами Survey і Navigate |
Останній
сигнал Exterme
Low Pover. Після
такого сигналу робочий файл закривається,
а приймач вимикається через 10 с. Потрібна
заміна батарей.
На
рис. ІІІ.3.20 показана заміна батарей.
Необхідно відгвинтити гвинт, зняти
кришку відділення для батарей. Замінити
старі батареї на нові, ураховуючи
полярність. Закрити кришку та загвинтити
гвинт.
387
Description
BENCHMARK
AS0t_
Shift
1. . .... {Bagfef
Receiver
IQ
1234
Рис
III 3 19 Вікна
Site
ID, Site description i Receiver ID
Об’єм
пам’яті приймача Pro
Mark-2 для
зберігання даних - 8
МБ. Мінімальний час спостереження 7
годин за умови, що збирання даних
виконується в найгірших умовах, коли
10
супутників відстежуються з 1-
секундним інтервалом. За 10-секундного
інтерваду можна зберегти дані 72-
годинного інтервалу спостережень.
Тому
рекомендується:
Щоденно
переписувати зібрані дані із приймача
до комп’ютера.
Переписувати
дані із приймача після опрацювання.
Оскільки
території України немає у картах Map
Send Streets, то
файли, відведені під ці карти, можуть
бути зайняті файлами, що стосуються
безпосередньо знімання.
На
закінчення цього параграфа подамо
технічні параметри та фізичні специфікації
системи Pro
Mark-2.
388


Можливі режими GPS-знімання |
Статичний, “стій/йди”, кінематичний |
Точність статичного методу знімання |
планова: 5 мм + 1 ppm висотна: 10 мм + 2 ppm |
Точність знімання (“стій/йди”) |
планова: 12 мм + 2,5 ppm висотна: 15 мм + 2,5 ppm |
|
<3 м із зовнішньою антеною та |
Точність навігації |
поправками WAAS 5 мм з внутрішньою антеною (з WAAS) |
Довжина векторів (статичний режим) |
до 20 км, більше від 20 км тільки в період малої іоносферної активності |
Довжина векторів (“стій/йди”) |
до 10 км |
Таймер спостережень (статичний режим) |
від 20 до 60 хв, залежно від довжини вектора |
Таймер спостережень (“стій/йди”) |
зазвичай 15 с |
Час ініціалізації (“стій/йди”) |
15 с на відомих пунктах, 5 хв з використанням рамки ініціалізації |
Канали супутників GPS |
10 |
Супутникові канали |
2 |
Висота захоплення супутників |
10° |
Інтервал запису даних |
1-999 с |
Робочий діапазон температур |
від-10 °С до+80 °С |
Тип акумуляторів |
2 АА, лужні або літієві |
Час експлуатації акумуляторів, за |
лужні - 8 год |
t = 20°С |
літієві - 13 ЩД |
Об’єм пам’яті для збереження даних |
8 Мб, 72 год збирання даних, 100 файлів даних |
Примітка:
за t
=
-10 °С яскравість дисплея зменшується,
а потім зникає, приймач ще працює, збирає
дані. За / = -20 °С дисплей може вийти з
ладу.
ІІІ.З. 7.
Підготування приймача Pro
Mark-2 до
роботи та виконання спостережень на
геодезичному пункті
Для
підготування приймача Pro
Mark-2
до
роботи необхідно:
З’єднати
штатив та трегер.
Зцентрувати
штатив із трегером над точкою за
допомогою оптичного центрира. Це
виконується так само, як і в електронного
тахеометра.
389
З’єднати
антену з вертикальним подовжувачем;
нижній кінець подовжувана з’єднати
з адаптером і його підставкою.
З’єднати
зібрану GPS-антену
із трегером, закріпленим на штативі.
Після цього перевірити центрування
антени над точкою.
Помістити
приймач Pro
Mark-2 у
польовий утримувач.
Приймач
разом з утримувачем закріпити на
штативі на такій висоті, щоб було зручно
працювати, як це показано на рис.
ІІІ.3.21.
Прикріпити
на антену кабельний з’єднувач.
Прикріпити другий кінець кабелю до
задньої частини приймача. Це робиться
простим засуванням з’єднувача в
названу частину приймача.
Виміряти
та записати висоту приймача та висоту
GPS-антени
за допомогою рулетки. Бажано записати
висоту як у метрах, так і у футах. Це
зменшить імовірність появи похибки
вимірювання висоти.
Рис.
111.3.21. Закріплення приймача на штативі
Ashtech
ftaTesnavigahon
com
Rev
2
00 NAmenca-107
© 2002 Thales
Nav
Рис.
III. 3.22. Вікно
Survey
390
Як
тільки приймач установлено над точкою,
можна починати підготування приймача
до спостережень, яке складається з
таких кроків:
Ввімкнення
приймача за допомогою червоної клавіші
on/off
на
лицевій частині приймача. З’явиться
вікно Mode
(Режими).
Вибір
пункту Survey
(Знімання)
за допомогою виділення Survey
та
натискання ENTER
для
входу до екрана Survey
(рис.
III.3.22).
Екранне
меню Survey
забезпечує
можливість налаштувати приймач і
функції параметрів знімання до початку
збирання даних (навіть до виїзду в поле,
тобто в камеральних, офісних умовах).
Під час вибору на екрані Survey
пункту
меню Setup
(Налаштування)
відкриється вікно Survey
Menu, де
можна встановлювати параметри знімання.
У разі вибору пункту Collect
Data (збирання
даних) починається знімання.
Допустимо,
приймач не підготований до знімання
ще до виїзду в поле. Тоді у пунктах 3-11
розглядаються функції приймача і
налаштування знімання безпосередньо
перед початком спостережень.
Немає
необхідності заново виконувати усі
налаштування кожен раз перед виконанням
знімання, оскільки деякі з них, наприклад,
такі, як вибір одиниць вимірювання
(Unit
of Measure) та
ідентифікаційний номер приймача
(Receiver
ID), будуть
однаковими для всіх геодезичних пунктів.
Усі пункти налаштування (3-11) необхідно
виконувати так:
Вибрати
з екранного меню Survey
(Знімання)
(рис. ІІІ.3.22) пункт Setup
(Налаштування),
натиснути ENTER
(Введення)
для відкриття Survey
Menu (Меню
у режимі Знімання) (рис. ІІІ.3.23).
P*in+
Attribute
І????
Site
Description
I
Save
Рис.
111.3.23.
Меню
Survey
Menu Рис. 111.3.24. Вікно
Point
Attribute
Саме
Survey
Menu забезпечує
доступ до функцій приймача і налаштування
параметрів знімання. Усі ці параметри
можна прочитати на екрані Survey
Menu.
Recording
inter Antenna File Manager Units
Receiver
ID Contrast *
©
2002 Thales Nau
391
тю
Першим
пунктом екрана є Survey
Mode (Режим
знімання). Необхідно вибрати у Survey
Menu пункт
Survey
Mode (Режим
знімання). Далі встановити режим Static
(Статичний).
У
Survey
Menu потрібно
вибрати Point
Attribute (Опис
точки). Якщо вибрано пункт меню Point
Attribute натиснути
ENTER
для
переходу у вікно Point
Attribute (рис.
ІП.3.24). Це вікно дає змогу вводити
атрибутивну інформацію про точку
спостережень, на якій установлено
приймач.
Інформація
містить:
чотиризначний
ідентифікатор пункту. Потрібно присвоїти
ідентифікаційний номер кожній
точці, що визначається. Номер повинен
залишатися однаковим під час багаторазових
спостережень на одній точці;
довільний
20-значний
опис кожної точки.
Щоб
ввести атрибутивну інформацію про
точку, необхідно виділити поле Point
Attribute, натиснути
клавішу ENTER.
Далі
поміняти значення на необхідні. У кінці
вибрати (натиснути) Save
(Зберегти),
щоб повернутися в меню Survey
Menu.
У
меню Survey
Menu вибрати
пункт Antenna
(Антена).
Установити висотні параметри антени
для точки. Вибрати Slant
(Нахилена
висота), якщо потрібно виміряти висоту
GPS-антени
від центра до точки, що розташована на
боковому краю корпусу антени, або
Vertical
(Прямовисна
висота), якщо потрібно виміряти
висоту антени по вертикалі від її
нижньої частини до центра знака. Ввести
виміряні значення висоти антени.
Вибрати одиниці вимірювання висоти
антени, натиснувши пункт Units
(Одиниці)
у Survey
Menu.
У
Survey
Menu потрібно
вибрати пункт File
Menager (Файловий
менеджер). Тут можна звільнитися від
старих файлів даних, якщо необхідна
додаткова пам’ять для закінчення
сеансу (сесії) знімання. Виділивши
пункт File
Menager, натиснути
ENTER
для
відкриття вікна Fil6
Manager, рис.
III.3.25.
Hie
Manager
♦R1234B01131
♦R1234B01129
-Ц1234С01.129
>R1234C01131
Size 7117 KB Free 7416 32 KB
Рис.
II 1.3.25. Вікно
File
Menager
Рис.
111.3.26. Вікно
Unit
of Measure
392

Вікно
File
Menager дає
змогу видалити непотрібні файли даних
і тим самим звільнити пам’ять для
збирання даних у поточному сеансі
спостережень. У вікні подано список
файлів, що займають пам’ять і клавіші,
що відповідають командам, які виконують
їхнє виведення. Кожний файл має символ,
що характеризує його так:
>
- файл є поточним файлом, у який заносяться
дані;
+
- файл ще не був вивантажений із приймача;
-
- файл був вивантажений із приймача.
Для
вибору файла, який необхідно видалити,
використовують стрілки “вверх/вниз”.
Для вибору Delete
(Видалити)
або DeLAll
(Видалити
все) використовують праву і ліву стрілки.
Під час вибору пункту Delete
буде
видалений тільки вибраний файл. Якщо
вибрати пункт Del.AU,
видаляться
всі файли.
Натисніть
клавішу ESC
(Відміна)
для закінчення роботи із цим вікном і
повернення у попереднє меню Survey
Menu.
У
Survey
Menu потрібно
вибрати пункт Units
(Одиниці).
Пункт призначений для зміни одиниць
вимірювань, якщо встановлений варіант
не задовольняє.
Виділивши
пункт Units,
потрібно
натиснути ENTER,
щоб
відкрити вікно Unit
of Measure (Одиниці
вимірювань), рис. ІП.3.26.
Вікно
Unit
of Measure дає
змогу вибрати одиниці, у яких вводиться
інформація щодо висоти антени. Крім
того, вибрані одиниці використовуються
таймером спостережень.
Для
доступу до вибраного списку одиниць
натиснути ENTER.
Тут
вибирають потрібний варіант і знову
натискають ENTER.
Далі
вибирають Save
(Зберегти)
для повернення в Survey
Menu.
У
Survey
Menu потрібно
вибрати Receiver
ID (Ідентифікатор
приймача). Тут змінюється
ідентифікаційний номер приймача, якщо
не задовольняє поточний номер.
Виділивши
пункт Receiver
ID, натискають
ENTER
(Введення)
для відкриття вікна Receiver
ID (Ідентифікатор
приймача), рис. ІІІ.3.27.
Вікно
Receiver
ID (Ідентифікатор
приймача) уможливлює введення
горизонтального ідентифікатора (ID)
приймача,
який використовується під час формування
назви файла необроблених даних. Кожний
такий файл, записаний у цьому приймачі,
буде мати чотиризначний ідентифікаційний
номер. Цей номер приймача повинен бути
унікальним (єдиним). В іншому разі
виникнуть проблеми під час постопрацювання
зібраних даних. Для редагування
ідентифікатора приймача натискають
ENTER.
Можна
змінити наявні значення ID
на
393
бажані.
Після введення ID
потрібно
вибрати Save
(Зберегти)
для збереження та повернення в Survey
Menu.
У
Survey
Menu вибирають
пункт Contrast
(Контраст).
Якщо погано відображається текст на
дисплеї, то можна змінити контрастність
дисплея.
Виділивши
Contrast,
натискають
ENTER,
щоб
відкрити вікно Contrast
(рис.
ІІІ.3.28).
Receiver
lb
1234
Save
А*т*я*
JL» і..,..,., і
©
2002 Thales
Nav
Рис
III 3 27. Вікно
Receiver
ID
Рис
III 3 28 Вікно
Contrast
Для
зміни контрастності дисплея приймача
використовують праву і ліву стрілки
для налаштування контрастності.
Виконавши цю операцію, натискають
клавішу ENTER
для
повернення в Survey
Menu.
Щоб
вийти з Survey
Menu і
повернутися до вікна Survey
(“Знімання”),
натискають клавішу ESC
(див.
рис. ІІІ.3.22).
Отже,
на цьому закінчилося налаштування
приладу для спостережень. Далі описується
збирання даних. Для цього:
У
вікні Survey
вибирають
пункт Collect
Data (збирання
даних), натискають ENTER
для
відкриття вікна Satellite
Status (Статус
супутника), рис. ІІІ.3.29.
Вікно
Satellite
Status (Статус
супутника) показує супутники, які
відстежує приймач. На схематичному
зображенні небесної сфери відображені
номери супутників, які доступні для
спостереження на цей час. Якщо сигнал
супутника захоплений GPS-приймачем,
зображення номера цього супутника
інвертовано (чорне віконце з білим
номером). Шкала під зображенням небесної
сфери показує потужність сигналу
супутника. Під час приймання сигналів
від чотирьох супутників, що розміщені
вище від 10°
над горизонтом, автоматично починається
збирання даних. Автоматично буде
викликано вікно Survey
Status Можна
повернутися у вікно Satellite
Status, натиснувши
клавішу Nav/Surv
(Навігація/Знімання).
У
нижній частині вікна Satellite
Status є
два індикатори: стану джерела струму
(ліворуч) та кількості вільної пам’яті
(праворуч). Індикатор вільної
394

пам’яті
показує в графічному вигляді вільну
пам’ять, що залишилася для зберігання
даних. Як тільки починається зберігання
даних, процентне число починає миготіти,
що означає: збирання даних почалося.
Індикатор стану джерела струму графічно
показує заряд батареї, що залишився.
Якщо зовнішнє джерело струму під’єднане
до приймача, то на дисплеї з’явиться
віконце зі значком вилки електричного
з’єднання.
Для
оцінки впливу перешкод на пункті
знімання використовують схему небесної
сфери для візуалізації тих супутників,
які будуть блоковані перешкодами. Це
допоможе визначити, чи цей пункт
сприятливий для GPS-
спостережень.
Далі,
щоб відкрити вікно Survey
Status, у
вікні Satellite
Status натискають
клавішу Nav/Surv
(рис.
ІІІ.З.ЗО).
8
3 59 1 4693
31
1
Static
Site
ID ?
|asoi
Qb&Ttmer
Elapsed
ГТГ
MX
f
00
04 30
ГТ
poop
f
4.0
ГШГ
Рис.
111.3.29. Вікно
Satellite
Status Рис. 111.3.30. Вікно
Survey
Status
Це
вікно інформує про хід збирання даних.
Ця інформація допомагає визначити, чи
достатня кількість даних зібрана для
якісного майбутнього постопрацювання.
У цьому вікні можна спостерігати за
такими індикаторами якості спостережень:
•
Observation
Timer (таймер
спостереження). Поле Observation
Timer інформує
про поточний стан таймера спостережень.
Таймер
перевіряє, чи достатньо одержаних
супутникових даних для того, щоб після
їхнього опрацювання отримати якісні
дані. Для цього таймер враховує кількість
супутників, що захоплені, геометрію
супутників (
0
км- відображається у разі, коли зібраних
даних недостатньо для точного визначення
вектора;
395

PDOP),
а також перерви у спостереженнях,
викликані наявністю перешкод. Таймер
повідомляє, коли буде зібрано достатньо
даних для того, щоб забезпечити бажану
точність визначення вектора, що з’єднує
два пункти, у яких одночасно виконуються
спостереження. Проміжок часу, необхідний
для цього, залежить від віддалі між
пунктами спостережень. Можливі такі
граничні значення:
5
км - відображається в тому разі, коли
зібрано достатньо даних, якщо довжина
вектора не більша за 5 км;
10
км - коли довжина вектора не більша за
10
км;
15
км - коли довжина вектора не більша за
15 км;
20
км - коли довжина вектора не більша за
20
км.
Тому,
по-перше, необхідно наближено розрахувати
довжини векторів, які необхідно буде
визначити під час знімання, а, по-друге,
використовуючи як орієнтир найдовшу
з цих віддалей, зачекати, поки таймер
не покаже значення, що відповідає цій
віддалі. Коли це відбудеться, спостереження
на пункті можна вважати закінченими.
Примітка:
наявність перешкод може викликати
неточність у роботі таймера. Тому,
коли спостереження виконуються у
закритій перешкодами місцевості,
необхідно зібрати дещо більше даних
на цьому пункті, щоб гарантувати якісний
результат.
Elapsed
Time (Витрачений
час). Поле Elapsed
Time показує,
скільки часу пройшло з моменту початку
збереження даних у поточному
спостереженні. З досвідом спостережень
можна оцінювати, який проміжок часу
необхідний для збирання даних для
різних умов.
#
Sate
(Кількість
супутників). Поле # Sate
показує
поточну кількість супутників, які
розташовані вище за 10°
над горизонтом, інформація про які
занесена в пам’ять. Якщо для спостережень
доступна незначна кількість супутників,
то потрібна більша кількість даних,
щоб успішно виконати спостереження.
Цей параметр може бути використаний
на пункті спостережень як індикатор
впливу перешкод на збирання даних у
будь-який час знімання.
Отже,
під час виконання спостережень оператор
повинен стежити саме за цими двома
вікнами, щоб бути інформованим про хід
збирання даних.
Якщо
необхідно змінити якісь дані про
параметри знімання або приймач, потрібно
натиснути клавішу Menu
(Меню)
для доступу до Survey
Menu.
39§
PDOP
(Коефіцієнт
геометричного погіршення точності
вимірювання). Поле PDOP
відображає
значення цього коефіцієнта у будь-який
час. Це значення обчислює приймач,
аналізуючи взаємне розташування усіх
доступних для спостережень супутників,
які розташовані вище за 10°
над горизонтом. Якщо значення PDOP
велике,
то потрібно зібрати більше даних для
успішного закінчення спостережень.
Тому цей параметр також може бути
використаний, як і параметр # Sate.
Крім
інформації про параметри знімання
вікно Survey
Status, так
само, як і вікно Satellite
Status, відображає
стан джерела струму і кількість пам’яті,
зайнятої даними.
Важливо
пам’ятати, що Survey
Menu (Меню
в режимі “Знімання”) доступне в
будь-який час під час збирання даних
натисненням клавіші “Menu”
(Меню).
Це те саме меню, яке описане раніше. Усі
налаштування Survey
Menu (Меню
у режимі “Знімання”) можуть бути
встановлені в будь-який момент під час
виконання спостережень. Інакше кажучи,
дії 3-10, подані вище, можуть, за бажанням,
бути виконані одразу після початку
збирання даних. Це дає змогу розпочати
збирання даних ще до введення налаштувань,
що скоротить час перебування на точці
спостережень.
Треба
врахувати, що коли ідентифікатор
приймача змінюється під час збирання
даних, ім’я поточного файла активних
даних буде містити ID
приймача,
установлений на початку збирання даних.
Якщо
зібраних даних достатньо для виконання
постопрацювання, приймач вимикають.
Як
бачимо, виконання спостережень на
пункті у статичному режимі складається
з 15 підпроцесів (дій).
Примітка:
для уникнення можливих пошкоджень
необхідно від’єднати кабель зовнішньої
антени від приймача до того, як виймати
приймач із рами польового утримувача.
Необхідно
дотримуватися вищеподаної послідовності
дій у кожному сеансі (сесії) статичних
спостережень.
За
наявності каналу зв’язку оператор
повідомляє на центральний пункт, що
він готовий закінчити спостереження
або внести пропозицію про необхідність
продовження спостережень.
На
ділянці, що підлягає топографічному
зніманню, залежно від розміру ділянки,
вибирають одну або декілька базових
станцій, які, зазвичай, є пунктами
ДГМ.
Вибираючи
розташування базових станцій, необхідно
розмістити їх на точках з якомога меншою
кількістю перешкод (дерева, будинки,
зовнішні геодезичні знаки), що затримують
поширення супутникових сигналів до
приймача, який не зможе відстежити
мінімум п’ять супутників під час
збирання кінематичних даних рухомими
(роверними) приймачами. У результаті
можлива втрата деяких точок, що
спостерігаються в цей проміжок часу
роверними приймачами. Чим відкритіша
місцевість, тим успішніше пройде
знімання. Тому треба надати особливу
увагу вибору положення бази. Загальні
настанови, хід та
397
Застосування режиму “стій/йди” для визначення просторових координат під час топографічного знімання місцевості
послідовність
виконання робіт на базовому приймачі
абсолютно такі самі, як і під час
статичного режиму знімання, описані в
попередньому параграфі (пункти 1-15).
Різниця
тільки у можливості використання на
базовій станції ініціалізаційної
рамки для ініціалізації (хоча це не
обов’язково, оскільки є інші методи
ініціалізації).
Під
час використання рамки (рис. ІП.3.32)
базова антена центрується і приводиться
в горизонтальний стан над маркою
(центром) геодезичного пункту. Антена
ровера встановлюється зі зміщенням
відносно базової антени на рамку
ініціалізації (рис. III. 3.31).
Ця
рамка забезпечує формування точної
базової лінії між базою та ровером
завдовжки 0,2
м.
Після
виконання ініціалізації антена роверного
приймача переноситься на роверну віху
(рис. ІІІ.З.ЗЗ).
Рис.
111.3.31. Антена РгоМагк-2 із рамкою
ініціалізації
398

Рис III 3 32 Рамка ініціалізації
Рис.
111.3.33. Антена ровера, перенесена
з
ініціалізаційної рамки на віху
Усі
подальші дії виконують точно так само,
як описано у пунктах 1-15. Базовий приймач
повинен виконувати вимірювання весь
час, як це передбачено в плані польових
робіт. Далі детально буде описана робота
роверного приймача у режимі “стій/йди”
(“stop-and-go”).
Для
роверного приймача дії 1-3 абсолютно
аналогічні до дій під час статичного
режиму та дій на базовій станції.
У
меню Survey
Menu (Меню
в режимі “Знімання”) вибирають пункт
Survey
Mode (Режим
“Знімання”). Далі встановлюють режим
“стій/йди”.
У
Survey
Menu вибирають
Point
Attribute (Опис
точки). Вводять атрибутивну інформацію
про точку, на якій буде виконуватися
знімання.
Виділений
пункт Point
Attribute (Опис
точки) зображено на рис. ІІІ.3.34.
Екран
Point
Attribute містить
такі параметри:
чотиризначний
ідентифікатор пункту. Необхідно
присвоїти ідентифікаційний номер
кожній точці, що знімається;
таймер
перебування на пункті, який працює за
принципом секундоміра;
довільний
20-значний
опис пункту;
вибіркове
встановлення режиму ініціалізації: без
ініціалізації,
ініціалізація
на точці з відомими координатами,
ініціалізація на точці з використанням
рамки ініціалізації;
вибіркове
встановлення контрольної точки;
встановлюють “Yes”,
якщо
точка є контрольною. Ідентифікаційний
номер пункту копіюється у таблицю
ідентифікаторів пунктів, координати
яких відомі.
399
Ptint
Attribute
Init
mode
ШЮ...
,
Time oft site
joooi
По
I ^
%
Initialize
Control
|<None>
|No
Save
Рис.
111.3.34. Вікно
Point
Attribute Рис. 111.3.35. Вікно
Init.
Mode
Ініціалізація
є дуже важливим кроком для успішного
знімання в режимі “стій/йди”. Далі
поданий приклад, який ілюструє
ініціалізацію з використанням рамки
ініціалізації.
У
вікні Point
Attribute (Опис
точки) виділяють пункт Initialize
(Ініціалізація)
і натискають ENTER
для
переходу у вікно Init.
mode (Режим
ініціалізації), рис. ІІІ.3.35.
Виділяють
пункт Ваг (Панель) і натискають Save
(Зберегти)
для відображення вікна Point
Attribute (рис.
ІІІ.3.36).
Ptint
Attribute
IkB
faw.rn.4t.
}AS01
j 300
Save
ШВШШЯЖ
$top-and~go
,
шр
Jasoi
00
04
30
■J*.
4.0
ИЗИІ
Рис.
II 1.3.36. Вікно
Point
Attribute
Рис.
111.3 37. Вікно
Survey
Status
Зверніть
увагу на те, що значення параметра Time
on Site (Час
на пункті) встановлений за замовчуванням
300 с (5 хвилин).
У
Survey
Menu далі
вибирають пункт Antenna.
Тут
установлюють висотні параметри антени.
Якщо антена встановлена на віху, тоді
її висота буде залишатися постійною.
Постійними залишаються також Units
(Одиниці
вимірювань). За необхідності можна
змінити Unit
у
Survey
Menu.
Пункти
7, 8,
9, 10, 11 такі самі, як і під час статичного
знімання. Після їхнього виконання
налаштування обладнання закінчиться
і тепер можна виконувати спостереження.
Далі описується збирання даних, а також
буде показано, як необхідно стежити за
виконанням знімання.
400
m*
Description t.
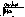
Пункт
12 такий самий, як і під час статичного
знімання.
Пункт
13.У вікні Satellite
Status (Статус
супутника) натискають клавішу Nav/Surv
(Навігація/Знімання),
щоб відкрити вікно Survey
Status (Статус
знімання), рис. ІІІ.3.37.
Вікно
Survey
Status “стій/йди”
інформує про збирання даних. У цьому
вікні можна спостерігати за такими
індикаторами якості спостережень:
Remain
-
поле Remain
показує,
як довго можна виконувати запис
атрибутивної інформації про цей пункт.
У полі Remain
іде
зворотний відлік часу, починаючи зі
значення, яке встановлено в полі
Time-on-site
у
меню Point
Attribute;
#
Sats
(Кількість
супутників), які розміщені на 10° вище
від горизонту та інформація яких
занесена в пам’ять;
PDOP
(Коефіцієнт
геометричного погіршення точності
вимірювання).
Крім
інформації про параметри знімання,
вікно Survey
Status “стій/йди”
так
само, як і вікно Satellite
Status (Статус
супутника), показує стан джерела струму
і кількість пам’яті, зайнятої даними.
14.
Клавіша Start
виділена
і приймач готовий до реєстрації
атрибутивної інформації про точку.
Натискають клавішу Enter,
щоб
почати збирання атрибутивних даних. У
полі Remain
починається
зворотний відлік часу. Коли значення
в полі Remain
досягне
значення 00.00.00, виділиться клавіша Stop
і
збирання атрибутивних даних для цієї
точки зупиниться, а ідентифікаційний
номер пункту автоматично збільшиться
на одиницю.
Увага:
Збирання
атрибутивних даних на цій точці можна
зупинити, натиснувши ENTER
за
виділеної клавіші Stop.
Реєстрація
даних починається відразу після вибору
пункту Collect
Data (Збирання
даних) і під час цього відстежуються
чотири або більше доступних супутників,
що розміщені на висоті більше ніж 10°
над горизонтом. Дані реєструються
протягом кожного інтервалу запису.
Натискання на клавішу Start
або
Stop
не
приводить до переривання реєстрації
даних, а тільки дає змогу додати
атрибутивну інформацію про точку, на
якій накопичуються дані.
Як
тільки почалась робота в режимі
“стій/йди”, для нормальної роботи
системи Pro
Магс-2
повинна забезпечуватися пряма видимість
супутникових сигналів під час усієї
сесії спостережень. Якщо будь-який із
приймачів, що входить у систему, не може
підтримувати безперервний зв’язок не
менше ніж з п’ятьма супутниками,
пролунає попереджувальний сигнал
кінематичного режиму. Це означає, що
сигнал супутника загублений, тобто
знімання потрібно ініціалізувати
заново. Дані, зібрані до попереджувального
сигналу, можуть бути
401
використані.
Перед відновленням знімання необхідно
наново виконати процедуру ініціалізації.
Закінчивши
роботу, вимикають приймач. Далі всі
дані завантажують у комп’ютер. Окрім
роботи з приймачем, оператор безпосередньо
на пункті закінчує усі записи в польовий
журнал. У журналі повинна міститися
така інформація:
назва
пункту спостережень та його умовне
позначення, занесене в реєстраційний
файл;
прізвище
оператора;
серійні
номери антени, приймача;
висота
встановлення антени над геодезичним
пунктом;
час
початку і закінчення спостережень на
пункті;
номери
супутників;
приблизні
координати пункту;
усі
зауваження, що стосуються виконання
спостережень, які можуть виявитися
корисними під час камерального
опрацювання результатів вимірювання.
Якщо
дані знімання будуть використані для
складання топографічного плану, а
точки, просторові координати яких
визначались, є фактично пікетами
знімання, то необхідно подати зариси
певної групи пікетів зі стрілками
пікетів, висоти яких можна інтерполювати
для побудови горизонталей так, як це
робиться під час тахеометричного
знімання.
В
опрацюванні топографо-геодезичної
інформації, зібраної GPS-приймачами,
розрізняють:
попереднє
опрацювання;
кінцеве
опрацювання.
Часто
в попередньому опрацюванні виділяють
так зване первинне опрацювання.
До
первинного опрацювання належать
обчислення, що виконуються безпосередньо
під час вимірювання. Цей етап дає змогу
контролювати дані в польових контролерах
(приймачах). При цьому контролюються:
наявність
видимості неба (відсутність перешкод);
наявність
необхідної кількості супутників;
допустимість
геометричного фактора;
визначення
координат у навігаційному режимі.
402
Загальні відомості про опрацювання gps-вимірів
Попереднє
опрацювання виконується з використанням
стандартного програмного забезпечення
фірми-виробника супутникових приймачів.
Більшість
сучасних програм камерального опрацювання
вимірів (посто- працювання) поділяються
за методами опрацювання на:
обчислення
окремих ліній;
багатоточкові
розв’язки.
Метод
обчислення окремих ліній є найпоширенішим,
і його у будь-якому разі доцільно
застосовувати під час виконання
попереднього опрацювання, навіть коли
програмний пакет дає змогу реалізувати
багатоточкові розв’язки. Річ у тім, що
на цій стадії опрацювання зазвичай
впливає значна кількість грубих похибок,
а методом багатоточкового розв’язання
їх виключити складно.
Програмне
забезпечення, розраховане на опрацювання
окремих ліній, забезпечує кращий
контроль і локалізацію неякісно
виміряних ліній.
Як
правило, точність таких ліній істотно
гірша, ніж середня точність на цьому
об’єкті робіт. Іншим методом контролю
є контроль за замкнутими побудовами:
трикутниками, векторними ходами між
відомими точками. Якщо сума приростів
координат по цьому векторному ходу
відповідає паспортній точності приладу,
то лінії, що увійшли в цю побудову,
виміряні якісно.
Загальний
алгоритм обчислення методом окремих
ліній подано на рис. ІІІ.3.38.
Перед
обробкою результати супутникових
спостережень переписують на комп’ютер.
Переписування даних спостережень із
приймача на комп’ютер виконується за
допомогою відповідного кабелю, який
з’єднує комп’ютер із приймачем, або
карт пам’яті, які зчитуються комп’ютером.
Формат даних спостережень різних форм
та різними супутниками істотно
відрізняється. Зроблена спроба
стандартизації результатів вимірювання,
яка привела до появи формату RINEX
(Receiver Independent Exchange) -
уніфікованого текстового запису
результатів спостережень, який зчитує
будь-яке програмне забезпечення усіх
фірм-виробників супутникових приймачів.
Формат RINEX
складається
з трьох файлів:
файл
відцалемірних даних;
файл
метеорологічних даних;
файл
навігаційних повідомлень.
Метою
кінцевого опрацювання є отримання
готової продукції каталогів координат.
Це означає, що під час кінцевих обчислень
виконуються:
зрівноваження
мереж;
обчислення
координат у національній системі
координат (еліпсоїд Красовського);
403
Рис.
III.
3.38.
Загальний алгоритм обчислення окремої
лінії
визначення
координат у Європейській системі
координат;
виконання
супутникових координатних обчислень
під час виконання різноманітних
завдань, наприклад, геодинамічних, які
пов’язані з переходом від “статичної”
геодезії до “динамічної-”
геодезії;
застосування
супутникових технологій у прикладній
геодезії;
виконання
аерознімання з використанням супутникових
технологій, що приводять до виключення
прив’язування аерознімків;
застосування
супутникових технологій у морській
геодезії;
використання
супутникових
технологій
під час різного спеціалізованого
знімання.
Під
час опрацювання супутникових вимірів
виникає необхідність ретельного
дослідження впливів усіх можливих
джерел похибок, особливостей їхнього
виникнення й обґрунтування методів
їхнього обліку. Залежно від характеру
впливу зазначених джерел виниклі
похибки поділяються на дві основні
групи:
404
Основні джерела похибок супутникових вимірювань і методи послаблення їхнього впливу
Класифікація джерел похибок супутникових вимірювань
,99
шум
.
Для
похибок першої групи створюються
спеціальні методи їхнього обліку. Вплив
другої групи вдається, здебільшого,
мінімізувати за рахунок використання
великого масиву вимірів. У цьому
підрозділі основна увага приділена
похибкам систематичного характеру,
які викликають зсуви результатів
вимірювання.
На
підставі аналізу вимірювального
процесу, характерного для системи GPS,
усі
джерела систематичних похибок можна
ще умовно поділити на три групи:
похибки,
пов’язані з неточними вихідними
даними, з яких основними є похибки
ефемерид;
похибки,
викликані впливом зовнішнього
середовища;
інструментальні
джерела похибок, до яких, як правило,
зараховують невідоме положення фазового
центра антени приймача, невраховані
тимчасові паузи під час проходження
інформаційних сигналів через апаратуру,
а також похибки, пов’язані з роботою
пристроїв.
Поряд
із вищеназваними групами похибок
необхідно враховувати й окремі фактори,
які викликають виникнення похибок, що
не характерні для жодної з перерахованих
вище груп. Зокрема, до таких похибок
можуть бути зараховані похибки, що
виникають внаслідок неоптимального
взаємного розташування супутників
(геометричний фактор). Крім того, цілий
ряд похибок може виникати під час
переходу від однієї координатної
системи до іншої (наприклад, від
притаманної системі GPS
глобальної
координатної системи WGS-84
до
місцевої координатної системи). Також
необхідно враховувати вплив джерел
похибок, пов’язаних з “штучним
зашумленням” випромінюваних супутниками
радіосигналів.
Джерела
похибок,
пов'язані
з неточними ефемеридами супутників
та методи послаблення їхнього впливу
Під
час визначення координат точок на
земній поверхні супутниковими методами
необхідно, поряд із вимірюванням
відстаней до супутника, знати також
його ефемериди, тобто місцезнаходження
супутника на момент виконання
вимірювання. Неточна інформація про
ефемериди пов’язана, насамперед, із
розбіжностями, які спостерігаються на
практиці, між прогнозованою (незбуреною)
і реальною (підданою впливу сил, що
збурюють) орбітами. До
405систематичні
похибки,
які стосовно супутникових вимірів
отримали назву зсувів;похибки
випадкового характеру,
які часто порівнюють із поняттям
Збурювальні фактори |
Максимальне збурювальне прискорення, м/с2 |
Максимальне збурення за 1 годину, м |
Центральне поле Землі |
5,65 10'1 |
- |
Друга зональна гармоніка |
5,3 • 10-5 |
300 |
Гравітація Місяця |
5,5' 10'6 |
40 |
Гравітація Сонця |
3 Iff6 |
20 |
Четверта зональна гармоніка |
10‘7 |
0,6 |
Сонячна радіація |
10'у |
0,6 |
Гравітаційні аномалії |
fir5 |
0,06 |
Інші фактори |
кг8 |
0,06 |
Сумарний
гравітаційний вплив мас Місяця та Сонця
хоча й виявляється істотно меншим (для
тригодинних дуг відхилення від незбуреної
орбіти оцінюється величинами на
рівні від 50 до 150 м), проте під час
прогнозування значень ефемерид цей
вплив також варто враховувати.
Безпосередньо із гравітацією зв’язані
різні припливні явища, які спостерігаються
також на земній поверхні, і які через
перерозподіл мас призводять до змін у
розрахованому гравітаційному полі
Землі, а, отже, і до впливів на орбітальний
рух супутника. Виконана оцінка такого
впливу свідчить про те, що відхилення
супутника від розрахункової орбіти
через вплив цього фактора навіть для
дводобових дуг лежать у межах від 0,5 до
2 м. Цим впливом стосовно GPS-супутників
можна знехтувати.
406
Переходячи
до оцінки впливу факторів негравітаційного
походження, варто зазначити, що
найістотніший вплив на неточність
знання ефемерид GPS-
супутників має сонячний радіаційний
тиск. Як показують розрахунки, відхилення
супутників від розрахункової траєкторії
через вплив прямого сонячного радіаційного
тиску лежать у межах від 5-6 м (для
тригодинних дуг) і до 100- 800 м (для
дводобових дуг).
Іншим
фактором негравітаційного походження
є атмосферне гальмування. Оцінюючи
вплив цього фактора, варто мати на
увазі, що на характерній для GPS-супутників
висоті близько 20 тис. км атмосфера є
надзвичайно розрідженою і її впливом
під час розрахунків орбіт супутників,
як правило, нехтують.
Узагальнюючи
оцінку сумарного впливу усіх перерахованих
вище збурювальних факторів, зазначимо,
що ці дані використовуються тільки для
первинного, наближеного розрахунку
реальних орбіт супутників. Що стосується
отримання необхідних для наземних
спостерігачів значень ефемерид
супутників, то на практиці застосовують
ефективніші експериментальні методи,
які ґрунтуються на використанні опорних
станцій. Ці станції встановлені на
пунктах з відомими координатами та
виконують безперервні високоточні
спостереження супутників в автоматичному
режимі. Після відповідного оброблення
на центральній станції обчислюються
поправки до раніше розрахованих значень
ефемерид, які за допомогою передавальних
станцій систематично (три рази на добу,
а останнім часом один раз на добу)
передаються на відповідні супутники.
Значення ефемерид на супутнику
коректуються щогодини та залишаються
дійсними, принаймні, ще упродовж
півгодини після закінчення кожної
контрольної години. Точність переданих
по радіоканалах значень ефемерид
характеризується похибкою на рівні
близько 20
м,
що забезпечує точність геодезичного
супутникового диференціального
вимірювання на рівні близько 10"6
м. Ця точність задовольняє вимоги
більшості геодезичних робіт.
Спрощена
залежність похибок визначення бази
(вектора, що з’єднує два пункти
спостереження) від похибок орбіти
супутника має вигляд:
db
_
dr
Т~Т’
(ІІІ.4.1)
де
Нижче
у табл. ІІІ.4.2 подано дані про значення
похибок
407db
-
похибка бази 6,
dr
-
похибка розташування супутника, р-
топоцентрична віддаль до супутника
(наближено р = 20000
км).db
залежно
від довжин бази та похибок орбіт
супутників dr.
|
|
|
Відносні похибки |
10 |
50 |
2,5 |
1:400000 |
20 |
1,0 |
1:1000000 |
|
2 |
0,1 |
1:10000000 |
|
100 |
50 |
25 |
1:400000 |
20 |
10 |
1:1000000 |
|
2 |
1 |
1:10000000 |
|
500 |
50 |
125 |
1:400000 |
20 |
50 |
1:1000000 |
|
2 |
5,0 |
1:10000000 |
|
0,2 |
0,5 |
1:100000000 |
|
1000 |
50 |
250 |
1:400000 |
20 |
100 |
1:1000000 |
|
2 |
10 |
1:10000000 |
|
0,2 |
1 |
1:100000000 |
Вплив
зовнішнього середовища на результати
супутникового вимірювання проявляється
як через зміни часу проходження
радіосигналів від супутника до приймача,
так і через виникнення багатошляховості,
викликаної відбиттям згаданих
радіосигналів від тих чи інщих поверхонь,
розташованих у безпосередній близькості
від приймача.
Своєю
чергою, зміни у часі поширення
радіосигналів пов’язані зі швидкістю
поширення електромагнітних хвиль, що
в такому середовищі, як атмосфера,
відрізняється від швидкості світла у
вакуумі, причому зміни швидкості на
шляху поширення сигналу стають причиною
додаткових тимчасових запізнень,
наслідком яких є похибки в значеннях
вимірюваних відстаней.
Стосовно
системи GPS
радіосигнал
велику частину свого шляху проходить
у вакуумі, де не виявляються зазначені
вище впливи. Але на висотах близько
1000 км і до висоти 50-40 км від земної
поверхні розміщена область іонізованої,
розрідженої атмосфери, яка отримала
назву
408Оцінка впливу зовнішнього середовища на результати супутникового вимірювання
іоносфери.
Її характерною рисою є те, що вона
вносить дуже істотні запізнення в час,
який витрачає сигнал на проходження
через таке середовище. Також вона
зумовлює залежність таких запізнень
від частоти згаданого сигналу, тобто
іоносфера, на відміну від нейтральної
атмосфери, є диспергувальним середовищем
для радіосигналів.
На
висотах менше за 40 км від земної поверхні
розміщена газоподібна атмосфера, яка
одержала назву тропосфери. У цьому
середовищі практично відсутня залежність
швидкості радіохвиль від частоти, тобто
тропосфера не диспергує радіохвиль,
але починає проявлятися її залежність
від метеорологічних факторів
(температури, тиску й вологості), які у
приземних прошарках атмосфери можуть
змінюватися із часом у широких межах.
Поряд
з атмосферними впливами результати
супутникового вимірювання піддаються
впливу такого фактора, як багатошляховість,
що приводить до приймання приймачем
декількох ідентичних радіосигналів,
які пройшли різний шлях. У результаті
їхньої взаємодії виникає результуючий
сигнал, який містить дещо спотворену
інформацію про вимірювану відстань.
Далі розглянемо окремо ці впливи.
Іоносфера
- найвіддаленіша від Землі частина
атмосфери, яка зазнає впливу різних
космічних випромінювань і, передусім,
ультрафіолетового випромінювання
Сонця. У результаті такого “опромінення”
електрично нейтральні молекули й атоми
повітря іонізуються, тобто розпадаються
на вільні електрони та електрично
заряджені іони. Оскільки енергія
сонячного випромінювання залежить
від частоти цього випромінювання, то
й степінь іонізації залежить від частоти
названого випромінювання, і чим вища
частота, тим інтенсивніша природна
іонізація.
Виконані
дослідження показують, що іонізація
частинок повітря відзначається
тільки під час його опромінювання
електромагнітними променями з довжиною
хвилі, коротшою за 0,13 мкм, тобто
коливаннями ультрафіолетового діапазону.
Ці
випромінювання Сонця майже повністю
витрачаються на іонізацію верхніх
прошарків атмосфери, охороняючи тим
самим земну поверхню від шкідливих
впливів такої радіації.
Вільні
електрони під дією випромінюваних
супутником електромагнітних хвиль
самі стають джерелом вторинних хвиль.
Ці вторинні хвилі, взаємодіючи з
первинними, приводять до виникнення
результуючих хвиль із дещо іншою
швидкістю поширення, яка за величиною
може бути як нижчою, так і вищою за
швидкість світла у вакуумі.
Оскільки
в іоносфері швидкість ЕМХ залежить від
частоти, то доводиться вводити поняття
фазової та групової швидкості
показника
заломлення
409Вплив іоносфери
Vf,
Vgr
та
фазового і груповогопу
іи^.Тоді
(IIL4.2)
де
де
Із
супутника, крім передавальних гармонічних
коливань, передаються також і кодові
сигнали з використанням модуляції.
Формується група хвиль, для якої
Одержані
результати показують, що в іонізованому
середовищі фазовий показник заломлення
такому
середовищі більша за швидкість світла
у вакуумі; проходять через іоносферу
не повільніше, а швидше ніж у вакуумі.
Що
стосується групової швидкості, то вона
точно на таку саму величину відрізняється
від швидкості світла у вакуумі, але в
інший бік, тобто в бік зниження. Саме
ця швидкість характерна для кодових
сигналів, на основі яких виконують
вимірювання псевдовіддалей.
Величина
іоносферних запізнень визначається
за відхиленням показника заломлення
від одиниці.
З урахуванням
описаних закономірностей зміни показника
заломлення іоносферне запізнення (у
часі) описується співвідношенням
вигляду:
(ІІІ.4.3)
(ІІІ.4.4)
(ІІІ.4.5)
(ІІІ.4.6)
(ІІІ.4.7)
410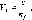
с
- швидкість світла у вакуумі. Але для
іонізованого газу фазовий показник Иу
можна розрахувати за такою наближеною
формулою:Ne
-
концентрація електронів, що виражена
кількістю вільних електронів в одиниці
об’єму (1
м3);
/ - частота радіосигналу, що проходить
через іоносферу.пу
завжди менший від одиниці, тобто фазова
швидкість у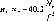

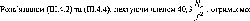

значення
якого
де
h
залежить
від концентрації електронів
Іоносферні
запізнення перераховують у поправки
до псевдовіддалей. їхні
значення
оцінюються величинами, що лежать у
межах від 5 до 50 м.
Зазначимо,
що робились неодноразові спроби
створення відповідних мо-
делей для
визначення іоносферних запізнень за
конкретних умов спостережень.
Найпоширеніша
модель, створена Дж. А. Клобушаром.
Вихідними поло-
женнями такої моделі
є припущення, що вночі рівень іонізації
залишається
незмінним, а, отже, і
запізнення є незмінними за величиною,
а вдень запізнення
можна описати
функцією косинуса. Не вдаючись у
подробиці, зазначимо, що
такий метод
за даними цілої низки досліджень для
випадку двомірних
навігаційних
визначень (тобто без висот) приводить
до виникнення похибок від
0,5 до 2,7 м,
тоді як похибки у висотах приблизно в
6
разів більші і становлять
від 4 до
16 м.
Такий
метод застосовується переважно у
навігації в абсолютних методах
визначення
координат.
Під
час геодезичного використання
супутникового вимірювання
найпоширеніший
метод “компенсації” запізнень, що
ґрунтується на вико-
ристанні двох
передавальних частот L,
та/^.
Під
час фазового супутникового вимірювання
справедливі формули:
ФЦ -
АФІ(
-
fi^geom
+
—і
J
Lj
Фі2 ~АФЬ2
=fl^'geom
+у~-
Jb2
(ІІІ.4.8)
де
т
приймача;
411К
= 40,3 j\'Ve
(A) dh;
К
- коефіцієнт пропорційності,Nc
та
від h
-
довжини шляху радіохвилі
в іоносфері.
Це, своєю чергою, приводить до залежності
запізнення від широти
точки
встановлення, періоду доби, сезону року
та дати в межах 11-річного
циклу
сонячної активності.fgeom
=
—+ (5,с
-8,и
j
-
час проходження радіосигналом
геометричної віддалі між супутником
та приймачем разом із поправками за
похибки годинників на супутнику 8^
і в приймачі 8^
; р - геометрична віддаль від супутника
доФ1{
і ФІ2
-
фазові зсуви; - частоти; NL{, -
кількість
jr
фазових
циклів;
/її
——
поправки,
що враховують іоносферу;
/і2
Перетворимо
останню систему рівнянь. Розв’яжемо
рівняння цієї системи відносно невідомого
*^І]
/і, ‘ ^geom
» “7 ^Іг
/і2
' ^geom
•
J
L\ JІУ2
Після
простих перетворень, виключивший,
отримаємо:
“
ФІ2
fL2
~
І
Розділивши
на/^ , будемо мати:
fb\
^Z-2 fL\
^geom f L2
^geom
*
J
Lj J
L\
(III.4.9)
(III.4.10)
Як
бачимо, в останній формулі
Особливістю
фазового зсуву , який знаходять за
(ІП.4.10), є те, що він
/і
2
- / 2
визначається
за допомогою комбінованої частоти =
—
/і,
від
впливу іоносфери. Цей вільний від впливу
іоносфери зсув позначимо
f
Під
час практичних розрахунків зазвичай
вводять поняття фактора
Ах
1227
6
який
для системи GPS
має
числове значення
1575,42
ням
фактора
~ФІ2
vgeom
(ІІІ.4.11)
fkQ-R2)
Фазовий
зсув, вільний від запізнення іоносфери,
можна записати так:
ФвІ,
=/l,
‘Xgeom- (ІІІ.4.12)
412АФц
і А- іоносферні запізнення у псевдовідцалі;
,с
- швидкість світла.К,
а потім виключимо це невідоме. Маємо:Фц
є величиною, вільною (незалежною) від
іоносферних запізнень. -2—
і є вільнимфв
ц .R
=
——,R
= 1—
= 0,779. З урахуван-R
остання
формула, розв’язана відносно x'geom,
набуде вигляду:R
Підставивши
в (ІІІ.4.12) значення т^ео/я
з (ПІ.4.11), отримаємо для
основної
частини вільний фазовий зсув:
■Фт.
R
(ІІІ.4.13)
ф
, =
в
L\
Фц-Фьг
R
1
-Л"
А
значення іоносферної поправки може
бути розраховане за формулою:
=<*>£,
"ф.А- (ША14)
З
урахуванням (ІІІ.4.13) формула (ІІІ.4.14)
набуває остаточного вигляду:
Дф-”=.
1-Л2
(ІП.4.15)
Подані
вище математичні співвідношення
свідчать про те, що на основі виконання
вимірювання на двох частотах з’являється
можливість не тільки обчислити практично
вільну від впливу іоносфери величину
віддалі до супутника, але й знайти
значення іоносферної поправки.
Залишковий
вплив на результати вимірювання
викликаний переважно не досить строгим
модельним поданням залежності іоносферної
поправки від частоти (ІІІ.4.7). У деяких
зарубіжних роботах показано, що зміна
тотальної кількості електронів (ТЕС)
проходить за складними законами, що
особливо проявляється під час магнітної
бурі.
Додаткових
послаблень впливу вдається досягти за
рахунок дифе- ренційних методів
вимірювання, коли під час розрахунків
використовуються не абсолютні значення
іоносферних запізнень, а їхні різниці,
характерні для траєкторій радіоприймачів,
що з’єднують супутник з двома віддаленими
на місцевості станціями.
Під
час виконання супутникового вимірювання,
поряд з іоносферою, необхідно враховувати
також вплив тропосфери, яка являє собою
найближчу до земної поверхні частину
атмосфери і яка сягає висот до 40-50 км.
Відмінна
риса тропосфери полягає в тому, що цей
компонент атмосфери є нейтральним
(тобто неіонізованим) середовищем. Тому
для частот радіодіапазону, менших
за 15 ГГц, таке середовище може розглядатися
як середовище, яке не піддається
дисперсії, внаслідок чого швидкість
поширення радіохвиль у ньому не залежить
від частоти. Фазова й групова швидкості
виявляються однаковими, а тому не
потрібно окремо вивчати вплив тропосфери
на фазові і на кодові вимірювання.
413II 1.4.5. Вплив тропосфери
Створюючи
методи урахування такого впливу,
неможливо використовувати описані
вище принципи вимірювання на двох
різних передавальних частотах, оскільки
вони спотворюються однаково.
Сьогодні
для урахування впливу тропосфери
запропонована значна кількість різних
моделей, які дають змогу оцінити
тропосферні запізнення під час
проходження сигналів від космічних
об’єктів до розташованих на земній
поверхні пунктів. Стосовно супутникових
систем типу GPS
найпоширеніша
модель Хопфілда. Під час створення
такої моделі була обґрунтована
доцільність поділу заломлювальних
властивостей тропосфери на “суху” і
“вологу” компоненти.
Ч-**
СО
;N„(h)
= Nt
(К.-Н'І
вл0
(ІП.4.16)
де
Формула
для підрахунку сумарного тропосферного
запізнення в зенітному напрямку має
вигляд:
ASmpon
=\lO-6(NCohc
+N„0h„). (ІІІ.4.17)
Під
час нахиленого проходження сигналів
через тропосферу використовують
формулу, яка в розгорнутому вигляді
запишеться так:
A-W^lO-6
NS0h*
^WQ
К
ylsin(E2
+6,25)
уІ&іп(Е2
+
2,25)
(ІІІ.4.18)
де
NSq
повідно
для сухої та вологої компонент;
Поряд
із тропосферною моделлю Хопфілда в
окремих типах супутникових приймачів
використовується модель Састамойнена,
яка описується таким емпіричним виразом:
AS,
0,002277
троп
COS
Z
' (1255
л
Р+
+ 0
I
Т
,05
je-
tg2z
(ІІІ.4.19)
де
Тропосферні
моделі інших авторів застосовуються
на практиці рідко.
414h
-
висота точки встановлення над рівнем
моря; hc
і
hejl
-
висоти політропного прошарку, до яких
температура лінійно пов’язана з висотою
для “сухого” та “вологого” компонентів.
Наближено hc
=
40 км, hejl
=
11 км.
і
NWq
-
індекси показника заломлення пбвітря
в точці спостережень відЕ
- вертикальний кут між напрямком на
супутник та горизонтом.z
-
зенітний кут у напрямку на супутник;
Р,
Ті е -
тиск, температура і вологість повітря.
Сумарна
тропосферна поправка для зенітного
напрямку становить близько 2,3 м. Проте
з наближенням супутника до горизонту
це значення значно зростає, а на висоті
близько 10°
над горизонтом сягає 20
м.
Варто
зауважити, що вплив тропосфери на
результати супутникового вимірювання
істотно послаблюється за рахунок
використанця диференціальних методів
спостережень, під час яких на остаточні
результати впливають не абсолютні
значення тропосферних запізнень, а
їхні різниці. Накопичений дотепер
досвід супутникового GPS-вимірювання
свідчить про те, що метод тропосферного
моделювання в поєднанні з диференціальними
принципами вимірювання дає змогу
доволі надійно оцінювати вплив тропосфери
на сантиметровому рівні точності.
Деякі складності можуть виникати під
час моделювання впливу вологості
повітря. Для їхнього подолання в тих
випадках, коли потрібно реалізувати
максимальну точність супутникового
вимірювання, рекомендується
використовувати спеціальні прилади,
які отримали назву радіометрів і
які дають змогу визначати з необхідною
точністю інтегральне значення вологості
на шляху проходження радіосигналу від
супутника до приймача.
Під
час супутникового вимірювання під
багатошляховістю прийнято розуміти
таке поширення радіосигналів, за якого
згадані сигнали сягають антени
супутникового приймача не тільки за
прямим шляхом, який з’єднує супутник
із пунктом спостереження, але і за
ламаним шляхом, який утвориться за
рахунок відбиття від різних об’єктів,
що оточують приймач (поверхня землі та
води, будівлі і споруди, зовнішні
геодезичні сигнали тощо).
За
наявності відбитих радіосигналів на
результати радіовіддалемірного
вимірювання діє додаткова похибка, яка
впливає на кінцеву точність супутникового
вимірювання. Багатошляховість може
бути причиною істотного послаблення
сигналів, які надходять на вхід приймача
і порушують його нормальну роботу.
Особливості
впливу відбитих радіосигналів на
результати відцалемірного вимірювання
доволі детально вивчені під час створення
і дослідження наземних радіовідцалемірних
пристроїв. Було встановлено істотне
розходження в механізмі впливу
відображень на передавальні коливання
і коливання, що їх модулюють. У зв’язку
з тим, що в супутниковому GPS-вимірюванні
використовують два типи зазначених
вище коливань, можна оцінити цей вплив
як на фазові вимірювання, які ґрунтуються
на використанні передавальних коливань,
так і на кодові вимірювання, які основані
на застосуванні сигналів, що їх модулюють.
415
Бвгатошляховість
Оскільки
вплив багатошляховості безпосередньо
на передавальні коливання описується
набагато простіше і наочніше, то
розглянемо механізм такого впливу на
характерні для супутникового вимірювання
фазові вимірювання, які належать до
передавальних коливань.
Припустимо,
що відбитий від того чи іншого об’єкта
радіосигнал проходить надлишковий
шлях Др, в результаті чого він набуває,
порівняно із прямим сигналом, додатковий
фазовий зсув Д'Р, що в частках фазового
циклу може бути оцінений на підставі
такого співвідношення:
дч#
=
у^Р, (ІІІ.4.20)
1)
де
/ - частота передавальних коливань, г>-
швидкість поширення електро
магнітних
хвиль.
Результуючий
сигнал, який виявляється зсунутим за
фазою щодо прямого сигналу на величину
АФ, оцінюється співвідношенням:
£(ДФ)
=
1
+ yfc cos(A'F) ’
(ІП.4.21)
де
Епр
нює
коефіцієнту відбиття відбивної поверхні.
Аналіз
(ІІІ.4.20) свідчить про те, що максимальна
похибка за багатошляховість за умови,
що
цих
сигналів, причому розглянута взаємодія
супроводжується не тільки виникненням
похибки у результатах супутникових
вимірювань, але й послабленням амплітуди
результуючого сигналу, що може приводити
до неможливості фіксації таких сигналів
через їхню малу величину і, як наслідок,
до пропуску фазових циклів під час
взяття послідовних відліків під час
орбітального руху супутника. Що
стосується кількісної оцінки фазових
зсувів, то з урахуванням того, що в
системі GPS
довжина
хвилі передавальних коливань близька
до 20 см, максимальна похибка фазового
вимірювання може сягати значень,
близьких до 5 см [24].
Під
час виконання псевдовіддалемірного
(кодового) вимірювання механізм
розрахунку похибок через багатошляховість
істотно ускладнюється. Не виконуючи
громіздкого математичного аналізу,
зазначимо, що під час підрахунку похибок
у результатах кодового вимірювання
відбувається перехід розглянутих вище
фазових зсувів, характерних для
передавальних коливань, у
416к
sin(A'P)к
= — коефіцієнт послаблення відбитого
сигналу, що наближено дорів-Евд
< Епр,
спостерігається у разі протифазності
фазові
зсуви модульованих (тобто кодових)
сигналів. Різниця ходу в кілька
сантиметрів, характерна для передавальних
коливань, трансформується у різницю
шляху для модульованих коливань, яка
оцінюється десятками метрів. Так,
наприклад, фазовий зсув на рівні близько
90°, якого набувають сигнали, які містять
інформацію про загальнодоступний
На
основі виконання як теоретичних, так
і експериментальних досліджень прийнято
такі рекомендації для послаблення
впливу джерел похибок, викликаних
багатошляховістю:
місця
розташування пунктів спостереження
варто вибирати з таким розрахунком,
щоб виключити наявність відбивних
об’єктів поблизу антени системи
супутникового приймача;
під
час створення антенних систем для
супутникових приймачів варто звертати
увагу на необхідність установлення
додаткових пристроїв, які екранують,
перешкоджають променям відбитих
радіосигналів на вхід антени (наприклад,
установлення екранів під антеною, що
дає змогу усунути вплив сигналів,
відбитих від підстилаючої поверхні);
на
пунктах, які піддаються впливу відбиття,
варто передбачати сеанси спостережень
більшої тривалості для того, щоб
отримати циклічну криву зміни похибок
через відбиття. Подальше усереднення
дає змогу істотно послабити розглянутий
вплив.
Сукупність
перерахованих вище заходів допомагає
мінімізувати вплив багатошляховості
до рівня, за якого це джерело похибок
не перешкоджає виконанню високоточного
супутникового вимірювання.
Під
час оцінки результуючої точності
супутникового вимірювання поряд із
похибками, викликаними неточною
інформацією про місцезнаходження
супутників на момент вимірювання, їхнє
взаємне розташування і вплив зовнішнього
середовища, ми повинні враховувати
також й інструментальні
417С/А-код,
і хвилі, які мають довжину, близьку до
300 м, викликає похибку, що оцінюється
величиною, близькою до 75 м. З урахуванням
вищевикладеного на підвищену увагу
заслуговують заходи, спрямовані на
послаблення впливу багатошляховості,
насамперед на результати кодового
вимірювання. Варто зазначити, що за
рахунок використання диференціальних
методів вимірювання не вдається
послабити розглянутий вплив, тому що
обставини, які породжують виникнення
багатошляховості, характерні для
кожного конкретного пункту спостережень.
Інструментальні джерела похибок
джерела
похибок, які пов’язані з недосконалістю
роботи тих чи інших вузлів, що входять
до складу апаратури.
Виконані
досі дослідження в цій галузі свідчать
про те, що основні джерела інструментальних
похибок пов’язані з похибками ходу
годинників на супутнику та приймачі,
з особливостями роботи передавальної
і приймальної антен, із урахуванням
часових запізнень в апаратурі передавача
і приймача, а також із недосконалістю
роботи відлікових пристроїв, за допомогою
яких визначається час (чи фазовий зсув),
що відповідає проходженню радіосигналу
від супутника до приймача.
Розглянемо
характерні риси кожного з перерахованих
вище інструментальних джерел похибок,
їхній вплив на результуючу точність
супутникового вимірювання і методи
мінімізації такого впливу.
Незважаючи
на всі заходи, спрямовані на підвищення
стабільності роботи відзначених
генераторів, вони за своїми показниками
не відповідають необхідним вимогам,
а тому, щоб уникнути істотного зниження
точності вимірювання, виконують
періодичне коректування показів
годинників, а також застосовують
спеціальні прийоми, які дають змогу
врахувати чи виключити похибки, викликані
неточністю показів годинників на
супутниках і в приймачах.
Для
урахування похибок показів годинників
супутникових приймачів застосовують
принцип вимірювання псевдовіддалей,
який ґрунтується на спостереженнях
чотирьох супутників.
Розглянутий
вище метод урахування впливу зміщення
руху годинників на супутнику і приймачі
набув найбільшого поширення під час
спостережень, які виконані однією
станцією, тобто під час абсолютних
визначень.
Під
час розв’язання геодезичних задач
вплив розглянутого вище джерела похибок
практично зводиться до нуля завдяки
застосуванню уже відомого нам методу
других різниць.
418Похибки,
викликані
нестабільністю ходу годинників супутника
і приймача. Похибки,
пов’язані з нестабільністю ходу
годинників, під час використання
однобічного методу віддалемірного
вимірювання є визначальними у всьому
комплексі похибок, характерних для
супутникового вимірювання. Роль
годинника на супутнику і в приймачі
виконують, як уже зазначалося,
високостабільні опорні генератори,
які є базовою основою для часу і частоти
під час реалізації шкали, відомої в
літературі як час GPS.
Через
високі вимоги до стабільності ходу
таких годинників на супутниках
використовують стабільні атомні
генератори. У приймальних пристроях,
які є у розпорядженні споживачів,
обмежуються застосуванням дешевших й
економічніших кварцових генераторів.
Похибка
визначення фазового центра та антени,
встановленої на супут- нику, сприймається
як неточність інформації про ефемериди,
які визначаються ца метровому рівні
точності.
Тому
споживачі основну увагу приділяють
проблемі встановлення фазового центра
супутникового приймача. Оскільки в
сучасних GPS-приймачах
переважно використовуються мікросмугові
антени, які мають симетричну конструкцію
щодо осі обертання антенного пристрою,
то місцезнаходження фазового центра
в горизонтальній площині, як правило,
з’єднують зі згаданою віссю обертання.
Що стосується фіксації фазового центра
в напрямку вертикальної осі, то цю
величину, визначає зазвичай фірма-виробник
приймальної апаратури і вносить в
паспорт приймача. Виробники прагнуть,
щоб згадана величина була однаковою
для всіх приймачів того самого типу.
Фірми- виробники GPS-приймачів
гарантують точність визначення і
стабільність положення фазового центра
на рівні одиниць міліметрів.
Стосовно
сучасних приймачів із мікросмуговими
антенами зсув фазового центра, як
правило, не перевищує декількох
міліметрів [24].
Для
боротьби із зазначеним впливом
фірми-виробники вживають заходів для
калібрування і компенсації запізнень
у трактах приймальної апаратури
споживача. З цією метою в деяких типах
приймачів вводиться спеціальний
контрольний канал, що дає змогу оперативно
оцінювати розбіжності у запізненнях,
які виникають у різних робочих каналах.
Увесь
комплекс заходів дає змогу звести
викликані такого роду джерелами
похибки до величини, яка обчислюється
декількома міліметрами.
419Похибки,
викликані неточною інформацією про
точки відносності.
Під час виконання високоточного
вимірювання від супутників до розташованих
на поверхні Землі приймачів дуже
важливим фактором є інформація про
положення точок, від яких вимірюються
віддалі. Щодо супутникового GPS-
вимірювання, то такими точками є фазові
центри антен супутника та приймача.Похибки,
пов \язані із впливом нестабільності
апаратурних часових запізнень і
внутрішніх шумів приймача.
Поряд із розглянутими вище джерелами
похибок, виникає також необхідність
урахування похибок вимірювання,
викликаних змінами в часі проходження
електричних сигналів в апаратурі
споживача. Впливам такого роду піддаються,
зокрема, багатоканальні GPS-
приймачі, у яких для проходження сигналів
від різних супутників відводиться
окремий, реально існуючий канал. Часові
запізнення в згаданих каналах можуть
помітно відрізнятися, що може призводити
до появи додаткових похибок у результатах
вимірювання.
Під
час проходження сигналів по електричних
ланках приймача спостерігається не
тільки їхнє запізнення в часі, але і
вплив на них внутрішніх шумів приймача.
Останній фактор має важливе практичне
значення, оскільки рівень внутрішніх
шумів визначає роздільну здатність
методів вимірювання. Зокрема, стосовно
GPS-вимірювання
через вплив зазначеного фактора
потенційна точність обмежується
величиною, що дорівнює близько 1%
від довжини хвилі, що для С/
Як
уже неодноразово зазначалося, одна з
характерних для системи GPS
особливостей
визначення місцезнаходження точок на
основі використання просторової
лінійної засічки полягає в тому, що
результуюча точність визначення
координат залежить не тільки від
точності віддалемірного вимірювання,
але і від геометрії розташування
супутників.
У
п. ІІІ.2.2 вказано, що фактор зниження
точності прийнято позначати абревіатурою
Залежно
від того, які параметри повинні бути
визначені під час розв’язання
поставленої задачі, використовують
різні модифіковані поняття
GDOP-
mN
+тЕ
+mh
+
mfc2
Щ
(ІІІ.4.22)
дет#,
Попередній
розрахунок значення геометричного
фактора може бути вико- аний перед
початком польового супутникового
вимірювання на підставі інформації
про розташування супутників на
відповідний момент часу і наближеної
інформації про координати пункту
спостереження, яка міститься в альманасі.
420А
-коду відповідає 3 м, для Р-коду - ЗО см,
а для фазового вимірювання, які
стосуються передавального коливання
- близько 2
мм. Найефективнішим засобом послаблення
такого роду впливів є використання
нової низькошумної елементної бази.Геометричний фактор
DOP.DOP.
Найуніверсальнішим
показником є параметр GDOP
(геометричний
фактор зниження точності з урахуванням
похибки визначення часу), що характеризує
точність тривимірного позиціонування
і часу:тЕ,
mh
-
середні квадратичні похибки визначення
координат за напрямками на північ, на
схід і за висотою; щ
-
середня квадратична похибка визначення
часу; с-
швидкість електромагнітних хвиль; т0-
похибка вимірювання віддалі до
супутників.
Зазначимо,
що фірма Leica
(Швейцарія)
не рекомендує виконувати високоточні
супутникові геодезичні вимірювання
для значень
Якщо
Найефективнішим
методом послаблення впливу геометричного
фактора на точність GPS-вимірювання
є вибір сприятливих періодів спостережень,
які визначаються під час складання
розкладів сесій GPS-вимірювання
на стадії планування супутникових
спостережень [23].
421GDOP,
більших за 8.
І це, безперечно, справедливо, оскільки
результуюча похибка вимірювання,
яка визначається за формулоютрез
= GDOP
■
т0. (ІІІ.4.23)GDOP
>8,
то результуюча (тобто загальна) похибка
визначення координат збільшується,
порівняно з т0,
практично на порядок - у десять разів.
РОЗДІЛ
IV. ВЕЛИКОМАСШТАБНЕ ТОПОГРАФІЧНЕ ЗНІМАННЯ
Під
час створення топографічних карт
зазвичай застосовується конформна
проекція еліпсоїда на площині,
запропонована Гауссом-Крюгером. Головні
властивості конформної проекції:
Зображення
нескінченно малого контуру еліпсоїда
на площині є подібним.
Кутові
спотворення відсутні.
Масштаб
зображення в кожній точці залежить
тільки від її координат і не залежить
від напрямку.
На
перехідний період (до введення референцної
системи координат України) для обчислення
координат пунктів Державної геодезичної
мережі (ДГМ) залишається референцна
система координат 1942 року (СК-42).
Висоти
точок під час складання топографічних
карт та планів визначають у Балтійській
системі висот 1977 року й відраховуються
від нуля Кронштадтського футштока.
Під
час використання проекції Гаусса-Крюгера
земний еліпсоїд розділяють меридіанами
на зони. Кожна зона - це сфероїдальний
двокутник, побудований від одного
полюса до другого й обмежений меридіанами
зі сталою різницею довгот.
Для
топографічних карт у масштабах 1:10000 і
менших застосовують шестиградусні
зони. Для України основними меридіанами
шестиградусних зон є меридіани з
довготами 21°, 27°, 33°, 39°. Початком
прямокутних координат у кожній зоні є
точка перетину осьового меридіана з
екватором; значення ординат у цій точці
на екваторі приймається таким, що
дорівнює 500 км.
4221. Загальні відомості про великомасштабне топографічне знімання
1.1. Топографічні плани та карти
Топографічною
картою
називають побудоване у картографічній
проекції, спотворене, зменшене,
узагальнене зображення значної ділянки
земної поверхні, що дає змогу визначати
як планове, так і висотне положення її
точок. Державні топографічні карти
України видаються у масштабах 1:1000000 і
більших.Топографічний
план
- подібне зображення на площині в
ортогональній проекції у великому
масштабі ситуації та рельєфу обмеженої
ділянки місцевості, у межах якої кривина
рівневої поверхні Землі не враховується.
Для
топографічних карт масштабів 1:5000 і
1:2000 для ділянок знімання більше за 20
км2
застосовують триградусні зони та
обчислюють прямокутні координати в
цих триградусних зонах. Осьовими
меридіанами триградусних зон для
території України є меридіани з довготами
21°, 24°, 39°. За основу
розграфлення
карт масштабів 1:5000 і 1:2000 беруть аркуш
карти масштабу 1:100 000, який поділяють
на 256 частин.
Номенклатура
аркуша карти масштабу 1:5000 складається
з номенклатури аркуша карти масштабу
1:100000 (наприклад, М-36-112), а потім далі, у
дужках, від 1
до 256 (наприклад, М-36-112-(256)). Номенклатура
аркуша карти масштабу 1:2000 складається
з номенклатури аркуша карти 1:5000 та
однієї з дев’яти букв українського
алфавіту (а, б, в, г, д, є, ж, з, і), наприклад,
М-36-112- (256-і).
Схема
створення номенклатури листів
топографічних карт масштабів 1:100000,
1:50000, 1:25000 та 1:10000, а також карт масштабів
1:5000, 1:2000, показана на рис. IV. 1.1.
Як
створюється номенклатура аркуша карти
масштабу 1:1000000, студентам відомо з курсу
“Топографії”. Нагадаємо, що цей аркуш
у нашому прикладі, на рисунку, має певний
пояс (буква М латинського алфавіту) і
номер колони 36, тому показаний на схемі
аркуш має номенклатуру М-36. Як будуються
номенклатури карт більших масштабів,
зрозуміло зі схеми. У нижньому правому
куті кожного прямокутника на схемі
вказана кількість аркушів топографічних
карт, на які поділено аркуш меншого
масштабу, а всередині прямокутника
вказаний масштаб карти та номенклатура
останнього аркуша карти цього масштабу.
Рис.
IV. 1.1. Схема створення номенклатури
аркушів топографічних карт
423
Масштаби |
Розмір |
Позначення (номенклатура) |
||
широти |
довготи |
|||
1:1000000 |
4°00'00" |
6°00'00,0" |
М-36 |
|
1:100000 |
20'00" |
30'00,0" |
М-36-144 |
|
1:50000 |
ІО'ОО" |
15'00,0" |
М-36-144-Г |
|
1:25000 |
5'00" |
7'30,0" |
М-Зб-144-Г-г |
|
1:10000 |
2'30" |
3'45,0" |
М-36-144-Г-Г-4 |
|
1:5000 |
1'15" |
1'52,5" |
М-36-144-(256) |
|
1:2000 |
0'25" |
0'37,5" |
М-36-144-(256-і) |
|
На
всіх топографічних картах обов’язково
показують лінійну рамку трапеції, тобто
виходи меридіанів та паралелей через
вказану в табл. IV. 1.1 кількість градусів,
мінут та секунд, і сітку плоских
прямокутних координат Гаусса-Крюгера.
Лінії сітки плоских прямокутних
координат проводять через 10
см на аркушах карт масштабу 1:10000
та більших масштабів; на аркушах
топографічних карт масштабу 1:25000 - через
4
см.
Отже, у масштабах 1:10000 і 1:25000 стороні
квадрата карти (10 см, 4
см)
на місцевості відповідає 1 км. Тому цю
мережу квадратів ще називають
Під
час складання топографічних планів на
забудованій та незабудованій території,
якщо ділянки менші за 20
км2,
а під час меліоративного будівництва
навіть більші за 20
км2,
застосовують прямокутне розграфлення
з розмірами рамок для планів масштабу
1:5000
- 40x40
см
(на місцевості (2x2
км),
а для масштабу 1:2000
із
розміром рамок 50x50
см
(1x1
км)).
Топографічні
плани у масштабах 1:1000, 1:500 завжди
складають тільки в ортогональній
проекції з прямокутним розграфленням
розмірів рамок 50x50
см.
На місцевості це відповідно будуть
квадрати 0,5x0,5
км
та 0,25x0,25
км.
Рамки
всіх цих топографічних планів масштабів
1:5000-1:500 не є частинами картографічної
сітки меридіанів та паралелей. Отже,
такі аркуші втрачають усі ознаки карт
і насправді є не картами, а планами.
За
основу розграфлення під час створення
номенклатури топографічних планів
беруть аркуш плану масштабу 1:5000 (див.
рис. IV. 1.2). Номенклатурою
424кілометровою
мережею (сіткою).
плану
масштабу 1:5000 є його номер, що позначається
арабською цифрою (на рис. цифра 5).
Змістова суть прийнятих позначень на
рис. IV. 1.2 така сама, як і на рис. IV. 1.1.
Рис.
IV. 1.2. Схема створення номенклатури
аркушів
топографічних планів
На
основі рис. IV. 1.2 неважко здогадатися,
що для отримання плану масштабу 1:2000
план масштабу 1:5000 поділяється на чотири
частини, які позначаються великими
буквами слов’янського алфавіту: А, Б,
В, Г. Із плану масштабу 1:2000
одержують чотири плани масштабу 1:1000,
які позначають цифрами римської системи
нумерації: I,
II,
III,
IV,
або 16 планів масштабу 1:500, які позначають
арабськими цифрами.
Топографічне
знімання - комплекс робіт, що виконується
для отримання оригіналу топографічної
карти та плану або топографічної
інформації в іншій формі [1].
Метою
топографічного знімання (створення
планів та карт) є вивчення у топографічному
аспекті території всієї держави для:
правильного
використання та розвитку виробничих
сил країни;
економії
технічних засобів;
економії
коштів;
економії
часу;
оборони
країни (“Карта - очі армії”).
До
великомасштабного топографічного
знімання належать знімання у масштабах
1:10000, 1:5000, 1:2000, 1:1000, 1:500.
Топографічні
плани можуть бути подані:
у
графічному вигляді;
у
вигляді цифрової моделі місцевості
(ЦММ) або цифрових моделей рельєфу
(ЦМР).
425
1.2. Мета та призначення топографічного знімання
Побудова
ЦММ та ЦМР виконується з використанням
комп’ютера перетворенням:
початкової
топографічної інформації (журналів
польового знімання);
картографічного
(графічного) зображення на цифрову
форму.
Топографічні
плани масштабів 1:5000-1:500 створюються:
методом
топознімання;
картоскладанням
за матеріалами більшого масштабу (крім
масштабу 1:500).
Що
підлягає зніманню? Усі об’єкти й контури
місцевості та рельєфу. Наприклад, на
планах масштабів 1:5000, 1:2000, 1:1000, 1:500
зображаються: пункти тріангуляції,
полігонометрії, трилатерації, репери
нівелювання, пункти робочої та знімальні
основи, закріплені на місцевості. Ці
об’єкти наносяться на плани за своїми
координатами.
На
незабудованих територіях - наносять
усі опорні пункти з їхніми висотами, а
на забудованих територіях - не всі,
залежно від навантаження плану та
його масштабу; наносять стовпи телефонних,
телеграфних, електричних мереж; проїжджі
частини вулиць з Обов’язковим позначенням
матеріалу покриття; стічні ґратки,
каналізаційні люки, тепломережі, інші
виходи підземних інженерних мереж;
промислові об’єкти: заводи, фабрики,
електростанції, шахти, кар’єри,
торфорозробки, нафтові вежі, цистерни,
склади корисних копалин, тощо;
гідрографія: берегова лінія моря, рік,
озер, струмків з позначенням зрізів
води та датою їхнього визначення;
гідрографічні об’єкти: канали, канави,
греблі, пристані, маяки, навігаційні
знаки; об’єкти водозабез- печення:
криниці, резервуари, джерела; лінії
електропередач та зв’язку: телефон,
телеграф, електромережі; лінії підземних
комунікацій, рослинність: дерева, кущі
і трави, сади, ягідники, виноградники,
технічні культури тощо; кордони:
політико-адміністративні, міські, смуги
шосейних доріг, ґрунтових доріг, захисних
зон, зон санітарної охорони тощо.
Розрізняють:
топоплани
та топокарти;
спеціалізовані
топоплани.
На
спеціалізованих топопланах зображають,
наприклад, тільки контури або тільки
рельєф чи тільки гідрографію. Спецплани
чи карти складають на основі спецінструкцій,
які вимагають знімання не усіх, а лише
певних контурів, нестандартних перерізів
рельєфу, зниження або підвищення вимог
стосовно точності.
Призначення
топографічних планів залежить від
масштабу знімання й подається в
інструкціях з топознімання.
426
Топографічні
плани масштабу 1:2000 використовуються
для:
створення
генеральних планів малих міст, селищ
міського типу та сільських населених
пунктів;
проектів
детального планування забудови міських
промислових районів;
проектів
осушення та зрошення;
проектів
залізниць та автодоріг тощо.
Плани
масштабу 1:1000 використовуються переважно
для складання технічних проектів і
робочих рисунків малоповерхової, а
плани масштабу 1:500 - для багатоповерхової
забудови. Тому під час вибору масштабу
знімання виходять із призначення плану
чи карти.
Наприклад,
замовнику необхідне знімання деякої
ділянки для створення генерального
плану забудови сільського населеного
пункту, і він просить виконати знімання
у масштабі 1:5000. Геодезист, виконавець
робіт, користуючись інструкцією,
інформує замовника, що у такому разі
потрібен план масштабу 1:2000. Це, звичайно,
дорожче, однак необхідно, інакше не
буде розв’язана інженерна задача
забудови на потрібному технічному
рівні.
Детальніше
це дуже важливе питання - обґрунтування
необхідного масштабу знімання, яким
керувались укладачі інструкції,
установлюючи той чи інший масштаб
знімання, для тих чи інших призначень,
- ми розглянемо дещо пізніше.
Як
відомо, карта виникла раніше ніж
писемність. Багатовіковий пошук методів
топографічного знімання виявився
плідним і привів до створення значної
кількості різноманітних способів
картографування. Для наочності спробуємо
класифікувати відомі методи, користуючись
наведеними нижче схемами.
Рис.
IV. 1.3. Методи топографічного знімання
427
1.3. Методи топографічного знімання. Їхня суть
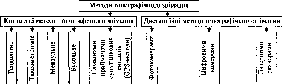
На
цій схемі показано дві великі групи,
на які поділяються усі відомі методи
топографічного знімання:
Суть
контактних методів - бусольного,
теодолітного, тахеометричного,
мензульного - студентам відома з курсу
“Топографії*”. Нагадаємо, що бусольне
та теодолітне знімання визначає тільки
планове положення предметів місцевості.
Інші, контактні методи дають змогу
складати повноцінні карти із зображенням
на них ситуації та рельєфу.
Основи
супутникових методів викладено у
розділі III цього підручника. Зауважимо,
що наземні приймачі GPS
визначають
своє положення на підставі інформації
з космосу, проте приймачі GPS
контактують
з об’єктом, координати якого визначають,
і тому зараховуються до контактних
методів.
З
появою супутникової геодезії вважалось,
що її можна застосовувати тільки для
створення геодезичних мереж. Проте
надзвичайно швидкий розвиток техніки
супутникової геодезії, особливо
приймачів GPS,
зменшення
розмірів та ваги приймачів фактично
без втрати їхньої точності розширив
застосування супутникової геодезії й
для топографічного знімання, оскільки
вона починає конкурувати із найшвидшими
й найточнішими традиційними методами
знімання. Методами космічної геодезії
можна створювати як графічні, паперові
плани та карти, так і електронні, цифрові
плани та карти.
Наземні
контактні методи знімання (окрім методу
GPS)
застосовуються
для знімання незначних ділянок, коли
методи аерознімання економічно
недоцільні. Тільки методи супутникової
геодезії (методи GPS),
що
також зараховані до контактних, набувають
останнім часом все більшого поширення
та конкурують з іншими контактними
методами.
Зауважимо:
необхідно розрізняти космічні методи
фотознімання, які виконуються з космосу,
та методи супутникової геодезії -
GPS-методи,
основою яких є просторове визначення
координат.
Що
стосується безконтактних методів, то
необхідно окремо розглядати кожну із
трьох груп таких знімань.
Наземне
фотознімання виконується приладами,
що поєднують теодоліт та фотокамеру і
мають назву “фототеодоліти”. Карти
складають на основі наземних фотознімків.
428контактні,
тобто, такі, що виконуються приладами,
здатними виконувати знімальні
вимірювання, торкаючись (контактуючи)
об’єкта картографування (з поверхнею
Землі), та дистанційні,
такі, що дають змогу виконувати знімання,
не торкаючись об’єкта, що картографується.
Крім того, у схемі коротко названі
методи знімання. В основу назв методів
покладено назви найголовніших приладів,
якими виконується знімання.
Рис.
IV. 1.4. Топографічне знімання фотокамерами
В
останньому методі комбінується
(поєднується) аерофотознімання й наземне
знімання. Найчастіше вживається
мензульне знімання або електронна
тахеометрія.
До
2000 року основними методами знімання,
які використовувалися для знімання
значних територій, тобто методами
державного знімання, були: 1)
стереознімання; 2) комбіноване
знімання. Найширше застосовувалось
стереознімання. Комбінований метод
використовувався у закритих, лісових
районах, а також на рівнинній місцевості
з високою чагарниковою й трав’яною
рослинністю.
Безконтактні
методи фотознімання за своїми
властивостями здавалися такими, що не
можуть бути перевершеними. Але з появою
цифрових камер фотознімання витісняється
цифровим топографічним зніманням.
Рис.
IV. 1.5. Топографічне знімання цифровими
камерами
429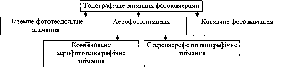
У
стереоаерофототопографічному методі,
який скорочено будемо називати методом
стереознімання,
використовуються для складання
повноцінних топографічних планів
аерофотознімки, виконані фотокамерами
(які встановлені на борту літака або
іншого літаючого апарату), та методи
фотограмметрії (науки про вимірювання
на фотознімках). У результаті отримують
карти та плани із зображеними на них
ситуацією та рельєфом місцевості.Комбінований
аерофототопографічний метод,
який будемо скорочено називати
комбінованим
методом,
використовує аерофотознімки тільки
для складання контурної частини планів,
а рельєф місцевості на цих планах
знімають і зображають горизонталями
наземними методами топографії.
Спочатку
цифровими методами опрацьовувалися
аерознімки. Але з появою на початку
третього тисячоліття цифрової аерокамери
цифрові методи топознімання набувають
державного значення, а методи фотознімання,
напевно, повністю заміняться цифровими
методами.
Проте
одним із найновіших топографічних
методів є
Рис.
IV. 1.6. Топографічне знімання лазерними
сканерами
Цей
метод застосовується як самостійний,
у наземному варіанті, і реалізується
особливими приладами - сканерами. Суть
технології полягає у визначенні
просторових координат точок поверхні
об’єкта з дуже високою швидкістю -
тисячі і десятки тисяч вимірювань на
секунду. Окрім того, лазерне сканування
комбінується із цифровим аерозніманням.
Найчастіше
рельєф зображають на топографічних
планах та картах горизонталями.
Людство
навчилося зображати схили крутістю до
45°. Тому схили до 45° ще зображаються за
допомогою горизонталей; крутіші схили
(яри, обриви, зсуви) зображаються умовними
знаками.
На
рис. IV. 1.7 показано вертикальний розріз
рельєфу за лінією
де
Тоді
для v
=
45° (коли горизонталі будуть найгустіщими)
закладення дорівнює перерізу. На рис.
IV. 1.8 зображені дві горизонталі, накреслені
завтовшки 0,1 мм, з проміжком між краями
горизонталей 0,1 мм. Отже, віддаль між
осями горизонталей становитиме 0,2 мм.
Ці горизонталі проведені
430метод
лазерного сканування.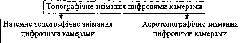
1.4. Обґрунтування вибору перерізу рельєфу
АВ.
Горизонтальні
лінії, що проходять через точки А
та В,
є зображеннями площин перерізу рельєфу.
Із трикутника ABC
можемо
записати формулу:a
= hctgv, (IV.1.1)а
-закладення
(віддаль між горизонталями на плані);
h-
переріз
рельєфу; v
-
вертикальний кут нахилу рельєфу. Для
v
=
45°, ctgv
=
1, і формула (IV. 1.1) набуває вигляду:a
= h. (IV.
1.2)
найгустіше:
проміжок, менший за 0,1
мм, вже майже не розрізняється неозброєним
оком людини.
Отже,
у такому разі А =
Рис
IV. 1.7 До вибору перерізу рельєфу
Товщина
горизонталі 0,1 мм
Товщина
горизонталі 0,1 мм
Рис
IV 1 8 Мінімально можливі віддалі між
горизонталями, що межують
Підкреслені
числа і є розрахованими мінімальними
перерізами.
Проте
такі перерізи рельєфу не можуть бути
реалізовані: у горбистій місцевості
горизонталі будуть накреслені занадто
густо і не буде місця на карті чи плані
для зображення ситуації масштабними
та позамасиггабними умовними знаками;
навпаки, на рівнинній місцевості
горизонталі будуть зображені дуже
рідко або їх узагалі не буде.
Тому
на практиці, зважаючи на необхідність
зображення на планах не тільки рельєфу,
але й ситуації, для масштабів 1:5000 на
рівнинних ділянках зменшують перерізи
рельєфу від розрахованого до 0,5 м.
Навпаки, у гірських районах перерізи
збільшують до 2-5 м. Для всіх інших
масштабів А, як правило, збільшують до
0,5-2 м.
431а
= 0,2 мм плану. Товщину горизонталі - 0,1
мм (коричнева лінія) та проміжок між
горизонталями - 0,1
мм (білий проміжок) будемо вважати
мінімальною двійковою одиницею (дв.
од.). її сумарна товщина - 0,2
мм.
Проміжок між осями горизонталей 0,2 мм

Ширина білого проміжку між горизонталями 0,1 мм
Як
відомо, точністю масштабу знімання
називають горизонтальний відрізок на
місцевості, якому на плані відповідає
0,1 мм. У табл. IV. 1.2 подано відрізки на
місцевості, яким у масштабі плану
відповідає 0,2
мм, тобто отримані теоретично, на
підставі формул (IV. 1.1) та (IV. 1.2) мінімально
можливі перерізи рельєфу для
великомасштабного знімання.
Масштаб знімання |
1:5000 |
1:200 |
1:1000 |
1:500 |
1 см плану відповідає на місцевості |
50 м |
20 м |
10 м |
5 м |
1 мм плану відповідає на місцевості |
5 м |
2 м |
1 м |
0,5 м |
0,1 мм плану відповідає на |
0,5 м |
0,2 м |
0,1 м |
0,05 м |
місцевості |
||||
0,2 мм плану відповідає на |
1 м |
0,4 м |
0,2 м |
0,1 м |
місцевості |
|
У
результаті отримаємо перерізи
рельєфу, що рекомендує чинна інструкція
великомасштабного топографічного
знімання [5]. Рекомендовані перерізи
подано у табл. IV. 1.3.
Таблиця
IV. 1.3
Рекомендовані
чинною інструкцією перерізи рельєфу з/п |
Характеристика рельєфу та максимально переважаючі кути нахилу |
Масштаби знімання |
||
1:5000 |
1:2000 |
1:1000, 1:500 |
||
Висоти перерізу рельєфу, м |
||||
1 |
Рівнинний, з кутами |
(0,5) |
0,5 |
0,5 |
|
нахилу до 2° |
1,0 |
(1,0) |
|
2 |
Горбистий, з кутами |
(1,0) |
0,5* |
0,5 |
|
нахилу до 4° |
2,0 |
1,0 |
|
'і |
Пересічений, з кутами |
2,0 |
(1,0) |
0,5 |
j |
нахилу до 6° |
(5,0) |
2,0 |
1,0* |
4 |
Гірський та передгір’я, з |
2,0* |
2,0 |
1,0 |
|
кутом нахилу понад 6° |
5,0 |
|
1 5V |
Примітка:
Перерізи, відмічені зірочкою, на планах
населених пунктів не використовуються.
Для планів населених пунктів допускаються
перерізи, взяті в дужки, але вони повинні
бути обґрунтовані проектами на виконання
знімання.
Дуже
складне питання, яке ще не отримало
повного теоретичного розв’язання
[4].
Численні
фактори, які впливають на вибір масштабу
знімання, можна об’єднати у чотири
групи:
432
1.5. Обґрунтування масштабу знімання
виробничі
(вид будівництва, розмір ділянки
знімання, стадії проектування,
способи проектування, розміри й види
об’єктів, що проектуються, наявні
топоматеріали, інженерні пошуки, час
пошуків);
природні
(характер та розташування території,
що піддягає зніманню, наявність
контурів, рельєф, пора року);
технічні
(вимоги до графічної точності, висота
перерізу, методи знімання, прилади, що
використовуються);
економічні
(терміни знімання, вартість робіт).
Карта
є засобом пам’яті інформації. Чим
більший масштаб (менший ступінь
зменшення), тим більше інформації
містить карта. Вибір масштабу
топографічного знімання на основі
певного математичного апарату можливий
за допомогою створення відповідних
критеріїв. Одним із таких критеріїв,
напевно, доволі вдалим, є критерій
мінімальної надлишкової інформації
(мінімальних затрат на знімання
amin).
Критерій
надлишкової інформації має вигляд:
1-
Ro_
(IV.
1.3)
де
omin
-
надлишкова інформація; Rq-
характеристика
інформативності топографічної карти
або плану, під якою розуміють кількість
двійкових одиниць на один гектар (дв.
од. / га), тобто достатню для користувача
кількість інформації для розрахунку
конкретної проектно-планувальної
задачі;
Зміст
цього критерію можна пояснити, ввівши
поняття інформаційної густини
топографічного плану чи карти
(IV.
1.4)
Зрозуміло,
що для
Для
433Rm-
масштабозадавальна
інформаційна місткість топографічної
карти або плану (дв. од. / га), під якою
розуміють максимальну кількість
інформації, що відповідає максимально
можливому завантаженню карти (плану)
без втрати її наочності та читабельності
(умовний знак не може бути викреслений
поверх іншого знака).Q>\
ємність
карти (плану) недостатня, не дає змоги
розв’язати поставлену задачу, оскільки
багато необхідних об’єктів місцевості
не будуть відображатися у прийнятому
масштабі. Інформаційна густина повинна
бути більшою за нуль, але не більшою за
одиницю.Q>
1
вважають, що інформаційна густина
генеративна,
тобто інформаційна місткість карти
(плану) через недостатність не дає змоги
розв’язати задачі проектувань, оскільки
необхідні об’єкти місцевості не
зображаються у вибраному масштабі
карти (плану).
|
Місцевість |
|
План (1:500) |
100 м |
Рм=10000 м2 |
20 см |
Рпл-40000 мм2 |
Рис.
IV. 1.9. До підрахунку Rm
масштабозадавальної
місткості
плану масштабу 1:500.
Тоді
40000
мм2
=
500 дв. од./га.
80
мм2
На
плані одну двійкову одиницю можна
зобразити квадратом зі стороною
5
м
Площа
такого квадрата місцевості » 20 м2.
Як бачимо, це площа житлової забудови
4x5
м.
Таких забудов на 1 гектар плану масштабу
1:500 може поміститися не більше ніж 500.
434Rm
плану
цього масштабу становить:[ZZ
2
nr.*
,т _ 1
см 0,894 см .a=yl80
мм
=8,94
мм.
На місцевості це буде = ; ам
-
4,47 м.а,.
Площа
в 1 гектар на місцевості має розмір,
незалежний від масштабу, що дорівнює
100x100
м.
На планах у масштабах 1:1000,
1:2000, 1:5000, 1:10000 - 1 гектар
подамо квадратами відповідно 100x100
мм,
50x50
мм,
20x20
мм,
10x10
мм,
тобто квадрати будуть меншими, порівняно
з масштабом 1:500,
у
2,4,10,20
разів.
Тому значення
1:500
1:1000
1:2000
1:5000
1:10000
Насправді
площі масштабних і позамасштабних
умовних знаків неоднакові; також
неоднакова їхня кількість на один
гектар. Достатньо, наприклад, прийняти,
що ширина двійкової одиниці позамасштабного
знака 0,3 мм. Тоді такий знак для довжини
100 мм (це сторона квадрата площею в 1
гектар плану масштабу 1:1000) матиме площу
30 мм2.
Кількість таких знаків на площі в 1
гектар масштабу 1:1000
дорівнюватиме
Точніші
розрахунки, коли враховуються різниці
в площах знаків та в кількості масштабних
та позамасштабних умовних знаків,
елементи генералізації та деякі інші
фактори дають такі значення
1:500
1:1000
1:2000
1:5000
1:10000
Порівнюючи
наближені значення
Характеристику
інформативності
10000
мм2
ЗО
мм2
=
333 дв. од. / га, а не 250 дв. од. / га.
(IV.
1.5)
435Rm
відповідно
для цих масштабів будуть:-Rm
—
500
дв. од. / га;-Rm=
250
дв. од. / га;-Rm-
125
дв. од. / га;-Rm
=
50
дв. од. / га;-Rm—
25
дв. од. / га.Rm,
які рекомендуються настановами щодо
вибору масштабу знімання:-Rm
=
500
дв. од. / га;-Rm-
330
дв. од. / га;-Rm-
1Ю
дв. од. / га;-Rm=
ЗО
дв. од. / га;-Rm-
Ю
дв. од. / га.Rm
і
ті, що рекомендуються, неважко побачити,
що вони мають один порядок.R()
рекомендується
розраховувати за такою емпіричною
формулою:
де
1,2
- стала;
урахуванням
інформаційних вимог спеціалістів. Ці
вимоги також уже встановлені і становлять
3,0; 2,7; 2,5; 2,3 і 1,8 дв. од. відповідно до
мінімальних площ на місцевості 1, 5, 10,
20 і 100 м2.
Як
бачимо, під час розрахунку критерію
надлишкової інформації Gmin
необхідно
знати:
кількісні
дані про середню кількість об’єктів
площу
мінімального з них
Ці
дані можуть бути отримані в управліннях
будівництва та архітектури та інших
відповідних організаціях. Для цієї
самої мети можна використати дані
польового обстеження двох-трьох типових
ділянок, що характеризують топографічні
умови об’єкта знімання.
Без
цих даних встановлення необхідного
масштабу знімання методом, що описується,
унеможливлюється.
Подамо
приклад обґрунтування масштабу знімання
для реконструкції забудованої території
(табл. IV. 1.4).
Нехай
/^іп
= 20 м2
(площа капітальної господарської
забудови). Розрахуємо за IV. 1.5 характеристику
інформативності Rq
:
Rq=
2,3x20+1,2x23=73,6 дв.
од. /
га.
Результати
розрахунків надлишкової інформації
подано у табл. IV. 1.5.
За
мінімумом надлишкової інформації (33
%) з табл. IV. 1.5 визначаємо необхідний
масштаб топографічного знімання для
реконструкції населеного пункту -
1:2000.
Існують
й інші критерії обґрунтованого вибору
масштабу знімання. Розглянемо ще один
із них -
де
436Ni
п
-
відповідно середня кількість ділянок
і предметів місцевості, які необхідно
відобразити масштабними і позамасштабними
умовними знаками на 1
гектар площі під час розв’язання певної
проектно- планувальної задачі; К
-
кількість двійкових одиниць, що залежить
від мінімальної площі ділянки Pg
(м2),
яку потрібно відобразити на плані чи
карті з
N
і
п,
які потрібно буде відобразити на одному
гектарі;Pg,
м2.критерій
допустимої похибки визначення віддалі.
Якщо
задана допустима середня квадратична
похибка вимірювання віддалі за планом
т0,
виражена в метрах, то обґрунтування
вибору масштабу знімання можна зробити
на підставі мінімальних затрат на її
виконання на основі умовиМ0<МР, (IV.
1.6)Мр
- знаменник розрахованого масштабу
знімання; М0-
знаменник найближчого стандартного
масштабу знімання.
Назва ділянок та предметів місцевості |
Середня кількість об’єктів на 1 га |
А. Ділянки, що зображаються в масштабі плану: |
|
житлові будинки |
10 |
господарські капітальні будови |
5 |
адміністративні та інші приміщення |
2 |
окремі ділянки (площі, сквери тощо) |
1 |
інші об’єкти |
2 |
|
|
Б. Об’єкти, що зображаються позамасштабними умовними знаками: |
|
виходи на поверхню мережі інженерного обладнання |
6 |
території |
|
стовпи лінії зв’язку, електропередач |
5 |
газорегулювальні пункти |
2 |
висоти точок |
5 |
інші об’єкти |
5 |
|
|
Таблиця
IV. 1.5
Розрахунок
надлишкової інформації залежно від
масштабу знімання топо- знімання |
Інформаційна ємність D ДВ.од. Кт га |
Інформатив ність D ДВ.ОД. *0 га |
Інформативн а густина ^-г Кт |
Надлишковість
(,
До
)
V. т / |
1:500 |
500 |
73,6 |
0,15 |
85% |
1:1000 |
330 |
73,6 |
0,22 |
78% |
1:2000 |
по |
73,6 |
0,67 |
33% |
1:5000 |
зо |
73,6 |
генеративна |
- |
1:10000 |
10 |
73,6 |
генеративна |
- |
Приблизне,
але доволі точне співвідношення між
середньою квадратичною похибкою (у
метрах) вимірювання віддалі за планом
437т0
і розрахованим знаменником масштабу
МР
можна записати так:Щцн)
=
0,3 (ММ)
-МР. (IV.
1.7)
Формула
(IV.1.7)
отримана
з таких міркувань. Лінія на плані чи
карті вимірюється циркулем-вимірником.
Квадратична похибка суміщення голок
вимірювача з кінцями лінії, що вимірюється,
дорівнює 0,2
мм.
Тому
відрізок на плані вимірюється з
абсолютною квадратичною похибкою
0,272=0,3 мм. Йому відповідає відрізок на
місцевості
Тому
МР=-
т.
0(м)
п
і (ІУЛ-8)
3
мм
Наприклад,
в умовах забудованої території з
капітальними будинками та густою сіткою
виходів на поверхню інженерних підземних
комунікацій можна прийняти
Розрахований
знаменник масштабу знімання становитиме:
0,15(М)-1000
0,3
мм
=
500.
Ще
приклад. Необхідно вимірювати лінії
на плані з точністю 0,6 м. Тоді
1#
0>6(м)-1000
Мр
=
3
мм
=
2000.
Обґрунтування
вибору масштабу топографічного знімання
можна виконувати і без розрахунків, на
підставі рекомендацій Основних положень
[14]. Критеріями слугують два типи
територій, що картографуються:
І тип
- територія з багатоповерховою забудовою,
територія великого
міста;
П
тип - територія переважно з малоповерховою
забудовою та неза- будована територія.
Масштаби
топографічних карт та планів, а також
масштаби топографічного знімання
залежно від типу території картографування
подано у табл. IV. 1.6.
Основні
положення дають змогу за необхідності
для створення робочих креслень на
території II типу плани масштабу 1:1000
збільшувати до масштабу 1:500 і для
складання проекту детального планування
на території II типу плани масштабу
1:5000 збільшувати до масштабу 1:2000.
Доволі
вдало можна вибрати масштаб знімання
за допомогою наближеної формули, якщо
вже заданий переріз рельєфу. Формула
має вигляд:
438(щ-
похибка вимірювання лінії у метрах).
т0
= 0,15 м.МР
= -М0=
МР
= 500. Необхідний масштаб знімання 1:500.
М0=
Мр
= 2000. Необхідний масштаб знімання 1:2000.
Масштаби топографічних планів або карт |
Тип І |
Тип II |
1:500 |
1:500 |
- |
1:1000 |
- |
1:1000 |
1:2000 |
1:2000 |
- |
1:5000 |
картоскладання |
1:5000 |
1:10000 |
1:10000 або картоскладання |
- |
Приклад:
1)
нехай переріз
0
10%
2)
нехай переріз
1-Ю4
0 5%
Навпаки,
якщо визначений масштаб знімання, то
за (IV. 1.9) можна визначити необхідний
переріз рельєфу. Справді, розв’язавши
(IV. 1.9) відносно
к
=
і%
■ М0
їо4
Нехай
М0
= 5000; v
=
4°;
Л
(м) =
7%-5000
104
=
3,5 м.
Стандартного
перерізу
K^hp,
(IV.1.10)
(IV.1.11)hp
=
1 м, vcep
=
6°;
tg6°
=
і
= 0,1 = 10%. Тоді 1
104М0
=—— = 103
=1000; масштаб 1:1000;hp
=
1 м, \сер
=
3°; tg3°
=
і
= 0,05 = 5%. ТодіМ0
= =
2000;
масштаб 1:2000.hp
(у
метрах), отримаємо:і
= tg
4°
= 0,0699 = 7 %. Тодіh$
=
3,5 м у табл. IV. 1.3 немає.
Кінцевий
переріз вибирається на підставі
нерівності
де
У
табл. IV. 1.3, для v
=
4° і масштабу 1:5000, Ад=
2
м - найближчий переріз до розрахованого.
Тобто для знімання потрібний переріз
Ад = 2 м. Формули (IV. 1.9) та (IV. 1.10) наближені,
проте доволі широко застосовуються
під час знімання сільських населених
пунктів.
Технічний
проект (програма) визначає призначення,
зміст та обсяг робіт, їхню кошторисну
вартість, термін виконання та інші
важливі показники топографо-геодезичних
робіт на об’єкті знімання.
Попередньо,
до складання проекту, виконуються
збирання та аналіз топографо-геодезичних
матеріалів, які дають змогу встановити
топографічну вивченість ділянки робіт
і можуть бути використаними у ході
знімання. Необхідні матеріали отримують
у територіальних інспекціях державного
геодезичного нагляду ГУГК, в управлінні
по справах будівництва та архітектури
в обласних та райдержадміністраціях.
Топографо-геодезичні
роботи, що здійснюються для створення
планів масштабів 1:5000-1:500, виконують на
основі держзамовлення, замовлень
окремих міністерств, відомств,
підприємств та організацій різних форм
власності.
Роботи
виконуються організаціями і суб’єктами
підприємницької діяльності, які
мають ліцензії на виконання
топографо-геодезичних робіт.
Проект
складається із трьох частин: 1) текстової;
2) графічної; 3) кошторисної.
У
текстовій частині описуються:
призначення
топографо-геодезичних робіт;
коротка
фізико-географічна характеристика
ділянки знімання;
відомості
про топографо-геодезичну вивченість;
обґрунтування
вибору масштабу знімання і висоти
перерізу рельєфу;
способи
побудови планових та висотних геодезичних
мереж з урахуванням фізико-географічних
умов місцевості та наявності відомих
геодезичних пунктів;
організація
та терміни виконання робіт, заходи з
техніки безпеки та охорони праці тощо.
Графічна
частина проекту містить схеми, матеріали
аерознімання, картографічні матеріали,
на яких зображена:
440hp
-
розрахована висота перерізу (hp=
3,5
м); Ад-
найближчий
до розрахованого переріз.
1.6. Технічний проект топографо-геодезичних робіт
ділянка
знімання;
відомі
геодезичні пункти;
пункти
планової Та висотної робочої основи
знімання;
номенклатура
і розграфлення аркушів карт та планів
тощо.
Кошторисна
частина проекту обґрунтовує необхідні
грошові витрати на
організацію
робіт, на матеріали, виготовлення
геодезичних планових та висотних
знаків, закладання цих знаків, дослідження
приладів, виконання польового геодезичного
вимірювання, попереднє та кінцеве
опрацювання вимірів, складання технічного
звіту, припинення робіт.
Топографо-геодезичні
роботи виконують тільки після погодження
із замовником і затвердження технічного
проекту організаціями, що видають
дозвіл на виконання цих робіт.
Основа
великомасштабного топографічного
знімання поділяється на:
Основну
(геодезичну).
Робочу.
Геодезцчною
основою великомасштабного знімання
слугують:
Планова
державна мережа, як відомо, поділяється
на: астрономо-геоде- зичну мережу 1
класу; геодезичну мережу 2
класу; геодезичні мережі згущення З
класу.
Висотна
державна мережа поділяється на нівелірні
мережі I,
II,
III та IV класів.
До
геодезичних мереж спеціального
призначення належать:
просторові
геодезичні мережі на геодинамічних
полігонах;
спеціальні
геодезичні мережі для інженерно-геодезичного
забезпечення будівництва, гірничої
справи та інші мережі.
Розрядні
мережі згущення,
які поділяються на:
мережі
полігонометрії, трилатерації,
тріангуляції 4 класу;
мережі
полігонометрії, трилатерації й
тріангуляції 1-2
розрядів;
мережі
технічного та тригонометричного
нівелювання.
441
2. Робочі (знімальні) мережі великомасштабного топографічного знімання
2.1. Види геодезичної основи великомасштабного знімання. Розрахунок необхідної щільності робочої основи
Державна
геодезична мережа (ДГМ)
України, яка складається із планової
та висотної мереж, а також мереж
спеціального призначення.
Державні
мережі - частково, а розрядні мережі
згущення - детально описано у розділі
II цієї книги.
Густота
(щільність) пунктів геодезичної основи
великомасштабного знімання.
Щільність
пунктів геодезичної основи визначається:
а) масштабом знімання; б) перерізом
рельєфу; в) цілями знімання.
Для
геодезичного забезпечення топографічного
знімання встановлюються такі норми
щільності пунктів ДГМ:
• для
знімання у масштабах 1:25000 і 1:10000 - 1 пункт
на 30 км2
і 1 репер на трапецію масштабу 1:10000.
Середня
щільність пунктів державної геодезичної
мережі повинна бути доведена під час
знімання у масштабі 1:5000 до одного пункту
на 20-30 км2
і одного репера на 10-15 км2.
Під час знімання у масштабі 1:2000 - один
пункт ДГМ на 5-15 км2
та один репер на 5-7 км2.
Подальше згущення геодезичної основи
виконується за рахунок розрядних мереж
згущення та знімальних мереж. Мережі
згущення доводяться до щільності: 4
пункти на 1 км2
у забудованих територіях та 1 пункт на
1 км2
у незабудованих територіях. У районах
меліоративного будівництва щільність
повинна бути доведена до 1-2
реперів
на 4 км2.
Для інженерних пошуків та будівництва
у містах та промислових майданчиках -
8
пунктів на 1 км2.
Знімальна основа доводиться до щільності,
що забезпечує безпосередньо знімання
тим чи іншим методом. Для наочності
вимоги до щільності пунктів наведені
в табл. IV.2.1.
Виконаємо
розрахунки необхідної щільності пунктів
робочої основи.
У
наш час, як уже зазначалось, під час
знімання значних територій застосовують
переважно стереознімання або комбіноване
знімання. За комбінованим методом
знімання рельєфу та дешифрування
виконуються за допомогою мензульного
знімання або оптичної чи електронної
тахеометрії. Наземне топографічне
знімання ситуації та рельєфу невеликих
ділянок також найчастіше виконують
електронними тахеометрами. Тому
розрахуємо необхідну щільність точок
робочої основи для цих методів знімання.
Для таких розрахунків необхідно,
передовсім, мати на увазі, що під час
мензульного та тахеометричного знімання
віддалі визначаються оптичними
віддалемірами з відносною помилкою
близько 1/300 і довжини ліній до пікетів
не повинні бути більшими за 300 м.
442
Знімальна
геодезична мережа
- планові, висотні й планово-висотні
знімальні мережі або окремі пункти
(точки), а також точки фотограмметричного
згущення.
№ з/п 1 |
Види геодезичної основи |
Масштаби знімання |
|
1:5000 |
1:2000 |
||
Державні планові мережі |
1 пункт на 20-30 км2 |
1 пункт на 5-15 км2 |
|
2 |
Державні висотні основи |
1 репер на 10-15 км2 |
1 репер на 5-7 км2 |
3 |
Мережі згущення на забудованій території |
4 пункти на 1 км2 |
|
4 |
Мережі згущення на незабудованій території |
1 пункт на 1 км2 |
|
5 |
Мережі згущення під час інженерних пошуків та будівництва у містах і на промислових майданчиках |
8 пунктів на 1 км2 |
|
6 |
Знімальна (робоча) основа |
Доводиться до щільності, що забезпечує виконання знімання запроектованим методом |
|
Електронний
тахеометр дає змогу вимірювати в
декілька разів більші довжини і його
точність вища в десятки разів.
Тому
наперед зрозуміло, що щільність робочої
основи для традиційних методів знімання
повинна бути значно більшою, ніж для
електронної тахеометрії.
Розглянемо
випадок, коли робоча основа будується
методом аналітичної мережі ідеальної
форми. Нехай (на рис. IV.2.1)
З
рівностороннього трикутника
S_
S 2
;
2S
= 2S' j3.
S'
2
s
= s'js. (IV.2.2)
443ABC-
рівносторонній
трикутник зі стороною S,
що є елементом цієї ідеальної мережі.
Точки D,
Е,
F,
К
-
перехідні точки, тобто точки, на яких
також буде встановлюватися мензула чи
оптичний тахеометр для знімання рельєфу
та дешифрування.АЕК
можемо записати:—
=
sin
60°
= —. (IV.2.1)
F
Рис.
IV.2.1. Аналітична
мережа ідеальної форми
Щоб
виконати знімання усієї території,
необхідно записати:
S'
= 2x,
(IV.2.3)
де
Припустимо,
що лінії відкладають на плані із
наближеною точністю 0,2
мм. Максимальну
відносну похибку визначення віддалі
нитковим віддалеміром
приймемо
1/150. Відповідно до графічної й польової
точності повинно бути:
2мм_
1
х
150
(IV.2.4)
На
основі (IV.2.4)
маємо:
до
(IV.2.3),
5'=
6
см, а, враховуючи (IV.2.2),
5
= 6
см
Для
масштабу 1:5000 - S
=
500 м;
для
масштабу 1:2000 - S
=
200 м.
Отже
(рис. IV.2.2),
якщо
будемо будувати мережу у вигляді
прямокутних трикутників із катетами
«10
см, на плані отримаємо для трапеції
масштабу 1:5000 (розмір 40x40
см)
- 25 пунктів, а для трапеції масштабу
1:2000 (розмір 50x50
см)
- 36 пунктів. Фактична кількість пунктів
може бути дещо більшою або меншою. Але
розрахунок дав кількість цих пунктів,
якщо мережі були б ідеальної форми.
444х
-
віддаль (максимальна) від приладу
(мензули чи оптичного тахеометра)
до
рейки.
х-0,2
мм • 150 = 30 мм = 3 см. Тому, відповідноу/ї
= 10,32 см. Оскільки пікети із Суміжних
станцій повинні перекриватися, приймемо
5
= 10
см.
40
см 2 км
50
cm
1
км
30
пунктів
1:2000
Рис.
IV. 2.2. До
розрахунку щільності пунктів робочої
основи
Якщо
ж знімання буде виконуватися електронним
тахеометром, то, по- перше, зникне
необхідність у перехідних точках, а
по-друге, можна будувати робочу мережу
зі сторонами аналітичної мережі, як
мінімум вдвічі більшими: 400-1000 м. Тоді
й кількість необхідних точок зменшиться
вдвічі і майже повністю зникне потреба
у перехідних точках.
Робоча
(знімальна) основа створюється у вигляді:
Аналітичних
мереж. Такі мережі, як і геометричні
мережі, будуються у вигляді мережі
трикутників. Проте у геометричних
мережах горизонтальні кути не
вимірюються, а будуються на мензульному
планшеті, тоді як в аналітичних мережах
ці кути вимірюються теодолітами 2Т30,
2Т5, 2Т5К або іншими такої самої точності.
Теодолітних
ходів.
Висотно-теодолітних
ходів, у яких окрім горизонтальних
кутів, вимірюють і вертикальні кути.
Останні використовуються для визначення
висот пунктів теодолітних ходів методом
тригонометричного нівелювання. У таких
ходах лінії вимірюють переважно мірною
стрічкою. Можна застосовувати
світловіддалеміри та оптичні віддал
еміри.
Тахеометричних
ходів.
Мензульних
ходів.
Окремих
точок, що визначаються прямими оберненими
та комбінованими засічками.
445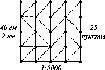
2.2. Методи створення знімальної (робочої) основи. Закріплення пунктів мережі на місцевості
Перехідних
точок - висячі мензульні та інші ходи.
Такі ходи мають 1-
точки
(не більше), а лінії вимірюються переважно
мірною стрічкою або світловіддалеміром.
Під
час побудови знімальних мереж одночасно
визначають положення пунктів як у
плановому, так і у висотному аспектах.
Гранична похибка положення пунктів
планової знімальної мережі щодо пунктів
державної мережі та розрядних мереж
згущення не повинна перевищувати 0,2 та
0,3 мм у масштабі плану відповідно на
відкритій і забудованій місцевості та
на лісовій або зарослій високими кущами
території.
Пункти
знімальної мережі закріпляють
довготривалими знаками (рис.
1.14)
з таким розрахунком, щоб на ділянці
місцевості, що відповідає знімальному
планшетові масштабу 1:5000, як правило,
було закріплено не менше від трьох
пунктів, а в масштабі 1:2000
- двох пунктів, враховуючи пункти ДГМ
та мережі розрядного згущення.
На
території населених пунктів та
промислових майданчиків пункти робочої
основи закріплюють тільки довготривалими
знаками.
Якщо
робоча мережа є самостійною основою
(без мереж вищої роз- рядності) тоді не
менше від однієї п’ятої частини пунктів
закріплюють знаками за типом центрів
тріангуляції та полігонометрії 1 і 2
розрядів (рис. II. 1.14). На забудованих
територіях населених пунктів застосовують
знаки типу чавунного репера (рис. II.
1.15).
Пункти
знімальної мережі нумерують. Номер
пункту наносять безпосередньо на
знаках або на встановлених сторожках.
На забудованих територіях номер ставлять
на стовпах ліній електропередач, на
близьких будинках та інших предметах
місцевості.
одним.
У такій мережі кути трикутників не
вимірюються, а будуються під час
створення робочої основи мензульного
знімання. Така мережа називається
Довжини
сторін трикутників аналітичної мережі
значно коротші, ніж у тріангуляції (min
-
150 м; шах - 2 км). Кути не менші за 20°. Кути
вимірюються
446
2.3. Аналітичні мережі (польові роботи)
Аналітичні
мережі,
як і тріангуляція - мережі трикутників.
Як відомо, існує ще одна побудова, що
будується у вигляді трикутників, які
межують один
геометричною.
Ми розглянемо мережу трикутників, у
яких кути вимірюються. Тому часто в
геодезичній літературі такі мережі
називають робочими (знімальними)
мережами, що будуються методом
тріангуляції. Проте, щоб відрізняти
ці мережі від геометричної мережі та
від тріангуляції, цілком виправдано
називати їх аналітичними
мережами.
двома
круговими прийомами теодолітами
(точності, не нижчої за ЗО") з
перевстановленням лімба через 90°.
Допустима нев’язка трикутника не
більша за 1,5'. Найчастіше використовуються
такі аналітичні побудови:
1)
геодезичний чотирикутник (рис. IV.2.3,
а):
3)
центральна система (рис. IV.2.3,
в):
4)
ланка трикутників з двома вихідними
сторонами (рис. IV.2.3,
г):
5)
ланка між стороною й пунктом (рис.
IV.2.3,
д):
447
6)
ланка, побудована на стороні (рис.
IV.2.3,
е):
Нехай
під дією похибок
М
N
Рис.
IV.2.4.
До
визначення похибки у положенні точкиР,
що
визначається прямою засічкою
Із
трикутника
(IV.2.5)
Із
трикутника
(IV.2.6)
На
підставі (IV.2.5)
(IV.2.6) запишеться
так:
(IV.2.7)
446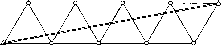
2.4. Розрахунок точності ланки трикутників аналітичної мережі
dSx
у
довжині сторони S
та
в дирекційному куті dax
точка
Р
змістилась у положення Р”
на величину q
.
Це зміщення можна розкласти на dSx
-уздовж
лінії Sl
йна
г
-
перпендикулярно до S{.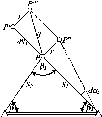
Р
Р' Р"
маємо: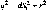
N
Р
Р*
(рис.
IV.2.4,):
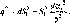
Переходячи
від диференціалів до квадратичних
похибок, отримаємо:
(IV.2.8)
9 9 ■>
та
МР
= ms
+
Sl
~~
Р
Як
відомо, у ланках трикутників сторони
визначаються з відносними похибками,
що описуються формулою
Ж-
Ь
2*4’
(IV.2.9)
s
J і
ь
і
+-j^r{cte2Pi
+ctS2h
+^gPiC/gp3}-
Переходячи
до абсолютної похибки та нехтуючи
похибкою в базисі
3
Р Крім того, як відомо
т\
=\S\~l2
[ctS2Pi
+
ctS2Рз
+
c&Pl<*gP3}
•
Wa,=mrj-'
(IV.2.10)
(IV.2.11)
Формулі
(IV.2.8)
можна
надати вигляду:
2
або
М2р 2tg2p!
+
ctg%
+cteftctek} + !^S?, (IV.2.12)
2
Mp
кутників:
Р,
= 60°;
ctg%
=0,58;
ctg2
р,-
=0,34.
Тоді
вираз формули (IV.2.13),
що
в дужках, буде дорівнювати 2.
Тому
формулі (IV.2.13)
можна
надати простішого вигляду:
МР=
1,15^5. (IV.2.14)
Р
Якщо
діють переважно випадкові похибки,
тоді їхнє накопичення буде пропорційне
до
Похибка
кінцевої точки ланки визначиться за
формулою
МР
ГП
(IV.2.15)
449Ь,
одержимо:
=lsl^{l + ctg2h
+ctg% +ctg^ctg^).
(IV.2.13) Припустимо,
що аналітична ланка складається з
рівносторонніх три-Jn
,
де п
-
кількість трикутників ланки.
Розрахуємо
максимально допустиму кількість
трикутників у ланці. Як відомо, гранична
похибка в розташуванні робочої основи
відносно найближчих пунктів геодезичної
основи на плані - 0,2 мм. Для масштабу
1:5000 0,2 мм становить 1 м. Підставивши в
(IV.2.15)
замість
формулу
відносно л/й, одержуємо:
Гп
=
1,15-S-
(IV.2.16)
Нехай
сторони мережі дорівнюють 1000 м, а похибка
вимірювання кута
_ 1•206265*
1,15
-1000-45' ’ ’
Для
масштабу 1:2000 на плані 0,2 мм відповідає
0,4 м, тобто
1,15-500-45
3,19
Наші
розрахунки зроблені для висячої ланки
трикутників. Якщо ланка спирається на
дві вихідні сторони, то максимальна
похибка буде всередині
ланки
і кількість трикутників такої ланки
можна збільшити в
Тоді
отримаємо: для масштабу 1:5000
для
масштабу 1:2000
Як
бачимо, хоча наші ррзрахунки спрощені,
похибки вихідних даних не враховані,
але одержана кількість трикутників
ланки майже така сама, що і допускається
інструкцією.
І. Висяча
ланка ув’язує тільки кути трикутників.
Поправки в окремий /в
кут
обчислюються
дирекційні кути та довжини сторін.
Координати кожної точки мережі
обчислюються два рази, з контролем (за
двома сторонами трикутника). За кінцеві
значення координат беруть середні
значення.
450М?п
1 м і розв’язавши цющ*
= 45". Тодіп=
16 трикутників.МР
= 0,4 м. Тому для такого масштабу, прийнявши
S
=
500 м, тяр*= 45", отримаємо:Г
0,4-2062265'\п
= -п=
10
трикутників.-J2
раза.п
=22 трикутники;п
= 14 трикутників. Інструкція [5] допускає
відповідно 20 та 17 трикутників.2.5. Спрощені способи зрівноваження аналітичних мереж
V/
=
—, де /р - нев’язка трикутника. 'Далі
розв’язуються трикутники і
Ланка
між вихідними сторонами:
Ув’язуються
всі кути.
Вибирається
середня лінія, наприклад
Координати
точок С і
Надалі
по кожному з чотирьох ходів між точками
Ланка
трикутників між двома пунктами
(побудована на вихідній стороні) (рис.
IV.2.5):
Ув’язуються
кути у трикутниках.
Вибирають
ходову лінію (див. рис. IV.2.5),
показану
пунктирною ламаною лінією і ув’язують
кути за ходовою лінією. Якщо, наприклад,
кількість
кутів,
враховуючи ті, що межують, дорівнює
v п
вводяться
тільки в ходові кути. До того ж, у ліві
кути поправки додаються, а від правих
віднімаються.
У
трикутниках знову з’являються нев’язки.
Для ліквідації нев’язок в
f
інші
(не ходові кути) вводяться поправки —.
Якщо кут Р, з отримав поправку
2п
—,
тоді кожний із кутів pj
j та
Р12
повинен одержати поправку, що дорівнює
Л.
п
За
кінцево ув’язаними кутами обчислюють
дирекційні кути ходових ліній та
координати всіх точок, зокрема точки
Рис.
IV.2.5.
До
зрівноваження аналітичної мережі,
побудованої на стороні AN
451
CD
(рис.
IV.2.3,
г).D
обчислюються
два рази, як у висячої ланки. Знаходять
середнє з них.AD,
ВС,
NC,
MD
виконуються
обчислення, як у теодолітних ходах.
п,
а нев’язка /в,
то поправки —
п
N.
Отже, отримують координати X'
та Y'
точки
N.
Оскільки координати X'
та Y'
точки N
не
збігаються з відомими координатами
точки N,
то одержимо рис. IV.2.6.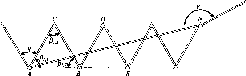
|
(IV.2.17) |
|
(IV.2.18) |
^ * 1 1 II а •ЙР |
(ГУ.2.19) |
, Yn-Ya
|
(IV.2.20) |
Обчислюють:
|
|
Поперечний
зсув u
= Р £
Коефіцієнт
|
|
Усі
дирекційні кути ходових сторін змінюють
на 6. Ще раз обчислюють координати усіх точок за |
ходовою лінією за |
виправленими
а;
та Sr
Якщо
ланка побудована між вихідною стороною
та відомим пунктом, то ув’язування
мережі виконується, як і в попередньому
випадку.
452
У
мензульному ході будуються з певною
точністю горизонтальні кути та
вимірюються довжини ліній. Тому для
розрахунків мензульного ходу можна
користуватися формулами, виведеними
для кутомірних ходів: полігоно- метричного
або теодолітного. Скористаємося відомою
формулою для висячого кутомірного
ходу:
[5]2="UJ+
3
V2’
(TV.2.21)
де
М - похибка в положенні кінцевої точки
ходу; [5]-
довжина ходу;
кількість
сторін; відносна похибка вимірювання
сторін; /ир- абсолютна
S
похибка
горизонтальних кутів.
Як
видно з (TV.2.21),
її
перший член зменшується зі збільшенням
АГ
їм)
1
rms
42
дп
.
т'2
1
Щ
+ тг
= 0.
З
о'2
(IV.2.22)
Розв’яжемо
(IV.2.22)
відносно
1
ms
S
1
./2
;„2=Г^2.3Р'2!*L.pL.J3. (IV.2.23)
[s
) ntf
s
Довжини
ліній вимірюються у мензульному ході
нитковим віддалеміром.
Нехай
^- = —!—. Орієнтування планшета за довгими
лініями можна
S
400
виконати
з похибкою /ир = 3'.
Підставивши
в (IV.2.23)
ці
числові значення, отримаємо:
п-
1 3438'
400
’ З'
•а/з
=4,96 = 52.6. Розрахунок планової точності та допустимої довжини мензульного ходу
М2
_ 1 Гf
я+
1,5п-п;
другий
член, навпаки, зростає зі збільшенням
п.
Необхідно знайти екстремальне значення
п.
Для цього треба (IV.2.21)
продиференціювати
по п
і прирівняти до нуля. Отримаємо:п:
сторін
Для
S
=
200 м; [.S]
=
200 м • 5 = 1000 м інструкція допускає 1000 м
для масштабу 1:5000 та 500 м для масштабу
1:2000.
453
Масштаб знімання |
Максимальні довжини ходу, м |
Максимальні довжини ліній, м |
Максимальна кількість ліній у ході |
1:5000 |
600 |
200 |
3 |
1:2000 |
250 |
125 |
2 |
1:1000 |
100 |
50 |
2 |
1:500 |
50 |
50 |
1 |
Хід
масштабу 1:500 може складатися із двох
ліній по 25 м кожна. Зауважимо, що в
розрахунках допустимої довжини висячих
мензульних ходів (саме такі ходи часто
використовуються) брались до уваги
тільки похибки вимірювання ліній та
похибки побудови горизонтальних кутів.
Неминучі,
454
абсолютні,
випадкові похибки відкладання ліній
за допомогою циркуля-вимір- ника та
поперечного масштабу, які дорівнюють
0,1-0,2 мм плану (граничні - 0,3 мм), практично
незалежні від довжин ліній (зазвичай,
декілька сантиметрів у цьому масштабі
плану), не враховувались.
Тому
для компенсації впливу цих похибок
доцільно виконувати вимірювання
ліній для мензульних ходів мірною
стрічкою або рулеткою не тільки під
час знімання у масштабі 1:500, але й у
масштабах 1:1000, 1:2000, 1:5000.
Заміна
висячих ходів ходами між точками з
відомими координатами також підвищує
їхню точність.
Інструкція
дає змогу використовувати під час
мензульного знімання геометричну
мережу трикутників, але тільки під час
знімання у масштабі 1:5000.
Нехай
теодолітний хід прокладено між відомими
пунктами. Скористаємось формулою,
виведеною в розділі II:
4
+
3
тр
(IV.2.24)
Знайдемо
екстремальне значення кількості сторін
ходу
[5]
дп
_
М ms
п2
-2
і 5
+2-4-0.
12
р'2
Після
перетворень отримаємо:
/
\2
. _2
1
п
fa.) .12..є!
UJ
>v2
М
v
п
= -
1
2000
0,5
«
= ^-P-VT2.
S
тф
•-^22.7. Розрахунок точності та допустимої довжини теодолітного ходу
S
) 12п.
Для цього продиференціюємо (IV.2.25)
по
п
і результат прирівняємо до нуля:
(IV.2.25)
Кути вимірюють теодолітом із точністю відліку / < 30" двома прийомами, а труба наводиться на віху з віхоутримувачем. Тому приймемо = 0,5'. Нехай
лінії вимірюються стрічкою з відносною похибкою 1/2000.
455
Масштаб |
Максимальні довжини |
Довжини |
Кількість |
знімання |
ходів, м |
сторін, м |
сторін у ході |
1:5000 |
9000-7500 (4500-3700) |
750-250(375-125) |
12/30 |
1:2000 |
4000-3200(2000-1700) |
400-100 (200-60) |
10/30 |
1:1000 |
2000-1700 (1000-850) |
200-85 (100-40) |
10/20 |
1:500 |
1000-850 (450-400) |
125-40 (60-20) |
8/20 |
Для
визначення екстремального значення
кількості сторін
тахеометричного
ходу скористаємося формулами (IV.2.24)
та
(IV.2.25).
Проте
необхідно врахувати, що лінії в
тахеометричному ході вимірюються
оптичними відцалемірами з відносною
похибкою
т
■S2.8. Розрахунок планової точності та допустимої довжини тахеометричного ходу
п
та Mdon=fL^
1
S
400
а горизонтальні кути вимірюються не грубіле за Г.
(ГУ.2.26)
456
Масштаб знімання |
Ц, м |
Доцільна кількість сторін пі |
Середня довжина сторін Sj, м |
Очікувані (допустимі) нев’язки ходу, м |
1:5000 |
2100-3000 (1100-1500) |
8/30 (8/30) |
260/100 (130/50) |
2,0 (1,0) |
1:2000 |
900-1200 (450-600) |
8/30 (8/30) |
100/40 (50/20) |
0,8 (0,4) |
1:1000 |
400 (200) |
8 (8) |
50 (25) |
0,4 (0,2) |
1:500 |
200 (100) |
8 (8) |
25 (15) |
0,2 (0,1) |
Оскільки
під час знімання у масштабі 1:1000 та 1:500
тахеометричні ходи короткі, то в них
лінії необхідно вимірювати металевою
або л^ктронною рулеткою, мірною стрічкою.
Інструкція рекомендує вимірювати лінії
стрічкою тільки для масштабу знімання
1:500. Розраховані тут допуски стосовно
параметрів ходів дещо відрізняються
від указаних в інструкції. У табл. IV.2.4
наведено
допустамі параметри ходів електронної
тахеометрії.
457
Масштаб знімання |
Гранична похибка вимірювання кутів =20” |
Граничні (очікувані) нев’язки ходів, м |
||
Відносні похибки вимірювання ліній 1:33000 |
||||
L, м |
П |
S, м |
||
1:5000 |
18000-12000 (9000-6000) |
12/30 |
1500/400 (750/200) |
2,0 (1,0) |
1:2000 |
7500-5000 (4000-2500) |
10/30 |
750/170 (400/80) |
0,8 (0,4) |
1:1000 |
4000-2500 (2000-1300) |
10/30 |
400/80 (200/40) |
0,4 (0,2) |
1:500 |
2000-1300 (1000-700) |
10/30 |
200/40 (100/20) |
0,2 (0,1) |
У
таблиці наведені допустимі довжини
ходів за оптимальної і значної кількості
сторін. Якщо
Технічне
нівелювання виконується як робоча
висотна основа топографічного
знімання з перерізом рельєфу 0,25; 0,5 і
1,0 м.
Допускається
технічне нівелювання й для перерізів,
більших за 1 м. У ходи технічного
нівелювання включають пункти теодолітних
ходів, аналітичних мереж, а також
окремі місцеві предмети, такі, наприклад,
як виходи підземних комунікацій.
Для
такого нівелювання застосовують
нівеліри із ціною поділки рівня не
більше за 45" на 2 мм та збільшенням
труби не менше ніж 20* типу Н-10 КЛ, а також
рейки нівелірні, двосторонні, шашкові
типу РН-10 із ціною найменшої поділки
10 мм. Нівелювання виконується ізсередини
в одному напрямку; віддалі від нівеліра
до рейок вимірюють віддалемірними
нитками труби.
458и
> t,
то під час збільшення п
Ldon
зменшиться,
якщо и
< t,
Ьдоп
збільшиться. У круглі дужки взято
значення параметрів ходів, за яких
очікувані нев’язки вдвічі менші за
допустимі.
2.9. Технічне нівелювання для створення робочої основи топографічного знімання
Нормальна
довжина плечей технічного, геометричного
нівелювання - 120 м.
Під
час спокійних зображень допускаються
плечі завдовжки до 200 м. Нерівність
плечей на станції -10 м. Накопичена
нерівність - 50 м. Плечі під час вибору
місця встановлення нівеліра та рейок
спочатку вимірюють кроками. Рейки
встановлюють на башмаки або кілки.
Відліки беруться за допомогою тільки
середньої нитки сітки ниток.
Послідовність
відліків рейок: задня чорна, передня
чорна, передня червона, задня червона.
Розходження перевищень на станції не
повинно перевищувати 5 мм.
Розрахуємо
допустиму довжину ходу технічного
нівелювання. Дойустима нев’язка ходу
визначається за формулою
Інструкція
[5] допускає похибку у висоті точок
робочої основи 1/10 від перерізу рельєфу.
Якщо нев’язка ходу 1/5 від перерізу
рельєфу, то після ув’язування ходу
максимальна похибка у висоті буде
всередині ходу й виявиться такою, що
дорівнює ~ 1/2 від нев’язки, тобто 1/10 від
перерізу. Тому приймемо
носно
m2h
"доп
(50
мм)2
(200)2
2500
40000
2500
=
16 км.
Для
Наші
розрахунки довжин ходів збігаються з
екстремальними допусками інструкції.
З методами
тригонометричного нівелювання студенти
знайомі з курсу “Топографія”. Саме
метод тригонометричного нівелювання
застосовують для визначення перевищень
та висот під час тахеометричного
знімання. Тут ми розглядаємо тригонометричне
нівелювання як метод побудови висотних
робочих мереж ДЛЯ
будь-якого
способу ТОПОЗНІмаННЯ.
Кути
налплу
місцеві
V
вимірюють
оптичними або електронними тахеометрами.
Рекомендується виконувати вимірювання
кутів нахилу трьома прийомами за двох
положень вертикального круга. Коливання
значень місця нуля (М0) та кутів нахилу
V
не
повинно перевищувати 15".
459fhdon
=
Щдоп
=
50 мм JL
km
. (IV.2.27)mhdo„
=1/5
від перерізу h.
Для
перерізу 1 м = 100 см,mhdo„
=1/5-100
см = 20 см = 200
мм. Розв’яжемо рівняння (TV.2.27)
відL.
Отримаємо:L(
км)
=h
=
0,5 м L
=
4 км; для h
=
0,25 м L
-
1 км.2.10. Тригонометричне нівелювання для створення висотної знімальної основи
Інструкція
рекомендує використовувати прилади з
точністю відліків вертикального круга
1-2".
Повна
формула тригонометричного нівелювання
має вигляд:
h
= S tgv + i-l + f, (IV.2.28)
де
Допустима
нев’язка тригонометричного нівелювання
визначається за формулою
A.»)'0'04!!' <rv-2-29)
У
(IV.2.29)
/Л-
нев’язка, см; [5] - довжина ходу, м;
ходу.
Розрахуємо
допустиму довжину тригонометричного
ходу на підставі (IV.2.29).
Тригонометричне
нівелювання допускається інструкцією
для перерізу
пдоп пдоп
=
40 см.
Розв’яжемо
(IV.2.29)
відносно
[5]:
(IV.2.30)
Як
бачимо з (IV.2.30),
допустима
довжина ходу буде зростати у разі
збільшення
кількості сторін ходу. Це закономірно,
оскільки нівелювання з
короткими
сторонами виконується точніше.
Інструкція, без обґрунтування,
приймає
допустиму кількість сторін 5, проте
допускає збільшення кількості
сторін
в 1,5 раза у гірських районах. Без втрати
точності нівелювання кількість
сторін
ходу можна збільшити.
Нехай
1
Отже,
допустима довжина ходу » 3 км. Для
перерізу рельєфу більше ніж 2 м допустимі
довжини ходів, зрозуміло, будуть
зростати.
Може
виконуватися спеціальне тригонометричне
нівелювання, коли перевищення
визначаються зі значно більшою точністю,
ніж передбачено (IV.2.29).
Тригонометричне
нівелювання широко застосовується під
час визначення висот перехідних точок,
а також окремих точок, планове положення
яких визначається прямими й оберненими
та комбінованими засічками.
460S
-
горизонтальне прокладення довжини
лінії; v
-
кут нахилу; і
- висота тахеометра; /- довжина рейки
(труба наводиться на верх рейки); / -
поправка за сумісний вплив кривини
Землі та рефракції.п-
кількість лінійh
=
2 м і більше. Якщо h
=
2 м, тоді /і, =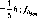
п
= 9. Тоді [S]
м
= ^
°М
^
=
3000 м.1 0,04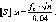
Детально
питання визначення координат окремих
точок засічками описано у розділі, де
розглядається прив’язування пунктів
полігонометрії до пунктів тріангуляції
або до пунктів полігонометрії старших
класів. Там також подано й розрахунки
точності визначення планових координат
прямими, оберненими та комбінованими
одноразовими та багаторазовими
засічками.
Коротко
зупинимося на вживаних методах визначення
висот цих точок.
Зазвичай
висоти визначаються методом “на себе”,
тобто знаходять висоту тієї точки, де
встановлено тахеометр, за відомими
висотами мінімум трьох найближчих
точок, що розташовані навколо шуканої
точки. Горизонтальні віддалі
Рис.
IV.2.7. До визначення висот окремих точок
Кути
нахилу v
вимірюють
трьома прийомами (кожний прийом при
двох положеннях вертикального круга).
Розраховують середнє значення кутів
нахилу із трьох вимірів. Нехай ці кути
будуть
знаходять
середні перевищення
їїА\
~ її і
+ ^сері
9 їїа2
~ її2 ^сер2 9 їїАз
— Я3
4- hcep3
.
Знаки
перевищень
визначається
висота
нА]Рі+нА2р2
+ нАір2
На
=-
(IV.2.31)
ДЄЛ=-^
;
461S29
S3
від
шуканої
точки А
до відомих точок 1, 2, 3 визначають з
аналітичного розв’язання трикутників
або вимірюють світловідцалемірами
(рис. IV.2.7).
vcep[9
vcep2,vcep3.
Далі за (IV.2.28)hcepi,
hcep2,
hcep3.
Визначають три значення висоти шуканої
точки А:hcep.
беруть оберненими до виміряних, оскількиНА
точки А,
а не висоти Я,. За кінцеву висоту точки
А
береться
її середнє вагове значенняР\
+ Р'У
+ jPl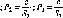
с
-
довільний коефіцієнт пропорційності.
В
аналітичних мережах, а також під час
тахеометричного знімання для визначення
перевищень вимірюють кути нахилу v.
У тріангуляції, коли виконується
тригонометричне нівелювання для
визначення висот пунктів тріангуляції,
вимірюють не кути нахилу V
,
а зенітні кути Z.
Хоча Z
-
це кути, їх часто називають ще й зенітними
віддалями. Залежність між кутами нахилу
v
та
зенітними кутами Z
показана
на рис. IV.2.8.
Рис.
IV.2.8.
Залежність
між кутами нахилу
V
та
зенітними кутами Z
Нехай
маємо нахилену пряму
Z
=
90°-v, (IV.2.32)
або
V
=
90° - Z. (TV.2.33)
Як
відомо, для вимірювання кутів нахилу
v
вводиться
поняття
h
= S ctg Ze
+i-l
+
f, (TV.2.34)
де
Як
і в (IV.2.28),
/
- поправка за кривину Землі
4622.11. Вимірювання зенітних віддалей. Вертикальна рефракція
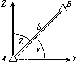
АВ,
початкова точка якої А
збігається з початком системи прямокутних
координат ZAY.
Площина ZAY
-
вертикальна. Як видно з рис. IV.2.8:“місце
нуля”
(М0). Під час вимірювання зецітних кутів
(віддалей) вводиться поняття “місце
зеніту”
(MZ).
Це
відлік вертикального круга тахеометра,
коли зорова труба спрямована в зеніт,
а бульбашка циліндричного рівня, що
скріплений із вертикальним кругом,
розміщена у нуль-пункті. Формула
(IV.2.28)
набуває
вигляду:і
-
висота
тахеометра; /-довжина рейки (труба
наведена на верх рейки).к3
та рефракцію г.f
= k3-r. (IV.2.35)
(IV.2.36)
k3
~
2 R3
1^1
2
Rc
'
(IV.2.37)
У
(IV.2.36)
кривої
поширення світла. Виникає запитання:
як визначити/?,.? На жаль, у неоднорідній
за густиною атмосфері світло від точки
2.9.
У
результаті достатньо спрямувати трубу
по дотичній
Рис.
IV.2.9. Спотворення вертикальною
рефракцією
виміряних \в
та ZB
Спостерігач
вважає, що труба спрямована по хорді
Урахування
рефракції 8
або
Для
визначення 8
або
463R3
-
радіус
Землі, що дорівнює 6371 км. У (IV.2.37)
Rc-
радіусВ
(де встановлена візирна ціль) до точки
А
(де встановлено тахеометр) поширюється
не прямолінійно, як показано на рис.
IV.2.8,
а
по деякій складній кривій, як це показано
на рис.
АС
до кривої АВ,
щоб спостерігач бачив у трубі точку
В.
АВ
=S.
Насправді труба спрямована по дотичній
АС.
Тому вимірюються не теоретичні кути
V, та Z,,
а спотворені рефракцією кути vB
та
ZB.
Кут 5 називається частковим кутом
вертикальної рефракції. Це кут між
дотичною АС
та хордою АВ.
Куту 8
відповідає
лінійна рефракція г.
Саме на величину г
спотворюється правильне перевищення
h
між
точками А
та 5.г
виявилось надзвичайно складним,
оскільки крива поширення світла
може бути повернута опуклістю вверх
або вниз. Окрім того, у різних частинах
кривина кривої різна.г
необхідно знати густину повітря у
багатьох точках на шляху світла. А
оскільки світло поширюється часто
доволі високо над
земною
поверхнею, то це майже неможливо. Це
питання досліджується майже 400 років.
Спочатку
дослідники покладали великі надії на
визначення єдиного коефіцієнта
рефракції. Під коефіцієнтом рефракції
к
*3
(IV.2.38)
Справді,
вплив кривини Землі
Для
відомого
R,=-
Отже
або
_
1 S2
_
1 S2
r~2RL~2R3
к
Як
бачимо з (IV.2.39), і
У
наш час абсолютно точно доведено, що
про єдиний коефіцієнт рефракції упродовж
доби не може йтися. Тільки під час
нормальної стратифікації температури
коефіцієнт
Нормальна
стратифікація настає уранці, приблизно
через годину після сходу Сонця й у разі
ясної погоди продовжується близько
півгодини. Ввечері нормальна стратифікація
настає десь за 1,5 години до заходу Сонця
й також триває півгодини. Отже, нормальна
стратифікація під час антициклонної,
ясної погоди продовжується усього
близько 1 години на добу. Під час похмурої
погоди ці періоди можуть розширитися
й сумарно становитимуть не більше за
3-3,5 години. Нормальна стратифікація
повітря характеризується нормальними
вертикальними градієнтами температури.
Під час підйому на 100 м температура
падає майже на 1 °С. Спостерігач ці
періоди може визначати за майже
спокійними зображеннями візирної цілі.
У
ці періоди діє нормальна рефракція,
яка визначається за формулою
8
=0,198-^-5'. (IV.2.40)
Т2
464к
розуміють відношенняк3
на перевищення визначається достатньо
точно (за (IV.2.36)).к
знайдемо Rc.r
= kk3. (IV.2.39)г
визначалось би просто, якби к
було сталою величиною.к
можна вважати сталим і таким, що дорівнює
кн
= 0,14 [27].
|
(IV.2.43) |
Враховуючи (IV.2.41), запишемо: |
|
0,23
10-2
|
(IV.2.44) |
Тому (IV.2.42) можна надати вигляду: |
|
|
(IV.2.45) |
Підставивши у (IV.2.45) числове значення радіуса Землі |
|
секунд у радіані, отримаємо: |
|
/(м) = (0,78 * 10-7 -0,11-Ю-7) S2. |
(IV.2.46) |
Або маємо: |
|
/(м) = 0» 6749 • 10-7 • 52(м) . |
(IV.2.47) |
Одержимо (для контролю) (IV.2.4I) іншим способом: із |
залежності між |
кутом
рефракції 8
та коефіцієнтом рефракції |
|
,
|
(TV.2.48) |
Враховуючи,
що |
|
(IV.2.48): |
|
0,14-р |
(IV.2.49) |
Підставляючи
числове значення р* та |
|
8^ = 0,227 • 10-2 • S(m) . |
(IV.2.50) |
Формули
(IV.2.50)
та
(IV.2.41)
фактично
не відрізняються. Отже, питання урахування
нормальної рефракції можна вважати
вирішеним.
465
Точність
визначення за (IV.2.47)
достатня.
Навіть для
Удень,
між ранковими й вечірніми періодами
нормальної стратифікації повітря,
установлюється термічна турбулентність
атмосфери, значні коливання зображень
візирної цілі та аномальна рефракція,
які визначаються за формулами
6^=8,132^-
5
2
5
Уан.ек.сер
~ с2
J
Уащ
I
dl. (IV.2.52)
У
(IV.2.51)
та
(IV.2.52)
найскладніше
знайти аномальний еквівалентний
середній градієнт температури
потрібно
знати
віддалених
від візирної цілі на /z
(тобто
у точках інтегрування). Про цей бар’єр
вище говорилося. Бар’єр вдалося
подолати. Відомості зі всієї траси
кажуть,
діє термічна турбулентність атмосфери.
Доведена
теорема [15]: максимальна
амплітуда коливань зображень візирної
цілі за час 1-2 секунди дорівнює середній
аномальній рефракції за той самий
проміжок часу.
Отже,
якщо виміряти розмах максимальних
коливань зображень (частота цих коливань
1-0,5 Гц), наводячи трубу на максимально
верхнє та нижнє розташування візирної
цілі, що коливається, і супроводжувати
наведення труби двома відліками шкали
мікрометра, то різниця цих відліків
дає розмах (подвійну амплітуду) коливань
Якщо
кутова рефракція
^ан.сер
*ан.сер
(TV.2.53)
відома,
поправку у перевищення за
аномальну
рефракцію знаходять за формулою
Формула
(IV.2.54)
отримана
на підставі (IV.2.43),
в
якій замінено нормальна рефракція 6'
на аномальну
Поправка
466S
—
10 км похибка в / не перевищує 1-2
мм.Чялкмр, (ГУ.2.51)S
оУанеКіСЄр-
Для цього, як видно з (IV.2.52),уан.
в багатьох нескінченно малих відрізках
dl
9
у точках,S
про
градієнт Уан£к
сер
дають видимі коливання зображень
візирної цілі, або, як ниніо'.
Тоді
ган
= +0,4848 • 1СГ5
Ь'ан
сер
• S
. (IV.2.54)Ь”ан
та враховано значення р'.гт
вдень, під час термічної турбулентності
(коли вимірюється куту ) завжди із
плюсом. Зауважимо, що знаки поправок
за рефракцію вказані
для
випадку, коли вимірюються кути наХилуV
. Для вимірювання зенітних кутів поправки
будуть із протилежними знаками. Справді,
як видно з рис. IV.2.9,
коли
Аномальна
рефракція під час нестійкої стратифікації
й за довжини лінії візування
97".
перерізу
рельєфу 0,25 м, 0,5 м з такими поправками
не можна не рахуватися. Зауважимо, що
коли
Залишається
зауважити, що упродовж нічного періоду
доби, а також в години після сходу Сонця
й години до його заходу, як правило, діє
інверсія температури, росте температура
з висотою. У ці періоди, під час відсутності
вітру, коливання зображень також
відсутні. Під час вітру (динамічна
турбулентність) діють коливання
зображень, але вони зовсім інші, ніж
під час термічної турбулентності:
коливання “ліниві”, поривчасті, з
малими частотами. Досвідчений спостерігач
легко відрізнить ці коливання від
термічних.
Під
час інверсії існує значна додатна
аномальна рефракція, яка складається
(додається) з нормальною рефракцією
(кривина світлової кривої повернута
випуклістю вверх). Для інверсійного
періоду поки що не створені кардинальні
методи урахування рефракції. Для
визначення рефракції у нічні години
необхідні, наприклад, градієнтні
вимірювання температури. Тому ми не
рекомендуємо виконувати тригонометричне
нівелювання під
Зауважимо,
що з появою приладів зарядного зв’язку
(ПЗЗ), які вбудовані в деякі електронні
теодоліти, тахеометри, нівеліри, створені
методи автоматизованого урахування
вертикальної рефракції [16]. Детальніше
це описано в розділі V.
467vB>vT
-
поправка в кут нахилу буде з мінусом.
Але ZB<ZT,
тому поправка за зенітний кут буде з
плюсом (кривина кривої повернута
випуклістю вверх). Під час аномальної
рефракції (нестійка стратифікація,
день) кривина повернута випуклістю
вниз. Тоді, навпаки, VB<vT,
a
ZB>ZT,
Змінюються й знаки поправок.S
^
1000
м може досягти величини (якщо Уан.ек.сер
~
1
градЛм) Ьан
=ган
становитиме 0,47 м. Навіть для УаН£К.сер
= 0,5 град/м ган
= 0,24 м. ДляS
=
1000 м, поправка за нормальну рефракцію
становитиме тільки ган
= - 0,011 м « — 11 мм. Вкажемо, що існує
простіший метод урахування аномальної
рефракції під час коливання зображень
візирної цілі. Можна відмовитися від
вимірювання розмаху коливань. Достатньо
наводити зорову трубу не на середнє
розташування візирної цілі, що
коливається, а на її максимально верхцє
положення за 1-2
с і брати відліки (якщо труба має обернене
зображення - на максимально нижнє
розташування цієї самої цілі протягом
1-2 с). У такому разі зенітні кути будуть
вільні від аномальної рефракції.
Достатньо ввести поправку за (IV.2.47).ч?
.
ісмператур- них інверсій. Для цього
достатньо використовувати денний
період доби.
Аерофотознімання
вважається одним із головних методів
складання та оновлення великомасштабних
планів та карт. Хоча в наш час підвищується
зацікавленість космічними знімками
високої роздільної здатності, проте
ще недавно не було сумніву щодо того,
що в найближчі роки аерофотознімання
залишиться головним методом
великомасштабного картографування.
Сьогодні можна стверджувати, що
перспективнішим є
Найпершу
серійну аерофотознімальну камеру С2
випускала з 1925 року швейцарська фірма
Wild
(тепер
це фірма Leica).
Аерофотознімання
(АФЗ) - це фотографування земної поверхні
з літального апарата (літака,
гелікоптера, повітряної кулі тощо).
Якщо АФЗ виконують для отримання
топографічних матеріалів, тоді його
називають
Лінію,
що є траєкторією польоту літака під
час фотографування, називають
горизонтальні
(кут нахилу а = 0);
планові
(кут нахилу а не перевищує ± 3°);
перспективні
(кут нахилу | а
|
> 3°).
Масштаб
знімання залежить від висоти літального
апарата над земною поверхнею 3. Комбіноване топографічне знімання
3.1. Виконання аерофотознімання
цифрове
аерофотознімання. Стосовно
космічного фотознімання, згідно з
оцінками американських спеціалістів,
станом на 2002
рік частка космічних даних становила
6
%, аерофотознімання - 94 %.топографічним
аерофотозніманням.
В інших випадках його називають
спеціальним АФЗ.маршрутом.
Якщо ця лінія пряма, то маємо прямолінійний
маршрут; існують також криволінійні
та ламані маршрути. Якщо фотографування
виконувалося у межах одного маршруту,
тоді це одномаршрутне АФЗ. Якщо
фотографують певну територію з кількох
паралельних маршрутів, то маємо
багатомаршрутне АФЗ. Залежно від кута
нахилу аерофотокамери а під час знімання
розрізняють такі аерознімання:
Н
та фокусної віддалі аерофотокамери fK
(рис.
IV.3.1).
Залежно
від масштабу аерознімків розрізняють:
дрібномасштабне
АФЗ, масштаб знімків 1:50000
і дрібніший;
середньомасштабне
АФЗ, масштаб знімків - у межах від
1:50000 до 1:10000;
великомасштабне
АФЗ, масштаб більший від 1:10000.
fk
\І/
Земна
поверхня
А В
Рис.
IV. 3.1. До визначення масштабу знімання
Аерофотознімання
виконують із використанням фотоплівок:
чорно-білої, спектрозональної або
кольорової. Нині для топографічних
цілей найчастіше застосовують кольорову
плівку, тому що такі знімки значно
інформативніші.
Для
виконання АФЗ потрібна аерофотокамера
та інша спеціальна апаратура, яка
забезпечує всі вимоги до АФЗ.
Аерофотокамера,
розріз якої показано на рис. IV.3.2
-
це складний автоматичний прилад з
дистанційним керуванням. Камера має
металевий корпус 1,
у який вмонтовано оптичну систему 2,
касету 3 для фотоплівки. Момент
фотографування (відкривання затвора)
визначається поданим імпульсом від
керуючого блока, так званого командного
приладу. У цей час відбувається
автоматичне вирівнювання аерофотоплівки
у площину з використанням механічної
плити або пневматичним способом (вакуум
або надування повітря). Затвор (відкривач)
пропускає світловий потік від земної
поверхні до плівки, тобто відбувається
експонування фотоматеріалу. Автоматично
відбувається перемотування фотоплівки.
Час відкриття затвора (витримка) дуже
короткий - 1/70, 1/100, 1/500 або 1/1000 секунди
залежно від
469
—;
1°—
Площина
знімка—*ф—Об’єктив
фотокамери
чутливості
фотоматеріалів. Важливими параметрами
фотокамер є кут поля зору та фокусна
відстань
Рис.
IV. 3.2. Будова аерофотокамери
Камери
поділяють на:
вузькокутні,
довгофокусні (10-20°, / = 610-950 мм);
нормальнокутні,
середньофокусні (50-70°, / = 210-300 мм);
надширококутні,
короткофокусні (110-130°, / = 88
мм і менше).
Чому
аерофотокамера та інша спеціальна
апаратура працюють
автоматично?
Політ літака відбувається дуже швидко
і людина не завжди встигає вносити
відповідні корективи як у траєкторію
польоту, так і в роботу камер. Сучасний
стан розвитку електроніки, радіотехніки
дає змогу повністю автоматизувати АФЗ.
Фірма Leica,
яка
створила першу аерокамеру, розробила
аерофотознімальну систему ASCOT
(Aerial Survey Control Tool - дослівно
“засіб для контролю за аерофотозніманням”).
Ця система складається з декількох
складових:
аерокамера
RC-30;
змінні
об’єктиви з / = 153 мм та / = 303 мм;
гіростабілізувальна
платформа PAV-30;
система
керування й контролю знімання (власне
ASCOT
з
антеною GPS
на
Літаку);
наземна
опорна станція GPS;
програмне
забезпечення постопрацювання.
Камера
RC-30,
одна
з найкращих у світі, має прямий інтерфейс
із бортовою навігаційною системою.
Діапазон поздовжнього перекриття
регулю
470fK.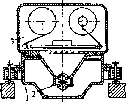
|
гп |
ргп |
|
рг- |
0 |
|
|
|
|
|
|
|
|
|
|
І
«
І
Рис.
IV.3.3.
Зовнішній
вигляд маршруту знімання з використанням
гіроплатформи
Система
ASCOT
-
засіб для контролю за аерофотозніманням,
що дає змогу виконувати АФЗ відповідно
до проекту, витримувати навігаційні
параметри АФЗ, а також фіксувати
координати центра аерофотознімка у
момент відкриття затвора. Технічні
засоби системи показано на рис. IV.3.4,
а
на рис.
3.5
-
дія системи разом з GPS.
Саме
методом GPS
визначаються
просторові координати центра проекції
у момент фотографування.
471
До
топографічного фотознімання ставлять
певні вимоги стосовно параметрів
польоту, які виконує ASCOT,
а
саме:
прямолінійність
маршруту;
горизонтальність
траєкторії;
витримування
поздовжнього перекриття: між знімками
одного маршруту (найчастіше 60 %);
витримування
поперечного перекриття між сусідніми
маршрутами (здебільшого 20-40 %).
Аерофотокамера,
а, отже, і знімок повинні бути правильно
зорієнтовані щодо траєкторії польоту,
тобто кут скосу
6
^щотабіліщтьШ
* ;
платформі
Leica
PA V30;
-
навігаційний
пристрій;
“
дисплей
пілота;
6-
GPS-приймач
*
«f
%
і
? ч
Рис.
IV. З 4. Технічні засоби системи ASCOT
472
К
(рис. IV.3.6)
не
повинен перевищувати 3°, інакше під час
накладання знімків виникне так звана
“ялинка”, що зробить подальше
фотограмметричне опрацювання ускладненим
і неефективним. Значну частину цих
вимог задовольняє гіроплатформа. Для
великомасштабного картографування
рекомендується у гірській місцевості
або на території, забудованій високими
будівлями, використовувати камери з
fK
=
200,
350 або 500 мм. Під час картографування
рівнинних територій застосовують
короткофокусні камери з fK
=
70,100, 140, 150 мм.

Рис.
IV. 3.5. Дія системи ASCOT
разом
з GPS
Рис.
IV. 3.6. Поздовжнє, поперечне перекриття
знімків та геометрія “ялинки”:
1,2-
знімки одного маршруту; 3, 103 - знімки
двох сусідніх маршрутів;
к-
кут
“ялинки”
Задаючись
масштабом знімання (зазвичай масштаб
знімання в 6-10 разів мілкіший, ніж масштаб
плану чи карти, складання яких
проектується), розраховують за (IV.3.1)
висоту
фотографування
473

Н
над середньою висотою
ділянки
знімання. Середню висоту на території,
що підлягає аерофотозніманню, прийнято
позначати
Набс=Н
+ Аа6с. (IV.3.2)
Оскільки
наперед задаються поздовжнім та
поперечним перекриттям знімків, то
можна розрахувати базис фотографування
(віддаль між суміжними точками відкриття
затвора)
*100
та
віддаль між суміжними аерофотознімальними
маршрутами
100-Pv
у
100
у
де
Кількість
знімків у маршруті
dx
,
я
= —+ 1,
5.
(IV.3.5)
а
кількість маршрутів - розміром дшянки
в поперечному до маршрутів напрямку
Загальна
кількість знімків:
(IV.3.6)
Звідси
можна знайти потребу в аероплівці для
АФЗ цієї території. Обчислюють також
інтервал фотографування т - час прольоту
літака від моменту виконання попереднього
знімка до моменту виконання наступного
знімка:
т
=
V
v
-
швидкість літака.
Знімання
можна виконувати тільки в ясну безхмарну
погоду, або коли хмари вище від висоти
474Аабс.
Знаючи Я та Аабс,
знайдемо висоту польоту над рівнем
моря Набс:В
=1-°~Р*
./ (TV.3.3)В= y--L, (IV.3.4)lx,
Іу
- розмір кадру, тобто знімка; зазвичай
1Х
=Іу.
Розміри найчастіше бувають 18x18
см,
30x30
см.п
визначається його довжиною dx
та
базисом Вг:dy
та
віддаллю між маршрутами Ву:
N
= n K. (IV.3.7)-А-. (IV.3.8)Н
-
висоти літака над середньою висотою
цієї території.
Якщо
під час АФЗ не використовуються
GPS-приймачі,
тоді пілотування літака та подальше
опрацювання матеріалів знімання для
складання планів та карт ускладнюються.
Під
час знімання забудованих територій
(для дво- і більше поверхових будинків),
для яких основою топографічного плану
буде фотоплан, фотографування місцевості
необхідно виконувати двічі:
довгофокусними
АФА для виготовлення фотопланів;
короткофокусними
або нормальними камерами для рисування
рельєфу.
Знімання
довгофокусними камерами виконується
у мілкішому масштабі, ніж короткофокусними.
Аерофотознімання
рівнинних, незабудованих територій із
переважно одноповерховою забудовою
можна виконувати в одному масштабі -
короткофокусними АФА для виготовлення
фотопланів та рисування рельєфу.
Детально вибір масштабів АФЗ описано
в інструкції з топознімання [5].
Напрямки
маршрутів під час фотографування
повинні бути за напрямком “захід-схід”,
хоча допускається й інше орієнтування
маршрутів. Знімання міст та заселених
районів потрібно виконувати ранньою
весною, після того, як зійде сніг та до
того, як розпуститься листя. Такі
території рекомендується фотографувати
на кольорову плівку, а території з
різноманітною рослинністю та надмірною
вологістю - на спектрозональну аероплівку.
Експоновану
фотоплівку проявляють, закріпляють і
розрізають негативну плівку на окремі
знімки. Нумерація знімків виконується
під час аерофотознімання. Далі
виконується контактне друкування,
тобто виготовляються позитивні
аерознімки без зміни масштабу (фотопапір
та негативні знімки контактують).
Позитивні знімки називають
475
3.2. Складання накидного монтажу. Оцінка якості аерофотознімання
контактними
відбитками.
Потім на великих столах (стелажах)
контактні відбитки укладають помаршрутно
так, щоб точно перекривались ідентичні
контури місцевості, що зобразилися на
знімках. Оскільки поздовжнє перекриття
більше за 60 % від Іх
- розміру знімка вздовж маршруту, то
частина однієї й тієї самої території
зображена на трьох суміжних знімках.
Укладені знімки прикріпляють найчастіше
спеціальними важелями або канцелярськими
кнопками. Уклавши перший маршрут,
починають складання наступного маршруту,
щоб ідентичні контури місцевості, що
зобразилися на знімках, перекривалися.
Нагадаємо, що поперечне пере
криття
знімків наближено становить ЗО
Головна
мета складання накидного монтажу -
оцінка якості виконаного аерофотознімання.
Для цього на кожному знімку знаходять
центральні точки знімків. Потім
визначають прямолінійність маршруту.
Для цього центральні точки першого й
останнього знімків з’єднують прямою
лінією. За умови абсолютної прямолінійності
маршруту - центральні точки всіх інших
знімків повинні розміщуватися на цій
прямій. За допомогою міліметрової
лінійки вимірюють віддалі між цією
лінією й центральними точками на
знімках. За цими віддалями роблять
висновок про непрямолінійність маршруту.
Далі визначають витриманість поздовжнього
перекриття: порівнюють фактичні значення
перекриття А/ з розміром
А/,
100
• (IV.3.9)
Ч
Аналогічно
визначають витриманість поперечного
перекриття:
Д/„
100
РУі
% = — . (IV.3.10)
ht
Відхилення
60
% та 30 %, також вказує на якість знімання.
Якщо є поздовжні перекриття 50 % або
менше, такі місця називають
“фотограмметричними дірками”. Подальше
опрацювання таких знімків викликає
багато ускладнень. Крім уже згаданих
параметрів, оцінюють фотографічну
якість знімків. Перевіряють правильність
вибраної витримки, відсутність на
знімках “плям” від тіні хмар, які
інколи виникають, якщо знімання
виконувалося під час похмурої погоди
та хмари виявляються нижче від висоти
літака, з якого виконується знімання.
Якість оцінюється за чотирибальною
системою: “відмінно”, “добре”,
“посередньо”, “брак”. Зрозуміло, що
у разі “браку” необхідно виконувати
повторне знімання.
Нині
комбінований метод зазвичай застосовується
тільки у рівнинних, закритих районах
під час знімання у масштабах 1:5000 і
1:2000 із перерізом
476%.
Так на стелажах укладають усі знімки
на територію, що була покрита
аерофотозніманням. Складені та скріплені
у такий спосіб знімки називаються
накидним
монтажем.
Накидний монтаж фотографують й
отримують репродукцію накидного монтажу
в декілька разів мілкішому масштабі.
Репродукцію монтажу, закріплену на
фанері або товстому папері (картоні),
часто використовують для знаходження
потрібних під час роботи номерів знімків
(номери знімків видно на репродукції
її накидного монтажу).Іх:Рх.,
Ру.
від заданого перекриття, наприклад,
відповідно від
3.3. Технологічна схема комбінованого методу знімання
рельєфу
1 м та 0,5 м, та у масштабах 1:1000-1:500 на
об’єктах із суцільною багатоповерховою
забудовою, для малих перерізів рельєфу.
Взагалі комбінований метод усе
частіше витісняється стереометодом.
Рис.
IV.3.7. Технологічна схема комбінованого
методу знімання
Застосовані
скорочені позначення: О. П. - опознак
плановий; О. П. В. - опознак планово-висотний.
Комбінований
метод відповідно до чинної інструкції
[5] можна використовувати у двох
варіантах: І варіант та П варіант.
Головна відмінність варіантів: у
варіанті І - складають фотоплан, у
варіанті II - графічний план. Далі буде
розглянуто суть складання фотопланів
та графічних планів. Наведемо рекомендації
щодо застосування варіантів:
під
час знімання у масштабі 1:5000 застосовують
перший варіант для будь-якого характеру
забудови;
під
час знімання у масштабі 1:2000
перший варіант використовують тільки
для розрідженої та малоповерхової
забудови;
на
територіях із густою, багатоповерховою
забудовою у масштабі 1:2000 знімання
виконується із застосуванням II варіанта;
під
час знімання у масштабах 1:1000 і 1:500 II
варіант застосовується на територіях
як з малоповерховою, так і з багатоповерховою
забудовами;
477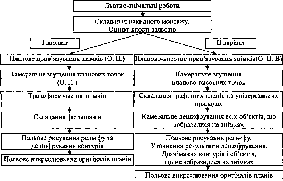
комбінований
метод (II варіант) застосовується також
під час знімання в масштабах 1:5000, 1:2000
на територіях, покритих суцільною
високою рослинністю (ліси, парки,
чагарники, очерет).
Рисування
рельєфу відповідно до інструкції може
виконуватися мензульним або тахеометричним
зніманням. Знімання рельєфу тахеометричним
зніманням може виконуватися не на
фотопланах, а на окремих знімках.
Окремі
аерофотознімки не є ділянками планів,
тому що мають спотворення: на одному
й тому самому знімку масштаб у різних
його частинах різний, неоднаковий.
Як
відомо, цього на планах не повинно бути.
Назвемо
причини спотворення знімків:
Невертикальність
оптичної осі фотокамери у момент
експозиції (у момент відкриття затвора).
Це видно з рис. IV.3.8,
на
якому точка
J.
Ь\
Нахилений
знімок Горизонтальний знімок
СІ
—Об
’єктив фотокамери
\
Я
\
Земна
noeePxW
N
В
Рис.
IV.3.8.
Спотворення
нахиленого знімка
На
горизонтальному знімку маємо відрізки
Різні
висоти літака в моменти експозиції.
Ця причина приводить до різних масштабів
на знімках, що межують. Висота в марйіруті
коливається у межах 20-30 м і більше.
4783.4. Прив’язування знімків
п
- точка надиру.
па
та nb.
На нахиленому знімку відповідно маємо
відрізки па'
та пЬ'.
Тоді nb'
<
nb,
а
па'
> па.
Отже, на нахиленому знімку маємо різні
масштаби у різних його частинах.
Рельєф
місцевості. На рис. IV.3.9
показано,
як рельєф спотворює масштаб знімка.
Точки
Густина
опознаків залежить від масштабу плану,
що складається, перерізу рельєфу,
масштабу аерознімків, способів
прив’язування опознаків. Розрізняють
479А
та В
- точки на місцевості; Я-Я - середня
площина; А',
В'-
проекції точок місцевості на середню
площину.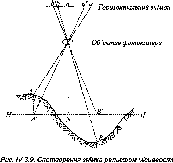
А
та В
зобразяться на знімку в точках а,Ь.
Правильне їхнє розміщення у разі
відсутності рельєфу було б у точках а
,Ь'.
Отже, похибки через рельєф а
а і b
Ь'.
Як видно з рисунка, якщо точка розташована
вище від середньої площини, то її
зображення віддаляється від центральної
точки п;
а якщо нижче від середньої площини -
наближається до центральної точки п.
Щоб
уникнути спотворень на аерознімках,
виконують прив’язування знімків. Під
прив’язуванням знімків розуміють
визначення координатX,
Y,
Я
деяких точок знімка, розпізнаних на
місцевості та на знімку. Такими точками
слугують чітко виражені на знімку
контурні точки, такі, як перехрестя
доріг, кути, близькі до прямих на межах
угідь, основи стовпів тощо. Ці точки
достатньо точно розпізнаються як на
знімку, так і на місцевості. На
малоконтурних територіях виконують
штучне маркування точок та знаходять
координати саме цих, маркованих точок.
Такі точки скорочено називають
“опознаками” - розпізнавальними
знаками. Визначають координати точок,
тобто виконують прив’язування
знімків як польовими, так і камеральними
методами.
суцільне
та розріджене прив’язування. Щоб
уникнути спотворення знімків, на знімку
повинно бути не менше від чотирьох
точок із відомими координатами (три -
необхідні і хоча б одна - контрольна).
Складаються проекти прив’язування
знімків. На ділянках знімання, завдовжки
160-200 см у масштабі плану, що створюється,
опознаки розташовуються так, як показано
на рис. IV.3.10.
80-100
см
Вісь
маршруту
}
Зона
поперечного
перекриття
о
$
4, *
Л?
*
V? Iі
і-н
4-5
км
Зона
поперечного
перекриття
Рис
IV 3 10 Схема положення планових опознаків
(О П) на маршрутах знімання
На
ділянках меншої довжини кожна секція
забезпечується на кінцях парами точок
по різні боки від осі маршруту. Опознаки
можуть розташовуватись по кутах
трапеції плану, що створюється. Початок
і кінець кожного маршруту мають бути
забезпечені двома плановими опознаками,
один із них повинен бути розміщений за
межею ділянки знімання. Межі знімання,
що збігаються із напрямком маршрутів,
забезпечують додатково плановими
точками через 40-50 см, якщо кількість
маршрутів більша від трьох. Для знімання
у масштабі 1:5000 із перерізом рельєфу 2
м і більше та для масштабів аерознімання
1:7000 опознаки розташовуються через 4-5
базисів фотографування. У разі
необхідності виконується маркування,
про що вже говорилось.
Проекти
прив’язування знімків складають на
картах, що є на цю територію.
Запроектовані точки - опознаки наколюються
голкою вимірника і позначаються кружками
на контактних відбитках, які будуть
використовуватися для розпізнавання
місцевості. Обов’язково розпізнаються
пункти геодезичної основи, зображені
на знімках. На місцевості опознаки
закріплюються постійними знаками.
Найпоширенішими є дерев’яні стовпи
завдовжки 115 см діаметром не менше ніж
15 см із перекладиною в нижній частині.
В яму завглибшки 100
см закладається бетонний моноліт, що
є чотиригранною зрізаною призмою
заввишки 20
см, нижньою основою 20x20
см,
верхньою 15x15
см.
На верхній грані моноліту цементується
центр (зазвичай головка цвяха). Стовп
ставиться на моноліт, засипається
землею й виконується зовнішнє оформлення
у вигляді кола радіусом 1
м, насипається земля навколо верхнього
480

зрізу
стовпа. Стовп виступає над поверхнею
землі на 10-15 см. Як вихідні пункти для
прив’язування знімків використовуються
пункти тріангуляції, полігонометрії
1, 2, 3, 4 класів, нівелірні марки та репери
I,
II,
III,
IV
класів.
Прив’язування
виконується побудовами таких геодезичних
мереж: тріангуляції 1, 2 розрядів;
висотно-теодолітні ходи; полігонометрія
4 кл. 1, 2 розрядів, трилатерації 4 кл. 1,2
розрядів; прямі, зворотні, комбіновані
засічки - дуже ефективні під час
прив’язування знімків аналітичної
мережі. Для висотного прив’язування
використовують технічне та тригонометричне
нівелювання.
Перерахуємо
стадії польових робіт під час
аерофототопографічних методів знімання:
комбінованих та стереозніманнях.
Маркування
розпізнавальних знаків (опознаків).
Виконання
аерофотознімання (АФЗ) розглянуто у
п. IV.3.1.
Планове
підготування аерознімків (планове
прив’язування).
Висотне
прив’язування аерознімків (висотне
прив’язування).
Висотне
та планове прив’язування доцільно
об’єднувати, тобто виконувати
одночасно. Нагадаємо: якщо координати
центра знімка визначаються методом
GPS,
то
польове прив’язування знімків не
потрібне, оскільки відомі координати
усіх центрів знімків; виконується
тільки камеральне згущення точок.
Дешифрування
контурів під час стереознімання.
Знімання
рельєфу та дешифрування контурів під
час комбінованого знімання.
Польове
викреслювання оригіналів планів
(можливе викреслювання в офісних,
камеральних умовах).
Частина
перелічених процесів польових робіт
уже називалась у технологічній схемі
комбінованого методу знімання.
Потреба
в маркуванні розпізнавальних знаків
виникає не тільки під час знімання
малоконтурних територій, але й у
забудованих територіях під час
великомасштабного знімання, для яких
підвищується точність ідентифікації
точок на знімку та на місцевості. Чинна
інструкція вимагає виконувати
ідентифікацію з точністю 0,1 мм. Обов’язково
маркуються точки геодезичної основи,
якщо вони не зобразяться на знімках,
люки підземних комунікацій, вхідні та
вихідні орієнтири на осях маршрутів.
481
3.5. Польові роботи під час аеротопографічного знімання
3.6. Маркування розпізнавальних знаків
Якщо
є стінні знаки, то біля них маркуються
тимчасові знаки або близькі місцеві
предмети. Для маркування використовують
дешеві матеріали: пісок, крейду, вапно,
марлеві тканини. Обов’язкова умова
маркування - контраст між фоном і
маркувальним знаком. Інколи створюють
штучний фон. На забудованих територіях
маркувальні знаки повинні мати форму
хреста, що складається з чотирьох
променів із вільним простором у центрі
(квадрата чи кола). Розміри маркованих
знаків нижче подаються у масштабі
фотографування: довжина і ширина
променя - 0,16 і 0,05 мм відповідно, сторона
квадрата або діаметр кола -0,1
мм.
0,16
'—N
4—'
0,05
Рис.
IV.3.11.
Маркувальний
знак у вигляді хреста
Якщо
хрест темного кольору, ширина променя
збільшується в 1,5 раза. Знаки осей
маршрутів - стрілки або прямокутники
завдовжки 0,6 мм, ширина - 0,1-0,15 мм. Якщо
аерофотознімання виконується, наприклад,
у масштабі 1:10000 (оскільки в 1 см - 100 м, в
1 мм - 10 м), то в 0,6 мм -6
м. Тому довжина опознака-стрілки на
місцевості 6
м, ширина 1
м - 1,5 м, товщина сторони квадрата - 50 см.
Маркування
виконують перед зніманням, за можливістю
з мінімальним розривом у часі. На кожний
маркований знак заводять спеціальну
картку, де вказана номенклатура трапеції,
на якій марковано розпізнавальний
знак. Марковані точки на знімках не
наколюються, оскільки точка на знімку
не розпізнана (фактично контуру немає).
Проте на лицьовій стороні аерознімка
креслять коло червоним кольором
діаметром 10
мм з центром у маркованій точці. На
звороті знімка олівцем обводять місце
цієї точки кружком діаметром З мм, а
праворуч роблять короткий запис,
наприклад: марковано пункт тріангуляції,
№ пункту, форма знака “хрест”. Виконав
(прізвище). Підпис. Дата.
Загальні
питання планового підготування
аерознімків, тобто визначення координат
розпізнавальних знаків, розглянуті в
п. IV.3.4
-
прив’язування знімків. Тут опишемо
безпосереднє підготування великомасштабних
аерознімків.
482
3.7. Планове підготування аерознімків
На
знімках контурні точки, вибрані як
розпізнавальні знаки, обводяться на
лицьовій стороні знімка кружком,
червоним кольором, діаметром 10
мм; точка чіткого контуру наколюється
голкою вимірювача; на звороті олівцем
обводять місце цієї точки кружком
діаметром 3 мм та роблять короткий
запис, як і під час маркування,
наприклад: розпізнано знак полігонометрії
(№ Пункту).
Розпізнавання
виконав. Прізвище виконавця. Підпис.
Дата. Далі на звороті подається зарис
розпізнаного пункту (зарис під час
маркування не роблять). Зарис повинен
полегшити знаходження цієї точки іншим
виконавцем, який, можливо, буде виконувати
контрольне визначення координат цього
самого опознака.
Розпізнавальні
знаки (опознаки) закріплюються на
місцевості центрами тривалого збереження:
дерев’яними стовпами (описаними у п.
IV.3.4),
бетонними
паралелепіпедами, а в місцях з твердим
покриттям - металевими трубами, штирями,
залізничними костилями. Такі типи
центрів показано на рис. IV.3.12.
Рис.
IV.3.12.
Типи
центрів знімальної основи тривалого
збереження
Висотне
підготування аерознімків полягає у
визначенні висот планових опорних
точок (опознак планово-висотний О. П.
В) або висот чітких контурів - висотні
розпізнавальні знаки (опознак висотний
О. В.), тобто точок, що зобразилися на
знімках, але не були використані як
планові опознаки О. П. Неважко зрозуміти,
що доцільно виконувати сумісне визначення
(X,
Y,
Н
). Як уже зазначалось, може виконуватись
повне (суцільне) або розріджене висотне
підготування залежно від масштабу
знімання, перерізу, рельєфу,
Бетонний
паралелепіпед
Металева
труба, штир, Пень із забитим
залізничний
костиль, які цвяхом, штирем
забетоновані
(забиті) у
тверде
покриття
483
3.8. Висотне підготування аерознімків
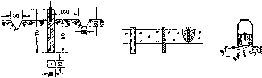
|
щ |
f 80% * |
|
||||
|
|
|
|
||||
|
|
|
|
|
|||
|
О О |
|
|
j |
|||
|
|
|
|
|
|
|
|
60% □ □ □ 1 2 3 |
|||||||
|
|
|
о о |
|
|
■“ *\ |
|
* |
|
|
|
|
|||
£ |
|
|
|
||||
£ 3-й |
|
/ |
|||||
знімки
Поперечне
перекриття
Поперечне
перекриття
Рис.
IV. 3.13. Розміщення висотних опознаків
на стереопарі
під час поздовжнього
перекриття 80 % (потрійне перекриття 60
%)
По
суті, на рис. IV.3.13
є
дві стереопари:
стереопара
першого та другого знімків;
стереопара
другого та третього знімків.
Отже,
чотири висотні точки, показані на
рисунку кружками, є точками висотного
прив’язування двох стереопар. Під час
розрідженого висотного прив’язування
знаки розташовуються попарно по обидва
боки від осі маршруту, у зонах поперечного
перекриття знімків, подібно до розміщення
планових
484
опознаків
за стандартною схемою. Крім того, на
кожні дві секції в зоні поперечного
перекриття маршрутів на віддалі 3-4
базисів
дається один знак.
Висотні
опознаки не вибираються на крутих
схилах. Якщо висотний опознак - контур
або маркована точка, тоді цю точку
позначають наколом, а на звороті знімка
точку наколу обводять кружком, підписують
її номер, висоту. Положення висотних
точок на місцевості можна визначати
промірами довжин від трьох контурних
точок. Такі висотні точки обводяться
на звороті пунктирним кружком, і
складається схема промірів від контурних
точок, вказуються довжини промірів.
Висотні
точки закріплюють як тимчасові - це,
зазвичай, дерев’яні кілки, діаметром
5-8 см, забиті в ґрунт на 0,4-0,6
м нарівні із поверхнею землі, а поряд
забивають сторожки. Виконується контроль
розпізнавання точок: для розрідженого
прив’язування усіх точок; для повного
- 25 % точок.
Висоти
розпізнавальних знаків визначають для
перерізів рельєфу h
=
0,25 м; 0,5 м; 1,0 м - технічним нівелюванням
і для перерізів h
=
2 м і більше - тригонометричним
нівелюванням.
Нагадаємо
принципову відмінність між методами
стереознімання та комбінованого
знімання. Під час виконання стереознімання
рельєф рисують в офісних умовах,
наприклад, на універсальних приладах.
Під час комбінованого методу знімання
рельєф рисується в полі наземними
геодезичними методами. За комбінованим
методом висотне прив’язування може
виконуватись під час знімання рельєфу
в полі. За стереометодом без попереднього
висотного підготування аерознімків
про камеральне рисування рельєфу не
може навіть йтися. Винятком є випадок,
коли виконується супроводження
аерофотознімання GP
S -технол
огіями.
Доцільно
також нагадати, що великомасштабне
картографування суцільно забудованих
територій стереометодом вимагає
здійснювати фотографування місцевості
двічі: довгофокусними АФК - для складання
фотоплану;
короткофокусними
АФК - для рисування рельєфу.
Зрозуміло,
що комбінованим методом друге знімання
не потрібно виконувати, оскільки
рельєф знімають наземними методами.
Метою
створення методів камерального згущення
планової та висотної основ аерознімання
є зменшення обсягів польових робіт, на
виконання яких витрачається значна
частина кошторису, що виділяється на
створення планів та карт.
485
3.9. Камеральне згущення планових та висотних ггзчок. Мета. Суть. Методи
Як
уже зазначалося, на кожний знімок має
бути не менше від трьох точок з відомими
координатами, щоб виключити спотворення
на знімках. Якщо всі точки визначати
польовими методами, то зрозуміло, що
це вимагає виконання великих обсягів
польових робіт. Тому завдання створення
методів камерального прив’язування
знімків - одне із найактуальніших у
геодезії. У результаті створено низку
методів камерального згущення планових
та висотних розпізнавальних знаків.
Планові
методи
Г
рафічна фототріангуляція.
Аналітична
фототріангуляція.
Фотополігонометрія.
Фототріангуляція
вимагає вимірювання за знімками
горизонтальних кутів. До того ж під час
побудови графічної фототріангуляції
горизонтальні кути не вимірюють, а
будують на прозорому папері (на кальці).
Під час побудови аналітичної
фототріангуляції горизонтальні кути
вимірюють на спеціальних приладах -
стереометрах. Точність камерального
вимірювання кутів за знімками близько
Г.
Взагалі
метод фототріангуляції ґрунтується
на тій властивості фотознімка як
центральної проекції, що напрямки,
проведені із центральної точки знімка
на будь-які інші точки, не спотворюються.
Завдяки саме такій властивості
фотознімків, користуючись знімками,
можна вимірювати кути. Якщо вершина
кута вибрана на знімку не в центральній
точці, а в будь-якій іншій точці знімка,
то напрямки, проведені із цієї (іншої)
точки, спотворюються, й кути р, будуть
не такими, як на місцевості. Не
спотворюються тільки напрямки, проведені
із центральних точок знімка, та з точок,
що розташовані близько біля центрів.
Покажемо,
як можна знайти планове положення
деякої точки методом фототріангуляції
без польових робіт. Нехай, наприклад,
відоме положення двох центральних
точок суміжних знімків, що перекриваються
(рис. IV.3.14),
і
на обох цих знімках є зображення деякої
контурної точки
Побудуємо
на кальці або виміряємо стереометром
кути
Аналогічно
можна знайти положення усієї мережі
точок, маючи на плані положення тільки
двох точок, координати яких визначались
методом польового прив’язування.
Аналітична фототріангуляція точніша
за графічну й, до того ж, вона може
врівноважуватися з урахуванням як
випадкових, так і систематичних похибок.
486
А,
яка є вершиною кута межі поля.$х
тар2.
Оскільки відомі координати центральних
точок 1 та 2 Хх,
Yx;
Х2
, Y2
і
ці точки нанесені на план, то положення
точки А
на плані знайдемо методом звичайної
кутової засічки. Маючи положення точки
А
на плані, можемо графічно визначити
координати ХА,
YA
точки
Я.
Рис.
IV. 3.14. Вимірювання або побудова на
знімках кутів та
(52
Рис.
IV. 3.15.
Визначення
положення точки А
методом
фототріангуляції
Далі
розглянемо суть фотополігонометрії,
що ґрунтується на визначеннях базисів
фотографування
Розглянемо
рис. IV.3.16.
З подібності
відповідних трикутників можемо записати:
в\
=
Ві
.
«2_ =
А
/
Н2
’ / я, ■
Звідси
отримаємо Д з контролем:
(IV.3.11)
в
в11н^=в2щ_
'
/ /
Аналогічно
можна визначити всі базиси фотографування,
які, фактично, є сторонами фотополігонометрії.
Кути визначаються, як і у фототріангуляції.
Якщо відомі координати кінцевих точок
маршруту, визначених наземними
геодезичними методами, тоді знайдемо
координати центральних точок усіх
знімків маршруту.
487
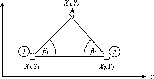
В{
та кутів між напрямками, що виходять
із центральних точок на сусідні
центральні точки знімків. Висотомірами
вимірюють висоти літака Н{.
Пі
Площини
знімків
П2
Пі
*3
об
єктивів
Поверхня
Землі
Рис.
IV. 3.16. До пояснення суті фотополігонометрії:
fK
-
фокусна
віддаль фотокамери; Нх,
Н2-
висоти літака або іншого апарата;
в\,
в2
- базиси на знімках; Sx,
S2
-
оптичні
центри об’єктива; щ,
п2-
точки надиру
на знімках; Bt
-
шуканий
базис фотографування
Висотні
методи
Для
згущення висот використовуються
прилади, які дають змогу будувати
стереомоделі місцевості, тобто бачити
просторове зображення предметів. Проте
для побудови стереомоделі на кожну
стереопару знімків необхідно мати три
точки з відомими координатами
Окремо
коротко зупинимося на камеральному
постопрацюванні даних АФЗ, якщо знімання
виконувалося із застосуванням системи
ASCOT
-
засобом для контролю за аерозніманням.
Припустимо, знімання виконане і ми
маємо рулон або декілька рулонів з
експонованою аероплівкою, GPS-дані
із приймача, що розташований на літаку,
дані з однієї або декількох наземних
станцій, часові
488
^ Оптичні
центри2X,
7,Z.
Дають
змогу створювати стереомоделі такі
прилади: стереопланіграфи, стереокомпаратори,
мультиплекси. Згущення висотних точок
відбувається на підставі вимірювання
різниці висот та визначення висот не
на місцевості, а на стереомоделі.
Вивчення цих приладів виходить за межі
курсу геодезії. Зауважимо, що за
комбінованим методом знімання висотні
камеральні згущення, як правило, не
виконуються. Визначення висот під час
стереознімання на основі аерофотознімків
залишається значно грубілим, ніж
безпосереднім вимірюванням на місцевості.
Тому чинна інструкція пропонує рисування
рельєфу з перерізом 0,25 м на планах
масштабів 1:1000, 1:500 (населені пункти,
промислові майданчики) виконувати
наземними методами.
миті
спрацювання затвора камери, кутові
дані з гіроплатформи. Далі використовується
програмне забезпечення ПЗ, створене
провідною канадською фірмою GEOSURV.
ПЗ
є ланкою зв’язку між зібраними даними
АФЗ та фототріангуляцією, яка створюється
за умови, що координати усіх центрів
знімків визначено GPS-методом.
Програмне забезпечення дає змогу
виконувати таке опрацювання:
конвертування
GPS-даних
із форматів Rinex,
Trimble, Leica Geosystems, Ashtech, Motorola, Novatel (це
фірми, що виготовляють приймачі GPS)
у
внутрішній формат - формат ПЗ;
обчислення
векторів (віддалей від літака до базової
станції, якщо одна базова станція, тоді
віддаль може бути до 500 км; якщо декілька
базових станцій - 20-60 км);
відновлення
траєкторії літака, вектор антена-фотокамера;
конвертування
координат з однієї системи в іншу,
залежно від використаного еліпсоїда;
зрівноваження
фототріангуляційної мережі (блока)
двома методами - OTF
(on The Fly -
“на льоту”) і СВА (Combined
Block Adjustment -
комбіноване зрівноваження блока).
Результуюча
точність визначення координат центра
фотографування <10 см. Приблизно така
сама точність фототріангуляції.
Камеральні
фотограмметричні методи побудови
планових мереж, наприклад, метод
фототріангуляції, дає змогу не тільки
будувати мережі у наперед заданому
масштабі. Цей метод має значно більші
можливості будувати мережі в одному,
але довільному масштабі. Довільний
масштаб, як правило, невідомий. Приведення
цього довільного, невідомого масштабу
мережі до заданого масштабу, тобто до
масштабу плану, що створюється,
називається
Побудова
фототріангуляційної мережі у довільному
масштабі також виконується методом
кутових засічок, як це показано на рис.
IV.3.17.
Проте
для такої побудови ми вважали координати
центральних точок 1
та 7 відомими. Припустимо, що координати
цих точок невідомі. Тоді також невідома
й віддаль між ними, тобто невідомий
базис фотографування
489
3.10. Редукування фототріангуляційної мережі
редукуванням
фототріангуляційної мережі.b.
Віддалимо ці дві точки на довільну
віддаль Ь'
та побудуємо в точках 1
та 2
виміряні на знімках кути Pj
та
Р2
(рис. IV.3.17).
Тоді на перетині ліній засічки отримаємо
точку А7.
А |
|
ь |
|
§ |
|
§ |
§ |
|
□ |
□ |
|
□ |
|
□ |
|
□ |
□ |
1 |
2 |
|
3 |
|
|
|
5 |
6 |
О |
|
о |
|
о |
|
О |
А |
|
|
|
х4 |
|
х6 |
|
х» |
ХІ0 |
|
Рис.
IV. 3.18. Вигляд фототріангуляційної мережі
для шести знімків у маршруті
На
рисунку
Фоторедуктор
за будовою нагадує фотозбільшувач,
тільки значно більших габаритів.
Фототріангуляційна мережа довільного
масштабу наноситься на прозору кальку
та вкладається в касету. На екран
фоторедуктора ставлять майбутній план,
на якому вже нанесені точки
490Xj
-
точки, координати яких необхідно
визначити в камеральних умовах. Це
можна зробити, якщо редукувати цю
мережу, тобто привести її до потрібного
нам масштабу. Для цього необхідно мати
особливий прилад, який називається
фоторедуктором. Крім того, необхідно,
щоб хоча б дві точки мережі, наприклад
Х{
таХ10,
показані на рис. IV.3.18
-
трикутниками, мали відомі координати,
визначені польовими геодезичними
методами і були за своїми координатами
нанесені на оригінал майбутнього плану.Хх
та *10-
Коли касета освічується, тоді оптична
система редуктора проектує всі точки
мережі на
екран.
Змінюючи масштаб зображення мережі,
наближаючи або віддаляючи касету
стосовно екрана, добиваються, щоб
проекції точок Хх
та
*10
збігалися з відповідними точками на
плані Хх
та
Ххо
Під
Фотопланами
називають контурні (ситуаційні) плани
місцевості з фотографічним зображенням
ситуації, складені із трансформо ^их
аерознімків. На трансформованих,
позитивних аерознімках у місцях, де
зобразилися розпізнавальні знаки
(опознаки), які на чорно-білих фотознімках
виглядають найтемнішими точками,
пробивають круглі отвори діаметром ~
1,0-1,5 мм. Для цього використовують
спеціальний пуансон, робоча частина
якого - загострений край (зріз)
металевого циліндра такого самого
діаметра.
491.
Якщо зображення цих точок і ці дві точки
сумістяться, то й усі інші проекції
точок займуть правильне положення на
плані. Необхідно тільки наколоти на
плані центри кружків цих точок, і мережа
буде редукована. Зазначимо, що аналітичні
фототріангуляційні мережі будуються
в потрібному масштабі, тому редукування
не потребують.
3.11. Трансформування знімків
трансформуванням
фотознімків розуміють виключення
спотворень,
що
виникають на знімках.
У результаті побудови фототріангуляційної
мережі на кожному знімку є п’ять точок
з відомими координатами - центральна
точка знімка та чотири X
-точки (рис. IV.3.17).
Наприклад,
для знімка 2, крім центра знімка точки
2, відомі ще координати точок Хх,
Х2,
Х3,
Х4.
Далі, на негативах аерознімків у місцях
розміщення цих розпізнаних контурних
точок голкою роблять проколи. Потім,
для трансформування кожного знімка,
його негатив встановлюють у касету
фототрансформатора. Цей прилад подібний
до фоторедуктора, але складніший, і
його екран має всі степені свободи,
тобто може обертатися як завгодно. На
екран установлюють план із нанесеними
на ньому точками. Вмикається електрична
лампа, що просвічує негатив. На екран
від отворів у негативі проектуються
яскраві точки. Тоді, використовуючи
степені свободи екрана та касети,
добиваються накладання точок, що
світяться, на відповідні їм точки на
плані. Після цього світло вимикається,
на план кладуть чутливий фотопапір, на
короткий період світло вмикається,
відбувається експонування. Фотопапір
проявляють та закріплюють. У результаті
отримують трансформовані, позитивні
фотознімки. Якщо через значні спотворення
негативів, викликані рельєфом, не
вдається досягти одночасного накладання
всіх точок, що світяться, на відповідні
точки на плані, то виконують трансформування
знімків частинами.
3.12. Складання фотопланів
Аерознімки
накладають на наклеєний на тверду
основу (фанера, картон, алюміній)
креслярський папір, з нанесеними на
ньому (за своїми координатами) точками
планового підготування (основи) знімків.
Знімки накладають так, щоб через пробиті
в них отвори було видно відповідні
точки планової основи. Знімки будуть
перекриватися так само, як і під час
побудови накидного монтажу. Спочатку
накладені знімки, щоб уникнути їхніх
зміщень, закріплюють спеціальними
важелями, виготовленими з дешевого
важкого металу. Потім гострим ножем
роблять непрямолінійні, хвилясті
розрізи знімків так, щоб залишалась
тільки центральна частина кожного
знімка й не були розрізані вздовж
прямолінійні контури (границі угідь,
дороги тощо). Потім відрізані периферійні
частини знімка забирають, а центральні
частини суміжних знімків доторкаються
один до одного, без проміжків між ними.
Залишається ці центральні частини
знімків приклеїти й отримаємо так
званий мозаїчний фотоплан. На якісно
складеному мозаїчному фотоплані місця,
де доторкаються суміжні знімки,
малопомітні. Щоб одержати суцільний
(не мозаїчний) фотоплан, виконується
спеціальне фотографування мозаїчного
фотоплану без зміни його масштабу.
Так
отримують кінцевий фотоплан, без
спотворень, притаманних аеро- знімкам,
на якому зображена ситуація, але не в
умовних позначеннях, а у фотографічному
вигляді.
Графічні
плани складають за допомогою універсальних
приладів. Універсальними називають
прилади, які за двома суміжними
фотознімками будують стереомодель
місцевості і здатні виконувати на цій
моделі вимірювання просторових координат
Спостерігач,
який бінокулярно (дивлячись одночасно
двома очима) бачить об’ємну модель
місцевості, переміщає по контурах
моделі вимірювальну марку. Переміщення
марки складною механічною системою
передається олівцю, який на горизонтально
встановленому аркуші креслярського
паперу креслить графічний план у
заданому масштабі.
492
3.13. Складання графічних планів
X,
Y,
Н
точок та будувати повноцінні плани з
контурами та горизонталями. Під час
побудови графічних планів використовують
не всі можливості універсальних
приладів, а тільки можливість такого
приладу будувати контурний план (без
горизонталей). Як це зрозуміло,
універсальні прилади працюють на
принципі стереоскопічного зору, тобто
на властивості бінокулярного зору
будувати об’ємне зображення. В
універсальний прилад закладають два
знімки, що створюють стереопару (мають
зображення однієї і тієї самої території
на певних частинах обох знімків).
Зрозуміло,
що для складання трапеції графічного
плану заданого масштабу на цей план
переносяться дані з декількох стереопар.
Графічні плани викреслюють спочатку
олівцем відповідно до умовних знаків
цього масштабу. Для цього на основі
стереомоделі виконується камеральне
дешифрування (розпізнавання) за
фотографічним зображенням реальної
суті предметів місцевості та контурів.
На
основі камерального дешифрування не
всі предмети ситуації та контури будуть
розпізнані та викреслені в умовних
знаках. Надалі графічний план буде
доповнюватися даними польового
дешифрування під час знімання рельєфу
наземними геодезичними методами.
Мензула
для знімання встановлюється на геодезичні
пункти та пункти робочої основи, а також
на планово-висотні розпізнавальні
знаки. Встановлення мензули над точкою
виконується за допомогою центрувальної
вилки і виконується спочатку наближене
встановлення у послідовності:
орієнтування, горизонтування, центрування
(все це на око), потім точне встановлення
у зворотній послідовності: центрування
(вилкою), горизонтування (за допомогою
циліндричного рівня, що на лінійці
кіпрегеля), орієнтування планшета з
контролем (за двома напрямками), з
використанням труби кіпрегеля. Точність
прокреслених на планшеті напрямків і
побудованих кутів залежить від:
Точності
орієнтування планшета
34'
(IV.4.1)
де
є' - похибка прокресленого напрямку в
кутових мінутах;
493IV.4. Знімання рельєфу та дешифрування фотопланів під час комбінованого методу топознімання
IV.4.1. Встановлення мензули над точкою
Як
вже відзначалося, під час комбінованого
методу топографічного знімання знімання
рельєфу часто виконується методами
мензульного знімання, яке відоме з
курсу “Топографія”. Одночасно з
рисуванням рельєфу виконується польове
дешифрування контурів. На мензульну
дошку прикріплюється не чистий
креслярський папір, а фотоплан або
графічний план та захисна “сорочка”,
якою слугує аркуш креслярського паперу
або калька.
S
-
довжина лінії у сантиметрах на планшеті.
Як бачимо, похибка орієнтування обернено
пропорційна до довжини лінії на планшеті
в сантиметрах. Якщо необхідно викреслювати
лінії з похибкою, не більшою за є' = 3-4’,
довжина лінії на
планшеті
повинна бути не меншою за
масштаб
1:5000, 5= 500 м; масштаб 1:1000, 5= 100 м.
масштаб
1:2000,
Точності
центрування планшета. Допустиму похибку
центрування
Р
У
(IV.4.2)
Для
Колімаційної
похибки
/
У'
= ——, (IV.4.3)
СОЛ"0
де
о - кут нахилу візирної осі труби
кіпрегеля;
Нахилу
горизонтальної осі обертання труби
кіпрегеля, викликаної неточним
приведенням верхньої площини планшета
в горизонтальний стан:
X'
= i'tgx>, (IV.4.4)
де
призначенням,
на: а) топографічне; б) спеціальне;
виконанням
на: а) польове; б) камеральне (офісне);
в)
комбіноване.
У
топографії користуються як польовим,
так і камеральним та комбінованим
дешифруванням. Під час камерального
дешифрування користуються:
Геометричною
особливістю зображення предметів,
їхньою формою. Хвиляста лінія - річка,
ґрунтова дорога; ламана із правильним
заокругленням - канал, шосе; круглий
предмет - копиця сіна, цистерна, силосна
вежа.
494S
=
10 см. На місцевості, залежно від масштабу
знімання, матимемо:S
=
200 м; масштаб 1:500, S
=
50 м.
X
в
см з похибкою прокреслених напрямків
е'
=
Г можна визначити за формулоюХ=—,. (IV.4.2)X
-
допустима похибка центрування; S-
довжина
лінії (за якою орієнтується планшет) у
метрах; р' = 3438'.S
=
500 м, X
= 15 см; для S
=
200 м, X
=
6
см.
с
труби кіпрегеля. ТодіУ'-
похибка прокресленого на планшеті
напрямку (в кутових мінутах). Ця похибка
виключається, якщо увесь час працювати
кіпрегелем при одному крузі.
X’
- похибка напрямку; і'- нахил планшета
у кутових мінутах; ц- кут нахилу візирної
осі труби кіпрегеля у градусах.IV. 4.2. Польове та камеральне дешифрування
Дешифрування
- розпізнавання предметів за їхнім
фотографічним зображенням на знімках
є важливим процесом топографічного
знімання. Дешифрування поділяється
за:
Розмірами
предметів залежно від масштабу.
Необхідно знати масштаб, щоб визначити
ширину річки, дороги, довжину моста,
розмір будинку. Багато предметів мають
однакові форму й розмір. Тоді під час
дешифрування може допомогти колір
(тональність) зображення.
Тональністю
зображення. Сухі дороги - майже білі;
світлі -т- оголена земля, дахи будівель;
водойми - темні, мутні води - сірі. Ґрунт
- чим вологіший, тим темніший.
Рослинність - темно сіра й чим темніша,
тим густіша.
Тінями.
Розрізняють: власні та тіні, що падають.
Різна яскравість випуклих та увігнутих
(понижених). Тіні, що падають, підняті
на північ, понижені - на південь. Форма
тіні дає змогу розрізнити сосну,
водонапірну вежу, вітряк.
Взаємним
розташуванням. Часто сукупність
предметів уможливлює дешифрування.
Так, розташування залізниці й поруч
будівлі - залізнична будка,
дорога-річка-дорога - брід. Правильне
розташування дерев - фруктовий сад.
Висотою
предметів, яка може бути визначена за
тінями або стереоскопічно. Під час
польового дешифрування часто достатньо
побачити предмет, щоб визначити його
суть та призначення. Розпізнані на
місцевості предмети та контури наносять
на карти та плани відповідно до умовних
знаків цього масштабу. Одночасно з
дешифруванням виконується знімання
важливих предметів, що не зобразилися
на фотознімку. Взагалі комбінація
камерального та польового дешифрування
дає змогу повністю розпізнати
різноманітні предмети та зобразити
їх на карті.
Рисування
рельєфу та дешифрування на мензулі
виконує бригада з 3-4 працівників:
топограф, його помічник, 1-2 рейковики.
Робота на окремій станції виконується
в такій послідовності:
Встановити
мензулу над точкою. Мензула може
встановлюватись не тільки на завчасно
закріплених точках, але й на додаткових
точках, які вибираються під час виконання
знімання, так званих перехідних точках,
які визначаються, як правило, полярним
методом. Окрім перехідних точок,
користуючись фотопланом, можна
встановити мензулу на будь-якому чітко
зображеному контурі, тобто на точці з
відомим плановим положенням. Висоту
цієї точки найпростіше визначити
методом тригонометричного нівелювання,
вимірявши кути нахилу на три інші точки
(для контролю) з відомими висотами.
Довжини ліній можна виміряти графічно
- на фотоплані. Якщо потрібно
495IV. 4.3. Послідовність роботи на станції під час рисування рельєфу й дешифрування фотопланів
встановити
планшет у деякій точці, якої немає на
графічному плані, тоді планове положення
цієї точки найпростіше визначити
графічним розв’язанням однократної
оберненої засічки (розв’язанням задачі
Потенота), а висотне положення -
тригонометричним нівелюванням, як і
на фотоплані. Висоти перехідних точок
можна також визначати горизонтальним
візирним променем зорової труби
кіпрегеля.
Виміряти
висоту горизонтальної осі труби
кіпрегеля
Виконати
інструктаж рейкарів. Рейкарам вказують
місця, у яких треба встановити рейку,
а також послідовність її встановлення.
Виконати
набір пікетів. Вважатимемо, що знімання
виконується номограмним кіпрегелем
КН, за допомогою якого можна за рейкою
визначити горизонтальну віддаль
Лінійка
кіпрегеля повертається у горизонтальній
площині навколо точки встановлення
мензули, позначеної на планшеті, й
труба наводиться на рейку, встановлену
на пікеті.
Відлічується
Основна
крива номограми наводиться на нульову
поділку рейки або на перев’язане
місце на рейці й визначається перевищення
Нт
=
Hcm+h-
(IV.4.5)
Топограф
уздовж додаткової лінійки кіпрегеля,
скошений край якої доторкається до
точки встановлення мензули на планшеті,
відкладає у масштабі довжину
1.2
(у
чисельнику: 1
- номер станції, 2
- номер пікету, у
наприклад,
о-
175,20
знаменнику
- висота пікету в метрах). Для перерізу
рельєфу 1 м і більше висоти пікетів
обчислюються до 0,01
м, а записуються на плані із заокругленням
до 0,1 м. Для перерізу рельєфу до 1 м висоти
пікетів обчислюються й записуються з
точністю до 0,01 м. Для кутів нахилу до
3° висоти пікетів визначаються
496
і
над центром знака. Висоту і
відкласти на рейках. Відповідне місце
на рейці перев’язується шнурком. Якщо
рейка розсувна, нульова поділка рейки
встановлюється на висоті кіпрегеля
і.S
та
перевищення h
між
станцією (точкою встановлення мензули)
й пікетом. Для визначення положення
окремого пікету виконуються такі дії:
S.
Помічник записує значення S
в
журнал знімання.h.
Перевищення голосно повідомляють
помічнику. Помічник, знаючи висоту
станції Нст,
розраховує висоту пікету Нпк
за формулою
S,
наколює
положення пікету. Накол обводиться
кружком діаметром 2
мм, а праворуч від пікету підписують
номер пікету та його висоту,
горизонтальним
візирним променем кіпрегеля. Для кутів
нахилу більше за 3° перевищення визначають
нахиленим променем - за допомогою
номограми. Під час роботи кіпрегелем
КН дозволяється не записувати в польовий
журнал вимірювання, що виконуються для
визначення розміщення пікетів.
Набравши
необхідну кількість пікетів для
зображення рельєфу, топограф виконує
інтерполювання висот і будує горизонталі.
Одночасно
виконується польове дешифрування
фотоплану.
Бригада
не повинна залишати точку стояння доти,
доки олівцем не будуть
викреслені
горизонталі та виконане дешифрування
контурів, сусідніх із точкою установлення
мензули. Повинні бути визначені й
записані на плані, крім пікетів, висоти
характерних точок рельєфу: вершин, дна
котлованів,
водорозділів,
сідловин, тальвегів. Підписуються також
висоти гребель, мостів, шлюзів, колодязів,
верху та підошви насипів, інших
характерних точок рельєфу. Обчислення
висот усіх характерних точок необхідно
виконувати в журналі.
Знімання
(рисування) рельєфу для першого варіанта
комбінованого знімання (на фотоплані)
має певні особливості, порівняно зі
зніманням на графічному плані та чистій
основі; назвемо основні із цих
особливостей:
Можливість
використання так званих безрейкових
точок. Оскільки на фотоплані є зображення
цілої низки характерних точок ситуації,
що спостерігаються з точки встановлення
планшета, з’являється можливість
визначати висоти цих точок, не посилаючи
в ці точки рейковика з рейкою, а візуючи
безпосередньо на ці точки на земній
поверхні. Висоти цих точок визначаються
за формулою
Можливість
встановлення мензули на будь-якій
контурній точці. Про це вже говорилось.
Така можливість значно полегшує
знімання.
Оскільки
на фотоплані видні межі контурів, то
рисування рельєфу виконується точніше,
ніж на чистій основі, до того ж для
значно меншої кількості пікетів.
Найголовнішим
є те, що виконується тільки знімання
рельєфу та дешифрування, а знімання
ситуації - не виконується, окрім
предметів, що не зобразилися на знімках.
Основні
вимоги до комбінованого методу знімання
задаються інструкцією великомасштабного
знімання. Точність планової геодезичної
основи має бути
497
Нш
= Нст
+ S
•
tgv
+
і.
Як бачимо, достатньо виміряти кут
нахилу v;
S
визначається
графічно з фотоплану. Нагадаємо, що
кіпрегель КН має вертикальний круг із
градусними поділками.IV.4.4. Основні офіційні вимоги до точності зображення контурів та рельєфу
Масштаб знімання |
Переріз рельєфу, м |
Максимальні віддалі між пікетами, м |
Максимальні віддалі між станцією і пікетами |
||
під час знімання рельєфу |
під час знімання контурів |
||||
чітких |
нечітких |
||||
1:5000 |
0,5 |
75 |
250 |
150 |
200 |
1,0 |
100 |
350 |
150 |
200 |
|
2,0 |
120 |
350 |
150 |
200 |
|
5,0 |
150 |
350 |
150 |
200 |
|
1:2000 |
0,5 |
50 |
200 |
100 |
150 |
1,0 |
50 |
250 |
100 |
150 |
|
2,0 |
60 |
250 |
100 |
150 |
|
- |
- |
|
- |
- |
|
1:1000 |
0,5 |
зо |
150 |
80 |
100 |
1,0 |
40 |
200 |
80 |
100 |
|
1:500 |
0,5 |
20 |
100 |
60 |
80 |
|
1,0 |
20 |
100 |
60 |
80 |
Зауважимо,
що допустимі похибки в розташуванні
контурів беруться вдвічі більшими, ніж
середні похибки. Проте допустимі похибки
у розташуванні контурів безпосередньо
стосуються знімання на чистій основі,
частково - знімання на графічних планах,
оскільки на фотопланах контури вже є.
Під час складання фотопланів також є
допуски похибок у розташуванні контурів
щодо робочої основи та розпізнавальних
знаків (опознаків). За величинами ці
допуски такі самі, які подані вище.
Нагадаємо також, що знімання рельєфу
можна виконувати не тільки за допомогою
мензули, а й тахеометрами. Незалежно
від методів такого знімання інструкція
вимагає
498
певної
густоти пікетів та обмежує віддалі від
станції до пікетів (висотних та
контурних). Ці вимоги, залежно від
масштабу знімання, подано в табл. IV.4.1.
Допускається
також за час знімання зміна орієнтування
планшета та тахеометра. Допуск 1,5’.
Під
час знімання рельєфу та дешифрування
ввечері або в дощову погоду виконують
камеральні роботи. До таких робіт
належить передовсім калька висот.
Кальку складають на кожний планшет,
частинами, доповнюючи її даними щоденних
польових робіт.
На
кальку наносять пункти геодезичної
основи, точки основних висотних і
знімальних ходів з їхніми номерами і
висотами, зрізи води та всі пікети.
Перед
складанням кальки необхідно перевірити
правильність обчислення висот, точок
ходів, зрізів води та характерних точок
рельєфу (пікетів).
Фотоплани
або графічні плани, складені на
універсальних приладах, оформляють у
кольорах, що передбачені “Умовними
знаками для топографічних планів
масштабів 1:5000, 1:2000, 1:1000 та 1:500”. Контури,
підписи, зарамкове оформлення викреслюють
чорним кольором, рельєф - коричневим,
гідрографію - зеленим, водні простори
- голубим, площі з твердим покриттям -
рожевим. На кожному квадратному дециметрі
плану масштабів 1:5000 і 1:2000 повинні бути
підписані не менше ніж 10 висот характерних
точок. На планах масштабів 1:1000 і 1:500
підписують висоти усіх пікетів. Якщо
топографічні плани створюються для
потреб меліорації, будівництва,
енергетичних, промислових та інших
об’єктів, на територіях яких пройдуть
значні зміни ситуації та рельєфу, і
якщо ці плани не будуть використані
іншими організаціями, дозволяється
польові оригінали оформляти в олівці.
Кількість підписаних висот точок на
топографічних планах, складених для
цілей меліорації, може сягати 30 на один
квадратний дециметр.
Кожний
топографічний план повинен мати
формуляр. Формуляр трапеції - це як
паспорт особи.
організацію,
що виконала знімання;
розміри
рамок трапеції;
координати
вершин (кутів) трапеції;
схему
геодезичної основи;
499IV.4.5. Камеральні роботи під час знімання рельєфу на фотопланах (калька висот, викреслювання польового оригіналу, формуляр трапеції)
Формуляр
- це документ, в якому записується всі
основні дані вибраної технологічної
схеми і точності знімання, наводяться
дані про:
координати
та висоти геодезичної основи;
назву
об’єкта знімання;
номенклатуру
трапеції;
масштаб
знімання;
переріз
рельєфу;
метод
знімання;
систему
координат;
систему
висот;
рік
виконання;
адміністративний
поділ;
інші
дані.
На
формулярі подаються прізвища та посади
виконавця та того, що перевіряє складання
формуляра.
Усі
елементи змісту топографічних планів
повинні бути зведені з відповідними
елементами суміжних трапецій по тих
сторонах рамки, з якими межують плани
такого самого або більшого масштабів,
що виконані в тій самій системі координат
та висот.
Якщо
знімання на суміжних планах виконано
в тому самому масштабі, але в іншій
системі координат та висот, то зведення
в плані здійснюється копіюванням на
кальку контурів, що розташовані на двох
суміжних планшетах; зведення за висотою
не виконується, але по цій рамці
прокладають нівелірний хід, а позначки,
отримані з цього ходу, підписують на
кальці висот через 3-5 см і з’єднують
червоною тушшю.
За
відсутності на суміжних рамках знімання
або якщо знімання виконано в дрібнішому
масштабі (не менше за 1:2),
рамка вважається вільною, але
забезпечується в плановому аспекті
прокладанням теодолітного ходу, яким
координуються значні контури.
Припустимо,
на двох суміжних трапеціях дві бригади
незалежно виконують топознімання.
Кожна бригада на суміжній рамці виконує
знімання не тільки до рамки трапеції,
але й за межами рамки завширшки 1,5-2,0
см. Після закінчення знімання кожний
топограф копіює на кальку рельєф і
ситуацію завширшки 2-3 см від рамки і
передає керівнику робіт, який здійснює
контроль накладанням смуг кальок одна
на одну. Розходження в контурах не
повинно перевищувати:
500IV.4.6. Зведення за рамками суміжних топографічних планів
1,0
мм основних контурів (межі, залізниці,
шосейні та поліпшені дороги, вулиці,
берегові лінії, інші чітко окреслені
контури, будівлі);
1,5
мм - для інших контурів.
Розходження
за висотою не повинні перевищувати
подвійної величини допустимих середніх
похибок (тобто граничних похибок)
знімання рельєфу. Для забудованих
територій під час знімання у масштабах
1:1000, 1:500 допуски зменшуються у 1,5 раза.
Для знімання ділянок лісу, навпаки,
допуски збільшуються у 1,5 раза. Розходження
у розташуванні контурів та рельєфу
усувається переміщенням контурів та
горизонталей на половину розходження,
але із збереженням виміряних розмірів
споруд. За недопустимих розходжень
виконують польову інструментальну
перевірку і керівництво підрозділу
приймає рішення про можливість
використання результатів робіт. Якщо
нове знімання вважається якісним, то
на полях знімального планшета і у
формулярі роблять відповідний запис,
а матеріали контролю зберігаються
разом із формуляром. За правильність
зведення за всіма сторонами рамки
топографічного плану відповідає
виконавець. Матеріали про зведення по
рамках підписує топограф-виконавець
і керівник робіт.
Постановою
Кабінету Міністрів України від 24 вересня
2005 р. № 979 затверджено Положення про
Державну службу геодезії, картографії
та кадастру, скорочено Укргеодезкартографія.
Державна геодезична служба діє в складі
Міністерства охорони навколишнього
природного середовища (скорочено
Міністерство природи - Мінприроди).
Голова Державної служби геодезії,
картографії та кадастру - Макаренко
Іван Дмитрович. Основним завданням
Укргеодезкартографії є реалізація
державної політики у сфері топографо-
геодезичної, картографічної та
кадастрової діяльності.
До
складу Укргеодезкартографії входять
державні аерогеодезичні підприємства,
державні науково-виробничі інститути,
геодезичні підприємства. Очолюють
підприємства директори підприємств
та головні інженери. Підприємства
часто поділяються на геодезичні
підрозділи. У цих підрозділах є відділи
технічного контролю. Контролювати
виконання топографо-геодезичних робіт
мають повноваження директори та головні
інженери підприємств. Проте найчастіше
контролюють роботи працівники відділів
технічного контролю - інспектори ВТК.
Види
контролю. Контроль можна поділити на
польовий та камеральний. Польовий
контроль поділяють на: контроль оглядом,
контроль об’їздом
501IV.4.7. Контроль робіт та приймально-здавальні роботи
території,
на яку створені плани. Але найефективніший
приладний, інструментальний контроль.
Під
час камерального контролю перевіряють
журнали польових робіт, обчислення
координат, зрівноваження мереж, планшети
планів та карт тощо.
Контролі
оглядом, об’їздом - це попередні
контролі. Наприклад, контролююча особа,
користуючись планшетом, з новим планом
чи картою на певну територію, об’їжджаючи
дорогами, зображеними на планшеті,
контролює, чи немає пропусків ситуації,
правильність дешифрування тощо.
Під
час інструментального контролю
контролюючий набирає контрольні пікети
в різних частинах планшета з двох-трьох
станцій. Обчислюються висоти контрольних
пікетів. Висоти цих точок визначаються
також за горизонталями, вже викресленими
на планшеті. Різниця цих висот Д
В
акті контролю подається оцінка робіт
у чотирибальній системі (відмінно,
добре, посередньо, брак).
Під
час повторних контролів передусім
перевіряють усунення недоліків у
роботі, виявлених попереднім контролем.
Після закінчення робіт на об’єкті
виконавець здає, а замовник чи
відповідальні особи підприємств
приймають результати знімання. Також
обов’язковим є інструментальний
контроль та акти приймання робіт.
Контрольні пікети наносяться червоним
кольором на кальку висот. Усі матеріали
комбінованого знімання перевіряє,
приймає та підписує керівник робіт.
Виконання приймально-здавальних робіт
завжди передбачається та фінансується
кошторисом на виконання
організаційно-ліквідаційних робіт
(оргліки).
Після
закінчення комбінованого знімання
здають такі матеріали:
фотоплан
(графічний план);
формуляр
до плану;
журнали
знімання та створення висотної
знімальної основи;
калька
висот (для планів масштабів 1:5000 і
1:2000);
копіювання
зведень за рамками;
акти
перевірки Та приймання польових робіт.
На
весь об’єкт знімання, крім цього,
здають:
схему
розміщення планшетів з номенклатурною
розграфкою;
502hj
=
Ні
- Нк
вказує на похибки у рисуванні рельєфу
(Ht-
висоти,
обчислені за горизонталями, Нк-
висоти,
обчислені за контрольними пікетами).
Різниці Ahj
не
повинні перевищувати офіційних
допусків, наведених вище у п. IV.4.4.
Складають
акти контролю в трьох примірниках: один
примірник надається виконавцю, другий
- контролюючій особі, третій - у вищі
геодезичні підрозділи.
схему
гідрографічної мережі зі зрізами води;
схему
шляхів сполучення з написами назв
пунктів та віддалей до них;
список
встановлених назв населених пунктів,
озер, вулиць, площ, інших об’єктів
державною мовою, засвідчений органами
місцевої влади;
пояснювальну
записку.
Комбінований
метод, створений у 1926-1928 роках проф.
М.М. Алексопольським, забезпечує
продуктивність у 1,5-2,0 рази більшу, ніж
мензульне знімання.
Проте
комбіноване знімання вимагає значних
затрат праці і залежить від
фізико-географічних і кліматичних умов
місцевості, оскільки значна частина
робіт виконується у полі.
Пошуки
заміни польових вимірювань на місцевості
на вимірювання в офісних (камеральних)
умовах привели до створення
Ідея
стереознімання полягає в тому, що коли
зображення місцевості на парі суміжних
аеронегативів (стереопарі), що
перекриваються, спроектувати на єдиний
екран, зберігши розташування негативів,
яке було в момент фотографування,
то в перетині однойменних світлових
променів отримаємо модель місцевості
- просторову фігуру, подібну до місцевості,
але зменшену залежно від масштабу
знімання. На створеній моделі, а не на
місцевості, виконуються вимірювання
для визначення просторових координат
точок земної поверхні.
Фотограмметрія,
яка починається з фотографування
об’єктів і продовжується опрацюванням
фотознімків на оптично-механічних
приладах, називається аналоговою
фотограмметрією.
Перший
аналоговий прилад (стереоплотер) для
просторових (тривимірних) вимірювань
був створений ще в 1901 р.
Прилади,
що дають змогу будувати моделі місцевості,
виконувати просторові вимірювання на
цих моделях (а не в полі) та будувати в
камеральних умовах плани із ситуацією
й горизонталями, називають
Удосконалення
цих приладів та методів вимірювання
на моделях місцевості привели до появи
аналітичної фотограмметрії. Аналітична
фотограмметрія також спирається на
фотографічні знімки, але увесь
фотограмметричний процес виконується
за технологією електронного опрацювання
IV.5. Стереоаерофотограмметричне знімання
IV.5.1. Загальні відомості про стереоаерофотограмметричне знімання
стереознімання.універсальними
приладами.
даних
(ЕОД) і, передусім, аналітичного обчислення
координат точок знімка на
електронно-обчислювальних машинах
(ЕОМ) або комп’ютерах. Сьогодні,
незважаючи на бурхливий розвиток
цифрової фотограмметрії, залишається
актуальною аналітична фотограмметрія,
оскільки є ціла низка задач, розв’язання
яких із застосуванням аналітичної
фотограмметрії єдино можливе. Там, де
потрібна велика роздільна здатність,
поки що важко обійтись без людського
зору та можливостей аналогового та
аналітичного опрацювання.
Необхідно
зазначити, що універсальні прилади -
складні та дорогі, і спочатку ввозилися
з-за кордону. Тому в СРСР у 1931—1936 роках
був створений оригінальний, диференціальний
метод стереознімання. Важлива роль у
створенні цього методу належить проф.
Ф.В. Дробишеву, який сконструював
спеціальний прилад - топографічний
стереометр. Цей прилад дає змогу рисувати
за стереомоделлю тільки рельєф
місцевості. Отже, отримання карт
поділяють на:
Контурну
частину плану отримують складенням
фотоплану, як у першому варіанті
комбінованого знімання.
Рельєф
рисують на окремих стереопарах
стереометрами Дробишева, а потім
горизонталі переносяться на фотоплан.
Саме
цей, диференційований метод дав змогу
отримати карту масштабу 1:100000 на всю
територію країни (СРСР) уже на початку
1950-х років. У США на той час таких карт
на всю країну ще не було.
II
варіант - універсальний метод
стереознімання, коли контури й рельєф
рисуються на універсальних приладах.
Універсальний метод постійно
удосконалюється. Річ у тім, що під час
виконання аерофотознімання у великих
масштабах основним, фактично єдиним
джерелом зображень ще недавно було
аерофотознімання із застосуванням
топографічних аерофотокамер. Цифрових
аерознімальних систем не було. Між
іншим, під час використання цифрових
методів для фотограмметричної обробки
матеріалів аерознімання, здійсненого
фотокамерами, потрібно виконувати
додаткові процеси фотохімічної обробки
аерофільмів та сканування знімків із
метою перетворення їх на цифрову форму.
Це вимагає істотних затрат і робить
значно тривалішим технологічний цикл
робіт. Тому невипадково фірма Leica
Geosystem, особливо
з отриманням прав на компанії ERDAS
і
LH
Systems, активно
веде виробництво обладнання для
аналітичної фотограмметрії, ґрунтуючись
на досвіді колишніх компаній Кет і
Wild.
Оптика
та високоточна механіка цих компаній
стали фактично стандартом в усьому
світі. Серія станцій для аналітичної
фотограмметрії SD
2000/3000
випускається з 1991 року. Про технічні
можливості цих станцій йтиметься у п.
IV.5.3.
504
Нижче
подано технологічну схему стереознімання
у двох варіантах: диференційного та
універсального методів. Технологічні
схеми відображають стереознімання без
застосування під час аерознімання
GPS-технологій,
які дають змогу визначати координати
центрів проекції кожного знімка. У
такому разі виконується польове
планово-висотне прив’язування знімків.
Рис.
IV.5.1. Стереофотограмметричне топографічне
знімання
На
технологічній схемі додатковими
стрілками об’єднані процеси, які
доцільно виконувати одночасно, до того
ж зрозуміло, що ці процеси (польове
прив’язування та дешифрування) можна
виконувати до складання фотопланів чи
графічних планів і цим скоротити Термін
складання карт або планів.
Різниця
двох поданих варіантів стереознімання
не тільки у відмінності процесів
складання карт, але й у тому, що
Диференційний метод не потребує складних
(універсальних) дорогих приладів. Проте
диференційний метод вимагає значної
“ручної*” праці й не піддається
автоматизації. Тому поши- реніший
універсальний метод.
505IV.5.2. Технологічна схема стереофотограмметричного методу знімання
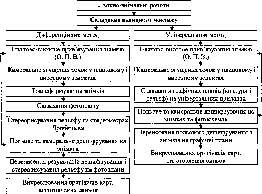
Як
вже зазначалося, найдосконалішими є
станції аналітичної фотограмметрії
(по суті, універсальні прилади), які
випускає фірма Leica
Geosystems. Ці
станції дають змогу значно автоматизувати
складання планів та карт методом
стереознімання. Такі станції називають
аналітичними стереоп- лотерами. Серед
істотних переваг цих станцій перед
іншими можна назвати:
використання
досвіду створення попередніх аналітичних
фотограмметричних приладів;
автоматизацію
фототріангуляційних вимірювань;
застосування
спеціальних ручних коліс та ножних
дисків;
стандартний
інтерфейс LMT
(Leica Mapping Terminal) між
аналітичною частиною станції й
прикладним програмним забезпеченням
(ПЗ);
концепцію
двокомп’ютерної станції; один із
комп’ютерів із прикладним ПЗ, другий
для LMT;
спільне
із цифровими фотограмметричними
станціями програмне забезпечення
ORIMA
і
PRO
600,
для блокової фототріангуляції та
збирання даних.
Остання
перевага є дуже важливою з погляду
паралельного використання цифрових
та аналітичних станцій. Не менш важливим
є те, що в цих аналітичних стереоплотерах
можна використовувати ПЗ інших фірм.
Наведемо технічні дані найновішої
аналітичної фотограмметричної станції
SD
3000.
Рис.
IV.5.2.
Аналітична
фотограмметрична станція
SD
3000
506IV. 5.3. Сучасні станції аналітичної фотограмметрії

Назва параметра |
Значення, матеріал параметра |
Матеріал зображення |
Плівка, скло, негатив або діапозитив |
Корекція фокуса |
Для скла 0,8-1,6 мм |
Збільшення оптики |
3-, 18-кратне |
Поле зору |
60 мм для 3, та 10 мм для 18-кратного збільшення |
Вимірювальна марка |
Освічується, налаштовується за інтенсивністю і розміром |
Роздільна здатність |
>160 лін/мм для 18-кратного збільшення |
Роздільність системи приводу |
1 мкм |
Точність системи приводу |
2 мкм |
Швидкість системи приводу |
60 мм/с |
Розміри |
854x1057x735 мм |
Маса |
198 кг |
Кінцева
продукція станції: оригінал плану або
карти.
Як
нам уже відомо, аерознімання є основним
методом створення та оновлення
великомасштабних топографічних планів
та карт. Але аерознімання виконувалося
топографічними аерофотокамерами. З
переходом від паперових, графічних
планів та карт до цифрових моделей
місцевості (ЦММ) та цифрових моделей
рельєфу (ЦМР) з’явилась необхідність
виконувати аерознімання не фотокамерами,
а цифровими камерами. Проте цифрових
камер, здатних виконувати аерознімання
з високою точністю та високою роздільною
здатністю, не було. Це гальмувало
широке застосування цифрової
фотограмметрії. Проте опрацювання
матеріалів аерофотознімання цифровими
методами вимагало істотних виробничих
затрат і розтягувало технологічний
цикл робіт, оскільки фотознімки, як уже
відзначалося, необхідно піддавати
фотохімічному опрацюванню й скануванню
з метою перетворення їх на цифрову
форму. Природним розв’язанням цієї
складної задачі могло стати безпосереднє,
дистанційне отримання аерознімків
цифровими камерами з високою роздільною
здатністю й точністю. Цю задачу вдалось
розв’язати тільки у кінці XX століття.
Першою такою цифровою аерознімальною
системою, яка ґрунту
507IV.6. Цифрове аерознімання
IV. 6.1. Цифрова аерознімальна система
валася
на літаку, стала ADS40,
створена
компанією LH
Sistems і
була показана на XIX конгресі Міжнародного
фотограмметричного товариства в 2000 р.
З того часу фотограмметрія стає повністю
цифровою.
В
основі технічного рішення ADS40
лежить
концепція трилінійного сканера, уперше
запропонована в 1970 році, яку активно
використовувала компанія DRL
(Німецький
аерокосмічний центр) у системі
дистанційного зондування, як космічного,
так і літакового. Відповідно до цієї
концепції у фокальній площині об’єктива
системи паралельно розташовані три
лінійки - прилади зарядного зв’язку
(ПЗЗ), віддалені один від одного у такий
спосіб, що одна з них забезпечує
панхроматичне знімання в напрямку
“вперед”, друга - у напрямку точки
надира, а третя - у напрямку “назад”
(рис. IV.6.1).
Рис.
IV.6,1.
До пояснення принципу роботи цифрової
камери ADS
Істотною
особливістю конструкції ADS40
є
те, що замість однієї лінійки ПЗЗ
використовуються пари лінійок, зміщені
одна щодо одної на 0,5 поділок (піксела).
Кількість елементів у лінійці ПЗЗ
дорівнює 12000, а в результаті використання
здвоєної лінійки зі зміщенням
забезпечується результуюча роздільність,
як під час використання лінійки, що має
24000 елементів. Крім панхроматичних
лінійок, у фокальній площині розташовані
чотири поодинокі лінійки по 12000
елементів у кожній для мультиспектрального
знімання в чотирьох вузьких зонах
спектра: червоного (610-660 мм), зеленого
(535-585 мм), синього (430-490 мм) та ближнього
інфрачервоного (835-885 мм). На рис. IV.6.2
показано
загальний вигляд діючого комплексу в
салоні носія (літака або гелікоптера).
У
табл. IV.6.1
подано
основні технічні характеристики
системи, які дають змогу оцінити
можливості використання системи ADS40
як
джерела інформації для цифрової
фотограмметрії.
508
№ з/п |
Характеристика |
Значення |
1 |
Кут поля зору (поперек напрямку польоту) |
64° |
2 |
Фокусна віддаль об’єктива |
62,77 мм |
3 |
Розмір піксела із ПЗЗ-лінійок |
6,5 мкм |
4 |
Час запису інформації із ПЗЗ-лінійок |
1,2 мс |
5 |
Реєструвальна кількість пікселів для панхроматичної лінійки (йому відповідає розмір піксела у фокальній площині 3,25 мм) |
2 х 1200 |
6 |
Радіометрична роздільність |
8 bit |
7 |
Куги стереоспостережень |
16°, 26°, 42° |
Як
бачимо, цифрова аерознімальна система
має багато технічних показників,
необхідних для точного знімання.
Цифрова
аерознімальна система ADS40
мас
як переваги, так і недоліки порівняно
з фотокамерою. Фактором, що обмежує
роздільну здатність зображення на
місцевості для системи, є інтервал часу
(період) між зчитуванням інформації з
лінійок, що дорівнює 1,2 мс. Для швидкості
літака 100 м/с
509IV. 6.2. Порівняння технічних можливостей фотограмметричної та цифрової камер. Опрацювання цифрових знімків системою ads40
Характеристики |
Значення |
|
ADS40 |
RS30 |
|
Масштаб фотографування |
- |
1:10000 |
Розмір піксела під час сканування |
Сканування не потрібне |
12 мкм |
Роздільна здатність на місцевості, що відповідає розміру піксела |
0,25 м |
0,25 м |
Ширина ділянки знімання |
3000 м |
2300 м |
З
поданих даних видно, що знімання цифровою
системою за роздільною здатністю
однакова з аерофотозніманням, але в
масштабі 1; 10000. Тільки за умови сканування
знімків із розміром піксела 12
мкм можна говорити про можливість
картографування території у масштабі
1:2000
за матеріалами цифрового знімання.
Цифрова система забезпечує ширину
смуги знімання, на 30 % більшу.
Отже,
система ADS40
поєднує
роздільну здатність топографічного
аерофотоапарата й інформативність
засобу дистанційного зондування.
На
жаль, треба зазначити, що геометричні
властивості зображення, одержаного
таким способом, принципово відрізняються
від геометрії звичайних аерофотознімків,
отриманих за допомогою топографічного
фотоапарата, які є центральною проекцією
точок знімка. У випадку описаного вище
формування зображення кожний рядок,
отриманий у результаті зчитування
інформації із ПЗЗ-лінійки, є центральною
проекцією деякої лінії на поверхні
Землі. Значення як лінійних, так і
кутових елементів внутрішнього
орієнтування для кожного такого рядка
відрізняються між собою через зміни
кутового орієнтування та переміщення
літака у просторі під час знімання.
Працювати з такими, довільно геометрично
спотвореними зображеннями, зокрема
спостерігати їх стереоскопічно,
неможливо. З цієї причини вихідні
зображення (рівень 0)
потрапляють під геометричне трансформування
з урахуванням значень елементів
внутрішнього орієнтування кожного
рядка, отриманих за допомогою системи
510
позиціонування
та орієнтування POS
(Position and Orientation System). Одержані
результати такого трансформованого
зображення (рівень 1)
можна вже спостерігати стереоскопічно,
виконувати необхідні вимірювання для
цілей фототріангуляції. Після цього
можна виконувати всі інші процеси
фотограмметричного опрацювання на
цифровій фотограмметричній станції
(створення цифрової моделі рельєфу
(ЦМР), ортофототрансформування й монтаж
ортофотоплану стереознімання) з метою
отримання кінцевого продукту -
геокодованого зображення або ортофотоплану
(рівень 2). Зазначимо, що через особливості
геометричних властивостей зображень,
отриманих за допомогою цифрової
знімальної системи такого типу, ці
зображення можна буде опрацювати тільки
з використанням спеціального програмного
забезпечення (ПЗ), яке дає змогу врахувати
ці особливості. Це є істотним недоліком
описаної цифрової системи.
В
останнє десятиліття у зв’язку з
бурхливим розвитком обчислювальної
техніки й засобів приймання зображень
на основі приладів зарядного зв’язку
(ПЗЗ), тобто комп’ютерного бачення,
з’явилась можливість перейти від
методів аерофотознімання до методів
цифрового знімання. Так, уже на початку
1990 р. значна частина робіт з опрацювання
матеріалів була комп’ютеризована.
Матеріали знімання - фотонегативи -
оцифровувались за допомогою сканерів.
Така технологія й сьогодні залишається
доволі поширеною. Проте послідовне
використання фотографічної та
оптично-електронної техніки спонукає
не тільки до необхідності виконання
додаткових процесів, таких, як фотохімічна
обробка та сканування знімків, що
затягує технологічний цикл і збільшує
матеріальні затрати, але й призводить
до втрати якості матеріалів знімання.
Напевно, саме цим пояснюється те, що в
середині 1990 років за кордоном з’явились
дослідні зразки цифрових аерофотокамер,
а першим комерційним зразком стала
камера ADS40
тільки
в 2000 році. Широке впровадження цифрової
фотограмметрії вимагає розв’язання
цілої низки супутніх задач. Принциповим,
наприклад, виявився вибір типу цифрових
камер. Основним недоліком камери ADS40,
як
уже зазначалося, є те, що вона дає
зображення, яке принципово відрізняється
від центральної проекції, тобто дає
іншу геометрію зображення. Перетворення
таких знімків на центральну проекцію
вимагає спеціального обладнання та
спеціального програмного забезпечення.
511IV. 6.3. Цифрові аерознімальні комплекси із лазерним скануванням
Камера
ADS40
працює
на ПЗЗ-лінійках. Саме така будова камери
приводить до істотного спотворення
принципу центральної проекції. Цифрові
камери, побудовані на ПЗЗ-матрицях,
дають змогу зберегти центральну проекцію
й ліквідують цей недолік. Але поки що
не вдається створити цифрові камери з
великоформатними ПЗЗ-матрицями й
високою роздільною здатністю та з
великим захопленням місцевості. Тому,
наприклад, і в Росії також були створені
цифрові камери ЦТК-140, ЦМК-70 на ПЗЗ-лінійках.
Остання камера ЦМК-70 за своїми
характеристиками близька до ADS40.
Російські
камери мають такий самий головний
недолік: спотворюють центральну
проекцію.
Технічне
вирішення цього складного питання
знайдене в застосуванні так званих
інтегральних навігаційних комплексів
типу GPS/IMU,
які
дають змогу, по-перше, з достатньою
точністю визначати шість параметрів
зовнішнього орієнтування кожного
знімка, що забезпечує можливість без
прив’язування знімків істотно спростити
створення фототріангуляційної мережі
та, по-друге, одночасно виконувати
аерофотографічне та лазерно-локаційне
знімання.
І
і
Рис.
IV.6.3.
Аерознімальний
комплекс із лазерним скануванням
512
Групи |
Довжина хвилі, см |
Частота, ГГц |
X |
3,0 |
9,6 |
с |
5,3 |
5,6 |
L |
24,0 |
1,3 |
Р |
68,0 |
0,3 |
Два
зображення IfSAR
можуть
бути об’єднані, щоб використовувати
техніку інтерферометри для генерування
(створення) DSM-цифрової
моделі рельєфу. Принцип роботи IfSAR
показаний
на рис. IV.6.4.
На
рисунку показані два положення антени
в точках
513А1
ІЛ2.
Нехай Н
- висота точки Ах
над референц-еліпсоїдом, a
h
-
висота поверхні Землі (перевищення,
яке визначають). Базова лінія В,
тобто віддаль між антеною в
положеннях
1
і 2. Похила віддаль від антени
h
= H-p
-cos©. (IV.6.1)
Рис.
IV. 6.4. Геометрія однопрохідного
інтерферометра SAR
Із
трикутника
\2
(/н-5р)
=
р2
+В2
-2рВ-cos(90°
-0 + а), (IV.6.2)
де
8
=
(IV.6.3)
де
Дф_
2л~
зміна
фази між двома відбитками (від дерева
та ґрунту). Ця зміна фази може бути
виміряна тільки під час зміни фази в
межах від 0 до 2 л. Визначити Дф
(кількість
разів по 2л
) можливо завдяки супутниковим даним
про розташування антени в пунктах
514Ах
до цілі А
дорівнює Р
і є відомою. Кут 0 в точці Ах
між вертикаллю й напрямком на ціль А
також відомий - це кут між осями цифрових
камер: вертикальною і спрямованою
вперед. Кут а між базовою лінією і
горизонтальним напрямком. Як видно з
рисунка: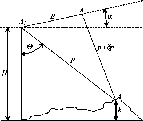
ААХА2
можемо записати:Ьр
- зміна нахиленої віддалі, яка визначається
за формулоюр
2л’N
-
кількість хвиль; А,- довжина хвилі, яку
випромінює радар; Дф-Ах
і А2.
Проте проникнення лазера в поверхню
дерев може спотворити їхню істинну
висоту. Отже, вимірювання у місцях,
покритих деревами, містять більше
“шуму” (похибок) вимірювання, ніж у
місцях з “дзеркальними” відбивними
поверхнями. Проникнення сигналу в
поверхню
дерев
різне для різних довжин хвиль, наприклад,
групи
515X
та L.
Це дає змогу визначити ступінь
“проникнення” сигналу. Якщо дерева,
кущі близько розташовані до дороги,
тоді це сприяє підвищенню точності
побудови цифрової моделі рельєфу DSM.
Саме
для побудови DSM
-
цифрової моделі рельєфу та DEM
-
цифрової моделі місцевості і
використовуються комплекси LIDAR
і
IfSAR.
Зазначимо,
що фіксація відбиття хвиль від поверхні
дерев та від ґрунту дасть змогу виконувати
цифрове аерознімання у місцевості,
вкритій рослинністю. До цього часу такі
райони знімались тільки наземними або
комбінованими методами.
РОЗДІЛ
V. АВТОМАТИЗАЦІЯ НАЗЕМНИХ
ТОПОГРАФО-
ГЕОДЕЗИЧНИХ РОБІТ. ЦИФРОВІ
ПЛАНИ ТА КАРТИ
Серед
таких напрямків виділимо:
автоматизацію
польових робіт;
застосування
комп’ютерів для математичного
опрацювання вимірів;
використання
автоматизованих та автоматичних
графопобудовувачів та координатографів
для складання графічних планів на
папері, пластиках та інших основах;
перехід
від графічних паперових планів та карт
до цифрових моделей місцевості (ЦММ)
та цифрових моделей рельєфу (ЦМР) із
застосуванням перетворювачів аналогової
(безперервної) інформації на цифрову,
дискретну, так званих дігітайзерів -
оцифровувачів (digit
-
від англ. цифра) та сканерів.
Автоматизація
технологічних процесів у будь-якому
виробництві є найперспективнішим,
революційним напрямком розвитку галузей
народного господарства.
Проте
об’єктивна оцінка показує, що стан
автоматизації у різних галузях
неоднаковий. Тоді як низка галузей,
особливо машинобудування, хімічне
виробництво та деякі інші галузі
сьогодні на високому рівні, передусім
завдяки розв’язанню найважливіших
комплексних задач за допомогою
комп’ютера, що дає змогу виділити
загальні ланки автоматизації та
систематизувати їх на державному рівні,
то одночасно існують галузі, у яких
домінує ручна, низько- кваліфікована
та малопродуктивна праця.
Автоматизація
технологічних процесів топографічного
виробництва не досягла ще тієї широти,
яка притаманна високоавтоматизованим
галузям виробництва. Особливо це
стосується камерального (офісного)
виробництва.
Для
ілюстрації характеру розподілу затрат
та сучасної тенденції автоматизації
геодезичного виробництва доцільно
навести таблицю за даними США, узяту з
роботи [19], де наводиться порівняльний
аналіз продуктивності п’яти видів
технічних засобів, що застосовуються
під час наземного топографічного
знімання однієї й тієї самої території
послідовно трьома виконавцями (рейкарів
- два).
5161. Автоматизація топографо-геодезичних робіт
1.1. Основні напрямки та технології автоматизації топографо- геодезичного вимірювання
Тип приладу |
Час у полі, ч/м |
Обчислення, ч/м |
Креслення, ч/м |
Загальний час, ч/м |
Кіпрегель |
4-50 |
- |
- |
4-50 |
Теодоліт |
2-50 |
0-40 |
5-30 |
8-15 |
Тахеометр круговий |
3-10 |
0-40 |
5-45 |
9-35 |
Тахеометр |
3—40 |
0-20 |
4-05 |
8-05 |
номограмний |
-//- |
-//- |
2-15* |
6-15 |
Тахеометр |
2-00 |
0-08 |
3-25 |
5-33 |
електронний |
-//- |
-//- |
2-13* |
4-21 |
*
Викреслювання на автоматичному
графопобудовувачі.
Аналізуючи
таблицю, неважко зауважити, що подані
технології автоматизації малоефективні
навіть порівняно з неавтоматизованим
мензульним зніманням. Нижній рядок
таблиці ілюструє межу перспектив у
продуктивності праці навіть одним із
найавтоматизованіших приладів -
електронним тахеометром.
Хоча
час затрат зменшився, проте ефективність
від’ємна через велику вартість приладу.
У чому тоді зміст автоматизації?
Відповідь на ці питання треба шукати
у визначенні: що таке автоматизація та
який ступінь перспективності мають
ті чи інші технічні рішення, спрямовані
на автоматизацію.
Підвищення
ефективності суспільного виробництва
за рахунок зниження частки живої праці
та підвищення продуктивності обладнання.
Виконання
робіт у небезпечних умовах або в місцях,
недоступних людині.
Підвищення
об’єктивності та точності результатів.
Джерелами
ефективності автоматизації є:
Різке
підвищення швидкості виконання
технологічних операцій за рахунок
ліквідації фізіології ручної праці,
притаманної людині-оператору.
Поєднання
часу виконання технологічних операцій
через універсалізацію технічних
засобів, тобто об’єднання технічних
засобів зі збереженням їхніх функцій.
Підвищення
частки чистого часу виконання
технологічних процесів за рахунок
підготовчих та допоміжних операцій.
517Автоматизація
-
це такий розвиток виробництва, під час
якого людина звільняється від
безпосередньої участі в ланках
технологічного процесу. Враховуючи
таке визначення, можна сформулювати
цілі автоматизації:
Заміна
технологічного процесу відповідно до
вимог технічних засобів автоматизації
(за умови збереження якості кінцевого
продукту).
Отже,
необхідно ретельно аналізувати
технологічні процеси, щоб відшукати
технічні засоби для автоматизації всіх
операцій. Звернемо увагу на те, що майже
половина затрат (див. табл. V. 1.1)
припадає на викреслювання паперових
планів та карт навіть за умови застосування
автоматизованих графопобудовувачів.
Щоб подолати цю перепону, є лише
Одним
із засобів підвищення швидкості
виконання технологічних циклів є
використання транспорту. Беззаперечно
застосування транспорту в топографо-
геодезичному виробництві необхідно
удосконалювати. Питання автоматизації
аерофотознімання розглянуто в розділі
IV.
Надалі
ми розглянемо автоматизацію наземних
методів визначення висот, планового
та просторового положення точок земної
поверхні.
Геометричне
нівелювання - поки що неперевершений
за точністю метод визначення висот.
Проте метод вимагає значних затрат
праці, особливо, якщо необхідно визначити
перевищення між значно віддаленими
точками. Автоматизація нівелірних
робіт починається із застосування
компенсатора. Зауважимо, що перший
рідинний компенсатор був запропонований
конструктором Г.Ю. Стодолкевичем
(СРСР) ще в 1945 році. Поширеніші маятникові
компенсатори.
Проте
насправді автоматичними нівелірами
стали електронні, цифрові нівеліри,
описані у розділі І. Класична форма
нівелювання - ходами із застосуванням
компенсаторів та спеціальних транспортних
засобів дає змогу на 30-40 % підвищити
продуктивність робіт.
Подібна
технологія із застосуванням компенсаторів
місця нуля (місця зеніту) та автомашини
виявилась ефективною для нижчих за
точністю робіт - під час тригонометричного
нівелювання тахеометрами, що дало змогу
скоротити час ще на 25-50 % порівняно з
геометричним нівелюванням.
518один
шлях,
якому
немає альтернативи, а саме: для успішного
застосування сучасних комп'ютерів
та засобів автоматизації необхідно
замінити образно-знакові, паперові
плани та карти на цифрові карти місцевості
(ЦКМ).
Питанням цифрових карт відведено в
цьому підручнику окремий параграф.
Велике значення для підвищення
ефективності продуктивності праці має
універсалізація приладів. Нині це
створення тотальних наземних станцій,
а найновіші досягнення - це об’єднання
наземних станцій із методами супутникової
геодезії.
1.2. Автоматизація визначення висот
Лазерні
методи нівелювання підвищують
об’єктивність та оперативність
реєстрації результатів нівелювання.
Проте застосування позиційних
випромінювальних нівелірів не має
помітних переваг перед відомими
методами. Можна відзначити систему
контролю планування (СКП-1), що ґрунтується
на принципі лазерної площини та її
використання на ділянках місцевості
радіусом до 300 м.
Результати
дослідження цієї системи підтверджують
похибки системи ±3 см для вказаної
віддалі. Розширення просторового
діапазону під час використання променевих
лазерних систем приводить до збільшення
впливу рефракції, який може бути
враховано, наприклад, за коливаннями
зображень візирних цілей.
З
позицій автономності, незалежності
від зовнішніх умов та автоматизації
нагадаємо про маятникові висотоміри-автомати.
Отже, серед відомих та перспективних
геодезичних засобів нівелювання площ,
деякі з них, після включення в агрегати
комплексних засобів, мають чітко
виражені можливості автоматизації та
різкого підвищення продуктивності.
У
цьому питанні необхідно окремо розглянути
автоматизацію вимірювання кутів та
ліній.
Автоматизація
вимірювання горизонтальних кутів
Вимірювання
кутів складається з таких операцій:
Встановлення
приладу над точкою - центрування.
Горизонтування.
Наведення
візирної труби на ціль.
Відлічування
горизонтального круга.
Опрацювання
вимірів.
Урахування
зовнішніх та інструментальних похибок
кутомірних вимірів.
Для
кутових вимірів тією чи іншою мірою
автоматизуються всі перераховані
операції, окрім встановлення приладу,
точніше, встановлення горизонтального
круга та алідади в горизонтальний стан,
яке і нині виконується за допомогою
циліндричного рівня. Центрування
приладу виконується швидше і точніше
завдяки лазерним вискам. Давно відомі
методи автоматизованого наведення
труби на ціль.
Застосовуються
кодові, імпульсні або динамічні методи
електронних відліків та вимірів кутів.
Частіше перевагу віддають останньому.
Крім того, динамічний метод дає ще змогу
орієнтувати горизонтальний круг щодо
заданого напрямку.
519
1.3. Автоматизація визначення планового положення точок
Результати
кутових вимірів відображаються на
дисплеї і можуть бути записані в польовий
журнал або в пам’ять приладу, а потім
відправлені на зовнішній комп’ютер
для подальшого опрацювання.
Автоматично
компенсуються інструментальні похибки
кутомірних приладів. Для цього, як
відомо, у динамічній системі відліків
використовуються чотири зчитувачі
відліків (чотири маски). Над нульовим
діаметром лімба встановлюється одна
пара фотодіодів, а зорова труба наводиться
на другий напрямок кута. З цим напрямком
збігається друга пара фотодіодів.
Розташування обох пар фотодіодів точно
не збігається з напрямками нульового
діаметра та візирної осі труби. Проте
виміри виконуються двома протилежними
напрямками обертання круга. Завдяки
діаметральному розташуванню чотирьох
зчитувачів та обертанню круга під час
вимірювання у протилежних напрямках
виключаються похибки, викликані не
точним розташуванням кругів та
зчитувачів, а саме:
ексцентриситет
лімба;
ексцентриситет
алідади.
Крім
того, автоматично вводяться поправки
за кривину Землі та нормальну
рефракцію (на жаль, поправки за аномальну
рефракцію не вводяться).
Динамічний
прилад має додаткові, вмонтовані
системи, що автоматично компенсують
вплив нахилу вертикальної осі теодоліта
(неточного горизонту- вання приладу)
на значення горизонтальних та вертикальних
кутів (раніше ми розглядали пристрої,
які автоматично встановлюють МО (місце
нуля) таким, що дорівнює нулю).
Автоматизація
вимірювання ліній
Під
час наземного великомасштабного
знімання у наш час основним засобом
лінійного вимірювання є світловідцалеміри
з напівпровідниковими випромінювачами.
Як відомо, вимірювання ліній складається
з таких дій:
Центрування.
Встановлення
приладу в робочий стан (горизонтування).
Наведення
труби на відбивач.
Вимірювання
ліній, яке, своєю чергою, складається
з:
отримання
оптимального відбитого сигналу;
усунення
несиметричності вимірювальних каналів;
розв’язку
багатозначності;
виконання
внутрішнього калібрування приладу.
Вимірювання
та урахування параметрів зовнішнього
середовища (метеоданих).
Опрацювання
вимірів.
520
Щодо
другої дії (приведення в робочий стан),
аналогічної до тієї, що і під час кутових
вимірювань, ніколи не було навіть спроб
автоматизації. Перша дія - центрування
с/в до певної міри, як і для кутових
вимірювань, прискорюється тільки
завдяки лазерним центрирам, але
залишається ручним.
Спроби
автоматизувати наведення труби існують
і продовжуються. Але, по суті, сьогодні
автоматизація вимірювання довжин
починається якраз із автоматизації
саме лінійного вимірювання. Першим
приладом, у якому було автоматизовано
електро-механічним способом розв’язання
неоднозначності, був світловіддалемір
DI-10,
створений
у 1968 році фірмою Wild.
Надалі
автоматизація пішла шляхом використання
електронних пристроїв. У наш час у
світловіддалемірах усе “вимірювання
ліній” автоматизовано, проте різними
способами. Автоматизація урахування
метеопоправки реалізована майже у всіх
останніх моделях. Технічно цей процес
вирішується також по-різному. Вимірювання
метеопараметрів вдало реалізоване
тільки у світловіддалемірі МЕ-3000. Це
високоточний прилад, що вимірює віддалі
до 3000 м із приладною похибкою 0,2 мм.
Виробники цього приладу сконструювали
автоматизовану систему для вимірювання
та урахування метеопараметрів, яка
розташована всередині приладу. Проте,
як відомо, щоб забезпечити високу
точність вимірювання, недостатньо
виміряти метеопараметри в одній точці
лінії.
З
появою світловідалемірів із цифровими
лічильниками опрацювання результатів
стало практично складовою вимірювання
ліній. Деякі сучасні світловіддалеміри
відображають на дисплеї не тільки
багаторазово виміряне середнє значення
віддалі, але й середні квадратичні
похибки (DI-38,
3805,
Recota),
а
деякі виконують вимірювання доти, доки
точність вимірювання не буде відповідати
наперед заданій середній квадратичній
похибці. Тому вимірювання затягується
і, залежно від умов видимості, продовжується
від 6
до 60 с. На жаль, виявляється, що
автоматизація тільки лінійного
вимірювання, як і тільки кутового
вимірювання, малодоцільна, оскільки
не виконується принцип універсалізації
приладів. Тільки у разі конструктивного
поєднання лінійного та кутового
вимірювання, тобто, по суті, переходу
до планового, а ще краще, до просторового
вимірювання, автоматизація стає
доцільнішою та ефективнішою.
Основним
методом наземного визначення просторового
положення точок є електронна тахеометрія.
Взагалі тахеометричне знімання, як
відомо, означає швидке знімання.
Швидкість знімання досягалась насамперед
завдяки заміні мірної стрічки нитковим
віддалеміром: одним поглядом на рейку
визначались віддалі. Подальшим
удосконаленням була заміна кругового
тахеометра номо-
521
1.4. Автоматизація визначення просторового положення точок
грамним,
запропонованим Гамером у 1901 році -
більше ніж 100 років тому. Номограмний
тахеометр дає змогу без обчислень,
користуючись відліками рейки визначати
горизонтальні прокладення довжин ліній
від тахеометра до рейки
Компенсатори
нахилу - наступне важливе вдосконалення
тахеометра, яке звільнило спостерігача
від необхідності увесь час виводити
бульбашку рівня, скріпленого з
вертикальним кругом, у нуль-пункт.
Компенсатори
значно підвищили швидкість виконання
топографічного знімання. Але найважливішим
сучасним досягненням є електронні
тахеометри - прилади, які здатні
автоматизувати одночасне вимірювання
кутів і віддалей та їхнє комп’ютерне
перетворення на просторові координати
Детальний
опис будови електронних тахеометрів
подано в розділі II.
Нагадаємо,
що прилади, якими можна виконувати
електронне вимірювання горизонтальних
та вертикальних кутів і віддалей
(нахилених, горизонтальних,
вертикальних), називаються електронними
тахеометрами. Використовуються два
способи поєднання електронних теодолітів
з електронними віддалемірами. Перший
з них полягає у поєднанні відцалемірної
і кутовимірної частин в одну систему
вимірювання, що має спільну будову і
багато спільних елементів (наприклад,
спільна зорова труба, мікропроцесор,
фазометр, клавіатура, реєстратор).
Такі системи називають
Другий
спосіб полягає у поєднанні окремо
сконструйованого віддалеміра з
теодолітом (оптичним або електронним).
Ці два прилади можуть незалежно
виконувати своє призначення. Тоді це
-
Інтегровані
тахеометри з високоточним вимірюванням
кутів та ліній, автоматичним введенням
інструментальних та інших поправок
здатні на пунктах спостережень виконувати
широку програму опрацювання даних,
зокрема визначення просторових координат
Окрім
вимірювання кутів, ліній та координат
визначення
недоступної віддалі;
визначення
недоступної висоти;
522S,
а також перевищення h.X,
Y,
Z
пунктів,
що спостерігаються.інтегрованими
тахеометрами
[31].модульний
тахеометр.
У цих двох частинах (модулях) спільними
частинами є тільки відбивач, візирні
марки, штатив, інші деталі. У нових,
інтегрованих тахеометрах застосовують
фазові відцалеміри, а для кутового
вимірювання - один із методів електронного
вимірювання кута: кодовий, імпульсний,
частіше - динамічний.X,
Y,
Z
отримали
назву “тотальні станції” (Electronic
total stations).X,
Y,
Z
ці
станції здатні виконувати низку програм
завдяки внутрішньому програмному
забезпеченню, а саме:
винесення
в натуру точок за їхніми координатами;
визначення
дирекційного кута. За координатами
точки стояння і точки орієнтування
автоматично вираховується дирекційний
кут на точку орієнтування і
горизонтальний круг приладу може бути
встановлений за обчисленим дирекційним
кутом;
обернена
засічка: за кутовими і лінійними
вимірами на дві точки з відомими
координатами обчислює координати
точки стояння і дирекційного кута на
точку, що буде спостерігатись наступною.
Особливо
відзначимо компактні тотальні станції
фірми Sokkia
(Японія).
Усе керування приладом (SET-6E,
SET-6F)
виконується
за допомогою тільки декількох клавіш.
Найновіші моделі з цієї серії - електронні
тотальні станції SET500
та
SET600.
Вага
цих приладів з акумулятором - 5 кг.
Середня квадратична похибка вимірювання
кута одним прийомом - 5" (1,5 МГон).
Максимальна віддаль 4200 м. Точність
визначення віддалі ± (3+2* Ю6^),
(
Останнім
часом, як уже зазначалось, деякі фірми
почали випускати
Так,
для
Горизонтальні
кути вимірюються з похибками 6-7".
Горизонтальні кути, як і перевищення,
відображаються на дисплеї. Стандартні
мінімальні величини:
вимірювання
перевищень - 0,01
мм;
вимірювання
віддалей - 1
мм;
кутових
вимірювань - 5".
Тотальний
нівелір Dini
ЮТ
випущений до 150-річчя оптичної фірми
Karl
Zeiss. Подальше
вдосконалення тотальної нівелірної
станції - Dini
1
IT.
Дуже
важливо, що деякі тотальні станції,
наприклад, ТМ 3000 V фірми Leica
(Швейцарія)
відображають на дисплеї структурні
характеристики
турбулентності
атмосфери С^, а цифрові нівеліри SDL
30
фірми Sokkia
(Японія)
та Dini
22
фірми Zeiss-Trimble
(Німеччина),
відповідно, видають на
523D-
віддаль
у км).тотальні
електронні нівелірні станції,
якими можна не тільки точно вимірювати
перевищення, але й віддалі та горизонтальні
кути. Інакше кажучи, такі станції здатні
визначати просторові координати точок.
До таких станцій можна зарахувати Dini
ЮТ.
Точність одного кілометра подвійного
ходу - 0,3 мм. Лінії визначаються з
похибками:mD
=
0,5 D
х
0,001 м для інварних рейок; mD
=
1,0
Z)
х
0,001 м для інших рейок.D
=
100 м, mD
=
5 см (для інвару);mD
=
10
см (для інших рейок).
дисплей
квадратичні похибки
У
роботах [15, 16] показано, що під час
термічної турбулентності (яка діє у
світлий період доби) існують залежності
між
dn
вертикальним
градієнтом показника заломлення
повітря—, а також між
dz
Єї-'-
тому
(V.1.1)
Одночасно
лінійна рефракція г
може бути визначена за формулою
г-
(V.1.2)
У
цих формулах
Отже,
щоб автоматизувати урахування кутової
та лінійної вертикальних рефракцій,
достатньо у внутрішній або зовнішній
комп’ютер ввести програму розв’язання
простих формул.
Точність
урахування рефракції для
Під
динамічними топографічними системами
розуміють системи, що використовують
візирні цілі, розташовані на транспортних
засобах, які увесь час перебувають у
русі. Планове положення візирної цілі
визначають різними способами (переважно
лінійними, кутовими або комбінованими
засічками), а висоти вимірюють або
тригонометричним нівелюванням, або
використовуючи лазерну горизонтальну
площину [4].
Однією
з найвідоміших таких систем є
автоматизована топографічна операційна
система (АТОС), призначена для
топографічного знімання у масштабі
1:2000 із перерізом рельєфу 0,5 м.
524ткв
відліку рейки, які пов’язані переважно
з турбулентністю атмосфери, що викликає
коливання зображень візирної цілі
(поділок рейки). Нині ці дані можна
використати для визначення поправок
за кутову аномальну вертикальну
рефракцію 8'н
у виміряні вертикальні кути, а також
поправок за лінійну вертикальну
рефракцію г
(мм) у відліки рейок або у виміряні на
станції перевищення h.СІ
та аномальнимт
.
таг.
Виявилось, що
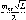
L
-
довжина лінії у метрах.L
=
100 м оцінюється в 0,7" (0,3 мм) і до того
ж ці (залишкові) похибки вже не
систематичні, а випадкові.1.5. Автоматизовані динамічні топографічні системи
Польовий
комплект АТОС встановлено на автомобілі
ГАЗ-66.
Він містить:
Висотомір
на базі опорної лазерної площини.
Чотири
геодезичні радіовіддалеміри (два
ведучі, два ведені) для визначення
планового положення пікетів знімання.
Автоматизований
реєстратор геодезичної інформації.
Висотомір
складається з трьох частин: 1) випромінювача
горизонтальної лазерної площини.
Випромінювач встановлюють на точках
знімальної (робочої) мережі; 2)
приймальної рейки, установленої на
кузові всюдихода; 3) блока підсилення,
також розміщеного на кузові.
Висота
випромінювача може змінюватися у межах
від 1 до 4,5 м за допомогою перевізної
металевої піраміди.
Фотоприймальна
рейка складається з 60 фотоелементів,
оснащених лінзами кругового огляду і
закріплених через 5 см на робочій частині
рейки завдовжки 3 м. Точність визначення
висот близько 7 см. Віддаль - 600 м. Чотири
радіовіддалеміри РДГВ (радіовідцалемір
геодезичний, високоточний) дають змогу
визначати планове положення пікетів
способом оберненої лінійної засічки
(віддалі 20-3000 м). Під час знімання ведені
станції розміщені на двох точках робочої
основи, ведучі - на транспорті. Транспорт
рухається по дузі. Створи радіовіддалемірів
повинні перетинатися під кутом, близьким
до 90 °.
Пікети
набираються по концентричних дугах на
віддалі 15-30 м один від одного. Середня
квадратична похибка визначення у русі
планового положення пікету - 0,5 м.
Реєстратор
польової інформації (РІП 01) - магнітофон,
що записує дані на компакт-касету. На
одну касету записується 600-650 пікетів.
Камеральний
комплекс складається з технічних
засобів опрацювання інформації на базі
експедиції або обчислювального центра.
Технічними засобами є: мінікомп’ютер,
автоматичний координатограф, пристрої
введення- виведення інформації. Склад
польової бригади - 5 осіб (водій, оператор
висотоміра, оператор радіовіддалеміра,
два оператори ведених станцій).
У.1.6.
Автоматизовані лазерно-паралактичні
топографічні системи
Такі
системи також використовують принцип
створення лазерної площини, але в іншому
варіанті. Випромінювач має лазерний
передавач з головкою, що повертається,
та радіопередавач. Лазерний передавач
формує два пучки променів: горизонтальний
і нахилений до горизонту під деяким
постійним кутом. Приймальний пристрій
виконано у вигляді фотоприймача з
об’єктивом кругового огляду, розміщеної
зверху телескопічної штанги, на якій
525
також
закріплені радіоприймач та обчислювальний
пристрій. Передавальний (випромінювальний)
пристрій встановлюють на точках
геодезичної основи, а приймальний - на
пікетах.
Висоту
пікетів визначають фіксацією фотоприймачем
країв горизонтального променя, а
віддаль - паралактичним методом,
використовуючи відомий вертикальний
кут (постійний) та виміряне перевищення
h
між
горизонтальним і нахиленим пучками
променя над пікетом.
Оскільки
ht
= •
tgv,
то, вимірявши h,
для відомого tgv
знайдемо:
Інформація
про кут обертання головки відносно
початкового напрямку передається
радіопередавачем і приймається
радіоприймачем приймального пристрою.
Описаний метод застосовний тільки на
відкритій, рівнинній місцевості.
Універсальнішим є спосіб електронної
тахеометрії.
Як
відомо, тахеометрія призначена для
визначення положення пунктів на основі
вимірів горизонтального кута а,
вертикального (зенітного) кута
,
де с
= tgv
.
с
А
і
Сенсор
і система
самонаведення
приладу
на рухому або
нерухому призму
Рис.
V.1.1.
Принцип
вимірювання кутів а та z,
нахиленої віддалі S
на
рухому або нерухому призму
526z
та
нахиленої від далі S
до
призми, що рухається або встановлена
нерухомо.
1.7. Електронна тахеометрія
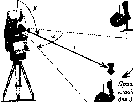

Кути
z,
а та нахилена віддаль
На
сучасних штангах призм-відбивачів
світла додатково кріпляться:
Сенсори-пристрої
для відшукування й автоматичного
наведення труби тахеометра на рухому
або нерухому призму.
Радіомодуль
(або лазерний модуль) з графічним
дисплеєм і клавіатурою (подібною на
ту, що в тахеометрі) для дистанційного
керування тахеометром (із точки
встановлення призми).
Комп’ютер
із системою електронного опрацювання
даних та пам’яттю, дисплеєм, клавіатурою,
бібліотекою програм вимірювань.
Середні
похибки вимірювання сучасними
тахеометрами, наприклад, фірми Leica
TPS 1100:
середня
похибка вимірювання кутів
середня
похибка вимірювання віддалів,
максимальна
віддаль - 3 км;
час
вимірювання -1с;
графічне
відображення - 8
ліній по 32 знаки;
вага
- 4,7 кг.
Зрозуміло,
що за такої точності вимірювання
тахеометр може використовуватися
не тільки для топографічного знімання,
але і для розв’язання багатьох задач
інженерної геодезії та геодинаміки.
Рис.
V. 1.2. До виведення формули тригонометричного
нівелювання
527S
вимірюються
автоматично.
maZ
=
1,5”;ms
=2+2S
(км)мм;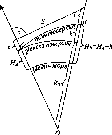
На
закінчення подамо формули, за якими
визначається перевищення
h
=
^j(R3
+if
+S2
+
2(j?3
+i)-ScosZ
-Щ-l. (V.1.3)
Ця
формула не враховує кривини Землі і
рефракції. Проте поправки можуть бути
введені окремо.
Автоматичні
координатографи (АК) є системами, що
складаються з:
Координатографа.
Обчислювальної
машини (ОМ), комп’ютера.
Робочих
пристроїв та приладів.
Допоміжного
обладнання.
Координатограф
складається зі стола, на якому розташовують
план чи карту, та обвідного, рухомого
пристрою (курсора), що, переміщуючись,
вказує точки або лінії, які треба
наносити. Робочими приладами є креслярські
пера, гравірувальні різці та різні
головки. У нових моделях координатографів
широко використовуються світлові
головки, що можуть гравірувати на
пластиках або креслити на фотоплівках
та інших основах. Переміщення креслярського
пера реалізується автоматично і
керується комп’ютером. До допоміжного
обладнання належить пульт керування,
пристрій введення та виведення
інформації. Інформація для АК може
подаватися безпосередньо з великої
ЕОМ або через проміжні носії: магнітні
стрічки, диски тощо. АК використовуються
під час виготовлення оригіналів карт
та планів на папері, пластиках та інших
основах, а також для отримання графічної
інформації у вигляді різних проектів,
схем, робочих креслень та інших
документів.
Існує
більше ніж 100
різних систем автоматичних координатографів.
Детальне описування їх не має змісту.
Описи та рекомендації доцільного
застосування координатографів зазвичай
подаються у відповідних інструкціях.
До
перетворювачів аналогової (безперервної)
інформації на цифрову (дискретну)
належать прилади, що дають змогу
перетворювати графічне зображення
карт, планів, аерофотознімків та наземних
на цифрову форму у вигляді координат
точок, що становлять елементи карти,
плану, фотознімка.
528h.
Ця формула дещо інша, ніж у класичній
тахеометрії і враховує безпосереднє
вимірювання тахеометром нахиленої
віддалі [ЗО]. Безпосередньо з рис. V.1.2
маємо:
1.8. Автоматичні координатографи
1.9. Перетворювачі аналогової інформації на цифрову
8 |
|
1 Xj |
7 |
|
Уі |
6 |
1 |
>2х2 |
2 J~~^5 |
|
У 2 |
|
|
Зхз |
Примітка.
Під час площинної дигіталізації
пікселами записується ступінь почорніння
(сірості) або кольору кожного елемента
образу. На рис. V.1.3
показано
у колі фрагмент поверхні з найпростішим
однобітовим запасом: 1
- відповідає чорному пікселу; 0
- навпаки, пікселу білому.
529
Якщо
зображеннями на екрані можна керувати
(виправляти, витирати, пересувати), то
дисплей - інтерактивний; у протилежному
випадку - пасивний. Сканери призначені
для площинного перетворення. У сканери
вмонтовано матриці пікселів, які здатні
перетворювати центральні проекції на
ортогональні, графічні на цифрові.
Сканери - складні електронно-оптичні
системи. Кольоровий сканер “Дельта”
може опрацьовувати знімки розміром до
470x320
мм
і рулонні фільми завширшки до 320 мм.
Сканер має 3175 пікселів розміром 8
(їм .
Оптичні
зчитувальні машини дають змогу читати
сторінки з текстом або символами.
Наземні
лазерні сканери є найсучаснішим,
оперативним, швидким та високопродуктивним
засобом просторового знімання не тільки
точок земної поверхні, але й, що дуже
важливо, просторового знімання споруд,
пам’ятників та інших культурних надбань
людства. Наземні лазерні сканери дають
змогу отримати найточнішу та найповнішу
інформацію про просторові об’єкти.
Суть технології у швидкому визначенні
одним візуванням просторових координат
багатьох точок поверхні об’єкта.
Процес
реалізується завдяки вимірюванню
віддалей до усіх точок об’єкта, положення
яких визначається за допомогою
імпульсного лазерного віддалеміра, що
працює без відбивача. Вимірювання
виконуються з дуже великою швидкістю
- тисячі, інколи десятки тисяч вимірів
на секунду.
На
шляху до об’єкта імпульси лазерного
віддалеміра проходять через систему,
що складається із двох дзеркал, які
можуть повертатися. Одне дзеркало
відповідає за вертикальне зміщення
променя, друге - за горизонтальне.
Дзеркала сканера керуються прецизійними
(точними) серводвигунами. В остаточному
результаті саме ці двигуни визначають
точність напряму променя лазера на
об’єкт, знімання якого виконується.
Знаючи кут повороту дзеркала в момент
спостереження та виміряну віддаль,
процесор вираховує координати кожної
точки. Керування роботою лазерного
сканера виконується портативним
комп’ютером за допомогою спеціальних
програм. Найвдалішими програмами
керування роботою сканерів вважається
комплекс програ^ “Cyclone”;
найдосконалішими
наземними сканерами в наш час вважаються
сканери HDS
3000
фірми Leica.
Назвати
цей сканер найкращим в своєму класі
дає змогу ціла низка його властивостей,
а саме:
•
область
сканування з однієї точки - 360 ° (по
горизонту та 270 ° по вертикалі);
5301.10. Наземні лазерні сканери
Характеристики |
Величини |
Точність визначення положення точки |
6 мм на 50 м |
Точність вимірювання віддалі |
4 мм |
Кутова точність, мікрорадіани |
60 (=12") |
Тип лазера |
імпульсний |
Максимальна віддаль |
100 м |
Частота сканування (точок на секунду) |
1800 |
Вибірковість по вертикалі (горизонталі), мм |
1,2 між точками для S = 50 м |
Максимум точок по вертикалі (горизонталі) |
5000 / 20000 |
Поле зору по вертикалі (горизонталі) |
270 ° / 360 ° |
Відеопошук |
вмонтована цифрова камера |
Відеонаведення |
визначається користувачем одне фото 24x24 1024x1024 пікселів |
Час роботи акумулятора, год |
до 6 |
Розмір сканера, мм |
265x370x510 |
Маса, кг |
16 |
• точність
визначення просторових координат точки
±6
* мля
віддалі
50
м;
діаметр
лазерної плями менше за 6
мм на віддалі 50 м;
спеціальна
цифрова фотокамера з можливістю
автоматичного калібрування;
531
вибірковість
області сканування;
гнучка
система енергозабезпечення із заміною
батарей у режимі “not-
swap” (без
зупинки).
На
рис. V.1.4
подано
загальний вигляд наземного сканера
HDS
3000.
У табл. V. 1.2 наведено його технічні
характеристики.
Комплекс
“Cyclone”
об’єднує
декілька програм. Серед них відзначимо
Cyclone
MODEL. Ця
програма володіє унікальним набором
функцій для створення тривимірних
моделей об’єктів на основі множини
визначених точок, що дістали назву
“хмари точок” і за допомогою яких
можна отримати тривимірні моделі
складних промислових об’єктів, знімання
яких традиційними способами зайняло
б неймовірно велику кількість часу.
Також у наборі засобів Cyclone
MODEL є
можливість побудови нерегулярних мереж
трикутників, що відображають поверхню
складних об’єктів. Такий підхід дає
змогу отримати просторові моделі
рельєфу у вигляді звичного для нас
фотоплану. Тобто програма дає змогу
вибрати з “хмари” точок необхідні
фрагменти та очистити цей об’єкт
знімання від непотрібних деталей,
спростити опрацювання та підвищити
точність.
На
закінчення опису сканерів ще раз
зазначимо, що сканування застосовується
у різних галузях діяльності людини в
архітектурі й археології, у промисловому,
цивільному та транспортному будівництві,
у машинобудуванні, у нафтово-газовій
та інших галузях.
У. 2.1.
Загальні відомості про цифрові моделі
місцевості
Під
цифровою моделлю місцевості (ЦММ)
розуміють множину, елементами якої
є топографо-геодезична інформація про
місцевість і правила
5322. Цифрові плани та карти
Цифрові
моделі місцевості
(ЦММ) створюються як за результатами
наземного знімання, без фотограмметричних
матеріалів, так і на основі матеріалів,
отриманих у результаті наземного
фототеодолітного або аерофотознімання.
Знімання значних територій, як відомо,
виконується переважно методами
аерознімання. Технології створення
ЦММ без фотограмметричних матеріалів,
переважно на основі електронної
тахеометрії значно відрізняються від
технологій створення цифрових планів
та карт на основі фотограмметричних
матеріалів. Тому в цьому підрозділі
описано основні технологічні процеси
створення ЦММ з використанням
фотограмметричних матеріалів і без
них [4].
користування
моделлю. Цифрова модель місцевості
(ЦММ) є
МПЗ
- це множина, елементами якої є
топографо-геодезична
МПЗ=(Ім,Пм). (V.2.1)
МПЗ
об'єднує
сукупність моделей ситуації та рельєфу,
а
також відповідну проекцію.
Модель
ситуації
(МС) - множина, елементами якої є інформація
про ситуацію
(Іс) та правила
користування цією моделлю
(Пс)
МС=(Іс,Пс). (V.2.2)
Цифрові
моделі місцевості (ЦММ) не тільки
призначені
замінити образно-знакові моделі
місцевості у вигляді різних паперових,
графічних
планів та карт, але й накопичувати
топографо-геодезичну інформацію в
інформаційно-пошукових системах
(ІПС), щоб розв'язувати за їхньою допомогою
цілу низку інженерних задач.
Саме
тому ЦММ є об’єднанням моделі
поверхні Землі
(МПЗ) і моделі
інженерного призначення
(МІП).
Дамо
визначення цій останній моделі. МІП -
множина, елементами якої є інженерна
Багато
тисячоліть графічні плани та карти,
які з’явилися раніше від писемності,
використовувались людьми і задовольняли
їхні потреби. Справді, паперові карти
на обмеженому аркуші паперу несуть
надзвичайно великий обсяг інформації,
завдяки не тільки накресленим графічним
знакам та символам, але й
асоціативно-образному сприйняттю
користувачем знакових комбінацій та
розміщень в умовно-тривимірному просторі
карти.
Виникає
запитання: що трапилось, чому виникла
необхідність замінити графічні плани
та карти цифровими?
Численні
спроби дати повний математичний опис
картографічної інформації, навіть
з урахуванням найостанніших досягнень
в області інформації з її комбінаторними
моделями, виявились невдалими. Одним
із недоліків матема
533об'єднанням
моделі поверхні Землі
(МПЗ) і моделі
інженерного призначення
(МІП).інформація
про
місцевість
у тому чи іншому вигляді (їм) і правила
користування моделлю (Пм),
які дають змогу однозначно й із заданою
точністю отримувати необхідні
характеристики місцевостіМодель
рельєфу
(МР) - множина, елементами якої є інформація
про рельєф
місцевості (Ір) і правила
користування цією моделлю
(Пр), які дають змогу однозначно й із
заданою точністю отримувати необхідні
характеристики рельєфу місцевості.інформація
про місцевість
(Іі) і правила
користування цією інформацією
(Пі), необхідною для безпосереднього
розв’язання цілої низки інженерних
задач та задач народного господарства.
тичного
опису інформації карт є дуже різноманітні
Цей
вид картографічної інформації, пов’язаний
з абстрактно-аналітичним мисленням
людини, і є результатом не тільки
сприйняття комплексних систем
образно-знакової інформації, але й
визначений рівнем підготовки карт у
відповідній галузі наукових знань,
наприклад, геоморфології, геоботаніці
тощо. Математичне формулювання цієї
частини образно-знакової інформації
є найскладнішою проблемою, вирішення
якої хоча й можливе, але, напевно, тільки
в далекому майбутньому.
Одночасно
сучасний розвиток науки й техніки,
пов’язаний із надзвичайно швидким
отриманням та опрацюванням великих
масивів інформації про Землю та простір
навколо неї, настійливо \ спонукає до
пошуку способів подання інформації
про місцевість у формі, зручній для
швидкого опрацювання на сучасних
комп’ютерах. Це стосується, передусім,
карт та планів, що використовуються
в науково-дослідних, проектних, пошукових
роботах, пов’язаних із будівництвом
великих інженерних споруд, транспортних
комунікацій, нафто- та газопроводів,
каналів, ліній електропередач,
автоматизованих інформаційно- пошукових
систем, а також різних засобів управління
й систем навігації.
Головний
недолік використання паперової
картографічної інформації полягає в
тому, що введення такої інформації в
комп’ютер займає вкрай багато часу, у
сотні разів більше ніж опрацювання
цієї інформації машиною, що є серйозним
бар’єром для розвитку автоматизованих
високоефективних технологій. Для
подолання цього бар’єра є лише один
шлях, якому немає альтернативи, а
саме: для успішного застосування
сучасних комп’ютерів та засобів
автоматизації необхідно замінити
образно-знакові карти та плани на
цифрові (ЦКМ, ЦПМ), які задовольняють
вимогу прямого введення й опрацювання
топографічної інформації на сучасних
комп’ютерах. Інформація, яка отримується
в результаті топографічного знімання,
фотограмметричного опрацювання
космічних та аерознімків або береться
з існуючих графічних карт та планів,
перетворюється на цифрову (двійкову)
систему числення й після відповідного
опрацювання на комп’ютері формується
в цифрові карти та плани.
Необхідно
також відзначити, що від вирішення цієї
проблеми залежить також розвиток
засобів автоматизації складання та
оновлення традиційних карт
534просторово-логічні
відношення
(ПЛВ) об’єктів місцевості у вигляді
їхніх сполук: перетинів, сусідства,
входжень, різновидів за рельєфом,
орієнтування за сторонами світу тощо.
Вони не мають на картах безпосереднього
ні умовно-знакового, ні текстового
позначення, але формуються в нашій
свідомості. Існує ще глибша аналітична
інформація карт. Так, за характером
рельєфу, видами рослинності, міграцією
рік визначають відповідні геоморфологічні
структури земної поверхні, прогнозують
місце залягання корисних копалин,
розташування підземних вод тощо.
та
планів, які залишаються необхідними в
багатьох галузях діяльності людини.
До того ж сьогодні у багатьох країнах
світу цифрові карти й плани переважно
створюються за традиційними графічними
оригіналами. Це пов’язано з тим, що
багато країн уже мають високоточні
плани та карти. Це по-перше. По-друге:
оновлення застарілих або створення
нових карт іншого масштабу та призначення
набагато ефективніше здійснювати
автоматизованим способом цифрової
картографічної інформації. Виявилось
найдоцільнішим мати наперед заготовлену
цифрову картографічну інформацію, так
званий банк картографічних даних
(БКД). Маючи такий банк, можна швидко
створити ЦКМ або ЦПМ будь-якого масштабу,
призначення й задовольнити вимоги
якого завгодно споживача.
Останнім
часом загальний банк картографічних
даних (БКД) країни називають
Крім
того, необхідно відзначити, що потреби
в цифрових планах та картах з часом
збільшуються.
Незалежно
від того, якими методами та технічними
засобами створюються карти та плани,
вони повинні задовольняти такі головні
вимоги.
За
змістом, проекцією, системою координат
та висот, точністю та розграфленням
(номенклатурою) цифрові карти та плани
повинні повністю відповідати вимогам,
які ставляться до традиційних
образно-знакових карт та планів.
Адекватне співвідношення властивостей
образно-знакових та цифрових карт
місцевості продиктовано тим, що сучасна
картографічна інформація за усіма
своїми параметрами, крім форми
відображення, задовольняє науково-
технічний прогрес відповідних галузей
науки й техніки і не виникає необхідності
у створенні особливих вимог до ЦКМ та
ЦПМ. Серед основних вимог можна назвати
також суворе дотримання
Ці
дві вимоги до ЦКМ та ЦПМ у деяких країнах
зведені до рівня державного стандарту,
що дає змогу за коротші терміни створити
єдиний національний банк картографічних
даних (БКД), тобто єдину національну
інфраструктуру геопросторових даних
країни. Зауважимо, що чим великомасш-
табнішою буде базова цифрова інформація,
тим ширшими будуть можливості БКД, тим
більше буде користувачів і тим дешевше
будуть коштувати цифрові плани та
карти.
535національною
інфраструктурою геопросторових даних.
2.2. Вимоги до цифрових карт та планів
єдиної
системи класифікації й кодування
інформації
(ЄСККІ) про місцевість усіма виробниками
цифрових планів та карт.
Необхідним
під час створення цифрових планів та
карт є урахування можливостей візуалізації
їхнього змісту в адаптованих (дещо
спрощених) або стандартних умовних
знаках та кольорах традиційних карт з
використанням програмно-технічного
комплексу (кольорових графічних
дисплеїв, графопобу- довувачів та інших
картографічних приладів). Це дасть
змогу автоматизувати картографічну
генералізацію, редагування та контроль
якості цифрових планів та карт.
Опрацювання
топографо-геодезичної інформації
(ТГІ), необхідне для введення в комп’ютер,
починається з кодування ТГІ. Відповідно
до теорії інформації система кодування
повинна бути економною. Економність
визначається кількістю елементарних
сигналів, необхідних для передавання
повідомлення. Чим менше елементарних
сигналів у коді, тим економніше кодування.
Система
кодування елементів знімання повинна
задовольняти такі вимоги:
Однозначність
- кожному елементу знімання відповідає
одне кодове позначення, яке не повинно
бути початком іншого, довшого, кодового
позначення.
Ефективність
- довжина кодового позначення обернено
пропорційна до частоти появи певного
об’єкта знімання.
Логіка
зв’язку з назвою об’єкта - швидше
запам’ятовується код.
Функціонування
інженерно пошукової системи (ІПС) та
банку даних - за будь-якою ознакою
виконується сортування кодів.
Повнота
передавання якісних ознак об’єкта
знімання. Наприклад, використовуючи
буквено-цифровий код.
Контроль
кодування вихідної ТГІ, як візуально,
так і машинним способом, наприклад,
завдяки чергуванню букв та цифр.
Розвиток
та вдосконалення системи - можливість
додавати нові коди, замінюючи попередні.
Окремо
кодуються три масиви інформації:
Загальна
інформація (на весь об’єкт знімання).
Метричний
і синтаксичний масив інформації.
Метрична інформація кодується переважно
числами. Її доповнює синтаксична
інформація (синтаксис - від грецького
- побудова, устрій, зв’язок).
Семантичний
і структурний масив інформації
(семантика - від грецького - означальний,
змістовний). Цей масив інформації
вказує на зміст та структуру об’єктів,
що підлягають зніманню.
536
2.3. Поняття про кодування топографо-геодезичної інформації (тгі)
№ з/п |
Класи елементів знімання |
Умовні позначення класів |
Коди |
і |
Опорні пункти |
Обоснование |
0 |
2 |
Споруди, будівлі, їхні частини |
Дома |
д |
3 |
Скульптури, місця захоронення |
Захоронення |
3 |
4 |
Об’єкти промислового і комунального господарства |
Хозобьектьі |
X |
5 |
Об’єкти зв’язку |
Связь |
с |
6 |
Залізниці і споруди біля них |
Железньїе дороги |
ж |
7 |
Шосейні та ґрунтові дороги |
Шоссейньїе дороги |
ш |
8 |
Гідрографія, гідротехнічні об’єкти |
Г идрография |
г |
9 |
Об’єкти водопостачання |
Водоснабжение |
в |
10 |
Мости та переправи |
Мостьі |
м |
11 |
Рельєф |
Рельєф |
р |
12 |
Рослинність |
Насаждения |
н |
13 |
Ґрунти і мікроформи земної поверхні |
Поверхность |
п |
14 |
Болота та солончаки |
Болота |
Б |
15 |
Межі |
Контурьі границ |
к |
іб |
Огорожі |
Изгороди |
и |
17 |
Водний транспорт |
Водньїй транспорт |
т |
*
Із незначними змінами може бути прийнятий
і в Україні.
Якщо
назви елементів складаються з двох
слів, то застосовують скорочений запис
із початкових букв: державна мережа -
ДМ, робоча мережа - РМ. Об’єкти, що часто
трапляються, повинні мати короткі
кодові позначення порівняно з тими, що
трапляються рідше, наприклад, на
забудованих територіях ліхтарі
трапляються частіше ніж фонтани, тому
їхні коди відповідно Ф і ФНТ.
Матеріал
об’єкта знімання кодується цифрами
1, 2, ... відповідно до їхньої наявної
частоти.
537
Приклади |
Прийняті зображення |
Стилізовані зображення (для комп’ютера) |
|
і |
Комунальний колодязь |
0 |
□ |
2 |
Дерево |
$ * |
Ч 4 |
3 |
Ліхтар |
V |
г |
4 |
Навіс |
г —п і і |
1 \ |
|
» і |
1 1 |
|
5 |
Дім, що будується |
|
ІЖ1 |
У
результаті топографічного знімання
(наприклад, електронного тахеометричного)
у журналах або машинних носіях створюються
три масиви інформації.
Загальна
інформація /0
на всю ділянку знімання:
/0=[4,
/0\
/0\
/0\
с], (V.2.3)
5382.4. Алгоритми опрацювання польової інформації

де
Iq
-
код об’єкта, залежний від інженерно-пошукової
системи (ІПС); /ц - код
масштабу
знімання;
Метрична
інформація для
Jj*=[(ftaUft,DUS,,(«-‘o))11;
(p,aUA,Z)US,(/-t>))12;
(р,о
U
(p,oUA,DUS,(/-‘o))je2;
(P.oUA^US.O-d))^]
де
(З та a
- відповідно
відліки горизонтального та вертикального
кругів тахеометра;
U
-
математичний знак об’єднання.
Семантична
інформація для
де
У
масивах (V.2.4),
(V.2.5) першим
пікетом є станція стояння, а першим
номером з’єднання номер станції
орієнтування тахеометра
Далі
вибирають код масштабу знімання, за
яким буде масштабуватися або вибиратися
цифрова інформація з бібліотеки умовних
знаків. За кодом типу приладу і методу
знімання масив (V.2.3)
перетвориться
за відомими формулами на масив
(V-
2-5)
(V-2.6)
де
5391%
- код методу знімання; /04
та С - відповідно код та стала (константа)
приладу, яким виконувалося знімання.т
станцій:h,D
U S,(i
-
ц))і;;
(p,a
U h,D
U S,
(і
- и))21
; (Р,<тUA,ZHJЯ',(*-;
...;(P,aU/^US,(/-'u))2.;h
-
перевищення; D-
нахилена
віддаль; S
-
горизонтальне прокладення до пікету,
що визначається; і
-
висота приладу; v
-
висота візування під час наведення
труби на ij
-й
пікет; р
-
останній пікет. Нагадаємо:т
станцій:NnK
-
номер ij
-го
пікету, що визначається; Nc
-
номер пікету, з яким треба з’єднати ij
-й
пікет; -
код ij
-го
елемента знімання.Nc.((A))
-
координати і висоти пікетів у відповідній
проекції: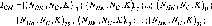
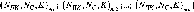

і
- номер станції, а j
-
номер пікета.
Після
обчислення координат та висот пікетів
у комп’ютері виконується
об’єднання
масивів (V.2.6)
і
(V.2.5)
у
масив
((B))
=
ІстС\
А =
[(Nm,
Nc,
К)..
П (Xv,
Ytj,
Щ)].
У
(V.2.7)f|-
математичний
знак перетину.
((B))=[{Nm,Nc,K,X,Y,H)u-,(Nm,Nc,K,X,Y,H)n-...
[Nm,NC,K,X,Y,H)u
-,{NnK,NC,K,X,Y,H)2l;
(Nm,Nc,K,X,Y,H)22-,...;(NnK,Nc,K,X,Y,H)2.;
{NnK,Nc,K,X,Y,H)mp.
Масив
Нагадаємо:
МС - це множина, елементами якої є
інформація про елементи ситуації (Іс)
і про правила її опрацювання (Пс), що
дають змогу з необхідною точністю
відобразити ситуацію місцевості. Отже,
складовими частинами МС є:
Іс
= [X,Y];
Пс
= [Nm
,Мс,КППк],
де
Потім
для кожного контуру разом із його кодом
комп’ютер формує ланку координат
пікетів за відповідними номерами.
Для
прискорення пошуку потрібних пікетів
використані пікети витирають з пам’яті
комп’ютера. Побудова МС продовжується
доти, доки не будуть вибрані усі пікети.
Масивів ситуації
(у.2.1)
(V.2.8)
540((B))
:{Nm,Nc,K,X,Y,H)mX
;(ЛГя/0ЛГс,^Х,Г,Я)т2
;...;((B))
у
вигляді (V.2.8)
є
каталогом координат та висот елементів
знімання з відповідними кодами. Наступним
завданням є формування моделі поверхні
Землі. Модель поверхні Землі (МПЗ), як
відомо, складається з моделі ситуації
(МС) та моделі рельєфу (МР). Ці моделі
формуються окремо з масиву ((B)).
Далі окремо розглянемо суть цих моделей
та їхні алгоритми.
2.5. Алгоритми формування моделі ситуації (мс)
Пк
-
правила декодування коду елемента
знімання і послідовності з’єднання
пікетів.((C))
з
кодами ((К))
буде стільки, скільки є контурів ситуації
на ділянці знімання. Координати пікетів
усередині масивів ((C))
будуть
розташовані у послідовності їхнього
з’єднання:
«0>=Щ,(х,г)и
.(*>>% (X>Y\,
•
K2,(x,Y)2l,(x,Y)21,...,(x,T)ll-
(V.2.9)
XAX-Y\AX-Y\i (X’TV
Для
кінцевого формування моделі ситуації
необхідно додати об’єднані
масиви
з бібліотеки умовних знаків, відповідно
до умови (V.2.10):
Пс
= К[)Пд9
де
У
кінцевому стані модель ситуації має
такий вигляд:
МС
= {[(X, ¥)иПх
ШХ,
Y)n
Я,
],...,[(X,Y)u
,Я,
];
[(X,Y)2ln2],[(X,Y)22n2],...,[(X,Y)li,nl];
[(X,Y)glIJg],(X,Y)g2
,ng],..„[(X,Y)gi,ng]}
де
Я є
Нарешті,
зауважимо, що під час відтворення
моделей ситуації (МС) масив (V.2.11)
поділяють на три підмасиви:
масштабних
умовних знаків (МС)м;
немаспггабних
умовних знаків (МС)Н;
лінійних
умовних знаків (МС)Л.
Така
суть побудови цифрової моделі ситуації
(ЦМС).
Розглядаючи
модель рельєфу як частину тривимірного
простору (
йому
просторі являє собою множину
P(tj,tk)
= yfrXk ~Xjf
+(Yk-Yjf
+(Hk
-Hjf
, (V.2.12)
де
X,
Отже,
тип моделі рельєфу залежить від виду
функції
(V.2.10)
(V.2.11)
541Пд
-
правила декодування множини кодів.ng
-
сукупність
команд з відтворювання певного типу
умовного знака.
2.6. Алгоритм формування моделі рельєфу (мр)
R3),
можна уточнити поняття МР з погляду
топології. Модель рельєфу в метрич-T
= (tx,t2,...,tn)
точок є R
,
що характеризується метрикою P(tj
,tk
)
,
яка обчислюється за формулою
Y,
H -
координати
тих точок, індекси яких збігаються з
індексами координат і задовольняють
умову: F[Xt,Yi,Hi(Xt,
Yt)]
= 0.Ні(Xt,Yt).
Тому моделі рельєфу можуть бути істотно
відмінними (різними). Можуть
використовуватися
поліноми будь-якого степеня,
мультиквадратичні рівняння, сплайни
й інші види функції. Вибір оптимального
виду функції
Вихідними
даними (СФМР) є масиви координат і висот
точок, що розміщені вздовж структурних
та ортографічних ліній, а також усередині
ділянки в довільній послідовності.
Така модель, напевне, має деякі переваги
порівняно з моделями, що використовують
одну функціональну залежність
ядад).
Проте
для повнішого розуміння суті створення
моделі рельєфу розглянемо це питання
на прикладі апроксимації рельєфу
мультиквадратичними функціями.
Вихідне
рівняння поверхні має вигляд:
Ні
=Нсер
+
tcjMxj-Xi)2
+(Yj-Yi)2
+D, (V.
2.13)
j=і
IHJ
де
у
п J
коефіцієнти.
Для знаходження коефіцієнтів
відомими
висотами розв’язується система із п
рівнянь
з п
невідомими
коефіцієнтами:
ЛіС1
+А12С2
+-
+ ЛпСп
-АЯ1
-0
^2[Q
+
А22С2
Н*... 4*
Л-2пСп
АН2 —
0
(V.2.14)
ЛіСі
+ А2С2
+ - +
А,пс„-ан„=
0
Де
An=0;AiJ=
y/(Xj -
Хі
f
+
{Yj
-Yif +D
; Ац
=
AJt
;C,, C2,
..., C„
- невідомі
Хя,-
коефіцієнти;
п
іншими
опорними точками.
542Hi(Xi,Yi)
-
складна
проблема, з якою студенти познайомляться
на старших курсах. Модель рельєфу, що
формується відповідно до (V.2.12),
коли
використовує різні види функцій Н1(Хі?,
Yt),
є структурно-функціональною моделлю
рельєфу (СФМР). Точніше, СФМР є
частково-функціональною моделлю,
розділеною структурними лініями на
земній поверхні.H
= — ; D
- коефіцієнт,
що залежить від типу рельєфу; С .•-
невідоміCj
за
п
опорними точками зХНІ
-
Ht
- — ;
і
-
опорна
точка, для якої будується поверхня за
Розв’язавши
систему (V.2.14)
відносно
невідомих коефіцієнтів, отримаємо
апроксимувальну поверхню для будь-якої
Нк
=Нсер
+ ± CjJ(XJ-Xk)2+(YJ-Yk)2+D. (V.2.15)
м
Але
для визначення положення точок
горизонталі
Створення
ЦММ за картографічними даними (без
фотознімків) можна розділити на чотири
основні етапи:
редакційні
роботи, які виконуються на усіх
технологічних етапах редакторами
центральних організацій;
перетворення
вихідної картографічної інформації
на цифрову форму.
Дуже
важливою роботою ще до оцифрування
вихідного картографічного
матеріалу
(ВКМ) є виготовлення кваліфікованими
спеціалістами оригіналів службової
інформації (ОСІ) та відомостей кодування
(ВК).
Під
час складання ОСІ виділяють такі
сукупності об’єктів карти - сегменти:
сегмент
1
- елементи математичної та планово-висотної
основи;
сегмент
2
- рельєф суші. Зазвичай розрізняють
підсегменти, призначені для оцифрування
горизонталей і форми рельєфу, що не
виражаються у горизонталях;
сегмент
3 - гідрографія і гідротехнічні споруди;
сегмент
4 - населені пункти;
сегмент
5 - промислові, сільськогосподарські
та соціально-культурні об’єкти;
сегмент
6
- дорожня мережа та дорожні споруди;
сегмент
7 - рослинне покриття та ґрунти;
сегмент
8
- межі, огорожі, окремі явища природи.
Відомості
кодування (ВК) призначені для числового
запису кодів семантичної інформації
про об’єкти з метою її оцифрування і
подальшого опрацювання сумісно з
метричною інформацією.
Подальшими,
ще двома технологічними процесами
створення ЦММ є:
опрацювання
даних і формування ЦММ на комп’ютері;
543к
-ї точки, що визначається через координати
та висоти опорних j
-х
точок:Нк
необхідно обчислити координати [Xk,Yk],
де Хк
є Hk
iYke
Нк.
В явному вигляді це зробити неможливо.
Тому задаються мережею точок з відомими
координатами, знаходять висоти вузлових
точок мережі і, інтерполюючи між вузлами,
визначають розташування горизонталей.
Таке спрощення неминуче спричинить
деяку втрату точності та інші недоліки
зображення рельєфу.
складання
оригіналів (паперових) карт за допомогою
автоматичних графопобудовувачів.
Зі
всіх чотирьох етапів створення ЦММ
досі недостатньо висвітлені суть і
значення редакційних робіт, про які
було тільки зазначено, що такі роботи
виконуються редакторами: виконуються
на всіх етапах створення цифрових карт.
Значення цих робіт важко переоцінити.
Редагування повинне забезпечити: високу
якість цифрової карти місцевості (ЦКМ);
економічність технології складання
карти; правильне розуміння і чітке
виконання усіма виконавцями створення
ЦКМ вимог редакційно-технічних вказівок;
єдиний підхід до вибору об’єктів
місцевості і їхня відповідна підготовка
до оцифрування.
У
редакційних вказівках центральних
організацій наводяться:
коротка
характеристика запланованих робіт і
району створення ЦКМ:
характеристика
картографічних і довідкових матеріалів,
рекомендації щодо їхнього використання;
порядок
зведення ЦКМ, що створюються різними
організаціями.
Ці
вказівки є керівним документом для
безпосереднього виконавця, що виконує
роботи із створення цифрових карт. Щоб
задовольнити редакційні вказівки,
підприємство, що безпосередньо виконує
складання цифрових карт, повинно
встановити: сучасність вихідних
картографічних матеріалів; повноту і
детальність відображення елементів
місцевості цими матеріалами; наявність
зведення із сусідніми організаціями
по всіх об’єктах місцевості, що готуються
до оцифрування; наявність даних для
заповнення формуляра ЦКМ; об’єкти
місцевості, характерні і типові для
району.
Зі
всього сказаного зрозуміло, що редактори
ЦКМ повинні мати високу кваліфікаційну
підготовку і від їхньої діяльності
залежить якість і детальність ЦКМ.
Надалі
будуть висвітлені питання створення
ЦММ з використанням фотограмметричних
матеріалів [10].
Для
розуміння всіх процесів створення ЦММ
(ЦКМ) на основі фотознімків необхідно,
насамперед, пояснити відмінність між
звичайним трансформуванням знімків
(за декількома опознаками) і диференційним
перетворенням знімків
(ортофототрансформуванням).
Основою
диференційного методу трансформування
фотознімків є теорія спотворень одного
знімка центральної проекції. Нехай
спотворення фотознімка- оригінала
задане координатами деформованої
сітки. На рис. V.2.1
поверхня
544
2.7. Диференційні перетворення або ортофототрансформування
сфотографованого
об’єкта відображена координатами Z
деякої
сітки точних квадратів (такі сітки
прийнято називати квадратними растрами).
У розумінні карти як ортогональної
проекції (проекції прямими, нормальними
до площини XY
)
квадратні растри - неспотворене
зображення. Інакше кажучи, у площині
XY
ми
маємо сітку точних квадратів, яка і є
ортогональною, неспотво- реною проекцією
сфотографованого об’єкта. Проте на
знімку як центральній проекції під
впливом рельєфу на об’єкті (різних^)
ми отримали спотворені вже не квадрати,
а чотирикутники. Ці спотворення (тобто
координати вершин спотворених квадратів)
можна обчислити за відомими формулами
фотограмметрії, які дають змогу за
координатами точок об’єкта знайти
координати точок знімка, або, навпаки,
за координатами точок знімка знайти
координати точок об’єкта. З цими
формулами студенти познайомляться під
час вивчення фотограмметрії. Поки що
нам достатньо знати, що існують такі
формули і виводяться вони в теорії
спотворення одного знімка.
Центр
проекції
Рис.
V.2.1.
Взаємозв’язок між сіткою квадратів
(АХ
= AY)
у площині XY
і
відповідною створеною сіткою квадратів
на знімку
545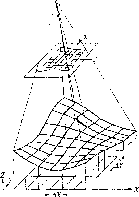
Нас
цікавить тільки результат обчислень,
тобто вигляд цих спотворених уже не
квадратів, а чотирикутників. Цей
результат схематично подано на рис.
V.2.2,
а.
Поряд із цим рисунком подано неспотворену
ортогональну проекцію об’єкта - точні
квадрати (рис. V.2.2,
б).
Як
бачимо з цих рисунків, чотирикутники
(центральна проекція), що були на
знімку-оригіналі, перетворилися на
ортогональні проекції - правильні
квадрати карти. Отже, завдання
трансформування полягає у перенесенні
фотографічного змісту деякого
чотирикутника (наприклад, Г-2’-3’-4’) в
квадрат (1-2-3-4). Звичайно, аналогічно
необхідно перетворити всі чотирикутники,
що створені на знімку-оригіналі.
а б
Рис.
V.2.2.
Сітка
квадратів на знімку (центральна
проекція)
і на карті (ортогональна
проекція)
Це
вже не просте трансформування знімка
на основі п’яти точок із
відомими
координатами. Йдеться про “перетворення”,
а не про “трансфор-
мування”.
Перетворення - поняття вищого порядку.
Під ним розуміють
утворення зображення
(на основі оригіналу) зі зміненими
геометричними
характеристиками.
Таке перетворення може бути виконане
аналітично. Нехай
всі операції в
чотирикутнику мають лінійний напрямок
вздовж сторін сітки,
тоді фотографічні
перетворення чотирикутника можна
записати у вигляді
математичної
залежності, використовуючи білінійну
трансформацію та її вісім
параметрів
x
= aoi
+anX
+ a2XY
+ a3lXY;
1
y~a02 +
a22^
+
Вісім
параметрів
(V.2.16)
546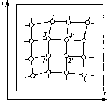

aik
:aik
можна
знайти за відомими координатами х,
у
чотирьох
точок чотирикутника і координатамиX,
Y
п’яти
точок (п’ята -
контрольна)
ортогонального квадрата. Рівнянь
(V.2.16)
при
п’яти точках можна скласти 10.
З їхнього розв’язання знайдемо (із
контролем) 8
параметрів %. Можна аналітично розв’язати
й обернену задачу: за координатами
Проте
нас більше цікавить прилад, що може
розв’язувати саме цю, обернену
задачу.
Інструментальна
(приладна) реалізація перетворення,
відома як білінійна трансформація,
може виконуватись по-різному. Один зі
способів - це оптичне перетворення із
цифровим керуванням, яке використано
у приладах фірми Wild-
Avioplan 0R1 та
Zeiss
Orthocomp Z2. Коротко
викладемо принцип такого перетворення.
Цифрове керування можливе, якщо відомі
координати вершин чотирикутників та
квадратів
а б
Рис.
V.2.3.
Диференційне
перетворення з лінійними елементами
У
площині
два
зміщення центральної точки (М' —>
поворот
на кут а =
547х,
у
точок знімка та параметрів аік
знайти координати X,
Y
точок
карти.xt,
уі
та Xt,
Yt.
Під час перетворення обчислення
координат та інших необхідних даних
виконує процесор приладу-перетво-
рювача. Звернемось до рис. V.2.3,
а,
б.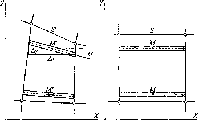
XY
(ортофотознімок)
у напрямку осі Y
рухається
вузька щілина завдовжки S',
що
дорівнює стороні елементарного квадрата
сітки. Під час цього безперервного руху
щілини відповідний лінійний елемент
у площині ху
проектується на площину XY,
причому
керування лінійним елементом відбувається
так:
М)
на Ах
та Ау;arctg{
Ах
/ Ау);
с)
зміна
масштабу
масштабний
,.
. S'
лі
Ах2
+ Ду2
коефіцієнт—
=
S S
Перетворивши
один чотирикутник, аналогічно перетворюють
наступний. Нарешті, відбувається
перетворення усієї смуги.
Рис.
V.2.4.
Цифрове
керування диференційним перетворенням
з
лінійними елементами
548(S'
—»
S);
Взаємодію
перетворення пояснимо на приладі
Wild-Avioplan
0R1, принципова
схема якого подана на рис. V.2.4.
Серцевиною
приладу є процесор (про який уже йшлося),
який, крім деякої додаткової інформації,
з магнітної стрічки одержує координати
Процесор
повертає барабан у напрямку осі
2.4,
знизу
вгору), а саме:
кут
а під час повороту призми Дове;
масштабний
коефіцієнт для зміни фокусної відстані
“гумових лінз” (зум-оптики);
дві
децентрації для переміщення каретки
зі знімком.
У
цей час джерело світла разом з проміжними
лінзами та іншими оптичними елементами
будують проекцію фрагмента знімка на
барабані з фотоплівкою; крізь щілину
освітлюється лише необхідний лінійний
елемент. Так отримують ортофотознімок.
Зауважимо, що описаний прилад, по суті,
є барабанним сканером. Проте
ортофотознімок має значні недоліки,
він не є цифровим зображенням,
оскільки всередині кожного з елементарних
квадратів знімка (сторона квадрата на
знімку, наприклад, 5 або 10 мм) можуть
бути розміщені будинки, дерева, інші
високі предмети, зображення яких на
ортофотознімку буде зміщеним відносно
їхнього справжнього розташування.
Проте диференційне перетворення
фотознімків дає уявлення, як створюються
отрофотоплани та ортофотокарти, а також
про те, як фотограмметрія поступово
розвивалась стосовно знешкодження
деформацій аерознімка, що притаманні
йому як центральній проекції. Подальший
крок цього розвитку - цифрова
фотограмметрія.
Як
уже зазначалося, фотограмметрія, що
починається з фотографування об’єктів
і продовжується фотограмметричним
опрацюванням знімків на оптично-механічних
приладах, називається аналоговою
фотограмметрією.
Фотограмметрія,
яка теж спирається на фотографічні
знімки, але в якій увесь фотограмметричний
процес опрацювання виконується
аналітично із
549х,
у
кутових точок деформованої сітки
квадратів та обчислює відповідні
координати^, Y.у.
Барабан розташований під стаціонарною
(нерухомою) щілиною. Одночасно процесор
зміщує барабан (у напрямку х).
На барабані натягнута світлочутлива
плівка, на якій і формується зображення.
Ціна поділки повороту барабана в
напрямку осі у
мала і становить Юрм . Відповідно
процесор обчислює та встановлює й інші
величини (див. рис.
2.8. Поняття про цифрову фотограмметрію та цифровий фотограмметричний знімок
застосуванням
ЕОД (електронного опрацювання даних),
зокрема ЕОМ (електронно-обчислювальні
машини) та комп’ютери, називається
аналітичною.
Третій
рівень - цифрова фотограмметрія. У
цифровій фотограмметрії силу освітленості
у площині знімка (освітленість виходить
від предмета, знімання якого виконується),
підтримує не фотографія, а електронно-технічні
засоби (ЕТЗ). Тобто у цифровій фотограмметрії
фотознімок замінено цифровим знімком
і все фотограмметричне опрацювання
виконують електронно-технічні засоби
(ЕТЗ), включаючи зорове сприйняття та
розпізнавання зображення, яке також
виконується не оком людини, а реалізується
за допомогою комп’ютера. У цьому
контексті вживають термін “комп’ютерне
бачення” (англ.: computer-
vision -
“розпізнавання образу”, “розпізнавання
знімка”). Отже, цифрова фотограмметрія
- це фотограмметрія комп’ютерного
бачення. Англійською мовою цифрова
фотограмметрія часто називається
“softcopy
photogrammetry”, що
можна перекласти як “не яскрава, сіра
фотограмметрія”. Мається на увазі, що
комп’ютер сприймає градації степеня
почорніння. Деталі зображення, що є на
чорно-білому знімку, змінюються у межах
від білого до чорного кольору, проходячи
через сірі відтінки різного ступеня
почорніння. Найпоширеніші сучасні
електронні приймачі ступеня почорніння
- сенсори (світлочутливі елементи)
розрізняють 256 (=28
бітів комбінацій) градацій (відтінків)
почорніння, який ще називають сірою
шкалою. Чорний колір має код 0, білий -
255. Така кількість градацій почорніння
значно перевищує здатність людського
ока, проте легко зчитується комп’ютером.
Цифрова фотограмметрія може розпочинатись
з фотознімка, отриманого звичайною
фотокамерою. Цифрова фотограмметрія
може сягати точності аналітичної
фотограмметрії, або ще вищої, але час,
витрачений на створення ЦММ або ЦМР,
буде значним, оскільки вже втратився
час на фотографування об’єкта та
створення фотознімка. Тепер цей знімок
необхідно перетворити на цифровий.
Якщо ж потрібна висока точність і від
знімання до виготовлення кінцевої
продукції необхідно витратити якомога
менше часу, тоді цифрову фотограмметрію
треба розпочинати з фотографування
об’єкта цифровою камерою, тобто
безпосередньо отримати цифровий
знімок. Перевага цифрової фотограмметрії
- беззаперечна, і з нею не може
конкурувати гіі аналогова, ні аналітична
фотограмметрія. Надамо визначення
цифрового знімка. Для цифрового знімка
краще підходила б назва “оцифрований
знімок”. Цифровий знімок складається
з двовимірної матриці
Оскільки
кожний елемент матриці відповідає
деякій поверхні (хоча й малій), то
говорять не про точку знімка, а про
елемент зображення. Замість двох слів
“елементи зображення” вживають одне
штучно утворене слово - піксел
550G
з
елементами зображення gtj.
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
І і t |
||
|
|
|
|
|
|
8І] |
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
н |
|
|
|
|
||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
г А і |
||||
|
|
|
|
|
|
|
|
♦ І |
||||
|
|
|
|
|
|
|
|
|||||
|
і -■*" |
-А У- |
j J |
|
||||||||
Рис.
V.2.5.
Визначення
цифрового фотограмметричного знімка
На
рис. V.2.5
прийнято
систему координат знімка.¥7, яка на
5511А
розміру піксела розташована поза
матрицею зображення і повернута на кут
в 100g
(90
°) за годинниковою стрілкою, порівняно
зі звичайною системою координат знімка.
Враховуючи, що розміри пікселів АХ,
А 7, під час зсуву системи координат на
УіАХ
та на ViAY
виявляється,
що добутки АХ
і
та А7 • j
проходять
через центри пікселів. Отже, ці добутки
роблять пікселі ідентифіко
ваними,
тобто вони визначають координати
центральної точки кожного піксела
У
цифровій фотограмметрії традиційне
вимірювання координат знімка замінюють
ідентифікацією окремих пікселів. Цю
ідентифікацію бажано автоматизувати.
Для фотограмметричного опрацювання
цифрового знімка необхідне внутрішнє
орієнтування. На рис. V.2.5
задано
положення головної точки цифрового
знімка
По
суті, диференційне перетворення або
ортофототрансформування зображень
також є скануванням. Проте розміри
квадратів - “елементів зображення”
були значні і виражались в одиницях-десятках
міліметрів. У цифровій фотограмметрії
йдеться про сканування малих елементів
зображень - пікселів, розміри яких
становлять тисячні частки міліметра
(мікрони). Проте принципова суть
сканування така сама, як і продемонстрована
на рис. V.2.4.
Нагадаємо,
що скануванням або дігіталізацією
називають перетворення звичайного
фотознімка на цифрову форму. Щоб не
втратити жодної інформації, яку дає
фотознімок, потрібно інтервал сканування
узгодити з роздільною здатністю знімка.
Роздільну здатність (РЗ) задають у
кількості ліній на один міліметр
(лін/мм), тобто роздільна здатність
означає, скільки штрихів та проміжків
між ними можна розрізнити на відрізку
в 1 мм. Теоретичні розрахунки з урахуванням
тільки дифракції дають навіть 250 лін/мм.
Насправді,
на практиці, враховуючи інші недоліки
лінз - “зернистість” фотознімка,
контрастність - ці можливості значно
менші, приблизно РЗ = 100 лін/мм. Кутова
роздільна здатність (КРЗ) = 35". Фактична
середня монокулярна гострота зору
людини становить ЗО". У геодезії
критичний кут зору звичайно беруть
60". Згідно з теоремою про сканування
можна отримати такий інтервал сканування:
АД,
мм<1/(2-
РЗ).
552gy.Н
у координатній системі Хн
, УН
. Враховуючи малі розміри пікселів,
достатньо знати лише піксел, у якому
розміщена головна точка. Неважко
зрозуміти, що для вибраної системи
координат індекси і
та j
і
є координатами центральних точок
пікселів. За умови квадратних елементів
зображення фокусну віддаль камери /
можна записати в одиницях АХ
або АУ. Задаючи таким, дещо незвичним,
способом масштаб цифрового зображення
(1 /
М =
/ / Н
),
ми зберігаємо справедливість відомих
у фотограмметрії рівнянь зв’язку
координат точок знімка та об’єкта.
2.9. Сканування фотознімків
На
практиці чисельник беруть таким, що
дорівнює 0,7, тобто:
Для
знімка низької контрастності роздільна
здатність становить 50 лін/мм. Тоді
Зі
зменшенням пікселів зростає співвідношення
сигнал-шум, тобто наявні спотворення
і згасання корисного сигналу. Строге
розв’язання цієї неузгодженості
виконане далеко не у всіх сучасних
сканерах. Залежно від розташування
детекторів - світлочутливих сенсорів
розрізняють три різні конструкції
сканерів:
Один
детектор, який проходить над знімком
по рядках (послідовно). Відомі фірми
Hell,
Optronigs, Scitex.
Ряд
детекторів по рядках рухаються над
знімком. В одному ряді розміщені 2048
детекторів. Найменша величина піксела
- 7,5 мм. Точність визначення позиції -
1 мм. За цим принципом працюють Photoscan
PS1, фірми
Zeiss
та
Intergraph.
Рис.
V.2.6.
Принцип
сканування за допомогою
сітки
регулярних хрестів “reseau”
553АД,
мм = 0,7 / (2 • РЗ).АД
=
0,7/(2*50)= 0,007 мм = 7цм. Розмір пікселів менше
за 7 рм у наш час вже досягнуто. Проте
інтервал сканування не можна порівнювати
із сенсорною величиною (світлочутливого)
елемента сканера. Тільки під час
ідеального сканування інтервал
сканування та величина сенсорного
елемента ідентичні. Тільки тоді маємо
ідеальну схему сканування, показану
на рис. V.2.5.
У
деяких сканерах інтервал сканування
дуже малий, а розмір сенсора значно
більший. Тоді буде перекриття пікселів
з певним розтягуванням вихідної
інформації.
Квадратна
матриця детекторів записує частину
знімка. Ці частини знімка можна об’єднати
за допомогою сітки регулярних хрестів.
У західній літературі сітку хрестів
називають “reseau”,
що
в перекладі із французької означає
“сітка” (рис. V.2.6).
За
цим принципом працює сканер RS1
фірми
Rollej
та
сканер VX
фірми
Vexel.
Є
дві технології використання “сітки”.
Перша: на фотознімок зверху накладають
сітку з награвійованими хрестами, а
після цього виконують сканування.
Друга: наявність сітки у фокальній
площині фотокамери або у площинах
знімка.
Цифрові
камери, як і звичайні камери, складаються
із власне камери, об’єктива, затвору,
блока запису та передавання зображення
до комп’ютера. У площині знімка цифрової
камери, якою знімають просторові
тривимірні об’єкти, встановлене плоске
двовимірне поле детекторів, яке, власне,
і є блоком запису зображення. У
завантажених станах ці детектори
подають спочатку аналогові (безперервні)
сигнали, які потім зчитуються комп’ютером
через певний інтервал. Як наслідок,
відбувається аналого-цифрове перетворення
- квантування. Отже, під квантуванням
необхідно розуміти перетворення
аналогових сигналів на цифрові. У
цифрових фотограмметричних камерах
використовуються переважно CCD-сенсори
(Charge
Coupled Device) -
прилад зі світлочутливими елементами
(українською мовою ПЗЗ - прилад із
зарядним зв’язком). Порівняно з оптичними
фотокамерами CCD-сенсорні
цифрові камери є дуже маленькими за
розмірами і порівняно стабільні. їх
називають CCD-
камерами. У сучасному серійному
виробництві є цифрові камери, чутлива
ділянка яких містить 500x500,
рідше
1000x1000
чутливих
елементів зображення (пікселів). Вже в
1991 р. існували камери з 2000x2000
пікселами
та з’являються цифрові камери з
4000x4000
елементами
зображення. А у 2000 р. обсяг інформації
в 1 гігабайт вже не вважається дуже
великим (1 гігабайт = 1024 мегабайт).
Зауважимо, що відеокамери (професійні
чи аматорські) також обладнані
CCD-сенсорами.
Камери підпорядковані прийнятим
стандартам. В Америці стандарт 30 знімків
на секунду; у Європі 25 знімків на секунду.
Професійні сучасні камери здатні робити
60 кадрів на секунду. Проте у деяких
камерах є можливість збільшити частоту
до 200 Гц. Цифрові камери широко
застосовуються не тільки під час
знімання місцевості для складання
карт, але й, наприклад, для визначення
турбулентності атмосфери, аномальної
рефракції, інших явищ. Відомо, наприклад,
що для розміру пікселів 9 мкм та об’єктива
з фокусною відстанню 400 мм та роздільною
здатністю камери близько 0,05 від
5542.10. Цифрові фотокамери
розміру
чутливого елемента можливо досягти
точності вимірювання коливань зображень
предмета 0,01 мм на віддалі 20 м.
Знімки,
отримані цифровою камерою, також
трансформуються. Проте зміст такого
трансформування дещо інший. Одержання
цифрового ортофо- тозображення
(трансформованого) полягає в тому, щоб
із цифрового знімка, заданого в системі
координат цифрової фотограмметричної
камери, перейти до деякої топоцентричної
системи координат матриці зображення
в площині XY,
причому
тут йдеться не про систему координат
об’єкта, а про систему координат у
площині XY
(координат
матриці зображень).
Цифрові
(трансформовані) ортофотознімки мають
переваги порівняно зі звичайними
знімками:
істотно
вища геометрична точність;
такий
знімок можна коригувати;
покращується
можливість монтажу декількох цифрових
трансформованих зображень, які
можна ідеально підібрати за рівнем
сірого тону в місцях з’єднань;
підсилення
контурів за допомогою відповідної
фільтрації;
цифровий
знімок можна розглядати як власну
інформаційну систему в геоінформаційній
системі; головне: можливість комп’ютерного
опрацювання цифрових ортофотозображень.
Цифровими
фотограмметричними станціями називають
інтегровані або модульні комплекси
приладів, призначених для розв’язання
фотограмметричних задач на базі
цифрових знімків. Загалом програмне
забезпечення для розв’язання
фотограмметричних задач можна встановити
на кожному комп’ютері. Проте периферійне
обладнання повинно бути доволі
різнобічним та нараховувати повний
набір основних технічних засобів, а
саме:
пристрій
для одержання зображень, який утворює
цифрові знімки від сканера, CCD-камери
або інші засоби;
графічний
екран (монітор) з 1024x768
пікселами
і більше;
диск
(зовнішня пам’ять) для збереження
зображень (наприклад, 10000x10000
пікселів);
глибини
зображення 8
байтів і більше (8
байтів для кожного основного кольору
- червоного, зеленого, синього);
швидкодіючий
процесор (12,5 мільйона операцій на
секунду (MIPS)
і
більше);
•
оперативна
пам’ять (1 Гбайт і більше).
555
2.11. Цифрові фотограмметричні станції
Таким
вимогам відповідають потужні PC
(Personal Computer) і
цифрові станції (Workstations).
Для
різногалузевого застосування цифрового
опрацювання зображень створено
системи електронного опрацювання даних
(ЕОД). Для геоінформаційних систем (ГІС)
також розроблено системи ЕОД. Проте
топографо-картографічні задачі
розв’язують цифрові фотограмметричні
станції. Виробники таких станцій -
фірми, що є не тільки за кордоном, але
й в Україні.
На
фотограмметричних станціях ведеться
стереоспостереження цифрових зображень.
Сьогодні існують чотири різні методи
отримання стереозображень:
стереоскопами
(лінзовими або дзеркальними);
кольоровими
окулярами (метод анагліфів);
окулярами
із затвором - рідким кристалом;
поляризаційними
окулярами; зауважимо, що нині
Нижче
подамо деякі технічні характеристики
цифрових фотограмметричних станцій
деяких відомих фірм.
Intergraph
(Huntsville, СІЛА)
пропонує систему Imagestation:
екран
1664x1248
пікселів;
глибина зображення 24 бітів. Стереоскопія:
за допомогою затворів - рідких кристалів
та інфрачервоного управління з частотою
120
або 60 Гц на один знімок. Комп’ютер: 14
MIPS
-
швидкодія процесора, 32-256 Мбайт оперативна
пам’ять; 1 Гбайт дискова пам’ять.
Leica
(Heerbrugg, Швейцарія)
пропонує DVP
(Digital Video Plotter). Програмне
забезпечення Laval
University (Quebec, Канада).
Екран: 800x600
або
1024x768
пікселів;
глибина зображення 8
бітів. Стереоскопія: половини зображень
з двох знімків зі стереоскопом. Комп’ютер
будь-який PC.
Zeiss
(Німеччина)
недавно розробила цифрову фотограмметричну
робочу станцію Phodis
ST (рис.
V.2.7).
Рис.
V.2.7.
Цифровий
стереоплотер Phodis
ST фірми
Zeiss
556
поляризаційна
техніка
також працює на основі оптичних
властивостей.
Основні
характеристики стереоплотера Phodis
ST: одержання
інформації зі сканованого Photo-Scan
PS1. Стереоскопія:
розділення зображень з використанням
затвора - рідкого кристала; “мишка” з
нерухомою позиційною маркою та рухомою
картиною (moving-image-fixed-cursor).
Комп’ютер:
Silicon
Graphic Workstation (обчислювач
SG1
з
64 Мбайт оперативної пам’яті, 2 Гбайт
дискової пам’яті та 85 MIPS).
За
допомогою програмного пакета Toposurf
можна
автоматично будувати цифрові моделі
поверхні, а за допомогою Phodis
OP -
цифрові ортофото.
Рис.
V.2
8.
Аналітична фотограмметрична
станція
“Стереоанаграф”
Науково-виробниче
підприємство “Геосистема” (Вінниця,
Україна) пропонує цифрову
фотограмметричну станцію “Дельта”
та аналітичну фотограмметричну
станцію “Стереоанаграф”. ЦФС “Дельта”
забезпечує повну технологічну ланку
фотограмметричного опрацювання:
тріангуляцію, орієнтування, векторизацію
(дігіталізацію) у моно і стереорежимі;
створення, оформлення та роздрук
електронних карт і мозаїчних ортофотокарт;
інтерполяцію та побудову горизонталей.
Працює із чорно-білими та кольоровими
растрами розміром до 4 Гб. “Дельта”
ґрунтується на стандартному Intel
сумісному
комп’ютері із системою Windows
98/МЕ/2000/ХР.
Аналітична фотограмметрична станція
“Стереоанаграф” є високоточним
стереоплотером, що використовується
для фототріангуляції і стереоскладання,
створення та редагування багатошарових
цифрових карт, працює з аерознімками
та космічними знімками, чорно-білими
та кольоровими до 300x300
мм.
Програма для створення та оновлення
557
електронних
карт “Digitals”
дає
змогу складати, редагувати і розмножувати
топокарти відповідно до вимог до умовних
знаків; створювати спеціальні та
кадастрові плани і топооснови для ГІС.
Керівний комп’ютер Intel/Windows.
Роздільна
здатність - 1 мм. Приладна середня
квадратична похибка - 3 мм. Маса АФС -
250 кг. Габаритні розміри у мм - 1600x1400x1000
(див.
рис. V.2.8).
“Геосистема”
також пропонує три види сканерів:
кольоровий
сканер “Дельта” для знімків розміром
470x320
мм
та рулонних фільмів завширшки до 320
мм, мінімальний розмір піксела - 8
рм, роздільна здатність - 1 рм, ПЗС-лінійка
- кольорова SONI
3x5300x8, освітлювач
- потужний світлодіод. Сканування
чорно-білого знімка розміром 230x230
мм
із роздільною здатністю 16 рм і 256
градаціями відбувається за 6
хвилин;
планшетний
сканер “Planscan”
для
сканування чорно-білих і кольорових
картографічних матеріалів розміром
до 800x600
мм
на носії будь- якої товщини та твердості.
Сканер має 600 dpi
(розмір
піксела 40 рм);
проекційний
картографічний сканер “ProScan”
(максимальний
розмір носія - 800x600
мм,
спеціально призначений для планшетів
на дуже деформованому носії). Має 400
dpi
(розмір
піксела - 60рм). Вихідні дані сканера
у форматі True
Color (24
бітів) або з 256 градаціями сірої шкали
(8
бітів). Час сканування відповідно 8
та 5 хвилин.
558
СПИСОК
ЛІТЕРАТУРИ
Баканова
Б.Б. Крупномасштабньїе топографические
сьемки. - М.: Недра, 1983. - 181 с.
Генике
А.А., Побединский Г.Г. Глобальньїе
спутниковьіе системьі определения
местоположения и их применение в
геодезии. - М.: Картгеоцентр, 2004. - 350 с.
Геодезія.
Ч. І / Під ред. д-ра техн. наук, проф. С.Г.
Могильного і д-ра техн. наук, проф. С.П.
Войтенко). - Чернігів, 2002. - 407 с.
Геодезия.
Топографические сьемки / Под ред. В.П.
Савиньїх и В.Р. Ященко. - М.: Недра, 1991. -
315 с.
Інструкція
з топографічного знімання у масштабах
1:5000, 1:2000, 1:1000 та 1:500.-К., 1999.-155 с.
Инструкция
по нивелированию I,
II,
III и IV классов. - М.: Недра, 1990.-167 с.
Инженерная
геодезия / Под ред. П.С. Закатова. - М.:
Недра, 1976. -
582
с.
Клюшин
Б.Б., Киселев М.Н., Михелев Д.ИІ. и др.
Инженерная геодезия: Учебник для вузов
/ Под ред. Д.Ш. Михелева. - М.: Вьісшая
школа, 2000.-464 с.
Костецька
Я.М. Геодезичні прилади. Ч. II. Електронні
геодезичні прилади. - Львів, 2000. - 320 с.
Краус
К. Фотограмметрія / Пер. з нім. 3. Кузик.
- Львівське астрономо-геодезичне
товариство, 2001. - 428 с.
Левчук
Г.П., Новак В.Е., Конусов В.Г. Прикладная
геодезия. - М.: Недра, 1981.
Мориц
Г. Фигура Земли. Теоретическая геодезия
и внутреннее строение Земли / Пер. с
англ.; Под ред. академика АН Украйни
Я.С. Яцкива. - К., 1944. - 239 с.
Моторний
А.Д. Новьіе системи звеньев полигонометрии.
- Львов: Издательство Львовского
государственного университета, 1955. -
36 с.
Основнне
положення по вибору масштаба и висоти
сечения рельефа топографических сьемок
населенннх мест / ГУГК СССР. - М., 1980.
Островский
А.Л., Мороз А.И. Теория и практика
флуктуационного метода определения
рефракции // Известия вузов. Геодезия
и азрофотосьемка. - 2000. - № 3. - С. 11-29.
559
Островський
А., Островська О., Новосад В., Кіселик
О. Порівняльні дослідження точності
автоматизованого визначення та
врахування аномальної вертикальної
рефракції // Геодинаміка. - Львів, 2004. -
№ 1 (4). - С. 17-24.
Островский
А.Л., Маслич Д.М., Гребенюк В.Г. Геодезическое
прибо- роведение. - Львов: Издательство
при ЛГУ издательского обьединения
“Вища школа”, 1983. - 206 с.
Практикум
по курсу прикладной геодезии / Под ред.
Н.Н. Лебедева. - М.і Недра, 1980.
Технические
средства автоматизации полевьіх
процессов наземньїх крупномасштабньїх
сьемок. - ЦНИИГАиК. Обзорная информация.
- М., 1983. - Вьіп. 75.-42 с.
Топографо-геодезична
та картографічна діяльність (законодавчі
та нормативні акти). Ч. І. Головне
управління геодезії, картографії та
кадастру. - К., 2000.-405 с.
Тревого
И.С., Шевчук П.М. Городская полигонометрия.
- М.: Недра, 1986.- 197 с.
Третяк
К.Р., Шушкова Т.М. До питання тривалості
GPS-вимірів
при побудові державних мереж 1-го та
2-го класів // Геодезія, картографія і
аерофотознімання. Нац. ун-т “Львівська
політехніка”. - 2001. - № 61. - С. 124— 132.
Третяк
К.Р., Романишин І.Б. До питання попереднього
розрахунку точності навігаційних
GPS-вимірів
// Сучасні досягнення геодезичної науки
та виробництва. - Львів, 2004. -С. 149-157.
Третяк
К.Р., Глотов В.М. Оцінка впливу додаткового
відбиття GPS-
сигналів
на точність визначення місцеположення
// Геодезія, картографія і
аерофотознімання: Міжвідомчий
науково-технічний збірник. Нац. ун-т
“Львівська
політехніка”. - 2004. - № 65. - С. 72-76.
Третяк
К.Р., Романишин І.Б. Методика оптимального
проектування мережі перманентних
станцій України // Вісник геодезії та
картографії. - К., 2004. - № 4(35). - С. 149-157.
Третяк
К.Р., Романишин І.Б. Оптимальна модель
мережі перманентних станцій України
// Сучасні досягнення геодезичної науки
та виробництва. - Львів, 2005. - С. 169-180.
Учет
атмосферних влияний на астрономо-геодезические
измерения // А.Л. Островский, Б.М. Джуман,
Ф.Д. Заблоцкий, Н.И. Кравцов. - М.: Недра,
1990.-235 с.
560
Чеботарев
А.С. Геодезия. Ч. II. - М.: Издательство
геодезической и картографической
литературьі, 1949. - 623 с.
Шевченко
Т.Г., Мороз О.І., Тревого І.С. Геодезичні
прилади. - Львів: Видавництво Нац. ун-ту
“Львівська політехніка”. 2006. - 459 с.
Osada
Е.
Geodezja.
-
Wroclaw:
Oficiyna Wydawnicza Politechniki Wroclawskej. - 2001. - 223 c.
Galda
M., Kujawski E., Przewlocki S. Geodezja I miernictwo budowlane. -
Warszawa-Wroclaw, 2000.-402 c.
561
НАВЧАЛЬНЕ
ВИДАННЯ
Островський
Аполлінарій Львович
Мороз
Олександр Іванович
Тарнавський
Володимир Левкович
ГЕОДЕЗІЯ
Частина
друга
Редактор
Оксана
Чернигевич
Коректор
Наталія
Колтун
Технічний
редактор
Лілія
Саламін
Комп
’ютерне верстання
Наталії
Максимюк
Художник-дизайнер
Уляна
Келеман
Здано
у видавництво 27.08.2008. Підписано до друку
28.12.2008.
Формат 70x100/16. Папір офсетний.
Друк офсетний.
Умови,
друк. арк. 45,5. Обл.-вид. арк. 32,70.
Наклад
1000 прим. Зам. 80679.
Видавництво
Національного університету “Львівська
політехніка”
Реєстраційне
свідоцтво серіїДКN9
751
від 27.12.2001 р.
Поліграфічний
центр Видавництва
Національного
університету “Львівська політехніка”
вул.
Ф. Колесси, 2, Львів, 79000