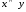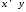Лекция 1Алгебра высказываний и алгебра предикатов Основные понятия математической логики

Информатика изучает знаковые (алфавитные) системы. Алгебра – наиболее адекватный математический аппарат описания действий в них, поэтому алгебраический аппарат наилучшим образом подходит для описания информационных систем общей природы, отвлеченно от их предметной направленности. Информационные процессы хорошо формализуются с помощью различных алгебраических структур.

Напомним, что алгеброй A называется некоторая совокупность определенных элементов X, с заданными над ними определенными операциями f (часто определяемые по сходству с операциями сложения и умножения чисел), которые удовлетворяют определенным свойствам – аксиомам алгебры А.

Операция f называется n-местной, если она связывает n операндов (объектов – участников этой операции).

Совокупность операций алгебры A называется ее сигнатурой, а совокупность элементов алгебры – носителем алгебры.

Определение 1.1. Утверждение (высказывательная форма) – основная единица, неделимая с точки зрения отражения смысла информации (семантики).

Определение 1.2. Высказывание – некоторое повествовательное утверждение, про которое можно однозначно сказать («сразу посмотрев на него»), истинно оно или ложно. Эти два значения всевозможных высказываний обозначаются «истина» и «ложь», «true» и «fаlse» или «1» и «0».

Определение 1.3. Переменная, значениями которой могут быть лишь значения «1» или «0», называется логической переменной или булевой переменной.

Пример 1.1. Рассмотрим словосочетания.

1. Москва – столица США.

2. Житель города Москва.

3. 5 – 7 + 8.

4. 5 – 9 + 28 = 4.

5. В пятую неделю зимы было очень холодно.

6. В Антарктиде живут тигры.

Высказывание должно быть однозначно истинным или однозначно ложным, поэтому высказываниями являются только утверждения 1), 4), 6).

Пример 1.2. Не является высказыванием «парадокс лжеца» (сформулировал Эвбулид, учитель Демосфена, около 350 лет до н.э.): «То, что я сейчас утверждаю, – ложно». Так как если оно истинно – то оно ложно, а если допустить, что оно ложно, то оно истинно. Это неопределенная высказывательная форма. Аналогичный пример принадлежит известному математику, логику Гёделю (1931 г.): «То, что утверждается в этом предложении, не может быть доказано». Если его можно опровергнуть, то его нельзя доказать, а если его можно опровергнуть, то его можно доказать. Предложения такого рода не могут быть доказаны или опровергнуты в пределах того языка (той теории, алгебры), с помощью которой они сформулированы. Известны многие подобные парадоксы.

Рассматривая высказывания, мы не обращаем внимания на их внутреннюю структуру и можем разлагать их на структурные части, равно как и объединять их.

Пример 1.3. Построим из ниже заданных простых высказываний составные, сложные высказывания:

1. Зима – холодное время года.

2. Пальто – теплая одежда.

3. Камин – источник тепла.

Сложные высказывания: «Зима – холодное время года и зимой носят пальто», или «Некоторые ходят в пальто, поэтому на улице зима».

Другим важным понятием математической логики является понятие предиката.

Определение 1.4. Предикат – высказывательная форма с логическими переменными (множество значений этих переменных вполне определено), имеющая смысл при любых допустимых значениях этих переменных.

Количество переменных в записи предиката называется его местностью.

Простые высказывания или предикаты не зависят от других высказываний или предикатов («не разбиваемы на более простые»), а сложные – зависит хотя бы от двух простых.

Пример 1.4. Выражение «х = у» – предикат, «х > 5» – предикат, а «7 > 5» – высказывание.

Утверждение «Хорошо» не является высказыванием, утверждение «Оценка студента Иванова по информатике – хорошо» – простое высказывание, утверждение «Вчера была ясная погода, я был вчера на рыбалке» – сложное высказывание, состоящее из двух простых.

Определение 1.5. Логической (булевой) функцией f(х) называется некоторая функциональная зависимость, в которой аргумент х – логическая переменная с заданным множеством изменений аргумента, а значения функции f(x) берутся из двухэлементного множества R(f) = {1,0}.

Пример 1.5. Заданы предикаты вида р = «число х делится нацело на 3» и q = «у – день недели». Найдем множество истинности предикатов р и q, если х{1, 4, 6, 16, 20, 24},

у{первый, вторник, среда, 1999, зима, выходной, праздник, воскресенье}.

Получаем, что D(p)=6, 24; D(q)=вторник, среда, воскресенье.

Из курса дискретной математики известны основные логические операции: отрицание, конъюнкция, дизъюнкция.

Напомним их определения.

Определение 1.6. Отрицанием (инверсией) высказывания х является новое высказывание, которое является истинным, если высказывание х ложно, и ложным, если х – истинно.

Обозначается отрицание ¬х или .

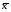Определение 1.7. Конъюнкция (логическое умножение) двух высказываний х и у – это новое высказывание, которое считается истинным только в том случае, если высказывания х и у истинны одновременно.

Обозначения конъюнкции: х  у, х & у, х  у.

Определение 1.8. Дизъюнкция (логическое сложение) двух высказываний х и у – это новое высказывание, которое считается ложным только в том случае, если высказывания х и у ложны одновременно.

Обозначения дизъюнкции: х  у.

Определение 1.9. Множество логических переменных х, уХ с определенными над ним операциями отрицания, дизъюнкции и конъюнкции называется алгеброй предикатов (высказываний), если эти операции удовлетворяют следующим аксиомам:

1. аксиома двойного отрицания: ¬(¬х) ₌ х;

2. аксиомы переместительности операндов (относительно операций дизъюнкции и конъюнкции): ;

3. аксиомы переместительности операций дизъюнкции и конъюнкции (относительно операндов): ;

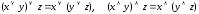4. аксиомы одинаковых операндов: ;

5. аксиомы поглощения (множителем – множителя-суммы или слагаемым – слагаемого-произведения): ;

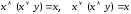6. аксиомы распределения операции (дизъюнкции относительно конъюнкции и наоборот): ;

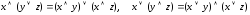7. аксиомы де Моргана (перенесения бинарной операции на операнды):

¬(х  у) = ¬х  ¬у, ¬(х  у) = ¬х ¬у;

8. аксиомы нейтральности (взаимноинверсных множителей или слагаемых): х  (у  ¬у) = х, х  (у  ¬у) = х;

9. аксиома существования единицы (истина, true, 1) и нуля (ложь, false, 0): ¬0=1, ¬1=0, ¬х  х=1, ¬х  х=0.

Из этих аксиом следует ряд полезных соотношений, например,

Три базовые операции алгебры предикатов определяются таблицей их значений, так как в алгебре предикатов из-за дискретности значений логических функций часто используется табличная форма задания функции. Булеву функцию n переменных можно полностью определить таблицей из 2ⁿ строк.

Итак, эти операции определяются совмещенной таблицей значений вида:

х	у	¬х
0	0	1	0	0
0	1	1	0	1
1	0	0	0	1
1	1	0	1	1

Такая таблица всех значений некоторой логической функции называется таблицей истинности этой функции.

Кроме указанных трех базовых операций можно с их помощью ввести следующие важные операции алгебры предикатов (можно их назвать небазовыми операциями):

1. импликация: х → у ≡ ¬х  у;

2. эквиваленция: х ↔ у ≡ х  у  ¬х  ¬у.

Определение 1.10. Импликация (следование) двух высказываний х и у – это новое высказывание, которое считается ложным только в том случае, если высказывания х – истинно, а высказывание у – ложно. Для остальных случаев новое высказывание – истинно.

Определение 1.11. Эквиваленция (равносильность) двух высказываний х и у – это новое высказывание, которое считается истинным только в том случае, если высказывания х и у имеют одинаковые истинностные значения.

Операции импликации и эквиваленции, хотя и являются часто используемыми, но не базовые, ибо они определяемы через три базовые операции. Нетрудно определить их таблицы истинности (проделайте это самостоятельно с помощью правых частей приведенных равенств).

При выполнении логических операций в компьютере они сводятся к поразрядному сравнению битовых комбинаций. Эти операции достаточно быстро (аппаратно) выполняемы, так как сводятся к выяснению совпадения или несовпадения битов.

В логических формулах определено старшинство операций, например: скобки, отрицание, конъюнкция, дизъюнкция (остальные, небазовые операции пока не учитываем).

Определение 1.12. Всегда истинные формулы называют тавтологиями.

Определение 1.13. Две формулы алгебры логики А и В называются равносильными, если они принимают одинаковые логические значения на любом наборе значений входящих в них высказываний.

Таблица 1.1. Основные законы алгебры логики

Переместительный закон	x  y = y  x	x Ú y = y Ú x
Сочетательный закон	(x  y)  z = x  (y  z)	(x Ú y) Ú z = x Ú (y Ú z)
Распределительный закон	x Ú (y  z) = (x Ú y)  (x Ú z) (x  y) Ú z = (x Ú z)  (y Ú z)	x  (y Ú z) = (x  y) Ú (x  z) (x Ú y)  z = (x  z) Ú (y  z)
Законы де Моргана	¬(x  y) = ¬x Ú¬y	¬(x Úy) = ¬x  ¬y
Закон идемпотентности	x  x = x	x Ú x = x
Закон поглощения	x  (x Ú у) = x	x Ú x  у = x
Закон склеивания	(x  у) Ú (¬x  у) = у	(x Ú у)  (¬x Ú у) = у
Операция переменной с ее инверсией	х  ¬х = 0	х Ú ¬х = 1
Операция с константой	х  1 = х х  0 = 0	х Ú 1 = 1 х Ú 0 = х
Закон двойного отрицания ¬(¬x) = x

Используя равносильности, можно часть формулы алгебры логики или всю формулу заменить равносильной ей формулой. Такие преобразования называются равносильными. Равносильные преобразования формул применяются для доказательства равносильности формул, для приведения формул к заданному виду, для упрощения формул.