Добавил:

AD Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тверской Государственный Университет

Предмет:

Математический анализ

Файл:

матанализ 1 курс 2 семестр Малышкин / Малышкин ответы на вопросы .docx

Скачиваний:

Добавлен:

19.06.2022

Размер:

35.04 Mб

Скачать

☆

<<< < Предыдущая 12 / 22

Предельный переход под знаком интеграла.

Обращаемся теперь к рассмотрению интеграла , зависящего от параметра у, ограничиваясь вначале случаем конечного промежутка и функции, интегрируемой в собственном смысле.

Предполагая, что область изменения параметра имеет точку сгущения поставим вопрос о пределе функции при

Теорема 1. Если функция при постоянном у интегрируема по и при стремится к предельной функции равномерно относительно х, то имеет место равенство

Доказательство. Интегрируемость предельной функции уже известна Задавшись произвольным числом

найдем такое число чтобы имело место. Тогда будем иметь

что и доказывает формулу.

Формула может быть переписана в виде:

При наличии ее говорят, что предельный переход по параметру допустим под знаком интеграла.

Предполагая, что все имеем:

Следствие. Если функция при постоянном у непрерывна по и при возрастании у стремится к непрерывной же предельной функции, монотонно возрастая, то справедлива формула

В предположении, что область сама представляет собой конечный промежуток рассмотрим в заключение вопрос о непрерывности функции.

Теорема 2. Если функция определена и непрерывна, как функция от двух переменных, в прямоугольнике то интеграл будет непрерывной функцией от параметра у в промежутке

Доказательство. Ввиду равномерной непрерывности функции по произвольному найдется такое что из неравенств

следует неравенство

Положим, в частности, тогда при каково бы ни было х, будем иметь

Таким образом, функция при стремлении у к любому частному значению стремится к равномерно

относительно В таком случае, по теореме 1,

или

что и доказывает наше утверждение.

Так, например, не вычисляя интегралов

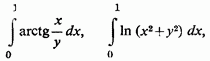
сразу видим, что они представляют собой непрерывные функции от параметра у для любых положительных его значений.

2.10

Дифференцируемость и интегрируемость по параметру несобственного интеграла.

Утверждение 6. Если:

a) функции непрерывны на множестве

b) интеграл сходится равномерно на множестве, а

c) интеграл сходится хотя бы при одном значении

то он сходится и даже равномерно на всем множестве К; при этом функция оказывается дифференцируемой и справедливо равенство

В силу условия а) при любом функция

определена и дифференцируема на промежутке и по правилу Лейбница

В силу условия семейство зависящих от параметра функций сходится равномерно на к функции при

Отсюда следует что само семейство функций сходится на равномерно к предельной функции, когда при этом функция оказывается дифференцируемой на промежутке и имеет место равенство. Но это как раз то, что и требовалось доказать.

Пример 12. При фиксированном значении интеграл

сходится равномерно относительно параметра любом промежутке вида это следует из оценки справедливой при всех достаточно больших значениях

Значит, по утверждению функция

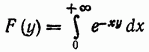
бесконечно дифференцируема при и

поэтому следовательно, можно заключить, Что

В частности получаем

Пример 13. Вычислим интеграл Дирихле

Для этого вернемся к интегралу (9) и заметим, что

поскольку интеграл (11) сходится равномерно на любом множестве вида

Интеграл (11) легко вычисляется через первообразную подынтегральной функции и получается, что

как видно из соотношения (9), поэтому из (12) следует, что из (10) и (12) получается, что

2.11

Несобственные двойные интегралы.

Рассмотрим неограниченную замкнутую область . Неограниченность означает, что вне любого кругаКр радиуса с центром в начале координат имеются точки области. Примерами таких областей могут служить полоса , или квадрант .

Определение 1. Говорят, что последовательность областей исчерпывает неограниченную область , если: 1) – ограничены и замкнуты; 2) ; 3) часть области , содержащаяся в кругеКр произвольного радиуса, целиком лежит в некоторой . Из этих условий вытекает, что .

Примером такой последовательности может служить . Пусть теперь в неограниченной замкнутой области задана непрерывная функция . Тогда она непрерывна и во всякой – ограниченной замкнутой части области и, следовательно, существует двойной интеграл

Определение 2. Несобственным двойным интегралом от функции по неограниченной области называют предел

где – исчерпывающая последовательность. Если этот предел существует, конечен и не зависит от выбора , то несобственный интеграл называют сходящимся, в противном случае – расходящимся.

Пусть область – правильная, т.е.

причём и могут равняться , а и – . Примем без доказательства теорему.

Теорема. Если функция непрерывна и неотрицательна в правильной неограниченной области , то

причём двойной интеграл сходится, если сходится повторный.

Используем понятие несобственного двойного интеграла для вычисления т.н. интеграла Пуассона

Прежде всего, отметим, что этот несобственный интеграл 1^го рода сходится по первому признаку сравнения. Действительно, для имеем:

Интеграл же – сходится.

Рассмотрим неотрицательную функцию и проинтегрируем её по 1^му квадранту:

Здесь последний интеграл является повторным лишь формально, на самом же деле – это произведение двух одинаковых интегралов.

Итак, повторный интеграл сходится, следовательно, сходится и двойной. Значит, при вычислении несобственного двойного интеграла по определению мы можем выбрать удобную для нас исчерпывающую последовательность областей. Пусть, например, – часть круга , расположенная в первой четверти. Тогда

и получим по определению

Отсюда получаем значение интеграла Пуассона

Примеры

Во внутреннем интеграле сделаем замену , тогда и . Получим для нашего интеграла

3.1

Определение определенного интеграла (интеграла Римана).

Грубо говоря, интеграл Римана-это предел римановых сумм функции по мере того, как разбиения становятся более тонкими. Если предел существует, то функция называется интегрируемой (или, более конкретно, интегрируемой по Риману).

Теорема об условиях существования интеграла.

Согласно теореме существования определенного интеграла, этот интеграл существует, если выполненные условия: 1) отрезок интегрирования [a, b] конечен; 2) подынтегральная функция f (x) непрерывная или ограничена и имеет конечное число точек разрыва.

3.2

Определение двойного интеграла.

Пусть в замкнутой области , принадлежащей плоскости , задана непрерывная функция . Разобьем эту область на элементарных областей , площади которых будем обозначать как , а наибольшее расстояние между точками соответствующей области – через (рис. 1).

В каждой элементарной области выберем произвольную точку . Значение функции в этой точке умножим на площадь соответствующей элементарной области и все такие произведения просуммируем:

Полученная сумма называется интегральной суммой функции в области .

Найдем предел указанной интегральной суммы при таким образом, чтобы . Если такой предел существует и не зависит ни от способа разбиения области на элементарные области, ни от способа выбора в них точек , то он называется двойным интегралом от функции по области и обозначается . Итак, двойной интеграл определяется равенством. Область называется областью интегрирования, и – переменные интегрирования, функция – подынтегральной функцией, которая является интегрируемой в области ; – элементом площади.

3.3

Функциональный определитель (Якобиан).

Якобиан (определитель Якоби, функциональный определитель) — определённое обобщение производной функции одной переменной на случай отображений из евклидова пространства в себя.

Преобразование плоских областей.

Предположим, что нам даны две плоскости, отнесенные одна — к прямоугольным осям х и у, а другая — к таким же осям Рассмотрим в этих плоскостях две замкнутые области: область (D) на плоскости и область (Д) на плоскости Каждая из этих областей может быть и неограниченной, в частности может охватывать и всю плоскость. Контур или границу области (если область не охватывает всей плоскости) мы будем предполагать простой кусочно-гладкой кривой; обозначим его символом для области (D) и символом для области (Д) (рис. 61).

Рис. 61.

Допустим, что в области (Д) дана система непрерывных функций:

которая каждой точке области (Д) относит одну определенную точку области (D), причем ни одна точка из (D) не будет пропущена, так что каждая такая точка отнесена хоть одной точке из (Д). Если различным точкам отвечают различные же точки (что мы впредь и будем предполагать), так что каждая точка отнесена лишь одной точке то формулы (1) однозначно разрешимы относительно Переменные в свою очередь являются однозначными функциями от х, у в области

Таким образом, между областями (D) и (Д) устанавливается взаимно однозначное или одно-однозначное соответствие. Говорят также, что формулы (1) осуществляют преобразование области (Д) в область (D), а формулы (1а) дают обратное преобразование области (D) в область (Д).

Если названные области заполняют соответствующие плоскости, то мы имеем дело с преобразованием одной плоскости в другую. Наконец, если обе плоскости совпадают, т. е. если точки рассматриваются как точки одной и той же плоскости, то налицо преобразование плоскости в самое себя.

Мы будем предполагать, далее, что функции (1) и (1а) не только непрерывны, но и имеют непрерывные частные производные (первого порядка). Тогда, как известно [п° 203, (4)],

так что оба функциональных определителя отличны от нуля и, по непрерывности, сохраняют постоянный знак.

Из того факта, что определитель

отличен от нуля в области (Д), уже следует, что внутренней точке области (Д) отвечает в силу формул (1) внутренняя же точка области ибо — по теореме о существовании неявных функций [п° 208] — этими формулами в целой окрестности точки переменные и определяются как однозначные функции от и у. Аналогично, внутренней точке области (D) отвечает всегда внутренняя точка области (Л). Отсюда уже ясно, что точкам контура (2) отвечают именно точки контура и обратно.

Если взять в области (Д) простую кусочно-гладкую кривую (Л), то с помощью преобразования (1) она перейдет в подобную же кривую в области Действительно, пусть уравнения кривой

причем (ограничиваясь гладким куском кривой) можно функции считать имеющими непрерывные производные не обращающиеся одновременно в нуль. Подставляя эти функции в формулы преобразования (1), мы получим параметрические уравнения соответствующей кривой

Легко видеть, что эти функции также имеют непрерывные производные

которые к тому же не могут одновременно обратиться в нуль, так что особых точек на кривой нет. Действительно, в противном случае, ввиду неравенства нулю определителя из (5) следовало бы, что одновременно что невозможно.

Если точка на плоскости описывает замкнутый контур , скажем, в положительном направлении, то соответствующая точка опишет также некоторый замкнутый же контур на плоскости но направление его может оказаться как положительным, так и отрицательным. Вопрос этот зависит, как мы увидим ниже [606, 1°], от знака якобиана (2).

Задание пары значений переменных из области однозначно определяет некоторую точку в области (D) на плоскости (и обратно). Это дает основание и числа называть координатами точек области По сути дела, уравнения (1) дают нам параметрическое представление плоской фигуры являющееся частным случаем параметрического представления поверхностей, о котором уже была речь [228].

Как и там, кривую, составленную из точек области которых одна из координат сохраняет постоянное значение, называют координатной линией. Например, полагая в мы получим параметрическое представление координатной линии:

(роль параметра здесь играет неявное уравнение той же линии получим, полагая во втором из уравнений (1а):

В связи с тем, что координатные линии, вообще говоря, будут кривыми, числа характеризующие положение точки на плоскости и в этом случае (как и в случае кривой поверхности) называют криволинейными координатами точки.

Придавая координате различные (возможные для нее) постоянные значения, мы получим целое семейство координатных линий на плоскости Фиксируя значение координаты Е, мы получим другое семейство координатных линий. При наличии взаимно однозначного соответствия между рассматриваемыми областями различные линии одного и того же семейства не пересекаются между собой, и через любую точку области (D) проходит по одной линии из каждого семейства.

3.4

Замена переменных в двойном интеграле.

Для того чтобы преобразовать двойной интеграл, заданный в декартовых координатах, в двойной интеграл в криволинейных координатах, нужно заменить в подынтегральной функции z=f(x, y) переменные x и yсоответственно через x=φ(u, v), y=ψ(u, v), а элемент площади dxdy– его выражением в криволинейных координатах: dxdy=|I|dudv, где I – якобиан.

3.5

Определение тройного интеграла.

Тройные интегралы – это аналог двойного интеграла для функции трёх переменных, заданной как f (M) = f (x, y, z). Записывается тройной интеграл так:. Здесь V – пространственная (трёхмерная) фигура, ограниченная плоскостями, выражения которых (равенства) даны в задании вычисления тройного интеграла. V называют также замкнутой ограниченной областью трёхмерного пространства.

Понятие тройного интеграла вводиться аналогично понятию двойного интеграла.

Пусть функция определена в ограниченной замкнутой области ,которая принадлежит трехмерному пространству с определенной декартовой системой координат . Разобьем заданную область на частей , которые не имеют общих внутренних точек и объемы которых равны соответственно . В каждой такой элементарной области возьмем произвольную точку и составим сумму, называемую интегральной суммой для функции по области .

Пусть – наибольшее из расстояний между точка элементарной области . Если существует предел , который не зависит ни от способа разбиения области на элементарные области , ни от выбора в них точек , то этот предел называется тройным интегралом по области

Пусть – замкнутая пространственная область, которая ограничена снизу и сверху поверхностями и соответственно сбоку – цилиндрической поверхностью с образующими, параллельными оси (рис. 1).

Переменные и изменяются в плоской области , которая является проекцией пространственной области на координатную плоскость .

В прямоугольной декартовой системе координат элемент объему вычисляется по формуле . Для указанной области тройной интеграл равен: Внутренний интеграл вычисляется по переменной , а переменные и в этом случае считаются постоянными. Результатом интегрирования есть функция переменных . Итак, вычисление тройного интеграла сводится к вычислению двойного интеграла.

3.6-3.18 3.6)

Длиной кривой (K) называется точная верхняя граница S=sup{p} для множества {p} периметров всевозможных вписанных в кривую ломаных.

где t1 и t2-значения,определяющие точки A и B

Если число S конечно, то кривая называется спрямляемой.

3.7) Если при стремлении L->0 интегральная сумма имеет определенный конечный предел 1, не зависящий от 1) способа дробления кривой(K), 2) выбора точек M; на участке Ai Ai+1 то он называется криволинейным интегралом кривого первого типа от функции f(M)=f(x,y) взятым по кривой (или по пути) (K), обозначаемый: