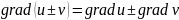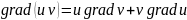0 группа (Элементы теории поля)
Скалярное и векторное поле.
Скалярное поле, это поле, которое в каждой точке характеризуется одним числом, т.е. каждой точкой M ∈ Ω ставится в соответствие некоторое число u (x, y, z), считаем что положение точки M определяется её координатами (x, y, z)
Таким образом u (x, y, z) можно рассматривать как некоторую функцию, заданную в области (x, y, z) ∈ Ω
В “чистой” математике скалярные поля рассматривают редко, ограничиваясь рассмотрением числовых функций.
Пример скалярного поля – температурное поле, поле давления, поле плотности
Далее будем
предполагать, что функция u (x, y, z) имеет
непрерывные частные производные по
всем переменным

Если эти производные не обращаются одновременно в 0, то уравнение u (x, y, z) = const определяет некоторую поверхность(без особых точек!)
Эта поверхность, вдоль которой величина u сохраняет постоянное значение, называется поверхностью уравнения, или изо- поверхностью. Примеры изотермы, изобары и т.д.
Вся рассматриваемая область Ω заполнена поверхностями уровня, причем между собой эти поверхности не пересекаются
Через каждую точку области проходит одна и только одна изо- поверхность.
Векторное поле,
это поле, которое в каждой точке
характеризуется вектором, т.е. каждой
точкой M ∈
Ω
ставится в соответствие по известному
закону некоторый вектор
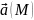
Таким образом, векторное поле задается с помощью векторной функции
Пусть
задана система координат Oxyz
и поле векторной величины
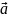 поскольку каждый вектор полностью
определяется своими координатами (P,
Q, R), то векторная функция
может быть реализована путем задания
её проекций на оси: P(x,
y,
z);
Q(x,
y,
z);
R(x,
y,
z)
поскольку каждый вектор полностью
определяется своими координатами (P,
Q, R), то векторная функция
может быть реализована путем задания
её проекций на оси: P(x,
y,
z);
Q(x,
y,
z);
R(x,
y,
z)
Причем каждая проекция по сути есть функция 3х переменных
Считается, что эти функции имеют непрерывные частные производные
При изучении векторного поля важную роль играет понятие
Векторная линия – кривая, направления которой в каждой точке M совпадает с направлением вектора , отвергающей этой точке.
Векторная
линия характеризуется равенством:
Мы уже имели дело с вектор-функцией, когда рассматривали криволинейные интегралы
Если
 ,
то вся рассматриваемая область Ω
заполнена векторными линиями, причем:
,
то вся рассматриваемая область Ω
заполнена векторными линиями, причем:
Через каждую точку ∊ Ω проходит одна и только одна линия
Векторными линии между собой не пересекаются
В физике, особенно при рассмотрении силовых полей (электрическое, магнитное и др.) векторные линии называют силовыми линиями поля
Градиент.
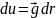
Вектор
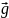 ,
определенный данным соотношением,
называется градиентом,
скалярного поля u(M)
в точке M
,
определенный данным соотношением,
называется градиентом,
скалярного поля u(M)
в точке M
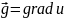
Градиет скалярного поля есть инвариант этого поля
Т.е. градиент не зависит от выбора систем координат
В тоже время, если
скалярное поле u(M)
задано в некоторой системе координат,
т.е. M(x,y,z)
=>
u(x,y,z),
вектор
в данной с.к. задается координатами
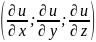 ,
и введя единичные орты
,
и введя единичные орты
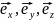 для данной С.К, получим для градиента
выражение:
для данной С.К, получим для градиента
выражение:
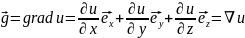
Важно: Если скалярное поле u(M), заданное в области Ω, дифференцируемо в этой области, то градиент grad u этого поля определен в каждой точке Ω и представляет собой векторное поле, заданное в Ω
Свойства градиента:
Пусть в области Ω заданны два дифференцируемых поля u(M) и v(M), тогда:
Дивергенция векторного поля.
Согласно формуле Остроградского-Гаусса поток вектора через поверхность (s) можно преобразовать в тройной интеграл:
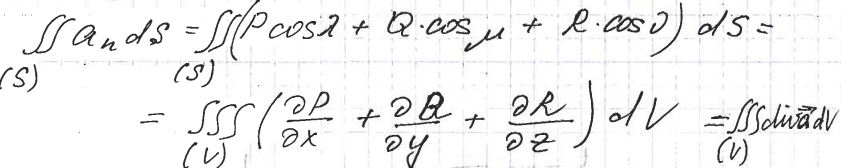
Выражение, стоящее под знаком тройного интеграла называется дивергенцией вектора в точке M
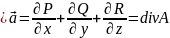
Дивергенция есть скаляр, но ее определение связано с выбором координатной системы (заданной ортонормированного базиса
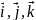 )
)
Формально,
дивергенцию можно представить как
скалярное произведение двух векторов:
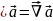
Таким образом
векторное поле
порождает скалярное поле
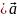 чтобы понять возьмем точку M
и окружность объемом (v)
с поверхностью (S)
тогда можно записать:
чтобы понять возьмем точку M
и окружность объемом (v)
с поверхностью (S)
тогда можно записать:
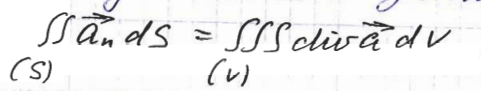
Разделим обе части
на V
и перейдем к пределу “стягивая” тело
(v)
в точку M,
получим:
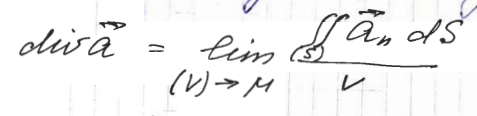 дивергенция
определена в каждой точке Ω,
т.е. имеет скалярное поле
дивергенция
определена в каждой точке Ω,
т.е. имеет скалярное поле
Циркуляция (ротор) векторного поля.
Рассмотрим теперь некоторую кривую (l) в рассматриваемой области Ω.
Интеграл, взятый
по этой кривой:
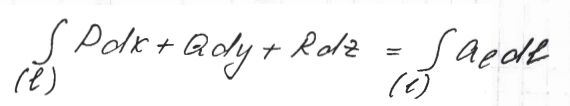 называется
линейным
интегралом
от вектора
вдоль кривой (l)
называется
линейным
интегралом
от вектора
вдоль кривой (l)
В случае замкнутой кривой, этот интеграл называют циркуляцией вектора вдоль (l).
Пример: если
– силовое поле, то
 есть работа сил поля при перемещении
точки по кривой
есть работа сил поля при перемещении
точки по кривой
![]()
Применим формулу
Стонкса, т.е. пусть кривая (l) ограничивает
некоторую поверхность (S),
тогда циркуляцию вектора может быть
выражена через поверхностный интеграл:
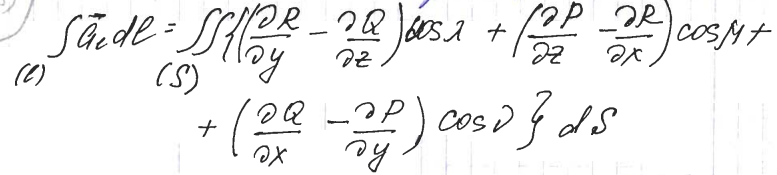
Т.е. мы получим некоторый вектор, имеющий координаты (проекции на оси):
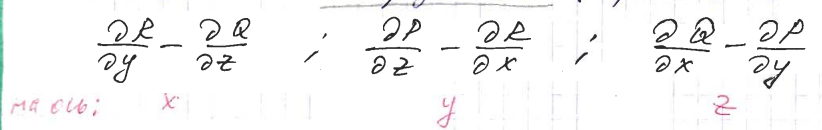
Данный вектор называется ротором вектора (или вихрем)
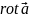
Имеем
Ротор — это вектор!!!
Поскольку в формуле
Стокса направление обхода и сторона
поверхности (задаваемая нормалью) должны
соответствовать друг другу, в векторной
форме она запишется в виде: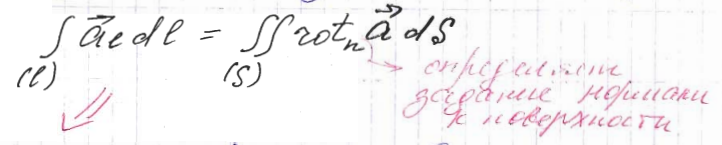
Циркуляция вектора вдоль замкнутого контура равна потоку ротора вектора через поверхность, ограниченную контуром
Следовательно, векторное поле порождает векторное поле ротора
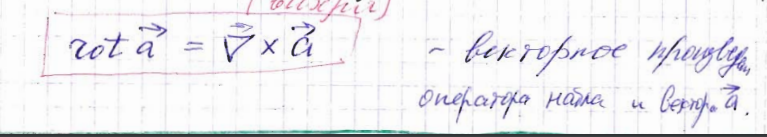
Оператор Лапласа.
Пусть в области Ω 3х мерного Евклидого пространства задано скалярное поле u(M), и все частные производные функции u(M) до второго порядка включительно непрерывны.
i, j, k – единичные орты пространства.
Тогда
 есть дифференцируемое векторное поле
в Ω.
есть дифференцируемое векторное поле
в Ω.
Вычислим
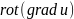
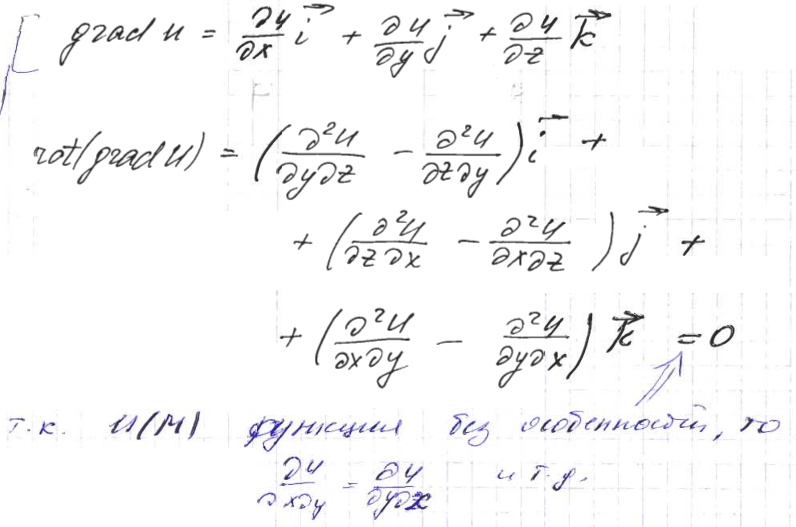
Основная, достаточно широко используемая операция теории поля, это:
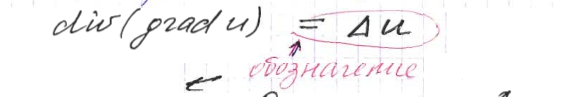
Называют Оператор Лапласа(Лапласиан)
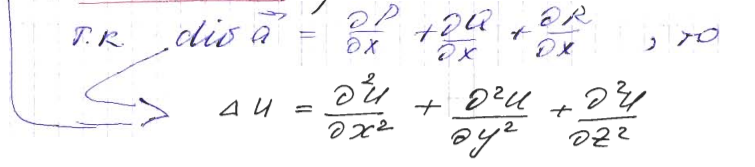
1-22 Первообразная – Первообразной называют такую функцию F (x), по отношению к которой исходная функция f(x) является производной
 .
.Неопределённый интеграл – Выражение
 называется неопределённым интегралом
f
(x)
и обозначает
называется неопределённым интегралом
f
(x)
и обозначает
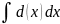
Правила интегрирования:
Если
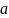 – постоянная
– постоянная
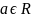 ,то
,то
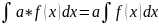 (постоянная выноситься за знак интеграла
)
(постоянная выноситься за знак интеграла
)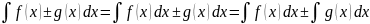 (интеграл суммы
двух или более равен сумме инетгралов)
F(x)
± G(x)
+ C
(C=
C1+C2)
(интеграл суммы
двух или более равен сумме инетгралов)
F(x)
± G(x)
+ C
(C=
C1+C2)
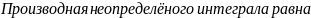 подынтегральной
функции
подынтегральной
функции
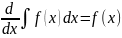
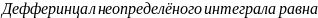 подынтегральному
выражению
подынтегральному
выражению
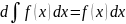
Неопределённый интеграл от дифференциала некоторой функции равна сумме этой функции и постоянной
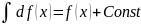
Свойство инвариантности неопределённого интеграла
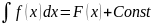 то
то

Интегрирование по частям – Пусть имеются две функции v(x) и u(x) имеющие непрерывные производные, то по правилу дифференцирования произведение имеем d(u*v) = udv + vdu, udv= d(u*v) + vdu возьмём интеграл и получим формулу (
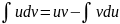 ) использование этой формулы является
интегрированием по частям
) использование этой формулы является
интегрированием по частям
Интегрирование путём замены переменных – Этот метод заключается в замене сложного выражения или некоторой функции какой-либо переменной.
Общая формула интегрирование по частям -Предположим, что функции u {\displaystyle u}г\ъuи v {\displaystyle v} в рассматриваемом промежутке X {\displaystyle {\mathcal {X}}}xXXsdfdsad обладают непрерывными производными всех порядков, до (n+1) {\displaystyle (n+1)}((9-го включительно, Тогда имеет место следующая формула
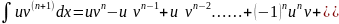
6)Интегрирование рациональных выражений – Вначале рассмотрим простые дроби у которых знаменатель раскладывается на множители, всего их существует четыре вида:
А)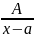
Б)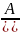
В)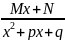
Г)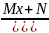
Где a p q M N A – вещественные числа
А
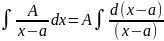 = A
= A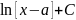
Б
В
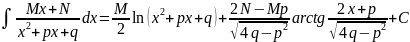
Г
7)
8) Свойства интегрируемых функций:
А) Если функция f(x) непрерывна в промежутке [a,b], то она интегрируема в этом промежутке.
Б) Если ограниченная функция f(x) в [a,b] имеет лишь конечное число точек разрыва, то она интегрируема (Критерий Лейбница)
В) Монотонная ограниченная функция f(x) всегда интегрируема
Г) Если функция f(x) интегрируема в промежутке [a,b] то и функция |f(x)| и r*f(x) интегрируема в этом промежутке
Д) Адаптивность: Если две функции f(x) и g(x) интегрируемы в промежутке [a,b] то их сумма, разность и произведение также интегрируемы
Е) Если функция f(x) интегрируема в промежутке [a,b], то она интегрируема и в любой части [A,B] c [a,b] этого промежутка. Наоборот если данный промежуток разложен на части, и в каждой из них функция интегрируема то она интегрируема и во всём промежутке [a,b]
Ё)Если изменить значение интегрируемой функции в конечном числе точек, то её интегрируемость не разрушиться.
9) Свойства определённых интегралов:
А) Если f(x)
интегрируема в промежутке [b,a]
то в промежутке [a,b]
мы имеем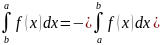
Б) Пусть f(x) интегрируема в наибольшем из промежутков [a,b],[a,c],[c,b] тогда она интегрируема в двух других и имеет равенство

Если a <c<b равенство очевидно
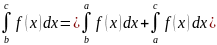
Если b<a<c имеем

В) Если f(x)
интегрируема в промежутке [a,b]
то и r*f(x)
интегрируема в этом промежутке
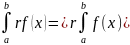
Г) Если f(x) g(x) интегрируемы в промежутке [a,b] то f(x) ± g(x) интегрируема в этом промежутке

Д) Если функция f(x) интегрируема в промежутке [a,b] неотрицательна и a<b то интеграл этой функции положителен или равен нулю
Е) Если две функуии f(x) и g(x) интегрируемы в промежутке [a,b] и всегда f(x)<=g(x) или f(x)<g(x) то если a<b
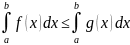
Ё) Пусть функция
f(x)
интегрируема на промежутке [a,b]
u
a<b,
тогда имеет место неравенство
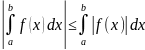
Ж) Пусть f(X) интегрируема в [a,b] и пусть во всём этом промежутке m≤f(x)≤M
Тогда
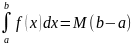
10) интеграл с переменным верхним пределом
Пусть функция f(x) интегрируема на промежутке [a,b] тогда она интегрируема и в промежутке [a,t] где t € [a,b] где t любое число из промежутка.
F(x)
=
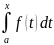
11) Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной.
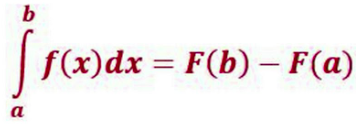
12) Формулы вычисления определенного интеграла
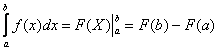 формулы
Ньютона-Лейбница:
формулы
Ньютона-Лейбница:
Интегрирование
по частям
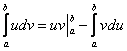
Замена переменной в определенном интеграле
Пусть
функция φ(t) имеет непрерывную производную
на отрезке [α,β], а=φ(α), в=φ(β) и функция
f(х) непрерывна в каждой точке х вида
х=φ(t), где t![]() [α,β].
[α,β].
Тогда справедливо следующее равенство:
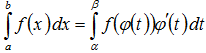
13) Геометрические приложения интеграла
Основными геометрическими приложениями определенного интеграла являются: вычисление площади плоской фигуры, вычисление объемов тел вращения вокруг осей координат и вычисление длины дуги плоской кривой.
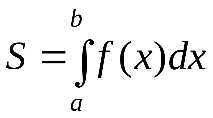
![]()
14) Свойства двойного интеграла
Постоянный множитель может быть вынесен за знак двойного интеграла
![]()
Линейность
![]()
Интеграл от единичной функции по области
![]()
Интегрирование неравенств
![]()
15) Вычисление двойных интегралов сведением к повторным



16) Понятие интегралов высшей кратности.
????
17) Замена переменных в кратных интегралах.



18) Переход к сферическим и цилиндрическим координатам


19) Формула Грина.

20) Следствия формулы Грина. Независимость криволинейного интеграла от пути интегрирования.
????
21) Формула Стокса

22) Формула Остроградского – Гаусса
Фо́рмула Гаусса —Остроградского связывает поток непрерывно-дифференцируемого векторного поля через замкнутую поверхность и интеграл от дивергенции этого поля по объёму, ограниченному этой поверхностью.
Формула применяется для преобразования объёмного интеграла в интеграл по замкнутой поверхности и наоборот.

2.1-2.8
2.1
Несобственные интегралы с бесконечным
пределом
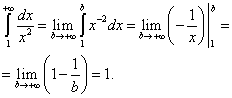
 2.2
Признак сходимости Коши несобственных
интегралов. Абсолютная сходимость.
Признаки сравнения.
Несобственный
интеграл
2.2
Признак сходимости Коши несобственных
интегралов. Абсолютная сходимость.
Признаки сравнения.
Несобственный
интеграл ![]() f(x)dx сходится
тогда и только тогда, когда
для любого
f(x)dx сходится
тогда и только тогда, когда
для любого ![]() >
0 существует
такое
>
0 существует
такое ![]() , что
для всех
'
и
", удовлетворяющих
условию
<
'
< b,
<
"<
b,
выполняется
неравенство
, что
для всех
'
и
", удовлетворяющих
условию
<
'
< b,
<
"<
b,
выполняется
неравенство
|
 Признаки
сравнения.
Признаки
сравнения.
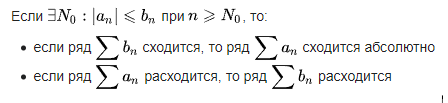
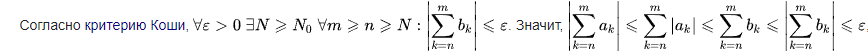
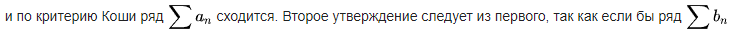
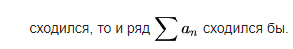
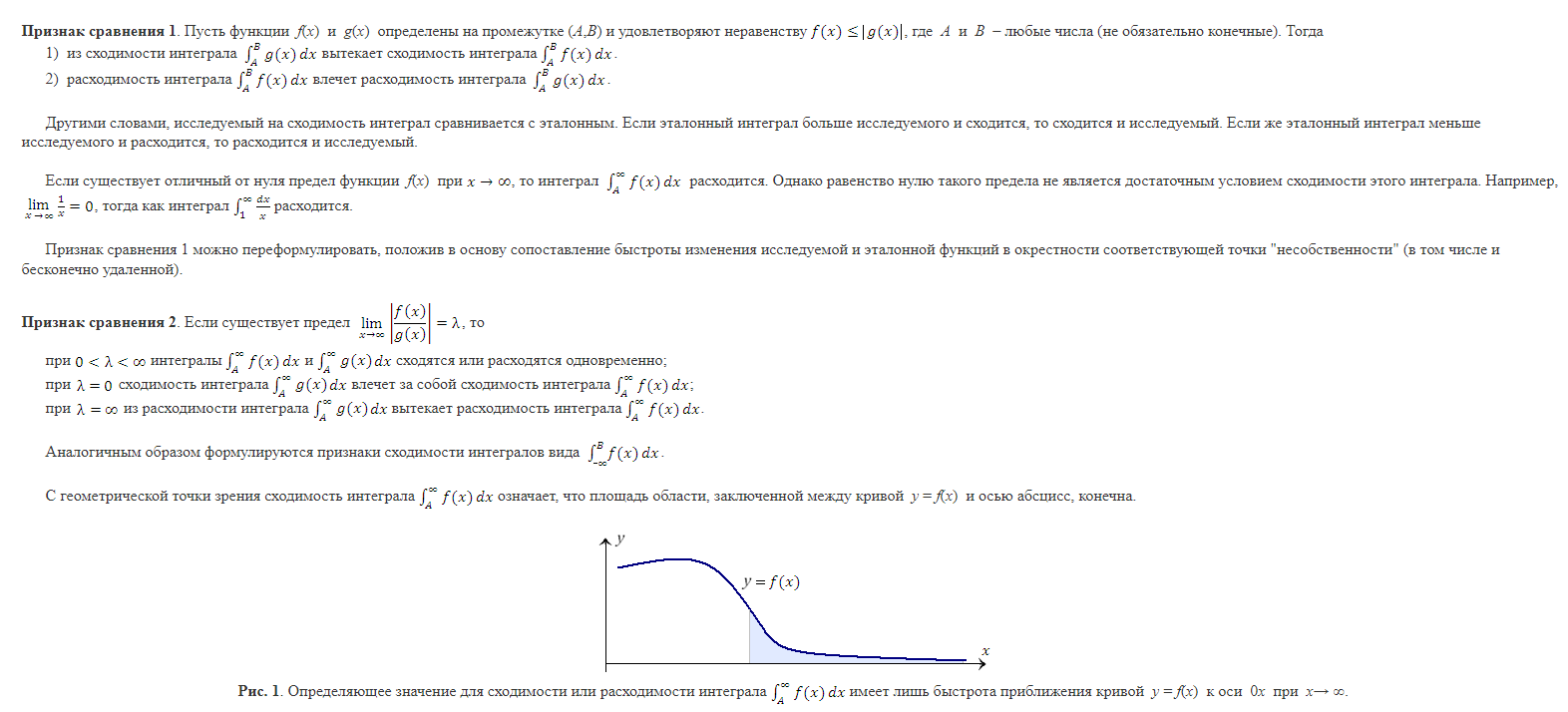 Абсолютная
сходимость.
Пусть
функция f(x)
интегрируема на полубесконечном
интервале [A, ∞).
Если наряду с интегралом
Абсолютная
сходимость.
Пусть
функция f(x)
интегрируема на полубесконечном
интервале [A, ∞).
Если наряду с интегралом 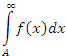 сходится и интеграл
сходится и интеграл 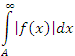 ,
то интеграл
называется абсолютно
сходящимся.
Говорят также, что функция f(x) абсолютно
интегрируема на
промежутке [A, ∞).
,
то интеграл
называется абсолютно
сходящимся.
Говорят также, что функция f(x) абсолютно
интегрируема на
промежутке [A, ∞).Пусть функция f(x) абсолютно интегрируема на промежутке [A, ∞). Если функция g(x) ограничена на этом промежутке, то и произведение
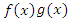 является
абсолютно интегрируемой функцией на
промежутке [A, ∞).
является
абсолютно интегрируемой функцией на
промежутке [A, ∞).
Если функция f(x) абсолютно интегрируема на промежутке [A, ∞) и | g(x) | ≤ | f(x) |, то и функция g(x) абсолютно интегрируема на промежутке [A, ∞).
2-3.
Признак Дирихле
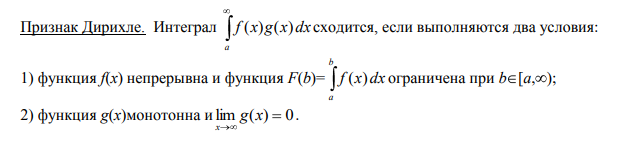 2-4.
Признак Абеля
2-4.
Признак Абеля
 2-5.
Несобственные интегралы от неограниченной
функции. Теорема об интегрируемости
неограниченных функций.
2-5.
Несобственные интегралы от неограниченной
функции. Теорема об интегрируемости
неограниченных функций.



 2.6
Равномерная сходимость.
2.6
Равномерная сходимость.
![]()
![]()
![]()
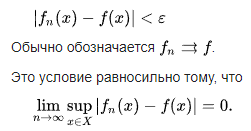 Cвойства
Cвойства
![]()
![]()
![]()
![]()
![]()
 2-7.
Собственные интегралы с параметрами.
Предельный переход под знаком
интеграла.
2-7.
Собственные интегралы с параметрами.
Предельный переход под знаком
интеграла.





 2-8
Интегрирование по параметру
2-8
Интегрирование по параметру
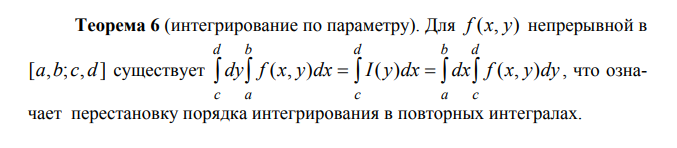
 Дифференцируемость
по параметру
Дифференцируемость
по параметру
 Вопросы
к мат анализу 2.9 – 3.5
Вопросы
к мат анализу 2.9 – 3.5
2.9
Несобственный интеграл называется равномерно сходящимся по параметру у на отрезке (с, d), если он сходится на этом отрезке и для любого е > 0 можно указать такое А ^ а, зависящее только от е, что для всех В > А и для всех у из отрезка (с, d) выполняется неравенство Имеет место следующий критерий Коши равномерной сходимости несобственных интегралов, зависящих от параметра.
+∞ 0∫e^-x cosxy dx
сходится равномерно по параметру у на интервале (−∞,+∞)=R(−∞,+∞)=R.
Для любого ε>0 существует b′=ln2ε такое, что для любого ξ∈[b′,+∞) и любого y∈Y выполняется неравенство
∣∫ξ+∞e−xcosxy dx∣≤∫ξ+∞e−x dx=e−ξ≤e−b′=ε2<ε.