9. Передаточные функции сау. Передаточная функция динамического звена.

Передаточная функция

Важной, очень удобной в практических приложениях характеристикой, компактно описывающей динамические свойства звена (или системы), является передаточная функция звена (или системы), определяемая как отношение изображений выходной переменной ко входной , взятое при нулевых начальных условиях:

В частности, для системы регулирования, описываемой уравнением (2.3), можно записать выражение для изображения выходной переменной:

Здесь

и

 

– передаточные функции системы регулирования по каналам «входной сигнал – выходная переменная » и «возмущение – выходная переменная ». Напомним, что уравнения (2.1) и (2.2) адекватны только при нулевых начальных условиях.

Динамическое звено САУ

Для математического описания работы САУ удобно разбивать её не на функциональные элементы автоматики, а на динамические звенья. Поэтому вводится понятие динамического звена. Динамическим звеном называется часть системы управления, либо вся система, описываемая дифференциальным (или иным) уравнением определенного вида. Приведённое определение является общим. Под него подходит любой элемент автоматики, совокупность таких элементов и даже вся система автоматического управления в целом.

Передаточные функции САУ

Передаточная функция динамического звена

Понятие передаточной функции динамического звена связано с операционным методом решения дифференциальных уравнений, основанном на применении преобразования Лапласа-Карсона. Преобразованием Лапласа называют соотношение:

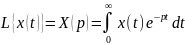(3.1)

где x(t) – оригинал; X(p) – изображение, ставящее функции x(t) вещественного переменного t в соответствие функцию X(p) комплексной переменной p (p = σ + jω).

Преобразование Карсона имеет вид:

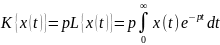. (3.2)

Обратное преобразование Лапласа:

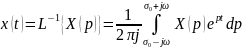(3.3)

Теорема смещения:

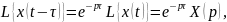
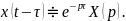(3.4)

Связь конечного значения функции с изображением:

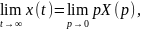(3.5)

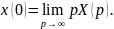
Изображение производных функций:

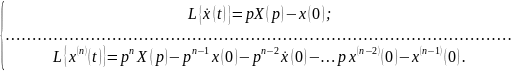
Рассмотрим пример. Пусть динамическое звено (рис 3.1) описывается дифференциальным уравнением:

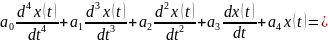
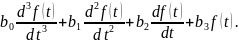= (3.7)

 

Рис. 3.1. Динамическое звено

Найдём изображение Лапласа уравнения (3.7). Для этого последовательно определим изображения левой и правой частей уравнения (3.7):

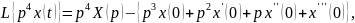
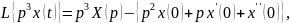
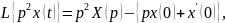
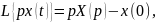
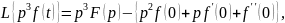
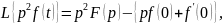
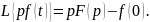(3.8)

С учётом (3.8) изображение уравнения (3.7) при нулевых начальных условиях принимает вид:

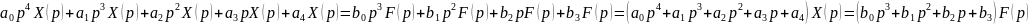
(3.9)

Тогда отношение изображения выходной координаты к изображению входной координаты рассматриваемого звена при нулевых начальных условиях примет вид:

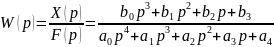. (3.10)

В общем виде передаточная функция динамического звена запишется:

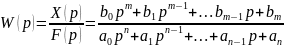. (3.11)

Таким образом, передаточная функция динамического звена есть отношение изображения (Лапласа-Карсона) выходной координаты звена к соответствующему изображению входной координаты звена при нулевых начальных условиях.

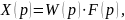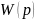При этом изображение выходной координаты динамического звена (рис. 3.2) равно где – передаточная функция динамического звена, а – изображение входного воздействия.

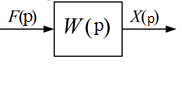
Рис. 3.2. Динамическое звено