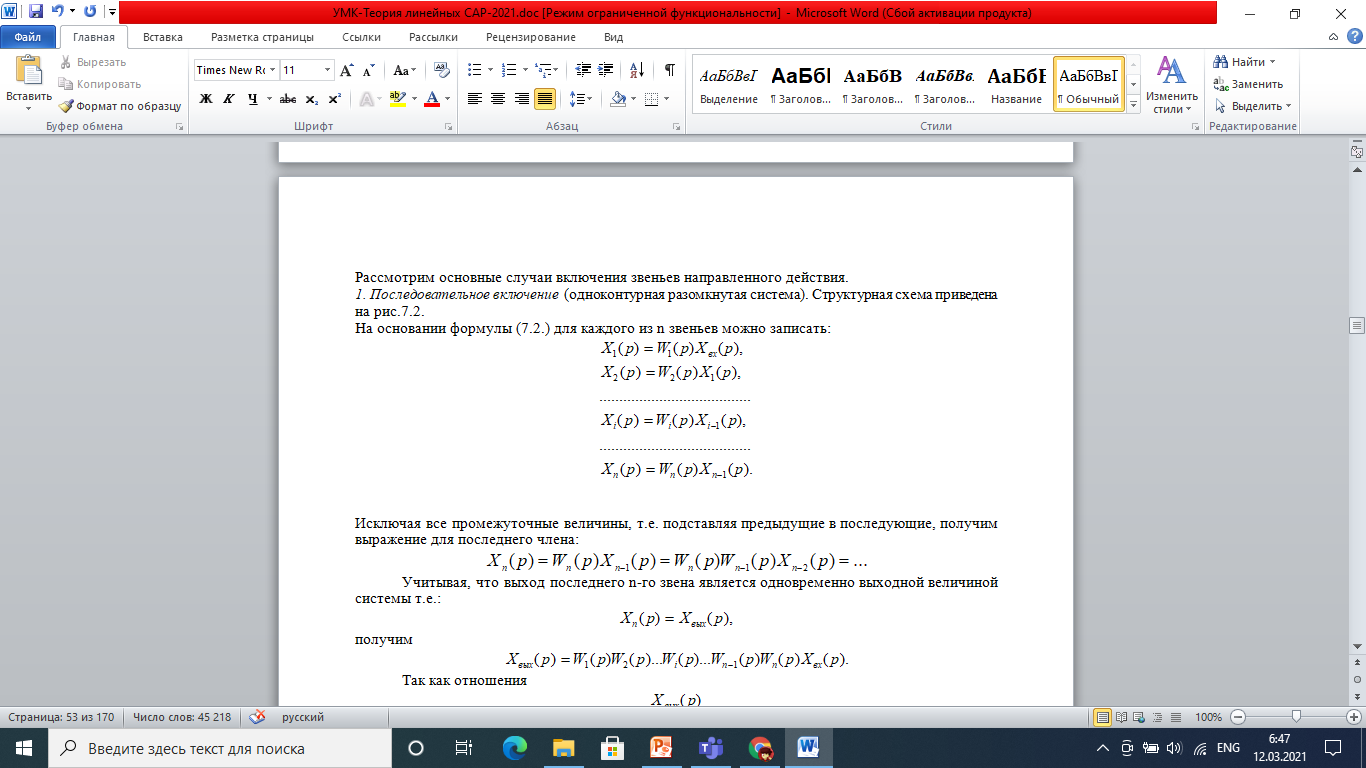
1. Последовательное включение
Рис.7.2. Последовательное включение звеньев направленного действия.
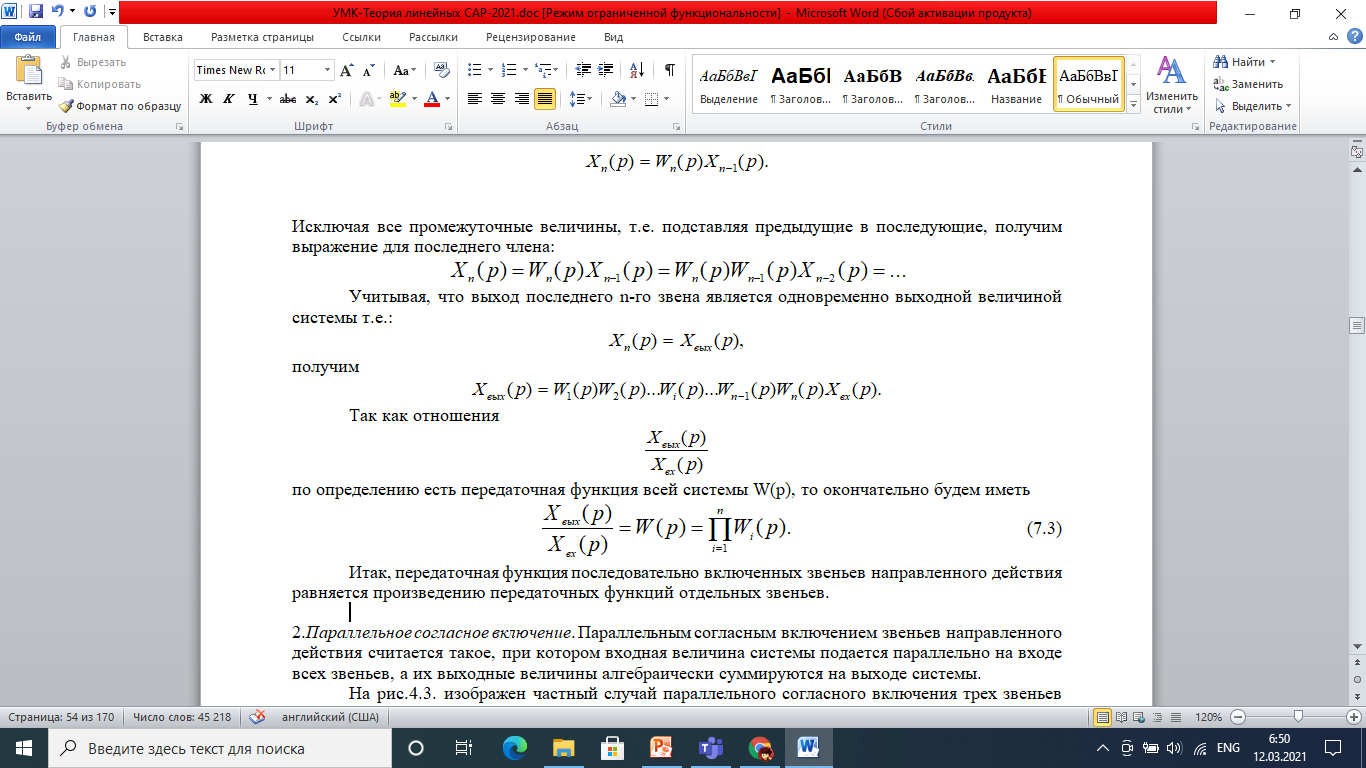
2. Параллельное согласное включение. Параллельным согласным включением звеньев направленного действия считается такое, при котором входная величина системы подаётся параллельно на входе всех звеньев, а их выходные величины алгебраически суммируются на выходе системы.
На рис.7.3. изображён частный случай параллельного согласного включения трех звеньев направленного действия.
Рис.7.3. Параллельное согласное включение звеньев направленного действия
На основании формулы (7.2) для каждого из n параллельно включенных звеньев можно записать:
Суммируя написанные равенства и принимая их во внимание, что по определению параллельного согласного включения звеньев направленного действия сумма левых частей является выходной величиной системы, получим
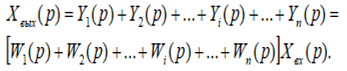
Согласно определению передаточной функции (4.1), из последнего выражения будем иметь
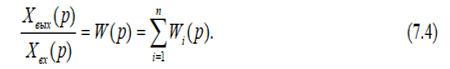
Таким образом, передаточная функция параллельных согласно включенных звеньев направленного действия равняется алгебраической сумме передаточных функций отдельных звеньев.
3. Параллельное встречное включение (обратная связь). Рассмотрим сначала основной случай – отрицательную обратную связь.
На рис. 7.4. изображена структурная схема замкнутый системы автоматического управления в наиболее общем виде, где G (p) и Z(p) - передаточные функции соответственно прямой цепи системы и цепи обратной связи.
Рис.7.4. Параллельное встречное включенье звеньев направленного действия (обратная связь).
Сигнал обратной связи Хо.с.(р) вычитается из входного сигнала Хвх (р) (в случае положительной обратной связи они не вычитаются, а складываются). Передаточные функции G(р) и 2(р) могут соответствовать как простым звеньям направленного действия, так и их любым комбинациям.
Для схемы, изображённой на рис.7.4,
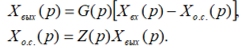
Исключив из них промежуточную величину Хо.с. получим передаточную функцию замкнутой системы
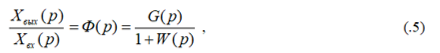
Где
есть передаточная функция разомкнутой системы. Смысл последнего названия становится понятным, если мысленно разомкнуть контур управления в любом месте и, «выпрямив» его, рассматривать прохождение сигнала, поданного в месте размыкания, по цепочке последовательно включенных звеньев направленного действия.
Итак, передаточная функция замкнутой системы автоматического управления равняется отношению передаточной функции прямой цепи к увеличенной на единицу передаточной функции разомкнутой системы.
При положительной обратной связи вместо плюса в знаменателе надо поставить минус.
Следует отметить, что этот вывод, равно как и формула (7.5), справедливы только для изображённого на рис.7.4 случая, когда внешнее воздействие поступает вход системы управления. Поэтому Ф(р) иногда называют передаточной функцией замкнутой системы по входному воздействию.
В действительности, кроме управляющего входного воздействия, всякая реальная система подвержена различным возмущающим воздействиям (колебания нагрузки, нестабильность характеристик элементов, помехи и т.д.), которые могут поступать в систему в любом месте. Для учёта их влияния нужно уметь при помощи структурной схемы устанавливать зависимости между этими возмущениями и изменениями управляемой (выходной) величины системы.
Рассмотрим структурную схему системы автоматического управления, изображённую на рис. 7.5. Прямая цепь системы состоит из последовательно включенных звеньев направленного действия с передаточными функциями G1(p), G2(p), G3(p). На входы двух последних звеньев поступают возмущающие воздействия F1(p) и F2(p), суммирующиеся с соответствующими выходными величинами предыдущих звеньев. Кроме того, возмущение F3(p) действует непосредственно на выходную величину системы, что обозначено на схеме специальным элементом суммирования. При этом принципиально важно, что место приложения возмущения F3(p) охвачено обратной связью, т.е. на звено с передаточной функцией Z(p) поступает выходная величина системы уже с учётом действия F3(p). В противном случае никакого эффекта регулирования не было бы, так как управляемая величина системы, искажённая влиянием возмущающего действия, не корректировалась бы обратной связью.
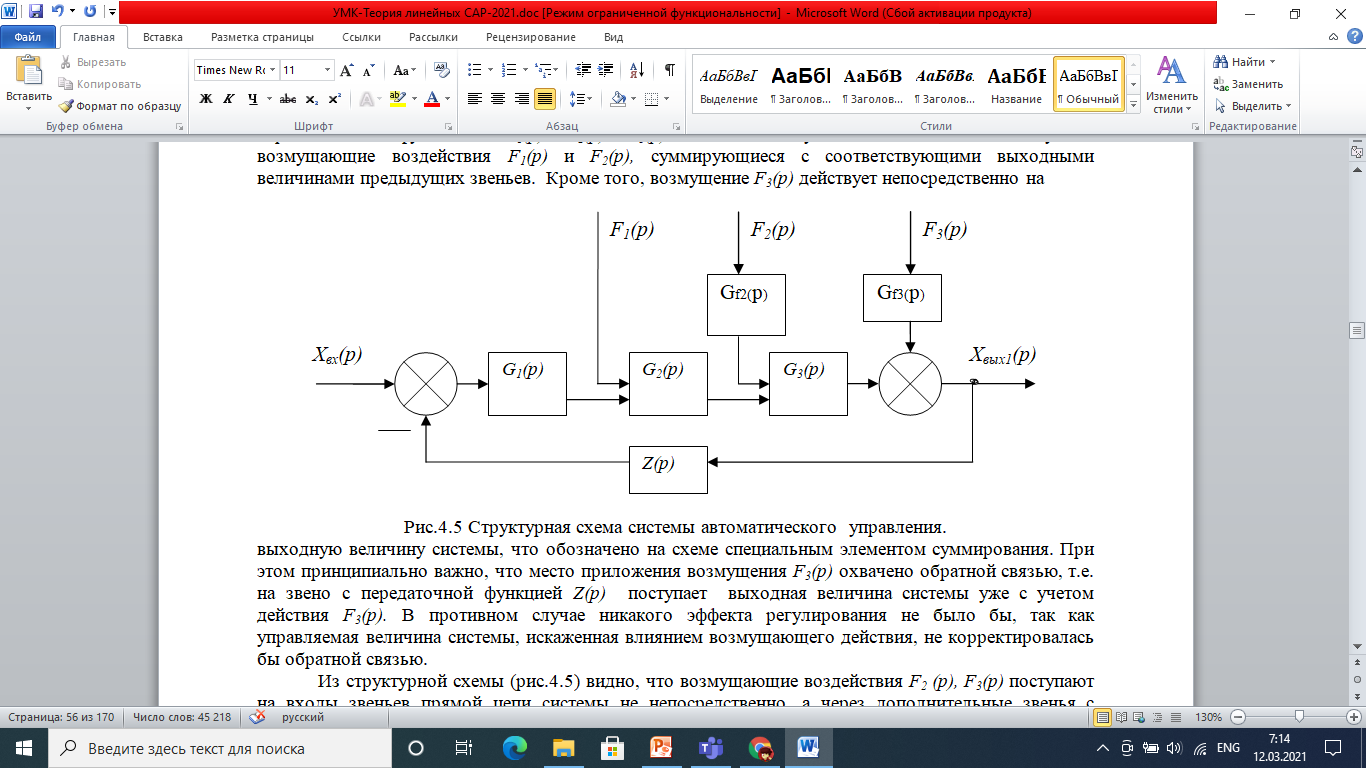
Рис.4.5. Структурная схема системы автоматического управления
Из структурной схемы (рис.7.5) видно, что возмущающие воздействия F2 (p), F3(p) поступают на входы звеньев прямой цепи системы не непосредственно, а через дополнительные звенья с передаточными функциями Gf2(p), Gf3 (p), которые отражают характер зависимости данной величины системы от конкретного возмущающего действия.
В силу линейности рассматриваемой системы управления к ней применим принцип наложения, дающий возможность определить общую реакцию системы (изменение выходной величины) как сумму частных реакций от каждого из внешних воздействий в отдельности.
Положим Xвх (р)=0, F2 (p)=0, F3 (p)=0 и определим зависимость Хвых (р) от F1 (p).
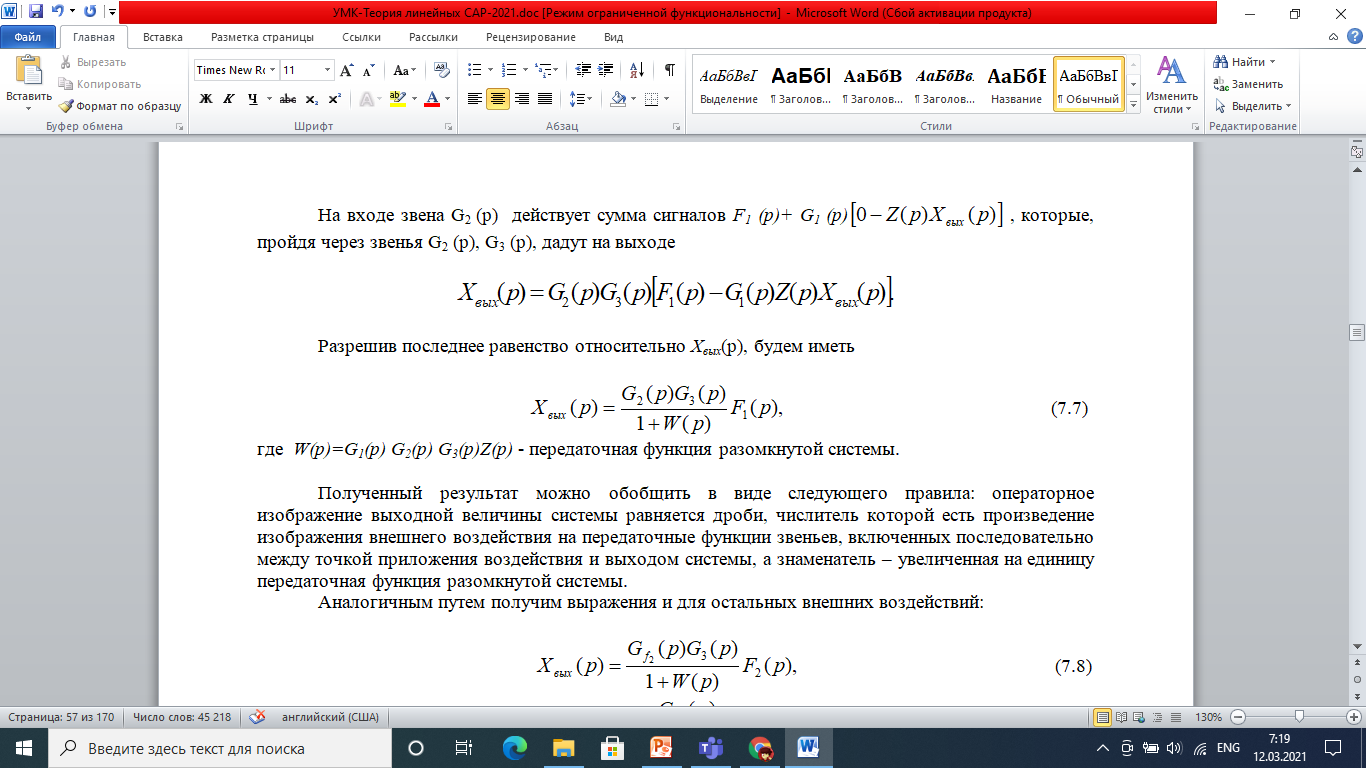
Полученный результат можно обобщить в виде следующего правила: операторное изображение выходной величины системы равняется дроби, числитель которой есть произведение изображения внешнего воздействия на передаточные функции звеньев, включенных последовательно между точкой приложения воздействия и выходом системы, а знаменатель – увеличенная на единицу передаточная функция разомкнутой системы.
Аналогичным путём получим выражения и для остальных внешних воздействий:
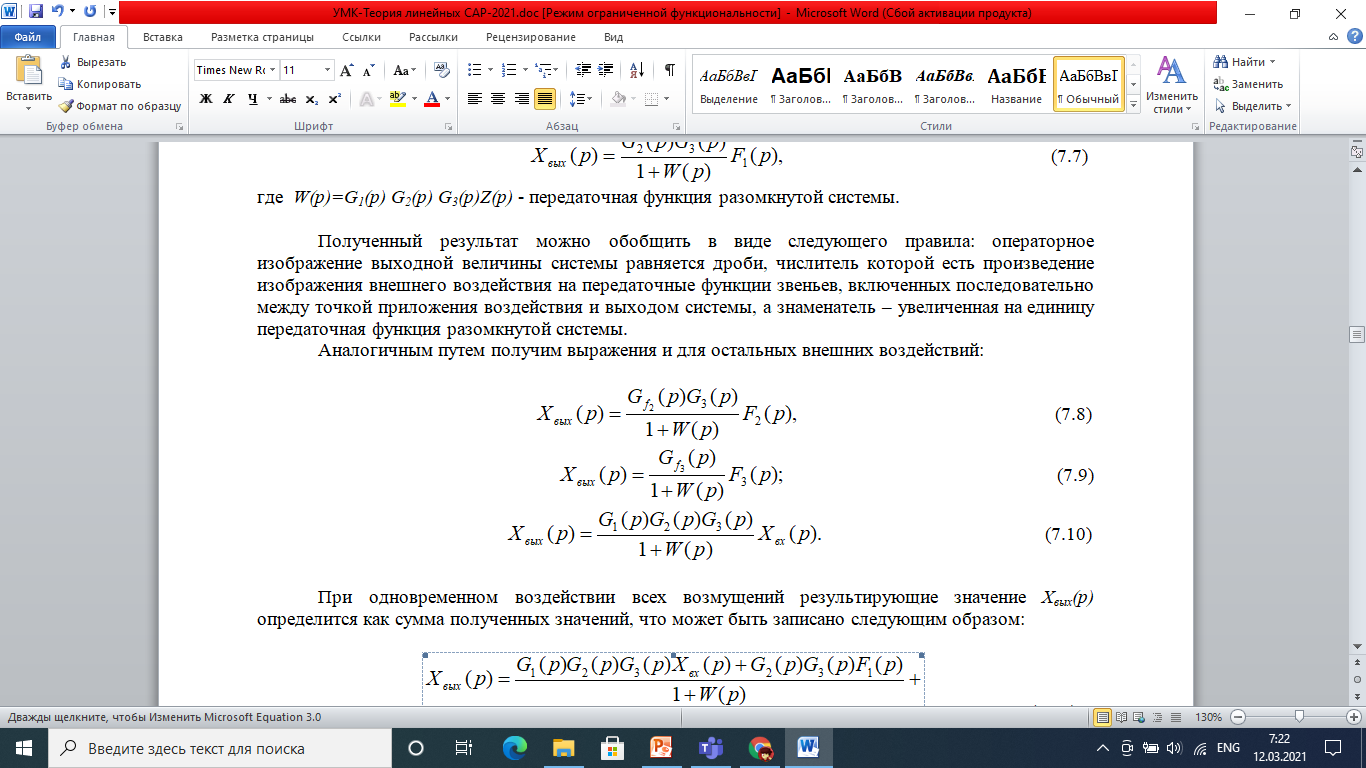
При одновременном воздействии всех возмущений результирующие значение Хвых(р) определится как сумма полученных значений, что может быть записано следующим образом:
Из выражения (7.5) можно получить (как частный случай) формулы, характерные для следящих систем. Особенностью последних является передача выходной величины Θвых к элементу сравнения, т.е. на вход системы, с коэффициентом передачи, равным единице. Кроме того, основным видом внешних воздействий в следящих системах обычно считают входное (управляющее) воздействие Θвх, отрабатываемое системой с некоторой ошибкой (рассогласованием)
Θ = Θвх - Θвых
С учётом сказанного, положив в (7.6) Z(p)=1, будем иметь W(p)=G(p), после чего, заменив в (7.5) обозначения входной и выходной величин, получим
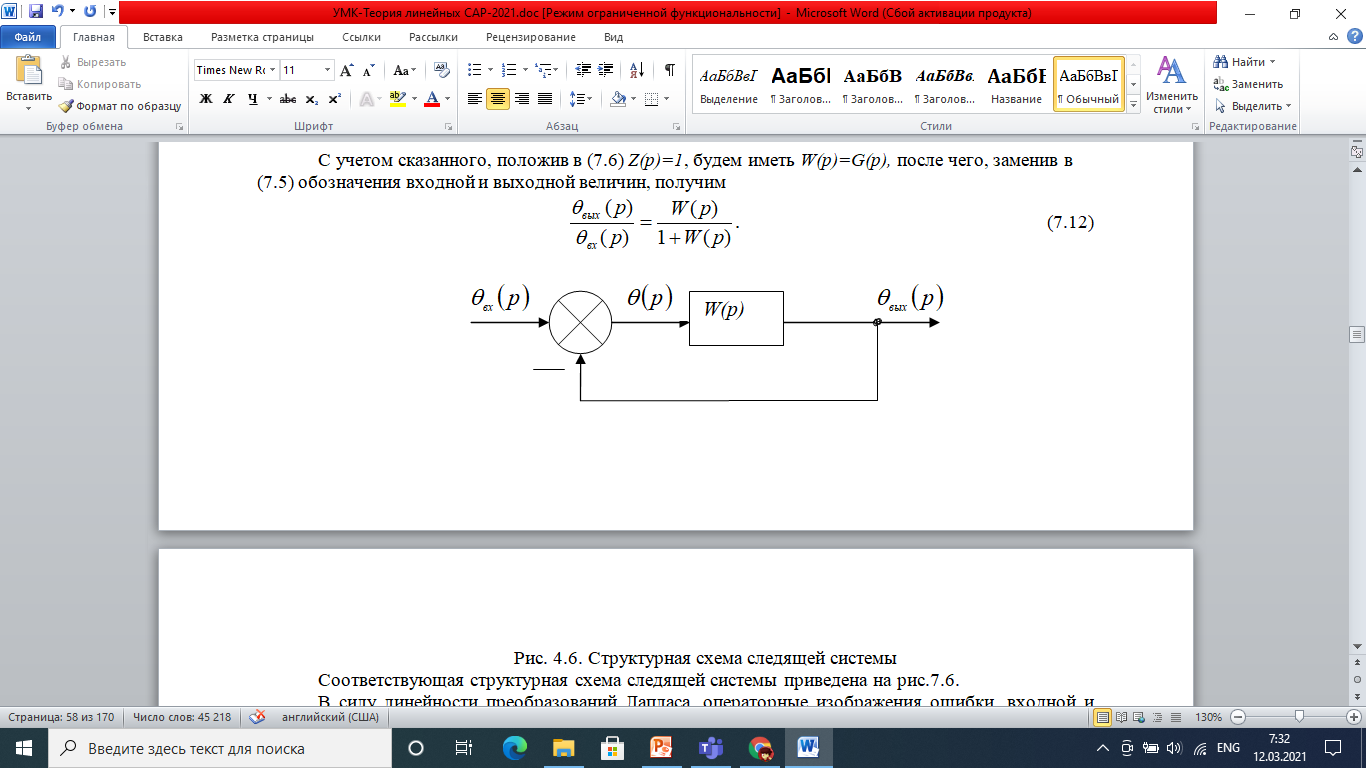
Рис. 7.6. Структурная схема следящей системы
Соответствующая структурная схема следящей системы приведена на рис.7. В силу линейности преобразований Лапласа, операторные изображения ошибки, входной и выходной величин связаны между собой так же, как и их оригиналы, т.е.
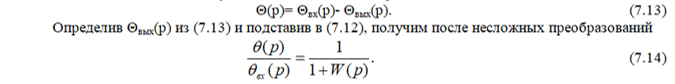
Выражения (7.12) и (7.14) называются соответственно передаточными функциями следящей системы по выходной величине и по ошибке. Во всех рассмотренных случаях передаточные функции замкнутых систем управления определялись через передаточную функцию разомкнутой системы W(p). Последняя обычно может быть представлена в виде
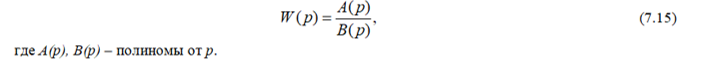
Подставив (7.15) в выражения (7.12) и (7.14), можно получить полезные для расчетов следящих систем формулы:
Выше рассматривались отрицательная обратная связь. Студентам предлагается в порядке упражнений самостоятельно убедиться. что в случае положительной обратной связи в знаменателе формул (7.5). (7.77.12), (7.14) знак плюс перед № (р) изменяется на минус. Преобразование многоконтурных структурных схем с перекрещивающимися связями производят по способу (перенесения) связей, сущность которого поясняется на примере ниже.
Пример определения передаточной функции системы с перекрёстными связями
Преобразование структурной схемы (рис. 7.7,а) системы автоматического управления и определение в общем виде передаточной функции замкнутой системы.
Структурная схема имеет перекрещивающиеся параллельные связи, поэтому преобразование её к виду, удобному для составления передаточной функции, будем производить с помощью способа переключения связей.
Местную обратную связь, поступающую через звено Z1, на вход звена W4, перенесём на вход звена W3. Чтобы результат не изменился, добавим в цепь этой связи последовательное звено. Обратную связь с передаточной функцией, равной единице подаваемую на вход звена Z2 с выхода звена W4, заменим связью с передаточной функцией с выхода звена W5. Параллельные, согласно включенные звенья с передаточными функциями 1 и W2 заменим одним звеном 1+W2. После этого структурная схема примет вид, изображённый на рис.7.7, б.
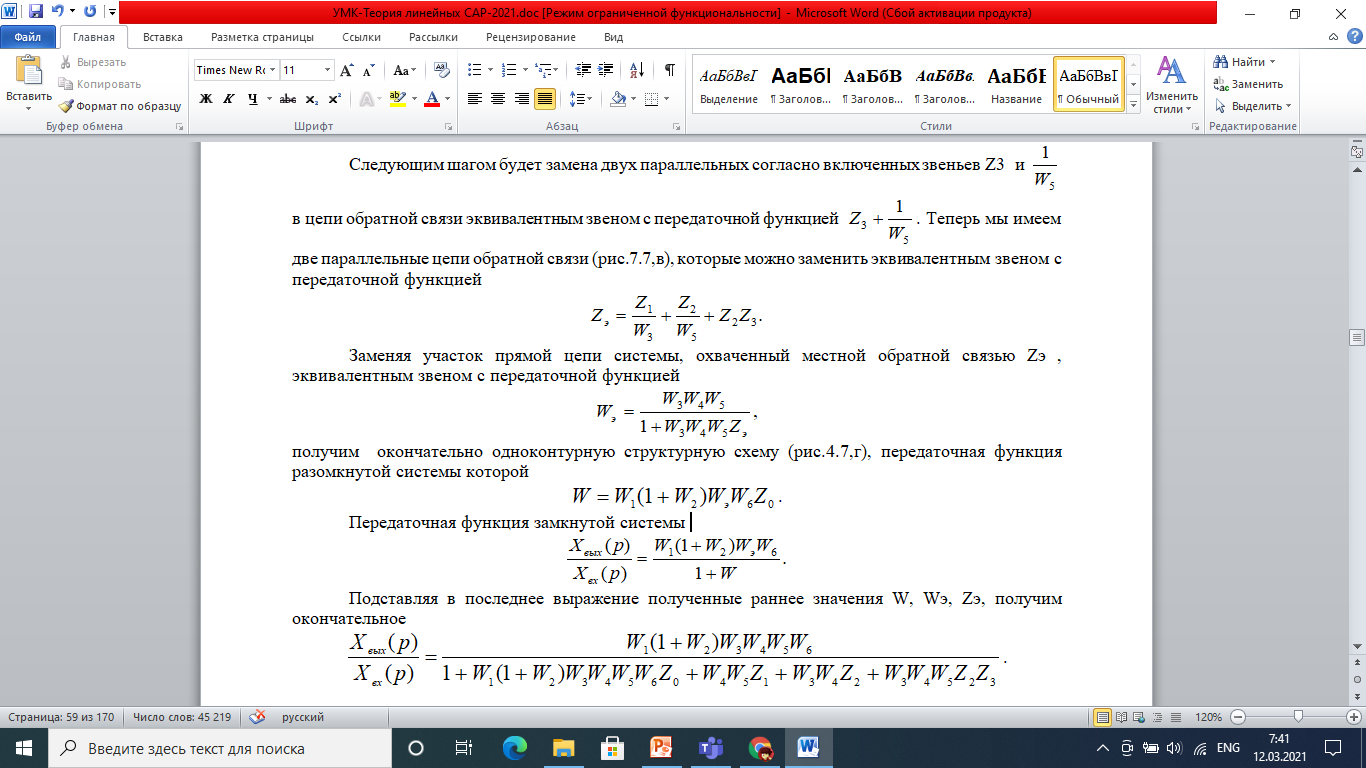
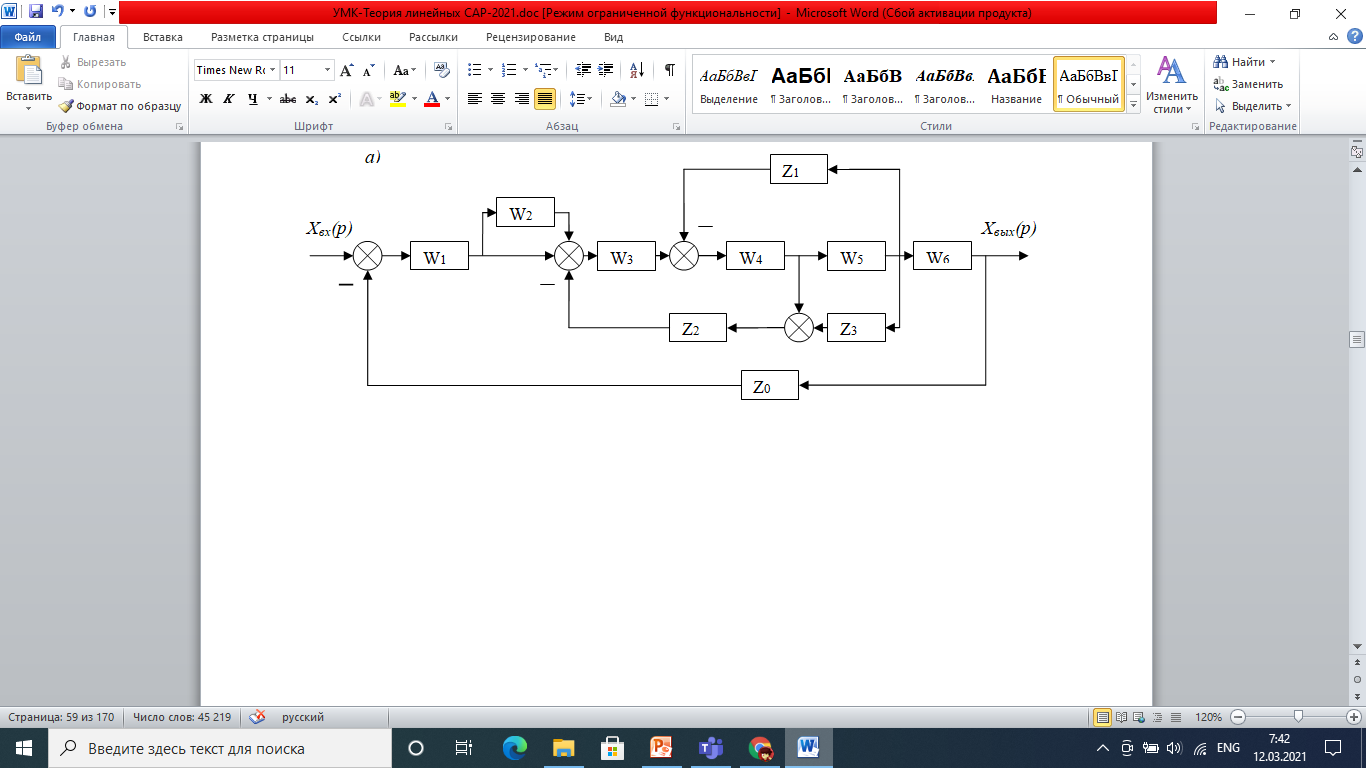
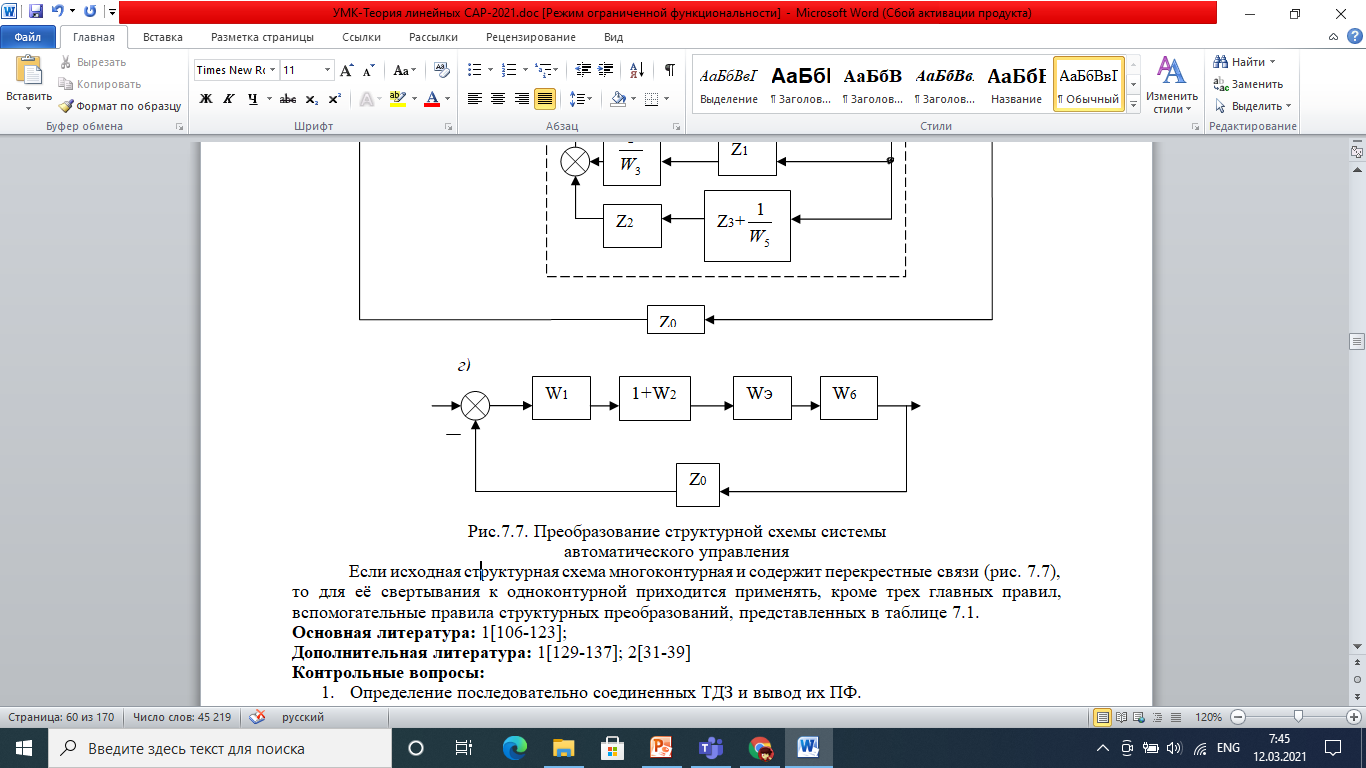
Рис.7.7. Преобразование структурной схемы системы
автоматического управления
Если исходная структурная схема многоконтурная и содержит перекрёстные связи, то для её свёртывания к одноконтурной приходится применять, кроме трех главных правил, вспомогательные правила структурных преобразований, представленных в таблице 7.2.
Таблица.7.2. Правила преобразования структурных и линейных систем
