Вопросы 5-7 общая часть:
Математическое описание элементов и систем автоматического управления
Для математического описания работы САУ удобно разбивать её не на функциональные элементы автоматики, а на динамические звенья. Поэтому вводится понятие динамического звена.
Динамическим звеном называется часть системы управления, либо вся система, описываемая дифференциальным (или иным) уравнением определенного вида. Приведённое определение является общим. Под него подходит любой элемент автоматики, совокупность таких элементов и даже вся система автоматического управления в целом.
Например, в качестве динамических звеньев рассматриваются отдельные части функциональных элементов автоматики и объектов управления (обмотки возбуждения электрических генераторов, якорные обмотки электродвигателей, отдельные каскады усилителей и т. д.).
Связь входа и выхода
Существует некоторое правило, по которому элемент преобразует вход x в выход y. Это правило называется оператором.
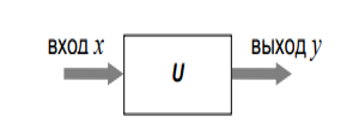
Запись y = U[x] означает, что выход y получен в результате применения оператора U ко входу x.
Построить модель – это значит найти оператор, связывающий входы и выходы. С его помощью можно предсказать реакцию объекта на любой входной сигнал.
Модель – это объект, который мы используем для изучения другого объекта (оригинала). Модель и оригинал должны быть в чем-то похожи, чтобы выводы, сделанные при изучении модели, можно было бы (с некоторой вероятностью) перенести на оригинал.
Пример – ДПТ, входная величина – напряжение питания, выходная – частота вращения. Будем считать, что при напряжении 1 В частота вращения равна 1 об/сек, а при напряжении 2 В – 2 об/сек, то есть частота вращения равна по величине напряжению1. Действие такого оператора можно записать в виде
U[x] = x
Если напряжение на входе x(t) меняется, угол поворота запишется в виде интеграла
.
Оператор, который действует по такому правилу, называется оператором интегрирования.
Обратный оператор – оператор дифференцирования – вычисляет производную:
Этот оператор играет очень важную роль в описании объектов управления.
Обычно оператор дифференцирования
обозначается буквой p. Интегрирование
это 1/p.
Запись
внешне выглядит как «умножение» оператора
p на сигнал
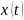), но на самом деле обозначает действие
этого оператора, то есть дифференцирование:
Примеры оператора дифференцирования – конденсатор (напряжение вход, ток выход), катушка (ток вход, напряжение выход).
5. Что такое линеаризация характеристики звена системы регулирования? в чем её польза? При выполнении каких условий она допустима?
Замена точного значения приращения
функции её дифференциалом в окрестности
принято называть линеаризацией
зависимости
.
Линеаризацию удобнее производить по
звеньям. Допустим, что в звене A
выходная величина y
является нелинейной функцией одной
входной величины x
(рис. 2.1 а). При
имеем
.
Пусть входная величина x
получила относительно начального
значения
приращение
,
так что
.
Тогда приращение выходной величины
Дифференциал функции y, определяемый как главная часть её приращения, при данном значении независимой переменной x равен значению производной при этом значении, умноженному на дифференциал независимой переменной:
Тогда для малых
.
Здесь
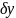– малая величина более высокого порядка,
чем
,
и которая обычно отбрасывается. В случае
необходимости величину погрешности
можно оценить, разложив функцию
в ряд Тэйлора в окрестности точки
.
Геометрически линеаризация нелинейной
зависимости между переменными x
и y (см. рис. 2.1 б) означает
замену исходной кривой AB
отрезком её касательной
в точке
,
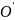соответствующей заданному режиму, и
параллельному переносу начала координат
в эту точку.
Её польза – представление сложной функции в виде линейных участков для упрощения выполнения математических операций с ними.
Линеаризация допустима только при существовании производной в данной точке. Если же вдруг там происходит в функции скачок, то тут мы и представляем нашу функцию в виде вертикальной прямой. Так же линеаризация недопустима если у нас из-за этого очень сильно снижается точность и сильно искажаются кривые процессов.
Пример 2.1.
Нелинейное статическое звено описывается
уравнением
.
Выполните линеаризацию характеристики
этого звена вблизи точки
.
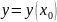Имеем:
При получим
.
Видим, что коэффициент усиления
линеаризованного звена зависит от
величины входного сигнала x.
В частности, при
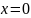он равен нулю.