29. Построение областей устойчивости в плоскости параметров системы автоматического управления. D–разбиение. Выделение областей устойчивости

С помощью рассмотренных выше критериев устойчивости можно определить, устойчива ли система автоматического регулирования с заданными параметрами. Однако критерии не дают возможности определить, в каких пределах можно менять тот или иной параметр или два параметра одновременно, чтобы система оставалась устой­чивой. Это можно сказать с помощью некоторых критериев устойчи­вости лишь по отношению к коэффициенту усиления.

Впервые вопросом выделения областей устойчивости занялись Вышнеградский и Неймарк. Этот метод по­лучил название Д-разбиения.

Построение областей устойчивости в плоскости параметров системы автоматического управления. D–разбиение.

При исследовании устойчивости большое практическое значение имеет построение областей устойчивости в плоскости одного или каких-либо двух параметров, влияние которых на устойчивость исследуют, а также построение семейства областей устойчивости в плоскости двух параметров при различных фиксированных значениях третьего параметра. Уравнение границ областей устойчивости можно находить, пользуясь любым критерием устойчивости. Часто для этих целей используют критерий Михайлова.

Понятие о d–разбиении

Характеристическое уравнение замкнутой системы n–порядка имеет вид:

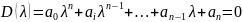(9.1)

или

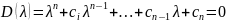(9.2)

где .

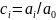Представим себе n–мерное пространство, по координатным осям которого отложены коэффициенты уравнения (9.2). Это пространство называют пространством коэффициентов. Каждой точке пространства коэффициентов соответствуют конкретные численные значения коэффициентов уравнения (9.2) и соответствующий им полином n-го порядка. Уравнение (9.2) имеет n корней, расположение которых на комплексной плоскости корней 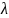зависит от численных значений коэффициентов .

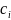Если изменять коэффициенты уравнения (9.2), то его корни, в силу их непрерывной зависимости от коэффициентов, будут перемещаться в комплексной плоскости корней, описывая корневые годографы.

Чтобы представить расположение корней геометрически, рассмотрим характеристическое уравнение третьего порядка (n = 3).

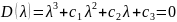. (9.3)

Если взять три взаимно-перпендикулярные оси и откладывать по ним значения коэффициентов 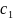, , 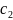, 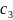то получим трехмерное пространство коэффициентов, каждой точке которого (рис. 9.1) соответствует вполне определенный полином (9.3) и вполне определенные три корня в комплексной плоскости корней (рис. 9.2).

Рис. 9.1. 3-мерное пространство коэффициентов полинома .

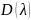Рис. 9.2. Расположение корней полинома на комплексной плоскости

При создании реальной системы управления бывает необходимо знать не только запас устойчивости, который можно оценить с помощью какого-либо критерия, но и всю область устойчивости по параметрам. Этой цели служит метод D-разбиения, позволяющий построить такую область в плоскости одного или двух параметров.

Рассмотрим суть метода D-разбиения по одному параметру D, который входит в характеристическое уравнение системы линейно:

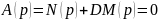(9.3)

Заменив в уравнении (9.1) р на 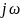, получим уравнение

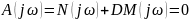(9.4)

соответствующее границе устойчивости согласно критерию Михайлова.

Разрешим его относительно D:

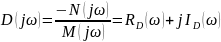. (9.5)

Получили комплексное представление параметра D, что позволяет изобразить его в виде вектора на комплексной плоскости. Конкретное числовое значение частоты определяет положение вектора 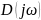. При изменении со в диапазоне от 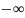до его конец выписывает на комплексной плоскости кривую D-разбиением, представляющую собой границу устойчивости (её также можно рассматривать как отображение мнимой оси плоскости корней).

Кривая D-разбиения симметрична относительно вещественной оси (рис. 9.3) поэтому достаточно построить её часть, соответствующую положительным значениям частоты, а вторую половину получить отображением относительно вещественной оси.

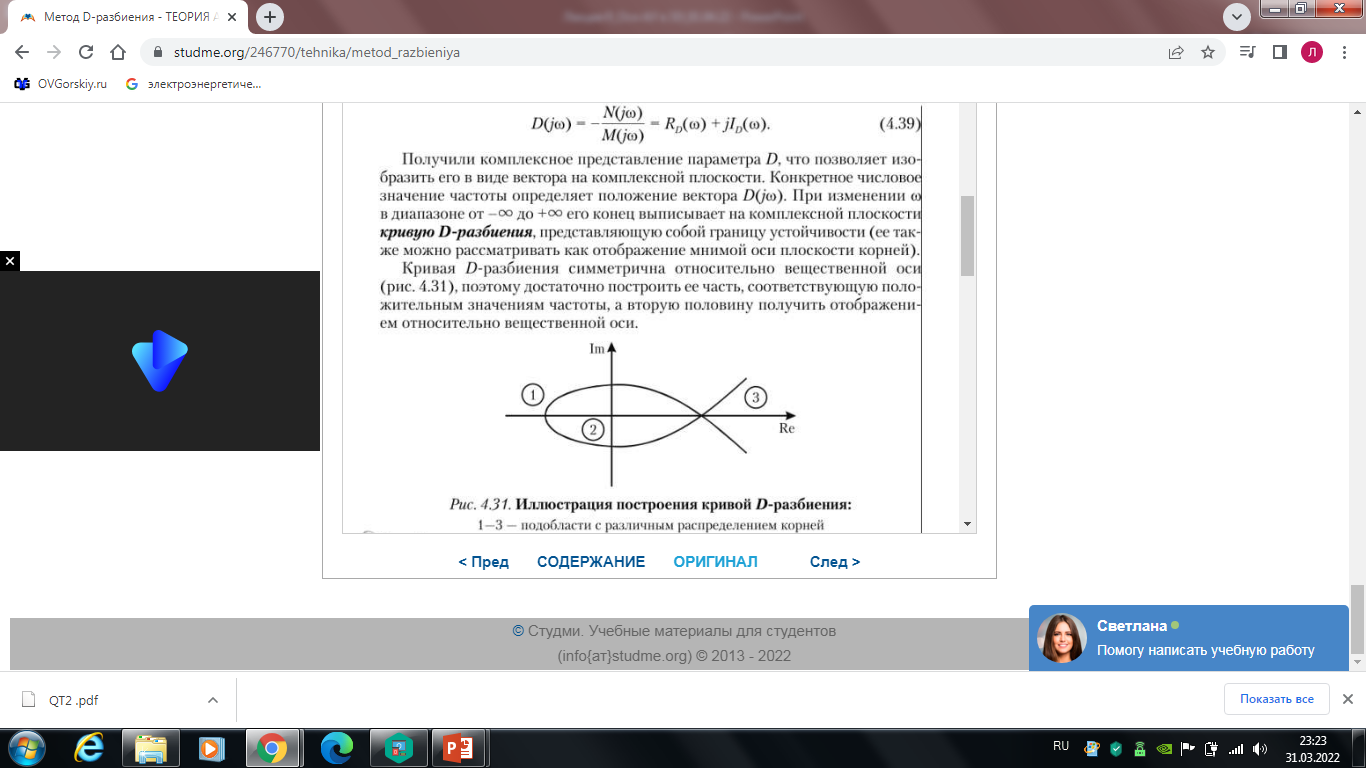
Рис. 9.3. Иллюстрация построения кривой D-разбиения:

1—3 — подобласти с различным распределением корней

Отметим, что эта кривая разбивает комплексную плоскость на несколько подобластей с различным соотношением корней. Для определения области устойчивости необходимо выбрать по одному значению D в каждой из них и проверить устойчивость с помощью какого-либо критерия. Если система устойчива при конкретном значении D, то она будет устойчива и при всех его значениях из этой области.

Обычно в качестве параметра D фигурирует реальный параметр системы (коэффициент усиления, постоянная времени, момент инерции и т.д.), который может иметь только вещественные значения. Представление его комплексным выражением носит формальный характер, а область устойчивости ограничивается отрезком вещественной оси.

Метод D-разбиения можно применять и для построения области устойчивости по двум параметрам 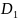 и 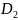, которые входят линейно в характеристическое уравнение

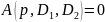(9.6)

В этом случае уравнение границы устойчивости имеет вид

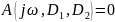(9.7)

и распадается на два независимых уравнения:

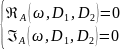(9.8)

Эти два уравнения параметрически задают кривую D-разбиения. Область устойчивости определяется аналогично случаю одного параметра D.

Д-разбиение плоскости одного параметра. Пусть какой-нибудь параметр Б (например, постоянная времени) входит линейно (в первой степени) в несколько коэффициентов характеристического уравнения, которое в этом случае можно записать в виде:

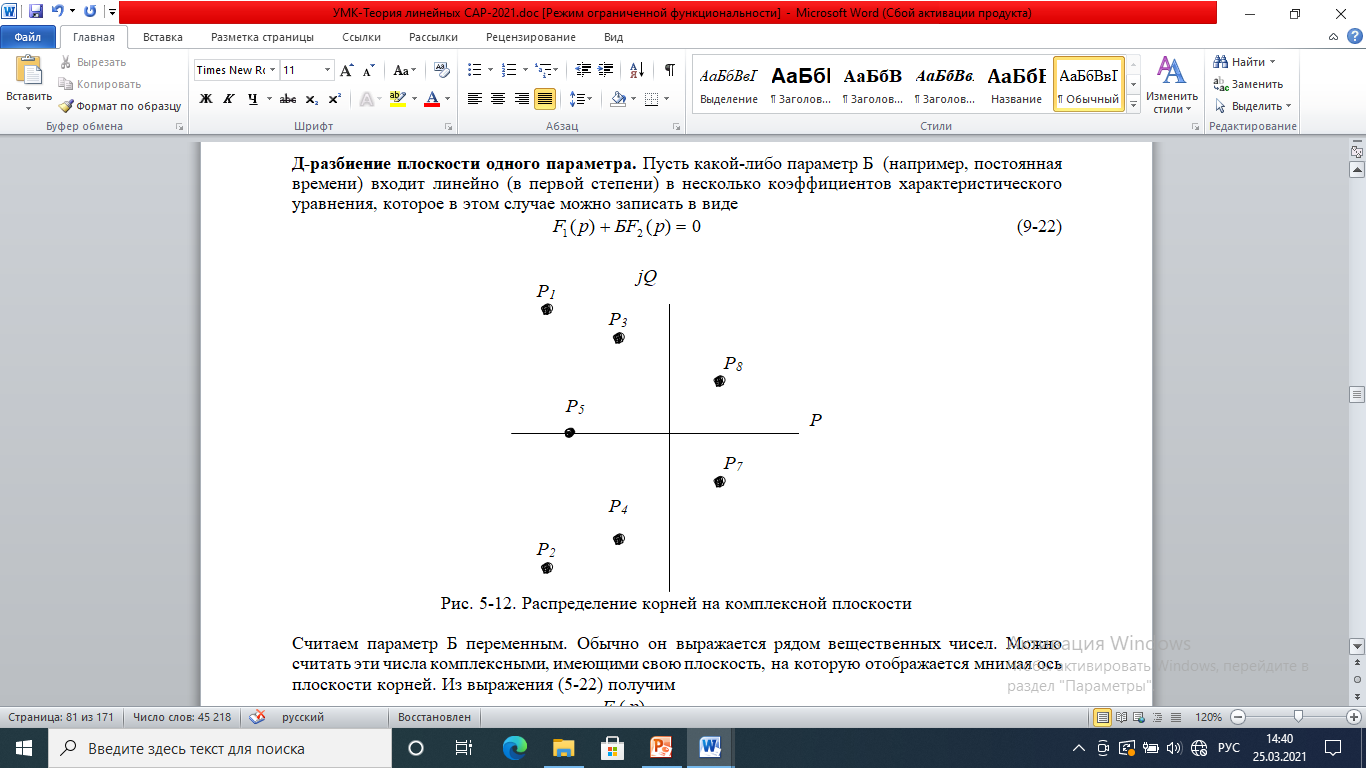
Рис. 9.6. Распределение корней на комплексной плоскости

Считаем параметр Б переменным. Обычно он выражается рядом вещественных чисел. Можно считать эти числа комплексными, имеющими свою плоскость, на которую отображается мнимая ось плоскости корней. Из выражения (9-22) получим:

Чтобы получить значения параметра Б, при которых хотя бы один корень находился на мнимой оси, в выражении (5-23) оператор р заменяем мнимым числом j и отделяем в полученном комплексном числе вещественную и мнимую части

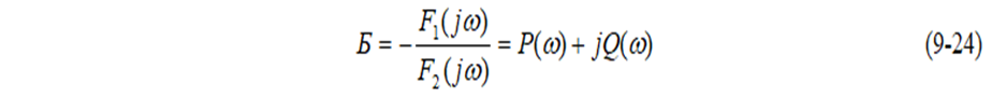
Чтобы получить все возможные значения параметра Б, соответствующие всем возможным мнимым корням, задаём в выражении (9-24) значения в пределах от -∞ до +∞, вычисляем соответствующие значения Р( ) и Q( ) и строим в этих координатах линию, которая является отображением мнимой оси плоскости корней на комплексную плоскость параметра Б или, иначе, границей Д-разбиения по параметру Б (рис. 9-8)

Рис. 9.7. Пример Д-разбиения плоскости параметров

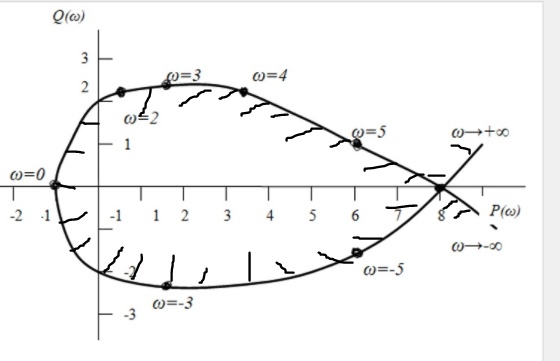
Рис. 9.8. Д-разбиение одного параметра

В устойчивой системе все корни находятся слева от мнимой оси, если двигаться в направлении от -∞ к +∞. Поскольку линия Д-разбиения является отображением мнимой оси, то область устойчивости также будет находиться слева от этой линии, если двигаться по ней в направлении от значения ω = -∞ к значению ω = +∞. Чтобы выявить область устойчивости, на линию Д-разбиения наносится штриховка слева при указанном перемещении -∞ к +∞.

Область, внутрь которой направлено больше штриховки, возможно является областью устойчивости. На рис. 9.8 –это область I. С помощью любого критерия устойчивости проверяется устойчивость системы для любой точки вещественной оси, лежащей в интересующей нас области. Если система устойчива для этой точки, значит, данная область является областью устойчивости. Может случиться, что область устойчивости отсутствует. Следовательно, система неустойчива при любом значении рассматриваемого параметра.