24. Критерии устойчивости критерий Михайлова.

Критерием устойчивости называется косвенный метод определения знаков вещественной части корней характеристического уравнения, не требующий решения этого уравнения.

Критерий Михайлова относится к частотным критериям устойчивости.

Критерий устойчивости Михайлова

Так же, как и критерий Гурвица, критерий Михайлова рассматривает характеристическое уравнение замкнутой системы. Выведем этот критерий. Разделим характеристическое уравнение системы (6.1) на коэффициент при высшей производной (при высшей степени p).

Это уравнение в общем случае имеет n комплексных корней

То есть мы можем разложить уравнение на множители:

Комплексное число может быть изображено на комплексной плоскости d, jω вектором, выходящим изначала координат (рис, 8-2).

Длина вектора равна модулю комплексного числа, а угол, образуемый вектором с положительным направлением вещественной оси, – его аргументу, если вектор записан в показательной форме p_i=A_i·e ^jθ. Координаты точки, лежащей в конце вектора, дают возможность записать его в форме (8-7).

Множители (р-р_i) выражения (8-8) представляют собой разность векторов, которая геометрически изображается вектором, проведённым из конца вычитаемого вектора р_i­ к началу уменьшаемого р (рис. 8-3).

Так как вектор р – произвольное комплексное число, то оно может быть принято и чисто мнимым. Вектор, изображающий это число, совпадает с направлением мнимой оси. Множители, входящие в уравнение (8-8), будут иметь вид

При меняющейся величине ω разность (8-9) представляет семейство векторов, показанное на рисунке 8-4.

Проследим за поворотом вектора jω-p_i при изменении ω от 0 до бесконечности. Начало этого вектора находится в неподвижной точке, соответствующей концу вектора p_i. Конец вектора будет скользить по мнимой оси от 0 до +∞, а сам вектор будет поворачиваться вокруг конца вектора p_i в ту или иную сторону в зависимости от того, по какую сторону от мнимой оси расположен вектор p_i.

Если корень p_i вещественный отрицательный, то вектор разности jω-p_i при изменении ω от 0 до +∞ повернётся против часовой стрелки на угол +π/2.

Если корень p_i вещественный положительный, то вектор разности при изменении ω от 0 до +∞ повернётся по часовой стрелке на угол -π/2.

При комплексных сопряжённых корнях с отрицательной вещественной частью углы поворота составят , при корнях с положительной вещественной частью

Характеристическое уравнение (8-8) можно рассматривать как произведение векторов вида jω-p_i, представляющие собой новый вектор, модуль которого равен произведению модулей векторов множителей, а аргумент – сумме аргументов векторов множителей. При изменении ω от 0 до +∞ угол поворота вектора произведения будет равен сумме углов поворота векторов множителей.

В устойчивой системе в характеристическом уравнении которой все вещественные части корней отрицательны и их n штук, суммарный угол поворота будет равен πn/2. В случае сопряжённых комплексных корней дополнительные углы +γ и -γ взаимно уничтожаются. В неустойчивой системе, в характеристическом уравнении которой содержатся отрицательные и положительные вещественные части корней, суммарный угол поворота вектора произведения меньше πn/2.

Чтобы получить наш критерий устойчивости – достаточно построить АФЧХ. Для этого надо сделать следующее. В наше характеристическое уравнение подставить p=jω, а затем отделить мнимую и действительную часть.

АФЧХ это график в координатах (P(ω), Q(ω)), поэтому подставляя значения ω от 0 до +∞ мы сможем построить график АФЧХ – эта характеристическая кривая называется годограф Михайлова. При изменении ω от 0 до +∞ вектор F(jω) будет перемещаться своим концом по годографу, поворачиваясь на некоторый угол.

В случае устойчивой системы, когда угол поворота вектора равен πn/2, годограф пройдёт через n квадрантов комплексной плоскости, не проходя через начало координат (рис. 8-5, кривая 1).

Если система неустойчива, то общий угол поворота будет меньше πn/2 и годограф не пройдёт через n квадрантов (рис. 8-5, кривая 2).

Формулировки критерия Михайлова:

Первая формулировка. Если при изменении частоты от нуля до бесконечности годограф Михайлова начинается на действительной оси в точке а_n‚ последовательно проходит против часовой стрелки n квадрантов комплексной плоскости, не проходя через ноль, и уходит в бесконечность в n-м квадранте, – система устойчива.

Вторая формулировка. Если при изменении частоты от нуля до бесконечности вектор комплексного частотного полинома F(jω) последовательно поворачивается против часовой стрелки на угол πn/2‚ где n — степень характеристического полинома, и нигде не становится нулём, – система устойчива.

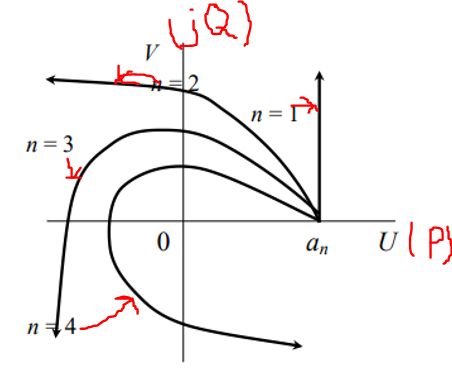Примеры годографов в зависимости от n.