Уравнение пятого порядка

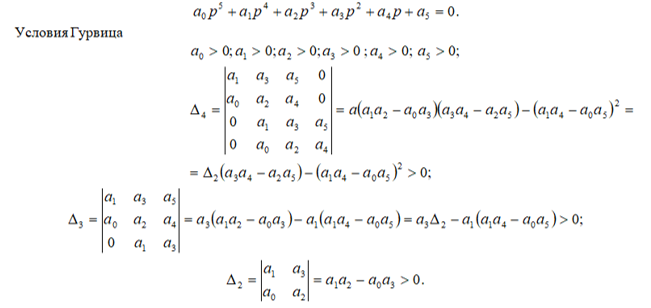
Из рассмотрения определителей следует, что если Δ₂>0 и Δ₄>0, то Δ₃ тоже положителен и его нет надобности вычислять.

Для того чтобы система, описываемая дифференциальным уравнением пятого порядка, была устойчивой, необходимо и достаточно, чтобы все коэффициенты характеристического уравнения и определители Δ₂ и Δ₄ были положительными.

Критерий устойчивости Рауса

Практически критерием Гурвица выгодно пользоваться при исследовании устойчивости САУ не выше пятого порядка, Для систем более высоких порядков удобнее применять критерии Рауса. Для этого необходимо составить таблицу – схему из коэффициентов характеристического уравнения (таблица–схема дана ниже).

В первую строку таблицы вписываются коэффициенты с чётными индексами, а во вторую — с нечётными. Все последующие строки получаются в результате деления разности перекрёстных произведений коэффициентов двух предыдущих строк на коэффициент первого столбца предыдущей строки.

Согласно критерию Рауса для устойчивости системы необходимо и достаточно, чтобы при a₀>0 все коэффициенты первого столбца таблицы были положительны, т.е. чтобы a₁>0, b₁>0, …

Всего таблица содержит n+1 строку.

23. Критерии устойчивости критерий Найквиста.

Критерием устойчивости называется косвенный метод определения знаков вещественной части корней характеристического уравнения, не требующий решения этого уравнения.

Критерий Найквиста относится к частотным критериям устойчивости.

Критерий устойчивости Найквиста

Критерий Найквиста позволяет судить об устойчивости замкнутой САУ (рис. 7.10) по амплитудно-фазовой частотной характеристике разомкнутой системы.

Передаточная функция замкнутой системы относительно сигнала рассогласования по задающему воздействию (видимо W_ос=1?):

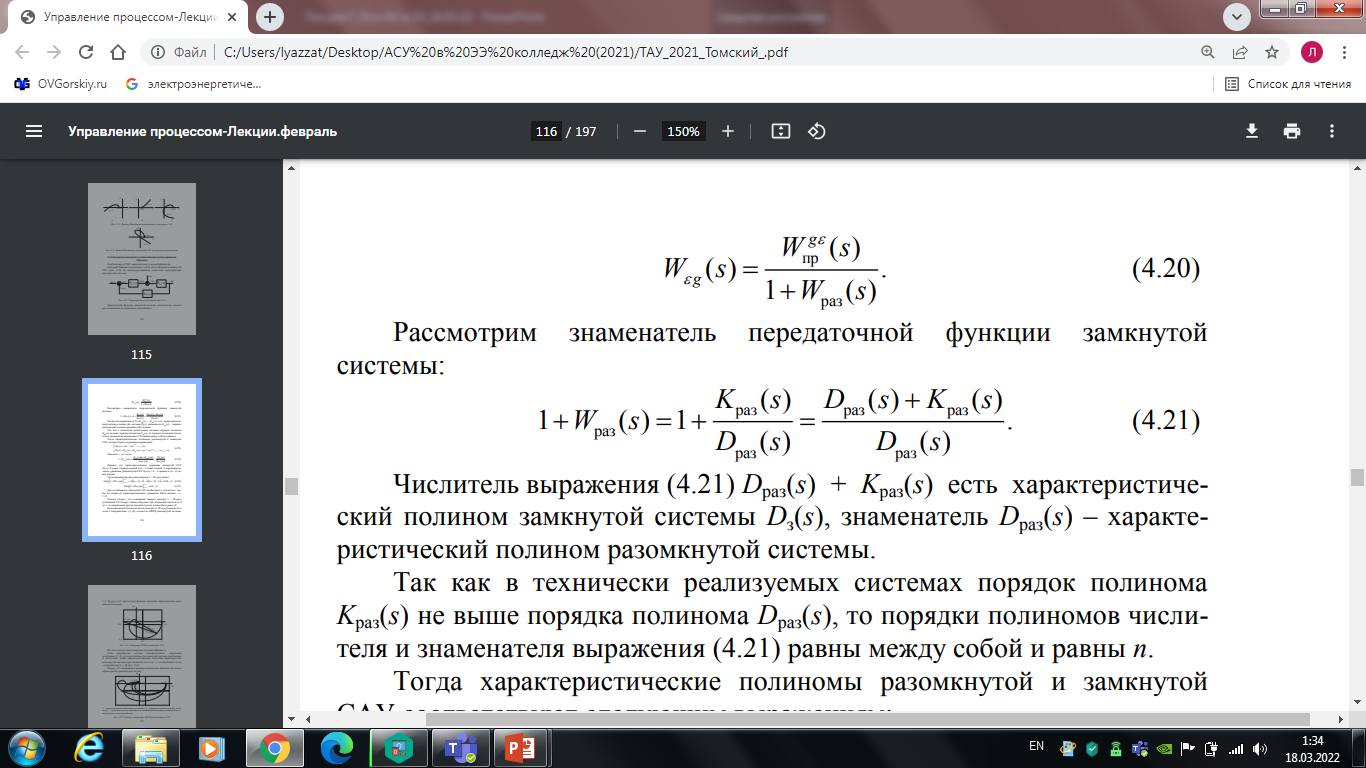(7.20)

Рассмотрим знаменатель передаточной функции замкнутой системы:

(7.21)

Числитель выражения (7.21) D_раз(s)+K_раз(s) есть характеристический полином замкнутой системы D_з(s), знаменатель D_раз(s) – характеристический полином разомкнутой системы. Так как в технически реализуемых системах порядок полинома K_раз(s) не выше порядка полинома D_раз(s), то порядки полиномов числителя и знаменателя выражения (7.21) равны между собой и равны n.

Тогда характеристические полиномы разомкнутой и замкнутой САУ соответствуют следующим выражениям:

(7.22)

(7.23)

Примем, что характеристическое уравнение замкнутой САУ D_з(s)=0 имеет l правых корней и (n–l) левых корней (тут имеется в виду вещественная часть положительная и отрицательная). А характеристическое уравнение разомкнутой САУ D_раз(s) = k правых и (n–k) левых корней.

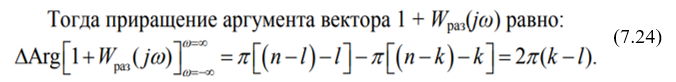
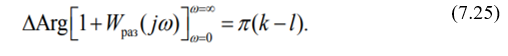
Бля, я честно не знаю, как эти аргументы были посчитаны, тут надо подумать толково, а мне лень, поэтому ниже попытался объяснить. Но она тоже не знает, откуда они берутся, так что пофиг.

Если как-то по-простому объяснять, то у нас есть числитель и знаменатель. Когда умножаем комплексные числа, то углы складываются, когда делим, то вычитаются. У нас числитель (D_з(s)=0) имеет l правых корней и (n–l) левых корней. Нам важны левые корни, потому что они нам дают отрицательную вещественную часть и поворот против часовой стрелки, который как раз берётся со знаком плюс. Теперь, когда мы меняли ω от 0 до +∞, то мы умножали количество корней на угол π/2, а здесь мы меняем ω от -∞ до +∞, поэтому умножаем и на угол π.

Для устойчивости замкнутой САУ необходимо и достаточно, чтобы все корни её характеристического уравнения были левыми, т. е. l = 0.

Отсюда следует, что суммарный поворот вектора 1+W_раз(jω) устойчивой САУ вокруг начала координат при изменении частоты от 0 до 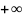в направлении против часовой стрелки должен быть равен .

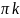На комплексной плоскости начало вектора (1+W_раз(jω)) находится в точке с координатами: (-1; j0), а конец на АФЧХ разомкнутой системы, т.к. W_раз(jω) есть амплитудно-фазовая частотная характеристика разомкнутой системы.

Из этого следуют формулировки критерия Найквиста.

1) Если разомкнутая система автоматического управления устойчивая (k=0), то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении от 0 до +∞ не охватывала точку с координатами [-1; j0] (рис. 7.11).

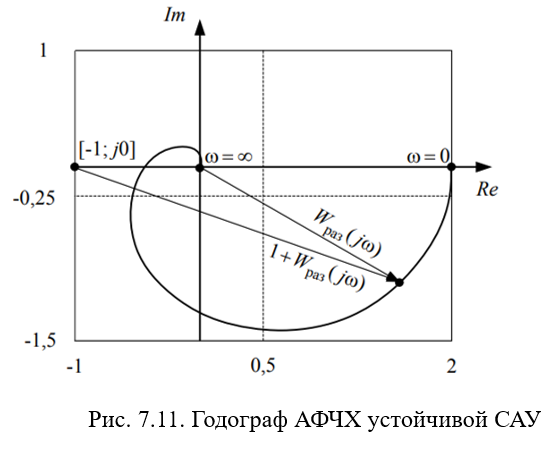
2) Если же разомкнутая система автоматического управления неустойчива, то для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы АФЧХ неустойчивой разомкнутой системы (k>0) при изменении частоты от 0 до +∞ охватывала точку 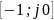в положительном направлении k/2 раз, где k – число правых корней характеристического уравнения разомкнутой системы.

Назовём переход W_раз(jω) через вещественную ось слева от точки , т.е. через интервал 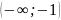, положительным, если он идёт сверху вниз, и отрицательным, если он идёт снизу вверх. Если W_раз(jω) начинается на интервале при 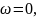или заканчивается на нем при 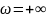, то в этих случаях считают, что она совершила полперехода.

На рис. 7.12 изображены примеры амплитудно-фазовых частотных характеристик разомкнутых систем.

Тогда критерий Найквиста можно сформулировать так: 3) если разомкнутая система автоматического управления неустойчива, то для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов АФЧХ разомкнутой САУ через отрезок вещественной оси 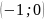при изменении частоты от 0 до +∞ была равна k/2, где k – число правых корней характеристического уравнения разомкнутой САУ.