21. Что такое критерий устойчивости?

Критерием устойчивости называется косвенный метод определения знаков вещественной части корней характеристического уравнения, не требующий решения этого уравнения.

Наиболее простым является условие устойчивости Стодолы, которое является необходимым, но недостаточным, однако оно позволяет по виду уравнения легко определить явно неустойчивую систему. Условие это формулируется следующим образом. Для того чтобы система была устойчивой, необходимо (но недостаточно), чтобы все коэффициенты характеристического уравнения имели одинаковые знаки. Если знаки при коэффициентах разные, это свидетельствует о том, что уравнение содержит положительные корни, хотя оно может содержать их и при одинаковых знаках перед коэффициентам.

Ценность критериев устойчивости не только в том, что они позволяют судить об устойчивости, не вычисляя корни характеристического уравнения, но также (и в большей степени) в возможности сравнительно просто выяснить причину неустойчивости, выявить, какие параметры и в какую сторону следует менять.

Все известные критерии делятся на две группы: алгебраические и частотные:

-к алгебраическим относятся критерии Вышнеградского, Рауса, Гурвица.

-к частотным относятся критерии Михайлова, Найквиста, когда об устойчивости системы судят по виду частотной характеристики разомкнутой или замкнутой системы.

22. Критерии устойчивости. Критерий Гурвица и критерий Рауса.

Критерием устойчивости называется косвенный метод определения знаков вещественной части корней характеристического уравнения, не требующий решения этого уравнения.

Критерии Гурвица и Рауса относятся к алгебраическим критериям устойчивости.

Критерий устойчивости Гурвица

Критерий Гурвица формулируется следующим образом: чтобы корни характеристического уравнения системы автоматического регулирования, имеющей вид

при а₀>0 имели отрицательные вещественные части, необходимо и достаточно, чтобы главный определитель и все его диагональные миноры были положительны.

Для составления главного определителя по главной диагонали выписывают все коэффициенты уравнения от а₁ до а_n-1 в порядке возрастания индексов. Столбцы вверх от элементов диагонали дополняют коэффициентами того же уравнения с последовательно возрастающими индексами, вниз – с последовательно убывающими индексами. На место коэффициентов, индекс которых больше n и меньше нуля, проставляют нули.

Диагональные миноры имеют следующий вид:

и т.д.

Если все коэффициенты характеристического уравнения отрицательны, то их можно сделать положительным, умножив обе части уравнения на -1.

Уравнение первого порядка

Для того чтобы система, описываемая дифференциальным уравнением первого порядка, была устойчивой, необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были положительными.

Уравнение второго порядка

Для того чтобы система, описываемая дифференциальным уравнением второго порядка, была устойчивой, необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были положительными.

Уравнение третьего порядка

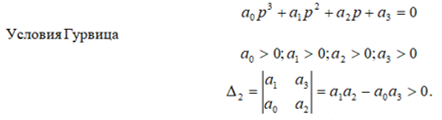
Для того чтобы система, описываемая дифференциальным уравнением третьего порядка, была устойчивой, необходимо и достаточно, чтобы все коэффициенты характеристического уравнения и определитель Δ₂ были положительными.

Уравнение четвёртого порядка

Для того чтобы система, описываемая дифференциальным уравнением четвёртого порядка, была устойчивой, необходимо и достаточно, чтобы все коэффициенты характеристического уравнения и определитель Δ₃ были положительными. Почему только Δ₃? Потому что диагональный минор Δ₂ входит множителем в положительную часть определителя Δ₃, поэтому Δ₃ может быть положительный только при условии, что Δ₂ положителен.