19. Получение передаточной функции и частотных характеристик сау по передаточным функциям и частотным характеристикам её звеньев.

Как получить передаточную функцию всей системы по передаточным функциям звеньев – рассмотрено в вопросах 7 и 8.

А вот как получить частотную характеристику системы по частотным характеристикам звеньев – мы не проходили))). Соответственно, я сейчас сам попробую что-то пояснить своими словами. Для этого воспользуемся следующим видом передаточной функции абсолютно любого звена, все частотные характеристики которого известны

1) Последовательное соединение

Передаточные функции умножаются. Значит будет следующее:

то есть ;

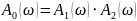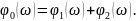
ВЧХ и МЧХ вычисляются сложнее (в плане формулы большеватые), но их легко вывести из АЧХ.

2) Параллельное соединение

Передаточные функции складываются. Значит будет следующее:

то есть ;

АЧХ и ФЧХ вычисляются сложнее (в плане формулы неприятные), но их легко вывести из ВЧХ и МЧХ.

20. Устойчивость линейных сау. Понятие об устойчивости.

В процессе работы системы автоматического регулирования подвергаются различным возмущающим воздействиям, которые выводят систему из установившегося режима, из состояния равновесия и отклоняют регулируемую величину от заданного значения. Регулятор стремится привести регулируемую величину к заданному значению. Переход системы из одного состояния в другое вследствие наличия инерции не может произойти мгновенно. В результате возмущающих воздействий и следующих за ними восстанавливающих воздействий регулятора в системе возникают переходные процессы.

При этом могут иметь место три вида переходных процессов:

1. Регулируемая величина, которая в результате возмущающих воздействий отклонилась от заданного значения, с течением времени под воздействием регулятора возвращается к заданному значению с точностью, отвечающей статической погрешности регулятора. Такой переходной процесс называется сходящимся, а система регулирования – устойчивой.

2. Регулируемая величина, которая в результате возмущающих воздействий отклонилась от заданного значения, с течением времени под воздействием регулятора не приближается, а теоретически беспредельно удаляется от заданного значения апериодически или с колебаниями, амплитуда которых непрерывно возрастает. Такой переходной процесс называется расходящимся, а система регулирования – неустойчивой.

Однако, в реальных условиях не может произойти беспредельное отклонение какого-либо физического параметра от заданного значения так же, как невозможны и колебания с беспредельно возрастающей амплитудой.

Отклонения ограничиваются свойствами элементов: насыщением электрических машин, максимальным ходом поршней, ограниченной мощностью двигателей и т. п. Однако возникающие колебания или неконтролируемые отклонения регулируемой величины могут быть недопустимы по соображениям сохранности оборудования, безопасности и др.

3. Регулируемая величина, которая в результате возмущающих воздействий отклонилась от заданного значения, с течением времени под воздействием регулятора к установившемуся значению не возвращается, а совершает незатухающие колебания с амплитудой, зависящей от начальных условий. Такой переходной процесс называется колебательным, а линейная система регулирования – находящейся на границе устойчивости.

Задачей замкнутой системы регулирования является поддержание выходной переменной в соответствии с сигналом задания. Это требует, чтобы неустановившийся процесс, вызванный случайным возмущением, затухал в самое короткое время после прекращения действия этого возмущения.

Системы, в которых процесс изменения регулируемой величины происходит беспорядочно, не соответствует входному сигналу, а также в которых возникают самовозбуждающиеся колебания, называют неустойчивыми.

Рис. 6.1. Структурная схема (а) и примеры переходных процессов в устойчивой (б) и неустойчивой (в) системах регулирования

То есть здесь мы подаём на вход X_вх и система может по-разному реагировать (монотонно – кривая 1, и колебательно – кривая 2).

Реакция линейной системы на внешнее воздействие состоит из двух составляющих:

где 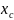– переходная составляющая, или составляющая собственных (свободных) движений системы; – составляющая вынужденного движения.

Чтобы система регулирования могла воспроизводить входной сигнал, переходная составляющая должна затухать. Если же собственное движение линейной системы расходится, то такая система неустойчива.

Переходная составляющая движения в линейной системе представляет собой сумму экспоненциальных составляющих. Переходная составляющая 𝑥_с будет затухать только в том случае, если будет затухать каждая из экспоненциальных составляющих в отдельности. Затухание или незатухание компоненты целиком определяется знаком соответствующего корня характеристического уравнения системы: в устойчивой системе все корни характеристического уравнения (или все полюсы передаточной функции) расположены слева от мнимой оси плоскости корней.

В нелинейных системах могут возникать устойчивые колебания постоянной амплитуды, величина которой не зависит от начальных условий, к которым система возвращается после снятия любого возмущающегося воздействия. Такие системы рассматривают, как имеющие устойчивые колебания.

Чтобы определить, устойчиво ли равновесие какой-либо статической системы, изучают поведение этой системы при малых отклонениях от положения равновесия.

Дальше идёт простой пример, чтоб понять, что происходит. Всё же решил написать его сюда, но не думаю, что надо его учить. Главное из него можно понять, что значит устойчивость в малом и устойчивость в большом.

Например, для того, чтобы определить устойчивость шара в положении А (рис. 6.2), можно задать ему малое отклонение и рассмотреть действие возникающих при этом сил. При любом малом отклонении шара от положения А возникают силы, возвращающие его в первоначальное положение, и, следовательно, это положение равновесия устойчиво.

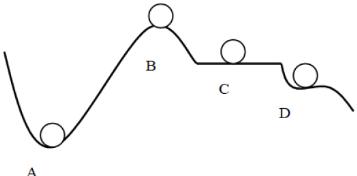
Рис. 6.2. Различные виды равновесия

При малом отклонении шара от положения равновесия в точке В возникают силы, продолжающие отклонять шар от положения равновесия, которое в данном случае является неустойчивым.

Шар, расположенный на горизонтальной плоскости в точке С, находится в безразличном равновесии, так как при отклонениях его от точки С никакие дополнительные силы не возникают. Шар, расположенный в точке D, находится в полуустойчивом равновесии.

Устойчивость системы при бесконечно малых отклонениях называется устойчивостью в малом. Часто системы, устойчивые в малом, оказываются устойчивыми и при конечных достаточно больших отклонениях, т. е. система оказывается устойчивой в большом. Встречаются системы, устойчивые в малом, но неустойчивые в большом.

На рис. 6.2 шар, расположенный в точке А, не теряет устойчивости до тех пор, пока отклонения не переходят за точку В. Система устойчива в малом, но в большом она устойчива лишь в ограниченной области.

При исследовании систем автоматического регулирования рассматривают устойчивость в малом, т.е. поведение системы при малых отклонениях регулируемой величины от установившегося значения.

В линейных системах устойчивость в малом обеспечивает устойчивость и в большом.

Нелинейная система, устойчивая в малом, может оказаться неустойчивой в большом и поэтому методы исследования устойчивости нелинейных систем существенно отличается от методов исследования линейных систем.

Свободное движение линейной системы автоматического регулирования, выведенной малым отклонением из состояния равновесия, описывается дифференциальным уравнением замкнутой системы. Представьте, что вместо y_c должно быть .

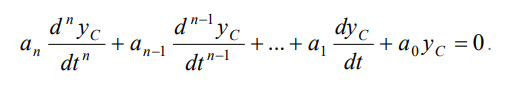
В операторном виде уравнение имеет следующий вид:

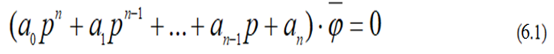
Система регулирования, описываемая таким уравнением, будет устойчива лишь в том случае, если все корни характеристического уравнения будут иметь отрицательные вещественные части.

Убедиться в правильности этого утверждения можно на основании следующих рассуждений. Предположим, что все корни характеристического уравнения, соответствующего дифференциальному уравнению (6.1) вещественны и различны и имеют значения p₁, p₂, …, p_n

Тогда решение уравнения (6.1) имеет вид:

Если хоть один из корней, например р₁, положителен, то соответствующий член c течением времени неограниченно возрастает и отклонение регулируемой величины . Система неустойчива.

При комплексных сопряжённых корнях в случае отрицательных вещественных частей отклонение регулируемой величины приходит к установившемуся значению с затухающими гармоническими колебаниями. Система устойчива.

При положительном значении вещественной части хотя бы одной пары корней отклонение регулируемой величины совершает колебания с неограниченно возрастающей амплитудой. Система неустойчива.

Если характеристическое уравнение линеаризованной системы, не имея положительных корней, имеет хотя бы один нулевой корень или пару чисто мнимых сопряжённых корней, то поведение реальной системы не может определяться её линеаризованным уравнением. В таком случае отброшенные при линеаризации уравнения члены со второй и высшими производными существенно влияют на устойчивость системы.

Таким образом, анализ устойчивости систем автоматического регулирования сводится к чисто алгебраической задаче – определению знака вещественных частей корней характеристического уравнения.

Для облегчения исследования устойчивости были предложены так называемые критерии устойчивости.

Итак, линейная стационарная система устойчива, если все вещественные корни её характеристического уравнения отрицательны, а все комплексные – имеют отрицательную вещественную часть.

Однако трудность заключается в том, что корни уравнений высоких степеней найти трудно. В связи с этим возникла необходимость судить об устойчивости системы регулирования, минуя задачу определения корней. Правила, которые позволяют анализировать устойчивость без решения характеристического уравнения системы, получили название критериев устойчивости.