15. Типовые звенья сау. Статическое звено, Апериодическое звено первого и второго порядков, колебательное.

Пропорциональное (безынерционное) звено. Пропорциональным звеном называют звено, которое описывается уравнением

,

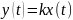где – коэффициент усиления звена.

Это – наиболее простое звено, процессы в котором протекают без запаздывания. Его передаточная функция

, амплитудно-фазовая характеристика вырождается в точку на действительной оси, логарифмическая амплитудная частотная характеристика параллельна оси частот во всем диапазоне частот и проходит на уровне , фазовая частотная характеристика совпадает с осью частот, так как и, наконец, переходная функция этого звена повторяет без искажений входную ступенчатую функцию (рис. 3.5).

Рис. 3.5. Пропорциональное звено:

а) передаточная функция;

б) амплитудно-фазовая характеристика;

в) логарифмические амплитудная и фазовая характеристики; г) переходная функция

Примерами пропорционального звена (рис. 3.6) можно назвать делитель напряжения (потенциометр), механический редуктор, пропорциональный, или П-регулятор. В последнем случае операционный усилитель ОУ, имеющий очень высокий (до нескольких сотен тысяч) коэффициент усиления, охвачен схемой, содержащей резисторы и . В результате регулятор – схема, представляющая собой совокупность ОУ и резисторов и , – имеет передаточную функцию вида:

.

Рис. 3.6. Примеры пропорциональных звеньев:

а) потенциометр;

б) механический редуктор; в) П-регулятор

Инерционное звено (апериодическое 1го порядка)

Во прикол, а она его подробно не объясняла, поэтому вот просто ловите скрин всех частотных характеристик и их построение.

И

1) Вещественная частотная характеристика (ВЧХ)

2) Мнимая частотная характеристика (МЧХ)

3) Амплитудная частотная характеристика (АЧХ)

4) Фазовая частотная характеристика (ФЧХ)

5) Логарифмическая амплитудная характеристика (ЛАЧХ)

6) Амплитудно-фазовая частотная характеристика (АФЧХ)

Колебательное звено

Колебательным (двухъёмкостным) называется звено второго по­рядка, в котором при получении на входе ступенчатого воздействия выходная величина стремится к новому установившемуся значению, совершая затухающие колебания.

К колебательным звеньям относятся устройства, в которых переходные режимы протекают с обменом энергией между двумя энергетическими ёмкостями, например, электрическая цепь, содер­жащая индуктивность, ёмкость и активное сопротивление; механи­ческое устройство, имеющее массу, пружину и силы трения; элек­трический двигатель постоянного тока с независимым возбуждением, способный накапливать кинетическую энергию в якоре и электро­магнитную энергию в магнитной цепи, для которого входной вели­чиной является напряжение, приложенное к якорю, а выходной — скорость вращения якоря.

Примерами колебательного звена могут служить: упругая механическая система с существенным влиянием массы, электрический колебательный контур и т. д

Где k₁ = kω₀; ω₀= – угловая частота свободных колебаний (при отсутствии затуханий);

ξ – параметр затухания, лежащий в пределах 0<ξ<1.

2. Передаточная функция звена:

3. Временные характеристики колебательного звена второго порядка:

3.1 Переходная функция (рис.5.2 б):

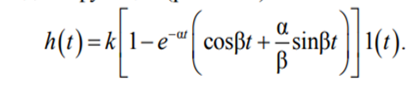
3.2 весовая функция

k – коэффициент, T – постоянная времени (в секундах), ξ – параметр затухания ( 0 < ξ < 1). Постоянная времени определяет инерционность объекта, чем она больше, тем медленнее изменяется выход при изменении входа. Чем больше ξ , тем быстрее затухают колебания.

При ξ = 0 в получается консервативное звено, которое даёт незатухающие колебания на выходе. Если ξ ≥ 1, модель представляет апериодическое звено второго порядка, то есть последовательное соединение двух апериодических звеньев.

Колебательное звено относится к позиционным звеньям, его статический коэффициент усиления равен W (0) = k .

Переходная и импульсная характеристики отличаются выраженной колебательностью, особенно при малых значениях параметра затухания ξ . На следующих двух графиках синие линии соответствуют ξ = 0,5, а красные – ξ = 0,25 .

Рис. 5.2 а. Переходная характеристика колебательного звена

Рис. 5.2.б Переходная функция колебательного звена второго порядка

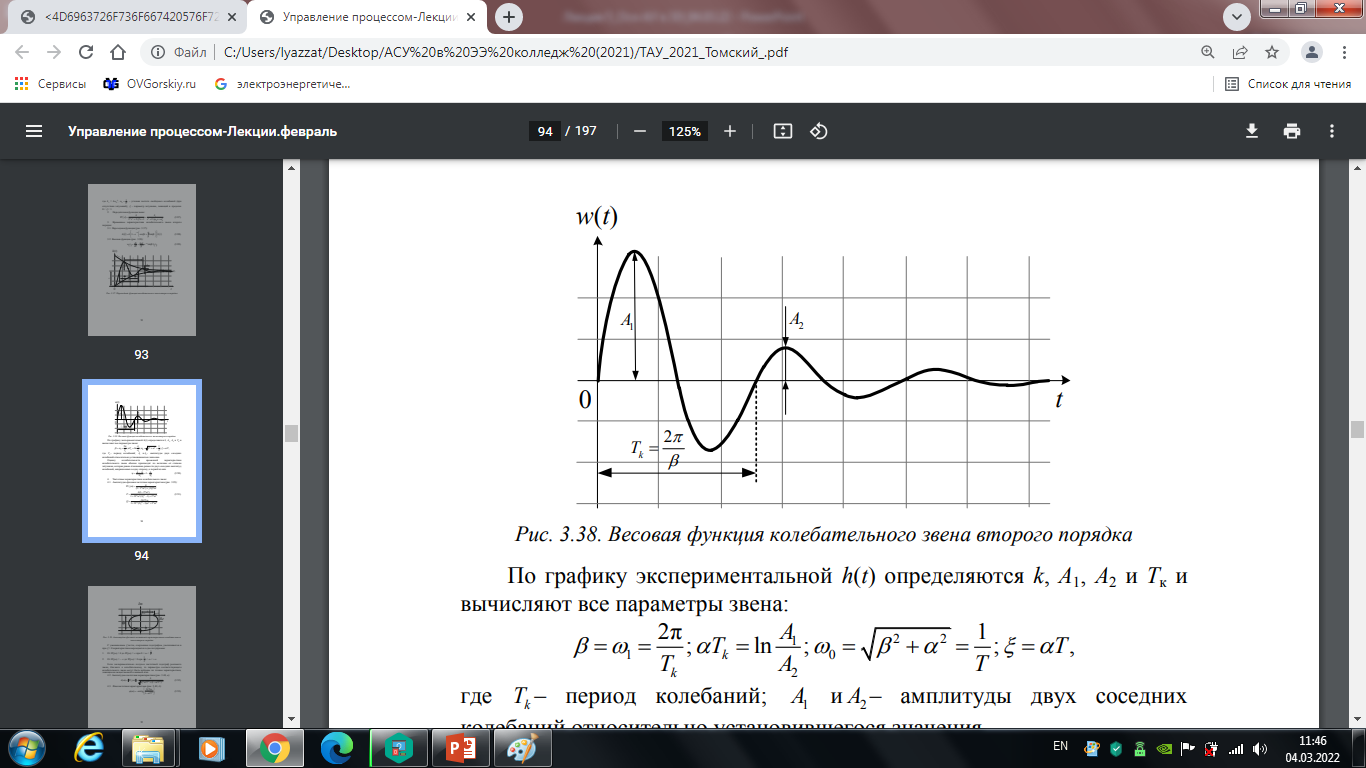
Рис. 5.3. Весовая функция колебательного звена второго порядка

По графику экспериментальной h(t) определяются k, А₁, А₂, и Т_k и вычисляют все параметры звена:

Где T_k – период колебаний, А₁ и А₂ – амплитуды двух соседних колебаний относительно установившегося значения.

Оценку колебательности временной характеристики колебательного звена обычно производят по величине её степени затухания, которая равна отношению разности двух соседних амплитуд колебаний, направленных в одну сторону, к первой из них.

Частотные характеристики

Частотные характеристики колебательного звена: 4.1. Амплитудно-фазовая частотная характеристика (рис. 5.4):

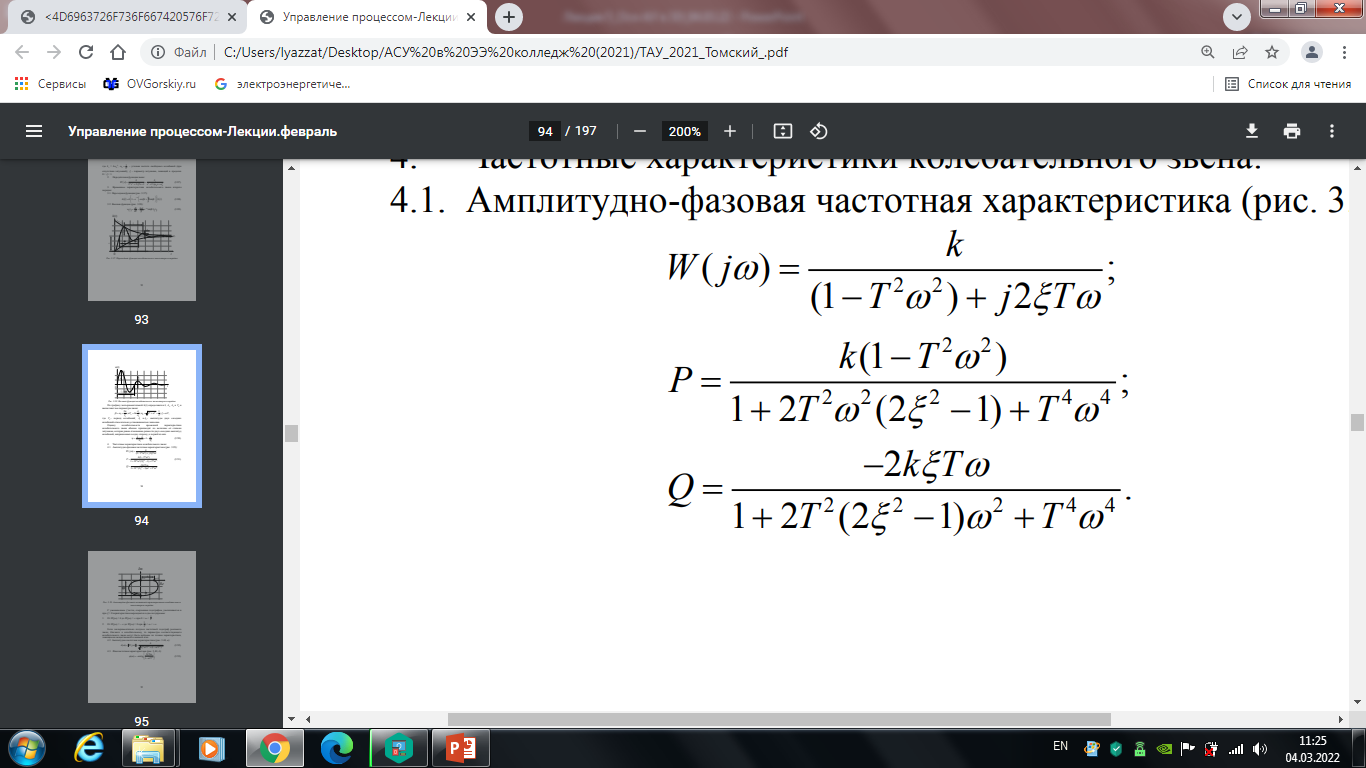
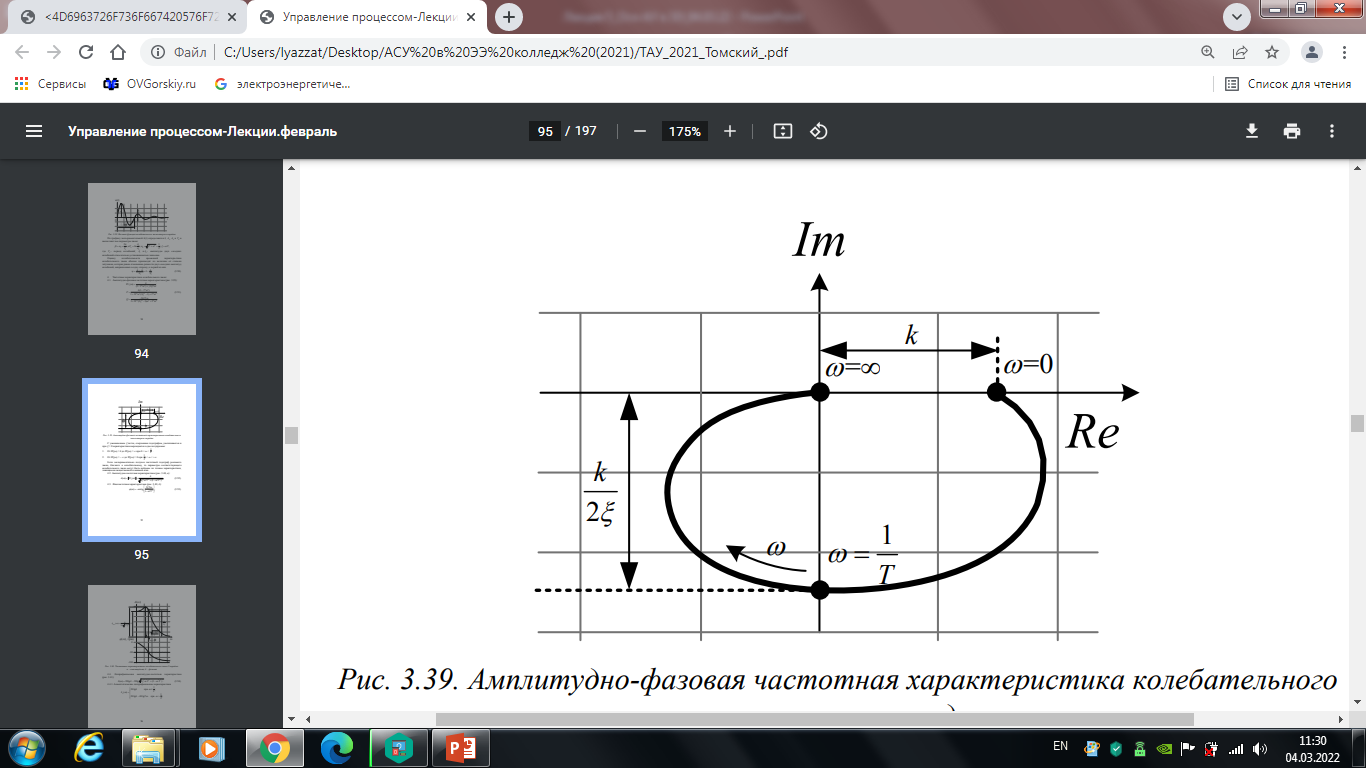
Рис. 5.4. Амплитудно-фазовая частотная характеристика колебательного звена второго порядка

С уменьшением ξ петля, очерченная годографом, увеличивается и

при & = 0 характеристика вырождается в две полупрямые:

Если экспериментально получен частотный годограф реального звена, близкого к колебательному, то параметры соответствующего колебательного звена могут быть найдены по точкам характеристики, лежащим на вещественной и мнимой осях.

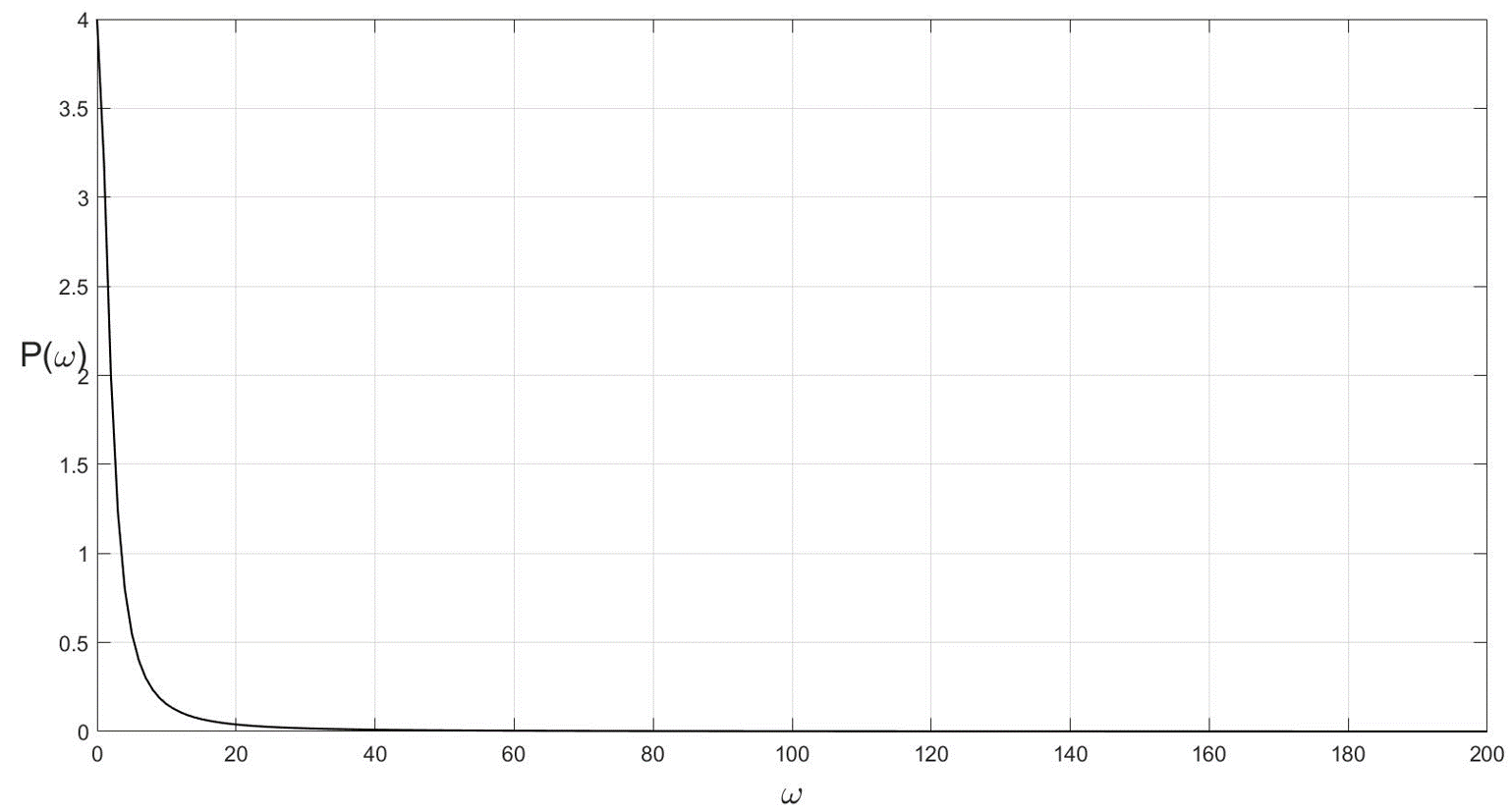
4.2. Амплитудно-частотная характеристика (рис. 5.5, а):

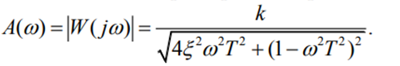
4.3. Фазочастотная характеристика (рис. 3.40, 6):

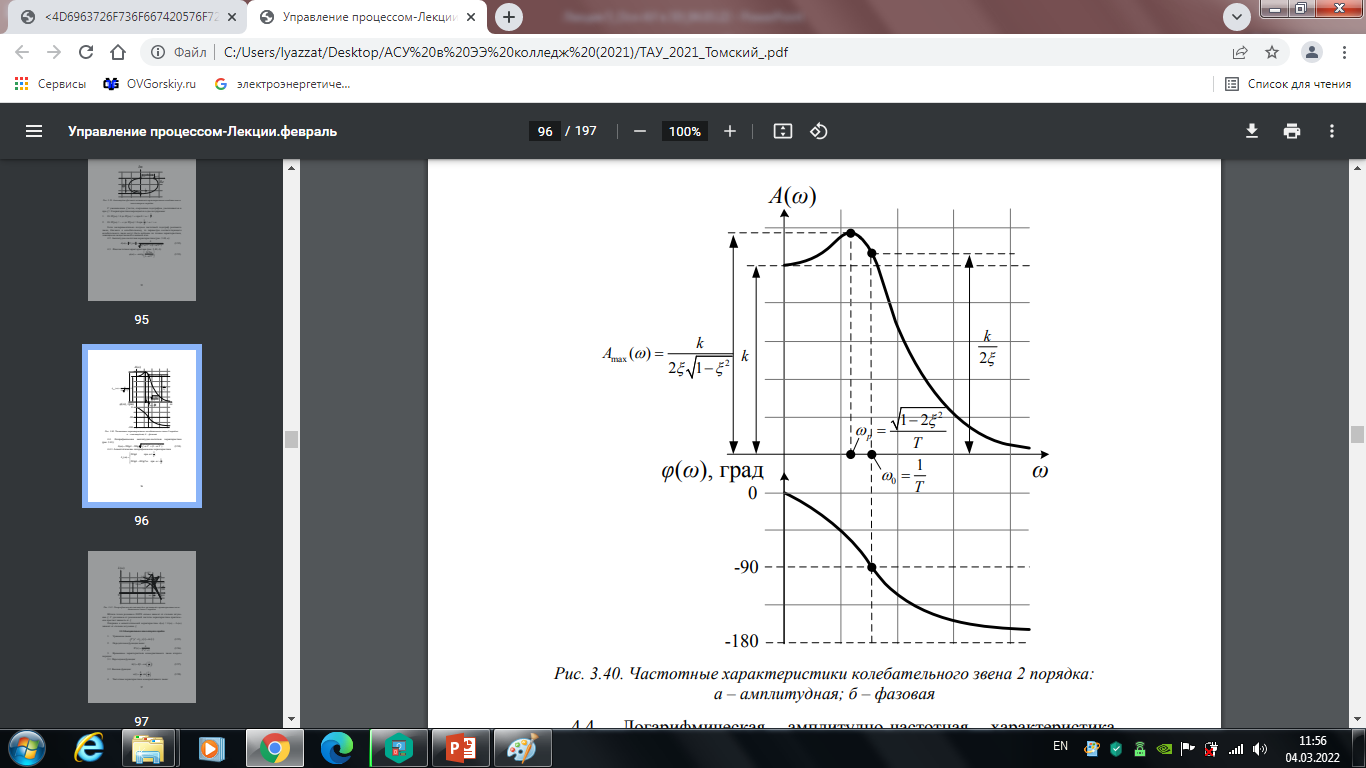
Рис. 5.5. Частотные характеристики колебательного звена 2 порядка: а – амплитудная; б – фазовая

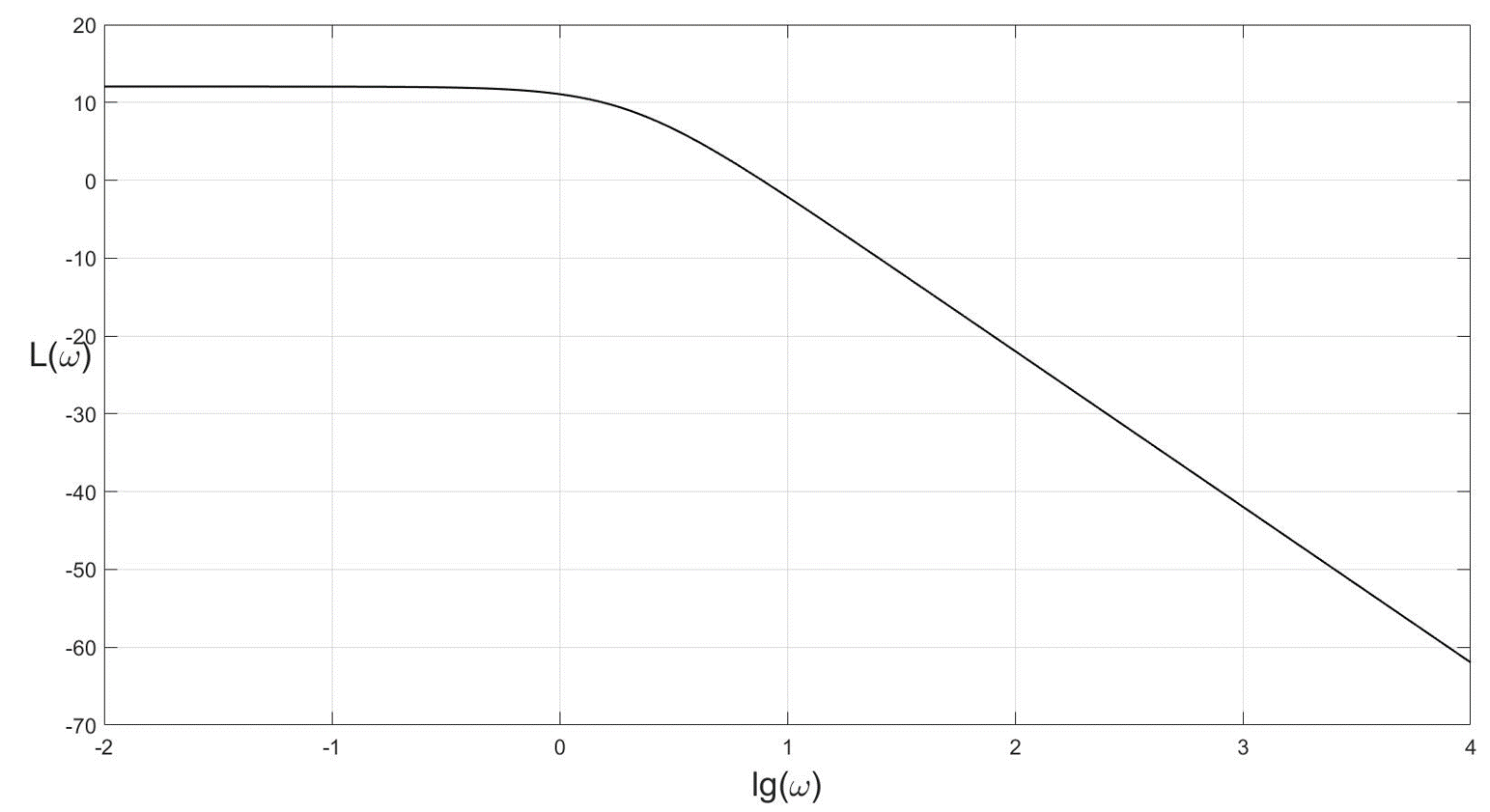
4.4. Логарифмическая амплитудно-частотная характеристика (рис. 5.6):

4.4.1. Асимптотические логарифмические характеристики

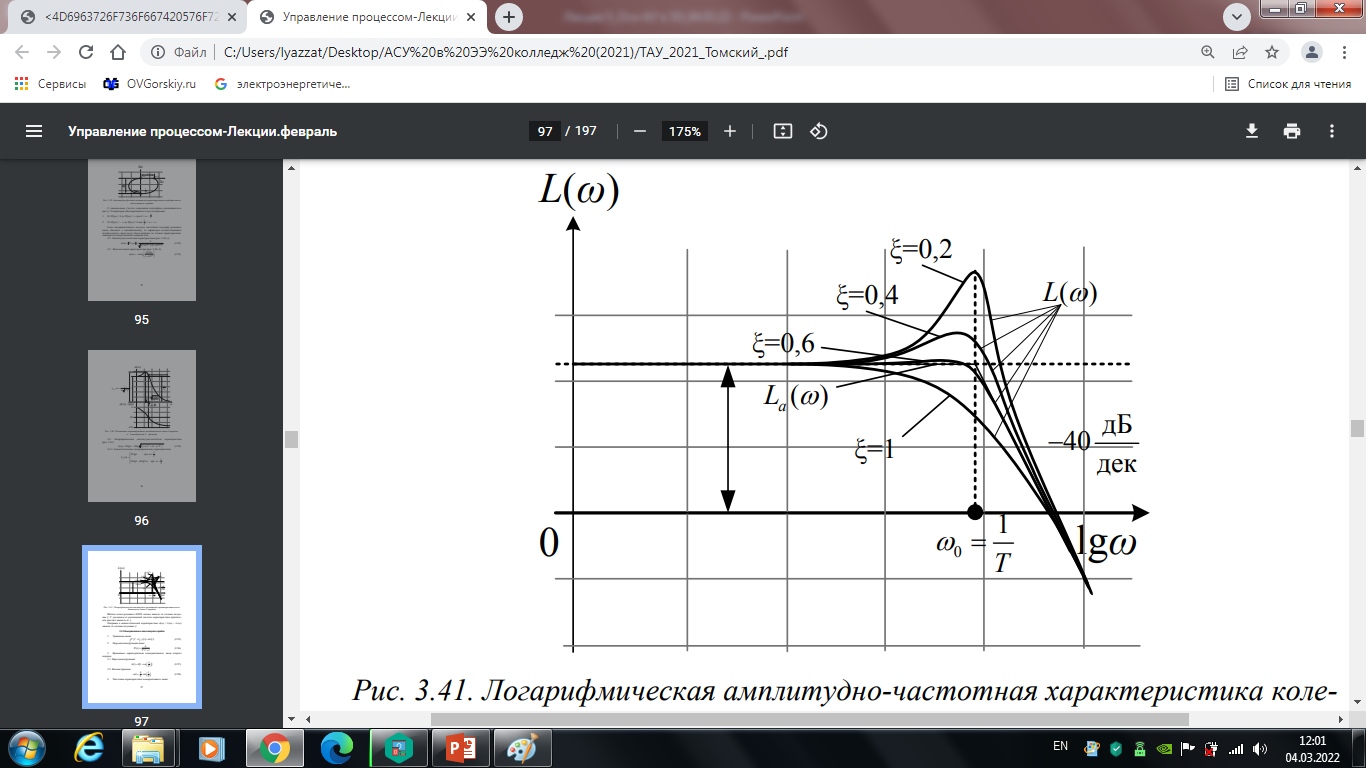
Рис. 5.6. Логарифмическая амплитудно-частотная характеристика колебательного звена 2 порядка

Вблизи точки резонанса ЛАЧХ сильно зависит от степени затухания . С удалением от резонансной частоты характеристика практически перестаёт зависеть от . Поправка к асимптотической характеристике δ(ω) = L(ω) – La(ω) зависит от степени затухания