14. Поясните и обоснуйте преимущества логарифмических частотных характеристик.

Логарифмические частотные характеристики

При расчётах в системах автоматического регулирования весьма удобными оказались логарифмические частотные характеристики. В этом случае угловая частота откладывается по оси абсцисс в логарифмическом масштабе, то есть откладывается десятичный логарифм частоты, а около отметки указывается само значение частоты (рис. 4.5а). Иногда на оси абсцисс указывают значение десятичного логарифма частоты 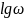, реже – логарифма при основании два – 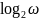(см. рис. 4.5 б, в).

Единица приращения десятичного логарифма соответcтвует удесятерению частоты, которое называется декадой. Единица приращения , соответствующая удвоению частоты, называется октавой. Одна октава соответствует 0,303 декады, так как .

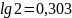Чтобы обосновать выбор масштабов по осям ординат для амплитуды и фазового сдвига , возьмем выражение для амплитудной частотной характеристики в показательной форме:

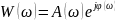
и прологарифмируем его:

.

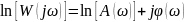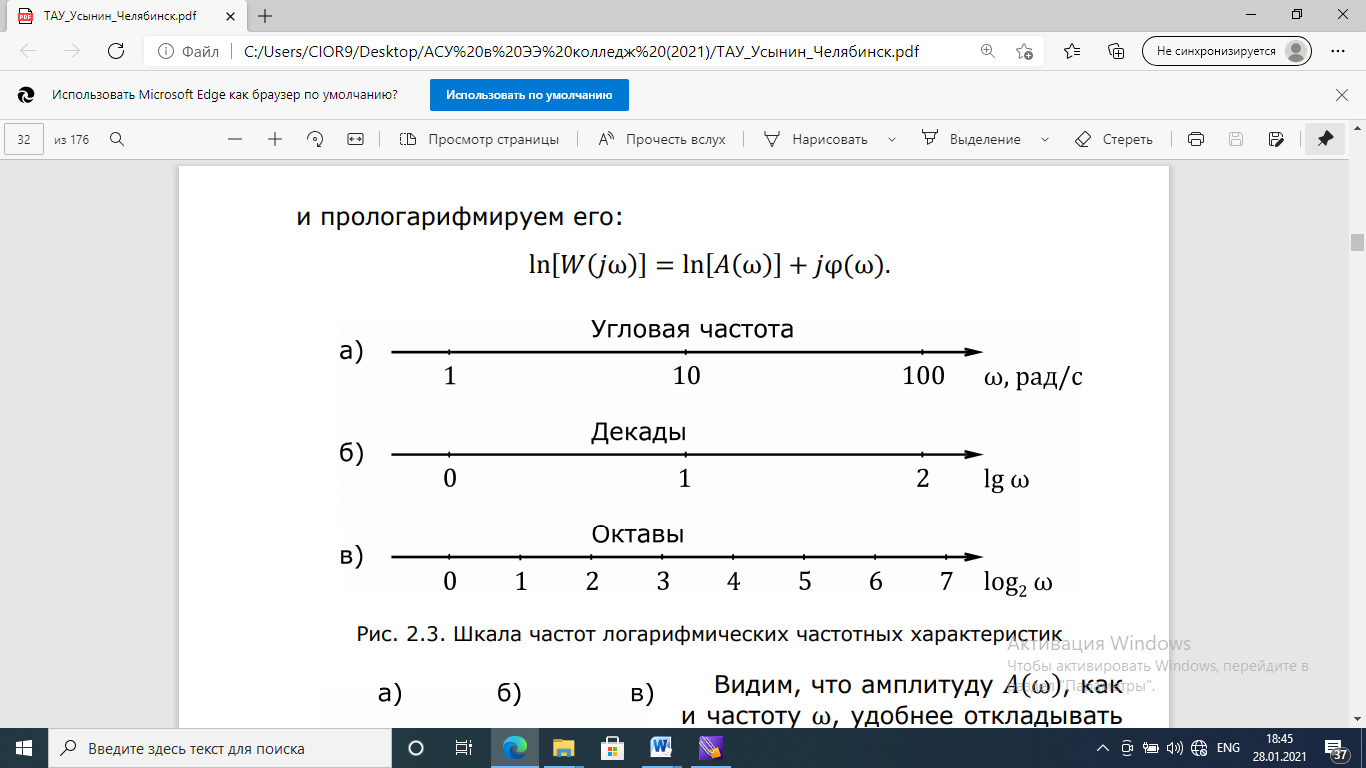
Рис. 4.5. Шкала частот логарифмических частотных характеристик

Рис. 4.6. Шкалы амплитуд логарифмических частотных характеристик

Амплитуду , как и частоту , удобнее откладывать в логарифмическом масштабе, а фазу – в линейном. Когда на оси амплитуд измеряемая величина откладывается в логарифмическом масштабе, то около отметок указываются сами значения амплитуды (рис. 4.6 а). Реже изменение амплитуды указывается в логах или децилогах (см. рис. 4.6 б). При этом один лог (или десять децилог) соответствует изменению амплитуды в 10 раз.

Единица измерения амплитуды сигнала бел (или децибел – одна десятая часть бела, см. рис. 4.6 в), которая определяется из соотношения:

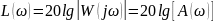
Аппарат логарифмических частотных характеристик получил большое распространение при расчёте систем автоматического регулирования, так как, во-первых, позволяет упростить расчёты (произведения величин заменяются суммой их логарифмов, шкалы частот логарифмических частотных характеристик, шкалы амплитуд логарифмических частотных характеристик степенные функции заменяются наклонными прямыми), а во вторых, и это главное, помогает выделить главный, доминирующий фактор в свойствах системы регулирования, обеспечивает наиболее ясную и простую связь частотной характеристики со структурой и параметрами системы регулирования.

В целом про ЛАЧХ, ЛФЧХ

Различают логарифмические амплитудно-частотные характеристики (ЛАЧХ) и логарифмические фазочастотные характеристики (ЛФЧХ).

При построении ЛАЧХ по оси ординат откладывают величину

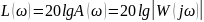4.3

единицей измерения для которой является децибел. По оси абсцисс откладывается частота ω [1/c] в логарифмическом масштабе. Равномерной единицей на оси абсцисс является декада – любой отрезок, на котором значение частоты увеличивается в десять раз (рис. 4.7).

Важно иметь в виду, что ось абсцисс (L(ω) = 0), согласно (4.3), соответствует значение A(ω) = 1, т. е. прохождению амплитуды сигнала через звено в натуральную величину. Верхняя полуплоскость ЛАЧХ соответствует значениям A(ω) > 1 (усилению амплитуды), а нижняя полуплоскость – значениям A(ω) < 1 (ослабление амплитуды).

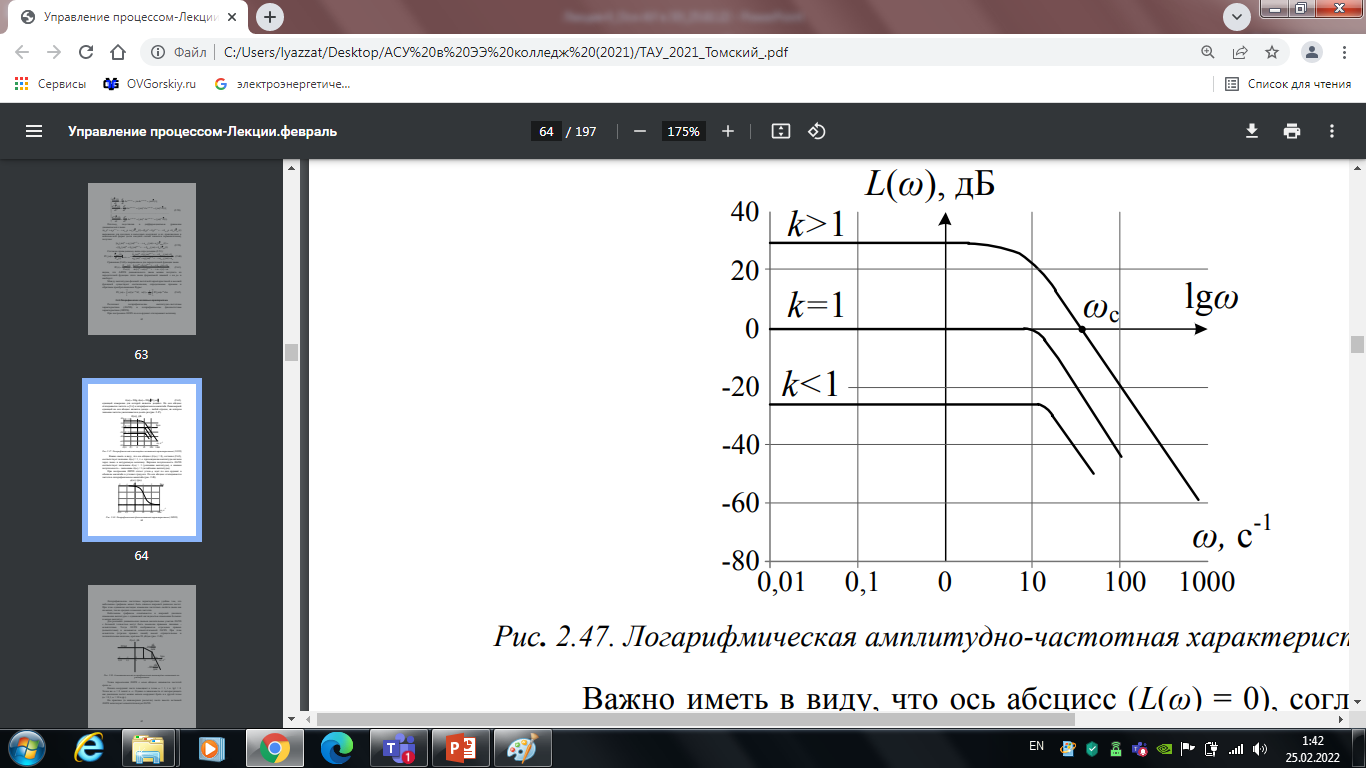
Рис. 4.7. Логарифмическая амплитудно-частотная характеристика (ЛАЧХ)

Важно иметь в виду, что ось абсцисс (L(ω) = 0), согласно (4.3), соответствует значение A(ω) = 1, т. е. прохождению амплитуды сигнала через звено в натуральную величину. Верхняя полуплоскость ЛАЧХ соответствует значениям A(ω) > 1 (усилению амплитуды), а нижняя полуплоскость – значениям A(ω) < 1 (ослабление амплитуды).

При построении ЛФЧХ отсчёт углов φ идёт по оси ординат в обычном масштабе в угловых градусах. По оси абсцисс откладывается частота в логарифмическом масштабе (рис. 4.8).

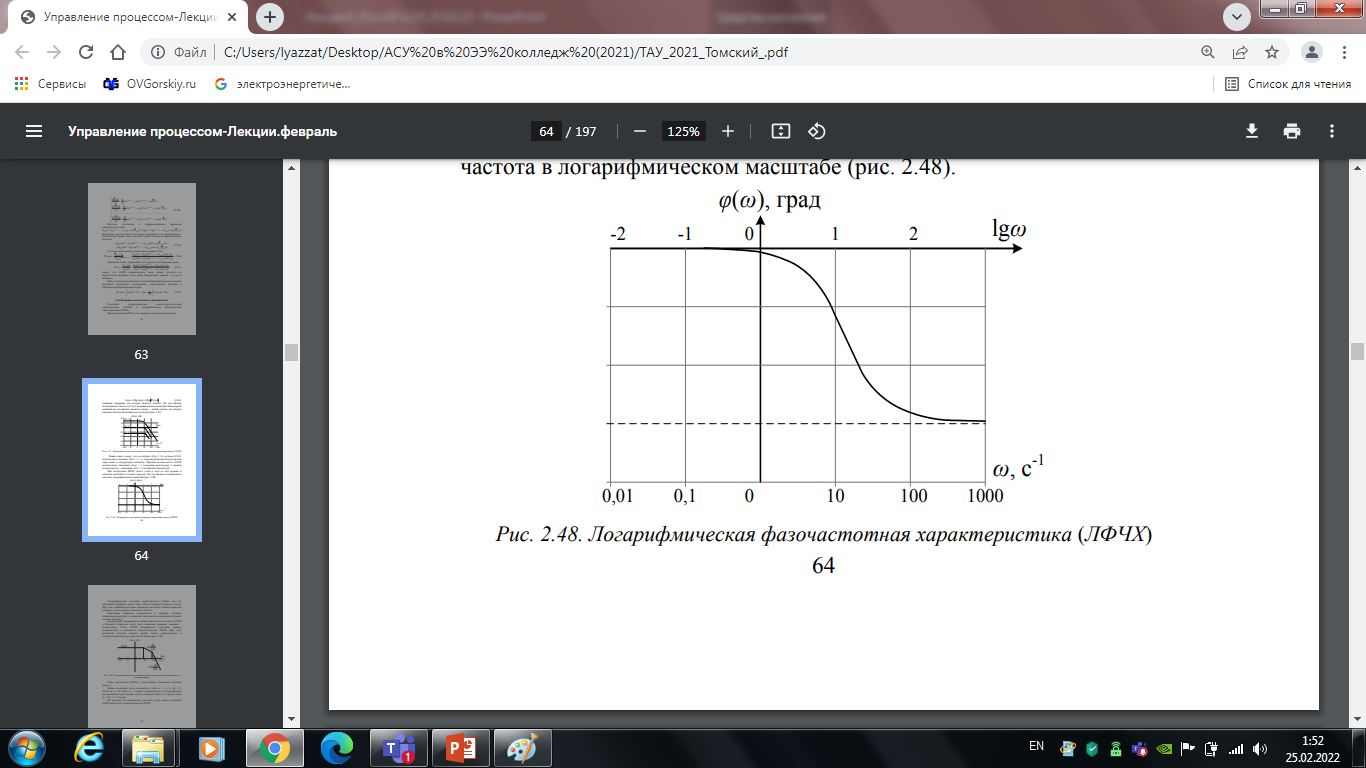
Рис. 4.8. Логарифмическая фазочастотная характеристика (ЛФЧХ)

Логарифмические частотные характеристики удобны тем, что небольшим графиком может быть охвачен широкий диапазон частот. При этом одинаково наглядно изменение частотных свойств звена как на малых, так на средних и высоких частотах.

Небольшим графиком охватывается и широкий диапазон изменения амплитуды с одинаковой наглядностью изменения больших и малых амплитуд.

Для реальных динамических звеньев значительные участки ЛАЧХ с большой точностью могут быть заменены прямыми линиями – асимптотами. Тогда ЛАЧХ изображается отрезками прямых (асимптотами) и называется асимптотической ЛАЧХ. При этом асимптоты (отрезки прямых линий) имеют отрицательные и положительные наклоны, кратные 20 дБ/дек (рис. 4.9). – это тоже преимущество логарифмических ЧХ. Оно относится ко второму преимуществу (помогает выделить главный, доминирующий фактор в свойствах системы регулирования, обеспечивает наиболее ясную и простую связь частотной характеристики со структурой и параметрами системы регулирования)

Рис. 4.9. Асимптотическая логарифмическая амплитудно-частотная характеристика

Точка пересечения ЛАЧХ с осью абсцисс называется частотой среза ωс .

Начало координат часто помещают в точке ω = 1, т. к. lg1 = 0. Точка же ω = 0 лежит в -∞. Однако в зависимости от интересующего нас диапазона частот можно начало координат брать и в другой точке (ω = 0,1; ω = 10 и др.).

На практике (в инженерных расчётах) часто вместо истинной ЛАЧХ используют асимптотическую ЛАЧХ.