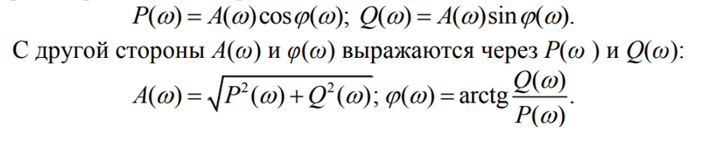11. Линеаризация системы автоматического управления.

Линеаризация уравнения, описывающего динамическое звено

Линеаризацию удобнее производить по звеньям. Допустим, что в звене A выходная величина y является нелинейной функцией одной входной величины x (рис. 2.1 а). При имеем . Пусть входная величина x получила относительно начального значения приращение , так что . Тогда приращение выходной величины

Дифференциал функции y, определяемый как главная часть ее приращения, при данном значении независимой переменной x равен значению производной при этом значении, умноженному на дифференциал независимой переменной:

Тогда для малых

.

Здесь – малая величина более высокого порядка, чем , и которая обычно отбрасывается. В случае необходимости величину погрешности можно оценить, разложив функцию в ряд Тэйлора в окрестности точки .

Рис. 2.1. Нелинейное звено (а) и его статические характеристики (б): АВ – исходная, А′В′ - линеаризованная

Замена точного значения приращения функции её дифференциалом в окрестности принято называть линеаризацией зависимости .

Геометрически линеаризация нелинейной зависимости между переменными x и y (см. рис. 2.1 б) означает замену исходной кривой AB отрезком её касательной в точке , соответствующей заданному режиму, и параллельному переносу начала координат в эту точку.

Для реальных динамических звеньев значительные участки ЛАЧХ с большой точностью могут быть заменены прямыми линиями – асимптотами (Тоже в какой-то мере линеаризация САУ). Тогда ЛАЧХ изображается отрезками прямых (асимптотами) и называется асимптотической ЛАЧХ. При этом асимптоты (отрезки прямых линий) имеют отрицательные и положительные наклоны, кратные 20 дБ/дек (рис. 4.9).

Рис. 4.9. Асимптотическая логарифмическая амплитудно-частотная характеристика

Точка пересечения ЛАЧХ с осью абсцисс называется частотой среза ω_с.

Начало координат часто помещают в точке ω = 1, т. к. lg1 = 0. Точка же ω = 0 лежит в -∞. Однако в зависимости от интересующего нас диапазона частот можно начало координат брать и в другой точке (ω = 0,1; ω = 10 и др.).

На практике (в инженерных расчётах) часто вместо истинной ЛАЧХ используют асимптотическую ЛАЧХ.

12. Временные характеристики динамических звеньев сау.

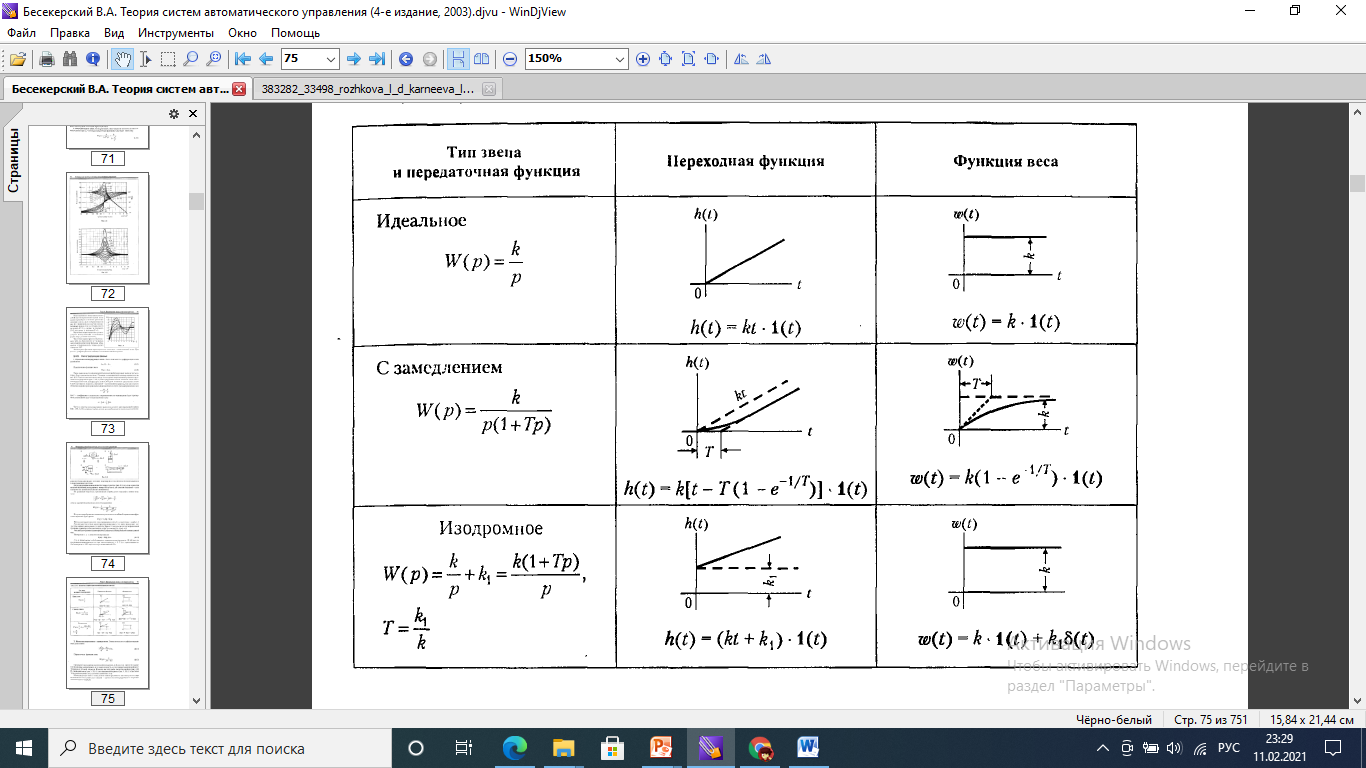
В принципе отсюда надо учить только эту таблицу и всё

Временные характеристики пропорциональных звеньев

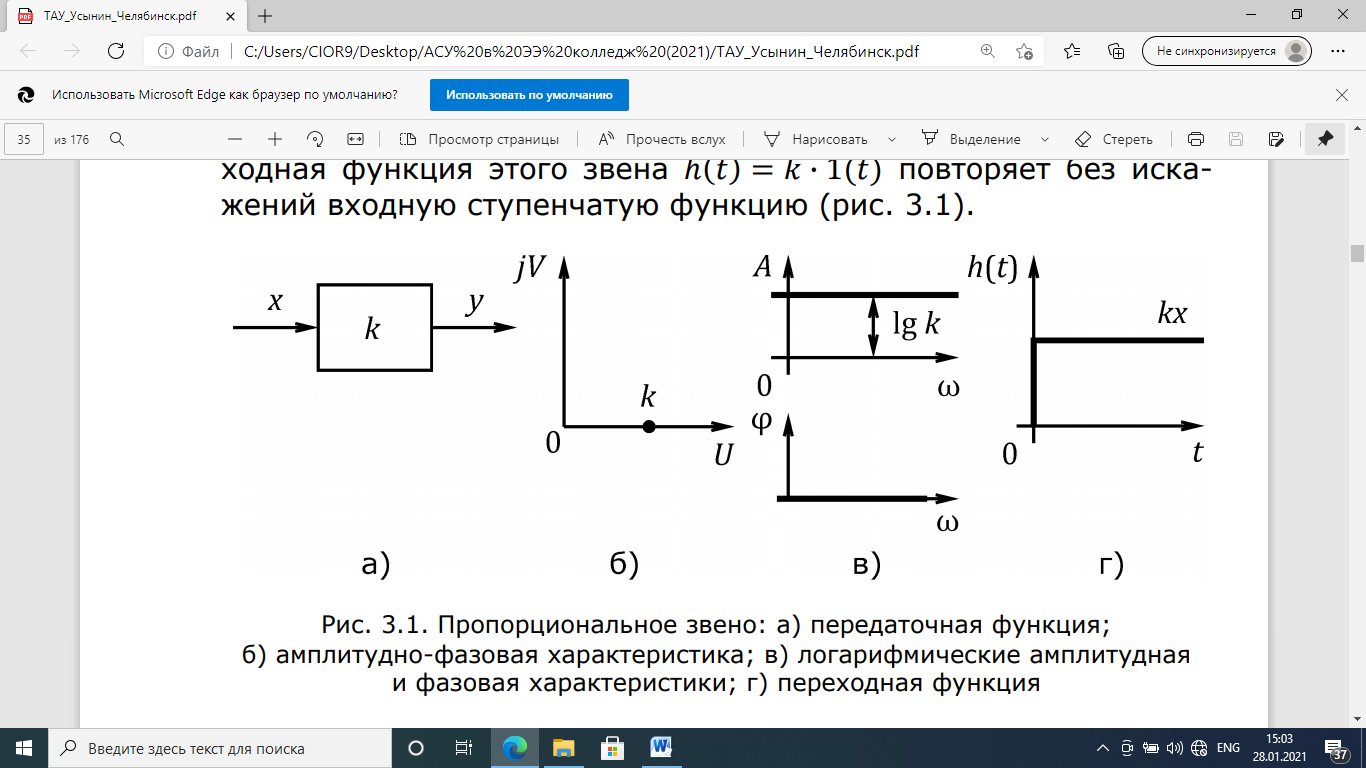
Рис. 3.5. Пропорциональное звено: переходная функция

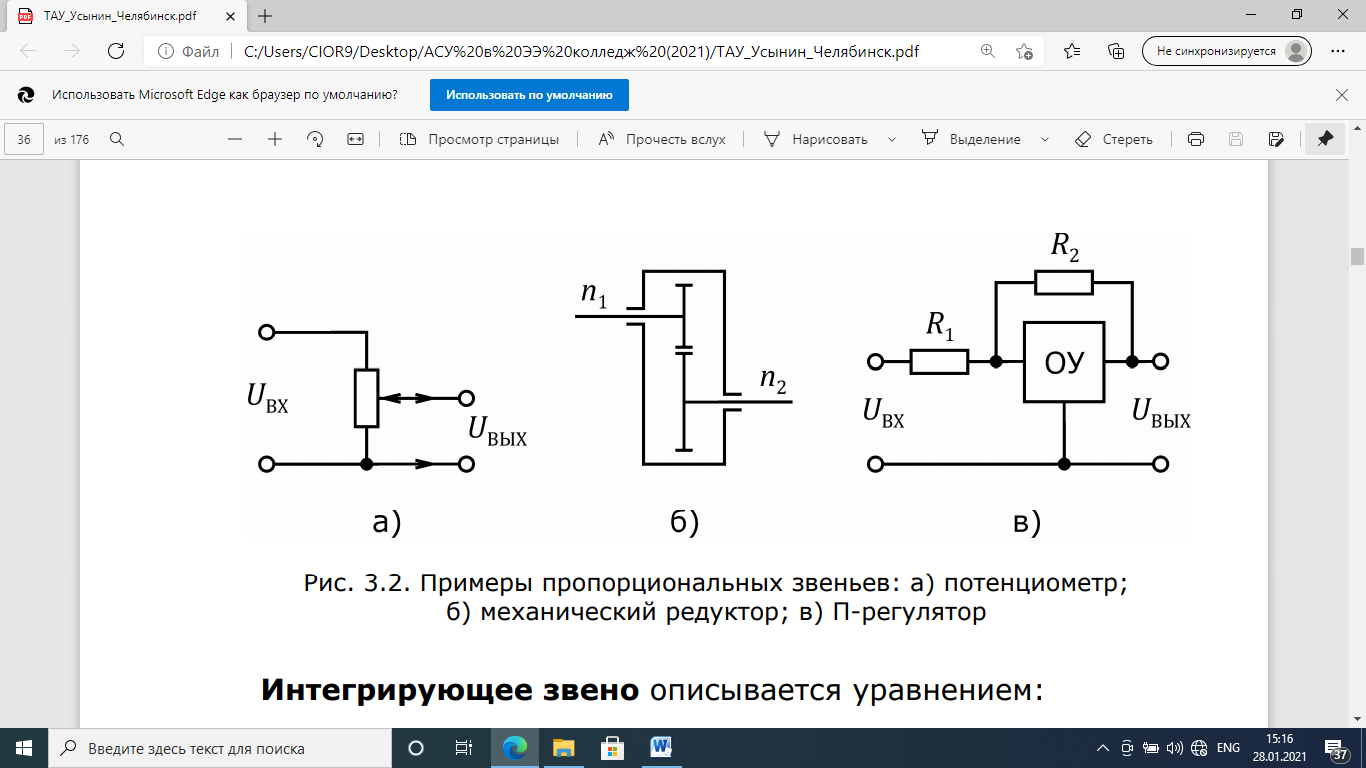
Рис. 3.6. Примеры пропорциональных звеньев:

а) потенциометр;

б) механический редуктор; в) П-регулятор

Временные характеристики интегрирующих звеньев

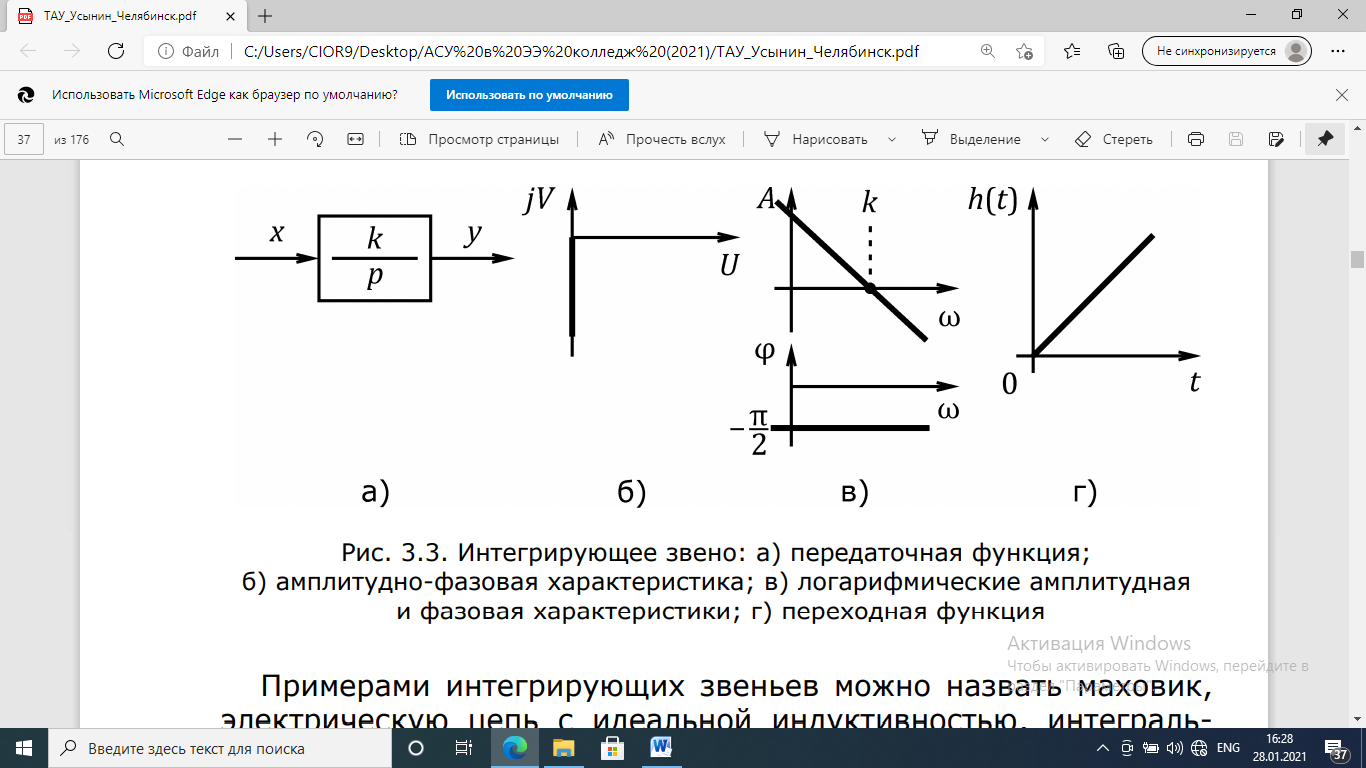
Рис. 3.7. Интегрирующее звено: переходная функция

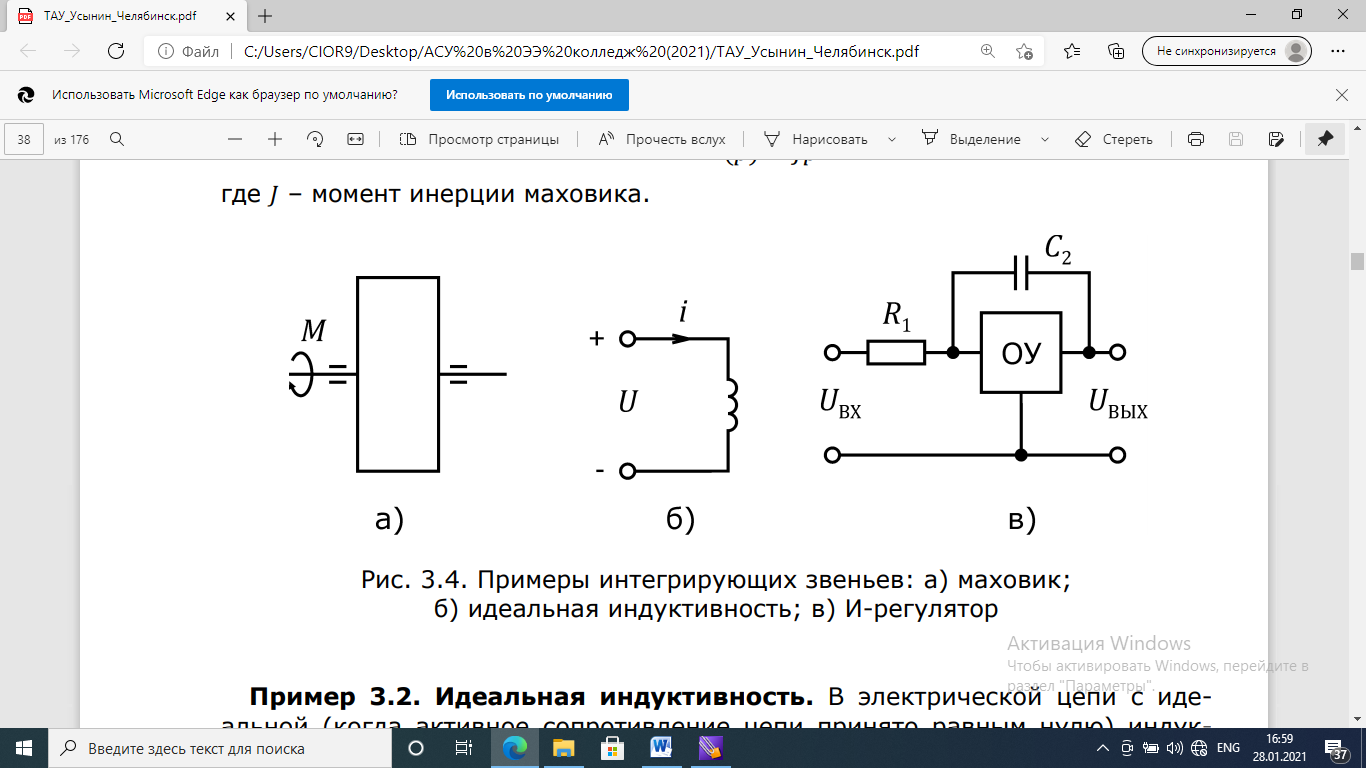
Рис. 3.8. Примеры интегрирующих звеньев:

а) маховик; б) идеальная индуктивность; в) И-регулятор

Временные характеристики дифференцирующих звеньев

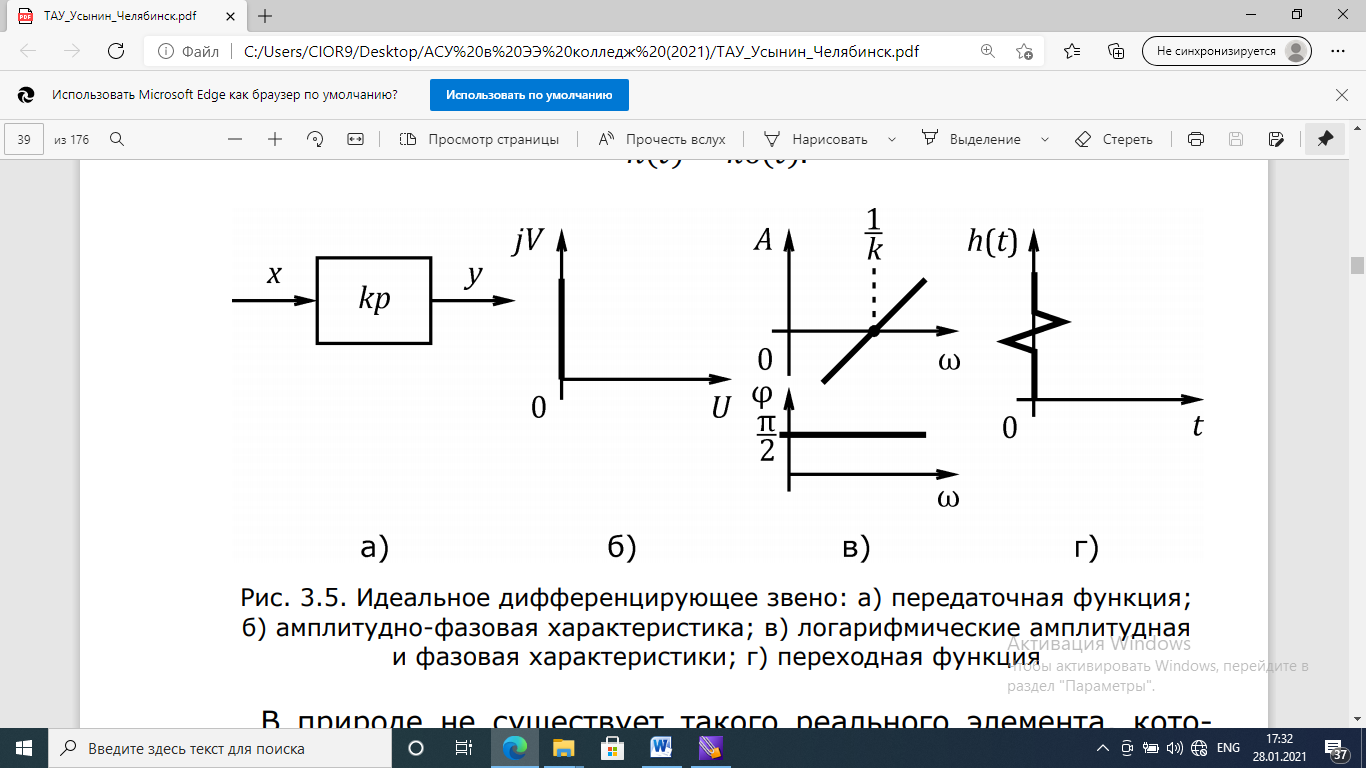
Рис. 3.10. Идеальное дифференцирующее звено: переходная функция

Примеры: идеальный конденсатор, Д-регулятор

13. Частотная передаточная функция и частотные характеристики. Частотные характеристики сау. Частотные характеристики динамического звена

Наряду с математическим описанием (дифференциальные уравнения, передаточные функции, временные характеристики) динамических звеньев и систем автоматического управления в целом в теории автоматического управления для математического описания звеньев и систем широко применяются также частотные характеристики, которые определяют поведение отдельных звеньев и системы в целом при действии на их входе гармонических колебаний.

Частотными характеристиками называются формулы и графики, характеризующие реакцию звена на синусоидальное входное воздействие в установившемся режиме (т. е. вынужденные синусоидальные колебания звена).

Известно, что гармонические колебания 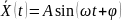, (A – амплитуда; φ – фаза; ω – частота колебаний) описываются периодической функцией времени 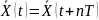, где 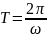– период колебаний; n – любое целое число.

Отличительной особенностью периодических функций является то, что они существуют на бесконечном отрезке времени от 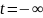до 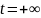. С этой точки зрения они являются математической абстракцией, т. к. любой реальный процесс имеет начало и конец. Однако, если реальный процесс длится достаточно долго с периодическим повторением предыдущих значений, то его можно с достаточной точностью считать периодическим.

Таким образом, в реальных условиях реакцией системы на периодические входные воздействия могут считаться только установившиеся колебания выходной величины, т. е. колебания, которые возникают в САУ по истечении достаточно большого времени после начала воздействия.

В этом принципиальное отличие метода частотных характеристик от метода временных характеристик, так как в последнем рассматривается поведение САУ в переходных режимах.

Несмотря на это, как увидим дальше, частотные характеристики также полно определяют поведение во времени управляемой величины, вызванное как периодическими, так и непериодическими воздействиями.

В линейной САУ установившиеся колебания выходной величины, вызванные гармоническими воздействиями на входе, являются гармоническими колебаниями той же частоты, но амплитуда и фаза их будут уже другими.

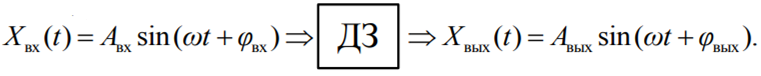
На вход линейного звена в момент времени подан сигнал, изменяющийся во времени по синусоидальному закону:

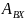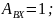
где – амплитуда входного сигнала; часто принимают 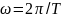– круговая частота колебания 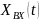; 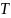– период колебаний; 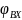– начальная фаза, обычно принимают .

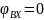Спустя некоторое время, достаточное для затухания свободной составляющей движения, на выходе звена установятся вынужденные колебания. При этом выходная переменная будет изменяться тоже по синусоидальному закону с той же частотой 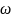, но с другой амплитудой 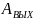и сдвинута по фазе относительно входной синусоиды на угол :

,

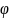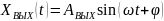Если теперь повторить эксперимент для другого значения частоты , то на выходе будут наблюдаться вынужденные колебания с другой амплитудой и другим фазовым сдвигом .

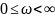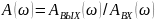Изменяя частоту входного сигнала в диапазоне , можно получить амплитудную частотную характеристику (АЧХ) – зависимость отношения амплитуд выходного и входного сигналов от частоты – и фазовую частотную характеристику (ФЧХ) 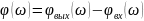– величину фазового сдвига выходной синусоиды относительно входной.

В ряде случаев бывает удобно амплитудную и фазовую частотные характеристики заменить одной – амплитудно-фазовой частотной характеристикой, – которая на комплексной плоскости может быть представлена в показательной форме:

.

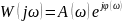По сут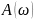и и 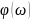– это параметрические уравнения переменного от частоты годографа вектора 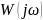в полярной системе координат.

Если уравнение вектора представить в параметрической форме в декартовых координатах, то ,

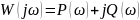где P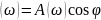 – вещественная частотная характеристика;

Q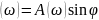 – мнимая частотная характеристика.

В электрических цепях вещественной частотной характеристике P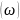 соответствует активная составляющая выходной переменной (тока или напряжения), а мнимой Q – реактивная. Очевидна связь между частотными характеристиками, заданными в полярной и декартовой системах координат:

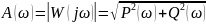и .

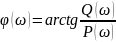Запишем гармонические функции входа и выхода динамического звена в символической (комплексной) форме:

; .

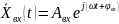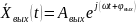И взяв их отношение, получим:

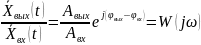
При изменении частоты от 0 до +∞ получаем комплексную функцию частоты W(jω), которая называется амплитудно-фазовой частотной характеристикой динамического звена. Её модуль 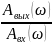определяет отношение амплитуд выходных и входных колебаний при изменении частоты ω от 0 до +∞. Эта зависимость отношения амплитуд выходных и входных гармонических сигналов от частоты называется амплитудно-частотной характеристикой (АЧХ) динамического звена (рис. 4.1).

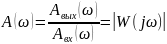
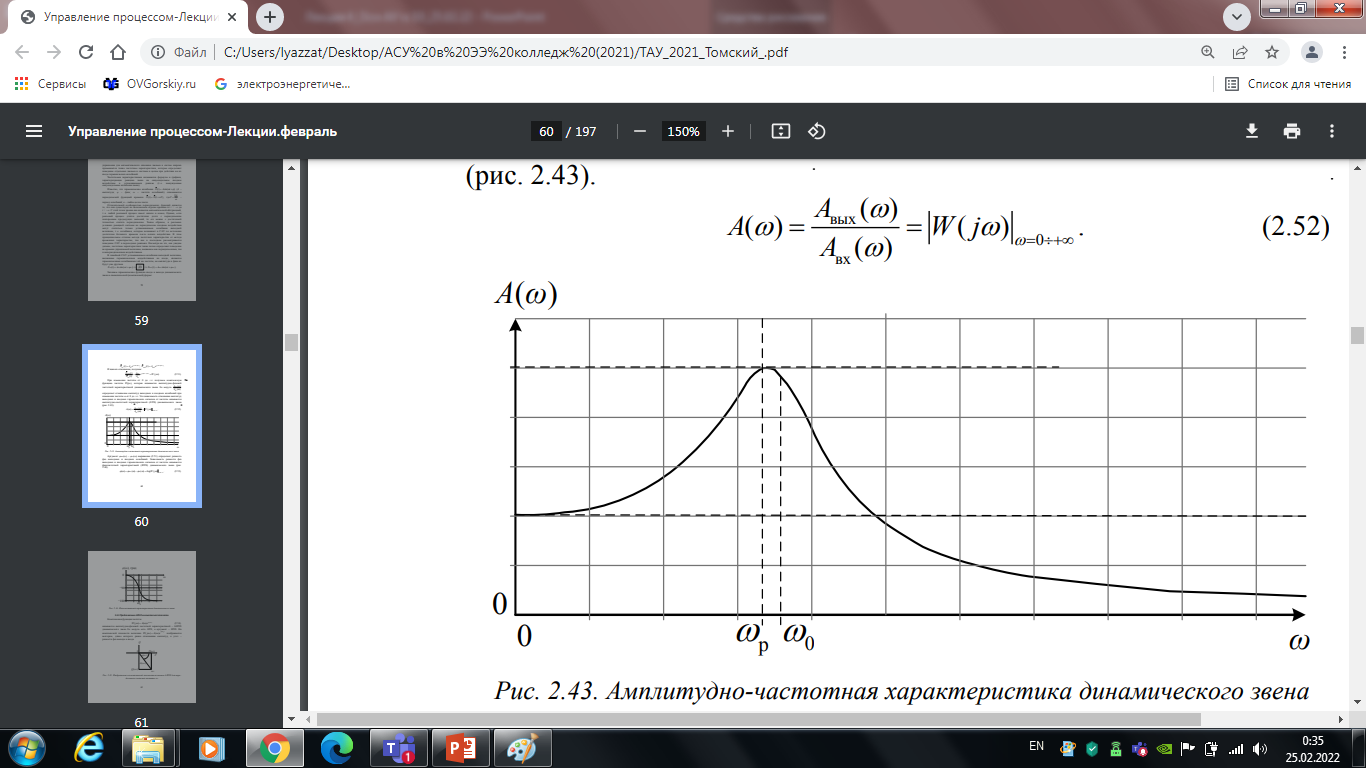
Рис. 4.1. Амплитудно-частотная характеристика динамического звена

Аргумент 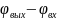выражения (4.1) определяет разность фаз выходных и входных колебаний. Зависимость разности фаз выходных и входных гармонических сигналов от частоты называется фазочастотной характеристикой (ФЧХ) динамического звена (рис. 4.2).

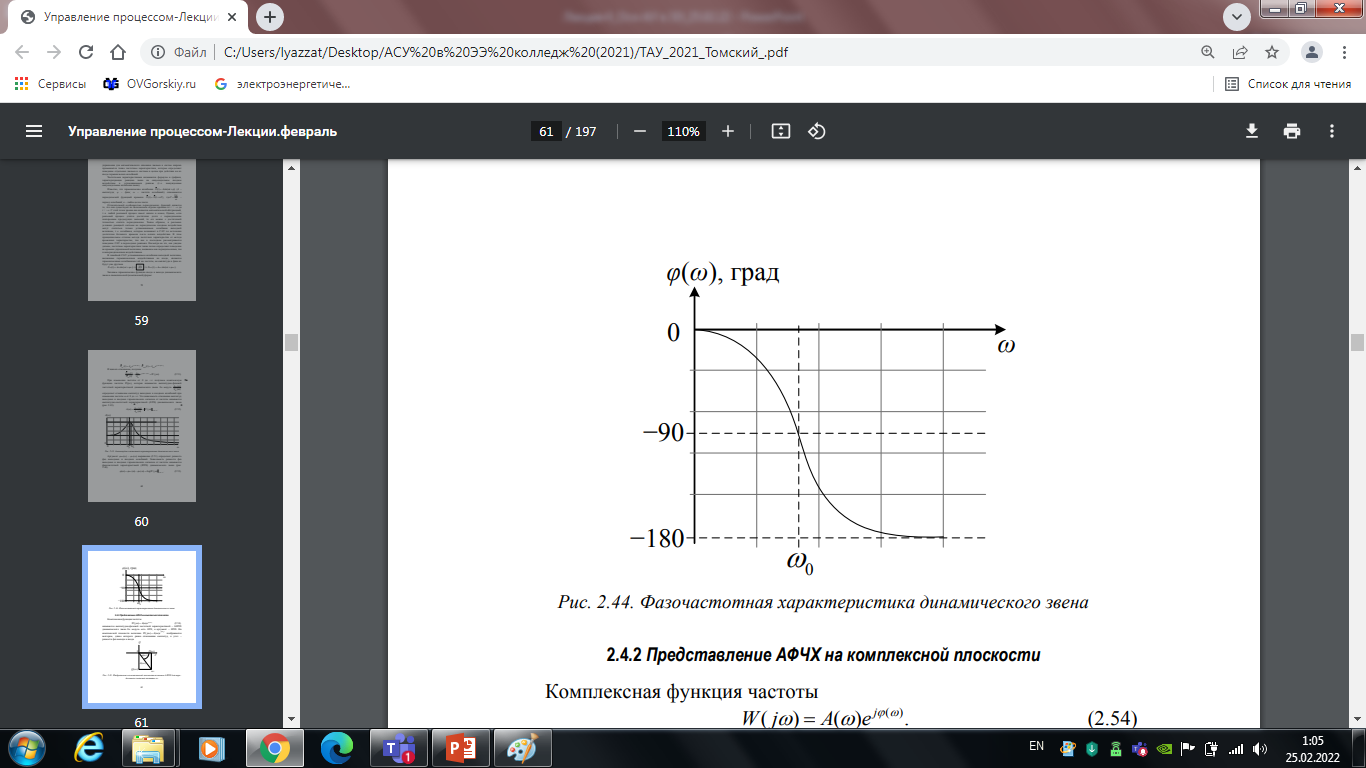
Рис. 4.2. ФЧХ динамического звена

Представление АФЧХ на комплексной плоскости

Комплексная функция частоты 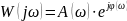называется амплитудно-фазовой частотной характеристикой – АФЧХ динамического звена, её модуль есть АЧХ, а аргумент – ФЧХ. На комплексной плоскости величина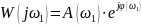 изображается вектором, длина которого равна отношению амплитуд, а угол – разности фаз выхода и входа.

Рис.4.3. Изображение на комплексной плоскости величины АФЧХ для определенного значения частоты ω1

Соответственно на комплексной плоскости АФЧХ представляется кривой – годографом, которую вычерчивает конец вектора 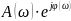при изменении ω от 0 до +∞.

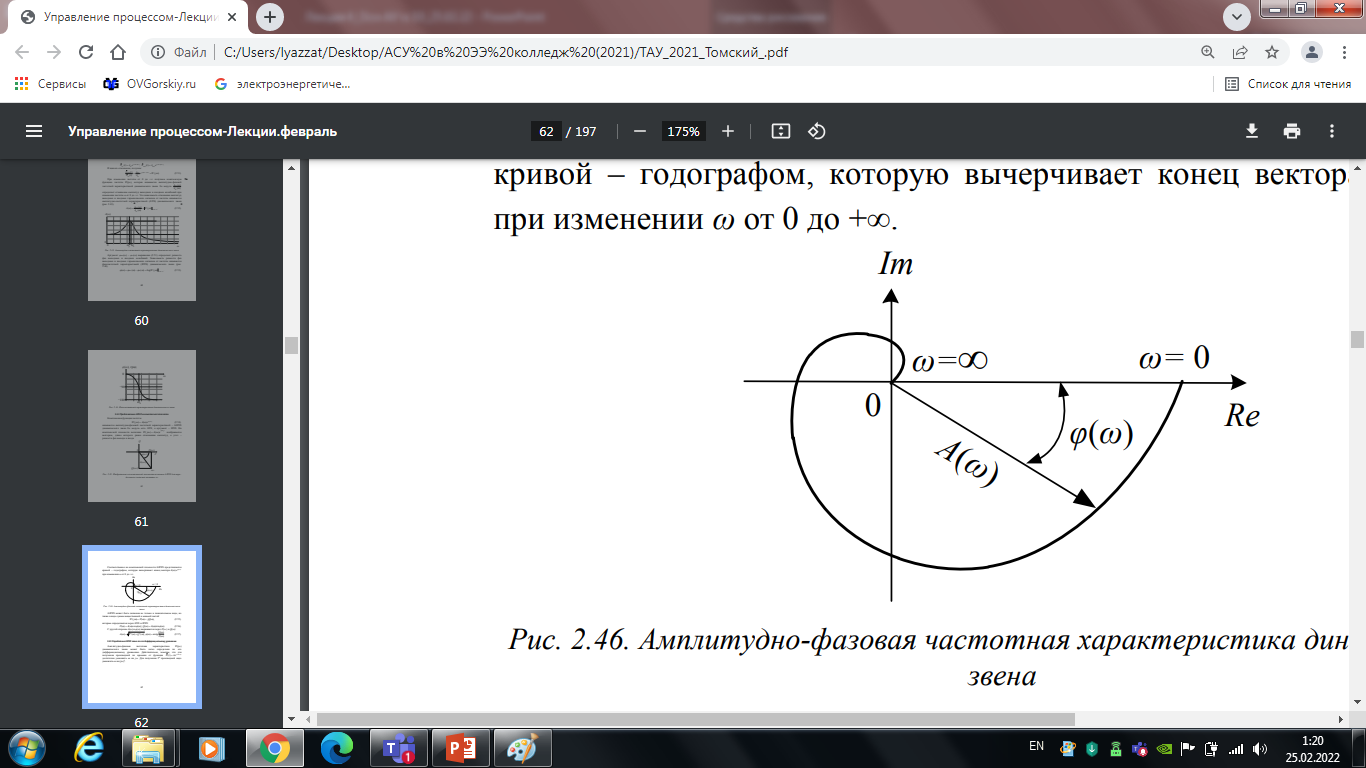
Рис. 4.4. Амплитудно-фазовая частотная характеристика динамического звена

АФЧХ может быть записана не только в показательном виде, но и также в виде суммы вещественной и мнимой частей:

Которые определяются через АЧХ и ФЧХ: