§ 5. Уширение спектральных линий

Мы принимали дискретные энергетические уровни атомов или молекул бесконечно узкими. Переход между ними давал бы квант строго фиксированной частоты , т.е. бесконечно узкую спектральную линию (идеально монохроматическую волну).

Но это принципиально невозможно, хотя бы потому, что существует соотношение неопределенности . Но есть и другие факторы, приводящие к уширению спектральных линий, т.е. излучение занимает спектр частот.

Распределение интенсивности излучения (или поглощения) по частоте в пределах данной линии характеризуется функцией , называемой форм-фактором спектральной линии или просто формой линии.

Эта функция нормирована

Для характеристики относительной ширины спектральной линии используют понятие добротности спектральной линии, которая численно равна отношению резонансной частоты ω₀ в максимуме интенсивности линии к ее ширине ∆ω на уровне половинной интенсивности

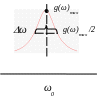
Рис. 10

Причины уширения спектральных линий:

1. Естественное уширение.

Атомы или молекулы пребывают в возбужденном состоянии конечное время τ, так что - «размытие» энергетического уровня – естественная ширина («толщина») уровня. Уровни на энергетической диаграмме – не бесконечно тонкие линии. Чем меньше время жизни, тем шире («толще») уровни (рис. 11).

Если действует только естественное уширение, спектральная линия называется Лоренцовой.

Если добавляются другие факторы уширения – форма линии называется Гауссовой.

Квантовомеханический расчет дает

, ( - функция Лоренца)

где ∆ω = А_тп – ширина линии на уровне 0,5 от max; ω₀ – резонансная частота;

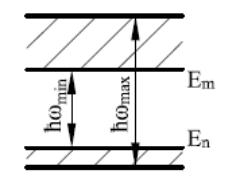
Рис. 11

Типичные значения (при v₀=5·10¹⁴ Гц порядка 20 МГц, а при переходе с метастабильных уровней много меньше – до сотен Гц). В радиодиапазоне естественная ширина линии существенно меньше, чем в оптическом. Например, для аммиака NH₃ спектральная линия перехода с частотой v₀=24870 МГц (λ₀ = 1,25 см) имеет естественную ширину ~ 10^-3 Гц.

2. Доплеровское уширение.

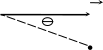
Эффект Доплера – изменение частоты, наблюдаемое при движении источника волн относительно приемника.

ист.

Ω ν

набл.

Рис. 12

ω – наблюдаемая частота;

ω₀ – испускаемая частота;

, - скорость источника;

θ – угол между направлением вектора скорости и направлением источник - наблюдатель

При << c формула упрощается

ω > ω₀ когда источник приближается к наблюдателю,

ω < ω₀ когда источник удаляется.

Атомы и молекулы движутся хаотично, они имеют разные и θ для наблюдателя. Это дает уширение спектра.

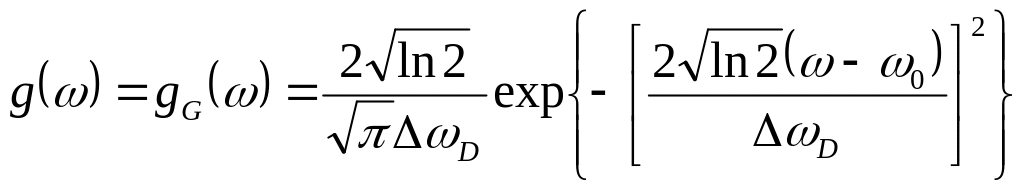
где - ширина доплеровской линии на уровне 0,5 от максимального значения при ω = ω₀; - функция Гаусса.

M - масса атома газа.

В газовом разряде для легких атомов .

Это для видимой части спектра при v₀ ≈ 5·10¹⁴ Гц дает .

В радиодиапазоне для аммиака v₀=24870 МГц при комнатной температуре и , т.е. в миллионы раз больше естественной ширины линии.

3. Уширение в результате столкновений.

Столкновения атомов с другими частицами, со стенками сосудов, с фононами (квантами тепловых колебаний) в твердом теле увеличивают скорость обмена энергией и, следовательно, уменьшают время пребывания атома в возбужденном состоянии. Форма спектральной линии такая же, как функция Лоренца, но вместо должно стоять , где τ_р – время релаксации (перехода из возбужденного состояния в невозбужденное), определяемое процессами столкновений.

Например для Ne при р ≈ 60 Па ≈ 0,5 мм рт. ст. :

Время релаксации примерно равно времени между двумя столкновениями атомов Ne, т.е. , где - средняя длина свободного пробега, - средняя тепловая скорость. Из кинетической теории газов

а – эффективный (боровский) радиус атома;

р – давление.

При комнатной температуре τ_ст ≈ 5 · 10^-7 с, т.е.

τ_ст ~ р^-1, следовательно ∆ω_ст ~ р, так что при р = 1 атм. ∆ω_ст может стать больше .

В твердых телах τ_р ≈ 10^-9 с ÷ 10^-11 с, что вызвано эффективной релаксацией возбужденных атомов при взаимодействии с колебаниями решетки. Поэтому уширение линий здесь велико.

4. Уширение за счет электрических и магнитных полей.

Уширение вызвано как внешними, так и внутрикристаллическими полями. Причина – эффекты Зеемана и Штарка. Если зеемановское и штарковское расщепления меньше ширины уровня, то рядом расположенные уровни частично перекрываются, а это вызывает уширение спектральных линий.

Например, рубин – окись Al, легированная хромом. В Al₂О₃ ионы G³⁺ замещают ионы Al³⁺ и находятся под действием сильного электрического поля соседних ионов алюминия и кислорода. Оно расщепляет и сдвигает энергетические уровни Cr³⁺. Из-за тепловых колебаний решетки это поле непрерывно и хаотически меняется, так что сдвиг уровней = f(t) – хаотичен и спектральная линия хаотически меняется по частоте, т.е. уширяется. Уширение можно снизить, уменьшив Т.

Различают однородное и неоднородное уширение. Однородное – если линии каждого атома и системы в целом уширяются одинаково (естественное и за счет столкновений). Неоднородное – если резонансные частоты отдельных атомов не совпадают и распределяются в полосе частот, так что уширение для системы в целом много больше уширения для отдельного атома (доплеровское).

Форма однородного уширенных линий описывается функцией Лоренца , неоднородного – функцией Гаусса .

Уширение линий необходимо учесть при вычислении коэффициентов Эйнштейна, которые будут зависеть от ω.

а_тп(ω) = А_тп

b_тп(ω) = B_тп

b_пm(ω) = B_пm

а, b – спектральные коэффициенты Эйнштейна.

А, В – интегральные коэффициенты Эйнштейна (по всем частотам).

Изменяется и понятие населенности. Теперь сюда нужно отнести все частицы единицы объема, энергия которых попадает в пределы размытости уровня по энергии.